1 引言
伴随着技术的进步和工业化的不断发展,数控领域各个场合对伺服控制系统的要求也随之提高,基于传统PI控制策略的伺服系统已很难满足控制性能的要求。例如在经编机高速横移领域,对位置控制要求十分苛刻,因为位置偏差会引起花型扭曲,导致产品质量下降[1]。
交流伺服控制系统并非是完全线性的,系统内部各参数也在不停地改变,而且它的负载也不是一成不变的,模型也不是完全整数阶的,各种因素的影响使得系统的动态性能呈现很大的差异。传统PI调节器具有很差的自适性能力,在高精度和高可靠性的场合,它的控制性能根本不能达到预想的效果。模糊自适应PI控制器为典型的整数阶控制器,对于分数阶模型同样难以达到理想的控制性能。针对以上问题,文章将广泛引用的模糊自适应控制、近来发展迅猛的分数阶控制理论与当前应用最广的经典PI控制相结合,设计了一种新型的模糊自适应分数阶PIλ交流伺服控制器[2,3,4,5,6]。最后在Simulink中搭建仿真模型,通过仿真验证其控制效果,经试验证实,其确有优越的控制性能。
2 永磁同步电机矢量模型
矢量控制是一种借助坐标变换实现对转矩更好控制的高性能交流电机控制技术,坐标变换方法包含Clark和Park变换两种[7]。永磁同步电机经过坐标变换后得到在dq坐标系中定子电压方程和磁链方程
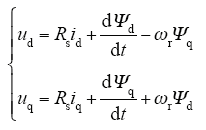
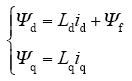
式中,ud、uq分别为定子电压矢量在dq轴的分量;id、iq分别为定子电流矢量在dq轴的分量;Ψd、Ψq分别为定子磁链在dq轴的分量;Ld、Lq分别为dq轴的同步电感;Rs为定子每相绕组电阻;ωr为转子旋转的电角度;Ψf为转子磁链。
转矩方程和运动方程为
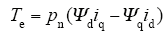
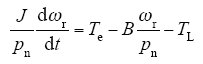
式中,pn为电机磁极对数;TL为负载转矩;B为黏滞摩擦系数;J为转动惯量。
从转子坐标来看,经过坐标变换后的三相定子电流最终被等效为力矩电流iq和励磁电流id两个分量。矢量控制有多种不同的控制方式,本文采用id = 0控制,这种方式可以使电机输出平稳而又最大的转矩。此时得到的电机转矩方程为
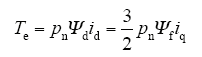
由式(5)可知,pn和Ψf是永磁同步电机的内部参数,其值固定。为了获得恒定的力矩输出,只要控制iq为定值即可。
3 模糊自适应分数阶PIλ控制器
3.1 分数阶微积分理论
分数阶微积分是一个古老而又新颖的研究课题,古老是指它的定义由来已久,而新颖指的是它的应用历史非常短暂,直到最近才被大家所关注。分数阶与整数阶微积分最大的不同点,即最重要的特征是,它的微积分算子并不是固定不变的整数阶次,它有可能是分数阶的,更广地来说,它是任意阶的。Grünwald-Letnikov和Riemann-Liouville是出现频率最高的两种分数阶微积分定义。aDtα为描述分数阶微分与积分算子,a和t为在微积分求解时变量取值的上下限,α为算子阶次。
(1)Grünwald-Letnikov 分数阶微积分定义为
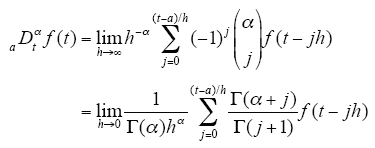
(2)Riemann-Liouville 分数阶微积分定义为
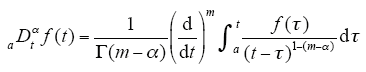
式中,m - 1<α<m,m∈N。
3.2 传统PID控制器
PID控制的微分方程如式(8)所示,式中,e(t)为系统给定值与反馈值之间的偏差量。
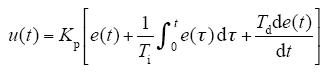
进行拉普拉斯变换得传递函数为
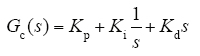
式中,Kp为比例系数;Ti为积分时间常数;Td为微分时间常数。
PID控制器由比例、积分、微分三个环节组成。比例环节有减小偏差的作用,但是存在稳态误差;积分环节能够消除稳态误差,但是会降低系统稳定性和动态响应速度;微分环节能够超前作用于偏差,提高系统动态性能,能够降低超调量。
3.3 分数阶PIλDμ控制器
分数阶PIλDμ控制器的微分方程为
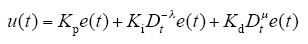
式中,λ>0,μ>0为任意实数,λ、μ分别为分数阶控制器积分和微分环节的阶次;Kp、Ki、Kd是控制器的比例、积分、微分系数。进行拉普拉斯变换得传递函数为
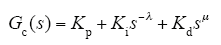
分数阶PIλDμ与传统PID相比增加了两个可调参数λ、μ,扩大了参数的可调节范围,拓宽了分数阶PIλDμ控制器的应用领域,控制器的应用方式也变得更加灵活多变,但同时也带来了参数整定困难的问题。
3.4 分数阶微积分的数字实现
分数阶毫无疑问不是一个简单系统,无法用有限的维度简单描述它,它的复杂程度决定了整数阶的控制方法不能直接应用于分数阶系统。面对这一情况,数学家们并没有知难而退,他们另辟蹊径,既然无法直接描述分数阶系统,那么就通过有限的微分方程近似地将它描述出来。本文所采用的逼近方法是Oustaloup方法,它属于间接近似化中的一种。
Oustaloup方法近似的传递函数形式为
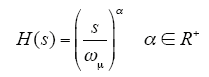
在给定频段[ωA,ωB]内,用C0[(1 + s/ωb)/(1 + s/ωh)]来代替s/ωμ,其中,(ωb ωh)1/2 = ωμ,ωb<ωA,ωh>ωB,且C0 = ωb/ωμ = ωμ/ωh,那么传递函数就能表示成
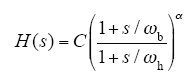
式中,C = C0α。
把式(13)写成零点、极点的形式,得到表达式
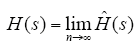
式中
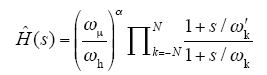
可求得
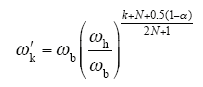
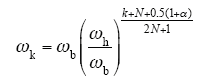
3.5 模糊自适应分数阶PIλ控制器设计
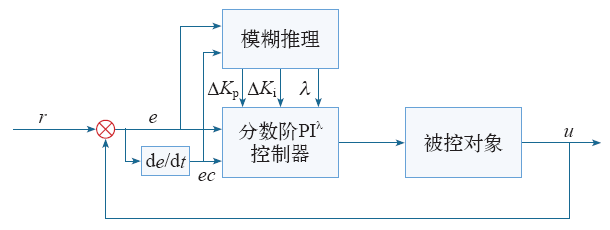
模糊自适应分数阶PIλ控制器如图1所示。
图1
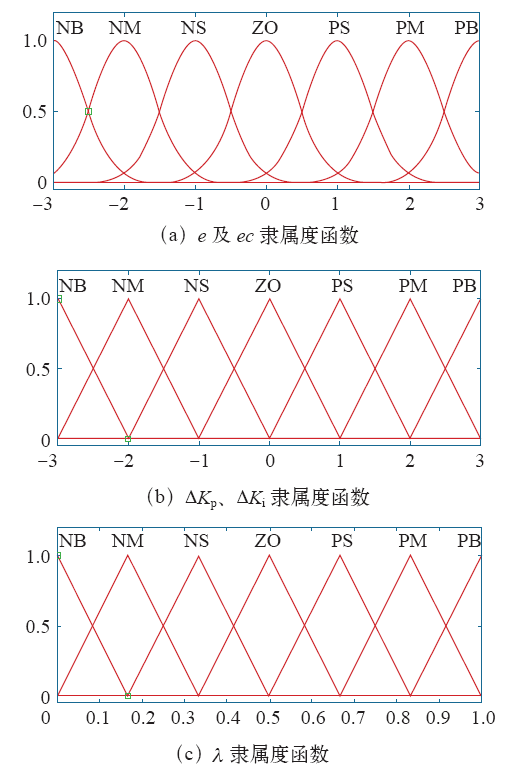
本文模糊自适应分数阶PIλ控制器的设计思路是,在分数阶PIλ控制回路中引入模糊推理模块,通过模糊控制规则周期性地推理出每个参数的当前值,再将本周期的参数值实时传递给分数阶PIλ控制器,从而实现参数在线整定。模糊推理模块输入变量为偏差e及其变化率ec,输出变量ΔKp、ΔKi、λ,各变量的模糊子集选取相同的{正大、正中、正小、零、负小、负中、负大},记为{PB、PM、PS、ZO、NS、NM、NB},选取输入变量e、ec的论域为[-3,3],输出变量ΔKp、ΔKi的论域为[-3,3],输出变量λ的论域为[0,1]。输入变量e和ec的隶属度函数采用高斯型隶属函数,输出变量ΔKp、ΔKi、λ的隶属度函数采用对称分布的三角型隶属函数,隶属度函数如图2所示。
图2
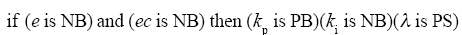
表1 ΔKp的模糊规则表
Tab.1
| ec e | NB | NM | NS | ZO | PS | PM | PB |
|---|---|---|---|---|---|---|---|
| NB | PB | PB | PM | PM | PS | ZO | ZO |
| NM | PB | PB | PM | PS | PS | ZO | NS |
| NS | PM | PM | PM | PS | ZO | NS | NS |
| ZO | PM | PM | PS | ZO | NS | NM | NM |
| PS | PS | PS | ZO | NS | NS | NM | NM |
| PM | PS | ZO | NS | NM | NM | NM | NB |
| PB | ZO | ZO | NM | NM | NM | NB | NB |
表2 ΔKi的模糊规则表
Tab.2
| ec e | NB | NM | NS | ZO | PS | PM | PB |
|---|---|---|---|---|---|---|---|
| NB | NB | NB | NM | NM | NS | ZO | ZO |
| NM | NB | NB | NM | NS | NS | ZO | NS |
| NS | NB | NM | NS | NS | ZO | PS | PS |
| ZO | NM | NM | NS | ZO | PS | PM | PM |
| PS | NM | NS | ZO | PS | PS | PM | PB |
| PM | ZO | ZO | PS | PS | PM | PB | PB |
| PB | ZO | ZO | PS | PM | PM | PB | PB |
表3 λ的模糊规则表
Tab.3
| ec e | NB | NM | NS | ZO | PS | PM | PB |
|---|---|---|---|---|---|---|---|
| NB | PS | NS | NB | NB | NB | NM | PS |
| NM | PS | NS | NB | NM | NM | NS | ZO |
| NS | ZO | NS | NM | NM | NS | NS | ZO |
| ZO | ZO | NS | NS | NS | NS | NS | ZO |
| PS | ZO | ZO | ZO | ZO | ZO | ZO | ZO |
| PM | PB | NS | PS | PS | PS | PS | PB |
| PB | PB | PM | PM | PM | PS | PS | PB |
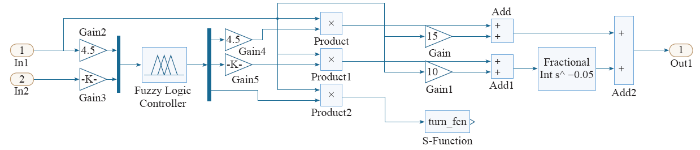
基于Matlab/Simulink的模糊自适应分数阶PIλ控制器的模型如图3所示。模糊控制器的模糊逻辑推理采用Mamdani法则,去模糊化方法选择重心法。模糊控制器周期性输出推理值ΔKp、ΔKi、λ,ΔKp、ΔKi分别与参数预先设定值Kp、Ki相加,λ设置为全局变量,在模型中引入S-Function模块,仿真过程中重复调用S函数,在S函数中添加修改变量λ的代码指令,这样就能够将每个周期修改后的λ值带入到分数阶微积分模块中,实现阶次周期性修改,从而实现分数阶PIλ控制器参数Kp、Ki和λ的在线整定。
图3
4 系统仿真
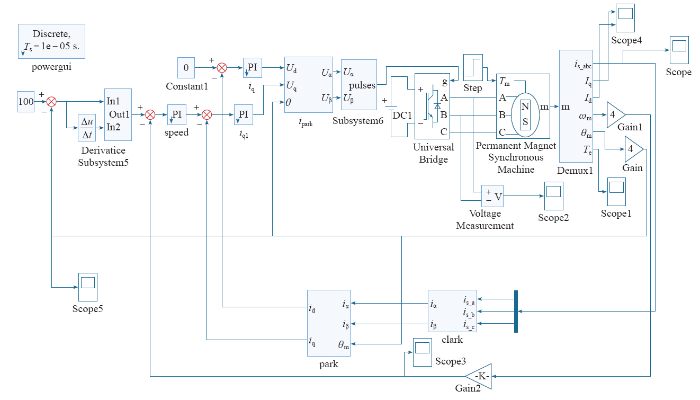
根据所建立的永磁同步电机矢量控制模型,利用Matlab的Simulink建立了基于模糊自适应分数阶PIλ控制器的交流伺服控制仿真系统,如图4所示。
图4
图4
基于模糊自适应分数阶PIλ控制器的交流伺服控制仿真图
Fig.4
Servo control strategy based on fuzzy adaptive fractional PIλ simulation chart
仿真系统由位置调节器、转速调节器、电流调节器,Park逆变换模块、SVPWM模块[8]、永磁同步电机、参数测量模块、Clark模块、Park模块等组成。系统采用位置、转速和电流三闭环控制方式,内部两控制环均采用数字PI控制器,最外环为位置环,采用本次设计的模糊自适应分数阶PIλ控制器作为位置调节器。位置给定θ*在与转子实际位置θ相比较并求出偏差值后,作为输入变量通过模糊自适应分数阶PIλ控制器,输出转速给定值ω*,与转速测量值ω比较并求出偏差值后,作为输入通过PI控制器,经调节后输出力矩电流给定值iq*,本文矢量控制选择最大转矩方式,取励磁电流给定值id* = 0。三相电流测量值ia、ib和ic经Clark和Park坐标变换后得到直、交轴电流反馈值iq、id,分别与前一步骤确定的力矩电流和励磁电流作比较并求出偏差值,经过电流调节器的调节和电流型逆变器后控制电机三相电流,从而完成对伺服电机的位置控制。
永磁同步电机采用的参数如下:定子绕组电阻Rs = 0.62Ω,d相绕组电感Ld = 0.008 5H,q相绕组电感Lq = 0.008 5H,转子磁场磁通Ψf = 0.175Wb,转动惯量J = 0.008kg·m2,极对数p = 4,B = 0。仿真系统采用ode3模式,仿真时间选择为0~10s,比较传统PI和模糊自适应分数阶PIλ控制器对伺服位置控制阶跃响应的控制效果。
图5
图5
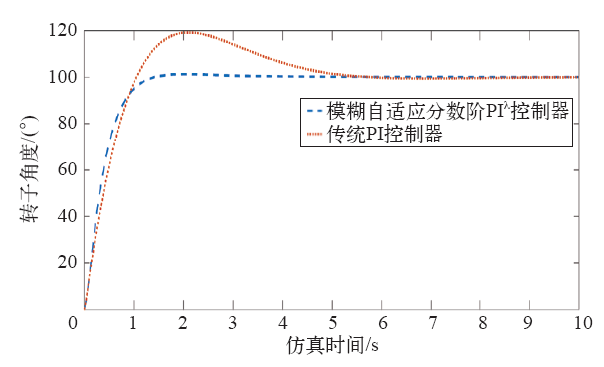
模糊自适应分数阶PIλ控制与PI控制下伺服位置控制阶跃响应曲线图
Fig.5
Fuzzy adaptive fractional PIλ and PI control result chart
表4 两种位置控制器的性能对照表
Tab.4
| 控制器 | 上升时间 /s | 超调量 (%) | 调节时间 /s |
|---|---|---|---|
| 传统PI控制器 | 0.790 | 19.3 | 5.6 |
| 模糊自适应分数阶PIλ控制器 | 0.745 | 1.3 | 4.8 |
通过表4各控制性能的数据对比可知,基于模糊自适应分数阶PIλ控制器的交流伺服控制系统大幅度地降低了超调量,具有更快的响应速度和更好的控制效果,其动态性、稳态性及鲁棒性都远优于传统PI控制的交流伺服系统。
5 结论
本文以提高交流伺服系统控制性能为最终目标,设计了一种基于模糊自适应分数阶PIλ的伺服控制器。其设计理念是在分数阶PIλ控制回路中引入模糊推理模块,运用模糊推理规则,得出推理结果,引用结果实时修改分数阶PIλ控制器参数。分数阶PIλ控制器增加的可调参数λ,扩大了参数的可调节范围,拓宽了分数阶PIλ控制器的应用领域,与此同时也使得它的应用方式变得更加灵活多变。此次研究工作的最后,根据建立的电机矢量模型,使用Simulink搭建了位置、转速及电流三闭环仿真系统,分别采用数字PI和模糊自适应分数阶PIλ控制器作为位置环调节器进行仿真实验,仿真研究结果表明:模糊自适应分数阶PIλ控制器产生了更小的超调量,具有更快的响应速度和更好的控制效果,其动态性、稳态性及鲁棒性都远优于传统PI控制的交流伺服系统。对于高精度伺服系统而言,基于模糊自适应分数阶PIλ控制器的伺服系统能够满足其苛刻的控制要求,是一个可行的方案。
参考文献
基于伺服控制经编机电子横移系统的研究
[J].
Research on electronic sway system of warp knitting machine based on servo control
[J].
基于Matlab的模糊PID控制系统设计及仿真
[J].
Design and simulation of fuzzy PID control system based on Matlab
[J].
模糊自适应PID控制器在交流伺服控制系统中的研究
[J].
Research on AC servo control system based on fuzzy adaptive PID controller
[J].
Research on the fuzzy PID speed control system of permanent magnet linear synchronous motor based on genetic algorithm
[J].
分数阶PID控制器的设计及仿真
[J].
Design and simulation of fractional-order PID controller
[J].
基于最优Oustaloup的分数阶PID参数整定
[J].
Fractional-order PID parameter tuning based on optimal oustaloup
[J].
SVPWM在永磁同步电机系统中的应用与仿真
[J].
Application and simulation of permanent magnet in PMSM system
[J].