基于D-H参数的磁阻式球形电机动力学建模*

doi:10.11985/2024.01.016

基于D-H参数的磁阻式球形电机动力学建模^*

李瑞英^,¹^,², 李国丽²^,³, 鞠鲁峰^,¹^,⁴, 王群京¹^,³

1.安徽大学电气工程与自动化学院合肥 230601

2.安徽大学高节能电机及控制技术国家地方联合实验室合肥 230601

3.安徽大学工业节电与用电安全安徽省重点实验室合肥 230601

4.安徽大学工业节电与电能质量控制安徽省级协同创新中心合肥 230601

Dynamic Modeling of Reluctance Spherical Motor Based on D-H Parameter

LI Ruiying^,¹^,², LI Guoli²^,³, JU Lufeng^,¹^,⁴, WANG Qunjing¹^,³

1. School of Electrical Engineering and Automation, Anhui University, Hefei 230601

2. National Engineering Laboratory of Energy-Saving Motor & Control Technology, Anhui University, Hefei 230601

3. Anhui Key Laboratory of Industrial Energy-Saving and Safety, Anhui University, Hefei 230601

4. Anhui Collaborative Innovation Center of Industrial Energy-Saving and Power Quality Control, Anhui University, Hefei 230601

通讯作者: 鞠鲁峰，男，1983年生，博士，讲师。主要研究方向为特种电机优化设计、电机电磁场分析计算。E-mail：julf@ahu.edu.cn

收稿日期: 2023-03-18 修回日期: 2023-09-4

基金资助:

国家自然科学基金(51637001)
安徽省自然科学基金面上(1908085ME168)

Received: 2023-03-18 Revised: 2023-09-4

作者简介 About authors

李瑞英，女，1997年生，硕士研究生。主要研究方向为磁阻式球形电机转矩建模等。E-mail：l_r_y@foxmail.com

摘要

三自由度球形电机的动力学模型是对转子运动过程的数学描述，在球形电机的闭环控制中用于计算转子从当前位置运动到期望位置时所需要的驱动转矩。以计算磁阻式球形电机驱动转矩为目标，提出一种动力学方程的建模方法。针对磁阻式球形电机的运动特征，将球形转子等效为三个串联旋转关节，推导出磁阻式球形电机基于D-H参数的动力学方程，再对方程中的未知参数进行辨识，最终模型的预测结果与仿真结果有较高的拟合度，试验验证了该模型在设定运动工况下的可靠性，为磁阻式球形电机驱动控制提供了理论基础。

关键词： 磁阻式球形电机; D-H参数; 动力学模型; 机器人; 参数辨识

Abstract

Dynamic model of 3-DOF spherical motor is a mathematical description of the rotor motion process. In the closed-loop control of spherical motor, it is used to calculate the drive torque required when the rotor moves from the current position to the desired position. Aiming at calculating the driving torque of reluctance spherical motor, a dynamic equation modeling method is proposed. According to the motion characteristics of reluctance spherical motor, the spherical rotor is equivalent to three rotary joints in series. The dynamics equation of reluctance spherical motor is derived based on D-H parameters. Then, the unknown parameters in the equation are identified. The prediction results of the final model agree well with the test data. Finally, the reliability of the model under a specific motion is verified by experiments, which provides a theoretical basis for the drive control of reluctance spherical motor.

Keywords： Reluctance spherical motor; D-H parameter; dynamics model; robot; parameter identification

PDF (32716KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

李瑞英, 李国丽, 鞠鲁峰, 王群京. 基于D-H参数的磁阻式球形电机动力学建模^*[J]. 电气工程学报, 2024, 19(1): 150-158 doi:10.11985/2024.01.016

LI Ruiying, LI Guoli, JU Lufeng, WANG Qunjing. Dynamic Modeling of Reluctance Spherical Motor Based on D-H Parameter[J]. Chinese Journal of Electrical Engineering, 2024, 19(1): 150-158 doi:10.11985/2024.01.016

1 引言

随着现代科学技术的发展，多自由度运动装置的研究受到越来越多国内外学者的关注^[1⇓⇓-4]。而传统装置总是由多台单自由度驱动元件等复杂装置构成，系统的复杂性会造成各部件间的协调性下降、响应延缓、精度减小等种种不可避免的情况^[5]。为了更好地满足多自由度驱动装置的需求，研究者们提出了球形电机^[5]的概念，可以在一个关节实现三自由度旋转运动，具有结构紧凑、精度高、没有回程误差积累以及力能指标高等显著优点。目前，球形电机研究的重点和难点主要是实现电机的闭环控制^[6]。围绕这一方向，众多学者在球形电机通电控制策略优化、转子空间位置检测和电磁模型及动力学模型^[6]建立等方面展开了研究。其中，球形电机动力学模型的建立是实现闭环控制的基础^[7]。该模型的主要作用是给出当转子从当前位置运动到期望位置时所需要的驱动转矩。同时，为了满足球形电机控制快速响应性，要求其动力学模型能根据转子位置的变化快速解算出驱动转矩。因此，如何建立高精度、高响应速度的球形电机动力学模型是球形电机研究的一个重要内容^[8]。

不同的建模方式体现在模型表达和运动描述方式两个方面。模型表达一般分为两类：一是简化为绕定点旋转的单刚体，该转子将以定子内球面和转子外球面作为支撑面作运动；另一类则是把运动件等效为由三个刚体组成的有约束的刚体系。作为单刚体进行的动力学研究在各坐标轴上依然存在耦合关系，未解耦系统提高了运动控制的难度。而对于刚体系来说，文献[5]用内外环做支撑框架来描述，文献[9]将球形转子等效为具有三个旋转关节的四杆串联机构。在运动描述方式中，文献[7]和文献[6]分别以广义欧拉角和四元数为姿态描述量，文献[9]以旋量理论和李群李代数作为基础，以POE指数积法表示运动学正逆解。以上学者采用了不同的方法作为建模基础，但建立的模型不够直观，不能对球形电机的复杂运动进行深入分析，且所需参数较多，验证过程较为复杂。

本文以一款新型磁阻式球形电机^[10-11]为研究对象，首先介绍了该电机的基本结构和工作原理，然后利用ADMAS仿真软件^[12]给出了该电机的动力学模型仿真，但是ADMAS仿真模型无法满足闭环控制实时响应的要求。因此，本文提出了一种基于D-H(Denavit-Hartenberg)参数法^[13]来建立三自由度^[14]磁阻式球形电机动力学模型方程的方法，并通过参数辨识^[15]对该模型的未知参数进行标定^[16]。最后，将基于D-H参数法建立的模型与ADMAS仿真模型进行了对比验证，研究结果表明该方法切实可行，为实现磁阻式球形电机的闭环控制提供了基础。

2 磁阻式球形电机结构

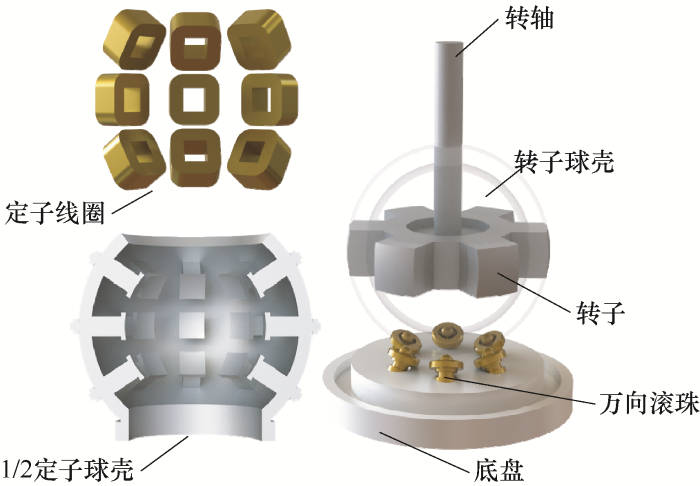
本文所研究的磁阻式球形电机结构如文献[10]所述，如图1所示，定转子均为凸极结构，定子球壳内侧均匀向心排布着三层呈环形阵列的定子极，赤道面排布中间层，上下两层对称，每层八极。转子的核心结构与传统开关磁阻电机转子一致，由硅钢片叠压而成，与中间层转子匹配即为常见的四相8/6极开关磁阻电机，外部套上非导磁结构的球壳，其余空间不做填充以减小自重。底座上均匀向心斜向呈圆周阵列排布着六个万向滚珠，一方面调节其高度可使定转子球心重合，另一方面减小转子运动时的机械摩擦，托举转子完成球心固定的任意三自由度运动。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 磁阻式球形电机结构

电机的主要结构参数如表1所示。

表1 仿真模型的参数

主要参数	数值
定子外径/mm	122
转子外径/mm	73
气隙长度/mm	1
线圈匝数	350
转轴长度/mm	40

新窗口打开| 下载CSV

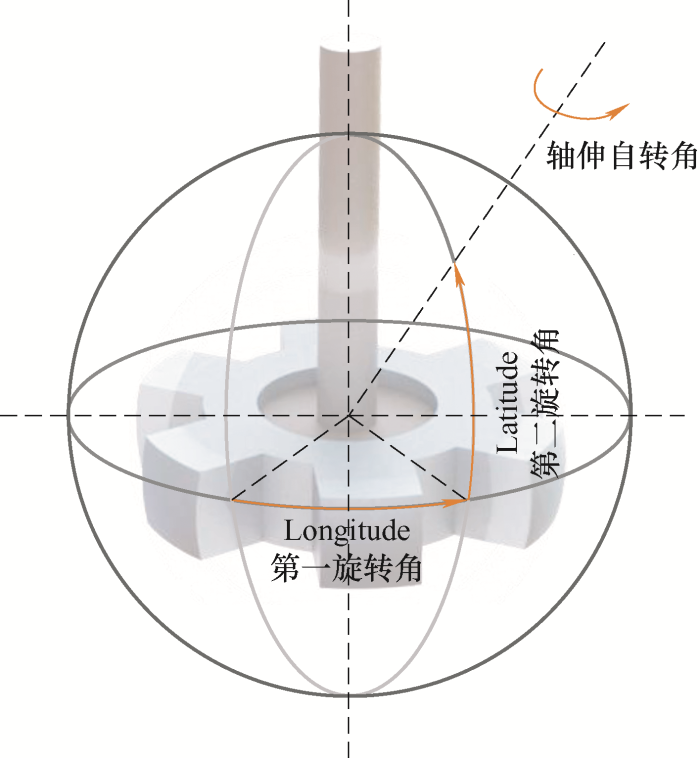
若要对转子运动进行系统的分析，先要建立固定的定子参考系，即形状、大小、位置和轴向完全确定的球体，使之既不变形、也不能平移和旋转。其次，在转子体的赤道面上构建辅助面，并以该辅助面为基准定义旋转角，旋转角相对于固定的定子坐标系表示转子所处的姿态。如图2所示，该坐标系中的旋转角类比于经纬度，维度对应偏航角^[13]，即第一自由度；经度对应侧倾角^[13]，即第二自由度；前两个自由度定位至球面一点，该点与球心连线为第三自由度旋转轴线，称为轴伸自转角^[13]，在该坐标系下的坐标表示为三个角度值。球形电机转子输出端的任务空间受定子外壳影响，侧倾角为±33°，其余两自由度无限制，末端可达到的空间位置为部分球面。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 球形转子坐标系

该模型更关注终端的空间位置。转子球心固定且与定子球心重合，当转子处于不同侧倾角时，与转子极所在球面距离最近的受激定子极对相互吸引，可产生不同侧倾角度下的旋转运动，即轴伸自转。旋转与侧倾的多种组合可驱动球形转子达到任意工作空间。

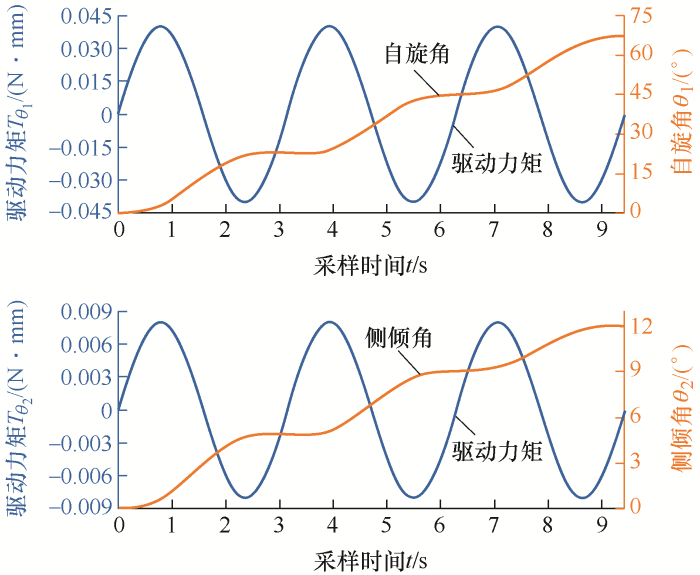
采用ADAMS虚拟样机技术使用正弦激励作为前两个独立自由度的驱动力矩，即第一第二旋转关节的驱动，表达式如下

$\left\{ \begin{matrix} {{T}_{{{\theta }_{1}}}}=0.04\sin \left( 2t \right) \\ {{T}_{{{\theta }_{2}}}}\text{=}0.008\sin \left( 2t \right) \\\end{matrix} \right.$

可得到输出结果，即自旋角θ₁、侧倾角θ₂，自旋力矩${{T}_{{{\theta }_{1}}}}$和侧倾力矩${{T}_{{{\theta }_{2}}}}$的对应变化情况，采样时长设为9.42 s，采样点数为187，具体结果如图3所示。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 ADAMS仿真结果

基于ADAMS的动力学仿真可以得到全面、准确的数据集，但无法应用于实时的闭环控制。设计电机控制器时，需要用到反映电机运行状态的数学模型，因此，提出该球形电机的动力学模型具有相当的必要性。

3 基于D-H参数的动力学模型

等效D-H参数动力学模型的建模灵感来源于机器人学中的手腕机构^[13]，二者的共同点是具有三个自由度。电机结构决定了转子的三自由度为围绕通过质心的三个轴线的旋转，对应三个旋转角。通过质心轴的三个旋转角中仅有两个相互独立，另外要再确定一个绕质心轴转过的角度，才能完全确定转子的姿态。

3.1 动力学模型的坐标系统

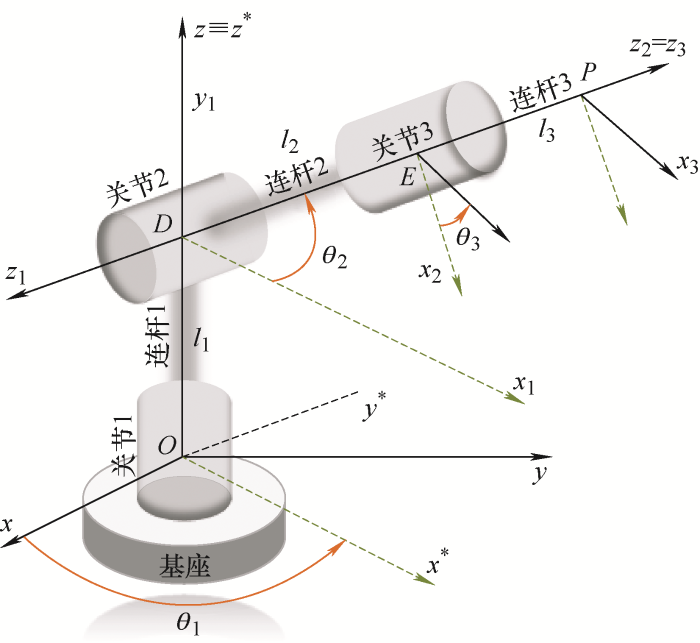
将球形转子虚拟为三个柱形旋转关节串联的运动模型，正运动学分析是由已知旋转关节的运动求解实际输出轴末端位姿的过程。等效模型如图4所示，可旋转关节1、2、3分别通过连杆1、2串联。关节1固连在基座上，执行机构的末端位置用点P表示。从图4可以看到，每个关节的旋转角度θ相对于一个固定的xyz坐标框架，绕z轴旋转。首先定义一个基于底座的固定坐标系O-xyz作为全局的参考标准，即定子坐标系，再用其余辅助坐标系与其之间的转换关系描述模型运动。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 等效模型坐标系统

设第i和i+1个关节连接点处为第i参考坐标系原点，各参考坐标系原点设为D点、E点、P点，位于连接两关节的连杆后端，最后一个连杆的后端P点对应输出轴末端，该坐标系与固定坐标系之间的转换关系对应球形电机运动姿态。z_i轴为连接点处第i关节旋转轴，相邻两个辅助坐标系z_i轴之间的公垂线为x_i轴，由右手坐标系建立原则可得到第三轴y_i，从而确定参考坐标系x_iy_iz_i，i=1，2，3。此类链式结构的每个关节都可由4个D-H参数描述。具体参数值如表2所示。

表2 D-H参数值

序号	a_i	α_i	d_i	变量
1	0	$\frac{\mathrm{ }\!\!\pi\!\!\text{ }}{2}$	l₁	θ₁∈[-180°180°]
2	l₂	$-\frac{\mathrm{ }\!\!\pi\!\!\text{ }}{2}$	0	θ₂∈[-33°33°]
3	0	0	l₃	θ₃∈[-180°180°]

新窗口打开| 下载CSV

为符合球形转子实体的特点，部分参数值做如下约定：设全局固定坐标系原点O对应转子球心，三个关节的旋转轴相交于该点，故旋转关节1和2之间，关节2和3之间的连杆长度l₁=l₂=0，旋转关节3之后的连杆长为转子球半径和输出轴总长，即l₃=76.5 mm。旋转关节的唯一变量旋转角θ_i(i=1,2,3)的取值范围由运动空间决定。根据齐次坐标的定义，每个关节运动的齐次坐标转换矩阵可由式(1)得到

(1)${{\mathbf{T}}_{i}}=\left[ \begin{matrix} \cos {{\theta }_{i}} & -\cos {{\theta }_{i}}\sin {{\alpha }_{i}} & \sin {{\theta }_{i}}\sin {{\alpha }_{i}} & {{l}_{i}}\cos {{\theta }_{i}} \\ \sin {{\theta }_{i}} & \cos {{\theta }_{i}}\cos {{\alpha }_{i}} & -\cos {{\theta }_{i}}\sin {{\alpha }_{i}} & {{l}_{i}}\sin {{\theta }_{i}} \\ 0 & \sin {{\alpha }_{i}} & \cos {{\alpha }_{i}} & {{d}_{i}} \\ 0 & 0 & 0 & 1 \\\end{matrix} \right]$

结合具体参数值，易得各齐次变换矩阵，不再列出，依次相乘构成的复合运动有

(2)$\begin{matrix} \mathbf{T}={{\mathbf{T}}_{\text{1}}}{{\mathbf{T}}_{\text{2}}}{{\mathbf{T}}_{\text{3}}}= \\ \left[ \begin{matrix} {{t}_{11}} & {{t}_{21}} & {{t}_{13}} & ({{l}_{2}}\cos {{\theta }_{2}}-{{l}_{3}}\sin {{\theta }_{2}})\cos {{\theta }_{1}} \\ {{t}_{21}} & {{t}_{22}} & {{t}_{23}} & ({{l}_{2}}\cos {{\theta }_{2}}-{{l}_{3}}\sin {{\theta }_{2}})\sin {{\theta }_{1}} \\ {{t}_{31}} & {{t}_{32}} & {{t}_{33}} & {{l}_{1}}+{{l}_{2}}\sin {{\theta }_{2}}+{{l}_{3}}\cos {{\theta }_{2}} \\ 0 & 0 & 0 & 1 \\\end{matrix} \right] \\ \end{matrix}$

其中

(3)$\left\{ \begin{matrix} {{t}_{11}}=\cos {{\theta }_{1}}\cos {{\theta }_{2}}\cos {{\theta }_{3}}\text{-}\sin {{\theta }_{1}}\sin {{\theta }_{3}} \\ {{t}_{21}}=\cos {{\theta }_{1}}\sin {{\theta }_{3}}+\cos {{\theta }_{2}}\cos {{\theta }_{3}}\sin {{\theta }_{1}} \\ {{t}_{31}}=\cos {{\theta }_{3}}\sin {{\theta }_{2}} \\ {{t}_{12}}=-\cos {{\theta }_{3}}\sin {{\theta }_{1}}-\cos {{\theta }_{1}}\cos {{\theta }_{2}}\sin {{\theta }_{3}} \\ {{t}_{22}}=\cos {{\theta }_{1}}\cos {{\theta }_{3}}-\cos {{\theta }_{2}}\sin {{\theta }_{1}}\sin {{\theta }_{3}} \\ {{t}_{32}}=-\sin {{\theta }_{2}}\sin {{\theta }_{3}} \\ {{t}_{13}}=-\cos {{\theta }_{1}}\sin {{\theta }_{2}} \\ {{t}_{23}}=-\sin {{\theta }_{1}}\sin {{\theta }_{2}} \\ {{t}_{33}}=\cos {{\theta }_{2}} \\ \end{matrix} \right.$

3.2 运动学分析

点$P$在固定坐标系中的位置可由式(2)与向量[0 0 0 1]^T相乘得到，即正运动学

(4)${{\left[ \begin{matrix} x \\ y \\ z \\ \end{matrix} \right]}_{P}}=\left\{ \begin{matrix} -{{l}_{3}}\sin {{\theta }_{2}}\cos {{\theta }_{1}} \\ -{{l}_{3}}\sin {{\theta }_{2}}\sin {{\theta }_{1}} \\ {{l}_{3}}\cos {{\theta }_{2}} \\ \end{matrix} \right\}$

显然，式(4)为一种球面螺旋线方程^[9]。据此方程，将三自由度运动进行不同的组合，可以归纳出球形电机转子输出轴末端不同的运动路径，如表3所示。

表3 转轴末端运动路径分析

序号	运动组合	运动形式	运动轨迹
1	θ₁	自旋	点
2	θ₂	侧倾	圆弧
3	θ₃	自旋	点
4	θ₁+θ₂	章动	球面螺旋线
5	θ₁+θ₃	自旋/旋进	点/圆
6	θ₂+θ₃	侧倾+轴伸自转	圆弧
7	θ₁+θ₂+θ₃	复合运动	球面螺旋线

新窗口打开| 下载CSV

由式(4)反解得到逆运动学^[17]

(5)${{\theta }_{1}}\text{=}\arctan \left( \frac{{{y}_{p}}}{{{x}_{p}}} \right)$

(6)${{\theta }_{2}}\text{=}\arccos \left( \frac{{{z}_{p}}}{{{l}_{3}}} \right)$

由于在E点处关节3以在球面任意位置进行旋转运动，θ₃取值不受θ₁和θ₂约束，故θ₃只能由旋转矩阵求得。当转子的侧倾角θ₂>0时，第三自由度运动的θ₃决定负载的姿态，对带负载情况下的轨迹规划、通电策略等有重要意义。此类腕关节的逆向运动学问题一般先解算姿态，再求可用位置。通过对关节坐标的公式进行微分得到雅可比矩阵为

(7)$\left[ \begin{matrix} {{l}_{3}}\sin {{\theta }_{1}}\sin {{\theta }_{2}} & -{{l}_{3}}\cos {{\theta }_{1}}\cos {{\theta }_{2}} & 0 \\ -{{l}_{3}}\cos {{\theta }_{1}}\sin {{\theta }_{2}} & -{{l}_{3}}\sin {{\theta }_{1}}\cos {{\theta }_{2}} & 0 \\ {{l}_{3}}\cos {{\theta }_{2}} & -{{l}_{3}}\sin {{\theta }_{2}} & 0 \\\end{matrix} \right]$

由式(7)可以看出，仅当第二自由度运动存在时，才能实现输出轴末端的空间位置移动。

3.3 动力学分析

在等效模型运动学分析的基础上，用拉格朗日能量法建立系统的动力学方程。先根据各关节变量${{\theta }_{i}}(t)$及速度变量${{\dot{\theta }}_{i}}(t)$写出系统的动能与势能表达式，再代入拉格朗日方程^[18]进行化简。拉格朗日方程的基本形式为

(8)$\frac{\mathrm{d}}{\mathrm{d}t}\left( \frac{\partial T}{\partial {{{\dot{\theta }}}_{j}}} \right)-\frac{\partial T}{\partial {{\theta }_{j}}}+\frac{\partial U}{\partial {{\theta }_{j}}}={{\mathbf{Q}}_{\text{j}}}$

式中，广义变量θ_j为关节处的旋转角；广义力Q_j为施加在关节${{M}_{\theta j}}$处分别进行三自由度运动的力矩。

球形转子被建模成由三个虚拟刚体串联的运动链，仅有刚体间约束允许的自由度，因此系统动能和势能表达式分别为

(9)$T\text{=}\sum\limits_{i=1}^{3}{\frac{1}{2}{{m}_{i}}\mathbf{V}_{{{\text{G}}_{\text{i}}}}^{\mathrm{T}}{{\mathbf{V}}_{{{\text{G}}_{\text{i}}}}}}+\sum\limits_{i=1}^{3}{\frac{1}{2}\mathbf{\Omega }_{\text{i}}^{\mathrm{T}}\mathbf{I}{{\mathbf{\Omega }}_{\text{i}}}}$

(10)$U=-\sum\limits_{i=1}^{3}{{{m}_{i}}{{\mathbf{g}}^{\mathrm{T}}}{{\mathbf{x}}_{\mathrm{0}{{\text{G}}_{\text{i}}}}}}$

式中，m_i为第i个关节的质量；${{\mathbf{V}}_{{{\text{G}}_{\text{i}}}}}$为关节质心${{G}_{i}}$相对于全局坐标系的平移速度；${{\mathbf{I}}_{\text{i}}}$为关节相对于其自身参考系的惯量；${{\mathbf{\Omega }}_{\text{i}}}$为关节的全局绝对角速度；$\mathbf{g}$为一个在全局坐标系中包含重力加速度的向量；${{\mathbf{x}}_{0{{\text{G}}_{\text{i}}}}}$为图4中标注出的连杆质心${{\mathbf{G}}_{\text{i}}}$在基础坐标系Oxyz中的位置坐标。在建模过程中，由于转子质心近似集中在球心处，故认为各关节中心位置均集中于球心，忽略连杆的质量和体积，又因球形转子在运动过程中质心无偏移，所以在能量表达式推导过程中势能不变，且去除平移动能分量，简化后的模型仅存在动能表达式(9)的第二项——旋转动能分量。

设每一关节固连坐标系的坐标轴平行于惯量主轴，则每个关节的惯量矩阵为斜对角矩阵

(11)${{\mathbf{I}}_{i}}=\left[ \begin{matrix} {{J}_{xi}} & 0 & 0 \\ 0 & {{J}_{yi}} & 0 \\ 0 & 0 & {{J}_{zi}} \\\end{matrix} \right]$

因关节设计为圆柱体，固连坐标轴原点位于圆柱体质心，空间旋转轴${{z}_{i}}$通过轴心，根据几何特征可以得到中心主转动惯量之间的关系

(12)${{J}_{xi}}={{J}_{yi}}\ne {{J}_{zi}}$

本文令${{J}_{xyi}}={{J}_{xi}}={{J}_{yi}}$。

因每个关节均围绕其自身的${{z}_{i}}$轴旋转，第i个关节相对于其自身参考坐标系的转动角速度为

(13)${{\mathbf{\Omega }}_{\text{i}}}={{R}_{i-1\to i}}\left\{ \begin{matrix} 0 \\ 0 \\ {{{\dot{\theta }}}_{i}} \\\end{matrix} \right\}+{{R}_{i-2\to i}}\left\{ \begin{matrix} 0 \\ 0 \\ {{{\dot{\theta }}}_{i-1}} \\\end{matrix} \right\}+{{R}_{i-3\to i}}\left\{ \begin{matrix} 0 \\ 0 \\ {{{\dot{\theta }}}_{i-2}} \\\end{matrix} \right\}+\cdots $

式中，${{R}_{i-j\to i}}$为一个旋转矩阵，由刚体i-j到刚i体的转换矩.阵连乘并取左上3×3子阵后的转置得到。因此角速度为

(14)${{\mathbf{\Omega }}_{\text{i}}}={{\mathbf{P}}_{\text{i}}}\left( \mathbf{\theta } \right)\mathbf{\dot{\theta }}$

得到平移速度和角速度后，进而得到关节链的总动能

(15)$T\text{=}\frac{1}{2}\sum\limits_{i=1}^{3}{{{{\mathbf{\dot{\theta }}}}^{\mathrm{T}}}\mathbf{P}_{\text{i}}^{\mathrm{T}}\left( \mathbf{\theta } \right){{\mathbf{I}}_{\text{i}}}{{\mathbf{P}}_{\text{i}}}\left( \mathbf{\theta } \right)\mathbf{\dot{\theta }}}=\frac{1}{2}{{\mathbf{\dot{\theta }}}^{\mathrm{T}}}\mathbf{M}\left( \mathbf{\theta } \right)\mathbf{\dot{\theta }}$

式中，矩阵$\mathbf{M}(\mathbf{\theta })$为关节质量矩阵。

将能量表达式代入拉格朗日方程

(16)$\frac{\mathrm{d}}{\mathrm{d}t}\left[ \mathbf{M}\left( \mathbf{\theta } \right)\mathbf{\dot{\theta }} \right]-\frac{1}{2}\frac{\partial }{\partial {{\theta }_{j}}}\left[ {{{\mathbf{\dot{\theta }}}}^{\mathrm{T}}}\mathbf{M}\left( \mathbf{\theta } \right)\mathbf{\dot{\theta }} \right]=M$

运动方程的简化形式为

(17)$\mathbf{M}\left( \mathbf{\theta } \right)\mathbf{\ddot{\theta }+V}\left( \mathbf{\dot{\theta },\theta } \right)\mathbf{=}{{\mathbf{M}}_{\text{ }\!\!\theta\!\!\text{ }}}$

式(17)表明该模型的动力学方程包含3个部分：惯性力项$\mathbf{M}\left( \mathbf{\theta } \right)\mathbf{\ddot{\theta }}$、科氏力与离心力项$\mathbf{V}\left( \mathbf{\theta,\dot{\theta }} \right)$以及包含所有非守恒外部力的广义力项${{\mathbf{M}}_{i}}$。科氏力与离心力项的数值取决于广义角速度${{\dot{\theta }}_{i}}$，并反映了机械臂的内部动态交互作用。一般来说，包含${{\dot{\theta }}_{i}}{{\dot{\theta }}_{j}}\left( i\ne j \right)$项的为科氏力项，而包含$\dot{\theta }_{i}^{2}$形式的项被称为离心力项。在简化模型的基础上，计算各部分结果如下所示

(18)$\mathbf{M}\left( \mathbf{\theta } \right)\text{=}\left[ \begin{matrix} {{M}_{11}} & {{M}_{12}} & {{M}_{13}} \\ {{M}_{21}} & {{M}_{22}} & 0 \\ {{M}_{31}} & 0 & {{M}_{33}} \\\end{matrix} \right]$

(19)$\mathbf{V}\left( \mathbf{\dot{\theta },\theta } \right)=\left[ \begin{matrix} {{V}_{11}}{{{\dot{\theta }}}_{1}}+{{V}_{12}}{{{\dot{\theta }}}_{2}}+{{V}_{13}}{{{\dot{\theta }}}_{3}} \\ {{V}_{21}}{{{\dot{\theta }}}_{1}}+{{V}_{22}} \\ {{V}_{31}}{{{\dot{\theta }}}_{1}}+{{V}_{32}} \\\end{matrix} \right]$

(20)$\left\{ \begin{matrix} \begin{align} & {{M}_{11}}={{J}_{xy1}}+{{J}_{xy2}}{{\sin }^{2}}{{\theta }_{2}}+{{J}_{z2}}c\text{o}{{\text{s}}^{2}}{{\theta }_{2}}+ \\ & \text{ }\ \ \ {{J}_{xy3}}{{\sin }^{2}}{{\theta }_{2}}\left( {{\cos }^{2}}{{\theta }_{2}}+{{\sin }^{2}}{{\theta }_{3}} \right)+{{J}_{z3}}{{\cos }^{2}}{{\theta }_{2}} \\ \end{align} \\ {{M}_{12}}={{J}_{xy3}}\sin {{\theta }_{2}}\sin {{\theta }_{3}}\left( \cos {{\theta }_{3}}-\cos {{\theta }_{2}} \right) \\ {{M}_{13}}={{J}_{z3}}\cos {{\theta }_{2}} \\ {{M}_{21}}={{M}_{12}} \\ {{M}_{22}}={{J}_{xy2}}+{{J}_{xy3}} \\ {{M}_{31}}={{M}_{13}} \\ {{M}_{33}}={{J}_{z3}} \\ \end{matrix} \right.$

(21)$ \begin{cases}\begin{aligned}&V_{11}=2\left(J_{xy2}-J_{z2}-J_{z3}\right)\sin\theta_{2}\cos\theta_{2}\cdot\dot{\theta}_{2}+\\&2J_{xy3}\sin\theta_{2}\cos\theta_{2}\cdot\dot{\theta}_{2}\left(\cos^{2}\theta_{2}-\sin^{2}\theta_{2}+\sin^{2}\theta_{3}\right)+\\&2J_{xy3}\sin\theta_{3}\cos\theta_{3}\cdot\dot{\theta}_{2}\cdot\sin^{2}\theta_{2}\\&2J_{xy3}\sin\theta_{3}\cos\theta_{3}\cdot\dot{\theta}_{2}\cdot\sin^{2}\theta_{2}\\&V_{12}=J_{xy3}\sin\theta_{3}\cos\theta_{2}\cdot\dot{\theta}_{2}\left(\cos\theta_{3}-\cos\theta_{2}\right)+\\&J_{xy3}\sin\theta_{2}\cos\theta_{3}\cdot\dot{\theta}_{3}\left(\cos\theta_{3}-\cos\theta_{2}\right)+\\&J_{xy3}\sin\theta_{2}\sin\theta_{3}\left(\sin\theta_{2}\cdot\dot{\theta}_{2}-\sin\theta_{3}\cdot\dot{\theta}_{3}\right)\\&V_{13}=-J_{z3}\sin\theta_{2}\cdot\dot{\theta}_{2}\\&V_{21}=V_{12}\\&V_{22}=\sin\theta_{2}\cos\theta_{2}\left[J_{xy2}-J_{z2}-J_{z3}+J_{xy3}\left(\cos^{2}\theta_{2}-\sin^{2}\theta_{2}+\sin^{2}\theta_{3}\right)\right]+\\&J_{xy3}\sin\theta_{3}\left(\cos\theta_{2}\cos\theta_{3}-\cos^{2}\theta_{2}+\sin^{2}\theta_{2}\right)-J_{z3}\sin\theta_{2}\\&V_{31}=V_{13}\\&V_{31}=J_{13}\end{aligned}\end{cases}$

经化简，式(20)和式(21)中未知参数为J_xy₁、J_xy₂、J_xy₃、J_z₂和J_z₃五项。

基于D-H参数的动力学模型存在的问题是建立模型的等效部件非真实存在，因此其各部件的转动惯量难以通过解析或有限元法得到，该模型存在待确定参数。

4 模型的参数辨识

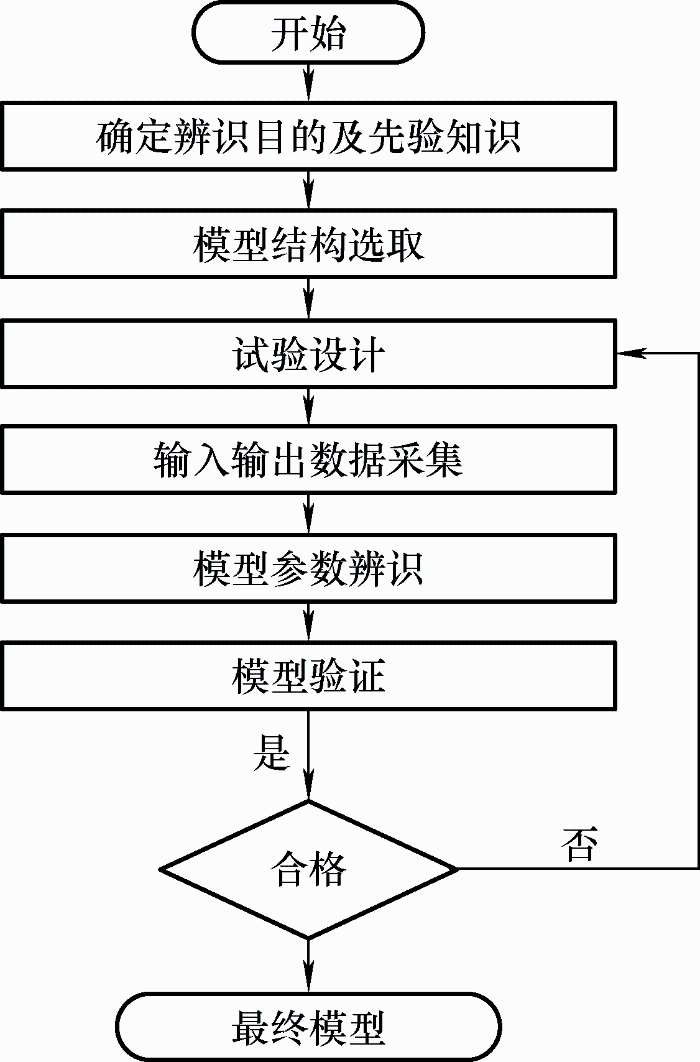
以上建立的动力学模型是一个多输入、多输出的非线性系统，可以表达为连续或离散时间下的非线性状态空间方程。对这类模型的参数估计，要在初始模型的基础上使用系统输入数据预测输出，通过不断更新参数使预测的输出结果与测量数据相拟合，当拟合度较高时，将此时的参数值作为参数辨识结果，其算法流程如图5所示。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 参数辨识流程

4.1 参数辨识方法

参数辨识方法的目标在于使预测值与真实值之间的误差更小，预测误差算法是参数辨识的基本方法之一，假设由某一模型$U\left( {{\theta }_{\text{*}}} \right)$给出的预测误差为

(22)$\varepsilon \left( t,{{\theta }_{*}} \right)=y\left( t \right)-\hat{y}\left( t\left| {{\theta }_{*}} \right. \right)$

设预测误差序列通过稳定滤波器L(q)滤波

(23)${{\varepsilon }_{F}}(t,\theta )=L(q)\varepsilon (t,\theta )\ \ \ \ \ \text{ }1\le t\le N$

对预测误差序列$\varepsilon_{F}(t, \theta)$求模

(24)${{V}_{N}}\left( \theta,{{Z}^{N}} \right)=\frac{1}{N}\sum\limits_{t=1}^{N}{l\left( {{\varepsilon }_{F}}(t,\theta ) \right)}$

再取式(24)的V_N(θ, Z^N)最小值，就获得了θ的估计值$\hat{\theta}_{N}$。在时间N内且已知数据集Z^N时，求模函数恰好是有限维实参数向量θ的普通函数。求解该问题的数值计算方法选择置信域：给定一点x⁽^k⁾后，指定x⁽^k⁾的变化范围，该范围通常取以x⁽^k⁾为中心的球域，称为信赖域。在此域内优化目标函数的二次逼近式，按照一定模式求出后继点x⁽^k⁺¹⁾，如果不满足要求，再定义以x⁽^k⁺¹⁾为中心的信赖域，并在此域内优化新的二次逼近式，重复以上步骤直到满足精度要求为止。

4.2 模型及数据处理

将前文推导出的动力学方程改写为一阶非线性状态空间方程来描述姿态特性和速度特性，忽略扰动e(t)得到

(25)$\left\{ \begin{matrix} \dot{x}(t)=F\left( t,x(t),u(t),par1,par2,\cdots,parN \right) \\ y(t)=H\left( t,x(t),u(t),par1,par2,\cdots,parN \right) \\ x(t)={{x}_{0}} \\\end{matrix} \right.$

式中，以角位移$\theta $和角速度$\dot{\theta }$为状态变量x(t)，则状态更新值，即连续时间情况下的状态导数向量$\dot{x}(t)$为相应的角速度$\dot{\theta }$和角加速度$\ddot{\theta }$，u(t)为输入激励，即转子上受到的力矩，y(t)为角度反馈值。选定模型之后使用参数向量θ将其参数化为一个模型结构的值域，参数辨识在这个集合内寻求最好的模型。

本系统的输入与响应数据涉及3个输入量，6个状态量，3个输出量。5个待辨识参数为等效关节的惯量矩阵主惯量：J_xy₁、J_xy₂、J_xy₃、J_z₂、J_z₃，单位为kg·mm²，依据物理推理与几何特征设定初值。

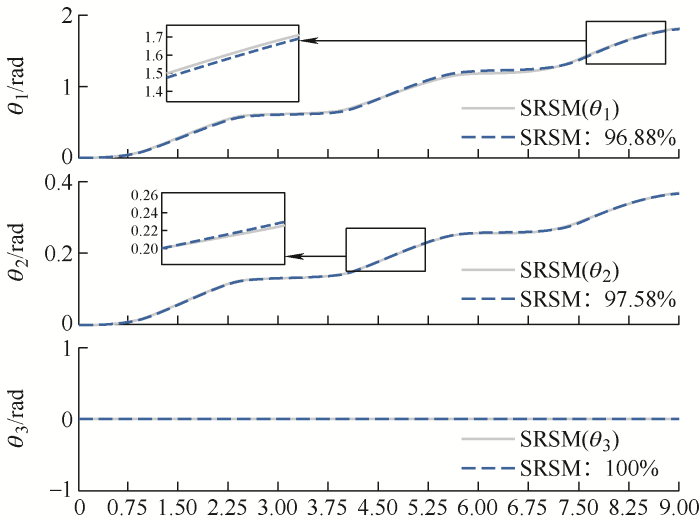
随后，使用最小二乘搜索算法，经过尝试不同初值的参数组合，选出拟合结果最优的一组。辨识后的模型输出和真实输出之间的比较如图6所示，实线为ADAMS仿真的真实输出，虚线为参数辨识后的输出。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 参数辨识结果

由图6右上角观察可得，辨识模型与系统原始模型在前两个自由度运动的匹配度为96.88%和97.58%，本次模拟不涉及第三自由度的运动，故结果恒为0，拟合度100%。辨识结果报告中提到，当在搜索方向上没有改进时终止，迭代次数为13，函数计算次数为14，终止预测误差FPE为2.98×10^-4，均方误差MSE为2.87×10^-4，说明该参数下的模型精度较高，辨识结果如表4所示。

表4 参数辨识结果

参数	辨识结果/(kg·mm²)
J_xy₁	32.531
J_xy₂	29.870
J_xy₃	30.001
J_z₂	56.014
J_z₃	89.235

新窗口打开| 下载CSV

动力学模型中的参数为表4中数值时，模型辨识结果与仿真结果相呼应，选择该条件下的辨识结果作为试验参照。

4.3 试验验证

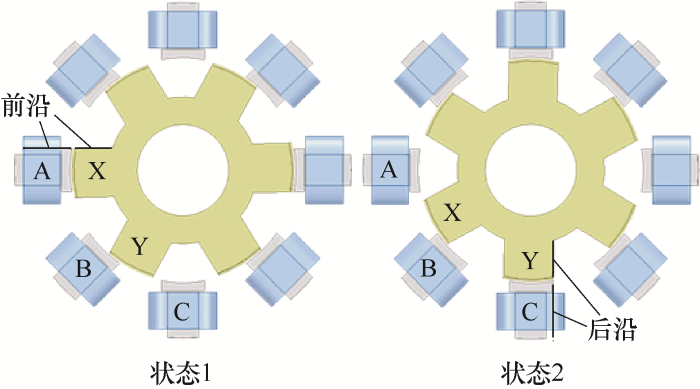
设计以下试验验证动力学参数辨识结果的准确性。在单线圈通电的条件下，吸引转子作单步步进运动，这一启停过程完全可以反映转子的动力学特性。已知转矩条件，可以分别获得理想和实际的运动状态。理想运动由虚拟样机仿真计算得出，实际运动通过传感器测量得到。但为了更加贴近建模目标，计算期望轨迹运动的需求力矩，用传感器获取的运动数据代入动力学方程计算需求力矩，与有限元分析软件中计算的转矩值进行比较，看结果是否吻合。如图7所示，转子由状态1运动至状态2，给中间层A相线圈通电，吸引距其较近的转子极使二者前沿重合，设此时转子姿态为初始位置，则C相线圈与转子极相距最远，给C相线圈通电就能获得较大自旋角度。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 运动状态描述

磁阻式球形电机通电控制系统^[1]主要由上位机、供电电源、控制电路、试验样机、陀螺仪传感器(MEMS)和力矩检测台架组成。MEMS可以测量运动过程中的角位移、角速度、角加速度。力矩传感器采取配用的XMT808-I型显示器测得转矩数值。试验平台如图8所示。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 试验平台

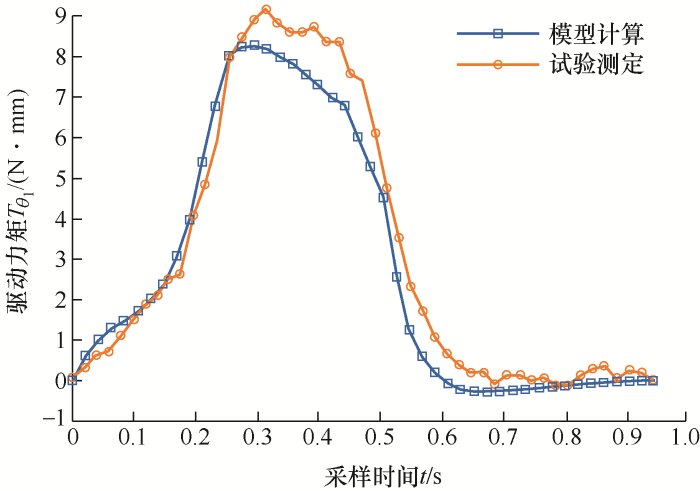
将试验测得的角位移${{\theta }_{1}}$、角速度$\dot{\theta}_{1}$、角加速度$\ddot{\theta}_{1}$代入含辨.识参数的动力学方程计算驱动力矩，与试验测量得到的转矩值比较，结果如图9所示。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 试验结果与计算结果对比

通过对比发现数学模型解算得到的力矩变化规律与试验得到的力矩变化规律基本吻合，最大绝对误差为0.870 1 N·mm，位于转矩输出峰值附近及以后。这是由于整个运动过程非常短暂，传感器的返回数据精度及采样时间间隔，再加上角位移、角速度、角加速度三者在计算中的累计误差，都对计算结果有影响，D-H参数等效模型下拉格朗日法的建模正确性得到验证，说明该模型可以应用于通电策略理论的研究中。

5 结论

动力学模型是三自由度球形电机闭环控制的核心工具之一。本文在研究球形电机的运动问题时，将三自由度运动进行拆分，把问题简化为三个等效旋转关节依次串联的运动链，对构件的D-H参数进行更贴合球形实体的近似处理，推导出含有不同自由度驱动力矩的动力学方程，最后利用系统参数辨识的结果对该方程的未知参数进行标定，得到完整的磁阻式球形电机动力学模型。试验和仿真的结果表明，该建模方式切实可行，为今后球形电机的运动规划与通电控制提供了理论依据。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

周睿.

永磁球形电机解析建模和基于粒子群算法的优化控制研究[D]. 合肥: 安徽大学, 2020.

[本文引用: 2]

ZHOU

Rui

Research on analytical modeling of permanent magnet spherical motor and optimization control based on particle swarm optimization algorithm[D]. Hefei: Anhui University, 2020.

[本文引用: 2]

[2]

郝春生, 李国丽, 王群京, 等.

感应式球形电机结构设计与参数分析

[J]. 微电机, 2021, 54(6):23-27,32.