电气工程学报, 2021, 16(4): 166-173 doi: 10.11985/2021.04.021

电力系统

基于模糊PID的液压杆塔调平控制方法研究*

胡燃,, 萧定辉, 卞佳音, 何泽斌, 陈建强, 林新生, 彭红刚

南方电网广东电网有限责任公司广州供电局 广州 510000

Research on Leveling Control Method of Hydraulic Tower Based on Fuzzy PID

HU Ran,, XIAO Dinghui, BIAN Jiayin, HE Zebin, CHEN Jianqiang, LIN Xinsheng, PENG Honggang

Guangzhou Power Supply Bureau, China Southern Power Grid, Guangzhou 510000

收稿日期: 2020-12-10   修回日期: 2021-06-8  

基金资助: * 广东电网有限责任公司广州供电局科技.  GZHKJXM20180107
基于智能控制技术的输电线路杆塔整体液压提升系统研究.  080044KK52180005

Received: 2020-12-10   Revised: 2021-06-8  

作者简介 About authors

胡燃,男,1990年生,硕士,工程师。主要研究方向为电力工程。E-mail： 1208319383@qq.com

摘要

针对输电线路杆塔需要在容易下陷的土壤上进行液压提升作业前进行调平控制的情况,对受压土壤下陷特性进行研究,得出在液压杆对土壤施压的情况下,土壤下陷程度与施压程度是线性关系。在此基础上利用惯性测量单元(Inertial measurement unit,IMU)和实时动态差分定位技术(Real time kinematic,RTK)对调平过程中的杆塔倾斜状态进行测量,并且在二者频率不一致的基础上以卡尔曼滤波进行数据融合后,再以模糊PID控制算法实现杆塔调平控制。文章在试验中对比IMU和RTK在卡尔曼滤波融合下和没有融合的杆塔状态估计,其融合数据更具鲁棒性。并且在控制算法上对比传统PID控制算法和模糊PID控制算法,在超调量和恢复稳态时间上,模糊PID控制更具优势。

关键词： 液压杆塔调平 ; 卡尔曼滤波 ; 模糊PID控制 ; IMU ; RTK

Abstract

Aiming at the situation that the transmission line tower needs leveling control before hydraulic lifting operation on the soil prone to subsidence, the subsidence characteristics of the soil under pressure are studied, and it is found that the subsidence degree of the soil is linear with the pressure degree under the pressure of the hydraulic rod. On this basis, IMU(Inertial measurement unit) and RTK (Real time kinematic) are used to measure the tilt state of the tower in the leveling process, and on the basis of their inconsistent frequencies, Kalman filter is used for data fusion, and then fuzzy PID control algorithm is used to achieve the tower leveling control. In the experiment, the state estimation of the tower with IMU and RTK are compared under Kalman filter fusion and without fusion, and the fusion data is more robust. In addition, compared with the traditional PID control algorithm, the fuzzy PID control has more advantages in overshoot and steady-state recovery time.

Keywords： Hydraulic tower leveling ; Kalman filtering ; Fuzzy PID control ; IMU ; RTK

PDF (586KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

胡燃, 萧定辉, 卞佳音, 何泽斌, 陈建强, 林新生, 彭红刚. 基于模糊PID的液压杆塔调平控制方法研究*. 电气工程学报[J], 2021, 16(4): 166-173 doi:10.11985/2021.04.021

HU Ran, XIAO Dinghui, BIAN Jiayin, HE Zebin, CHEN Jianqiang, LIN Xinsheng, PENG Honggang. Research on Leveling Control Method of Hydraulic Tower Based on Fuzzy PID. Journal of Electrical Engineering[J], 2021, 16(4): 166-173 doi:10.11985/2021.04.021

1 引言

随着城市的发展,输电杆塔周围的导线跨越道路、建筑物等导线对于跨域物净空距离不足的情况会发生,在这情况下需要对杆塔进行升塔作业,其升塔作业之前需要对杆塔在提升向土壤施压发生沉降后进行调平才可进一步对杆塔提升。目前国内行业中常规采用的解决方法是手动调平方式为主,过分依赖经验且不能够适应液压杆在土壤上受压后的不均匀沉降,所以有必要对电力杆塔调平技术进入深入研究,提出有效可行的解决方案。

杆塔整体调平实现传统的方法为借助经纬仪监视铁塔的高度,调节铁塔稳定拉线保证铁塔垂直水平[1,2,3]。调平过程中最重要的环节是在液压杆对土壤施压情况下发生沉降后对输电杆塔进行调平控制,要监控铁塔倾斜角度,根据倾斜角度合理调节不同液压杆上升速度和高度。目前调平控制研究中,房怀英等[4]提出以模糊PID算法作为调平控制方法来实现对沥青砂浆车液压进行调平。王冰[5]提出基于PID神经网络对调平系统进行控制的方案。史海 红[6]采用人工神经网络控制器对混凝土摊铺机调平。冯仪等[7]提出车载雷达机电式自动调平控制 系统。

结合以上文献,对受压土壤下陷特性进行研究,在土壤受压程度与下降程度为线性关系的条件下,提出利用IMU和毫米级的RTK传感器测量塔身倾斜角度,对土壤受压发生沉降导致杆塔倾斜的情况进行监控,并以卡尔曼滤波对其二者数据进行融合更新去噪,在该融合数据中利用模糊PID控制算法控制液压杆在沉降发生后进行调平控制,最终实现整体调平过程中塔身处于无倾斜的姿态,防止倾斜角度过大导致输电铁塔倾倒。此方案能够以电子设备代替人力,保证施工的安全性,提高施工效率。

2 调平过程分析

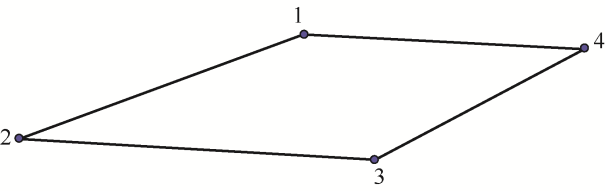
本文提出的方案是利用IMU和毫米级RTK传感器对塔身倾斜度测量,并以此测量数据来对杆塔进行调平控制。在调平过程中对杆塔状态的分析能够具体地使得调平策略更加有效。具体液压杆部署位置如图1所示。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   液压支撑杆塔模型


在液压杆对杆塔进行提升工作时,液压杆会对地面有反作用力,地面会因其特性导致液压杆下陷的可能。所以需要在提升作业之前,在液压杆在逐步提升压力为杆塔重力的情况下,确保液压杆在发生土地下陷后对液压杆进行调平控制,使得杆塔的倾斜度控制在允许的范围内。当塔身发生较大倾斜的时候需要对其进行调平,调平后才能继续增加液压杆压力直至总压力为杆塔重力而在一段时间内杆塔倾斜度无变化时认为其调平工作完成。

2.1 土壤下陷特性

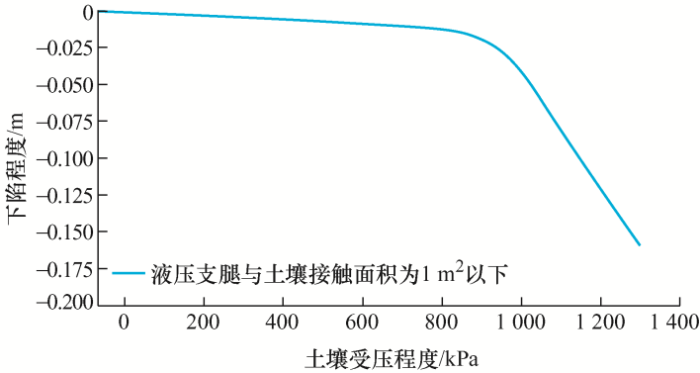
对土壤特性进行分析,其土壤受压下陷会经过三个阶段,分别为弹性变形、弹性变形到塑性变形的过渡阶段、完全塑性变形阶段[8]。在弹性变形过程中,土壤下陷程度随着压力载荷增大从零逐渐增大,压力载荷与沉陷量之间为线性关系;在弹性变形到塑性变形过渡阶段中,土壤弹塑性变形区分明显,极限承载力位置明显,其土壤发生整体剪切破坏;在完全塑性变形阶段,土壤达到极限承载力,进入完全塑性变形,土壤在较小的载荷增量的坐下发行失稳变形。其地面下陷特性与液压杆支腿与地面接触面积有关,在相同压力的情况下,同一沉陷地面处的极限载荷随接触面积增大而减少,随着面积减少而增大。其土壤在支腿对土壤一定的接触面积下进行不同压力作用,其压力与下陷程度的关系如图2所示。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   土壤受压压力与下陷程度的关系图


根据对土壤受压下陷特性,可以认为其调平过程中其土地受压下陷为非线性的下陷。

2.2 杆塔状态测量方法

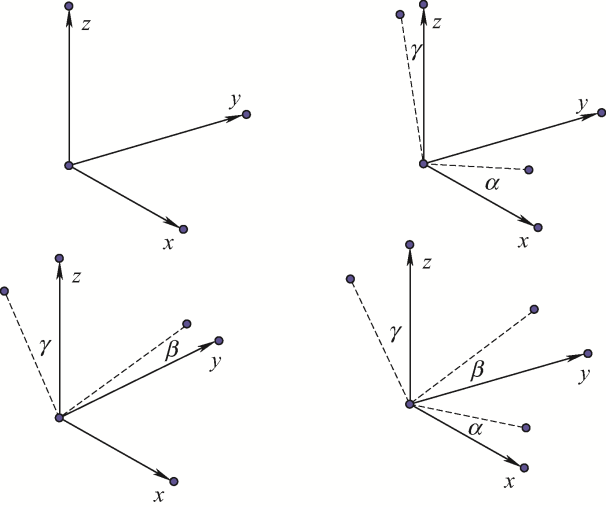
因为在实际作业过程中无法确定地面下面的主要构成,对于每个支腿发生下陷可能性并不一定相同,所以在发生下陷过程中,对于倾角的测量至关重要。本文利用IMU获取其x轴、y轴、z轴方向的加速度值和利用毫米级RTK获取塔身高度变化对铁塔的倾斜状态进行预估。对于输电铁塔的调平过程中,可以认为杆塔除重力和同一方向的液压杆提升力外并不受其他明显外力的作用。IMU传感器是利用三个轴向的加速度值之间的关系计算出物体的姿态角度。塔身在x轴、y轴、z轴的重力加速度分量与倾角的关系如图3表示。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   三轴加速度分量与倾角的关系


以x轴为正方向,则输电杆塔与y轴的夹角α、与x轴的夹角β、与z轴的夹角γ可以视为杆塔塔绕x轴、y轴和z轴的旋转角度,夹角值用x轴、y轴、z轴的测量加速度分量计算,考虑到反正弦函数的值域为(–π, +π),可以将α、β表示为以下公式

$\beta = \left\{ \begin{array}{l}\arcsin \left( {\frac{{{a_x}}}{{\sqrt {a_x^2 + a_y^2 + a_z^2} }}} \right)\;\;\;\;\;\;\;\;\;\;\;\;\;\;{a_z} > 0\\\pi - \arcsin \left( {\frac{{{a_x}}}{{\sqrt {a_x^2 + a_y^2 + a_z^2} }}} \right)\;\;\;\;\;\;\;\;\;{a_x} > 0,{a_z} < 0\\ - \left[ {\pi + \arcsin \left( {\frac{{{a_x}}}{{\sqrt {a_x^2 + a_y^2 + a_z^2} }}} \right)} \right]\;\;\;{a_x} < 0,{a_z} < 0\;\end{array} \right.$
$a = \left\{ \begin{array}{l}\arcsin \left( {\frac{{{a_y}}}{{\sqrt {a_x^2 + a_y^2 + } a_z^2}}} \right)\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{a_z} > 0\\\pi - \arcsin \left( {\frac{{{a_y}}}{{\sqrt {a_x^2 + a_y^2 + } a_z^2}}} \right)\;\;\;\;\;\;\;\;\;\;{a_y} > 0,{a_y} < 0\\ - \left[ {\pi + \arcsin \left( {\frac{{{a_y}}}{{\sqrt {a_x^2 + a_y^2 + } a_z^2}}} \right)} \right]\;\;\;\;{a_y} < 0,{a_z} < 0\end{array} \right.$

此外,塔体相对于自然重力轴线的倾角可以计算如下

$\gamma = \arcsin \frac{{\sqrt {a_x^2 + a_y^2} }}{{\sqrt {a_x^2 + a_y^2 + a_z^2} }}$

利用上述公式,可以计算出弧度值的数据,经过弧角度换算,可以算得角度值。本文利用这α、β两个夹角对塔身状态进行预估,利用γ作为调平误差的控制量。

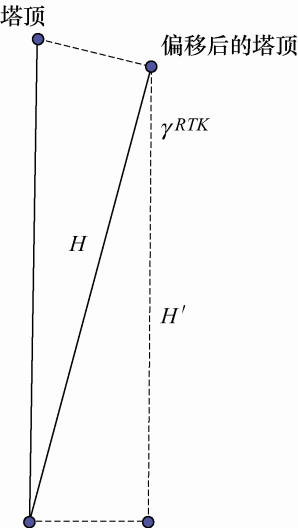
但由于杆塔处于野外环境中,由于外在气象、地质环境及自身因素的影响,除了实际的摇摆和倾斜之外,振动杂波的干扰总是存在的[9]。但是加速度传感器的灵敏度较高,上述的干扰会极大的影响其精确性,降低施工的安全性。因此单一倾角测量传感器远远不够,有必要增加毫米级RTK测量原本塔高与调平过程塔高的变化值来测量其倾斜角度,根据如图4所示的几何关系可知,其测量方式如下

${\gamma ^{RTK}} = \arccos \left( {\frac{{H'}}{H}} \right)$

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   塔身偏移示意图


在这基础上利用卡尔曼滤波算法多传感器融合算法下,对所采集到的IMU数据与毫米级RTK的数据进行融合。

3 基于卡尔曼滤波的多传感器融合 算法

对于多传感器数据进行融合,需要考虑不同传感器在输出频率快慢上的时间同步问题[10,11],在本文中采用传感器有IMU和RTK,两者的采集频率不一致,一般需要通过统一主机给各个传感器提供基准时间,各个传感器根据已经校准后的各自独立采集的数据加上时间戳信息,来做到传感器时间戳同步。另外还需考虑自身运动的补偿,传感器在采集时间内发生的变化需要考虑[12]。最后还需要对不同传感器测量值转换到同一个坐标系上。按其在融合系统中对信息进行抽象处理的话,可分为数据层、特征层、决策层上的融合。本文利用卡尔曼滤波实现对目标对象倾斜角进行估计,属于数据层上的融合。该算法将多个原始的观测数据直接融合,要求多个传感器观测的是同一物理量,或者对其进行尺度校准,最后得到融合数据的最优估计值。该算法从IMU加速度传感器读取三个轴的加速度值,通过换算公式计算上述α、β和γ角度值,另一方面根据毫米级RTK测量铁塔高度h也根据换算公式计算其倾斜角度,异步处理多传感器传输的数据。这时候能够得到由两个在不同时间频率上传感器采集的两个数据对同一个目标的描述。对于卡尔曼滤波而言,需要保证目标对象持续的观测,不然会有目标跟踪失败丢失的情况。

在一个相对较短的Δt得到角值数据序列,测量噪声在为高斯分布的前提下,可用一个线性微分方程来描述,使用IMU对倾斜角进行估计,铁塔在调平过程中定义其在t时刻的状态向量为

$x_{\rm{t}}^{{\rm{imu}}} = \left[ \begin{array}{l}\alpha \\\beta \\\gamma \end{array} \right]$

对$t + {\rm{\Delta }}t$时刻进行预测,方程为

$x_{t + \Delta t{\rm{|}}t}^{{\rm{imu}}} = {F^{{\rm{imu}}}}x_t^{{\rm{imu}}} + {u^{{\rm{imu}}}}$

式中,xt+Δt|t为基于t时刻的状态对铁塔状态进行预测;u为外部影响,在该模型中不受外力影响,无加速度,即${u^{{\rm{imu}}}} = {\rm{0}}$;${F^{{\rm{imu}}}}$为状态转移矩阵,如下 所示

${F^{{\rm{imu}}}} = \left[ {\begin{array}{*{20}{c}}{\rm{1}}&{}&{}\\{}&{\rm{1}}&{}\\{}&{}&{\rm{1}}\end{array}} \right]$

由此可得

$x_{t + \Delta t{\rm{|}}t}^{{\rm{imu}}} = \left[ \begin{array}{l}\alpha \\\beta \\\gamma \end{array} \right]$

再者,对其系统不确定性建模,对于t时刻的状态方差矩阵${P_t}^{{\rm{imu}}}$,一开始对其初始化

$P_{\rm{0}}^{{\rm{imu}}} = \left[ {\begin{array}{*{20}{c}}{{\rm{10}}}&{}&{}\\{}&{{\rm{10}}}&{}\\{}&{}&{{\rm{10}}}\end{array}} \right]$

再对其$t + {\rm{\Delta }}t$时刻的系统不确定性进行预测得

$P_{t + \Delta t}^{{\rm{imu}}} = F{P_t}^{{\rm{imu}}}{F^T} + Q$

其中,Q为过程噪声。预测完毕后对其进行测量数据更新

$y_{t + \Delta t}^{{\rm{imu}}} = z_{t + \Delta t}^{{\rm{imu}}} - x_{t + \Delta t{\rm{|}}t}^{{\rm{imu}}}$
$K_{t + \Delta t}^{{\rm{imu}}} = P_{t + \Delta t{\rm{|}}t}^{{\rm{imu}}}(P_{t + \Delta t{\rm{|}}t}^{{\rm{imu}}} + R{}^{{\rm{imu}}})$
$x_{t + \Delta t}^{{\rm{imu}}} = x_{t + \Delta t{\rm{|}}t}^{{\rm{imu}}} + K_{t + \Delta t{\rm{|}}t}^{{\rm{imu}}}y_{t + \Delta t}^{{\rm{imu}}}$
$P_{t + \Delta t}^{imu} = {P_{t + \Delta t | t}^{-1}}^{imu} - K_{t + \Delta t}^{imu} {P_{t + \Delta t|t}^{ - 1}}^{imu}$

式中,$z_{t + \Delta t}^{{\rm{imu}}}$为$t + {\rm{\Delta }}t$时刻IMU测量值,${R^{{\rm{imu}}}}$为IMU测量误差,$K_{t + \Delta t}^{{\rm{imu}}}$为此过程卡尔曼增益。$z_{t + \Delta t}^{{\rm{imu}}}$为

$z_{t + \Delta t}^{{\rm{imu}}} = \left[ \begin{array}{l}{\alpha _{{\rm{imu}}}}\\{\beta _{{\rm{imu}}}}\\{\gamma _{{\rm{imu}}}}\end{array} \right]$

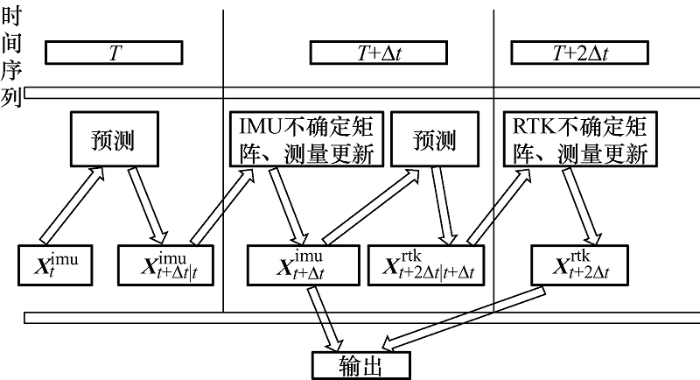
毫米级RTK同样使用上述卡尔曼滤波进行预测和更新,最后因为RTK和IMU的输出频率不同,对其进行融合,其融合流程如图5所示。由此可得可靠性较高的倾斜角度误差值和误差值变化值,并且以此作为PID模糊推理的输入。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5   数据融合流程图


4 液压缸模糊控制算法

4.1 控制策略

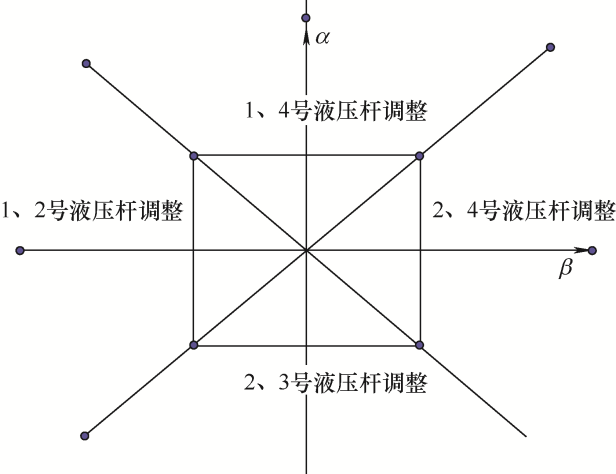
在卡尔曼滤波下从IMU获取α、β作为控制器调平策略选择变量,根据液压杆特性,液压杆若允许下降导致电力塔抖动,使得铁塔造成更大的倾斜,所以液压升塔过程中的液压杆控制策略采取只升不降,并采取追逐最高点调平策略[13]。

如图6所示对四个液压杆分别编号,然后制定如图7所示的液压提升控制策略。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6   四个液压杆编号图


图7

新窗口打开| 下载原图ZIP| 生成PPT

图7   调平控制策略图


4.2 控制算法

模糊控制[14]是一种基于自然语言控制规则、模糊逻辑推理的智能控制技术,不依赖于被控系统的数学模型,而是根据人的控制经验形式化后的模糊规则对其进行模糊推理,得到模糊推理判断,再将其转化为具体数值作为输出量向执行单元发送。

PID控制器因其鲁棒性好、简单、可靠性高,在工业控制中被广泛使用。但常规的PID控制存在其参数整定困难、修改的参数不能自适应调节的缺点,而结合模糊控制和PID控制的优点,能将模糊控制于PID控制融合形成模糊PID控制,对于非线性、具有滞后性的工业控制有较好的控制效果。针对本文中由于液压施压土壤,土壤发生非线性变化后模糊PID控制具有较好的效果。选取杆塔倾斜角度与预设倾斜角度误差E及误差变化率EC作为模糊输入的变量,模糊输出变量ΔKP、ΔKI、ΔKD选为PID的三个参数的修正值。

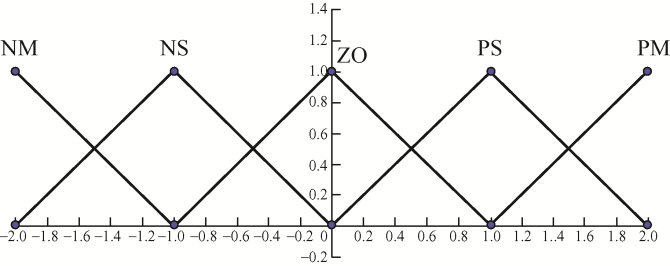
对于杆塔液压调平系统,倾斜角度设定值为0°,采集范围为(-2, 2),其倾斜角度误差值论域为(-2, 2),误差值的变化率论域为(-1, 1),其误差的量化因子为KE=1,误差变化率量化因子为KEC=2,那么可以将误差值和误差变化值的论域划分为5个等级,他们分别为E=EC=[-2, -1, 0, 1, 2],其中将分别用E=EC=[NM, NS, ZO, PS, PM]表示。

结合实际的工程经验和PLC参数设置,ΔKP的取值区间分别为[-2, 2],ΔKI的取值区间分别为[-1.8, 1.8],ΔKD的取值区间分别为[-1.6, 1.6],输出量的量化因子

$\left\{ \begin{array}{l}K(\Delta {K_p}) = 4/10 = 0.4\\K(\Delta {K_I}) = 3.6/10 = 0.36\\K(\Delta {K_D}) = 3.2/10 = 0.32\end{array} \right.$

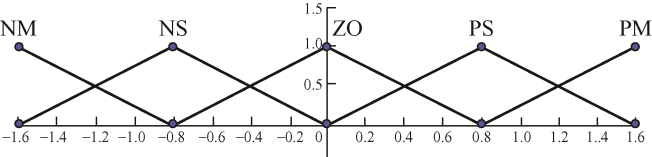
相应输出量的划分为ΔKP=ΔKI=ΔKD=[-4, -2, 0, 2, 4],输出量相对应的模糊子集为ΔKP=ΔKI=ΔKD= [NM, NS, ZO, PS, PM]。

接下来对E、EC、ΔKP、ΔKI、ΔKD的隶属度函数均取三角形。E和EC的隶属度函数如图8所示。ΔKP、ΔKI、ΔKD的隶属度函数如图9所示。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8   E和EC的隶属度函数图像


图9

新窗口打开| 下载原图ZIP| 生成PPT

图9   ΔKP、ΔKI、ΔKD的隶属度函数


根据常规PID控制算法进行控制,表达式为

$u(t) = {K_p}e(t) + {K_I}\int_{\;0}^{\;t} {e(\tau )} d\tau + {K_D}\frac{{de(t)}}{{dt}}$

式中,u(t)是被控制量;e(t)是实际输出值和期望输出值之间误差;KP是比例系数;KI是积分系数;KD是微分系数。PID控制原理是基于系统输出值的反馈控制的,关键是把系统的输出值和期望值的误差作为控制量。其中Kp是直接影响到实际控制效果的,在合理的数值范围内Kp越大,控制效果越好,越短时间回到期望值,但也容易导致抖动,无法稳定于期望值;KD影响的是控制量向期望值靠近时的加速度,即使得靠近期望值的过程相对平滑;而只有KD控制会导致控制量一直与期望保持一个恒量差值[15],再者KI是用来抵消这个恒量的。总结上述整定原则和结合专家实践操作经验总结,可得到下列模糊控制规则,见表1~3。

表1   Kp的规则表

ECE
NMNSZOPSPM
NMPMPMPMPSZO
NSPMPMPMZOZO
ZOPMPSZOPSNS
PSZOZONSPMNS
PMZONSNSPMNM

新窗口打开| 下载CSV


表2   KI的规则表

ECE
NMNSZOPSPM
NMNMNMNMNSZO
NSNMNSNSZOPS
ZONSNSZOPSPS
PSNSZOPSPSPM
PMZOPSNSPMPM

新窗口打开| 下载CSV


表3   KD的规则表

ECE
NMNSZOPSPM
NMNSNSNSZOPS
NSNBNMNSZOPS
ZONMNMNSZOPS
PSNMNSNSZOPS
PMNSNSNSZOPS

新窗口打开| 下载CSV


建立好模糊控制规则表后,可进一步得到模糊关系矩阵R,$R = \mathop \cup \limits_{i = 1}^{25} {R_i}$,总共25条模糊规则,误差取模糊集E,误差变化率取模糊集EC,PID的3个输出控制量由模糊关系合成法则可得到如下推理

$U = (E \times EC) \circ R$

从模糊近似推理模块得到模糊控制量后,对于实际的控制系统必须要对模糊量再转化为清晰量后才能实际对系统实现控制。清晰化的方法有面积均分(中位数)法、重心(面积中心)法等方法。为了简便,本文采用面积中心对输出的模糊控制量进行清晰化处理。具体表示为

$u(\Delta {K_P},\Delta {K_I},\Delta {K_D}) = \frac{{\sum\limits_{i = 1}^{25} {{u_i}} A({u_i})}}{{\sum\limits_{i = 1}^{25} {A({u_i})} }}$

式中,u(ΔKP, ΔKI, ΔKD)为输出精确控制量;A(ui)为出的隶属度;ui为相应的面积。

由此可得到PID具体修正参数,代入修正表达式为

$\left\{ \begin{array}{l}{K_{\rm{p}}} = {K_{\rm{p}}}_{_{\rm{0}}} + \Delta {K_{\rm{p}}}\\{K_{\rm{I}}} = {K_{\rm{I}}}_{_{\rm{0}}} + \Delta {K_{\rm{I}}}\\{K_{\rm{D}}} = {K_{\rm{D}}}_{_{\rm{0}}} + \Delta {K_{\rm{D}}}\end{array} \right.$

式中,KP、KI、KD为PID修正后的参数值;KP0、KI0、KD0为PID参数整定的初始值。

5 试验分析与结果

5.1 试验条件

为了验证以上方法的可行性和有效性,在实验室搭建了液压杆塔调平模型来进行仿真试验。在模型塔顶中搭载IMU传感器和毫米级RTK传感器监测调平过程中杆塔状态,仿真其土壤的下陷情况采用支腿提升压力的时候随机选择支腿根据土壤特性建模的线性函数下降,在这过程中测试了所提出的杆塔调平方案。在试验中记录其调平过程中IMU和RTK信息,对比没有进行卡尔曼滤波和经过卡尔曼滤波的效果,并在实际调平过程要求铁塔倾斜角不可以超过2°,当超过2°后杆塔会因重力影响杆塔发生持续倾斜导致倒塌,所以在控制试验过程中以是否超出该值来判断该方案的可行性。进一步利用常规PID控制算法和模糊PID控制算法对调平控制效果进行对比。

5.2 试验结果分析

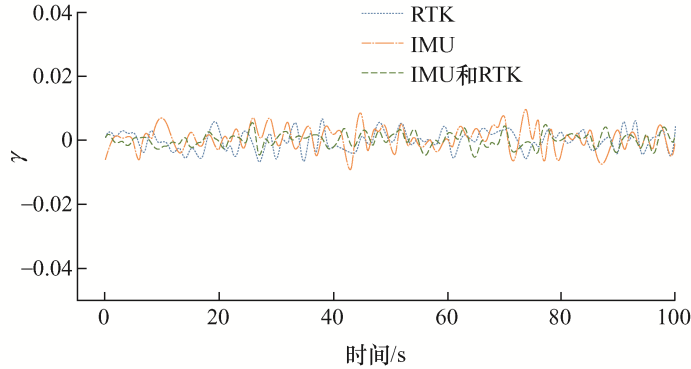
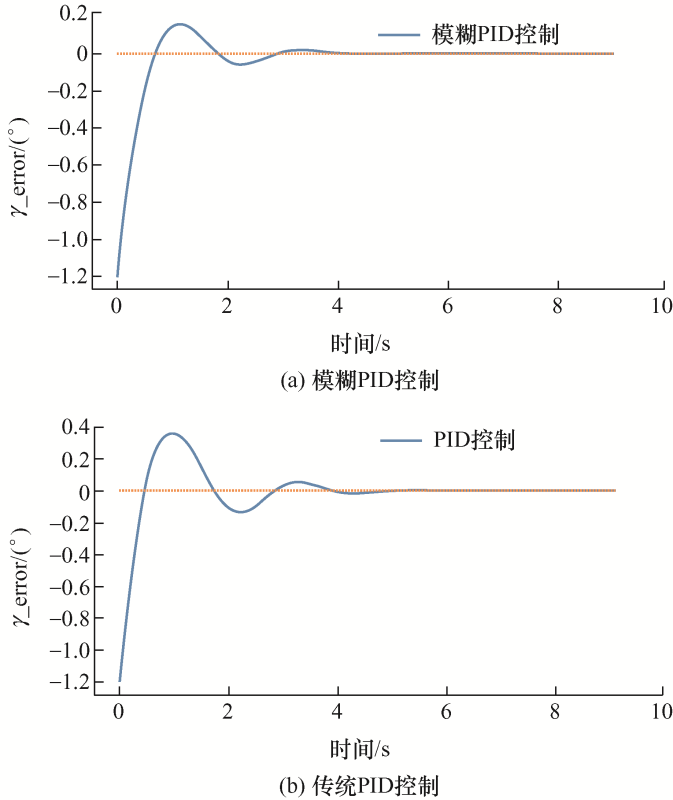
采集IMU传感器的γ的变化曲线和RTK传感器的高度$H'$利用换算公式算得的γRTK,在卡尔曼滤波对二者数据融合效果如图10所示。另外在对塔身调平控制过程中记录了杆塔调平过程中倾斜角误差如图11所示。

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10   γ的三种变化曲线比较


图11

新窗口打开| 下载原图ZIP| 生成PPT

图11   不同控制算法测量下的响应曲线比较


可以看出利用卡尔曼滤波使得传感器返回的数据更加平稳,去噪效果更好,而IMU传感器返回的数据会随着时间误差会逐渐变大,这是由于IMU传感器本身的特性所导致的,所以利用IMU和毫米级RTK传感器进行数据融合,使得IMU传感器本身误差会累积的特性得到很好的消除。

从图11中可以看出在调平过程中,模糊PID控制下和传统PID控制下的倾斜角误差变化曲线之间的差别,模糊PID控制的超调量比PID控制要多,且恢复稳态的时间模糊PID控制也比传统PID控制要快,再者器控制算法能够将倾斜角误差被控制在阈值范围内,说明其控制是有效的,可以得出此升塔控制方案是可行的。

6 结论

(1) 提出了在对受压土壤下陷特性研究基础上对杆塔升塔前的调平工作使用模糊PID控制算法进行控制,在IMU和毫米级RTK的传感器对杆塔调平过程中对倾斜角度进行测量,并且基于卡尔曼滤波算法状态估计,对二者传感器在不同频率上进行数据融合。

(2) 在试验中验证其测量数据在卡尔曼滤波融合下更具鲁棒性。在保证数据真实可靠的前提下,提出以模糊PID控制,根据以往工程经验和专家指导,制定其模糊化策略和清晰化策略,得到相对应的PID控制量,对铁塔的倾斜角度设计了调平控制策略,并在试验中对比传统PID和模糊PID的倾斜角度误差变化,验证了模糊PID控制调平策略的有效性和可行性。

参考文献

李忠信.

带电升塔技术在大房500 kW线路的应用

[J]. 电力建设, 1995, 16(7):28-30,43.

[本文引用: 1]

LI Zhongxin.

Application of live lifting tower technology in 500 kW line of large building

[J]. Power Construction, 1995, 16(7):28-30,43.

[本文引用: 1]

卓高智.

浅论500 kV拉V型直线铁塔整体提升方法

[J]. 广东科技, 2007(11):209-210.

[本文引用: 1]

ZHUO Gaozhi.

Brief discussion on integral lifting method of 500 kV pull V Type straight line tower

[J]. Guangdong Science and Technology, 2007(11):209-210.

[本文引用: 1]

SKELTON H E, ORDE C L.

Lifting of transmission towers under liver line conditions

[J]. IEEE Transactions on Power Apparatus and Systems, 1982, PAS- 101(9):3018-3021.

[本文引用: 1]

房怀英, 杨建红, 吴仕平.

基于模糊PID控制沥青砂浆车液压调平系统

[J]. 长安大学学报, 2011, 31(1):98-101.

[本文引用: 1]

FANG Huaiying, YANG Jianhong, WU Shiping.

Control of hydraulic leveling system of asphalt mortar truck based on mould and PID

[J]. Journal of Chang’an University, 2011, 31(1):98-101.

[本文引用: 1]

王冰.

基于神经网络的车载平台自动调平控制系统的研究

[D]. 哈尔滨:哈尔滨工业大学, 2012.

[本文引用: 1]

WANG Bing.

Research on automatic leveling control system of vehicle platform based on neural network

[D]. Harbin:Harbin Institute of Technology, 2012.

[本文引用: 1]

史海红.

摊铺机模型研制及调平系统神经网络控制技术研究

[D]. 哈尔滨:哈尔滨工业大学, 2006.

[本文引用: 1]

SHI Haihong.

Development of paver model and research on neural network control technology of leveling system

[D]. Harbin:Harbin Institute of Technology, 2006.

[本文引用: 1]

冯仪, 陈柏金.

车载雷达机电式自动调平控制系统

[J]. 华中科技大学学报, 2004(6):66-68,71.

[本文引用: 1]

FENG Yi, CHEN Baijin.

Electromechanical automatic leveling control system for vehicle-mounted radar

[J]. Journal of Huazhong University of Science and Technology, 2004(6):66-68,71.

[本文引用: 1]

冯文选, 马吉胜, 吴大林, 等.

不同条件下土壤压力沉陷关系有限元分析

[J]. 火炮发射与控制学报, 2019, 40(1):53-58.

[本文引用: 1]

FENG Wenxuan, MA Jisheng, WU Dalin, et al.

Finite element analysis of soil pressure-settlement relationship under different conditions

[J]. Journal of Artillery Launch and Control, 2019, 40(1):53-58.

[本文引用: 1]

钟铁.

基于现代统计理论的陆地地震勘探随机噪声特征研究

[D]. 长春:吉林大学, 2016.

[本文引用: 1]

ZHONG Tie.

Study on random noise characteristics of land seismic exploration based on modern statistical theory

[D]. Changchun:Jilin University, 2016.

[本文引用: 1]

周军, 魏国亮, 田昕, 等.

融合UWB和IMU数据的新型室内定位算法

[J]. 小型微型计算机系统, 2021, 42(8):1741-1746.

[本文引用: 1]

ZHOU Jun, WEI Guoliang, TIAN Xin, et al.

A novel indoor location algorithm combining UWB and IMU data

[J]. Journal of Small Microcomputer Systems, 2021, 42(8):1741-1746.

[本文引用: 1]

李睿, 冯庆善, 蔡茂林, 等.

基于多传感器数据融合的长输埋地管道中心线测量

[J]. 石油学报, 2014, 35(5):987-992.

[本文引用: 1]

LI Rui, FENG Qingshan, CAI Maolin, et al.

Measurement of long-distance buried pipeline centerline based on multi-sensor data fusion

[J]. Acta Petrolei Sinica, 2014, 35(5):987-992.

[本文引用: 1]

张新宇.

基于互补滤波的汽车姿态数据采集系统研究

[J]. 电子器件, 2021, 44(4):994-999.

[本文引用: 1]

ZHANG Xinyu.

Research on vehicle attitude data acquisition system based on complementary filter

[J]. Electronic Devices, 2021, 44(4):994-999.

[本文引用: 1]

张毅.

基于液压支腿的电力杆塔自动调平系统研究

[D]. 太原:太原理工大学, 2016.

[本文引用: 1]

ZHANG Yi.

Research on automatic leveling system of electric pole and tower based on hydraulic outrigger

[D]. Taiyuan:Taiyuan University of Technology, 2016.

[本文引用: 1]

杨辉, 严永锋, 陆荣秀.

基于模糊PID控制算法的管廊通风系统设计

[J]. 控制工程, 2019, 26(12):2181-2187.

[本文引用: 1]

YANG Hui, YAN Yongfeng, LU Rongxiu.

Ventilation system design of urban utility tunnel based on fuzzy PID control algorithm

[J]. Control Engineering of China, 2019, 26(12):2181-2187.

[本文引用: 1]

王旭元.

锂电池放电仪器的研究与开发

[D]. 长沙:中南大学, 2010.

[本文引用: 1]

WANG Xuyuan.

Research and development of discharge instrument for lithium battery

[D]. Changsha:Central South University, 2010.

[本文引用: 1]

/

〈 〉