1 引言
移动机器人涉及速度和转向的精确控制,由于反馈误差和机器人运动时扰动等误差的累积,影响执行机构的精确控制。而高效的驱动控制系统能提高机器人的精确性、快速性和稳定性[1]。
控制器的设计,要求响应超调量小,调节时间短,稳态误差小。传统的滞后超前校正,手动调节的PID控制器,不能满足高精度控制的要求。而神经网络、蚁群算法和遗传算法等智能控制策略,使控制系统结构简单,响应速度快,抗干扰能力强,控制精度高,提高了系统的综合能力[2]。
本文针对差速驱动和转向的轮式移动机器人,从永磁无刷直流电机驱动系统出发,基于基本物理定律,根据电机的运行原理,推导出电机数学模型的线性微分方程,在考虑负载的情况下,得到以电压为输入和角速度为输出的电气特性传递函数。从空间向量方程,对系统可控性进行分析,在传统PID控制的基础上,结合粒子群算法和蚁群优化设计,自动调整PID控制参数,并对两种优化设计性能进行分析,为移动机器人速度和转向控制设计了高效和精确的控制系统。
2 永磁无刷直流电机的数学模型
忽略定子谐波磁场在转子中产生的感应电流,同样忽略铁损和杂散损耗;无刷直流电机中不含阻尼绕组[6]。
2.1 电机的数学模型
磁阻不随角度变化,假设电机三相对称,各相自感记为L,互感记为M,L1 = L - M。定子相电流是平衡的,无刷直流电机简化的数学模型表示为
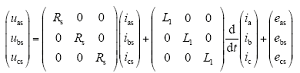
三相定子相绕组Rs相等,反电动势eas、ebs、ecs认为是梯形波,Ep为其峰值。
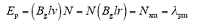
式中,N为每相串联导体数;v为速度;l为导体长度;r为转子外径;Bg为磁通密度。Bglr与φa有相同量纲,与气隙磁通φg成正比,即
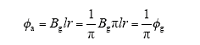
由磁通与每相串联导体数的乘积和磁链有相同的量纲,记为λp。
电磁转矩方程为
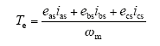
式中,ωm为角速度。
由于反电动势为平顶梯形波,故取fis(θ) ≈ 1。
用转动惯量J、摩擦系数B1和负载转矩T1表示的简单系统中的运动方程为
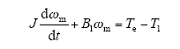
电机中转子速度和位置有如下关系
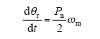
式中,Pn为极数;θr为弧度表示的转子位置。
综上,系统状态空间形式为
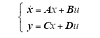
其中 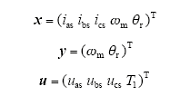
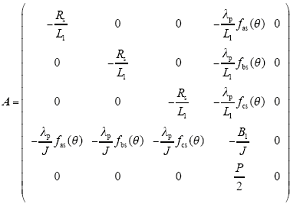
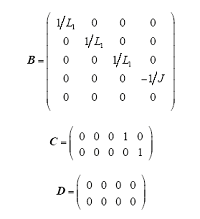
2.2 电机和负载的传递函数
全桥整流运行中,任意时刻电机中只有两相导通,并且这两相是串联的,所以两相电流和电动势在数值上相等,但符号相反[6],即
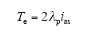
定子电压方程为
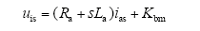
式中,各相反电动势合并成一个常数Kb = 2λp,假定负载转矩与转速成正比,T1 = B1ωm,Bt = 2B1。则传递函数分为速度和相电流、相电流和输入电压之间传递函数,带负载时驱动系统简化的控制框图如图1所示。
图1
可得电机特性的拉普拉斯变换定律中,电压作为输入,转轴速度ω作为输出的开环传递函数为
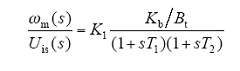
3 电机及驱动系统性能参数
为获得高精度的机器人驱动轮转速控制效果,选用转矩转速特性好,转速范围大,效率高,重量轻的永磁无刷直流电机。经减速器输出至传动轴,直接驱动车轮转速。所选用的永磁无刷直流电机主要性能参数见表1。
表1 永磁无刷直流电机参数
Tab.1
| 参 数 | 数 值 |
|---|---|
| 定子相电阻Rs /Ω | 0.7 |
| 各相自感L/mH | 2.72 |
| 总转动惯量J/kg·m2 | 0.000 2 |
| 各相互感M/mH | 1.5 |
| 电机极数Pn | 4 |
| 转矩常数Kt /(N·m/A) | 0.053 844 |
| 摩擦系数B1 /[N·m/(rad/s)] | 0.002 |
| 感应电动势常数Kb /[V/(rad/s)] | 0.512 8 |
3.1 系统可控性分析
依据电机参数,得到状态空间矩阵,经数学分析计算,得到系统的状态完全可控性矩阵的秩,等于系统的状态变量维数,系统的输出完全可控性矩阵的秩等于系统输出向量y的维数,所以系统可控,因此可以对系统进行控制器设计,使系统稳定。
3.2 设计标准参数
针对无刷直流电机驱动的差速轮式移动机器人,由于机器人的转向和行进速度均由电动机驱动车轮控制,通过改变所施加的输入电压信号,控制旋转轴的角速度,以实现对机器人的控制。控制设计标准按以下方式定义:对于阶跃输入角速度ω(rad/s)的参考角度,仿真机器人的转向,电机转速满足瞬态响应时间t≤0.1s,超调σ≤5%和稳态误差SSE≤0.1%。机器人速度控标准是能平滑跟踪正弦型输入信号。
4 控制器优化设计
PID控制器广泛应用,其一般形式为
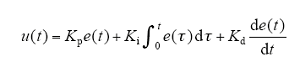
其性能取决于Kp、Ki和Kd 3个参数是否合理,但是目前PID参数主要由人工调整,不仅费时,而且不能保证获得最佳的性能,智能算法中的粒子群算法能自动调整参数,满足设计标准,并且更精确快速。
粒子群算法(Particle Swarm Optimization,PSO)是一种群体智能的优化算法,用位置、速度和适应度指标表示粒子特征,以粒子为桥梁,实现控制与粒子群算法的链接,根据自身和其他粒子的移动经验进行动态调整,用于求解优化问题[7]。
蚁群算法源于对蚂蚁搜索问题的研究,由Dorigo M等人于20世纪90年代提出的一种新型进化算法,具有分布计算群体智能等优势。
根据公式vt+1 = ωvt + c1r1(Pt - xt) + c2r2(Gt - xt),设置粒子群算法惯性因子ω为0.5,加速常数c1、c2均为2,维数为3,粒子群规模为200,编写算法程序,依据粒子群算法和Matlab/Simulink,自动获得了最优的控制器参数:Kp = 294.478 9,Ki = 284.074 8,Kd = 20.003 1。
表2 蚁群优化算法程序参数
Tab.2
| 名 称 | 参 数 |
|---|---|
| 蚂蚁数 | 300 |
| 迭代次数 | 25 |
| α | 0.8 |
| β | 0.2 |
| 蒸发率 | 0.7 |
| 下界 | (0.01).*ones(1,27) |
| 上界 | 10.*ones(1,27) |
| 每个节点的参数 | 10 000 |
以阶跃和正弦的输入信号驱动,根据图3中Simulink部分的仿真框图依次利用上述两组PID参数,仿真机器人位置和速度。
5 仿真结果分析
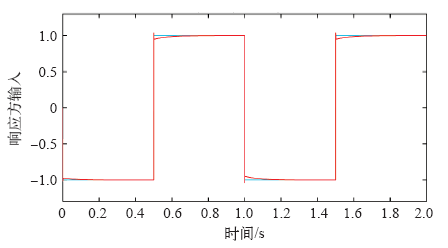
图4
图5
图5
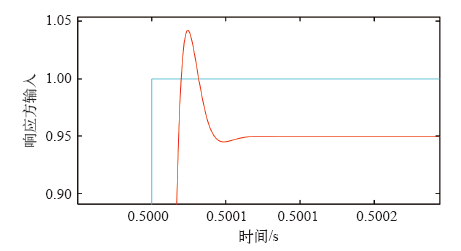
阶跃信号输入与响应图(0.5s 放大)(PSO)
Fig.5
The plot of step signal input and response(0.5s zoom in)(PSO)
阶跃响应参数与设计标准对比见表3,粒子群算法阶跃响应超调量<2.1%,调节时间<0.000 1s,稳态误差为0。蚁群优化算法阶跃响应超调量为0,调节时间,0.15s≤T≤0.3s,稳态误差为0。性能分析表明,基于粒子群算法的控制器,阶跃响应有很高的精确度。控制器的设计瞬态响应时间、超调量和稳态误差完全满足设计标准。蚁群优化的PID控制器,阶跃响应无超调,但调节时间长。
step input
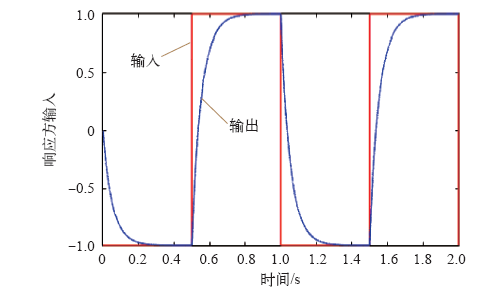
图6
图7
图8
图8
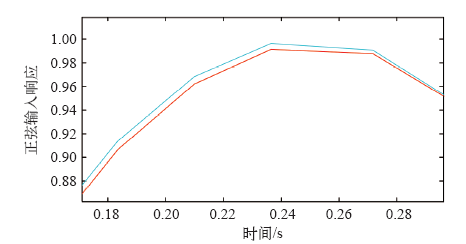
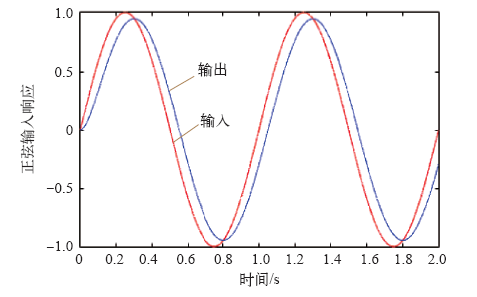
正弦信号输入与响应图(放大)(PSO)
Fig.8
The plot of sine signal input and response (zoom in)(PSO)
图9
图9
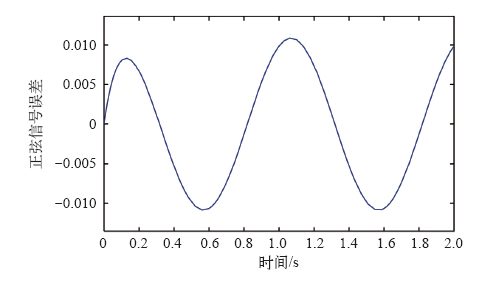
正弦信号控制器响应误差图(PSO)
Fig.9
The plot of error to the controller response for sinusoidal signal input (PSO)
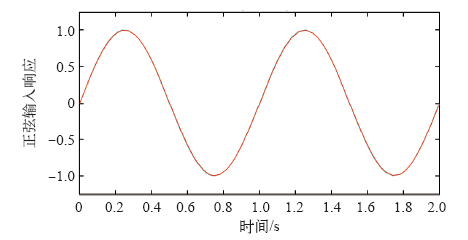
对于蚁群优化PID控制器,正弦信号输入和响应如图10所示。由图可知,系统输入输出误差大,性能差。
图10
两种优化算法分析结果表明,基于粒子群优化的控制系统具有良好的动态和稳态性能,能精确、快速且稳定地控制机器人的转向和速度。
6 结论
由实验表明,基于粒子群算法与蚁群算法优化的PID控制器相比,基于粒子群算法优化的PID控制器,阶跃响应超调量<2.1%,调节时间<0.000 1s,稳态误差为0,系统运行稳定,具有快速的响应速度,对机器人的转向和速度控制性能优良,满足设计标准,系统有良好的动态和稳态性能。采用粒子群智能算法优化设计,自动调整了PID控制参数,节省了时间,而且获得最优的性能,同时验证了该智能优化控制策略的可行性、有效性和优越性。
参考文献
轮式移动机器人电机驱动系统的研究与开发
[J].
Design and research on motor driving system of wheeled mobile robot
[J].
自适应模糊PID智能控制器在无刷直流电机速度控制系统中的应用
[J].
Application study in brushless DC motor speed control system based on intelligent controller of adaptive fuzzy PID
[J].
基于模糊PID算法的轮式移动机器人驱动轮控制器设计
[J].
Controller design of wheeled robot wheel based on algorithm of fuzzy PID
[J].
轮式机器人遗传模糊神经网络转向控制
[J].
Teering control of wheeled mobile robot using GA fuzzy neural network
[J].
Design and simulation of control systems for a field survey mobile robot platform
[J].
PID control system analysis and design
[J].
Kinematics/fuzzy logic combined controller for formation control of mobile robots
[J].
机器人技术研究进展
[J].
Researchprogress on robotics
[J].
四轮全向移动机器人的双闭环速度控制系统设计
[J].
Design of double closed-loop velocity control system for four-wheel omnidirectional mobile robot
[J].