电气工程学报, 2021, 16(4): 59-67 doi: 10.11985/2021.04.008

特邀专栏：高性能永磁电机驱动与控制

位置伺服电机系统的鲁棒性模型预测控制

温从剑,, 王政,, 张子越,

东南大学电气工程学院 南京 210096

Robust Model Predictive Control for Position Servo Motor System

WEN Congjian,, WANG Zheng,, ZHANG Ziyue,

School of Electrical Engineering, Southeast University, Nanjing 210096

收稿日期: 2021-06-30   修回日期: 2021-08-1  

Received: 2021-06-30   Revised: 2021-08-1  

作者简介 About authors

温从剑,男,1995年生,硕士研究生。主要研究方向为电机驱动及控制。E-mail： wcj19951026@163.com

王政,男,1979年生,教授,博士研究生导师。主要研究方向为电机系统及控制、电力电子功率变换、新能源与分布式发电。E-mail： zwang@seu.edu.cn

张子越,男,1998年生,硕士研究生。主要研究方向为电机驱动及控制。E-mail： 1922314678@qq.com

摘要

为提高永磁同步电机位置伺服系统的控制性能,提出一种鲁棒性模型预测直接转速控制(Model predictive direct speed control, MPDSC)策略。首先,介绍一种将有限集MPDSC和两矢量MPDSC相结合的混合MPDSC策略。该控制策略可以在电机稳态和动态运行过程中进行切换。然后,基于滑模控制理论设计一个参数扰动和负载观测器,用于消除电气参数和机械参数不匹配以及负载扰动带来的影响。最后,通过试验对所提控制策略的有效性进行验证。

关键词： 位置伺服系统 ; 模型预测直接转速控制 ; 滑模观测器

Abstract

In order to improve the control performance of permanent magnet synchronous motor position servo system, a robust model predictive direct speed control (MPDSC) strategy is proposed. Firstly, a hybrid MPDSC strategy which combine the finite control set MPDSC and double vector MPDSC strategy is introduced. It can switch between steady and dynamic state of the motor. Then, a parameters disturbance and load observer based on sliding-mode control theory is designed to eliminate the mismatch of electrical and mechanical parameters and the load disturbance. Finally, the experiments are presented to verify the validity of the proposed control schemes.

Keywords： Position servo system ; model predictive direct speed control ; sliding-model observer

PDF (2589KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

温从剑, 王政, 张子越. 位置伺服电机系统的鲁棒性模型预测控制. 电气工程学报[J], 2021, 16(4): 59-67 doi:10.11985/2021.04.008

WEN Congjian, WANG Zheng, ZHANG Ziyue. Robust Model Predictive Control for Position Servo Motor System. Journal of Electrical Engineering[J], 2021, 16(4): 59-67 doi:10.11985/2021.04.008

1 引言

永磁同步电机(Permanent magnet synchronous motor, PMSM)由于具有高功率密度、低转矩脉动和噪声小等特点[1],被广泛地应用于伺服系统中。磁场定向控制和直接转矩控制是PMSM驱动控制中两种常用的策略。然而位置伺服系统对动态性能要求高,这种级联形式的控制器带宽有限。

近些年来,随着数字处理器性能的不断提高,模型预测控制(Model predictive control, MPC)已成为提高系统性能的重要手段。其中,有限集MPC在预测模型的基础上,针对有限的开关状态进行遍历寻优,易于实现且灵活度高[2,3,4]。为了充分发挥MPC的动态性能,已有许多文献针对PMSM提出了模型预测直接转速控制(Model predictive direct speed control, MPDSC)的方法[5,6,7]。与模型预测电流控制和模型预测直接转矩控制相比,MPDSC具有更简单的结构,然而现有文献中很少涉及到基于MPDSC的位置伺服系统的 研究。

与其他形式的MPC相同,MPDSC的控制性能依赖于系统模型,包括电机电气参数、机械参数以及负载转矩[8]。电机电气参数会随电机工况的改变而不断变化,机械参数无法直接通过测量获得,而负载转矩的测量需要额外的装置。为了克服参数不确定带来的影响,对电机的全部参数及负载转矩进行在线的全局辨识是其中一种方法。文献[9]提出一种基于磁链注入的方法,能够实现对电机电气参数的辨识,但是额外的信号注入会影响系统正常的运行状态。文献[10,11]提出一种基于粒子群优化算法的全局参数辨识方法,但是这种生物启发式算法需要对大量数据进行迭代寻优,无法应用于数字处理器中。此外,在位置伺服系统中,电机常处于动态运行状态,在短暂的动态过程中对参数进行辨识仍是当前研究的一个难点。另一种方法是基于观测器[12,13,14]对参数不匹配和负载扰动进行整体补偿。其中,滑模观测器(Sliding-mode observer, SMO)由于具有较强的鲁棒性受到了广泛的关注。文献[13]提出一种SMO,可以对所有电气参数的不匹配进行观测。文献[14]针对变速和变负载条件提出一种SMO,实现对负载转矩的自适应辨识。然而电机参数不匹配和负载扰动通常是同时存在的,两者都会对MPDSC的控制性能造成影响。

本文首先对两电平三相PMSM伺服系统进行建模。在此基础上,设计了PMSM伺服系统MPDSC策略,针对位置伺服系统提出一种结合有限集MPDSC (Finite control set-MPDSC, FCS-MPDSC)和两矢量MPDSC (Double vector-MPDSC, DV-MPDSC)的混合MPDSC策略;然后根据滑模控制理论设计一种参数扰动和负载观测器增强系统的鲁棒性;最后通过试验验证了所提出的混合MPDSC策略的有效性。

2 永磁同步电机数学模型

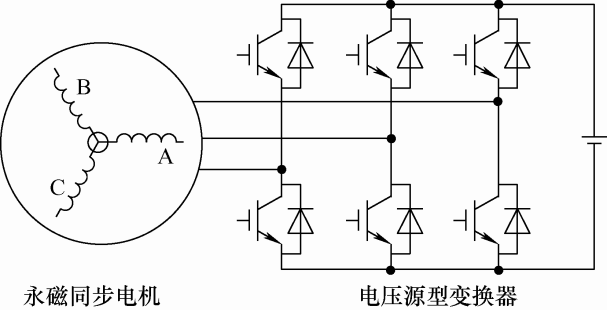
图1为本文研究的基于两电平变换器的三相PMSM伺服系统拓扑结构。在d-q参考坐标系中,定子电压和电磁转矩可以表示为

$\left\{ \begin{array}{l}{u_d} = {R_s}{i_d} + {L_d}\frac{{d{i_d}}}{{dt}} - {\omega _e}{L_q}{i_q}\\ {u_q} = {R_s}{i_q} + {L_q}\frac{{d{i_q}}}{{dt}} + {\omega _e}{L_d}{i_d} + {\omega _e}{\psi _f}\end{array} \right.$
${T_e} = 1.5p\left[ {{\psi _f}{i_q} + \left( {{L_d} - {L_q}} \right){i_d}{i_q}} \right]$

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   基于两电平变换器的三相PMSM伺服系统拓扑结构


式中,ud和uq分别为d、q轴电压,id和iq分别为d、q轴电流;Rs为定子电阻;Ld和Lq分别为d、q轴电感;${\psi _f}$为永磁磁链;ωe为电角速度;Te为电磁转矩;p为极对数。在表贴式PMSM中,有Ld=Lq=L。

PMSM的机械方程可表示为

$\frac{{d{\omega _m}}}{{dt}} = \frac{{{T_e} - {T_l} - B{\omega _m}}}{J}$

式中,ωm为机械角速度;Tl为负载转矩;B为粘滞摩擦因数;J为转动惯量。

3 模型预测直接转速控制

3.1 一拍延时补偿

由于数字控制中存在一拍延时,会对系统控制性能造成影响,需要对其进行补偿。在采样频率足够大的情况下,可采用前向欧拉法将电机电压方程式(1)进行离散化,根据k时刻电压、电流可得k+1时刻的电流为

$\left\{ {\begin{array}{*{20}{l}} \begin{array}{l} {i_d}(k + 1) = \left[ {{u_d}(k) + {\omega _e}(t)L{i_q}(k)} \right]\frac{{{T_s}}}{L} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {1 - \frac{{{R_s}}}{L}{T_s}} \right){i_d}(k) \end{array}\\ \begin{array}{l} {i_q}(k + 1) = \left\{ {{u_q}(k) - {\omega _e}(t)\left[ {L{i_q}(k) + {\psi _f}} \right]} \right\}\frac{{{T_s}}}{L} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {1 - \frac{{{R_s}}}{L}{T_s}} \right){i_q}(k) \end{array} \end{array}} \right.$

式中,Ts为采样周期;ωe(t)为t时刻的电角速度。

将式(4)代入电压离散方程,可得k+1时刻的电压方程

$\left\{ {\begin{array}{*{20}{c}} \begin{array}{l} {u_d}(k + 1) = \frac{L}{{{T_s}}}{i_d}(k + 2) + \left( {{R_s} - \frac{L}{{{T_s}}}} \right){i_d}(k + 1) - \\ {\rm{ }}\;\;\;\;\;\;\;{\omega _e}(t)L{i_q}(k + 1) \end{array}\\ \begin{array}{l} {u_q}(k + 1 = \frac{L}{{{T_s}}}{i_q}(k + 2) + \left( {{R_s} - \frac{L}{{{T_s}}}} \right){i_q}(k + 1) + \\ {\rm{ }}\;\;\;{\omega _e}(t)\left[ {L{i_d}(k + 1) + {\psi _f}} \right] \end{array} \end{array}} \right.$

3.2 参考电压计算

将式(2)代入式(3)并将其离散化可得t+1时刻的电机转速

$\begin{array}{c}{\omega _m}(t + 1) = {\omega _m}(t) + \frac{{{T_{sp}}}}{J}\left[ {1.5p{\psi _f}{i_q}(k + 2) - {T_l}} \right] - \\\frac{{B{T_{sp}}}}{J}{\omega _m}(t)\end{array}$

由于电机机械时间常数远大于电气时间常数,转速采样周期Tsp通常比采样周期Ts大。本文中Tsp=10Ts。

为了跟随下一时刻的参考转速,采用无差拍控制的方法,将式(6)中ωm(t+1)用$\omega _m^*$表示,iq(k+2)用$i_q^*$表示,则q轴电流的参考值可以表示为

$i_q^* = \frac{2}{{3p{\psi _f}}}\left\{ {\frac{J}{{{T_{sp}}}}\left[ {\omega _m^* - {\omega _m}(t)} \right] + {T_l} + B{\omega _m}(t)} \right\}$

采用同样的方法,将式(5)中的id(k+2)和iq(k+2)用$i_d^*$和$i_q^*$表示,可得k+1时刻的参考电压

$\left\{ {\begin{array}{*{20}{l}} {u_d^* = \frac{L}{{{T_s}}}i_d^* + \left( {{R_s} - \frac{L}{{{T_s}}}} \right){i_d}(k + 1) - {\omega _e}(t)L{i_q}(k + 1)}\\ \begin{array}{l} u_q^* = \frac{L}{{{T_s}}}i_q^* + \left( {{R_s} - \frac{L}{{{T_s}}}} \right){i_q}(k + 1) + {\omega _e}(t)L{i_d}(k + 1) + \\ \;\;\;\;\;\;\;{\omega _e}(t){\psi _f} \end{array} \end{array}} \right.$

本文采用$i_d^* = 0$的控制方法。

3.3 价值函数

在FCS-MPDSC中,价值函数由两个部分组成。第一部分为跟踪误差,如式(9)所示。由于参考电压中包含了参考转速与参考电流的信息,因此可以通过一个价值函数实现对转速和电流的跟踪。

${J_T} = {\left( {u_d^* - {u_d}} \right)^2} + {\left( {u_q^* - {u_q}} \right)^2}$

第二部分为控制约束。本文采用软约束的方法,控制器会尽可能满足约束,但允许违反约束的行为发生。电流约束可以表示为

${J_{L1}} = {\left( {{I_{\max }} - \sqrt {{i_d}^2 + {i_q}^2} } \right)^2}$

式中,Imax为变换器和电机允许通过的最大电流值。

由于在位置伺服系统中,电机会运行在高速状态,此时必须对电压限制进行考虑

${J_{L2}} = {\left( {\sqrt {{{(L{i_q})}^2} + {{(L{i_d} + {\psi _f})}^2}} - \frac{{{U_{dc}}}}{{\sqrt 3 \left| {{\omega _e}} \right|}}} \right)^2}$

式中,Udc为直流母线电压。

当6个有效开关矢量中存在满足控制约束的开关矢量,此时仅对满足约束的开关矢量进行遍历,价值函数仅包含跟踪误差,即

$J = {J_T}$

当6个有效开关矢量均不满足其中一个和两个控制约束,需要对违反约束的行为进行惩罚,此时根据新的价值函数选取最优开关矢量

$J = {J_T} + {\lambda _L}\left( {{J_{L1}} + {J_{L2}}} \right)$

式中,λL为控制约束项的权重系数。由于只允许违反约束的行为短时间地出现,因此λL通常选取一个较大值,使得控制约束在价值函数中所占比例远大于跟踪误差。本文λL选取105。

3.4 混合MPDSC策略

在位置伺服系统中,电机会在动态和稳态工作之间不断进行切换。FCS-MPDSC具有更快的动态响应,但稳态时电流纹波较大。为了在实现快速动态响应的同时优化电流纹波,本文将FCS-MPDSC和DV-MPDSC相结合,在动态情况下采用FCS-MPDSC策略,稳态情况下采用DV-MPDSC策略。两种控制策略切换原则如下所示

$\left\{ \begin{array}{l}\left| {\omega _m^*\left( k \right) - {\omega _m}\left( k \right)} \right| < {\omega _1}\\\left| {\omega _m^*\left( k \right) - \omega _m^*\left( {k - 1} \right)} \right| < {\omega _2}\end{array} \right.$

当电机转速满足式(14)的两个不等式时,可以判断此时电机处于稳态,否则电机处于动态。式(14)中,ω1为参考转速与实际转速差值绝对值的阈值,通常设为稳态时转速波动的10倍以上,防止稳态时转速出现少许波动引起误切换;ω2为k时刻与k-1时刻参考转速差值绝对值的阈值,通常选取的数值与稳态时转速波动为同一数量级,当系统由稳态向暂态过渡时,由于参考转速发生了变化,控制器能及时对电机运行状态进行判断并快速做出反应。

DV-MPDSC策略的实现分为两步,第一步根据FCS-MPDSC策略选择最优开关矢量,第二步将其与零矢量进行合成[15]。

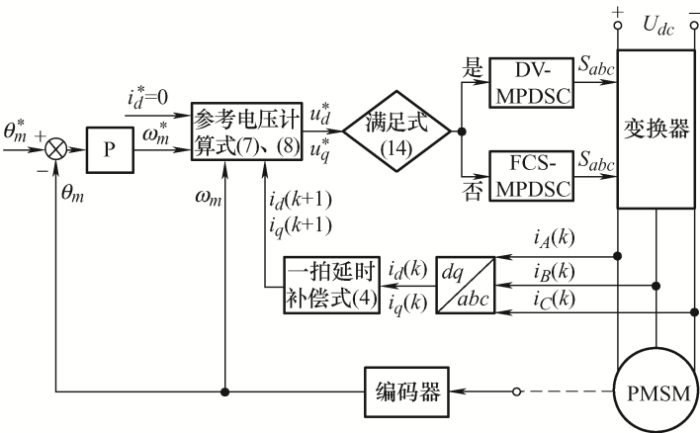
图2为基于混合MPDSC策略的PMSM位置伺服系统控制框图,具体步骤如下。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   基于混合MPDSC策略的PMSM位置伺服系统控制框图


(1) 根据式(4)对控制器一拍延时进行补偿。

(2) 根据式(7)和式(8)计算参考电压。

(3) 根据式(14)判断电机运行状态,确定所采用的控制策略。

(4) 判断开关状态是否满足控制约束,确定价值函数并筛选出最优开关矢量。

(5) 设置下一周期的开关矢量或开关矢量组合并返回步骤(1)。

4 参数扰动和负载转矩观测器

为了提高MPDSC的鲁棒性,本文基于滑模控制理论设计了一种参数扰动和负载观测器。

考虑到系统参数不匹配及负载扰动时,d、q轴参考电压方程和q轴参考电流方程如式(15)所示

$\left\{ {\begin{array}{*{20}{l}} \begin{array}{l} {u_d}(k) = \frac{L}{{{T_s}}}{i_d}(k + 1) + \left( {{R_s} - \frac{L}{{{T_s}}}} \right){i_d}(k) - \\ {\rm{ }}\;\;\;{\rm{ }}{\omega _e}(t)L{i_q}(k) + {f_d}(k) \end{array}\\ {\frac{{{f_d}(k + 1) - {f_d}(k)}}{{{T_s}}} = {F_d}}\\ \begin{array}{l} {u_q}(k) = \frac{L}{{{T_s}}}{i_q}(k + 1) + \left( {{R_s} - \frac{L}{{{T_s}}}} \right){i_q}(k) + \\ {\rm{ }}{\omega _e}(t)\left[ {L{i_d}(k) + {\psi _f}} \right] + {f_q}(k) \end{array}\\ {\frac{{{f_q}(k + 1) - {f_q}(k)}}{{{T_s}}} = {F_q}}\\ \begin{array}{l} {i_q}(k + 1) = \frac{{2J}}{{3p{\psi _f}{T_{sp}}}}\left[ {{\omega _m}(t + 1) - {\omega _m}(t)} \right] + \\ \;\;\;\;\;\;\;\;\;\;\;\frac{{2\left[ {{T_l} + B{\omega _m}(t)} \right]}}{{3p{\psi _f}}} + {f_\omega }(k) \end{array}\\ {\frac{{{f_\omega }(k + 1) - {f_\omega }(k)}}{{{T_{sp}}}} = {F_\omega }} \end{array}} \right.$

式中,fd、fq和fω表示参数不匹配和负载的扰动总 和,Fd、Fq和Fω表示扰动变化率。

根据式(15)可以得到如下所示的参数扰动和负载转矩观测器

$\left\{ {\begin{array}{*{20}{l}} \begin{array}{l} {u_d}(k) = \frac{L}{{{T_s}}}\mathop {{i_d}(k + 1)}\limits^ \wedge + \left( {{R_s} - \frac{L}{{{T_s}}}} \right)\mathop {{i_d}(k)}\limits^ \wedge - \\ {\rm{ }}{\omega _e}(t)L{i_q}(k) + \mathop {{f_d}(k)}\limits^ \wedge + {u_{dsmo}} \end{array}\\ {\frac{{\mathop {{f_d}(k + 1)}\limits^ \wedge - \mathop {{f_d}(k)}\limits^ \wedge }}{{{T_s}}} = {\lambda _d}{u_{dsmo}}}\\ \begin{array}{l} {u_q}(k) = \frac{L}{{{T_s}}}\mathop {{i_q}(k + 1)}\limits^ \wedge + \left( {{R_s} - \frac{L}{{{T_s}}}} \right)\mathop {{i_q}(k)}\limits^ \wedge + \\ \;\;\;\;{\omega _e}(t)\left[ {L{i_d}(k) + {\psi _f}} \right] + \mathop {{f_q}(k)}\limits^ \wedge + {u_{qsmo}} \end{array}\\ {\frac{{\mathop {{f_q}(k + 1)}\limits^ \wedge - \mathop {{f_q}(k)}\limits^ \wedge }}{{{T_s}}} = {\lambda _q}{u_{qsmo}}}\\ \begin{array}{l} {i_q}(k + 1) = \frac{{2J}}{{3p{\psi _f}{T_{sp}}}}\left[ {\mathop {{\omega _m}(t + 1)}\limits^ \wedge - \mathop {{\omega _m}(t)}\limits^ \wedge } \right] + \\ {\rm{ }}\frac{{2\left[ {{T_l} + B\mathop {{\omega _m}(t)}\limits^ \wedge } \right]}}{{3p{\psi _f}}}{\rm{ + }}\mathop {{f_\omega }(k)}\limits^ \wedge + {u_{\omega smo}} \end{array}\\ {\frac{{\mathop {{f_\omega }(k + 1)}\limits^ \wedge - \mathop {{f_\omega }(k)}\limits^ \wedge }}{{{T_{sp}}}} = {\lambda _\omega }{u_{\omega smo}}} \end{array}} \right.$

式中,$\mathop {{i_d}}\limits^ \wedge$和$\mathop {{i_q}}\limits^ \wedge$分别表示d、q轴电流的估计值;$\mathop {{\omega _m}}\limits^ \wedge$表示电机转速的估计值;$\mathop {{f_d}}\limits^ \wedge$、$\mathop {{f_q}}\limits^ \wedge$和$\mathop {{f_\omega }}\limits^ \wedge$分别表示fd、fq和fω的估计值;λd、λq和λω为滑模参数;udsmo、uqsmo和uωsmo为滑模控制函数。

分别定义滑模面和滑模趋近率如下

$\left\{ \begin{array}{l}{S_d} = \mathop {{i_d}}\limits^ \wedge - {i_d}\\{S_q} = \mathop {{i_q}}\limits^ \wedge - {i_q}\\{S_\omega } = \mathop {{\omega _m}}\limits^ \wedge - {\omega _m}\end{array} \right.$
$\left\{ {\begin{array}{*{20}{c}}{\frac{{d{S_d}}}{{dt}} = - {\beta _d}\left| {{S_d}} \right|sign({S_d})}\\{\frac{{d{S_q}}}{{dt}} = - {\beta _q}\left| {{S_q}} \right|sign({S_q})}\\{\frac{{d{S_\omega }}}{{dt}} = - {\beta _\omega }\left| {{S_\omega }} \right|sign({S_\omega })}\end{array}} \right.$

式中,βd、βq和βω为趋近率参数,sign( )表示符号函数。

可以推导出滑模控制函数表达如下

$\left\{ {\begin{array}{*{20}{l}} {{u_{dsmo}}{\rm{ = }}L{\beta _d}\left| {{S_d}{\rm{(}}k)} \right|sign\left( {{S_d}{\rm{(}}k)} \right) - {R_s}{S_d}(k)}\\ {{u_{qsmo}} = L{\beta _q}\left| {{S_q}{\rm{(}}k)} \right|sign\left( {{S_q}{\rm{(}}k)} \right) - {R_s}{S_q}(k)}\\ \begin{array}{l} {u_{\omega smo}} = \frac{{2J}}{{3p{\psi _f}}}\left[ {{\beta _\omega }\left| {{S_\omega }{\rm{(}}k)} \right|sign\left( {{S_\omega }{\rm{(}}k)} \right)} \right] - \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{2B{S_\omega }(k)}}{{3p{\psi _f}}} \end{array} \end{array}} \right.$

最终,参数扰动和负载转矩观测器可表示为如下形式

$\left\{ {\begin{array}{*{20}{l}} \begin{array}{l} \mathop {{i_d}(k + 1)}\limits^ \wedge = \frac{{{T_s}}}{L}\left[ {{u_d}(k){\rm{ + }}{\omega _e}(t)L{i_q}(k) - \mathop {{f_d}(k)}\limits^ \wedge } \right] - \\ {\rm{ }}\frac{{{T_s}}}{L}{u_{dsmo}}{\rm{ + }}\left( {1 - \frac{{{R_s}{T_s}}}{L}} \right)\mathop {{i_d}(k)}\limits^ \wedge \end{array}\\ {\mathop {{f_d}(k + 1)}\limits^ \wedge = {\lambda _d}{u_{dsmo}}{T_s} + \mathop {{f_d}(k)}\limits^ \wedge }\\ \begin{array}{l} \mathop {{i_q}(k + 1)}\limits^ \wedge = \frac{{{T_s}}}{L}\left\{ {{u_q}(k) - {\omega _e}(t)\left[ {L{i_d}(k) + {\psi _f}} \right]} \right\} - \\ {\rm{ }}\;\;\;\;\;\;\;\;{\rm{}}\frac{{{T_s}}}{L}\left[ {\mathop {{f_q}(k)}\limits^ \wedge + {u_{qsmo}}} \right] + \left( {1 - \frac{{{R_s}{T_s}}}{L}} \right)\mathop {{i_q}(k)}\limits^ \wedge \end{array}\\ {\mathop {{f_q}(k + 1)}\limits^ \wedge = {\lambda _q}{u_{qsmo}}{T_s} + \mathop {{f_q}(k)}\limits^ \wedge }\\ \begin{array}{l} \mathop {{\omega _m}(t + 1)}\limits^ \wedge = \frac{{3p{\psi _f}{T_{sp}}\left[ {\mathop {{i_q}(k + 1)}\limits^ \wedge - \mathop {{f_\omega }(k)}\limits^ \wedge - {u_{\omega smo}}} \right]}}{{2J}} - \\ {\rm{ }}\frac{{{T_{sp}}\left[ {{T_l} + B\mathop {{\omega _m}(t)}\limits^ \wedge } \right]}}{J} + \mathop {{\omega _m}(t)}\limits^ \wedge \end{array}\\ {\mathop {{f_\omega }(k + 1)}\limits^ \wedge = {\lambda _\omega }{u_{\omega smo}}{T_{sp}} + \mathop {{f_\omega }(k)}\limits^ \wedge } \end{array}} \right.$

根据上述参数扰动和负载转矩观测器可以对q轴参考电流和参考电压进行实时补偿。补偿后的q轴参考电流和参考电压如下所示

$\left\{ {\begin{array}{*{20}{l}} \begin{array}{l} \mathop {i_q^*}\limits^ \wedge = \frac{{2J}}{{3p{\psi _f}{T_{sp}}}}\left( {\omega _m^* - \mathop {{\omega _m}(t)}\limits^ \wedge } \right) + \mathop {{\rm{ }}{f_\omega }(k + 1) \times \;\;}\limits^{ \wedge \;\;\;\;\;\;\;\;} \\ \;\;\;\;\;\;\frac{{2\left( {{T_l} + B\mathop {{\omega _m}(t)}\limits^ \wedge } \right)}}{{3p{\psi _f}}} \end{array}\\ \begin{array}{l} \mathop {u_d^*}\limits^ \wedge = \frac{L}{{{T_s}}}i_d^* + ({R_s} - \frac{L}{{{T_s}}})\mathop {{i_d}(k + 1)}\limits^ \wedge + \mathop {{\rm{ }}{f_d}(k + 1)}\limits^ \wedge - \\ {\rm{ }}\;\;\mathop {\;{\omega _e}(t)}\limits^{\;\;\;\;\;\;\;\;\;\; \wedge } L\mathop {{i_q}(k + 1)}\limits^ \wedge \end{array}\\ \begin{array}{l} \mathop {u_q^*}\limits^ \wedge = \frac{L}{{{T_s}}}\mathop {i_q^*}\limits^ \wedge + ({R_s} - \frac{L}{{{T_s}}})\mathop {{i_q}(k + 1)}\limits^ \wedge + \mathop {{f_q}(k + 1)}\limits^ \wedge + \\ \mathop {{\rm{ }}\;{\omega _e}(t)}\limits^{\;\;\;\;\;\;\;\;\;\;\; \wedge } \left( {L\mathop {{i_d}(k + 1)}\limits^ \wedge + {\psi _f}} \right)\\ {\rm{ }} \end{array} \end{array}} \right.$

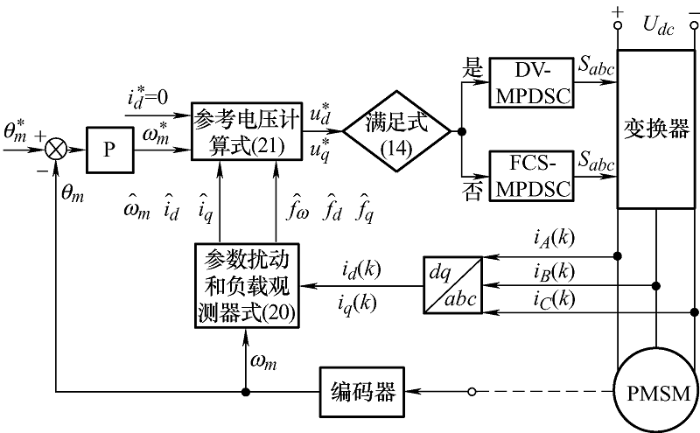
图3为基于参数扰动和负载观测器的PMSM位置伺服系统混合MPDSC策略的控制框图。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   基于参数扰动和负载观测器的PMSM位置伺服系统混合MPDSC策略控制框图


为了保证所设计SMO的稳定性,根据滑模稳定条件,李雅普诺夫函数V=1/2S2的导数需要保持为负数,即

$\mathop V\limits^ = S \cdot \frac{{dS}}{{dt}} < 0$

根据式(15)、式(16)和式(22)可推导出如下关系式

$\left\{ {\begin{array}{*{20}{c}}{{\beta _d} > \left| {\frac{{{e_{fd}}}}{{L \cdot {S_d}}}} \right|}\\{{\beta _q} > \left| {\frac{{{e_{fq}}}}{{L \cdot {S_q}}}} \right|}\\{{\beta _\omega } > \left| {\frac{{{e_{f\omega }}}}{{L \cdot {S_\omega }}}} \right|}\end{array}} \right.$
$\left\{ {\begin{array}{*{20}{l}}{{e_{fd}} = \exp \left( { - {\lambda _d}t} \right)\left( {{C_d} + \int {{F_d} \cdot \exp \left( {{\lambda _d}t} \right)dt} } \right)}\\{{e_{fq}} = \exp \left( { - {\lambda _q}t} \right)\left( {{C_q} + \int {{F_d} \cdot \exp \left( {{\lambda _q}t} \right)dt} } \right)}\\{{e_{f\omega }} = \exp \left( { - {\lambda _\omega }t} \right)\left( {{C_\omega } + \int {{F_\omega } \cdot \exp \left( {{\lambda _\omega }t} \right)dt} } \right)}\end{array}} \right.$

式中,Cd、Cq和Cω为恒定值;efd、efq和efω为扰动项估计值和实际值的误差。为了使efd、efq和efω收敛到零,λd、λq和λω显然须为正值。因此,当βd、βq和βω满足式(23)且λd、λq和λω为正值时,SMO是稳定的。

5 试验结果

为了验证本文所提出的控制策略,搭建了两电平三相PMSM试验平台。伺服电机系统的试验参数如表1所示。

表1   试验参数

参数数值参数数值
直流电压Udc/V100极对数p4
电感L/mH4.83永磁磁链ψf/Wb0.075
定子电阻Rs/Ω1.175转动惯量J/(kg·m2)0.000 029
最大电流Imax/A1.6采样频率fs/kHz20
权重系数λL105转速阈值ω1/(rad/s)3
转速阈值ω2/(rad/s)0.1

新窗口打开| 下载CSV


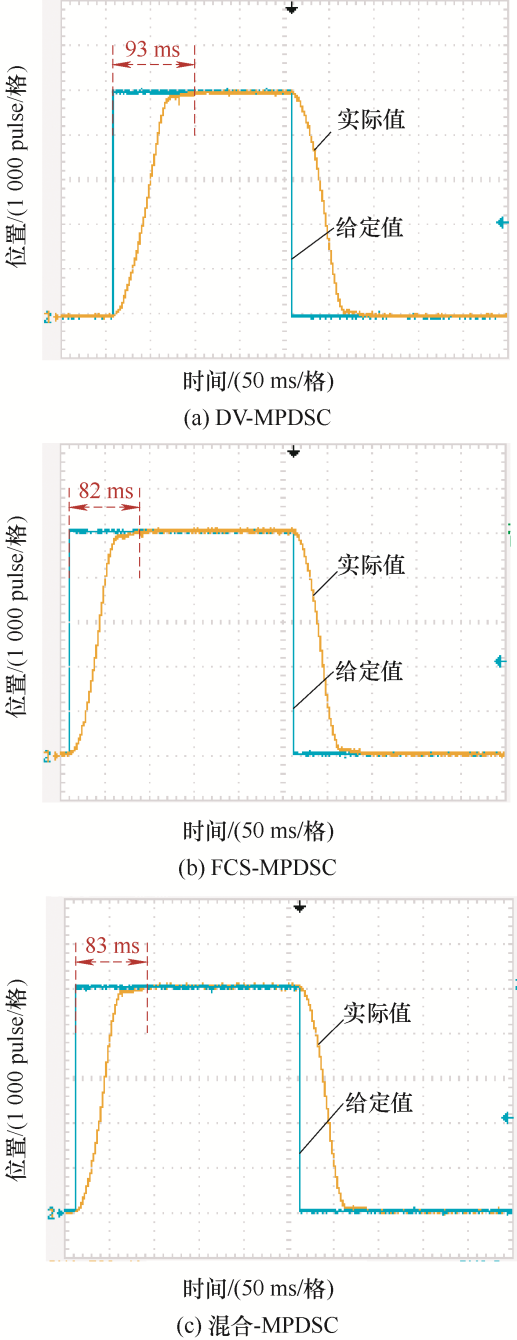
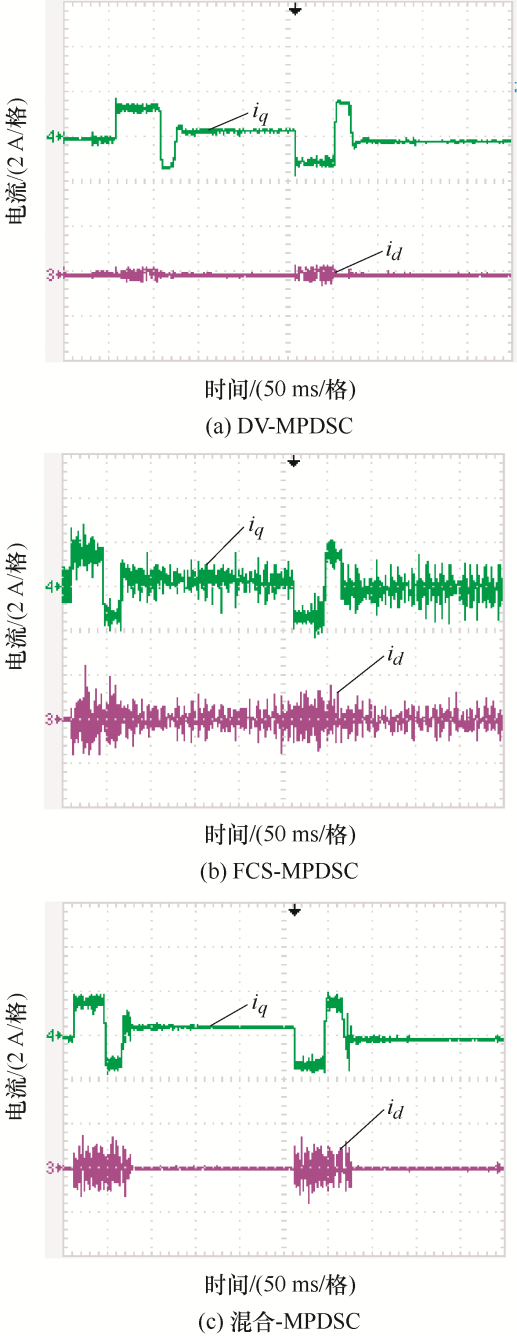
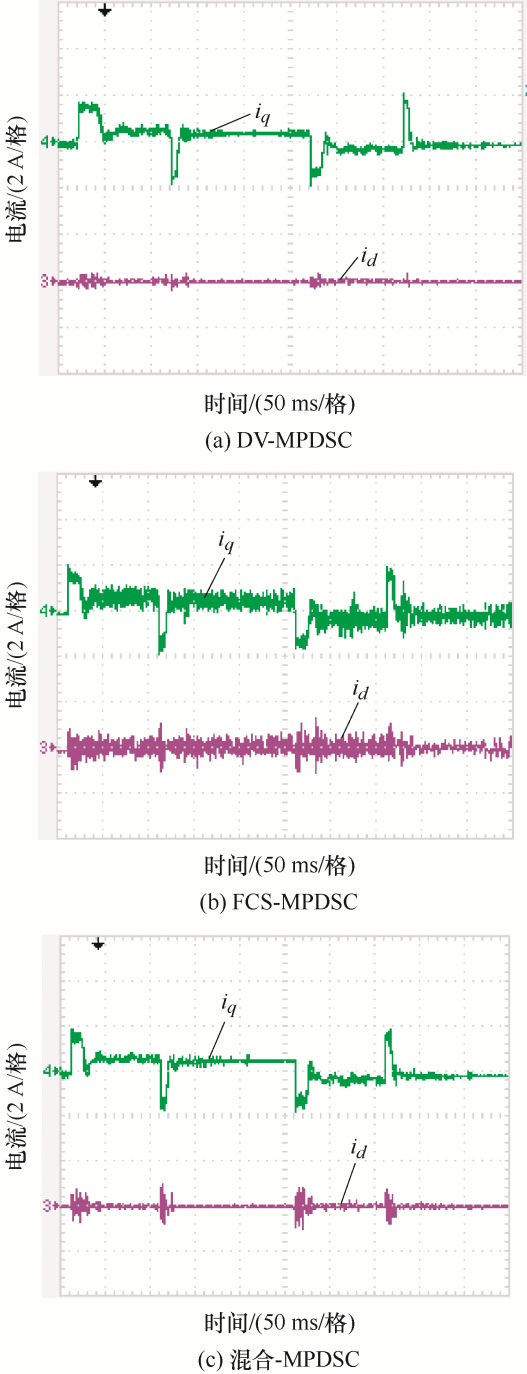
图4和图5所示为给定阶跃位置信号下系统位置跟随波形和d、q轴电流波形,采用DV-MPDSC策略时,到达给定位置的时间约为93 ms,此时电流纹波较小。采用FCS-MPDSC策略时,到达给定位置的时间约为82 ms,相较于DV-MPDSC动态响应更快,但电流控制效果不佳。采用混合MPDSC策略时,到达给定位置的时间与采用FCS-MPDSC策略时几乎一致,约为83 ms,并且稳态情况下电流控制效果与DV-MPDSC一致。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   给定阶跃信号的试验波形


图5

新窗口打开| 下载原图ZIP| 生成PPT

图5   给定阶跃信号的d轴和q轴电流波形


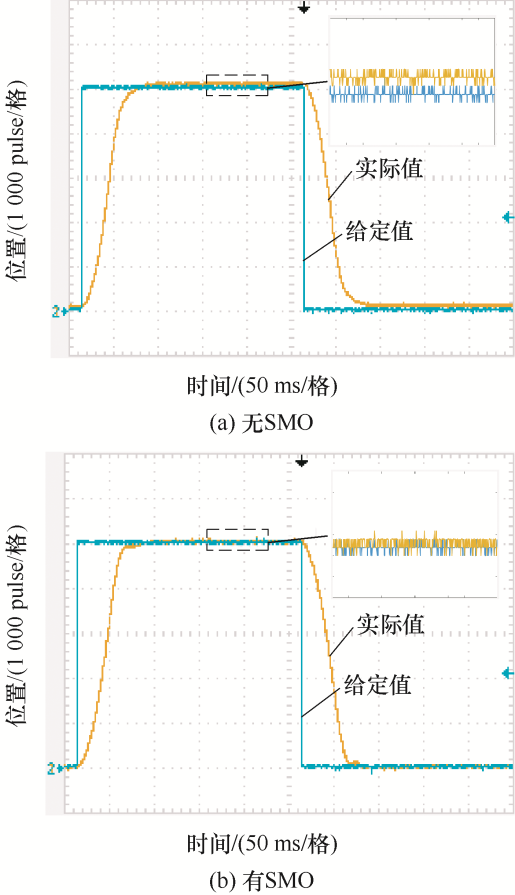
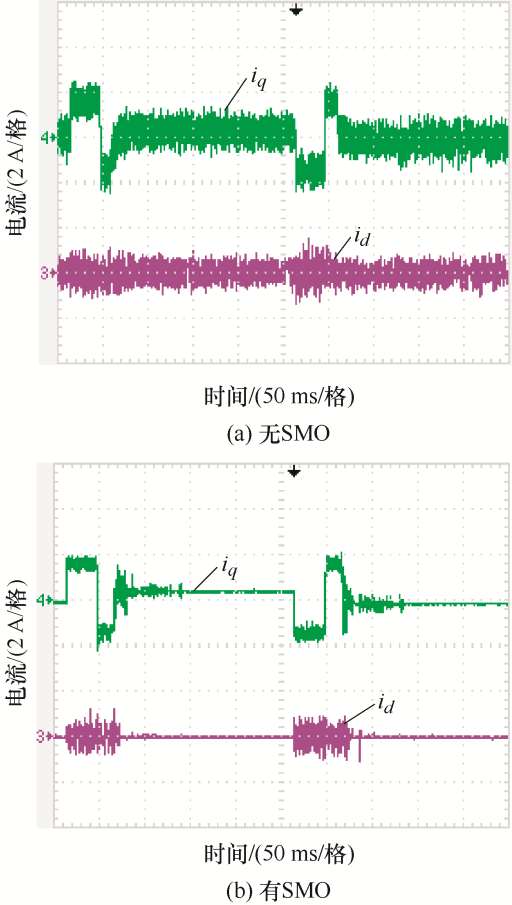
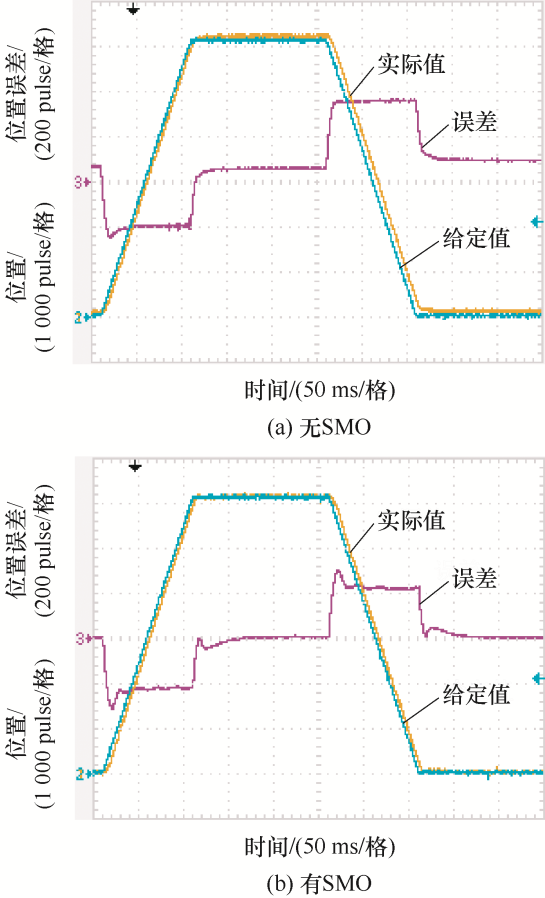
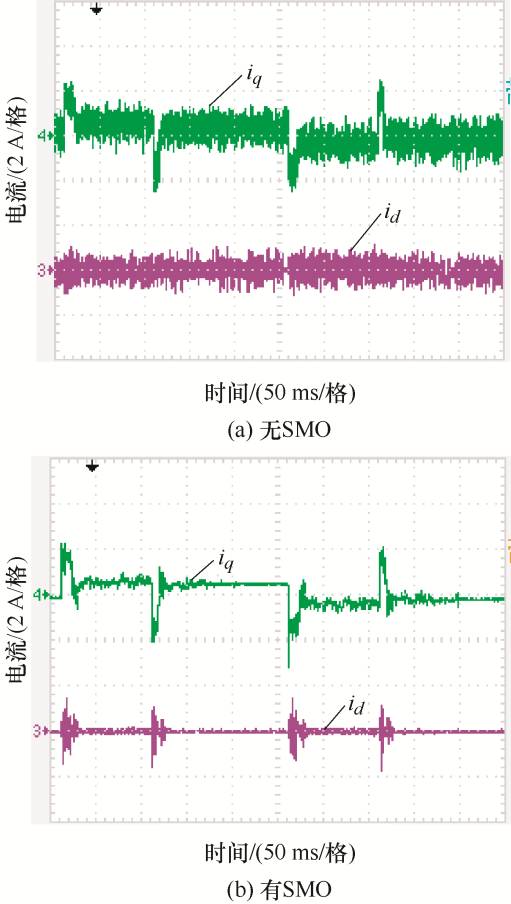
图6和图7所示为采用混合MPDSC策略时,系统在电机参数和负载信息不匹配情况下阶跃位置信号跟随波形和d、q轴电流波形。其中,控制程序中电感、电阻、永磁磁链和转动惯量的给定值均为电机标定参数值的两倍,负载转矩给定值为1 N·m,实际系统为空载。由图6a和图7a可以看出,在没有加入SMO的情况下,由于控制程序中负载转矩值与实际值不符,系统实际位置与给定位置存在60脉冲的误差,并且由于控制程序中电机参数值与系统实际值不匹配,d、q轴电流纹波增大。由图6b和图7b可以看出,在加入SMO后,系统实际位置与给定位置之间的误差得到了消除,并且d、q轴电流纹波明显减小。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6   参数不匹配情况下给定阶跃信号的试验波形


图7

新窗口打开| 下载原图ZIP| 生成PPT

图7   参数不匹配情况下给定阶跃信号的d轴和q轴电流波形


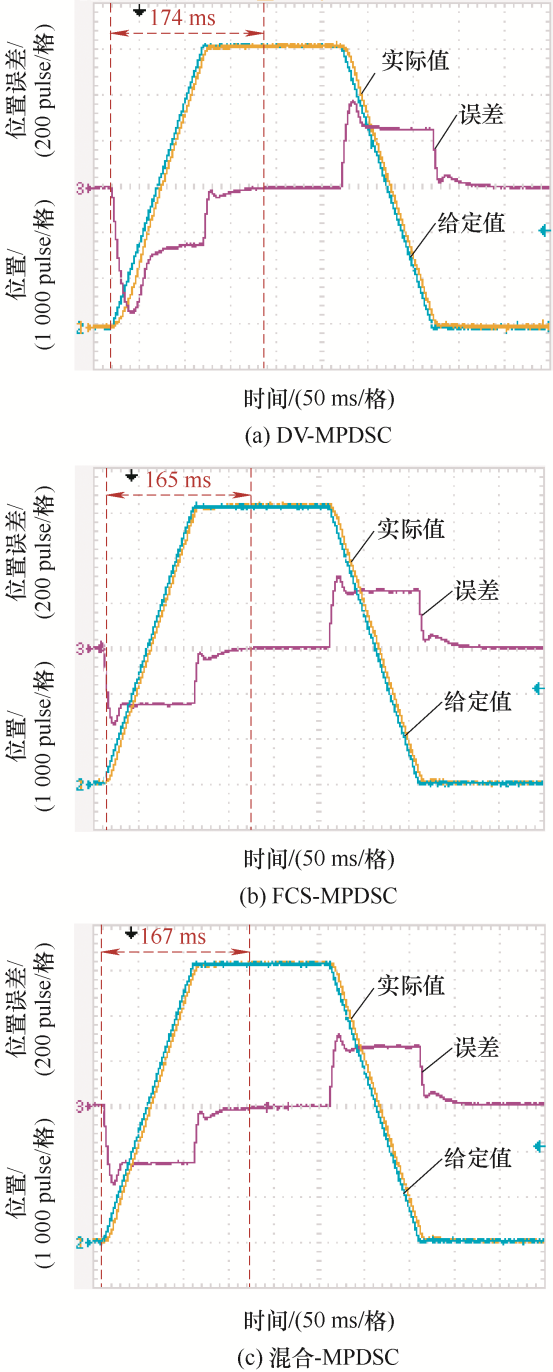
图8和图9所示为给定斜坡位置信号下系统位置跟随波形和d、q轴电流波形。采用DV-MPDSC策略时,系统到达给定位置的时间约为174 ms,位置上升阶段最大跟随误差和最小跟随误差分别为566脉冲和256脉冲,此时电流纹波较小。采用FCS-MPDSC策略时,系统到达给定位置的时间约为165 ms,位置上升阶段最大跟随误差和最小跟随误差分别为343脉冲和251脉冲,相较于采用DV-MPDSC策略具有更好的跟踪效果,但此时电流控制效果不佳。采用混合MPDSC策略时,系统到达给定位置的时间约为167 ms,位置上升阶段最大跟随误差和最小跟随误差分别为350脉冲和252脉冲,位置跟踪效果与采用FCS-MPDSC策略时相近,并且稳态情况下电流控制效果与DV-MPDSC一致。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8   给定斜坡信号的试验波形


图9

新窗口打开| 下载原图ZIP| 生成PPT

图9   给定斜坡信号的d轴和q轴电流波形


图10和图11所示为采用混合MPDSC策略时,系统在电机参数和负载信息不匹配情况下斜坡位置信号跟随波形和d、q轴电流波形。控制程序电机参数给定值为标定值的两倍,负载转矩为1 N·m,实际系统为空载。由图10a和图11a可以看出,在没有加入SMO情况下,上升位置信号不变时,系统实际位置与给定位置存在60脉冲的误差,并且d、q轴电流纹波增大。由 图10b和图11b可以看出,在加入SMO后,上升位置信号不变时,系统实际位置与给定位置之间的误差得到了消除,并且d、q轴电流纹波明显减小。

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10   参数不匹配情况下给定斜坡信号的试验波形


图11

新窗口打开| 下载原图ZIP| 生成PPT

图11   参数不匹配情况下给定斜坡信号的d轴和q轴电流波形


6 结论

本文研究基于MPDSC策略的鲁棒性位置伺服PMSM系统,得出如下研究结论。

(1) 设计的混合MPDSC策略根据电机实际转速和参考转速以及相邻时刻参考转速之间的关系判断电机运行状态,在电机动态运行时采用FCS-MPDSC策略,稳态运行时采用DV-MPDSC策略,在保证系统动态性能的同时优化电流纹波。

(2) 针对MPDSC依赖模型参数的特点,基于滑模控制理论设计了一种电气参数、机械参数和负载扰动观测器,以消除参数不匹配和负载扰动对系统造成的影响。

(3) 论文通过试验验证了上述控制策略的有 效性。

参考文献

WANG Z, CHEN J, CHENG M, et al.

Field-oriented control and direct torque control for paralleled VSIs fed PMSM drives with variable switching frequencies

[J]. IEEE Transactions on Power Electronics, 2016, 31(3):2417-2428.

DOI:10.1109/TPEL.2015.2437893      URL     [本文引用: 1]

徐质闲, 王政, 王学庆, 等.

T型三电平双三相永磁同步电机驱动零共模电压模型预测控制

[J]. 中国电机工程学报, 2020, 40(13):4301-4310.

[本文引用: 1]

XU Zhixian, WANG Zheng, WANG Xueqing, et al.

Model predictive control of zero common-mode voltage for T-type three-level dual-three phase permanent magnet synchronous motor drive

[J]. Proceedings of the CSEE, 2020, 40(13):4301-4310.

[本文引用: 1]

GEYER T, QUEVEDO D.

Multistep finite control set model predictive control for power electronics

[J]. IEEE Transactions on Power Electronics, 2014, 29(12):6836-6846.

DOI:10.1109/TPEL.2014.2306939      URL     [本文引用: 1]

GU M, WANG Z, YU K, et al.

Interleaved model predictive control for three-level neutral-point-clamped dual three-phase PMSM drives with low switching frequencies

[J]. IEEE Transactions on Power Electronics, 2021, 36(10):11618-11630.

DOI:10.1109/TPEL.2021.3068562      URL     [本文引用: 1]

PREINDL M, BOLOGNANI S.

Model predictive direct speed control with finite control set of PMSM drive systems

[J]. IEEE Transactions on Power Electronics, 2013, 28(2):1007-1015.

DOI:10.1109/TPEL.2012.2204277      URL     [本文引用: 1]

KAKOSIMOS P, ABU-RUB H.

Predictive speed control with short prediction horizon for permanent magnet synchronous motor drives

[J]. IEEE Transactions on Power Electronics, 2018, 33(3):2740-2750.

DOI:10.1109/TPEL.2017.2697971      URL     [本文引用: 1]

FUENTES E, SILVA C, YUZ J.

Predictive speed control of a two-mass system driven by a permanent magnet synchronous motor

[J]. IEEE Transactions on Industrial Electronics, 2012, 59(7):2840-2848.

DOI:10.1109/TIE.2011.2158767      URL     [本文引用: 1]

YU K, WANG Z, WANG X, et al,

An online flux estimation for dual three-phase SPMSM drives using position-offset injection

[J]. IEEE Transactions on Power Electronics, 2021, 36(10):11606-11617.

DOI:10.1109/TPEL.2021.3067669      URL     [本文引用: 1]

WANG K, LORENZ R, BALOCH N.

Enhanced methodology for injection-based real-time parameter estimation to improve back EMF self-sensing in induction machine deadbeat-direct torque and flux control drives

[J]. IEEE Transactions on Industry Applications, 2018, 54(6):6071-6080.

DOI:10.1109/TIA.2018.2855162      URL     [本文引用: 1]

LIU Z, WEI H, ZHONG Q, et al.

Parameter estimation for VSI-fed PMSM based on a dynamic PSO with learning strategies

[J]. IEEE Transactions on Power Electronics, 2017, 32(4):3154-3165.

DOI:10.1109/TPEL.2016.2572186      URL     [本文引用: 1]

LIU Z, WEI H, LI X, et al.

Global identification of electrical and mechanical parameters in PMSM drive based on dynamic self-learning PSO

[J]. IEEE Transactions on Power Electronics, 2018, 33(12):10858-10871.

DOI:10.1109/TPEL.63      URL     [本文引用: 1]

LI M, ZHAO J, HU Y, et al.

Active disturbance rejection position servo control of PMSLM based on reduced-order extended state observer

[J]. Chinese Journal of Electrical Engineering, 2020, 6(2):30-41.

DOI:10.23919/CJEE.7873788      URL     [本文引用: 1]

ZHANG X, HOU B, MEI Y.

Deadbeat predictive current control of permanent-magnet synchronous motors with stator current and disturbance observer

[J]. IEEE Transactions on Power Electronics, 2017, 32(5):3818-3834.

DOI:10.1109/TPEL.2016.2592534      URL     [本文引用: 2]

LU W, TANG B, JI K, et al.

A new load adaptive identification method based on an improved sliding mode observer for PMSM position servo system

[J]. IEEE Transactions on Power Electronics, 2021, 36(3):3211-3223.

DOI:10.1109/TPEL.63      URL     [本文引用: 2]

ZHANG X, HOU B.

Double vectors model predictive torque control without weighting factor based on voltage tracking error

[J]. IEEE Transactions on Power Electronics, 2018, 33(3):2368-2380.

DOI:10.1109/TPEL.2017.2691776      URL     [本文引用: 1]

/

〈 〉