1 引言
航天器姿态控制是航空航天领域中的关键技术之一。地球静止轨道(Geostationary Earth Orbit,GEO)航天器可以抽象为一个广义三自由度刚体摆等效模型(简称3D刚体摆模型),以该等效模型为对象,学者们开展了对航天器姿态控制问题的研究。
基于航天器动力学与运动学方程对3D刚体摆建立数学模型,对3D刚体摆的姿态稳定和PMSM输出转矩采用PID控制策略。其中对3D刚体摆采用PD控制,使其稳定在期望姿态,对位置伺服系统中的伺服电机实施PID控制,可使电动机输出满足3D刚体摆实际需要的输入力矩,在3D刚体摆伺服系统仿真及平台实验中,利用Matlab和Labview软件,设计PID算法流程及窗口监视界面,并通过3D刚体摆的姿态角和姿态角速度输出曲线验证了位置伺服系统控制策略的可行性。
2 3D刚体摆输入力矩
2.1 3D刚体摆数学模型
根据三自由度刚体摆动力学特性,未受控的三自由度刚体摆的动力学方程为
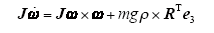
3D刚体摆的运动学方程为
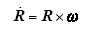
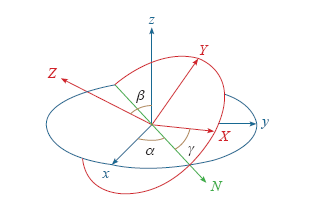
式中,J = diag(Jx,Jy,Jz)为3D刚体摆的转动惯量矩阵;m为3D摆的质量;g为重力加速度;ρ = (0,0,Г)T为原点与3D摆质心之间的矢量(Г是质心与支点之间的距离);e3为惯性坐标系Z轴方向上的单位矢量,且e3 = (0,0,1)T;ω∈R3为连体坐标系中3D摆的角速度矢量;R为连体坐标系与惯性坐标系之间的方向余弦矩阵[11]。从惯性坐标系[I]到本体坐标系[B]需要经过坐标变换,α、β、γ分别为绕Z轴、Y轴及X轴坐标变换转过的角度,记为偏航角、俯仰角及滚动角。
根据式(1)、式(2),得到未受控三自由度刚体摆的数学模型展开式为
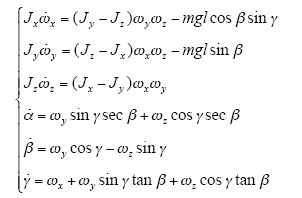
图1
2.2 3D刚体摆PD控制器设计
在仿真实验中,常将阶跃信号、斜坡信号等作为伺服系统输入力矩,本文以被控对象实际需要的控制力矩作为位置伺服系统的给定转矩输入,得到系统转矩输出曲线,能真实地模拟输入所需信号,较好地体现伺服系统的控制作用。根据运动学和动力学方程建立数学模型,需要通过下式实现三通道动态解耦,即
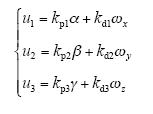
此处设计PD控制器。将控制量u1、u2、u3作为3D刚体摆的输入,式(4)中取Kp = diag(212,242,235),Kd = diag(400,375,312),得到摆姿态输出曲线。
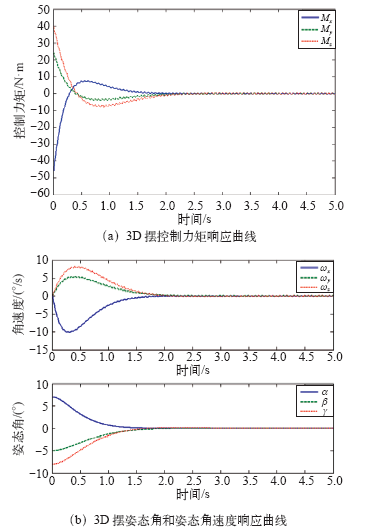
选取3D刚体摆的质量为m = 140kg,惯量矩阵J = diag(30,40,50)g·m²,Г = 0.1m,设定3D摆的初始状态姿态角(α,β,γ) = (5,5,-5)Trad,姿态角速度(ωx,ωy,ωz) = (0,0,0)Trad/s;得到3D刚体摆输出的角度、角速度和力矩响应曲线分别如图2所示。
图2
上述控制力矩是3D摆的期望输入,即PMSM的输出,这就需要对PMSM伺服系统实施恰当的控制策略。
3 基于PID的PMSM位置伺服系统
3.1 PMSM动态数学模型
PMSM是一个高阶、非线性、强耦合的多变量系统,其动态数学模型包括电压方程、磁链方程、转矩方程和运动方程。当永磁同步电机以转子磁场定向、忽略铁心饱和、不计涡流损耗和磁滞损耗、假设转子无阻尼绕组时,永磁同步电机在转子dq轴下的动态数学模型为
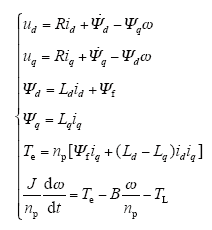
式中,ud、uq为定子电压矢量dq轴分量;id、iq为定子电流矢量在dq轴上的分量;Ψd、Ψq为定子磁链在dq轴上的分量;Ψf为永磁体磁链;ω为转子速度;J为转动惯量;B为摩擦系数;np为电机极对数;TL为负载转矩。
3.2 伺服系统PID控制器设计
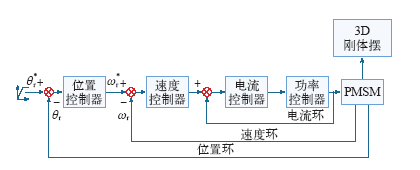
永磁同步电机位置伺服控制框图如图3所示。
图3
图3将电流和转速控制作为内环,位置控制作为外环;其中,θr*为位置参考输入;θr是电动机转子实际输出的位置角度;nr*为电动机转速参考输入;nr为电动机实际输出转速。
图3所示位置伺服系统中,位置环性能的好坏取决于系统内环尤其是电流环的稳定,提高电流环的快速性,可以实现定转子电流对矢量控制指令的准确跟踪,使伺服系统的动态特性得以提高。
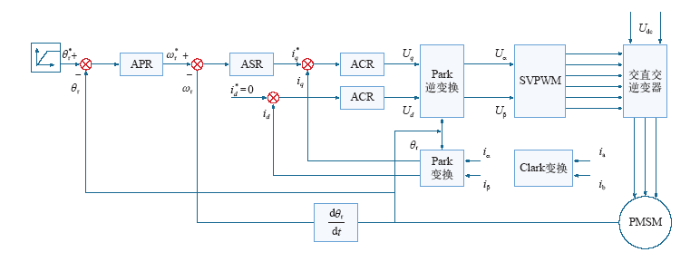
根据id = 0的矢量控制策略,得到PMSM矢量控制位置伺服系统原理图如图4所示。
图4
图4
PMSM 矢量控制位置伺服系统结构图
Fig.4
The block diagram of position servo systemfor PMSM vector control system
为了快速消除系统位置偏差,对图4中的位置控制器采取P控制策略;为了减小系统稳态误差,速度控制器采用PI控制策略;为了能够满足动态性能中快速性和稳定性的要求,电流环采取P控制策略。
4 3D刚体摆位置伺服系统实验
4.1 基于Matlab的仿真实验
在Matlab环境中,搭建PMSM位置伺服系统,仿真实验所用PMSM参数为:极对数np = 4,额定转速nr* = 1 500r/min,定子电阻R = 0.958 5Ω,dq轴电感Ld = Lq = L = 5.2mH,转子磁动势Ψf = 0.182 7Wb,转动惯量J = 0.6×10-3kg·m2,摩擦系数B = 0。实验以3D刚体摆偏航通道所需的控制力矩Mx作为PMSM的负载转矩,PMSM输出力矩如果满足负载力矩所需大小则满足负载的要求。
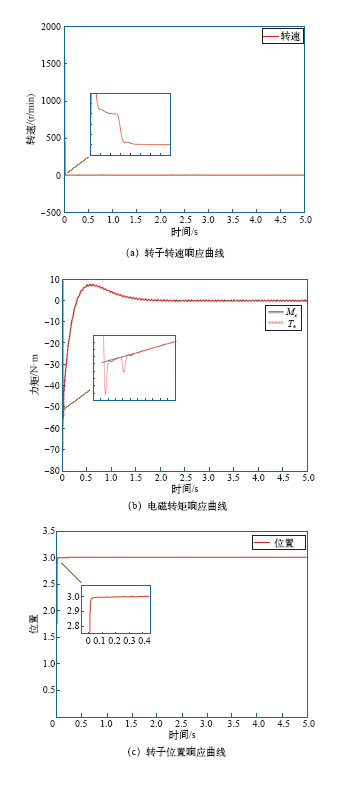
图5
图5b是电磁转矩响应曲线,电动机起动,电磁转矩从0N·m陡增,很快就能跟踪负载转矩,到达期望位置时,电磁转矩虽有抖动,但能快速恢复到稳定状态,表明电磁转矩可以快速响应负载输入,能够满足负载要求,控制3D刚体摆到达指定的姿态稳定位置。
图5c为位置响应曲线,转子在30ms后就达到指定位置并稳定,控制系统的性能指标见下表。
表 PID位置伺服系统性能指标
Tab.
| 控制策略 性能指标 | PID控制 |
|---|---|
| 上升时间tr(稳态值的10%上升到90%所需要的时间)/s | 0.015 |
| 调节时间ts/s | 0.019 |
| 超调量 δ% | 0 |
| 定位精度 | 准确 |
4.2 3D刚体摆伺服系统实验平台
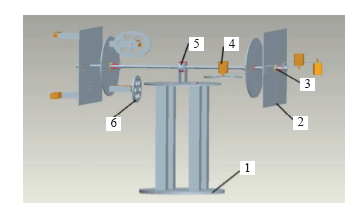
图6
图6
3D 刚体摆模拟装置
1—实验装置底座 2—实验装置安装面板 3—涨紧套 4—伺服电机 5—球轴承 6—惯性飞轮
Fig.6
The device of for 3D rigid pendulum
4.2.1 软件设计
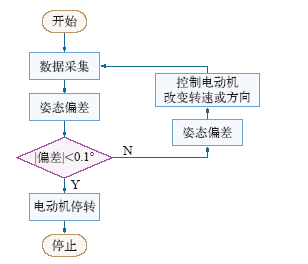
基于Labview软件,在上位机进行软件编程,实现3D刚体摆伺服系统的PID控制。软件设计流程如图7所示。
图7
Labview虚拟平台集成了大量的库函数,通过调用动态函数可以方便灵活地调取外部设备数据;运用PID控制得到控制器的输出;电动机控制模块的输出借助Labview中的“DAQ助手”,将PID控制器的输出值通过数据采集卡以模拟量电压的形式直接作用于电动机;采用Xsens公司的MTi传感器实现3D刚体摆实验平台的姿态数据测量,可同时输出欧拉角和角速度等数据。
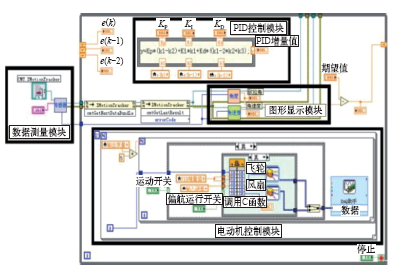
以偏航通道为例,对伺服系统控制电机的部分编程如图8所示。
图8
5 实验结果分析
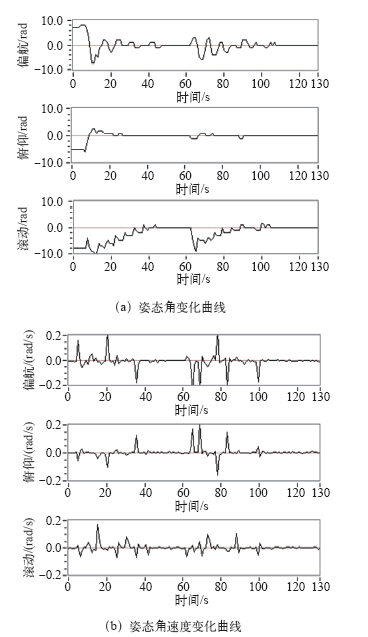
选取3D刚体摆实验平台的初始姿态角α = 7°,β = -5°,γ = -8°。利用Labview软件设计了3D刚体摆实验平台的监视界面,实时得到实验平台的姿态角和姿态角速度的变化曲线如图9所示。
图9
6 结束语
构建3D刚体摆数学模型,设计3D摆PD控制器,仿真实验验证了PD控制策略能够使控制对象达到期望姿态并稳定在指定的位置,得到了理想的3D刚体摆控制力矩;在3D刚体摆伺服系统平台上,对位置伺服控制系统采用PID控制策略,在抗干扰、定位精度及稳态性能方面能够满足系统控制性能的要求,编写Labview程序做出监视画面,可以观察3D刚体摆的运行状况,实时、准确地反映PID控制器对3D刚体摆位置伺服系统控制的有效性。实验还表明,由于对数学模型、伺服系统的部分简化,造成仿真实验和平台实验结果是有差别的,这些影响在实际工程应用中都应予以考虑。
参考文献
Dynamics and control of a 3D pendulum
[C].
Nonlinear dynamic of the 3D pendulum
[J].
Spacecraft attitude dynamics and control
[D].
基于滑模控制的3D刚体摆姿态稳定性
[J].
Position stability of 3D rigid body based on sliding mode control
[J].
3D刚体摆姿态稳定性的自适应滑模控制
[J].
Adaptive sliding mode control of 3D rigid body position stability
[J].
永磁同步伺服电机二自由度控制
[J].
Two degree of freedom control of permanent magnet synchronous servo motor
[J].
交流位置伺服系统自适应模糊PID控制器设计
[J].
Design of fuzzy PID adaptive controller for AC position servo system based on sliding surface
[J].
基于自抗扰控制器的永磁同步电机位置伺服系统
[J].
A novel position controller of PMSM servo system based on active-disturbance rejection controller
[J].
全局滑模控制在永磁同步电机位置伺服中的应用
[J].
Global sliding mode control for permanent magnet synchronous motor servo system
[J].
Chaotic attitude motion of the 3D rigid pendulum
[C].