1 引言
本文针对两自由度直驱感应电机[9]的特有结构,建立耦合模型分析行波磁场对运动轴旋转运动的影响,推导该电机转子磁场定向坐标系下的数学模型,在Matlab中搭建该电机的矢量控制系统,并加入对耦合效应的补偿。
2 电机结构与工作原理
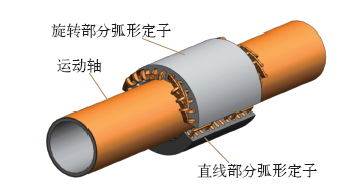
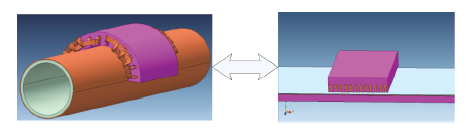
两自由度直驱感应电机的结构如图1所示。电机由旋转运动弧形定子、直线运动弧形定子和运动轴组合而成。旋转部分定子绕组通电时,运动轴输出旋转运动。直线部分定子绕组通电时,运动轴输出直线运动。当旋转部分定子绕组与直线部分定子绕组同时通电时,运动轴输出螺旋运动。因此该电机可以提供旋转运动、直线运动和螺旋运动三种运动形式。
图1
3 耦合特性分析
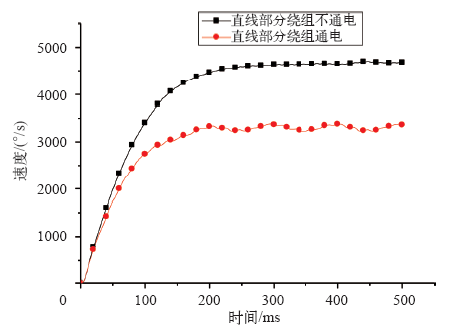
当旋转部分绕组通入127V/50Hz的电源,直线部分绕组在通电和不通电两种情况下运动轴的空载旋转速度如图2所示。
图2
如图2所示,当旋转部分绕组通127V/50Hz电源,直线部分绕组不通电时,运动轴的旋转速度为4 600°/s;当旋转部分绕组通入127V/50Hz电源,而直线部分绕组通入127V/50Hz电源时,则运动轴的旋转速度为3 300°/s,运动轴的旋转速度出现了显著的下降。这是由于直线部分绕组通电引起,因此推测直线部分的行波磁场会影响到旋转运动。
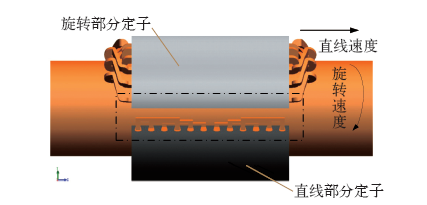
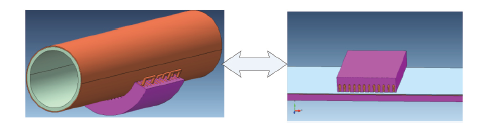
图3所示为两自由度直驱感应电机的侧视图。图中点划线框内为直线部分定子与旋转部分定子的端部部分。
图3
当旋转部分绕组通电时,运动轴产生旋转运动。如果此时直线部分绕组通电,直线部分定子内会产生行波磁场。由于运动轴旋转速度的存在,运动轴的导电层会由无行波磁场区域进入到行波磁场区域,必然会受到来自行波磁场的阻力。因此可以推测,运动轴旋转运动速度下降的原因是因为运动轴旋转运动时受到来自行波磁场的阻力矩。
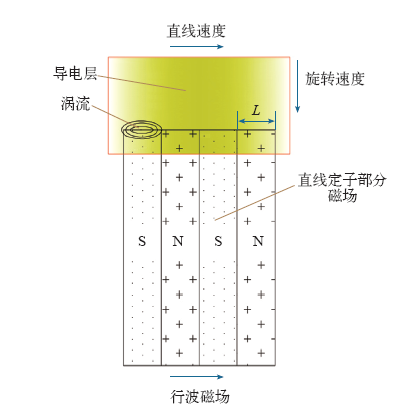
当导电层由无行波磁场区域进入到行波磁场区域,在直线部分定子端部处的导电层内会产生涡流,并受到行波磁场的阻力。
图4
导电层相当于由无数个导体组成, 当导电层进入直线部分行波磁场时,导体会切割行波磁场。假设此时导电层上有一段导体,它的长度为L。在某一时刻,该处的磁感应强度为B,导电层的运动速度为v,导体内的感应电动势为e,则
E=BLv(1)
此导体受到的力为
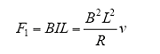
式中,R为此段导体的电阻值。
在此时刻,导电层所受到的力为
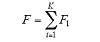
式中,K为在端部涡流部分的导体个数。
联立式(2)、式(3),可得
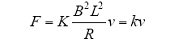
其中, 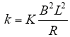
由式(4)可知,在行波磁场强度不变的情况下, k的值也不会发生变化。
通过上述分析可知,旋转运动受到的阻力矩T1与运动轴旋转速度成正比,即
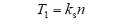
式中,ks为旋转耦合系数,其值与行波磁场磁感应强度有关;n为运动轴旋转速度。旋转部分的电磁转矩需要修正为
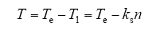
由于旋转部分定子与直线部分定子结构类似,因此运动轴的直线运动同样会受到来自旋转磁场的阻力,并且该阻力大小与直线运动的速度成正比。因此直线部分的电磁推力需要修正为
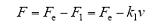
式中,kl为直线耦合系数,其值与旋转磁场磁感应强度有关;v为运动轴直线速度;ks与kl能够通过实际测定的方法得到。
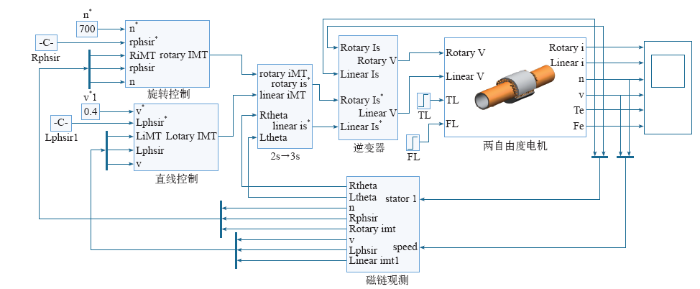
4 矢量控制系统建模
图5
图6
在转子磁场定向时,规定d轴为转子磁链方向,则此时q轴无磁链分量,因此纵向边端效应只影响到d轴,对q轴没有影响。转子磁场定向坐标系下两自由度直驱感应电机的数学模型为
(1)旋转部分电压方程为
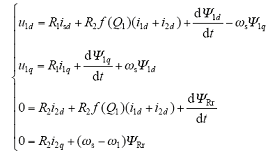
式中,(u1d,u1q)、(i1d,i1q)、(Ψ1d,Ψ1q)、ωs为旋转部分两相同步坐标系下的一次电压、一次电流、一次磁链和同步旋转角速度;(i2d,i2q)、ΨRr、ω1为旋转部分dq坐标系下的转子电流、磁链和转子角速度。f (Q1)为考虑旋转部分纵向端部效应的修正系数[10]。
(2)直线部分电压方程为
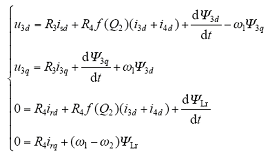
式中,(u3d,u3q)、(i3d,i3q)、(Ψ3d,Ψ3q)、ωl为直线部分dq坐标系下的一次电压、电流、磁链和同步旋转角速度;(i4d,i4q)、ΨLr为直线部分dq坐标系下的二次电流、二次磁链,ω2为直线部分次级角速度;f (Q2)为考虑直线部分纵向端部效应的修正系数。
(3)旋转部分磁链方程为
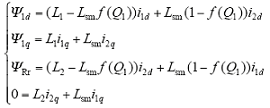
式中,L1、Lsm、L2分别为旋转部分同步坐标系下一次电感、一次与二次互感、二次电感。
(4)直线部分磁链方程为
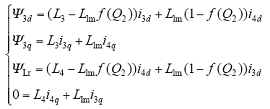
式中,L3、Llm、L4分别为直线运动部分两相同步坐标系下一次电感、一次与二次互感、二次电感。
考虑到旋转部分与直线部分的耦合效应,dq坐标系下旋转部分的转矩方程与直线部分的推力方程为
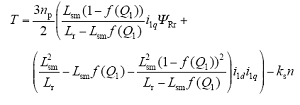
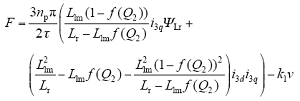
式中,ksn为行波磁场对旋转运动的阻力矩;klv为旋转磁场对直线运动的阻力。
(5)旋转部分的转子磁链为
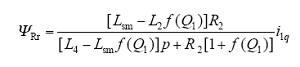
(6)直线部分的二次磁链为
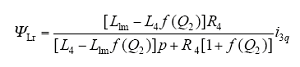
由于纵向边端效应以及耦合效应的影响,仅仅控制i1q与i3q难以达到控制转矩与推力的目的。因此,需要在矢量控制系统中对其进行补偿,由式(13)、式(14)变换可得
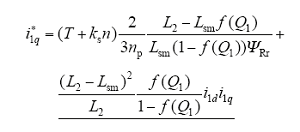
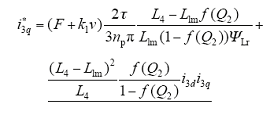
其中, 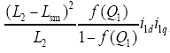
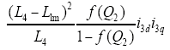
图7
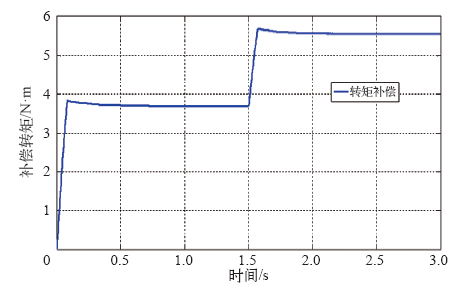
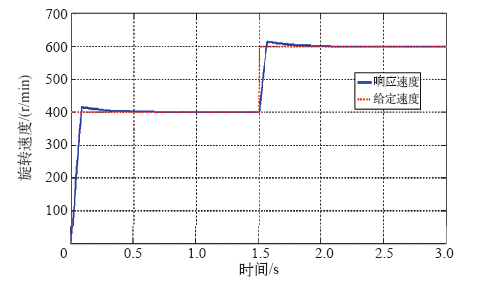
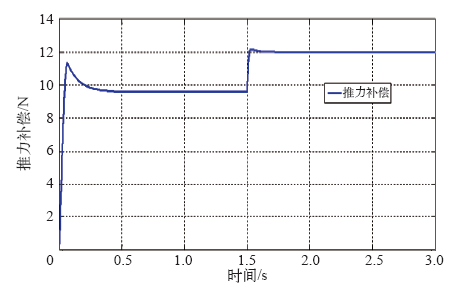
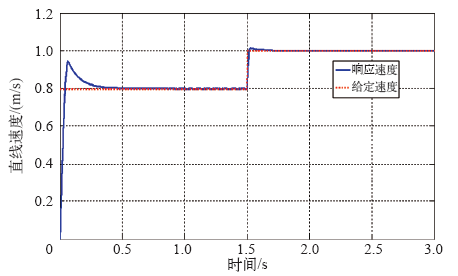
5 仿真结果
本文所采用的转子磁场定向矢量控制方法,将磁链与转矩解耦,保持旋转部分的转子磁场与直线部分的二次磁场不变。由于耦合系数ks只与行波磁场强度有关,耦合系数kl只与旋转磁场有关, 所以在转子磁场定向控制系统中,耦合系数ks、kl的值保持不变,其中ks = 0.009 222,kl = 11.897。
图8
图9
图10
图11
6 结论
本文分析了两自由度直驱感应电机的直线部分与旋转部分之间的耦合影响,直线运动会受到来自旋转磁场的阻力,阻力的大小与直线速度成正比,旋转运动会受到来自行波磁场的阻力矩,阻力矩大小与旋转速度成正比,在此基础上,修正了旋转部分的转矩方程和直线部分的推力方程。
本文推导出两自由度直驱感应电机在转子磁场定向坐标系下的数学模型,通过Matlab仿真平台建立两自由度直驱感应电机的矢量控制系统,并加入了对耦合效应的补偿。仿真结果表明,旋转速度和直线速度均能快速跟踪给定速度,验证了所提矢量控制方法的可实施性。
两自由度电机精确控制系统在工业中具有广泛的应用场景,本文所探讨的考虑耦合效应的矢量控制方法可以为两自由度直驱感应电机的驱动系统设计提供一些参考。
参考文献
Analysis on coupling effect of 2-DOF direct drive induction motor based on 3-D model
[C].
Direct-drive rotary-linear electromechanical actuation system for control of gearshifts in automated transmissions
[C].
Force control of a spiral motor and its application to musculoskeletal biped robot
[C].
Decoupling control of linear and rotary permanent magnet actuator using two-directional dq transformation
[J].
3-D analytical linear force and rotary torque analysis of linear and rotary permanent magnet actuator
[J].
Performance analysis and decoupling control of an integrated rotary-linear machine with coupled magnetic paths
[J].
Speed control of a two-degrees of freedom induction motor with rotor helical motion for industrial applications
[C].
3-D space modeling of rotary-linear induction motor with twin-armature
[C].
Design and analysis of a 2-DOF split-stator induction motor
[J].
Linear induction motor-equivalent-circuit model
[J].