电气工程学报, 2021, 16(4): 25-32 doi: 10.11985/2021.04.004

特邀专栏：高性能永磁电机驱动与控制

四象限运行磁通切换永磁直线电机的MRAS无位置传感器控制*

程明,, 王飒飒,, 王伟,

东南大学电气工程学院 南京 210096

MRAS Position Sensorless Control of Linear Flux-switching Permanent Magnet Motor for Four-quadrant Operation

CHENG Ming,, WANG Sasa,, WANG Wei,

School of Electrical Engineering, Southeast University, Nanjing 210096

通讯作者: * 程明,男,1960年生,教授,博士研究生导师,IEEE Fellow,IET Fellow。主要研究方向为电动车驱动控制技术、新能源发电技术、微特电机及测控技术等。E-mail：mcheng@seu.edu

收稿日期: 2021-08-9   修回日期: 2021-10-9  

基金资助: * 国家自然科学基金.  51977036
江苏省优秀青年基金.  BK20200066

Received: 2021-08-9   Revised: 2021-10-9  

作者简介 About authors

王飒飒,男,1994年生,硕士研究生。主要研究方向为电机驱动与控制。E-mail： ssw2013a@163.com

王伟,男,1985年生,副研究员,博士研究生导师。主要研究方向为电机系统及控制。E-mail： wangwei1986@seu.edu.cn

摘要

模块化磁通切换永磁直线电机(Liner flux-switching permanent magnet machines, LFSPM)的电枢绕组和永磁体均放置在初级短动子,次级长定子仅由导磁铁心组成,适合用于电梯等长距离轨道运输系统中。在电梯驱动系统中,上行时主要为电动运行,下行时在自重作用下常处于发电甚至制动运行,运行模式的交替变化给无位置传感器控制带来挑战。为此,基于LFSPM电机d-q轴数学模型,建立了LFSPM电机基于模型参考自适应法(Model reference adaptive system, MRAS)的无位置传感器控制系统,根据运行工况设计了混合控制策略。电梯上行时采用id=0控制,下行处于轻载制动发电状态,电压电流信号中基波含量占比小,进行增磁控制,利用id调节电压电流信号中基波占比来满足速度辨识的要求,实现LFSPM电机四象限无位置传感器控制。分析该无位置传感器控制系统的角位置估算误差原因,提出电流补偿方法。样机试验结果验证了所提混合控制策略的有效性。

关键词： 磁通切换永磁直线电机 ; 无位置传感器控制 ; 四象限运行 ; 增磁控制 ; 电流补偿 ; 电梯

Abstract

The armature windings and permanent magnets of the modular liner flux-switching permanent magnet machines (LFSPM) are placed in the primary short mover, while the secondary long stator is composed only of the conductive magnet core, which is suitable for elevators, etc. in long distance rail transport system. In the elevator drive system, the main operation is electric operation when going up, and it is often in power generation or even braking operation under the action of self-weight when going down. The alternating change of operation mode brings challenges to the position sensorless control. Therefore, based on the mathematical model of the d-q axis of the LFSPM motor, a position sensorless control system based on the model reference adaptive system (MRAS) of the LFSPM motor is established. A hybrid control strategy is designed based on operating conditions. When the elevator is going up, it adopts control with id=0. When the elevator is going down, it is in the state of light load braking power generation, the proportion of the fundamental wave in the voltage and current signal is small, so that flux-strengthening control is carried out. The id is used to adjust the proportion of the fundamental wave in the voltage and current signal to meet the requirements of speed identification. The reasons for the large error in the angle position estimation of the sensorless control system are analyzed, and a current-based compensation method is proposed. The prototype experiment results prove the effectiveness of the proposed hybrid control strategy.

Keywords： Liner flux-switching permanent magnet machines ; position sensorless control ; four-quadrant operation ; flux- strengthening control ; current compensation ; elevator

PDF (3755KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

程明, 王飒飒, 王伟. 四象限运行磁通切换永磁直线电机的MRAS无位置传感器控制*. 电气工程学报[J], 2021, 16(4): 25-32 doi:10.11985/2021.04.004

CHENG Ming, WANG Sasa, WANG Wei. MRAS Position Sensorless Control of Linear Flux-switching Permanent Magnet Motor for Four-quadrant Operation. Journal of Electrical Engineering[J], 2021, 16(4): 25-32 doi:10.11985/2021.04.004

1 引言

随着永磁材料的不断发展,永磁电机技术日新月异,应用领域不断拓展。永磁直线电机驱动的无绳电梯具有无需中间转换环节、提升高度没有限制、无需机房、同一个井道内可同时运行多个轿厢等优点,受到日益广泛的关注。与传统的曳引式电梯不同,由直线电机直接驱动的无绳电梯,一般难以安装对重,电梯上行时直线电机需要克服轿厢自重以及负载,处于电动运行状态;而电梯下行时,在轿厢自重和负载重力作用下运动,为保证下行速度安全、稳定,直线电机需要工作在制动发电状态。因此,无绳电机梯中的直线电机需要四象限运行。文献[1]提出一种应用于无绳电梯的新型磁通切换永磁直线电机(Liner flux-switching permanent magnet machines, LFSPM),永磁体和绕组安装在初级短动子上,次级长定子仅由导磁铁心组成。但电梯领域的永磁直线电机运行状态多变,既有电动运行,又有制动发电运行,对控制系统提出了更高的要求,因此研究永磁直线电机的控制系统具有重要的意义。

为了实现永磁直线电机高精度、高动态性能的速度和位置控制,一般需要沿着电梯的井道安装较长的位置传感器,包括磁栅式和光栅式传感器,增加了控制系统的成本,同时传感器容易受环境因素的变化而使永磁直线电机控制性能变差。因此,研究LFSPM电机无位置传感器控制算法可以减小系统成本,提高系统运行性能。

当前,虽然在永磁同步电机无位置传感器控制中已经提出了包括基于反电势和高频电压信号注入方法来估计电机转子位置和速度,但是关于LFSPM的无位置传感器控制的研究还不多。文献[2,3]基 于反电势估计方法,文献[4,5]基于电机静止坐标系下的磁链模型,均为开环观测器,缺乏误差校正环节,虽然实现简单,但过度依赖电机参数,误差较大。文献[6,7,8,9]利用磁饱和凸极性,通过检测绕组注入高频电压信号后的电流或电压响应来获取转子位置信息,但仅适用于凸极性较强的电机,且容易产生高频噪声。文献[10]采用卡尔曼滤波器法来估计电机速度,该算法需要大量的矩阵运算,对控制器MCU要求严格,且受噪声矩阵参数影响较大。文 献[11]设计了一种适用于同步电动机无传感器控制的自适应互联观测器,可以同时估计定子电感、定子电阻、负载转矩、转子速度和转子位置,减小了电机运行过程中定子电感、定子电阻参数变化对转子速度和转子位置估计观测精度的影响。文献[12]提出一种基于分段PI调节器的模型参考自适应控制方法,电机可以在全转速范围内得到较好的控制效果。文献[13]建立了MLFSPM电机基于模型参考自适应系统的无传感器控制系统,证明了系统的可行性,但该系统的电机在水平往复运行时,仅工作在电动状态,工况单一。文献[14]仅实现了LFSPM电机上行处于电动状态时的无位置传感器控制,在电机下行处于制动发电未能实现无位置传感器闭环控制。

在无绳电梯驱动系统中,LFSPM上行时主要为电动运行,下行时在自重作用下常处于轻载或制动发电运行,运行模式的交替变化给无位置传感器控制带来挑战。尤其电机下行时轻载发电,电流很小,采用id=0控制,电压电流信号中基波含量占比小,难以准确估计出电机角位置,从而造成控制失败。本文针对上述问题,提出了混合控制策略,即当LFSPM电机上行时,采用id=0控制;电机下行时,采用id>0的增磁控制,利用id调节电压电流信号中基波占比来满足速度辨识的要求,保证了LFSPM电机上下行时都能准确估计出电机动子速度和角位置,实现了LFSPM电机四象限无位置传感器控制。对可调模型计算出的电流进行补偿,减小可调模型中电阻、电感和永磁磁链幅值等固定参数、逆变器非线性以及其他干扰对动子速度和位置估计的影响。样机试验结果验证了本文混合控制策略的有效性。

2 LFSPM的数学模型

本LFSPM试验样机三相反电势基本为正弦波,磁场变化和普通的正弦波永磁同步电机类似,因此可以参照后者建立LFSPM电机的数学模型。为简化分析,首先假设LFSPM电机满足以下条件：初级三相绕组按Y型连接;不考虑铁心饱和;忽略涡流损耗和磁滞损耗;三相电流是对称正弦波电流。

和正弦波永磁同步电机类似,对于LFSPM电机来说,两相旋转坐标系下的数学模型如下所示。

d-q轴的磁链方程可表示成

$\left[ {\begin{array}{*{20}{c}} {{\psi _d}}\\ {{\psi _q}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{L_d}}&0\\ 0&{{L_q}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{i_d}}\\ {{i_q}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{\psi _{{\rm{mf}}}}}\\ 0 \end{array}} \right]$

电压方程可表示成

$\left[ {\begin{array}{*{20}{c}} {{u_d}}\\ {{u_q}} \end{array}} \right] = {R_{\rm{s}}}\left[ {\begin{array}{*{20}{c}} {{i_d}}\\ {{i_q}} \end{array}} \right] + \frac{{\rm{d}}}{{{\rm{d}}t}}\left[ {\begin{array}{*{20}{c}} {{\psi _d}}\\ {{\psi _q}} \end{array}} \right] - {\omega _{\rm{e}}}\left[ {\begin{array}{*{20}{c}} {{\psi _q}}\\ { - {\psi _d}} \end{array}} \right]$

电磁推力可表示成

${F_{\rm{e}}} = \frac{{3{\rm{\pi }}}}{{{\tau _{\rm{s}}}}}\left[ {{\psi _{{\rm{mf}}}}{i_q} + ({L_d} - {L_q}){i_d}{i_q}} \right]$

式中,id、iq分别为d-q轴电流;ψmf为永磁磁链,ψd、ψq分别为d-q轴磁链;Ld、Lq分别为d-q轴下的同步电感;Rs为相电阻;τs为定子极距;ωe为电角速度;Fe为电磁推力。

机械运动方程可以表示为

${F_{\rm{e}}} = m\frac{{{\rm{d}}v}}{{{\rm{d}}t}} + {F_{{\rm{load}}}} + {F_{{\rm{ripple}}}} + {F_{{\rm{fric}}}} + {F_{\rm{d}}}$

式中,m为动子质量;v为动子直线速度;Fload为负载拉力,Fripple为推力波动,Ffric为摩擦力,Fd为其他干扰力。

动子直线速度v和电角速度ωe之间的关系为

${\omega _{\rm{e}}} = 2{\rm{\pi }}\frac{v}{{{\tau _{\rm{s}}}}}$

3 LFSPM的MRAS无位置传感器控制

3.1 基于电流可调模型的MRAS

对LFSPM电机数学模型进行变换,将式(1)代入式(2)中,并写为电流模型格式

$\frac{{\rm{d}}}{{{\rm{d}}t}}\left[ {\begin{array}{*{20}{c}} {{i_d}}\\ {{i_q}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} { - \frac{{{R_{\rm{s}}}}}{{{L_d}}}}&{{\omega _{\rm{e}}}\frac{{{L_q}}}{{{L_d}}}}\\ {{\omega _{\rm{e}}}\frac{{{L_d}}}{{{L_q}}}}&{ - \frac{{{R_{\rm{s}}}}}{{{L_q}}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{i_d}}\\ {{i_q}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {\frac{{{u_d}}}{{{L_d}}}}\\ {\frac{{{u_q} - {\omega _{\rm{e}}}{\psi _{{\rm{mf}}}}}}{{{L_q}}}} \end{array}} \right]$

令

$\left[ {\begin{array}{*{20}{c}} {i_d^*}\\ {i_q^*} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{i_d} + \frac{{{\psi _{{\rm{mf}}}}}}{{{L_d}}}}\\ {{i_q}} \end{array}} \right]\;\;\;\;\left[ {\begin{array}{*{20}{c}} {u_d^*}\\ {u_q^*} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{u_d} + \frac{{{R_{\rm{s}}}}}{{{L_d}}}{\psi _{{\rm{mf}}}}}\\ {{u_q}} \end{array}} \right]$

则式(6)变换为

$\frac{{\rm{d}}}{{{\rm{d}}t}}\left[ {\begin{array}{*{20}{c}} {i_d^*}\\ {i_q^*} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} { - \frac{{{R_{\rm{s}}}}}{{{L_d}}}}&{{\omega _{\rm{e}}}\frac{{{L_q}}}{{{L_d}}}}\\ {{\omega _{\rm{e}}}\frac{{{L_d}}}{{{L_q}}}}&{ - \frac{{{R_{\rm{s}}}}}{{{L_q}}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {i_d^*}\\ {i_q^*} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {\frac{{u_d^*}}{{{L_d}}}}\\ {\frac{{u_q^* - {\omega _{\rm{e}}}{\psi _{{\rm{mf}}}}}}{{{L_q}}}} \end{array}} \right]$

将式(8)中的电流、电角速度替换为估计值,此时可得MRAS算法基于电流的可调模型为[15]

$\frac{{\rm{d}}}{{{\rm{d}}t}}\left[ {\begin{array}{*{20}{c}} {\hat i_d^*}\\ {\hat i_q^*} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} { - \frac{{{R_{\rm{s}}}}}{{{L_d}}}}&{{{\hat \omega }_{\rm{e}}}\frac{{{L_q}}}{{{L_d}}}}\\ {{{\hat \omega }_{\rm{e}}}\frac{{{L_d}}}{{{L_q}}}}&{ - \frac{{{R_{\rm{s}}}}}{{{L_q}}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\hat i_d^*}\\ {\hat i_q^*} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {u_d^*}\\ {u_q^*} \end{array}} \right]$

式中,“^”表示变量的估计值。

根据Popov超稳定理论,基于电流可调模型的MRAS控制策略的估计电角速度为[15]

$\begin{array}{c}{{\hat \omega }_{\rm{e}}} = ({k_{\rm{p}}} + \frac{{{k_{\rm{i}}}}}{s})\left[ {\frac{{{L_q}}}{{{L_d}}}{i_d}{{\hat i}_q} - \frac{{{L_d}}}{{{L_q}}}{{\hat i}_d}{i_q} + } \right.\\\frac{{{\psi _{{\rm{mf}}}}}}{{{L_d}}}({{\hat i}_q} - {i_q}) + \left. {(\frac{{{L_d}}}{{{L_q}}} - \frac{{{L_q}}}{{{L_d}}}){{\hat i}_d}{{\hat i}_q}} \right]\end{array}$

式中,kp为比例参数,ki为积分参数。

将式(10)进行积分,得到电角度的估计值

${\hat \theta _{\rm{e}}} = \int {{{\hat \omega }_{\rm{e}}}} dt + {\theta _{\rm{e}}}{\rm{(0)}}$

将式(10)代入式(5)得到电机直线速度的估计值

$\hat v = \frac{{{{\hat \omega }_{\rm{e}}}}}{{2{\rm{\pi }}}}{\tau _{\rm{s}}}$

3.2 辨识误差分析及补偿

为了减少传感器的数量,LFSPM电机的MRAS系统可调模型的电压输入采用三相占空比进行电压重构,但由于未考虑逆变器的非线性影响,此电压并不是实际电机端电压。此外,MRAS系统可调模型中的d-q轴电感、相电阻、永磁磁链都是静态测量的固定数值,电机运行时,这些数值和实际值均有误差。以上种种因素导致式(9)估计出来的d-q轴电流和电机的实际d-q轴电流不等,使电角速度出现稳态辨识误差,且误差波动,导致角度也会出现误差。如果要将这些参数变化均考虑在内,则模型会变得十分复杂甚至不可行。因此,本文从工程角度出发,结合试验对式(9)估计到的d-q轴电流进行补偿。

记d-q轴估计电流的补偿量分别为idcom、iqcom。令

$\left[ {\begin{array}{*{20}{c}} {{{\hat i}_{d{\rm{c}}}}}\\ {{{\hat i}_{q{\rm{c}}}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{{\hat i}_d} + {i_{d{\rm{com}}}}}\\ {{{\hat i}_q} + {i_{q{\rm{com}}}}} \end{array}} \right]$

式(10)变换为

${\hat \omega _e} = \left( {{k_p} + \frac{{{k_i}}}{s}} \right)\left[ {\frac{{{L_q}}}{{{L_d}}}{i_d}{{\hat i}_{qc}} - \frac{{{L_d}}}{{{L_q}}}{{\hat i}_{dc}}{i_q} + } \\ \frac{{{\psi _{mf}}}}{{{L_d}}}({\hat i_{qc}} - {i_q}) + {(\frac{{{L_d}}}{{{L_q}}} - \frac{{{L_q}}}{{{L_d}}}){{\hat i}_{dc}}{{\hat i}_{qc}}} \right]$

3.3 系统整体控制策略

与通常的水平运行的直线电机不同,电梯上行时电机处于重载电动状态,而下行时在轿厢自重作用下直线电机呈轻载发电/制动状态。因此,整个行程中,电机运行在四个象限,针对电动运行设计直线电机无位置传感器控制方法难以奏效,为此,需要设计新的控制策略。

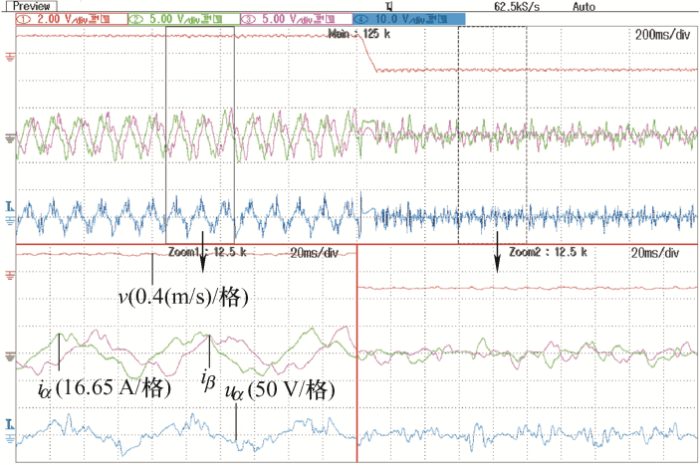
电机上行时,处于重载电动状态,电流幅值大,相电压、相电流基本呈现正弦波,谐波较小,因此采用id=0控制。但电机下行时,处于轻载发电/制动状态,电枢电流通常很小,导致基波含量较小,相电压、相电流谐波相对较大,图1给出了电机上、下行时的电压电流试验波形。Zoom1、Zoom2分别为电机上、下行时的波形放大。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   电机上下时的电压电流波形图


计算电机下行时静止两相电流iα、iβ及α轴电压uα的THD,iα的THD=92.73%,iβ的THD=95.81%,uα的THD=393.66%。可以看出电机下行时,在自重下,由于摩擦力向上,克服了一部分轿厢重力,所需要的电磁制动力较小,电机处于轻载发电状态,绕组上的电压和电流均较小,且电机由于加工制造原因,受到的干扰较大,静止两相电压、电流谐波含量较大,导致电压、电流信号中基波含量占比小,因此,难以利用基于电机基波模型的速度估计自适应律,即式(10)和式(11)不能准确估计出电机速度与位置,从而造成无位置传感器闭环控制失败。

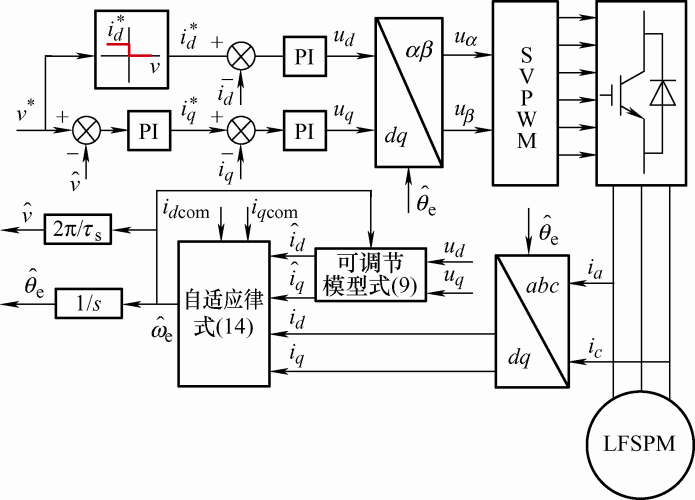
为此,本文提出了一种混合控制策略,如图2所示。控制策略基于矢量控制原理,主要功能模块包括LFSPM电机、坐标变换、PI控制器、SVPWM、三相逆变器、MRAS、电流给定等模块。在电机下行处于轻载制动发电状态时,采用增磁控制,人为增大d轴电流分量,利用id调节电压电流信号中基波占比来满足速度辨识的要求,保证电机下行时能准确估计出电机动子速度和角位置。为了保证电压电流信号中基波含量满足速度辨识的要求,d轴电流给定$i_d^*$设有最小值idmin;同时,为保证电机相电流is小于电机的最大电流ilim,d轴电流给定$i_d^*$还设定了一个最大值idmax,且电机电压us小于逆变器可线性调制的最大电压ulim

$i_{{\rm{lim}}}^2 \ge i_{\rm{s}}^2 = i_{d{\rm{max}}}^2 + i_q^2$
$\frac{{U_{dc}^2}}{3} = u_{\lim }^2 \ge u_s^2 = u_d^2 + u_q^2{\rm{ = }}{({R_s}{i_{d\max }} - {\omega _e}{L_q}{i_q})^2} + [{R_s}{i_q} + {\omega _e}{({\psi _{mf}} + {L_d}{i_{d\max }}]^2}$

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   基于MRAS的无位置传感器控制策略框图


这样,可以保持电机能够长时间稳定安全运行。因此,0≤idmin≤id*≤idmax,在电机下行轻载发电状态下,由于id为正值,增大了磁链,提高了电压和电流信号中基波含量占比,实现了电机速度的可靠辨识。

4 试验研究

为了验证上述设计方案,设计制作了模型电梯如图3a所示,LFSPM电机的主要参数列于表1,并基于dSPACE1104建立了磁通切换永磁直线电机无位置传感器控制系统,如图3b所示。

表1   电机参数

参数数值
定子极距τs/m0.036
动子质量m/kg18.5
额定速度vn/(m/s)1
相电阻Rs/Ω0.75
d轴电感Ld/mH6.54
q轴电感Lq/mH6.62
永磁磁链ψmf/Wb0.11

新窗口打开| 下载CSV


图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   试验平台


4.1 补偿电流的确定

本文采用试验方法获取d-q轴估计电流的补偿量idcom、iqcom。在电机自重情况下,先令idcom=0,电机上下行时,以固定步长逐步增加补偿电流iqcom,计算MRAS观测角位置与直线型磁栅编码器的平均误差θerror,如表2和表3所示。

表2   上行时,补偿电流iqcom与角位置误差θerror关系

iqcom/Aθerror/(°)iqcom/Aθerror/(°)iqcom/Aθerror/(°)
0-22.31.8-8.83.610.1
0.2-20.52.0-7.23.812.1
0.4-18.42.2-5.84.014.0
0.6-16.32.4-2.34.215.7
0.8-14.32.60.54.417.2
1.0-13.52.82.44.619.1
1.2-12.53.04.14.820.6
1.4-11.43.25.85.022.5
1.6-10.23.47.6

新窗口打开| 下载CSV


表3   下行时,补偿电流iqcom与角位置误差θerror关系

iqcom/Aθerror/(°)iqcom/Aθerror/(°)iqcom/Aθerror/(°)
033.0-1.85.2-3.6-17.5
-0.230.1-2.02.6-3.8-20.1
-0.425.3-2.20.1-4.0-23.0
-0.622.5-2.4-2.9-4.2-25.1
-0.820.0-2.6-5.1-4.4-27.1
-1.017.9-2.8-7.6-4.6-28.9
-1.215.1-3.0-9.9-4.8-31.2
-1.410.2-3.2-12.5-5.0-33.1
-1.67.5-3.4-15.0

新窗口打开| 下载CSV


从表2和表3中可以看出,电机上行时局部最佳补偿电流iqcom约为2.6 A;下行时局部最佳补偿电流iqcom约为-2.2 A。

在得到电机上下行局部最佳补偿电流iqcom后,同样以试验方法获取局部最佳补偿电流idcom,试验时已经可以利用局部最佳补偿电流idcom、iqcom对式(9)估计到的d-q轴电流进行补偿。最终微调,可以得到最优补偿电流idcom、iqcom。

4.2 试验验证

为验证本文所提出的混合控制策略及电流补偿的正确性,同时设置了直线型磁栅编码器以反馈的实际角位置与速度,与估计值进行比较,但不参与整个系统控制过程。根据设置在样机行程两端的限位开关,进行速度给定取反,使样机实际运行速度反向。

本试验中,电机下行时,取$i_d^*$=4 A。$i_d^*$最大值idmax和电机速度v有关,因为粘滞摩擦力Dv和速度v有关,下行时,速度v越大,粘滞摩擦力越大,所需要的电磁制动力就越小,iq越小,根据式(15)可知idmax越大,但需要满足式(16);在速度为0.5 m/s时,idmax为12 A。$i_d^*$的最小值需要保证电压电流信号中基波占比能够准确辨识出速度,本系统$i_d^*$最小取3.3 A,取整数4 A,既保证了能够准确估计出速度,又减小了相电阻消耗的功率。

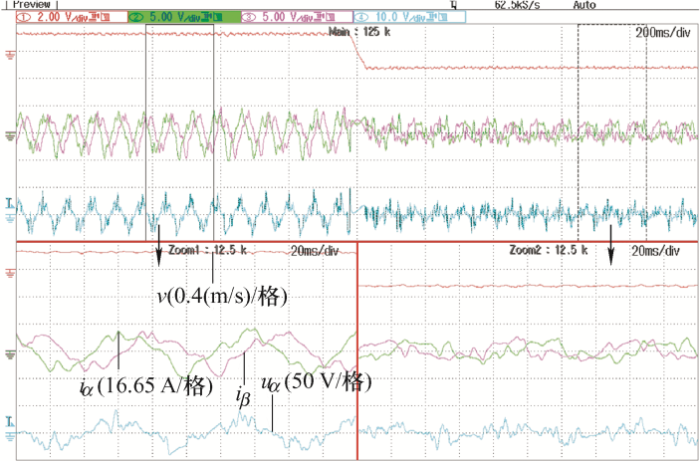
图4给出了电机上、下行时,$i_d^*$=4 A的电压电流试验波形。Zoom1、Zoom2分别为电机上、下行时的波形。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   id*=4 A,电机上下时的电压电流波形图


图4中各量的THD大小如下：iα的THD= 75.43%,iβ的THD=77.17%,uα的THD=320.46%。$i_d^*$=4 A的THD比$i_d^*$=0 A的THD减小,由于id的注入,提高了电流、电压的基波占比,从而满足了速度辨识的要求。

考虑到注入的id将在电机绕组和功率器件中产生损耗,因此,在满足位置和速度辨识需求的前提下,注入的id越小越好。

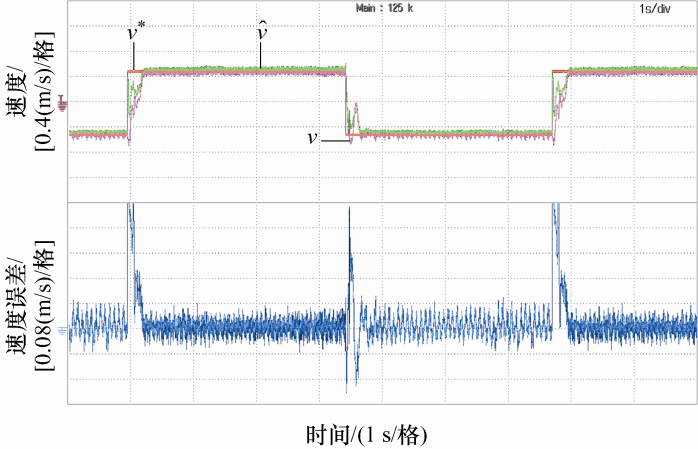
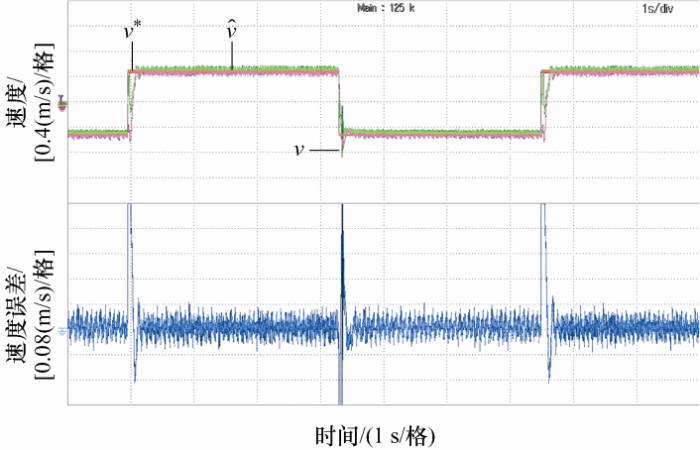
图5是补偿前,电机运行速度波形图,稳态时,估计速度误差为0.08 m/s。图6是补偿前,电机运行角位置波形图。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5   补偿前速度响应波形图


图6

新窗口打开| 下载原图ZIP| 生成PPT

图6   补偿前角位置波形图


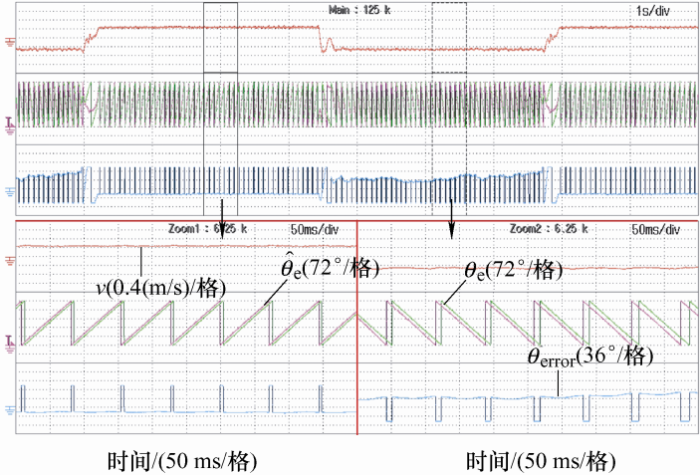
图6中,Zoom1和Zoom2分别是电机上下行稳定运行时波形的局部放大图。上行稳态时,估计角度与实际角度的最大误差为-20°,下行稳态时估计角度与实际角度的最大误差为36°。LFSPM电机上下行能够稳定运行,证明了本文提出的混合控制策略的有效性。

图7是补偿后电机运行速度波形图。稳态时,速度估计误差为0.08 m/s。图8是补偿后电机运行角位置波形图。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7   补偿后速度响应波形图


图8

新窗口打开| 下载原图ZIP| 生成PPT

图8   补偿后角位置波形图


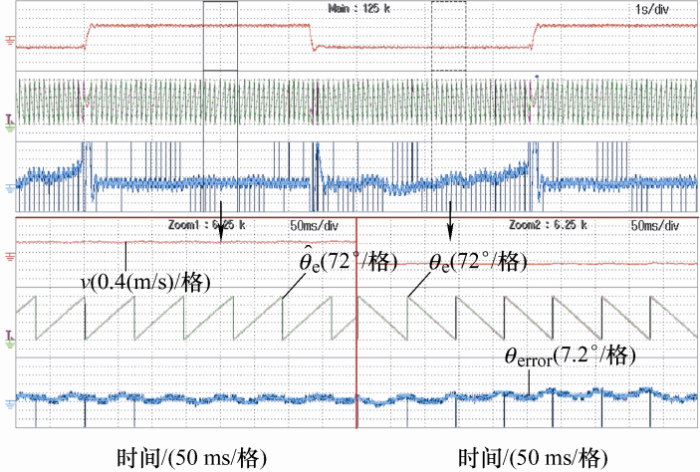
图8中,Zoom1和Zoom2分别是电机上下行稳定运行时波形的局部放大图。上行稳态时,估计角度与实际角度的最大误差为7.2°,下行稳态时估计角度与实际角度的最大误差为15°。且补偿后,速度给定突变时,速度响应时间明显减小。

5 结论

本文构建了LFSPM电机基于d-q轴数学模型的模型参考自适应系统,提出了混合控制策略,针对电机下行处于轻载制动发电状态,电压电流信号中基波占比低,提出增磁控制,利用id调节电压电流信号中基波占比来满足速度辨识的要求,实现了LFSPM电机四象限无位置传感器控制,证明了本文提出的混合控制策略的有效性。考虑到可调模型中d-q轴电感、相电阻和永磁磁链幅值等参数为静态测量的固定数值情况下,MRAS系统出现速度稳态估计误差,提出了电流补偿的方法,通过试验验证了可行性。结果表明,采用混合控制策略的LFSPM电机无位置传感器矢量控制系统运行稳定可靠,且在电流补偿后,估计角位置最大误差从36°减小到15°,位置估计精度提高了58.33%。

需要说明的是,本文控制策略虽然实现了LFSPM电机的四象限稳定运行,但位置角最大估计误差仍然偏大,这也是下一步的研究重点。

参考文献

程明, 张邦富, 王飒飒, 等.

模块化细轭部磁通切换永磁直线电机及其控制

[J]. 电气工程学报, 2021, 16(1):1-8.

[本文引用: 1]

CHENG Ming, ZHANG Bangfu, WANG Sasa, et al.

Modular thin yoke linear flux-switching permanent magnet machine and control system

[J]. Journal of Electrical Engineering, 2021, 16(1),1-8.

[本文引用: 1]

薛晓明, 杨翀.

一种统一的无刷直流电机直接反电动势法

[J]. 电工技术学报, 2010, 25(9):62-68.

[本文引用: 1]

XUE Xiaoming, YANG Chong.

A unified approach to direct back EMF detection for brushless DC motor

[J]. Transactions of China Electrotechnical Society, 2010, 25(9):62-68.

[本文引用: 1]

史婷娜, 吴曙光, 方攸同, 等.

无位置传感器永磁无刷直流电机的起动控制研究

[J]. 中国电机工程学报, 2009, 29(6):111-116.

[本文引用: 1]

SHI Tingna, WU Shuguang, FANG Youtong, et al.

Reasearch on sensorless PM brushless DC motor starting control

[J]. Proceedings of the CSEE, 2009, 29(6):111-116.

[本文引用: 1]

涂小涛, 辜承林.

新型横向磁通永磁电机无位置传感器磁链自适应直接转矩控制

[J]. 中国电机工程学报, 2013, 33(9):97-103.

[本文引用: 1]

TU Xiaotao, GU Chenglin.

Direct torque and adaptive flux sensorless control of novel transverse flux permanent magnet motors

[J]. Proceedings of the CSEE, 2013, 33(9):97-103.

[本文引用: 1]

GAO Jin, HU Yuwen.

Direct self-control for BLDC motor drives based on three-dimensional coordinate system

[J]. IEEE Transactions on Industrial Electronics, 2010, 57(8):2836-2844.

DOI:10.1109/TIE.2009.2036027      URL     [本文引用: 1]

周扬忠, 龙世鹏.

基于转子高频脉动电流注入的同步电动机无位置传感器型直接转矩控制

[J]. 中国电机工程学报, 2015, 35(1):223-230.

[本文引用: 1]

ZHOU Yangzhong, LONG Shipeng.

Sensorless direct torque control for synchronous motors based on injection of high-frequency ripple currents into the rotor winding

[J]. Proceedings of the CSEE, 2015, 35(1):223-230.

[本文引用: 1]

MEDJMADJ S, DIALLO D, MOSTEFAI M, et al.

PMSM drive position estimation:Contribution to the high- frequency injection voltage selection issue

[J]. IEEE Transactions on Energy Conversion, 2015, 30(1):349-358.

DOI:10.1109/TEC.2014.2354075      URL     [本文引用: 1]

刘海东, 周波, 郭鸿浩, 等.

脉振高频信号注入法误差分析

[J]. 电工技术学报, 2015, 30(6):38-44.

[本文引用: 1]

LIU Haidong, ZHOU Bo, GUO Honghao, et al.

Error analysis of high frequency pulsating signal injection method

[J]. Transactions of China Electrotechnical Society, 2015, 30(6):38-44.

[本文引用: 1]

ALMARHOON A H, ZHU Z Q, XU P.

Improved rotor position estimation accuracy by rotating carrier signal injection utilizing zero-sequence carrier voltage for dual three-phase PMSM

[J]. IEEE Transactions on Industrial Electronics, 2017, 64(6):4454-4462.

DOI:10.1109/TIE.2016.2561261      URL     [本文引用: 1]

SHI Yuchhao, SUN Kai, HUANG Lipei, et al.

Online identification of permanent magnet flux based on extended Kalman filter for IPMSM drive with position sensorless control

[J]. IEEE Transactions on Industrial Electronics, 2012, 59(11):4169-4178.

DOI:10.1109/TIE.2011.2168792      URL     [本文引用: 1]

HAMIDA M A, DELEON J, GLUMINEAU A, et al.

An adaptive interconnected observer for sensorless control of PM synchronous motors with online parameter identification

[J]. IEEE Transactions on Industrial Electronics, 2013, 60(2):739-748.

DOI:10.1109/TIE.2012.2206355      URL     [本文引用: 1]

钟臻峰, 金孟加, 沈建新.

基于分段PI调节器的模型参考自适应永磁同步电动机全转速范围无传感器控制

[J]. 中国电机工程学报, 2018, 38(4):1203-1211,1297.

[本文引用: 1]

ZHONG Zhenfeng, JIN Mengjia, SHEN Jianxin.

Full speed range sensorless control of permanent magnet synchronous motor with phased PI regulator-based model reference adaptive system

[J]. Proceedings of the CSEE, 2018, 38(4):1203-1211,1297.

[本文引用: 1]

孔龙涛, 程明, 张邦富.

基于模型参考自适应系统的模块化磁通切换永磁直线电机无位置传感器控制

[J]. 电工技术学报, 2016, 31(17):132-139.

[本文引用: 1]

KONG Longtao, CHENG Ming, ZHANG Bangfu.

Position sensorless control of modular linear flux-switching permanent magnet machine based on model reference adaptive system

[J]. Transactions of China Electrotechnical Society, 2016, 31(17):132-139.

[本文引用: 1]

张明利.

电梯用磁通切换永磁直线电机的驱动控制系统研究

[D]. 南京:东南大学, 2018.

[本文引用: 1]

ZHANG Mingli.

Research on control system of linear flux-switching permanent magnet motor for elevator

[D]. Nanjing:Southeast University, 2018.

[本文引用: 1]

王成元, 夏加宽, 孙宜标. 现代电机控制技术[M]. 北京: 机械工业出版社, 2009.

[本文引用: 2]

WANG Chengyuan, XIA Jiakuan, SUN Yibiao. Modern control technology for electric machines[M]. Beijing: China Machine Press, 2009.

[本文引用: 2]

/

〈 〉