1 引言
永磁同步电机(Permanent magnet synchronous motor,PMSM)与逆变器间加入LC滤波器是降低高频电流谐波的有效手段[1 ] 。考虑到体积和电磁干扰因素,滤波器更适宜独立于逆变器布置,电机控制系统相电流检测传感器由此便于布置在逆变器侧[2 -3 ] 。不同于传统电机系统,引入LC滤波器后,电流环控制器比例积分(Proportional integral,PI)参数不仅决定电机动态与稳态性能,还对系统稳定性和谐振性能及高频谐波产生影响[4 ⇓ ⇓ ⇓ -8 ] 。因此,研究电流环PI参数设计方法,对于改善前置滤波器电机系统性能极具实用价值。
传统电机系统PI参数设计方法的研究较多。其中,Ziegler-Nichols法[9 ] 和零极点相消法[10 ] 得到广泛应用。Ziegler-Nichols法不需要识别系统参数,通过寻找稳定极限确定PI增益,但未考虑其余性能指标。零极点相消法忽略影响中低频段较小的环节,结合截止频率调整PI参数,使电机传递函数极点与控制器零点相抵消,以提高系统动态性能。近年来,对传统参数整定方法也进行了不少改进。文献[11 ]基于零极点相消法和PMSM系统频域模型,考虑了逆变器死区和延时等因素,推导出电流环PI控制器参数与开环截止频率和相位裕度关系,受界定范围影响,其PI参数取值范围较大且需要多次比对。在文献[11 ]的基础上,文献[12 ]通过建立最小评价函数迭代学习最优开环截止频率,简化了计算步骤,提高了系统响应速度,但超调量等性能未能兼顾。文献[13 ]分析了电流环带宽、延迟与PI参数关系,进而通过改变PI参数以提高电流环动态响应能力。文献[14 ]通过预测控制与PI控制结合,提高了系统动态性能并拓展了PI参数稳定域。文献[15 ]建立了PMSM控制系统离散模型,将时域性能指标转换成频域特征量,通过频域分析进行PI参数整定。文献[16 ]提出一种多目标设计方法,通过分析PI参数与时域指标、频域指标和系统参数的关系,确定可直接取值的PI参数期望区域,但PI参数取值范围较广。
关于前置滤波器电机系统的电流环参数设计研究较少。传统的Ziegler-Nichols法与系统结构无关,零极点相消法着重关注中低频段,因而这两种方法可用于前置滤波器系统,但性能有限。在文献[11 ⇓ ⇓ ⇓ ⇓ -16 ]中,PI参数设计方法均面向无滤波器传统电机系统,均未涉及引入滤波器后的谐振和稳定性问题。可见,针对前置滤波器电机系统,其电流环参数设计问题尚未有效解决,还需要全面考虑PI参数对系统性能的影响,进而在满足稳定性基础上最大化兼顾系统综合性能需求。
本文针对前置LC滤波器PMSM系统,研究其电流环PI参数设计方法,推导逆变器侧电流反馈系统开环传递函数,分析PI参数对系统稳定性、动态性能、带宽以及谐振峰值的影响,在此基础上确定PI参数稳定域并给出优化目标及其约束范围,通过遗传算法求解电流环参数,并进行系统仿真验证。
2 逆变器侧电流反馈系统数学模型
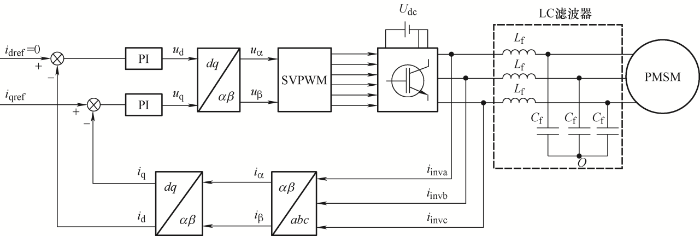
图1 为前置LC滤波器的PMSM系统矢量控制结构框图,其中的相电流i inva 、i invb 和i invc 检测位于逆变器侧。在d -q 旋转坐标系下,前置LC滤波器PMSM系统的电压和电流方程如式(1)~(6)所示。
(1) d i invd d t = 1 L f u invd − u sd + ω e i invq
(2) d i invq d t = 1 L f u invq − u sq − ω e i invd
(3) d u sd d t = 1 C f i invd − i sd + ω e u sq
(4) d u sq d t = 1 C f i invq − i sq − ω e u sd
(5) u sd = R s i sd + L d d i sd d t − ω e L q i sq
(6) u sq = R s i sq + L q d i sq d t + ω e L d i sd + ω e ψ f
式中,i invd 、i invq 分别为逆变器侧d 、q 轴电流;i sd 、i sq 分别为电机侧d 、q 轴电流;u invd 、u invq 分别为逆变器侧d 、q 轴电压;u sd 、u sq 分别为电机侧d 、q 轴电压;ω e 为电角速度;L d 、L q 分别为d 、q 轴电感;R s 为定子电阻;ψ f 为永磁体磁链。
图1
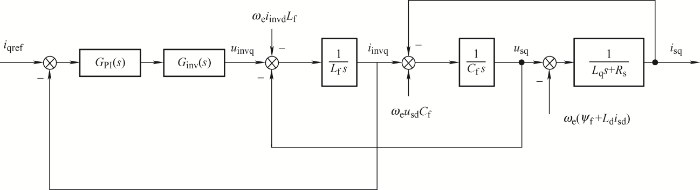
由式(1)~(6)可得前置滤波器PMSM系统的q 轴电流环框图如图2 所示。其中,PI控制器G PI (s )如式(7)所示,逆变器G inv (s )如式(8)所示,K p 、K i 分别为比例系数和积分系数,T d 为采样与传输延迟。
(7) G PI ( s ) = K p + K i s
(8) G inv s = 1 T d s + 1
图2
根据图2 ,由梅森公式计算可得电流环q 轴开环传递函数G q (s ),如式(9)所示
(9) G q ( s ) = ( K p s + K i ) ( C f L s s 2 + C f R s s + 1 ) s ( T d s + 1 ) [ L f C f L s s 3 + L f C f R s s 2 + L f + L s s + R s ]
3 电流环PI参数对系统性能的影响
3.1 电流环PI参数对系统稳定性的影响
由式(9)结合表1 参数可得,前置滤波器系统的电流环开环传递函数G q (s )如式(10)所示。其根轨迹增益K =3.124 7K i ,零点分别为z 1,2 =-88.9±2 633.7i,z 3 =-K i /K p ,极点为p 1,2 =-12.7±6 971.9i,p 3 =-6 666.6,p 4 =-152.4,p 5 =0。
(10) G q ( s ) = 3.124 7 K i K p K i s + 1 ( 1.44 × 10 − 7 s 2 + 2.56 × 10 − 5 s + 1 ) s ( 1.5 × 10 − 4 s + 1 ) ( 6.56 × 10 − 3 s + 1 ) ( 2.057 × 10 − 8 s 2 + 5.225 × 10 − 7 s + 1 )
(11) G cq s = G q s 1 + G q s = G q s D s
由闭环特征方程D (s )=0可知,K p 、K i 直接影响根轨迹走向,不当配置会出现右半平面极点,造成系统不稳定。由于系统特征根之和为常数,此时零点和与极点和相等,如式(12)所示
(12) ∑ i = 1 5 p i = ∑ j = 1 3 z j
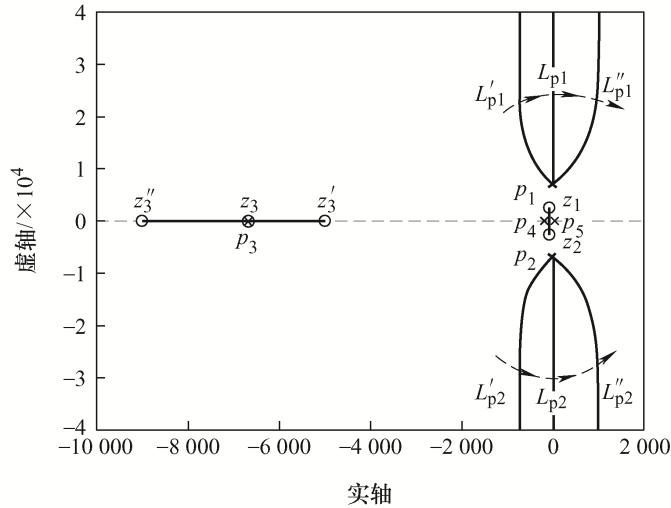
由式(12)计算得到,当K i /K p =6 666.6时,z 3 与p 3 重合;当K i /K p >6 666.6时,z" 3 位于p 3 左侧;当K i /K p <6 666.6时,z' 3 位于极点p 3 右侧。将对应三种PI参数代入式(10),可得根轨迹曲线如图3 所示。其中L p1 、L p2 ,L' p1 、L' p2 ,L" p1 、L" p2 分别受z 3 、z' 3 、z" 3 影响并以p 1 、p 2 为起点。由图3 可知,当K i /K p >6 666.6时,系统不稳定;当K i /K p =6 666.6时,系统临界稳定;当K i /K p <6 666.6时,系统稳定,此时根轨迹曲线位于左半平面,为最小相位系统。
图3
式(10)所示开环传递函数分母高于分子2个阶次,幅值裕度始终满足稳定要求[17 ] ,保证系统稳定只需要满足约束式(13)所示相位裕度即可。
(13) P m = 180 ∘ + ∠ G q j ω
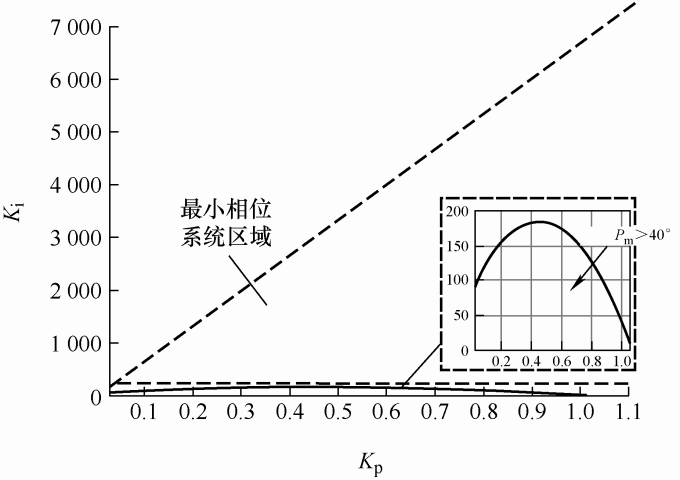
期望相位裕度P m ≥40°[11 ] ,结合最小相位系统稳定约束K i /K p <6 666.6,绘制PI参数取值范围如图4 所示。在图4 所示最小相位系统内,取P m ≥40°箭头所示区域作为本文所提方法的PI参数稳定域。
图4
3.2 电流环PI参数对谐振峰值的影响
前置滤波器会使系统在谐振频率ω res 处产生较大谐振峰值,ω res 可表示如下[18 ]
(14) ω res = L f + L s L f L s C f
由式(14)可得到本文系统ω res =6 972 rad/s,对应1 109 Hz。根据式(10)所示系统开环幅频特性,谐振峰值M r 可通过式(15)计算得出。
(15) M r = 20 lg G q j ω res
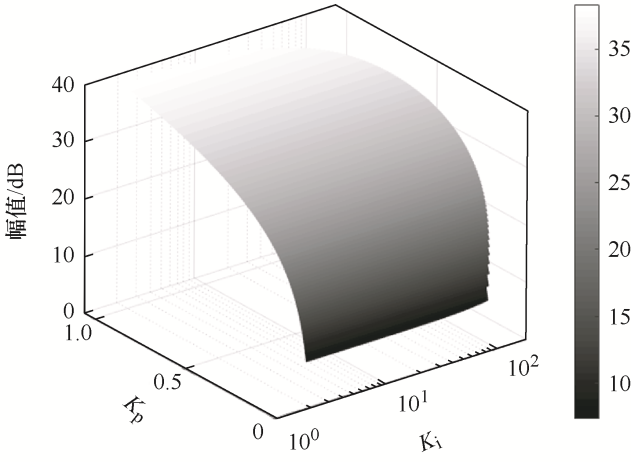
谐振峰会影响电流谐波幅值和谐波畸变率[3 ⇓ ⇓ ⇓ -7 ] ,应在保证系统稳定基础上削减谐振峰值。由式(15)绘制M r 与PI参数关系如图5 所示,可见,M r 与K p 和K i 有关,且K p 影响更明显,K p 应取小以降低M r 。
图5
3.3 电流环PI参数对系统动态性能的影响
动态性能由超调量σ %、上升时间t r 和调节时间t s 描述[19 -20 ] ,可由式(16)所示时域特性表达式得到,其中1/s 为单位阶跃输入传递函数,c (t )为系统输出,L -1 为拉普拉斯反变换算子。
(16) c t = L − 1 1 s ⋅ G q s 1 + G q s
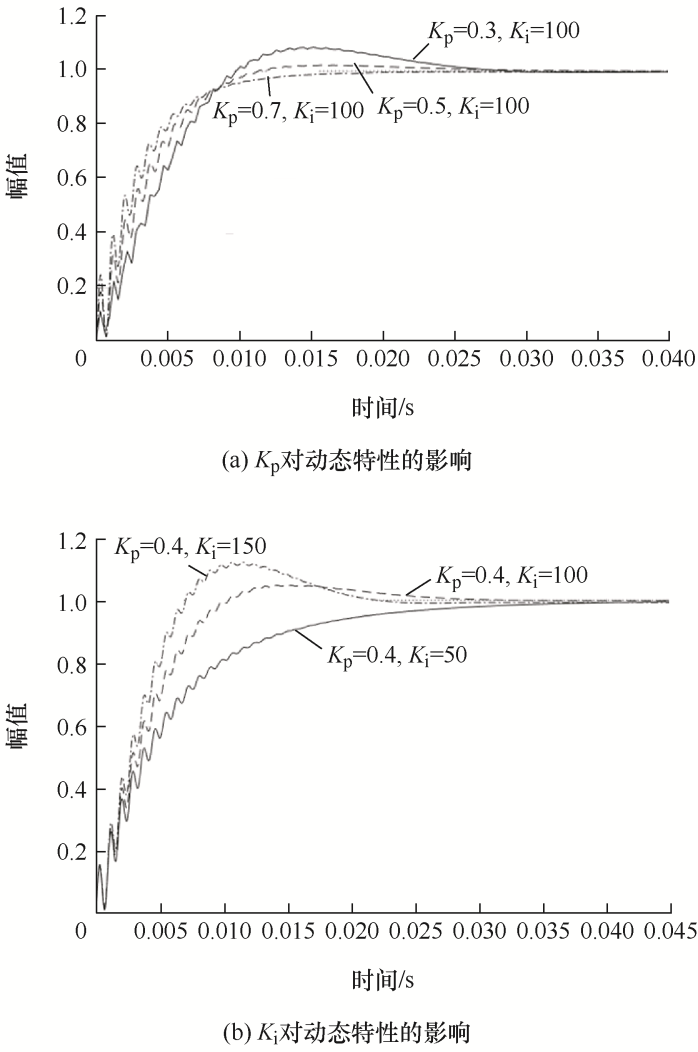
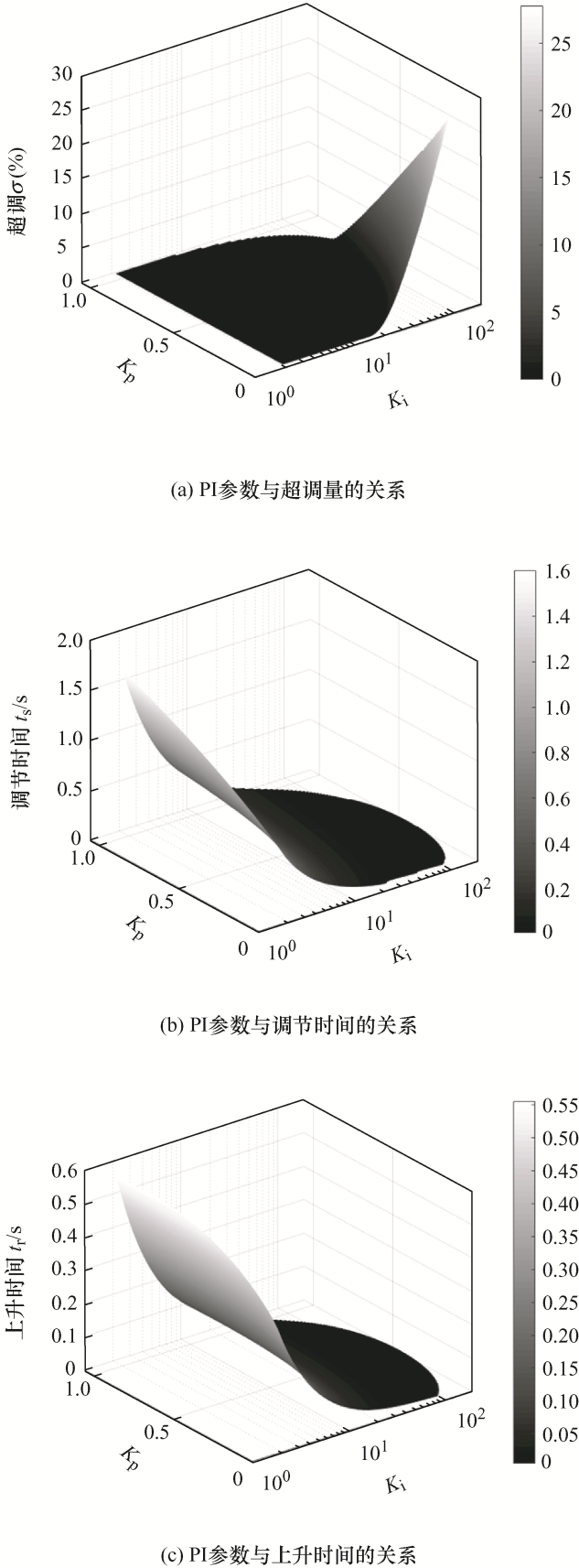
在图4 所示P m ≥40°区域内,选取三组K i 相同、K p 不同和K p 相同、K i 不同的PI参数,由式(16)绘制单位阶跃响应曲线如图6 所示。可见,当K i 不变时,σ %、t s 和t r 均随K p 增大而减小;当K p 不变而K i 增大时,σ %随之增大,t s 和t r 随之减小。绘制PI参数与动态性能指标的三维关系如图7 所示,结合图6 可见,K p 越小或K i 越大时,σ %越大,t s 和t r 越小。
图6
图7
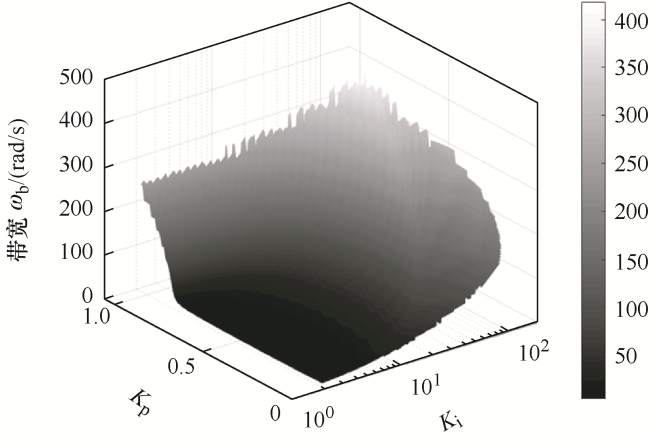
3.4 电流环PI参数对系统带宽的影响
电流环带宽取闭环幅频特性-3 dB或相频特性-90°对应频率中的较小值[13 ] ,即
(17) ω b = min ω b 1 , ω b 2 20 lg G cq j ω b 1 = − 3 dB ∠ G cq j ω b 2 = − 90 °
本文电机额定转速为500 r/min,对应角频率为209.4 rad/s,带宽ω b
(18) ω b > 209. 4 rad/s
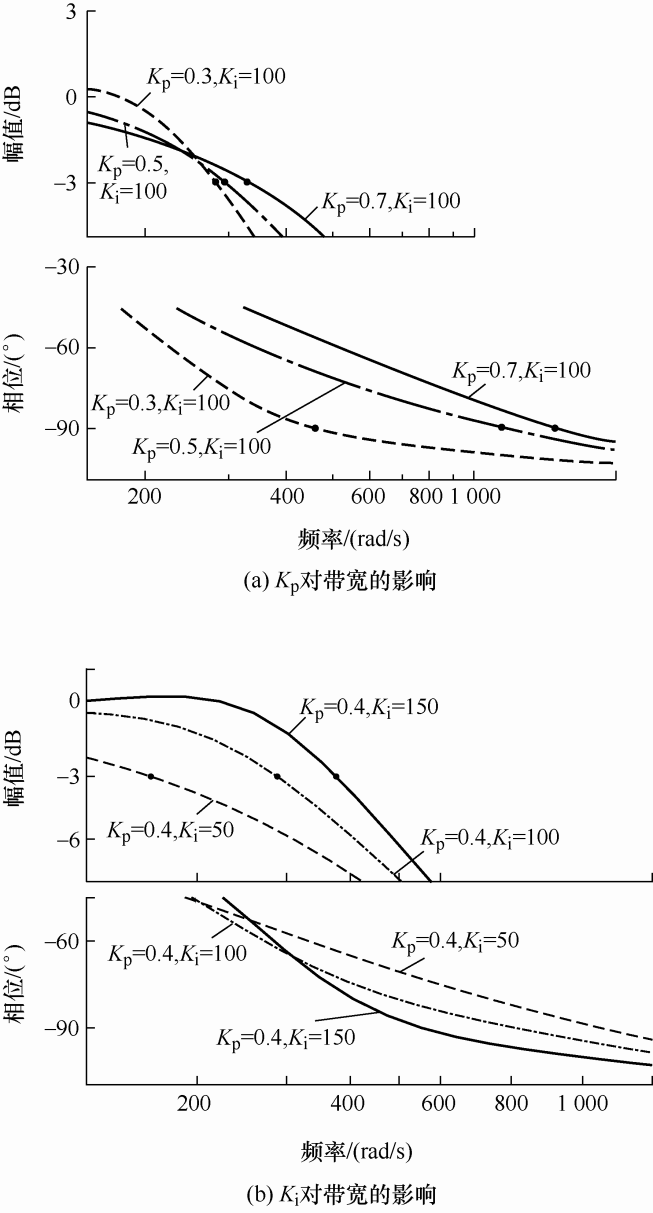
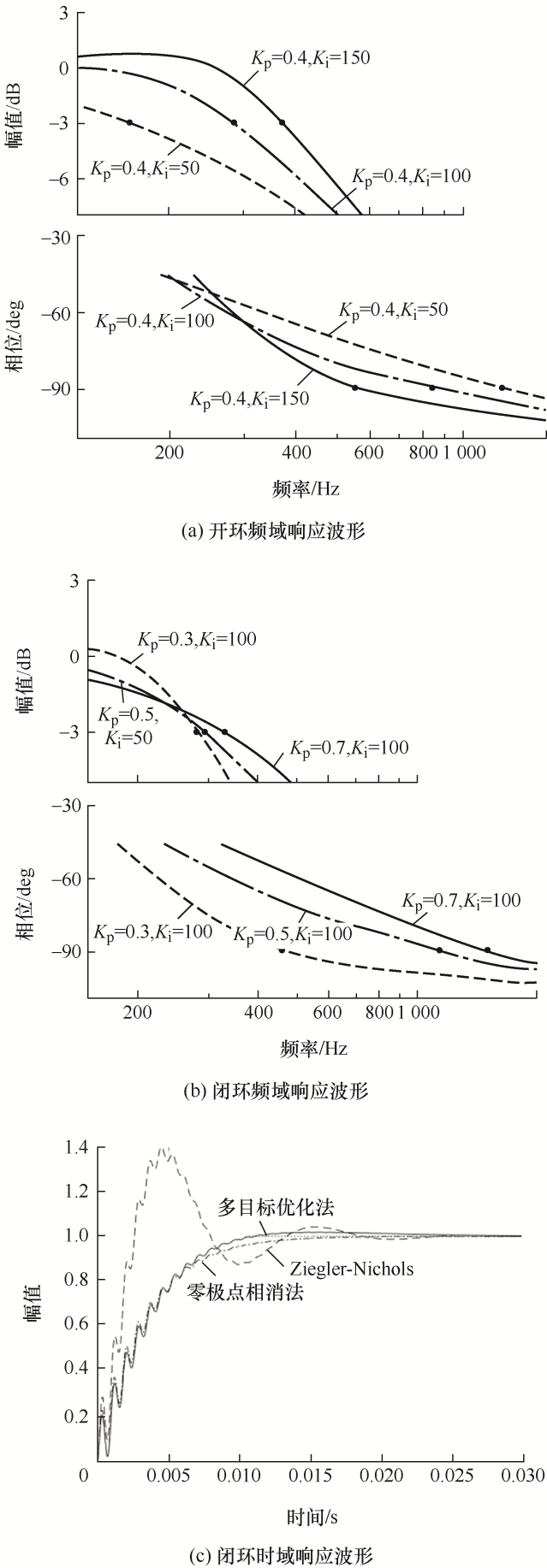
应用与图6 相同的PI参数,绘制闭环系统伯德曲线如图8 所示。图8a 为K i 不变时K p 对电流环带宽的影响。可见,带宽随K p 增大而变大,结合图6a 可知,带宽大的系统响应速度快,上升时间和调节时间小,超调量小。
图8
图8b 为K p 不变时K i 对带宽的影响,可见,带宽随K i 的增大而增大,结合图6b 可知,带宽越大,系统响应速度越快,上升时间和调节时间越小,超调量大。因此,可通过调节PI参数,使系统具有较大的带宽,进而提高系统响应速度,获得较小上升时间t r 和调节时间t s 。
4 电流环PI参数多目标优化
由以上分析可知,前置滤波器电机系统的带宽与动态性相关,高带宽系统响应速度快、调节时间t s 和上升时间t r 短,从动态性能角度可选取带宽ω b [21 ] 。超调量σ %单独作为优化目标之一。同时,为了降低谐振峰值减小高频电流谐波,将谐振峰值也作为一个优化目标。
针对闭环带宽、超调量和谐振峰值目标,本文采用遗传算法(Genetic algorithm, GA)优化设计电流环PI参数,设计过程如下所示。
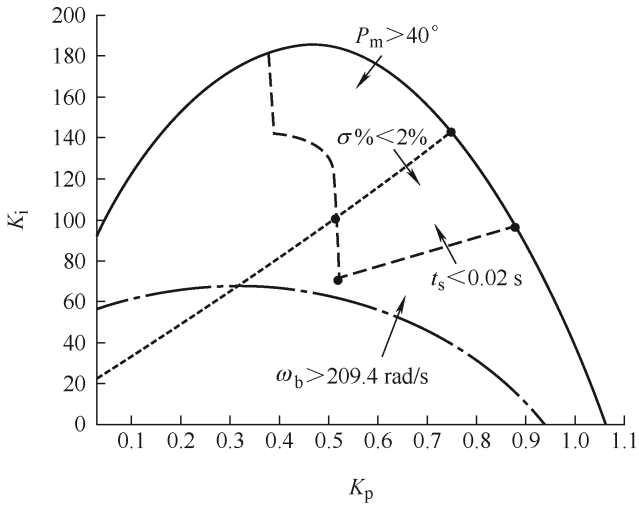
步骤1:PI参数取值范围确定。根据前述分析,系统各性能指标受PI参数的影响不同,为获得良好的综合性能,要求相位裕度P m ≥40°,带宽ω b t s <0.02 s,超调量σ %<2%,谐振峰值尽可能小。
绘制满足上述性能要求的PI参数范围如图9 所示。其中,四个标记点所围成的四边形区域即为满足上述性能要求的约束区域,也是PI参数多目标寻优的取值范围。
图9
步骤2:多目标优化模型构建。以闭环带宽ω b σ %和谐振峰值M r 最小作为优化目标,以图9 所示约束区域作为种群取值范围,以K p 和K i 作为设计变量,构建多目标优化模型如式(19) 所示
(19) max f 1 x = ω b K p , K i min f 2 x = σ K p , K i min f 3 x = M r K p , K i s . t . K p , K i ⊆ R P m ≥ 40 ° ∩ R σ % < 2 % ∩ R t s < 0.02 s ∩ R ω b > 209.4 rad/s
式中,f 1 (x )、f 2 (x )、f 3 (x )分别为ω b σ %和M r 的函数,描述三个优化目标与PI参数的关系;R (x )表示满足x 条件的PI参数取值范围。
当在稳定域内随机取值PI参数时,对应的f 1 (x )、f 2 (x )、f 3 (x )的值可分别通过式(17)、式(16)、式(15)计算得到。
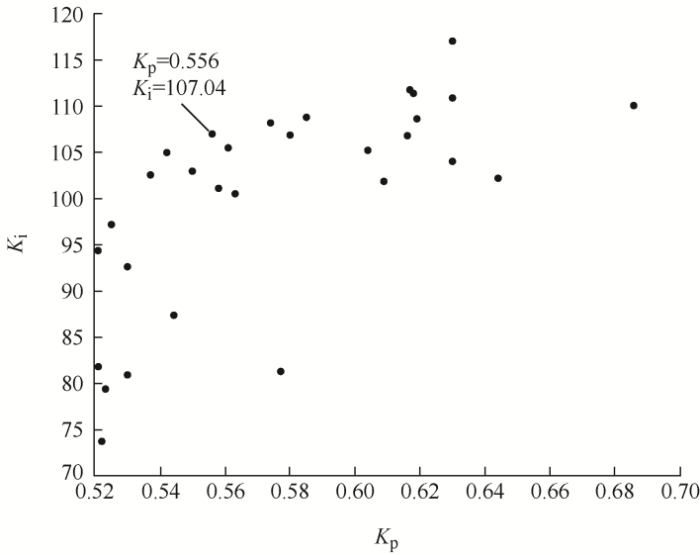
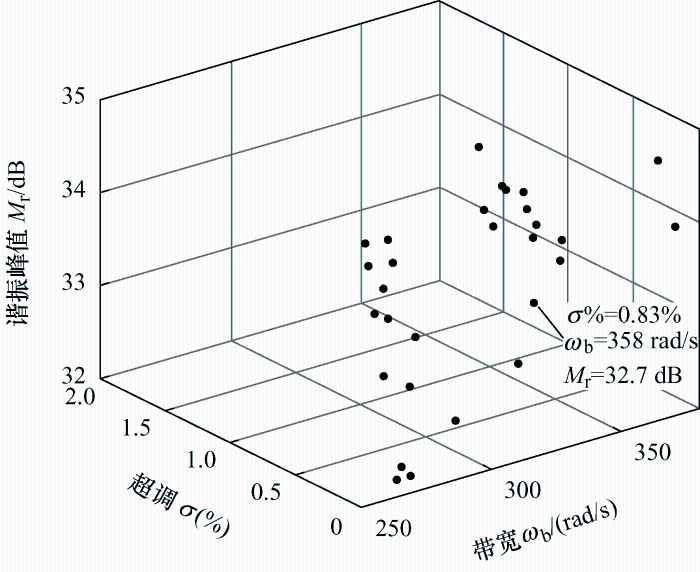
步骤3:遗传算法寻优。在图9 所示PI参数多目标约束范围中,配置种群规模为30,应用式(19)对种群中个体进行评价,将性能好的个体保存到下一代,两次迭代之间数据交叉概率取为0.8,变异概率取为0.2,迭代500次。遗传算法寻优得到的PI参数解集如图10 所示,其对应的优化目标数值构成图11 所示Pareto前沿。根据图10 和图11 ,考虑超调量小、谐振峰小和闭环带宽大的需求,本文选取K p =0.556,K i =107.04作为PI控制器参数,该取值可使系统有较小超调(σ %=0.83)和较小谐振峰值(M r =32.7 dB)及较大带宽(ω b
图10
图11
5 与传统参数设计方法的性能比较
应用传统Ziegler-Nichols法设计本系统参数,如图12 所示,当调节临界比例度K c =1.5时,系统临界振荡周期T c =0.001 s。由经验公式K p =0.45K c 、K i =K p /0.833T c 可得K p =0.675,K i =810.3。
图12
应用传统零极点相消法设计本文系统参数时,将表1 数据代入式(9),忽略较小影响中低频段环节,传递函数极点与控制器零点抵消,将电流内环校正为一阶系统。由此,PI参数设计为K p /K i = 6.56×10-3 ,电流环开环传递函数化简为G qx (s )= 3.124 7K i /s ,结合式(17)可求得带宽与PI参数关系为K i =ω b /3.124 7。再由式(19)可绘制P m ≥40°稳定域内PI参数与带宽关系如图13 所示,可以看出能实现的最大带宽约为300 rad/s,进而可计算出K p =0.63,K i =96。
图13
图14
由图14 和表2 可见,三种方法系统稳态误差均趋于0。Ziegler-Nichols法相位裕度较小(P m =31.8°),谐振峰值大(M r =34.5 dB),带宽大(ω b t r =2.4 ms),但超调过大(σ %= 37.72%),稳态调节时间长(t s =17.4 ms)。零极点相消法系统稳定性提高(P m =40.9°),谐振峰值降低(M r =33.8 dB),超调约为0,但带宽小(ω b t r =7.5 ms),稳态调节时间较长(t s =12.7 ms)。本文所提多目标优化方法通过对超调、带宽和谐振峰值进行综合寻优,系统稳定性好(P m =41°),谐振峰值低(M r =32.7 dB),带宽较大(ω b σ %= 0.83%,t r =6.8 ms,t s =9.5 ms)。
6 仿真验证
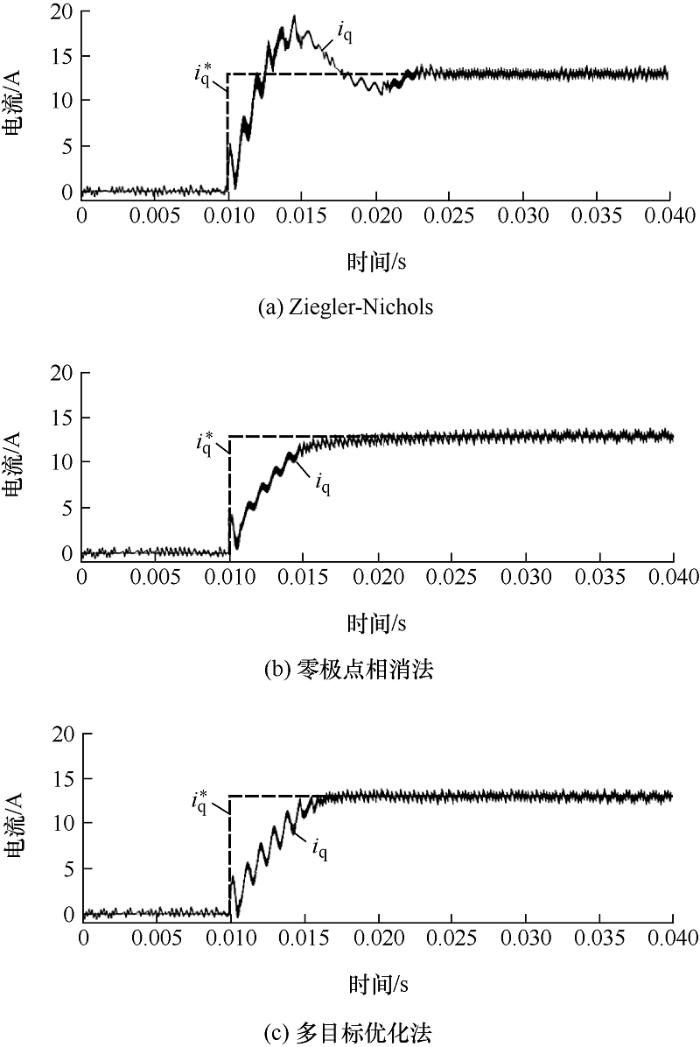
针对传统Ziegler-Nichols法、零极点相消法和本文多目标优化方法分别设计的PI参数,进行系统仿真。比较三组不同PI参数系统的如下性能:电流阶跃系统动态和稳态性能;正弦电流频率逐渐增加的电流环带宽;额定工况电流跟踪响应;谐振峰值和谐波抑制能力。
验证三种设计方法系统稳态和动态性能如下。图15 给出了q 轴给定13 A电流阶跃响应仿真波形。由图15 可见,不同参数系统均具有良好稳态性能。Ziegler-Nichols法的系统响应速度快,上升时间为2 ms,但超调量过大,约为33.33%,且调节时间长达16 ms。零极点相消法的超调量基本为0,但动态性能差,响应速度慢,t r =7 ms,t s =13 ms。多目标优化方法基本零超调,相较于零极点相消法响应速度也大大提升,t r =6 ms,t s =7 ms。上述指标与表2 相符。
图15
为验证三种设计系统电流环带宽,进行如下测试[22 ] 。给定幅值13 A、频率从1 rad/s逐渐增大的正弦信号,直至反馈信号幅值降至0.707倍或相位滞后90°。测试得到Ziegler-Nichols法、零极点相消法和多目标优化法对应的系统带宽分别为611 rad/s、280 rad/s和325 rad/s,如图16 所示。
图16
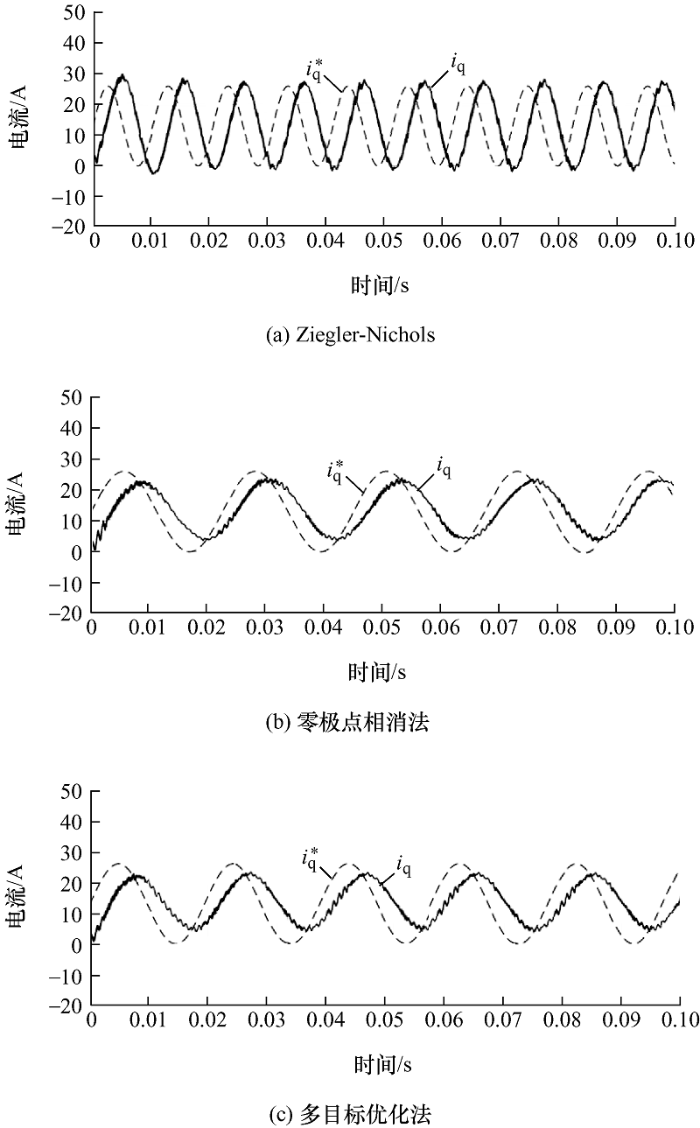
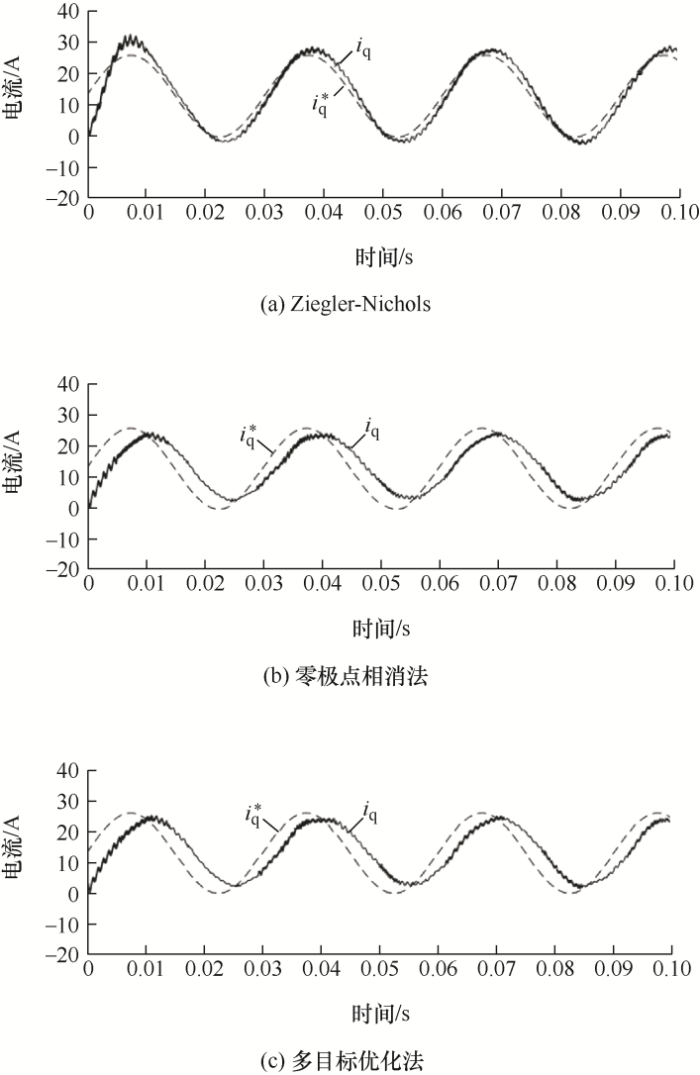
验证三种方法系统电流环跟踪性能如下。q 轴正弦给定幅值13 A、频率33.33 Hz (对应500 r/min),电流响应如图17 所示。可见,Ziegler- Nichols法可准确追踪给定信号,幅值几乎无衰减,跟踪延迟小(约为0.49 ms),对应相位滞后5.91°。零极点相消法的系统带宽最小,跟踪电流幅值衰减约2 A,约占给定幅值的15.3%,跟踪延迟约为2.99 ms,对应相位滞后35.99°。多目标优化方法中电流幅值衰减约1.49 A,占给定幅值的11.5%,跟踪延迟约为2.49 ms,对应相位滞后29.99°,优于零极点相消法的跟踪性能。
图17
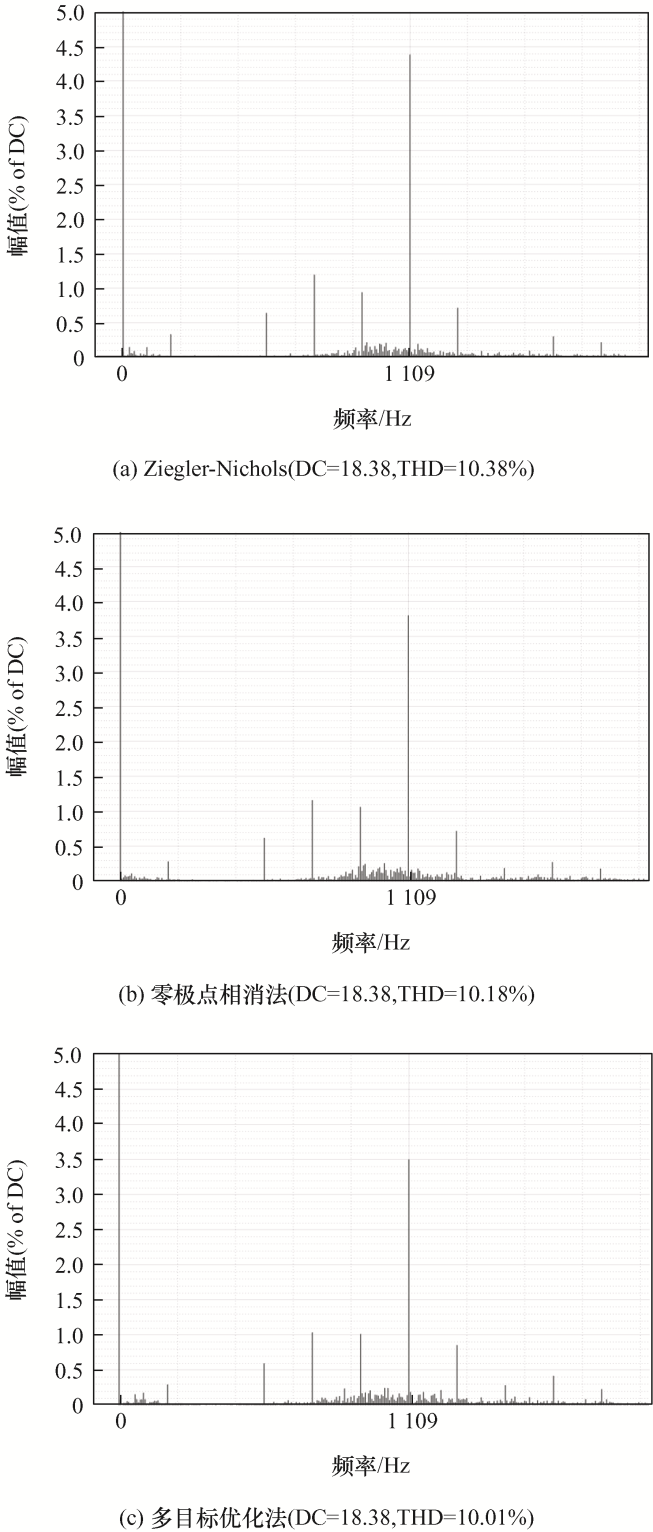
三种设计方法的系统谐振性能可通过谐振频率处(ω res =6 972 rad/s,对应1 109 Hz)的电流谐波进行比较分析。额定工况的逆变器侧q 轴电流频谱如图18 所示。由图18 可见,Ziegler-Nichols法系统谐振峰值最大,ω res 处电流谐波幅值占比H res =4.39%,谐波畸变率THD=10.38%。零极点相消法系统谐振峰值及谐波含量均有下降,H res =3.81%,THD=10.18%。与两种传统方法相比,多目标方法系统谐振峰值和谐波含量更低,H res =3.52%,THD=10.01%。
图18
综合上述仿真结果得到系统性能如表3 所示。三种设计方法系统仿真性能与表2 理论计算性能相符。其中,Ziegler-Nichols法系统带宽较大,但超调和高频谐波也最为严重。零极点相消法系统带宽小,电流响应速度较慢。多目标优化法系统可以权衡优化多项性能指标,在保证系统良好动态性能的同时,又能够有效抑制谐振峰和电流高频谐波。
7 结论
针对逆变器侧电流反馈的前置滤波器永磁同步电机系统,本文提出一种电流环PI参数多目标优化设计方法,进行了理论分析和仿真验证,并与两种传统参数设计方法进行了比较,得出如下结论。
(1) 多目标优化方法可兼顾超调量、带宽、谐振、谐波、上升和调节时间等系统多个性能指标,传统Ziegler-Nichols法及零极点相消法则难以做到。
(2) 与传统Ziegler-Nichols法相比,多目标优化方法系统通过适当减小带宽及电流跟踪能力,可以大大降低超调量、谐振峰值及逆变器侧电流谐波。
(3) 与传统零极点相消法相比,多目标优化方法系统超调同样较小,电流环带宽更大,电流跟踪能力更好,谐振峰值及高频电流谐波有效降低。
参考文献
View Option
[1]
MISHRA P MAHESHWARI R Design, analysis, and impacts of sinusoidal LC filter on pulsewidth modulated inverter fed-induction motor drive
[J]. IEEE Transactions on Industrial Electronics , 2020 , 67 (4 ):2678 -2688 .
DOI:10.1109/TIE.41
URL
[本文引用: 1]
[2]
赵仁德 , 赵斌 , 徐海亮 , 等 . 带LC滤波器的永磁同步电机控制系统及策略研究
[J]. 电工技术学报 , 2019 , 34 (S1 ):79 -86 .
[本文引用: 1]
ZHAO Rende ZHAO Bin XU Hailiang et al. Research on control method of permanent magnet synchronous motor with LC filter
[J]. Transactions of China Electrotechnical Society , 2019 , 34 (S1 ):79 -86 .
[本文引用: 1]
[3]
TANG Yi LOH P C WANG Peng et al. Exploring inherent damping characteristic of LCL-filters for three-phase grid-connected voltage source inverters
[J]. IEEE Transactions on Power Electronics , 2012 , 27 (3 ):1433 -1443 .
DOI:10.1109/TPEL.2011.2162342
URL
[本文引用: 2]
[4]
刘飞 , 查晓明 , 周彦 , 等 . 基于极点配置与重复控制相结合的三相光伏发电系统的并网策略
[J]. 电工技术学报 , 2008 , 23 (12 ):130 -136 .
[本文引用: 2]
LIU Fei ZHA Xiaoming ZHOU Yan et al. Research on grid-connected strategy combining pole-assignment and repetitive control in three-phase photovoltaic system
[J]. Transactions of China Electrotechnical Society , 2008 , 23 (12 ):130 -136 .
[本文引用: 2]
[5]
张宪平 , 林资旭 , 李亚西 , 等 . LCL滤波的PWM整流器新型控制策略
[J]. 电工技术学报 , 2007 , 22 (2 ):74 -77 .
[本文引用: 2]
ZHANG Xianping LIN Zixu LI Yaxi et al. A novel control strategy for PWM rectifier with LCL filter
[J]. Transactions of China Electrotechnical Society , 2007 , 22 (2 ):74 -77 .
[本文引用: 2]
[6]
侯朝勇 , 胡学浩 , 惠东 . 基于离散状态空间模型的LCL滤波并网变换器控制策略
[J]. 中国电机工程学报 , 2011 , 31 (36 ):8 -15 ,237.
[本文引用: 2]
HOU Chaoyong HU Xuehao HUI Dong Control strategy of grid-connected converter with LCL filter based on discrete state-space model
[J]. Proceedings of the CSEE , 2011 , 31 (36 ):8 -15 ,237.
[本文引用: 2]
[7]
刘计龙 , 马伟明 , 肖飞 , 等 . 一种LCL滤波器有源阻尼策略与设计方法
[J]. 电机与控制学报 , 2013 , 17 (5 ):22 -27 .
[本文引用: 2]
LIU Jilong MA Weiming XIAO Fei et al. An active damping control strategy and design method for LCL filter
[J]. Electric Machines and Control , 2013 , 17 (5 ):22 -27 .
[本文引用: 2]
[8]
MA Wenjie GUAN Yuanpeng ZHANG Bo et al. Active disturbance rejection control based single current feedback resonance damping strategy for LCL-type grid-connected inverter
[J]. IEEE Transactions on Energy Conversion , 2021 , 36 (1 ):48 -62 .
DOI:10.1109/TEC.60
URL
[本文引用: 1]
[9]
JAGANATHAN B SHARANYA R DEVI S K et al. Ziegler-Nichol’s method of online tuning of PMSM for improved transient response
[C]// 2010 International Conference on Power,Control and Embedded Systems , 2010 :1 -4 .
[本文引用: 1]
[10]
LEE S B Closed-loop estimation of permanent magnet synchronous motor parameters by PI controller gain tuning
[J]. IEEE Transactions on Energy Conversion , 2006 , 21 (4 ):863 -870 .
DOI:10.1109/TEC.2005.853742
URL
[本文引用: 1]
[11]
王莉娜 , 朱鸿悦 , 杨宗军 . 永磁同步电动机调速系统PI控制器参数整定方法
[J]. 电工技术学报 , 2014 , 29 (5 ):104 -117 .
[本文引用: 4]
WANG Lina ZHU Hongyue YANG Zongjun Tuning method for PI controllers of PMSM driving system
[J]. Transactions of China Electrotechnical Society , 2014 , 29 (5 ):104 -117 .
[本文引用: 4]
[12]
王爽 , 冯坚栋 , 丁雪 , 等 . 基于最优开环截止频率学习的永磁伺服系统PI控制器参数整定方法
[J]. 电工技术学报 , 2017 , 32 (21 ):44 -54 .
[本文引用: 2]
WANG Shuang FENG Jiandong DING Xue et al. PI controllers tuning method of permanent magnet servo system based on optimal open-loop cut-off frequency learning
[J]. Transactions of China Electrotechnical Society , 2017 , 32 (21 ):44 -54 .
[本文引用: 2]
[13]
肖海峰 , 贺昱耀 , 乔社娟 . 永磁同步电机电流环频率响应改进策略研究
[J]. 电机与控制学报 , 2018 , 22 (6 ):107 -113 .
[本文引用: 3]
XIAO Haifeng HE Yuyao QIAO Shejuan Current loop frequency response improvement strategy research for permanent magnet synchronous motor control system
[J]. Electric Machines and Control , 2018 , 22 (6 ):107 -113 .
[本文引用: 3]
[14]
王伟华 , 肖曦 . 永磁同步电机电流增量预测算法参数设计及性能分析
[J]. 电机与控制学报 , 2013 , 17 (12 ):98 -105 .
[本文引用: 2]
WANG Weihua XIAO Xi Parameters design and performance analysis of current incremental predictive algorithm for PMSM
[J]. Electric Machines and Control , 2013 , 17 (12 ):98 -105 .
[本文引用: 2]
[15]
刘景林 , 公超 , 韩泽秀 , 等 . 永磁同步电机闭环控制系统数字PI参数整定
[J]. 电机与控制学报 , 2018 , 22 (4 ):26 -32 .
[本文引用: 2]
LIU Jinglin GONG Chao HAN Zexiu et al. Tuning method for digital PI controllers of PMSM closed-loop driving system
[J]. Electric Machines and Control , 2018 , 22 (4 ):26 -32 .
[本文引用: 2]
[16]
LI Haoyuan ZHANG Xing YANG Shuying et al. Multi-objective controller design of IPMSM drives based on DTD D-partition method considering parameters uncertainties
[J]. IEEE Transactions on Energy Conversion , 2019 , 34 (2 ):1052 -1062 .
DOI:10.1109/TEC.60
URL
[本文引用: 2]
[17]
YANG Ming LYU Zekai XU Donglin et al. Resonance suppression and EMI reduction of GaN-based motor drive with sine wave filter
[J]. IEEE Transactions on Industry Applications , 2020 , 56 (3 ):2741 -2751 .
DOI:10.1109/TIA.28
URL
[本文引用: 1]
[18]
MISHRA P MAHESHWARI R A simple feedforward approach to stabilize VSI-fed induction motor with filter in RFOC
[J]. IEEE Transactions on Industrial Electronics , 2020 , 67 (12 ):10191 -10201 .
DOI:10.1109/TIE.41
URL
[本文引用: 1]
[19]
BAO Chenlei RUAN Xinbo WANG Xuehua et al. Step-by-step controller design for LCL-type grid-connected inverter with capacitor-current-feedback active-damping
[J]. IEEE Transactions on Power Electronics , 2014 , 29 (3 ):1239 -1253 .
DOI:10.1109/TPEL.2013.2262378
URL
[本文引用: 1]
[20]
鲍陈磊 , 阮新波 , 王学华 , 等 . 基于PI调节器和电容电流反馈有源阻尼的LCL型并网逆变器闭环参数设计
[J]. 中国电机工程学报 , 2012 , 32 (25 ):133 -142 .
[本文引用: 1]
BAO Chenlei RUAN Xinbo WANG Xuehua et al. Design of grid-connected inverters with LCL filter based on PI regulator and capacitor current feedback active damping
[J]. Proceedings of the CSEE , 2012 , 32 (25 ):133 -142 .
[本文引用: 1]
[21]
王宏佳 , 杨明 , 牛里 , 等 . 永磁交流伺服系统电流环带宽扩展研究
[J]. 中国电机工程学报 , 2010 , 30 (12 ):56 -62 .
[本文引用: 1]
WANG Hongjia YANG Ming NIU Li et al. Current loop bandwidth expansion for permanent magnet AC servo system
[J]. Proceedings of the CSEE , 2010 , 30 (12 ):56 -62 .
[本文引用: 1]
[22]
孙伟 , 于泳 , 王高林 , 等 . 基于矢量控制的异步电机预测电流控制算法
[J]. 中国电机工程学报 , 2014 , 34 (21 ):3448 -3455 .
[本文引用: 1]
SUN Wei YU Yong WANG Gaolin et al. A predictive current control scheme for induction motor with vector control
[J]. Proceedings of the CSEE , 2014 , 34 (21 ):3448 -3455 .
[本文引用: 1]
Design, analysis, and impacts of sinusoidal LC filter on pulsewidth modulated inverter fed-induction motor drive
1
2020
... 永磁同步电机(Permanent magnet synchronous motor,PMSM)与逆变器间加入LC滤波器是降低高频电流谐波的有效手段[1 ] .考虑到体积和电磁干扰因素,滤波器更适宜独立于逆变器布置,电机控制系统相电流检测传感器由此便于布置在逆变器侧[2 -3 ] .不同于传统电机系统,引入LC滤波器后,电流环控制器比例积分(Proportional integral,PI)参数不仅决定电机动态与稳态性能,还对系统稳定性和谐振性能及高频谐波产生影响[4 ⇓ ⇓ ⇓ -8 ] .因此,研究电流环PI参数设计方法,对于改善前置滤波器电机系统性能极具实用价值. ...
带LC滤波器的永磁同步电机控制系统及策略研究
1
2019
... 永磁同步电机(Permanent magnet synchronous motor,PMSM)与逆变器间加入LC滤波器是降低高频电流谐波的有效手段[1 ] .考虑到体积和电磁干扰因素,滤波器更适宜独立于逆变器布置,电机控制系统相电流检测传感器由此便于布置在逆变器侧[2 -3 ] .不同于传统电机系统,引入LC滤波器后,电流环控制器比例积分(Proportional integral,PI)参数不仅决定电机动态与稳态性能,还对系统稳定性和谐振性能及高频谐波产生影响[4 ⇓ ⇓ ⇓ -8 ] .因此,研究电流环PI参数设计方法,对于改善前置滤波器电机系统性能极具实用价值. ...
Research on control method of permanent magnet synchronous motor with LC filter
1
2019
... 永磁同步电机(Permanent magnet synchronous motor,PMSM)与逆变器间加入LC滤波器是降低高频电流谐波的有效手段[1 ] .考虑到体积和电磁干扰因素,滤波器更适宜独立于逆变器布置,电机控制系统相电流检测传感器由此便于布置在逆变器侧[2 -3 ] .不同于传统电机系统,引入LC滤波器后,电流环控制器比例积分(Proportional integral,PI)参数不仅决定电机动态与稳态性能,还对系统稳定性和谐振性能及高频谐波产生影响[4 ⇓ ⇓ ⇓ -8 ] .因此,研究电流环PI参数设计方法,对于改善前置滤波器电机系统性能极具实用价值. ...
Exploring inherent damping characteristic of LCL-filters for three-phase grid-connected voltage source inverters
2
2012
... 永磁同步电机(Permanent magnet synchronous motor,PMSM)与逆变器间加入LC滤波器是降低高频电流谐波的有效手段[1 ] .考虑到体积和电磁干扰因素,滤波器更适宜独立于逆变器布置,电机控制系统相电流检测传感器由此便于布置在逆变器侧[2 -3 ] .不同于传统电机系统,引入LC滤波器后,电流环控制器比例积分(Proportional integral,PI)参数不仅决定电机动态与稳态性能,还对系统稳定性和谐振性能及高频谐波产生影响[4 ⇓ ⇓ ⇓ -8 ] .因此,研究电流环PI参数设计方法,对于改善前置滤波器电机系统性能极具实用价值. ...
... 谐振峰会影响电流谐波幅值和谐波畸变率[3 ⇓ ⇓ ⇓ -7 ] ,应在保证系统稳定基础上削减谐振峰值.由式(15)绘制M r 与PI参数关系如图5 所示,可见,M r 与K p 和K i 有关,且K p 影响更明显,K p 应取小以降低M r . ...
基于极点配置与重复控制相结合的三相光伏发电系统的并网策略
2
2008
... 永磁同步电机(Permanent magnet synchronous motor,PMSM)与逆变器间加入LC滤波器是降低高频电流谐波的有效手段[1 ] .考虑到体积和电磁干扰因素,滤波器更适宜独立于逆变器布置,电机控制系统相电流检测传感器由此便于布置在逆变器侧[2 -3 ] .不同于传统电机系统,引入LC滤波器后,电流环控制器比例积分(Proportional integral,PI)参数不仅决定电机动态与稳态性能,还对系统稳定性和谐振性能及高频谐波产生影响[4 ⇓ ⇓ ⇓ -8 ] .因此,研究电流环PI参数设计方法,对于改善前置滤波器电机系统性能极具实用价值. ...
... 谐振峰会影响电流谐波幅值和谐波畸变率[3 ⇓ ⇓ ⇓ -7 ] ,应在保证系统稳定基础上削减谐振峰值.由式(15)绘制M r 与PI参数关系如图5 所示,可见,M r 与K p 和K i 有关,且K p 影响更明显,K p 应取小以降低M r . ...
Research on grid-connected strategy combining pole-assignment and repetitive control in three-phase photovoltaic system
2
2008
... 永磁同步电机(Permanent magnet synchronous motor,PMSM)与逆变器间加入LC滤波器是降低高频电流谐波的有效手段[1 ] .考虑到体积和电磁干扰因素,滤波器更适宜独立于逆变器布置,电机控制系统相电流检测传感器由此便于布置在逆变器侧[2 -3 ] .不同于传统电机系统,引入LC滤波器后,电流环控制器比例积分(Proportional integral,PI)参数不仅决定电机动态与稳态性能,还对系统稳定性和谐振性能及高频谐波产生影响[4 ⇓ ⇓ ⇓ -8 ] .因此,研究电流环PI参数设计方法,对于改善前置滤波器电机系统性能极具实用价值. ...
... 谐振峰会影响电流谐波幅值和谐波畸变率[3 ⇓ ⇓ ⇓ -7 ] ,应在保证系统稳定基础上削减谐振峰值.由式(15)绘制M r 与PI参数关系如图5 所示,可见,M r 与K p 和K i 有关,且K p 影响更明显,K p 应取小以降低M r . ...
LCL滤波的PWM整流器新型控制策略
2
2007
... 永磁同步电机(Permanent magnet synchronous motor,PMSM)与逆变器间加入LC滤波器是降低高频电流谐波的有效手段[1 ] .考虑到体积和电磁干扰因素,滤波器更适宜独立于逆变器布置,电机控制系统相电流检测传感器由此便于布置在逆变器侧[2 -3 ] .不同于传统电机系统,引入LC滤波器后,电流环控制器比例积分(Proportional integral,PI)参数不仅决定电机动态与稳态性能,还对系统稳定性和谐振性能及高频谐波产生影响[4 ⇓ ⇓ ⇓ -8 ] .因此,研究电流环PI参数设计方法,对于改善前置滤波器电机系统性能极具实用价值. ...
... 谐振峰会影响电流谐波幅值和谐波畸变率[3 ⇓ ⇓ ⇓ -7 ] ,应在保证系统稳定基础上削减谐振峰值.由式(15)绘制M r 与PI参数关系如图5 所示,可见,M r 与K p 和K i 有关,且K p 影响更明显,K p 应取小以降低M r . ...
A novel control strategy for PWM rectifier with LCL filter
2
2007
... 永磁同步电机(Permanent magnet synchronous motor,PMSM)与逆变器间加入LC滤波器是降低高频电流谐波的有效手段[1 ] .考虑到体积和电磁干扰因素,滤波器更适宜独立于逆变器布置,电机控制系统相电流检测传感器由此便于布置在逆变器侧[2 -3 ] .不同于传统电机系统,引入LC滤波器后,电流环控制器比例积分(Proportional integral,PI)参数不仅决定电机动态与稳态性能,还对系统稳定性和谐振性能及高频谐波产生影响[4 ⇓ ⇓ ⇓ -8 ] .因此,研究电流环PI参数设计方法,对于改善前置滤波器电机系统性能极具实用价值. ...
... 谐振峰会影响电流谐波幅值和谐波畸变率[3 ⇓ ⇓ ⇓ -7 ] ,应在保证系统稳定基础上削减谐振峰值.由式(15)绘制M r 与PI参数关系如图5 所示,可见,M r 与K p 和K i 有关,且K p 影响更明显,K p 应取小以降低M r . ...
基于离散状态空间模型的LCL滤波并网变换器控制策略
2
2011
... 永磁同步电机(Permanent magnet synchronous motor,PMSM)与逆变器间加入LC滤波器是降低高频电流谐波的有效手段[1 ] .考虑到体积和电磁干扰因素,滤波器更适宜独立于逆变器布置,电机控制系统相电流检测传感器由此便于布置在逆变器侧[2 -3 ] .不同于传统电机系统,引入LC滤波器后,电流环控制器比例积分(Proportional integral,PI)参数不仅决定电机动态与稳态性能,还对系统稳定性和谐振性能及高频谐波产生影响[4 ⇓ ⇓ ⇓ -8 ] .因此,研究电流环PI参数设计方法,对于改善前置滤波器电机系统性能极具实用价值. ...
... 谐振峰会影响电流谐波幅值和谐波畸变率[3 ⇓ ⇓ ⇓ -7 ] ,应在保证系统稳定基础上削减谐振峰值.由式(15)绘制M r 与PI参数关系如图5 所示,可见,M r 与K p 和K i 有关,且K p 影响更明显,K p 应取小以降低M r . ...
Control strategy of grid-connected converter with LCL filter based on discrete state-space model
2
2011
... 永磁同步电机(Permanent magnet synchronous motor,PMSM)与逆变器间加入LC滤波器是降低高频电流谐波的有效手段[1 ] .考虑到体积和电磁干扰因素,滤波器更适宜独立于逆变器布置,电机控制系统相电流检测传感器由此便于布置在逆变器侧[2 -3 ] .不同于传统电机系统,引入LC滤波器后,电流环控制器比例积分(Proportional integral,PI)参数不仅决定电机动态与稳态性能,还对系统稳定性和谐振性能及高频谐波产生影响[4 ⇓ ⇓ ⇓ -8 ] .因此,研究电流环PI参数设计方法,对于改善前置滤波器电机系统性能极具实用价值. ...
... 谐振峰会影响电流谐波幅值和谐波畸变率[3 ⇓ ⇓ ⇓ -7 ] ,应在保证系统稳定基础上削减谐振峰值.由式(15)绘制M r 与PI参数关系如图5 所示,可见,M r 与K p 和K i 有关,且K p 影响更明显,K p 应取小以降低M r . ...
一种LCL滤波器有源阻尼策略与设计方法
2
2013
... 永磁同步电机(Permanent magnet synchronous motor,PMSM)与逆变器间加入LC滤波器是降低高频电流谐波的有效手段[1 ] .考虑到体积和电磁干扰因素,滤波器更适宜独立于逆变器布置,电机控制系统相电流检测传感器由此便于布置在逆变器侧[2 -3 ] .不同于传统电机系统,引入LC滤波器后,电流环控制器比例积分(Proportional integral,PI)参数不仅决定电机动态与稳态性能,还对系统稳定性和谐振性能及高频谐波产生影响[4 ⇓ ⇓ ⇓ -8 ] .因此,研究电流环PI参数设计方法,对于改善前置滤波器电机系统性能极具实用价值. ...
... 谐振峰会影响电流谐波幅值和谐波畸变率[3 ⇓ ⇓ ⇓ -7 ] ,应在保证系统稳定基础上削减谐振峰值.由式(15)绘制M r 与PI参数关系如图5 所示,可见,M r 与K p 和K i 有关,且K p 影响更明显,K p 应取小以降低M r . ...
An active damping control strategy and design method for LCL filter
2
2013
... 永磁同步电机(Permanent magnet synchronous motor,PMSM)与逆变器间加入LC滤波器是降低高频电流谐波的有效手段[1 ] .考虑到体积和电磁干扰因素,滤波器更适宜独立于逆变器布置,电机控制系统相电流检测传感器由此便于布置在逆变器侧[2 -3 ] .不同于传统电机系统,引入LC滤波器后,电流环控制器比例积分(Proportional integral,PI)参数不仅决定电机动态与稳态性能,还对系统稳定性和谐振性能及高频谐波产生影响[4 ⇓ ⇓ ⇓ -8 ] .因此,研究电流环PI参数设计方法,对于改善前置滤波器电机系统性能极具实用价值. ...
... 谐振峰会影响电流谐波幅值和谐波畸变率[3 ⇓ ⇓ ⇓ -7 ] ,应在保证系统稳定基础上削减谐振峰值.由式(15)绘制M r 与PI参数关系如图5 所示,可见,M r 与K p 和K i 有关,且K p 影响更明显,K p 应取小以降低M r . ...
Active disturbance rejection control based single current feedback resonance damping strategy for LCL-type grid-connected inverter
1
2021
... 永磁同步电机(Permanent magnet synchronous motor,PMSM)与逆变器间加入LC滤波器是降低高频电流谐波的有效手段[1 ] .考虑到体积和电磁干扰因素,滤波器更适宜独立于逆变器布置,电机控制系统相电流检测传感器由此便于布置在逆变器侧[2 -3 ] .不同于传统电机系统,引入LC滤波器后,电流环控制器比例积分(Proportional integral,PI)参数不仅决定电机动态与稳态性能,还对系统稳定性和谐振性能及高频谐波产生影响[4 ⇓ ⇓ ⇓ -8 ] .因此,研究电流环PI参数设计方法,对于改善前置滤波器电机系统性能极具实用价值. ...
Ziegler-Nichol’s method of online tuning of PMSM for improved transient response
1
2010
... 传统电机系统PI参数设计方法的研究较多.其中,Ziegler-Nichols法[9 ] 和零极点相消法[10 ] 得到广泛应用.Ziegler-Nichols法不需要识别系统参数,通过寻找稳定极限确定PI增益,但未考虑其余性能指标.零极点相消法忽略影响中低频段较小的环节,结合截止频率调整PI参数,使电机传递函数极点与控制器零点相抵消,以提高系统动态性能.近年来,对传统参数整定方法也进行了不少改进.文献[11 ]基于零极点相消法和PMSM系统频域模型,考虑了逆变器死区和延时等因素,推导出电流环PI控制器参数与开环截止频率和相位裕度关系,受界定范围影响,其PI参数取值范围较大且需要多次比对.在文献[11 ]的基础上,文献[12 ]通过建立最小评价函数迭代学习最优开环截止频率,简化了计算步骤,提高了系统响应速度,但超调量等性能未能兼顾.文献[13 ]分析了电流环带宽、延迟与PI参数关系,进而通过改变PI参数以提高电流环动态响应能力.文献[14 ]通过预测控制与PI控制结合,提高了系统动态性能并拓展了PI参数稳定域.文献[15 ]建立了PMSM控制系统离散模型,将时域性能指标转换成频域特征量,通过频域分析进行PI参数整定.文献[16 ]提出一种多目标设计方法,通过分析PI参数与时域指标、频域指标和系统参数的关系,确定可直接取值的PI参数期望区域,但PI参数取值范围较广. ...
Closed-loop estimation of permanent magnet synchronous motor parameters by PI controller gain tuning
1
2006
... 传统电机系统PI参数设计方法的研究较多.其中,Ziegler-Nichols法[9 ] 和零极点相消法[10 ] 得到广泛应用.Ziegler-Nichols法不需要识别系统参数,通过寻找稳定极限确定PI增益,但未考虑其余性能指标.零极点相消法忽略影响中低频段较小的环节,结合截止频率调整PI参数,使电机传递函数极点与控制器零点相抵消,以提高系统动态性能.近年来,对传统参数整定方法也进行了不少改进.文献[11 ]基于零极点相消法和PMSM系统频域模型,考虑了逆变器死区和延时等因素,推导出电流环PI控制器参数与开环截止频率和相位裕度关系,受界定范围影响,其PI参数取值范围较大且需要多次比对.在文献[11 ]的基础上,文献[12 ]通过建立最小评价函数迭代学习最优开环截止频率,简化了计算步骤,提高了系统响应速度,但超调量等性能未能兼顾.文献[13 ]分析了电流环带宽、延迟与PI参数关系,进而通过改变PI参数以提高电流环动态响应能力.文献[14 ]通过预测控制与PI控制结合,提高了系统动态性能并拓展了PI参数稳定域.文献[15 ]建立了PMSM控制系统离散模型,将时域性能指标转换成频域特征量,通过频域分析进行PI参数整定.文献[16 ]提出一种多目标设计方法,通过分析PI参数与时域指标、频域指标和系统参数的关系,确定可直接取值的PI参数期望区域,但PI参数取值范围较广. ...
永磁同步电动机调速系统PI控制器参数整定方法
4
2014
... 传统电机系统PI参数设计方法的研究较多.其中,Ziegler-Nichols法[9 ] 和零极点相消法[10 ] 得到广泛应用.Ziegler-Nichols法不需要识别系统参数,通过寻找稳定极限确定PI增益,但未考虑其余性能指标.零极点相消法忽略影响中低频段较小的环节,结合截止频率调整PI参数,使电机传递函数极点与控制器零点相抵消,以提高系统动态性能.近年来,对传统参数整定方法也进行了不少改进.文献[11 ]基于零极点相消法和PMSM系统频域模型,考虑了逆变器死区和延时等因素,推导出电流环PI控制器参数与开环截止频率和相位裕度关系,受界定范围影响,其PI参数取值范围较大且需要多次比对.在文献[11 ]的基础上,文献[12 ]通过建立最小评价函数迭代学习最优开环截止频率,简化了计算步骤,提高了系统响应速度,但超调量等性能未能兼顾.文献[13 ]分析了电流环带宽、延迟与PI参数关系,进而通过改变PI参数以提高电流环动态响应能力.文献[14 ]通过预测控制与PI控制结合,提高了系统动态性能并拓展了PI参数稳定域.文献[15 ]建立了PMSM控制系统离散模型,将时域性能指标转换成频域特征量,通过频域分析进行PI参数整定.文献[16 ]提出一种多目标设计方法,通过分析PI参数与时域指标、频域指标和系统参数的关系,确定可直接取值的PI参数期望区域,但PI参数取值范围较广. ...
... ]基于零极点相消法和PMSM系统频域模型,考虑了逆变器死区和延时等因素,推导出电流环PI控制器参数与开环截止频率和相位裕度关系,受界定范围影响,其PI参数取值范围较大且需要多次比对.在文献[11 ]的基础上,文献[12 ]通过建立最小评价函数迭代学习最优开环截止频率,简化了计算步骤,提高了系统响应速度,但超调量等性能未能兼顾.文献[13 ]分析了电流环带宽、延迟与PI参数关系,进而通过改变PI参数以提高电流环动态响应能力.文献[14 ]通过预测控制与PI控制结合,提高了系统动态性能并拓展了PI参数稳定域.文献[15 ]建立了PMSM控制系统离散模型,将时域性能指标转换成频域特征量,通过频域分析进行PI参数整定.文献[16 ]提出一种多目标设计方法,通过分析PI参数与时域指标、频域指标和系统参数的关系,确定可直接取值的PI参数期望区域,但PI参数取值范围较广. ...
... 关于前置滤波器电机系统的电流环参数设计研究较少.传统的Ziegler-Nichols法与系统结构无关,零极点相消法着重关注中低频段,因而这两种方法可用于前置滤波器系统,但性能有限.在文献[11 ⇓ ⇓ ⇓ ⇓ -16 ]中,PI参数设计方法均面向无滤波器传统电机系统,均未涉及引入滤波器后的谐振和稳定性问题.可见,针对前置滤波器电机系统,其电流环参数设计问题尚未有效解决,还需要全面考虑PI参数对系统性能的影响,进而在满足稳定性基础上最大化兼顾系统综合性能需求. ...
... 期望相位裕度P m ≥40°[11 ] ,结合最小相位系统稳定约束K i /K p <6 666.6,绘制PI参数取值范围如图4 所示.在图4 所示最小相位系统内,取P m ≥40°箭头所示区域作为本文所提方法的PI参数稳定域. ...
Tuning method for PI controllers of PMSM driving system
4
2014
... 传统电机系统PI参数设计方法的研究较多.其中,Ziegler-Nichols法[9 ] 和零极点相消法[10 ] 得到广泛应用.Ziegler-Nichols法不需要识别系统参数,通过寻找稳定极限确定PI增益,但未考虑其余性能指标.零极点相消法忽略影响中低频段较小的环节,结合截止频率调整PI参数,使电机传递函数极点与控制器零点相抵消,以提高系统动态性能.近年来,对传统参数整定方法也进行了不少改进.文献[11 ]基于零极点相消法和PMSM系统频域模型,考虑了逆变器死区和延时等因素,推导出电流环PI控制器参数与开环截止频率和相位裕度关系,受界定范围影响,其PI参数取值范围较大且需要多次比对.在文献[11 ]的基础上,文献[12 ]通过建立最小评价函数迭代学习最优开环截止频率,简化了计算步骤,提高了系统响应速度,但超调量等性能未能兼顾.文献[13 ]分析了电流环带宽、延迟与PI参数关系,进而通过改变PI参数以提高电流环动态响应能力.文献[14 ]通过预测控制与PI控制结合,提高了系统动态性能并拓展了PI参数稳定域.文献[15 ]建立了PMSM控制系统离散模型,将时域性能指标转换成频域特征量,通过频域分析进行PI参数整定.文献[16 ]提出一种多目标设计方法,通过分析PI参数与时域指标、频域指标和系统参数的关系,确定可直接取值的PI参数期望区域,但PI参数取值范围较广. ...
... ]基于零极点相消法和PMSM系统频域模型,考虑了逆变器死区和延时等因素,推导出电流环PI控制器参数与开环截止频率和相位裕度关系,受界定范围影响,其PI参数取值范围较大且需要多次比对.在文献[11 ]的基础上,文献[12 ]通过建立最小评价函数迭代学习最优开环截止频率,简化了计算步骤,提高了系统响应速度,但超调量等性能未能兼顾.文献[13 ]分析了电流环带宽、延迟与PI参数关系,进而通过改变PI参数以提高电流环动态响应能力.文献[14 ]通过预测控制与PI控制结合,提高了系统动态性能并拓展了PI参数稳定域.文献[15 ]建立了PMSM控制系统离散模型,将时域性能指标转换成频域特征量,通过频域分析进行PI参数整定.文献[16 ]提出一种多目标设计方法,通过分析PI参数与时域指标、频域指标和系统参数的关系,确定可直接取值的PI参数期望区域,但PI参数取值范围较广. ...
... 关于前置滤波器电机系统的电流环参数设计研究较少.传统的Ziegler-Nichols法与系统结构无关,零极点相消法着重关注中低频段,因而这两种方法可用于前置滤波器系统,但性能有限.在文献[11 ⇓ ⇓ ⇓ ⇓ -16 ]中,PI参数设计方法均面向无滤波器传统电机系统,均未涉及引入滤波器后的谐振和稳定性问题.可见,针对前置滤波器电机系统,其电流环参数设计问题尚未有效解决,还需要全面考虑PI参数对系统性能的影响,进而在满足稳定性基础上最大化兼顾系统综合性能需求. ...
... 期望相位裕度P m ≥40°[11 ] ,结合最小相位系统稳定约束K i /K p <6 666.6,绘制PI参数取值范围如图4 所示.在图4 所示最小相位系统内,取P m ≥40°箭头所示区域作为本文所提方法的PI参数稳定域. ...
基于最优开环截止频率学习的永磁伺服系统PI控制器参数整定方法
2
2017
... 传统电机系统PI参数设计方法的研究较多.其中,Ziegler-Nichols法[9 ] 和零极点相消法[10 ] 得到广泛应用.Ziegler-Nichols法不需要识别系统参数,通过寻找稳定极限确定PI增益,但未考虑其余性能指标.零极点相消法忽略影响中低频段较小的环节,结合截止频率调整PI参数,使电机传递函数极点与控制器零点相抵消,以提高系统动态性能.近年来,对传统参数整定方法也进行了不少改进.文献[11 ]基于零极点相消法和PMSM系统频域模型,考虑了逆变器死区和延时等因素,推导出电流环PI控制器参数与开环截止频率和相位裕度关系,受界定范围影响,其PI参数取值范围较大且需要多次比对.在文献[11 ]的基础上,文献[12 ]通过建立最小评价函数迭代学习最优开环截止频率,简化了计算步骤,提高了系统响应速度,但超调量等性能未能兼顾.文献[13 ]分析了电流环带宽、延迟与PI参数关系,进而通过改变PI参数以提高电流环动态响应能力.文献[14 ]通过预测控制与PI控制结合,提高了系统动态性能并拓展了PI参数稳定域.文献[15 ]建立了PMSM控制系统离散模型,将时域性能指标转换成频域特征量,通过频域分析进行PI参数整定.文献[16 ]提出一种多目标设计方法,通过分析PI参数与时域指标、频域指标和系统参数的关系,确定可直接取值的PI参数期望区域,但PI参数取值范围较广. ...
... 关于前置滤波器电机系统的电流环参数设计研究较少.传统的Ziegler-Nichols法与系统结构无关,零极点相消法着重关注中低频段,因而这两种方法可用于前置滤波器系统,但性能有限.在文献[11 ⇓ ⇓ ⇓ ⇓ -16 ]中,PI参数设计方法均面向无滤波器传统电机系统,均未涉及引入滤波器后的谐振和稳定性问题.可见,针对前置滤波器电机系统,其电流环参数设计问题尚未有效解决,还需要全面考虑PI参数对系统性能的影响,进而在满足稳定性基础上最大化兼顾系统综合性能需求. ...
PI controllers tuning method of permanent magnet servo system based on optimal open-loop cut-off frequency learning
2
2017
... 传统电机系统PI参数设计方法的研究较多.其中,Ziegler-Nichols法[9 ] 和零极点相消法[10 ] 得到广泛应用.Ziegler-Nichols法不需要识别系统参数,通过寻找稳定极限确定PI增益,但未考虑其余性能指标.零极点相消法忽略影响中低频段较小的环节,结合截止频率调整PI参数,使电机传递函数极点与控制器零点相抵消,以提高系统动态性能.近年来,对传统参数整定方法也进行了不少改进.文献[11 ]基于零极点相消法和PMSM系统频域模型,考虑了逆变器死区和延时等因素,推导出电流环PI控制器参数与开环截止频率和相位裕度关系,受界定范围影响,其PI参数取值范围较大且需要多次比对.在文献[11 ]的基础上,文献[12 ]通过建立最小评价函数迭代学习最优开环截止频率,简化了计算步骤,提高了系统响应速度,但超调量等性能未能兼顾.文献[13 ]分析了电流环带宽、延迟与PI参数关系,进而通过改变PI参数以提高电流环动态响应能力.文献[14 ]通过预测控制与PI控制结合,提高了系统动态性能并拓展了PI参数稳定域.文献[15 ]建立了PMSM控制系统离散模型,将时域性能指标转换成频域特征量,通过频域分析进行PI参数整定.文献[16 ]提出一种多目标设计方法,通过分析PI参数与时域指标、频域指标和系统参数的关系,确定可直接取值的PI参数期望区域,但PI参数取值范围较广. ...
... 关于前置滤波器电机系统的电流环参数设计研究较少.传统的Ziegler-Nichols法与系统结构无关,零极点相消法着重关注中低频段,因而这两种方法可用于前置滤波器系统,但性能有限.在文献[11 ⇓ ⇓ ⇓ ⇓ -16 ]中,PI参数设计方法均面向无滤波器传统电机系统,均未涉及引入滤波器后的谐振和稳定性问题.可见,针对前置滤波器电机系统,其电流环参数设计问题尚未有效解决,还需要全面考虑PI参数对系统性能的影响,进而在满足稳定性基础上最大化兼顾系统综合性能需求. ...
永磁同步电机电流环频率响应改进策略研究
3
2018
... 传统电机系统PI参数设计方法的研究较多.其中,Ziegler-Nichols法[9 ] 和零极点相消法[10 ] 得到广泛应用.Ziegler-Nichols法不需要识别系统参数,通过寻找稳定极限确定PI增益,但未考虑其余性能指标.零极点相消法忽略影响中低频段较小的环节,结合截止频率调整PI参数,使电机传递函数极点与控制器零点相抵消,以提高系统动态性能.近年来,对传统参数整定方法也进行了不少改进.文献[11 ]基于零极点相消法和PMSM系统频域模型,考虑了逆变器死区和延时等因素,推导出电流环PI控制器参数与开环截止频率和相位裕度关系,受界定范围影响,其PI参数取值范围较大且需要多次比对.在文献[11 ]的基础上,文献[12 ]通过建立最小评价函数迭代学习最优开环截止频率,简化了计算步骤,提高了系统响应速度,但超调量等性能未能兼顾.文献[13 ]分析了电流环带宽、延迟与PI参数关系,进而通过改变PI参数以提高电流环动态响应能力.文献[14 ]通过预测控制与PI控制结合,提高了系统动态性能并拓展了PI参数稳定域.文献[15 ]建立了PMSM控制系统离散模型,将时域性能指标转换成频域特征量,通过频域分析进行PI参数整定.文献[16 ]提出一种多目标设计方法,通过分析PI参数与时域指标、频域指标和系统参数的关系,确定可直接取值的PI参数期望区域,但PI参数取值范围较广. ...
... 关于前置滤波器电机系统的电流环参数设计研究较少.传统的Ziegler-Nichols法与系统结构无关,零极点相消法着重关注中低频段,因而这两种方法可用于前置滤波器系统,但性能有限.在文献[11 ⇓ ⇓ ⇓ ⇓ -16 ]中,PI参数设计方法均面向无滤波器传统电机系统,均未涉及引入滤波器后的谐振和稳定性问题.可见,针对前置滤波器电机系统,其电流环参数设计问题尚未有效解决,还需要全面考虑PI参数对系统性能的影响,进而在满足稳定性基础上最大化兼顾系统综合性能需求. ...
... 电流环带宽取闭环幅频特性-3 dB或相频特性-90°对应频率中的较小值[13 ] ,即 ...
Current loop frequency response improvement strategy research for permanent magnet synchronous motor control system
3
2018
... 传统电机系统PI参数设计方法的研究较多.其中,Ziegler-Nichols法[9 ] 和零极点相消法[10 ] 得到广泛应用.Ziegler-Nichols法不需要识别系统参数,通过寻找稳定极限确定PI增益,但未考虑其余性能指标.零极点相消法忽略影响中低频段较小的环节,结合截止频率调整PI参数,使电机传递函数极点与控制器零点相抵消,以提高系统动态性能.近年来,对传统参数整定方法也进行了不少改进.文献[11 ]基于零极点相消法和PMSM系统频域模型,考虑了逆变器死区和延时等因素,推导出电流环PI控制器参数与开环截止频率和相位裕度关系,受界定范围影响,其PI参数取值范围较大且需要多次比对.在文献[11 ]的基础上,文献[12 ]通过建立最小评价函数迭代学习最优开环截止频率,简化了计算步骤,提高了系统响应速度,但超调量等性能未能兼顾.文献[13 ]分析了电流环带宽、延迟与PI参数关系,进而通过改变PI参数以提高电流环动态响应能力.文献[14 ]通过预测控制与PI控制结合,提高了系统动态性能并拓展了PI参数稳定域.文献[15 ]建立了PMSM控制系统离散模型,将时域性能指标转换成频域特征量,通过频域分析进行PI参数整定.文献[16 ]提出一种多目标设计方法,通过分析PI参数与时域指标、频域指标和系统参数的关系,确定可直接取值的PI参数期望区域,但PI参数取值范围较广. ...
... 关于前置滤波器电机系统的电流环参数设计研究较少.传统的Ziegler-Nichols法与系统结构无关,零极点相消法着重关注中低频段,因而这两种方法可用于前置滤波器系统,但性能有限.在文献[11 ⇓ ⇓ ⇓ ⇓ -16 ]中,PI参数设计方法均面向无滤波器传统电机系统,均未涉及引入滤波器后的谐振和稳定性问题.可见,针对前置滤波器电机系统,其电流环参数设计问题尚未有效解决,还需要全面考虑PI参数对系统性能的影响,进而在满足稳定性基础上最大化兼顾系统综合性能需求. ...
... 电流环带宽取闭环幅频特性-3 dB或相频特性-90°对应频率中的较小值[13 ] ,即 ...
永磁同步电机电流增量预测算法参数设计及性能分析
2
2013
... 传统电机系统PI参数设计方法的研究较多.其中,Ziegler-Nichols法[9 ] 和零极点相消法[10 ] 得到广泛应用.Ziegler-Nichols法不需要识别系统参数,通过寻找稳定极限确定PI增益,但未考虑其余性能指标.零极点相消法忽略影响中低频段较小的环节,结合截止频率调整PI参数,使电机传递函数极点与控制器零点相抵消,以提高系统动态性能.近年来,对传统参数整定方法也进行了不少改进.文献[11 ]基于零极点相消法和PMSM系统频域模型,考虑了逆变器死区和延时等因素,推导出电流环PI控制器参数与开环截止频率和相位裕度关系,受界定范围影响,其PI参数取值范围较大且需要多次比对.在文献[11 ]的基础上,文献[12 ]通过建立最小评价函数迭代学习最优开环截止频率,简化了计算步骤,提高了系统响应速度,但超调量等性能未能兼顾.文献[13 ]分析了电流环带宽、延迟与PI参数关系,进而通过改变PI参数以提高电流环动态响应能力.文献[14 ]通过预测控制与PI控制结合,提高了系统动态性能并拓展了PI参数稳定域.文献[15 ]建立了PMSM控制系统离散模型,将时域性能指标转换成频域特征量,通过频域分析进行PI参数整定.文献[16 ]提出一种多目标设计方法,通过分析PI参数与时域指标、频域指标和系统参数的关系,确定可直接取值的PI参数期望区域,但PI参数取值范围较广. ...
... 关于前置滤波器电机系统的电流环参数设计研究较少.传统的Ziegler-Nichols法与系统结构无关,零极点相消法着重关注中低频段,因而这两种方法可用于前置滤波器系统,但性能有限.在文献[11 ⇓ ⇓ ⇓ ⇓ -16 ]中,PI参数设计方法均面向无滤波器传统电机系统,均未涉及引入滤波器后的谐振和稳定性问题.可见,针对前置滤波器电机系统,其电流环参数设计问题尚未有效解决,还需要全面考虑PI参数对系统性能的影响,进而在满足稳定性基础上最大化兼顾系统综合性能需求. ...
Parameters design and performance analysis of current incremental predictive algorithm for PMSM
2
2013
... 传统电机系统PI参数设计方法的研究较多.其中,Ziegler-Nichols法[9 ] 和零极点相消法[10 ] 得到广泛应用.Ziegler-Nichols法不需要识别系统参数,通过寻找稳定极限确定PI增益,但未考虑其余性能指标.零极点相消法忽略影响中低频段较小的环节,结合截止频率调整PI参数,使电机传递函数极点与控制器零点相抵消,以提高系统动态性能.近年来,对传统参数整定方法也进行了不少改进.文献[11 ]基于零极点相消法和PMSM系统频域模型,考虑了逆变器死区和延时等因素,推导出电流环PI控制器参数与开环截止频率和相位裕度关系,受界定范围影响,其PI参数取值范围较大且需要多次比对.在文献[11 ]的基础上,文献[12 ]通过建立最小评价函数迭代学习最优开环截止频率,简化了计算步骤,提高了系统响应速度,但超调量等性能未能兼顾.文献[13 ]分析了电流环带宽、延迟与PI参数关系,进而通过改变PI参数以提高电流环动态响应能力.文献[14 ]通过预测控制与PI控制结合,提高了系统动态性能并拓展了PI参数稳定域.文献[15 ]建立了PMSM控制系统离散模型,将时域性能指标转换成频域特征量,通过频域分析进行PI参数整定.文献[16 ]提出一种多目标设计方法,通过分析PI参数与时域指标、频域指标和系统参数的关系,确定可直接取值的PI参数期望区域,但PI参数取值范围较广. ...
... 关于前置滤波器电机系统的电流环参数设计研究较少.传统的Ziegler-Nichols法与系统结构无关,零极点相消法着重关注中低频段,因而这两种方法可用于前置滤波器系统,但性能有限.在文献[11 ⇓ ⇓ ⇓ ⇓ -16 ]中,PI参数设计方法均面向无滤波器传统电机系统,均未涉及引入滤波器后的谐振和稳定性问题.可见,针对前置滤波器电机系统,其电流环参数设计问题尚未有效解决,还需要全面考虑PI参数对系统性能的影响,进而在满足稳定性基础上最大化兼顾系统综合性能需求. ...
永磁同步电机闭环控制系统数字PI参数整定
2
2018
... 传统电机系统PI参数设计方法的研究较多.其中,Ziegler-Nichols法[9 ] 和零极点相消法[10 ] 得到广泛应用.Ziegler-Nichols法不需要识别系统参数,通过寻找稳定极限确定PI增益,但未考虑其余性能指标.零极点相消法忽略影响中低频段较小的环节,结合截止频率调整PI参数,使电机传递函数极点与控制器零点相抵消,以提高系统动态性能.近年来,对传统参数整定方法也进行了不少改进.文献[11 ]基于零极点相消法和PMSM系统频域模型,考虑了逆变器死区和延时等因素,推导出电流环PI控制器参数与开环截止频率和相位裕度关系,受界定范围影响,其PI参数取值范围较大且需要多次比对.在文献[11 ]的基础上,文献[12 ]通过建立最小评价函数迭代学习最优开环截止频率,简化了计算步骤,提高了系统响应速度,但超调量等性能未能兼顾.文献[13 ]分析了电流环带宽、延迟与PI参数关系,进而通过改变PI参数以提高电流环动态响应能力.文献[14 ]通过预测控制与PI控制结合,提高了系统动态性能并拓展了PI参数稳定域.文献[15 ]建立了PMSM控制系统离散模型,将时域性能指标转换成频域特征量,通过频域分析进行PI参数整定.文献[16 ]提出一种多目标设计方法,通过分析PI参数与时域指标、频域指标和系统参数的关系,确定可直接取值的PI参数期望区域,但PI参数取值范围较广. ...
... 关于前置滤波器电机系统的电流环参数设计研究较少.传统的Ziegler-Nichols法与系统结构无关,零极点相消法着重关注中低频段,因而这两种方法可用于前置滤波器系统,但性能有限.在文献[11 ⇓ ⇓ ⇓ ⇓ -16 ]中,PI参数设计方法均面向无滤波器传统电机系统,均未涉及引入滤波器后的谐振和稳定性问题.可见,针对前置滤波器电机系统,其电流环参数设计问题尚未有效解决,还需要全面考虑PI参数对系统性能的影响,进而在满足稳定性基础上最大化兼顾系统综合性能需求. ...
Tuning method for digital PI controllers of PMSM closed-loop driving system
2
2018
... 传统电机系统PI参数设计方法的研究较多.其中,Ziegler-Nichols法[9 ] 和零极点相消法[10 ] 得到广泛应用.Ziegler-Nichols法不需要识别系统参数,通过寻找稳定极限确定PI增益,但未考虑其余性能指标.零极点相消法忽略影响中低频段较小的环节,结合截止频率调整PI参数,使电机传递函数极点与控制器零点相抵消,以提高系统动态性能.近年来,对传统参数整定方法也进行了不少改进.文献[11 ]基于零极点相消法和PMSM系统频域模型,考虑了逆变器死区和延时等因素,推导出电流环PI控制器参数与开环截止频率和相位裕度关系,受界定范围影响,其PI参数取值范围较大且需要多次比对.在文献[11 ]的基础上,文献[12 ]通过建立最小评价函数迭代学习最优开环截止频率,简化了计算步骤,提高了系统响应速度,但超调量等性能未能兼顾.文献[13 ]分析了电流环带宽、延迟与PI参数关系,进而通过改变PI参数以提高电流环动态响应能力.文献[14 ]通过预测控制与PI控制结合,提高了系统动态性能并拓展了PI参数稳定域.文献[15 ]建立了PMSM控制系统离散模型,将时域性能指标转换成频域特征量,通过频域分析进行PI参数整定.文献[16 ]提出一种多目标设计方法,通过分析PI参数与时域指标、频域指标和系统参数的关系,确定可直接取值的PI参数期望区域,但PI参数取值范围较广. ...
... 关于前置滤波器电机系统的电流环参数设计研究较少.传统的Ziegler-Nichols法与系统结构无关,零极点相消法着重关注中低频段,因而这两种方法可用于前置滤波器系统,但性能有限.在文献[11 ⇓ ⇓ ⇓ ⇓ -16 ]中,PI参数设计方法均面向无滤波器传统电机系统,均未涉及引入滤波器后的谐振和稳定性问题.可见,针对前置滤波器电机系统,其电流环参数设计问题尚未有效解决,还需要全面考虑PI参数对系统性能的影响,进而在满足稳定性基础上最大化兼顾系统综合性能需求. ...
Multi-objective controller design of IPMSM drives based on DTD D-partition method considering parameters uncertainties
2
2019
... 传统电机系统PI参数设计方法的研究较多.其中,Ziegler-Nichols法[9 ] 和零极点相消法[10 ] 得到广泛应用.Ziegler-Nichols法不需要识别系统参数,通过寻找稳定极限确定PI增益,但未考虑其余性能指标.零极点相消法忽略影响中低频段较小的环节,结合截止频率调整PI参数,使电机传递函数极点与控制器零点相抵消,以提高系统动态性能.近年来,对传统参数整定方法也进行了不少改进.文献[11 ]基于零极点相消法和PMSM系统频域模型,考虑了逆变器死区和延时等因素,推导出电流环PI控制器参数与开环截止频率和相位裕度关系,受界定范围影响,其PI参数取值范围较大且需要多次比对.在文献[11 ]的基础上,文献[12 ]通过建立最小评价函数迭代学习最优开环截止频率,简化了计算步骤,提高了系统响应速度,但超调量等性能未能兼顾.文献[13 ]分析了电流环带宽、延迟与PI参数关系,进而通过改变PI参数以提高电流环动态响应能力.文献[14 ]通过预测控制与PI控制结合,提高了系统动态性能并拓展了PI参数稳定域.文献[15 ]建立了PMSM控制系统离散模型,将时域性能指标转换成频域特征量,通过频域分析进行PI参数整定.文献[16 ]提出一种多目标设计方法,通过分析PI参数与时域指标、频域指标和系统参数的关系,确定可直接取值的PI参数期望区域,但PI参数取值范围较广. ...
... 关于前置滤波器电机系统的电流环参数设计研究较少.传统的Ziegler-Nichols法与系统结构无关,零极点相消法着重关注中低频段,因而这两种方法可用于前置滤波器系统,但性能有限.在文献[11 ⇓ ⇓ ⇓ ⇓ -16 ]中,PI参数设计方法均面向无滤波器传统电机系统,均未涉及引入滤波器后的谐振和稳定性问题.可见,针对前置滤波器电机系统,其电流环参数设计问题尚未有效解决,还需要全面考虑PI参数对系统性能的影响,进而在满足稳定性基础上最大化兼顾系统综合性能需求. ...
Resonance suppression and EMI reduction of GaN-based motor drive with sine wave filter
1
2020
... 式(10)所示开环传递函数分母高于分子2个阶次,幅值裕度始终满足稳定要求[17 ] ,保证系统稳定只需要满足约束式(13)所示相位裕度即可. ...
A simple feedforward approach to stabilize VSI-fed induction motor with filter in RFOC
1
2020
... 前置滤波器会使系统在谐振频率ω res 处产生较大谐振峰值,ω res 可表示如下[18 ] ...
Step-by-step controller design for LCL-type grid-connected inverter with capacitor-current-feedback active-damping
1
2014
... 动态性能由超调量σ %、上升时间t r 和调节时间t s 描述[19 -20 ] ,可由式(16)所示时域特性表达式得到,其中1/s 为单位阶跃输入传递函数,c (t )为系统输出,L -1 为拉普拉斯反变换算子. ...
基于PI调节器和电容电流反馈有源阻尼的LCL型并网逆变器闭环参数设计
1
2012
... 动态性能由超调量σ %、上升时间t r 和调节时间t s 描述[19 -20 ] ,可由式(16)所示时域特性表达式得到,其中1/s 为单位阶跃输入传递函数,c (t )为系统输出,L -1 为拉普拉斯反变换算子. ...
Design of grid-connected inverters with LCL filter based on PI regulator and capacitor current feedback active damping
1
2012
... 动态性能由超调量σ %、上升时间t r 和调节时间t s 描述[19 -20 ] ,可由式(16)所示时域特性表达式得到,其中1/s 为单位阶跃输入传递函数,c (t )为系统输出,L -1 为拉普拉斯反变换算子. ...
永磁交流伺服系统电流环带宽扩展研究
1
2010
... 由以上分析可知,前置滤波器电机系统的带宽与动态性相关,高带宽系统响应速度快、调节时间t s 和上升时间t r 短,从动态性能角度可选取带宽 ω b [21 ] .超调量σ %单独作为优化目标之一.同时,为了降低谐振峰值减小高频电流谐波,将谐振峰值也作为一个优化目标. ...
Current loop bandwidth expansion for permanent magnet AC servo system
1
2010
... 由以上分析可知,前置滤波器电机系统的带宽与动态性相关,高带宽系统响应速度快、调节时间t s 和上升时间t r 短,从动态性能角度可选取带宽 ω b [21 ] .超调量σ %单独作为优化目标之一.同时,为了降低谐振峰值减小高频电流谐波,将谐振峰值也作为一个优化目标. ...
基于矢量控制的异步电机预测电流控制算法
1
2014
... 为验证三种设计系统电流环带宽,进行如下测试[22 ] .给定幅值13 A、频率从1 rad/s逐渐增大的正弦信号,直至反馈信号幅值降至0.707倍或相位滞后90°.测试得到Ziegler-Nichols法、零极点相消法和多目标优化法对应的系统带宽分别为611 rad/s、280 rad/s和325 rad/s,如图16 所示. ...
A predictive current control scheme for induction motor with vector control
1
2014
... 为验证三种设计系统电流环带宽,进行如下测试[22 ] .给定幅值13 A、频率从1 rad/s逐渐增大的正弦信号,直至反馈信号幅值降至0.707倍或相位滞后90°.测试得到Ziegler-Nichols法、零极点相消法和多目标优化法对应的系统带宽分别为611 rad/s、280 rad/s和325 rad/s,如图16 所示. ...