永磁同步电机(Permanent magnet synchronous motor，PMSM)具备高功率密度、高能量转换效率等优点，近年来在高效能需求的场景，如电动汽车等，得到了广泛应用^[1⇓-3]。PMSM矢量控制系统的正常运行需要获取稳定可靠的转子位置信息，而无位置传感器算法因可靠性等因素而无法彻底取代编码器。但低分率编码器与无位置传感器算法相互配合的插值控制方案，既可以降低控制成本，又能保障控制系统的可靠性，因此极具应用前景^[4⇓⇓-7]。

目前主流的插值控制方案有平均速度法^[8⇓⇓-11]、平均加速度法^[12-13]、观测器法^{[14⇓⇓-17]}。文献[8]提出了平均速度法，利用前一个霍尔位置区间计算出平均速度，利用计算结果对当前霍尔位置区间实现位置插补，从而在当前霍尔位置区间位置缺省的状态下实现矢量控制。文献[12]提出了平均加速度法，利用前两个霍尔位置区间计算出的平均加速度，利用位置-加速度公式，实现当前霍尔位置区间的位置插补，在位置插补过程中引入平均加速度使得插值算法动态性能更好，能够在电机加减速情况下实现位置插值。观测器法中的主流方法是矢量观测器法^{[14⇓⇓-17]}，矢量观测器法利用旋转矢量观测器理论，采用位置观测器获取的位置信息用作实时位置插值，但此方法需要解决观测器相位滞后等问题。为了解决相位滞后对插值算法造成的不利影响，文献[18]提出基于观测器法的插值算法(Observer-based interpolation，OI)，采用位置增量差值信息实现插值算法。该方法不受观测器相位滞后的影响，消除了观测器相位滞后导致的位置误差，但在每个位置脉冲内，电机参数不精确等因素导致该算法出现累计误差，降低了控制系统的精度和稳定性。

为了降低基于观测器法的插值算法中误差累积现象带来的不利影响，本文提出一种基于累积误差补偿的插值控制算法(Accumulative error compensation based position interpolation control，AECPIC)。该方法利用误差累积方向的一致性，通过计算获知上一位置脉冲的累计误差，利用此信息构造误差补偿项，以降低当前位置脉冲的累计误差。最后，在750 W对拖控制系统进行了试验，验证了所提方法的有效性。

在运动坐标系中，PMSM电压方程为^[19]

式中，u_d、u_q为dq轴电压；i_d、i_q为dq轴电流；L_d、L_q为dq轴电感；ω_e为转子电气角速度；R为电机定子绕组；ψ_f为永磁体磁链；p为微分算子。

在两相静止坐标系中，PMSM电压方程为^[19]

式中，等式右边第二项为扩展反电势，其定义如下

将式(2)变更为电流状态方程，可得

式中，$Q=\frac{1}{{{L}_{d}}}\left[ \begin{matrix} -R & -\left( {{L}_{d}}-{{L}_{q}} \right){{\omega }_{e}} \\ \left( {{L}_{d}}-{{L}_{q}} \right){{\omega }_{e}} & -R \\\end{matrix} \right]$。依据电机参数模型与滑模理论^[20]，构造如下的电流状态预测方程

式中，$\hat{Q}=\frac{1}{{{L}_{d}}}\left[ \begin{matrix} -R & -\left( {{L}_{d}}-{{L}_{q}} \right){{{\hat{\omega }}}_{e}} \\ \left( {{L}_{d}}-{{L}_{q}} \right){{{\hat{\omega }}}_{e}} & -R \\\end{matrix} \right]$，${{v}_{\alpha \beta }}$表示滑模趋近律，定义如下：$\left[ \begin{matrix} {{\nu }_{\alpha }} \\ {{\nu }_{\beta }} \\ \end{matrix} \right]=\left[ \begin{matrix} ksign\left( {{{\tilde{i}}}_{\alpha }} \right) \\ ksign\left( {{{\tilde{i}}}_{\beta }} \right) \\ \end{matrix} \right]$ ，在表达式中，k表示滑模增益，sign(x)表示符号函数，函数定义如下：$sign\left( x \right)=\left\{ \begin{array}{*{35}{l}} 1\ \ \ \ \ \ \ x0 \\ -1\ \ \ \ x<0 \\ \end{array} \right.$。

预测模型与参数模型做差后可获取误差方程

式中，$\tilde{i}=\hat{i}-i$，$\hat{i}$是预测电流，i为实际量测电流，$\tilde{Q}=\frac{1}{{{L}_{d}}}\left[ \begin{matrix} -R & -\left( {{L}_{d}}-{{L}_{q}} \right){{{\tilde{\omega }}}_{e}} \\ \left( {{L}_{d}}-{{L}_{q}} \right){{{\tilde{\omega }}}_{e}} & -R \\\end{matrix} \right]$。

本文使用Lyapunov理论证明滑模观测器的稳定性^[21]，构造Lyapunov函数如下

由式(6)可知，V在非零且为正的时刻，因参数不精确等因素导致误差永远存续，故V永远为正。对构造的函数式(6)求导，可得

将误差方程${{\dot{\tilde{i}}}_{\alpha }}$、${{\dot{\tilde{i}}}_{\beta }}$代入式(7)，可得

由前文所述可知，${{\tilde{Q}}_{12}}+{{\tilde{Q}}_{21}}=0$，${{\tilde{Q}}_{11}}<0$，${{\tilde{Q}}_{22}}<0$，代入滑模趋近律后，$\dot{V}$为

易知，在式(9)中，${{\tilde{Q}}_{11}}\tilde{i}_{\alpha }^{2}+{{\tilde{Q}}_{22}}\tilde{i}_{\beta }^{2}<0$，依据Lyapunov稳定性判据，$\dot{V}$需要为负。由此，可获取约束如式(10)所示

当${{\tilde{i}}_{\alpha }}>0$，${{\tilde{i}}_{\beta }}>0$时，${{E}_{\alpha }}-k<0$，${{E}_{\beta }}-k<0$；当${{\tilde{i}}_{\alpha }}<0$，${{\tilde{i}}_{\beta }}<0$时，${{E}_{\alpha }}+k>0$，${{E}_{\beta }}+k>0$。联立求解不等式，可得

在k满足式(11)约束条件时，滑模增益可取任意数。在此前提下，可保证设计的扩展反电势观测器在有限的时间内收敛，从而保证了观测器的可观性存在。为了降低刚性切换函数sign引入的抖振，在后文试验过程中，使用sigmoid函数替代sign函数，替换后不影响上文的可观性证明^[22]。本文使用的sigmoid函数定义如下

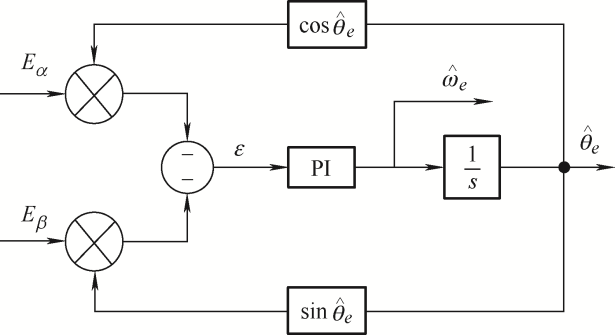
在上述滑模观测器得到扩展反电势信息后，可结合锁相环技术完成相位锁定，进而得到转子的位置信息，但滑模观测器获取的信息需要经过低通滤波器滤波后方可输入锁相环使用。锁相环的原理如图1所示，PI表示比例积分控制器，滑模观测器与锁相环共同构成了位置观测器。

通过插值算法可实现动态拟合转子实时运动轨迹，还可有效提高低线数编码器闭环控制精度。从位置观测器获取位置信息后，利用插值算法可实现电机转子位置插补。基于观测器法的插值算法实现表述如下^[18]：在控制策略中，每个采样时刻获取实时编码器位置信息。判断当前采样时刻与上一个采样时刻编码器的位置是否相同。若相邻采样时刻的编码器位置一致，则进入插值算法模块，在插值算法模块中，对位置观测器获取的位置信息进行做差运算，以获取当前采样时刻位置信息的增量，并将当前时刻的位置增量赋给存储增量值的静态变量，将静态变量值与当前时刻的编码器位置做和运算，从而获得当前插值位置，并用插值位置参与坐标变换运算，完成矢量控制闭环动作。在每个位置脉冲内，该静态变量可以记住上一时刻的累计位置增量。若相邻采样时刻的编码器位置信息发生跳动，表明此时编码器的位置信息发生变更，应将编码器位置信息赋给当前插值位置，进而参与矢量控制闭环，同时，此刻将静态变量清零，以便在下一个位置脉冲重新计数，此操作可以消除位置观测器相位滞后引入的不利影响。基于观测器法的插值算法的执行步骤表述如下，其中，下标enc表示从编码器中获取的离散位置信息，下标comp表示补偿值，即累积增量值，int表示插值位置，k表示不同的时序。

插值程序执行步骤如下所示。

步骤1：程序启动，获取当前编码器位置θ_enc[k+1]。

步骤2：判断θ_enc[k+1]与θ_enc[k]是否相等，若两者相等，进入步骤3；否则，将θ_enc[k+1]赋给θ_int[k+1]，进入步骤5，同时将θ_comp清零。

步骤3：计算当前时刻位置观测器的增量，并于上一时刻的累积增量θ_comp[k]相加，得到当前时刻的累积增量θ_comp[k+1]。

步骤4：将当前时刻的累积增量与θ_enc[k+1]相加，将结果赋值给θ_int[k+1]。

步骤5：输出θ_int[k+1]，程序结束。

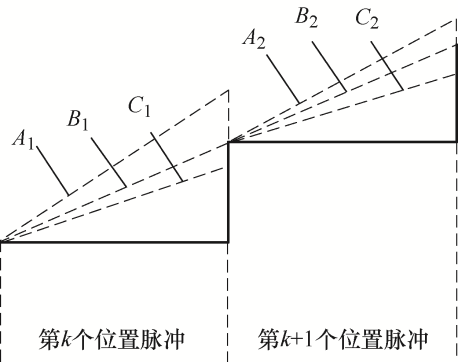
分析基于观测器法的插值算法可知，插值位置存在以下可能。出于简化分析的目的，取相邻两个位置脉冲的插值结果进行演示，可能情况如图2所示。从图2可看到相邻两个位置脉冲所有可能的插值情况。在理想情况下，即误差允许的范围内，认为存在B₁、B₂两种插值结果。实际上由于离散化误差的影响，完美拟合的情况并不存在。为了进一步简化分析，可将B₁、B₂两种插值结果去掉，通过排列组合可知，此时存在4种组合方式，即A₁A₂、A₁C₂、C₁A₂、C₁C₂。在上述四种插值结果中，认为A₁、A₂正向误差累积过多，相应地认为C₁、C₂负向误差累积过多，两类误差现象均可归类至同向累积误差，剩下的插值情况可分类至非同向累积误差。经过试验观察，在相邻位置脉冲中，A₁A₂、C₁C₂组合是最常见的两种插值结果，即最常见的误差累积现象表现出同向误差累积特点。分析常见的两个插值组合可知，插值误差在大多数情况下，表现出同向累积特性，即在相邻两个位置脉冲，误差累积方向同为正向累积或同为负向累积。

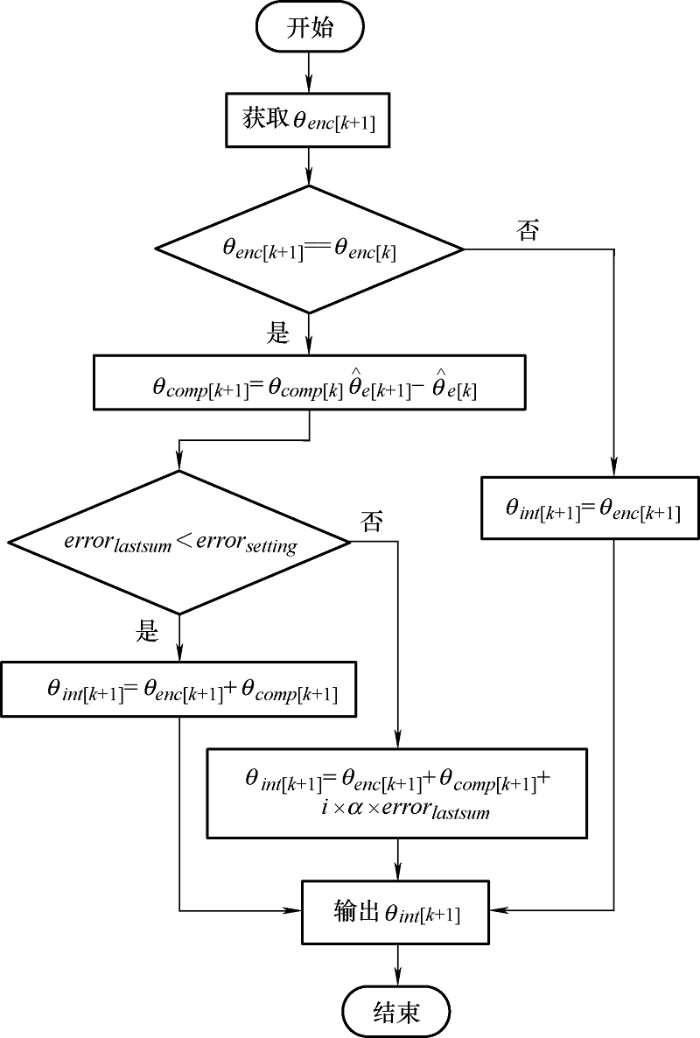
基于上述分析，为改善A₁A₂、C₁C₂两种插值结果带来的不利影响，本文引入累积误差补偿策略实现插值控制，即利用基于累积误差补偿的插值控制算法实现闭环控制。在每个位置脉冲的起始点，将前一个采样时刻插值位置与当前位置脉冲的起始位置做差，所得结果记为前一个位置脉冲的累积插值误差。考虑相邻位置脉冲的累积误差大致相当，将上一位置脉冲的累积误差视为当前位置脉冲结束时的累积误差，依据误差反向相消原理，在当前位置脉冲内逐采样周期做出位置补偿。在具备误差同向传递性的相邻位置脉冲，因累积误差相当但不相等，上一位置脉冲的累积误差不能直接作为当前位置脉冲的累积误差，需要引入缩放因子α构造当前位置脉冲的累积误差。整个插值控制程序框图如图3所示，图3中下标与基于观测器法的插值算法执行步骤中含义一致。

基于累积误差补偿的插值控制算法执行步骤如下所示。

步骤1：程序启动，获取当前编码器位置θ_enc[k+1]。

步骤2：进入判断模块，比较θ_enc[k+1]与θ_enc[k]是否相等，若两者相等，进入步骤3；否则，将θ_enc[k+1]赋给θ_int[k+1]，进入步骤5，同时，将θ_comp清零。

步骤3：计算当前时刻位置观测器的增量，并与上一时刻的累积增量θ_comp[k]相加，得到当前时刻的累积增量θ_comp[k+1]。

步骤4：若上一位置脉冲的累积误差超过误差限，进入基于累积误差补偿的插值控制算法，累积增量θ_comp[k+1]、误差补偿项i×α×error_lastsum、当前编码器位置θ_enc[k+1]三者相加，所得结果赋给θ_int[k+1]。在误差补偿项中，i为分式，初始值为0，分子在每个采样周期加1，分母为当前位置脉冲包含的采用周期总数，起到逐采样周期抵消累积误差的作用，α是缩放因子，在当前位置脉冲结束时，i重置为零，error_lastsum是上一位置脉冲的累积误差；否则进入基于观测器法的插值算法，累积增量θ_comp[k+1]与θ_enc[k+1]相加，所得结果赋值给θ_int[k+1]。

步骤5：输出θ_int[k+1]，程序结束。

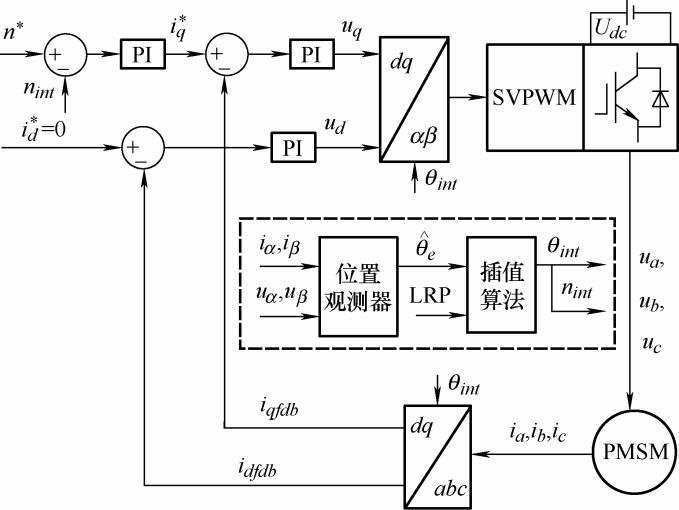
本文所有试验在750 W的IPMSM对拖控制系统完成，试验装置如图4所示。装置中IPMSM的参数如表1所示，负载电机是安川伺服电机，通过安川变频器控制，负载电机工作于转矩控制模式。考虑文中试验最高速度为50 r/min，位置观测器中的低通滤波器截至频率设置为：50×5×3/60 Hz= 12.5 Hz。sigmoid函数中的待定系数为a=5。锁相环中PI参数如下：k_p=150，k_i=250。文中利用光电编码器模拟低线数编码器，编码器线数为2 500线，依据降采样模块可得：2 500×250/10 000=62.5，此时模拟编码器为62.5线；同时，未经降采样模块的位置信息作为对照以评判插值算法的优劣，不参与闭环控制过程。误差补偿项中的缩放因子取α=0.9。误差限设置为error_setting=0.004 rad，当累积插值误差超过误差限，启动基于累积误差补偿的插值控制算法，否则，启动基于观测器法的插值算法进行插值控制。以下试验结果均是通过插值位置实现闭环矢量控制，依据速度-位置构成的积分链，反馈速度由实时插值位置计算获取。依前所述，总体控制框图如图5所示，PI表示比例积分控制器。

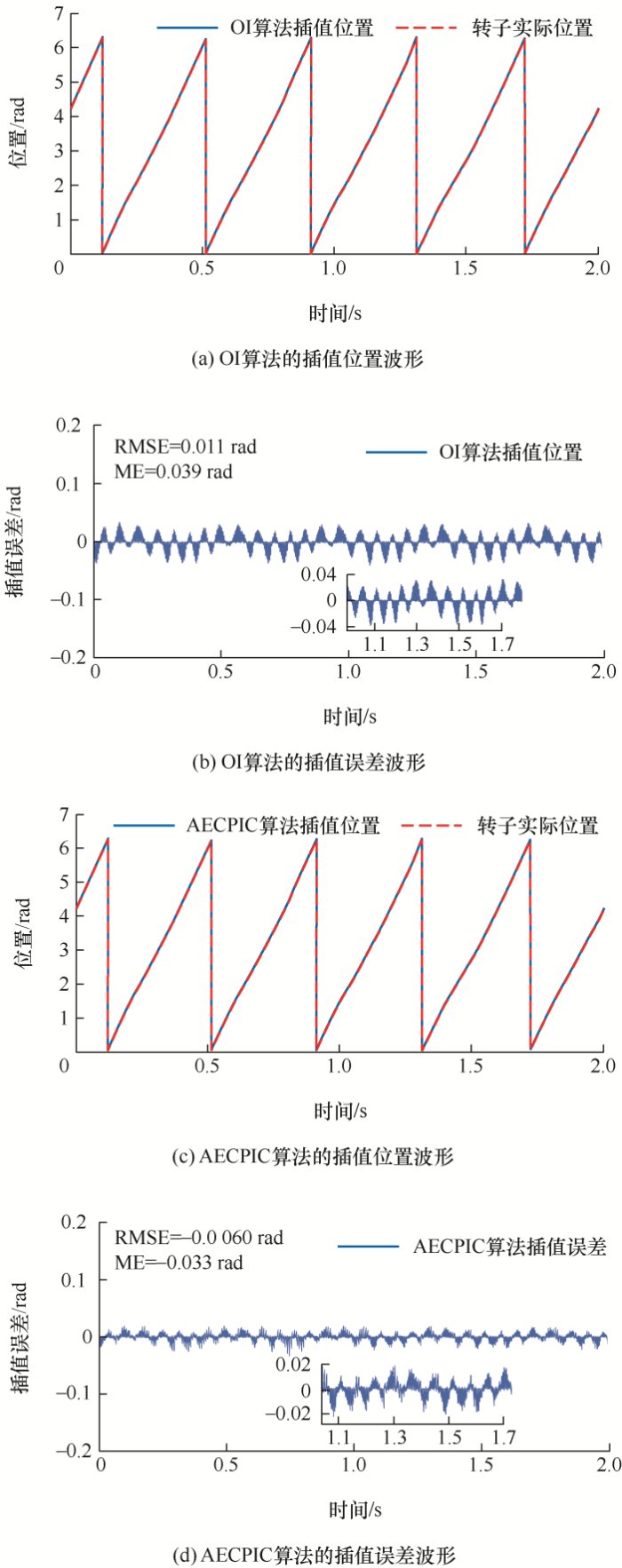
图6为参考转速30 r/min、空载条件下的试验波形，图6a、图6b表示基于观测器法(OI)的插值算法插值位置与插值误差，图6c、图6d表示基于累积误差补偿的插值控制算法(AECPIC)插值位置与插值误差，插值误差定义为位置降采样之前的编码器位置减去插值位置。RMSE表示插值误差的均方根误差，ME表示插值误差的最大误差，ME中数值前方的“-”表示超前误差，“+”表示滞后误差。表2为不同参考转速空载条件下的OI算法与AECPIC算法性能对比。从图6a、图6c可以分析出，在空载工况下，基于观测器法的插值算法和所提插值控制算法在参考转速30 r/min时均能很好地跟踪实际的转子位置；从图6b、图6d可以分析出，AECPIC算法插值误差减小，在低速域工况性能表现更好，其空载时插值位置误差的误差带稳定在0.02 rad (1.15°)内。

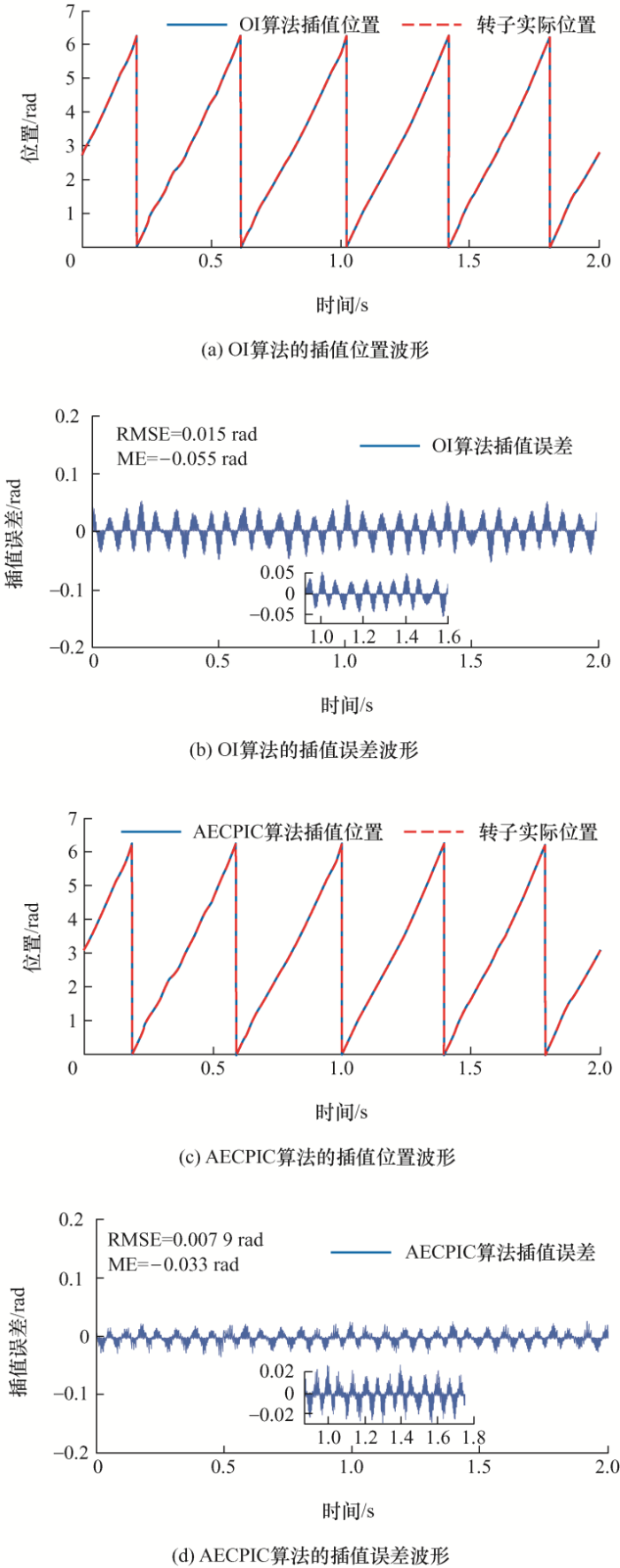
图7为参考转速30 r/min、恒定0.5 N负载条件下的试验波形，图片顺序信息与图6相同。表3为0.5 N负载、不同参考转速下OI算法与AECPIC算法性能对比。图7表明，在0.5 N负载条件下，从图7a可看出，OI算法表现出了位置谐波现象，从图7c则可看出，所提算法的插值位置中谐波更少，表明所提方法能有效改善位置谐波现象。综合表3可得出如下结论：在恒定负载工况下，所提算法能有效提高位置插值精度，提升效果与参考速度正相关；OI算法与AECPIC算法的插值误差的误差带与参考转速正相关。

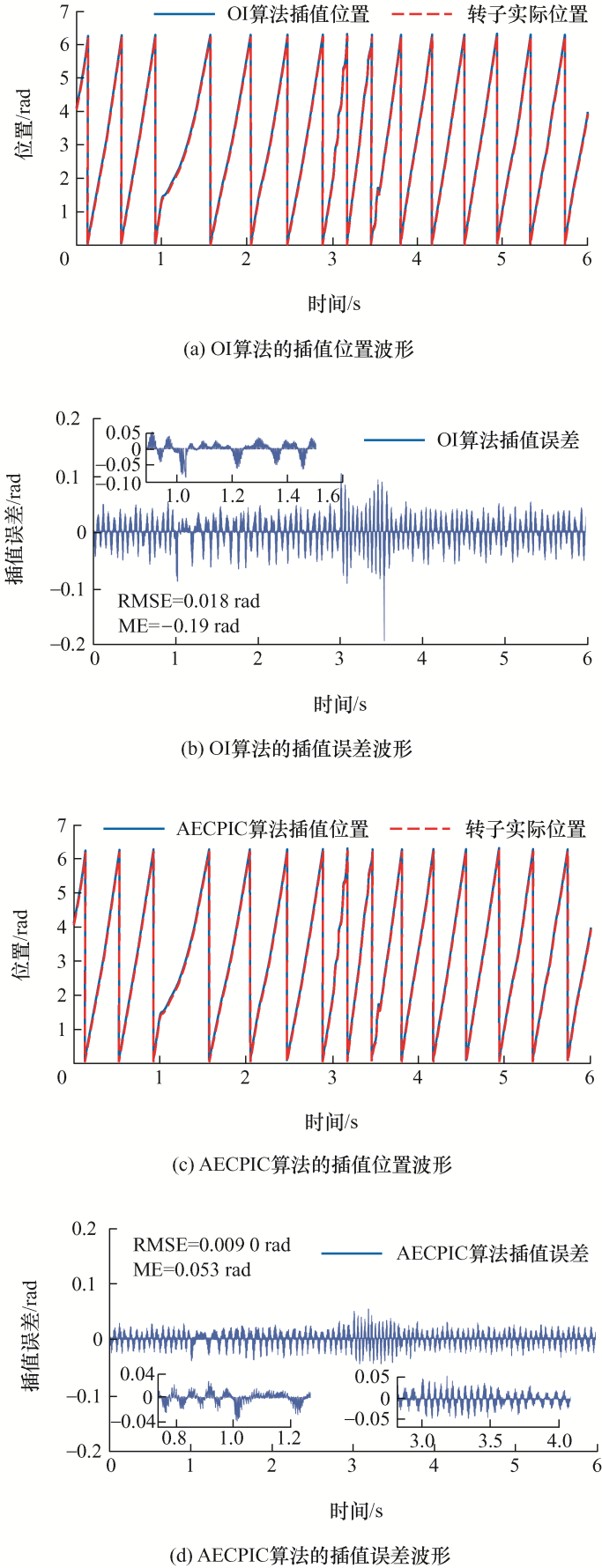
图8为参考转速30 r/min、恒定0.5 N负载、1~2 s施加0.5 N外界扰动条件下的试验波形图，顺序信息与图6相同，表4为恒定0.5 N负载、1~2 s施加0.5 N外界扰动、不同参考转速条件下OI算法与AECPIC算法性能对比。分析图8可看出，OI算法在该测试工况下同样表现出位置谐波现象。从图8b、图8d可看出，施加0.5 N外界扰动后，转子先减速，随后加速至给定转速。在此过程中，OI算法的插值误差峰值为0.19 rad，稳态误差带为 ±0.050 rad，AECPIC算法的插值误差峰值为0.053 rad，稳态误差带为±0.03 rad。

在每个编码器位置脉冲内，误差累积导致插值算法的控制精度和稳定性降低。针对此问题，本文基于误差补偿思想提出了一种插值控制策略，通过试验验证了所提方法的有效性和可行性。主要结论如下所述。

(1) 在不同负载、不同参考转速工况中对所提方法进行了试验，结果表明，与传统方法相比，所提方法有效抑制了位置脉冲间的同向误差传播现象，其控制精度和抗外部扰动能力更优。

(2) 所提方法不需要额外增加硬件，易于实现，具有一定的工程应用价值。

(3) 所提方法未考虑逆变器非线性因素环节，研究考虑非线性因素补偿的低速插值控制算法，这是今后本文的改进方向。