1 引言
随着能源和环境问题日益突出[1 ] ,水电、风电、光伏等可再生能源作为清洁能源的代表,对电网的渗透规模不断扩大[2 -3 ] 。然而,可再生能源具有波动性大和间歇性强等特点,这给电力系统的频率稳定带来了巨大压力[4 ] 。传统机组爬坡率低、响应速度慢,因此无法及时调节可再生能源不确定性对电力系统频率扰动的影响。随着电动汽车的普及,越来越多的电动汽车可作为移动储能系统和调峰装置接入电网[5 -6 ] ,其所发挥的削峰填谷、频率调节等功能可大大提高电力系统运行的可靠性和经济性[7 -8 ] 。为此,V2G(Vehicle-to-grid)技术引起了国内外学者的广泛关注。
车辆参与V2G服务意味着电池需要依据电网需求进行频繁充放电,这不可避免地加剧了电池的老化速度。JAFARI等[9 ] 发现电动汽车若每天执行V2G服务,则会显著缩短电池寿命。BISHOP等[10 ] 发现在不同的电池容量、充电方式和放电深度下,V2G服务对动力电池退化影响程度是不同的,其中电动汽车电池组的退化对充电方式以及单个电池的放电深度最为敏感。THINGVAD等[11 ] 研究了电动汽车长期执行V2G服务对电池容量衰退的影响,发现电池可用容量两年后平均降低了10%,五年后降低了17.8%。电池老化加剧会导致其维修保养成本的提升,从而降低V2G所带来的服务效益。ZHENG等[12 ] 发现在当前电池成本下,电动汽车提供V2G服务,车主极难从中获取利润。GOUGH等[13 ] 发现V2G服务可获得的利润无法弥补电动汽车参与辅助服务所造成的电池老化成本损失。LUNZ等[14 ] 发现V2G在电力市场能源交换所带来的收益与电池老化成本相比是极小的。此外,电池容量衰退还会造成车辆续航里程下降,引发用户“里程焦虑”[15 ] 。为此,研究如何抑制车辆参与V2G服务所引起的电池老化,从而延长电池寿命,具有重要意义。
目前,研究人员主要通过以下几个方面来延长电池寿命。第一,研发具有超长电池寿命的下一代电池技术。如ELDESOKY等[16 ] 开发的最新NMC811/Graphite电池在室温条件下工作寿命可长达数十年。第二,通过优化电池充电策略延长电池寿命。如ATTIA等[17 ] 开发了一种机器学习方法,通过优化电池充电协议,最大化电池循环寿命,同时还可以缓解电动汽车用户的续航焦虑。HUANG等[18 ] 基于模糊控制的充电协议设计了一种先进的电池充电器,有效缩短了充电时间,同时还提高了电池循环寿命和充电效率。第三,基于当前电池技术开发先进的V2G优化控制模型,以抑制电池老化。RENIERS等[19 ] 基于锂电池老化物理模型来计算能源交易收入并测量电池老化,从而在能源交易市场中弥补了技术保真度和经济调度之间的差距。数据分析表明,与传统启发式退化建模方法相比,该方法可以增加20%的收入,同时减少30%的电池老化。FORTENBACHER等[20 ] 提出了一种用于分布式电池存储的新型两阶段集中式MPC方案,该方案由调度实体和实时控制实体组成,研究发现,在实时控制阶段使用详细的电池模型,可以将电网调度对电池的损耗降低30%。PATSIOS等[21 ] 提出了一种集成的电-热-化学建模方法,并构建了一种从电池到电网的电网储能系统的集成建模框架。仿真发现其可将电力系统调度对电池的损耗减少两倍。UDDIN等[22 ] 构建了一种完整的电池退化模型,该模型综合考虑了电池所有的老化行为,结果表明,智能电网可将电动汽车电池组容量衰减最多减少9.1%。LI等[23 ] 提出了一种主动抑制电池老化的调度系统,采用雨流循环计数法量化电池老化,以电池老化最小化为优化目标之一,发现通过优化参与调度车辆规模以及各辆车充放电时间可以使电池充放电周期最小。综上可见,当前大部分研究聚焦于V2G在削峰填谷与能源交易市场电量调度过程中减少电池老化,但如何抑制V2G调频服务中的电池老化却鲜有研究。
当前有关V2G调频的研究主要集中在如何有效跟踪电网频率信号,忽略了V2G调频对电池老化的影响。BUŠIĆ等[24 ] 在满足电池约束界限情况下,为跟踪电网端调频功率需求信号,引入分布式随机控制构架,并为不同类型的电池定义不同的随机决策规则,以优化单个电池的静置时间和充电状态。RAJAMAND[25 ] 发现将电动汽车的荷电状态(State of charge,SOC)反馈到控制结构中,可以很好地改善微电网频率/电压调节。KAUR等[26 ] 针对电动汽车参与次级频率控制,提出了一种双层分级控制方案,以电动汽车车主使用需求为约束条件,结果显示,该方案减小了电网频率偏差。PENG等[27 ] 提出了一种智能充电算法,可以根据频率偏差信号协调电动汽车充放电,该算法可以改善低压配电网的负载系数和电压水平。REHMAN[28 ] 提出了一种最优分层双向聚合算法,通过优化电动汽车充放电功率,预测电力需求,并在智能电网中执行日前负载调度来实现为电网提供电压和频率调节服务。因此,研究如何抑制V2G调频过程中的电池老化,将对V2G调频的经济效益产生重要影响。
为了抑制V2G调频对电动汽车电池老化的影响,提升整个V2G系统的稳定性,本文提出了一种以抑制电池老化和跟踪电网端调频需求功率为目标的V2G最优调频控制策略。主要工作如下:① 通过引入基于机理的电池老化模型,建立了以抑制电池老化为目标的优化模型;② 应用fmincon函数对优化模型进行求解,进而基于模型预测控制理论,实现对电动汽车充放电功率的实时高效控制;③ 仿真结果表明,与基准优化控制策略相比,本文所提出的V2G调频策略,可将电池老化降低高达22.34%。
2 V2G工作原理与优化控制
2.1 V2G工作原理
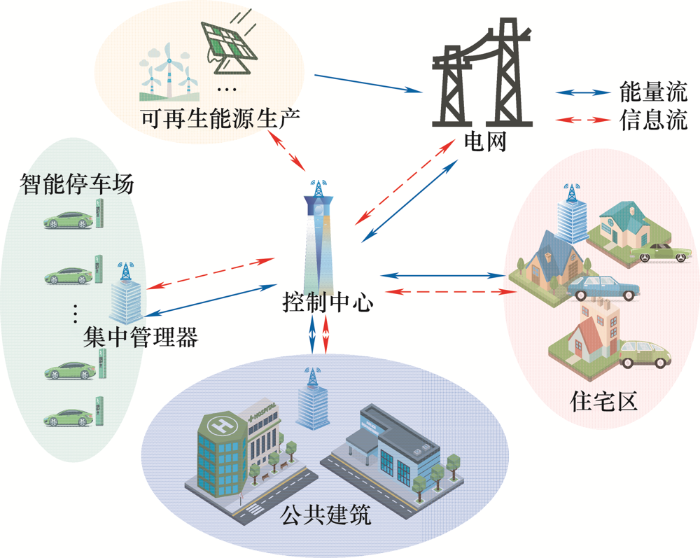
V2G技术可实现电动汽车与电网之间能量和信息的高效互动,为电动汽车并入电网提供辅助服务,并为优化电力系统运行提供了技术支持。图1 为电动汽车与电网之间的能量流和信息流示意图。其中,集中管理器由数据管理系统和控制系统两部分组成,可实现多辆电动汽车的统一管理与控制。数据管理系统负责收集电动汽车实时充放电功率、SOC信息、电网调度中心发送的实时调频功率需求数据以及相关历史数据等,然后上报给电网调度中心。控制系统则对调频功率需求数据和调度指令进行分析,优化车辆充放电策略并将控制指令发送到充电桩。例如,当电网频率出现扰动,调度中心将向集中管理器发送调频功率需求指令,集中管理器则通过控制系统控制充电桩以改变电动汽车充放电功率,使V2G提供的总功率满足调频需求。
图1
2.2 抑制电池老化的V2G优化控制原理
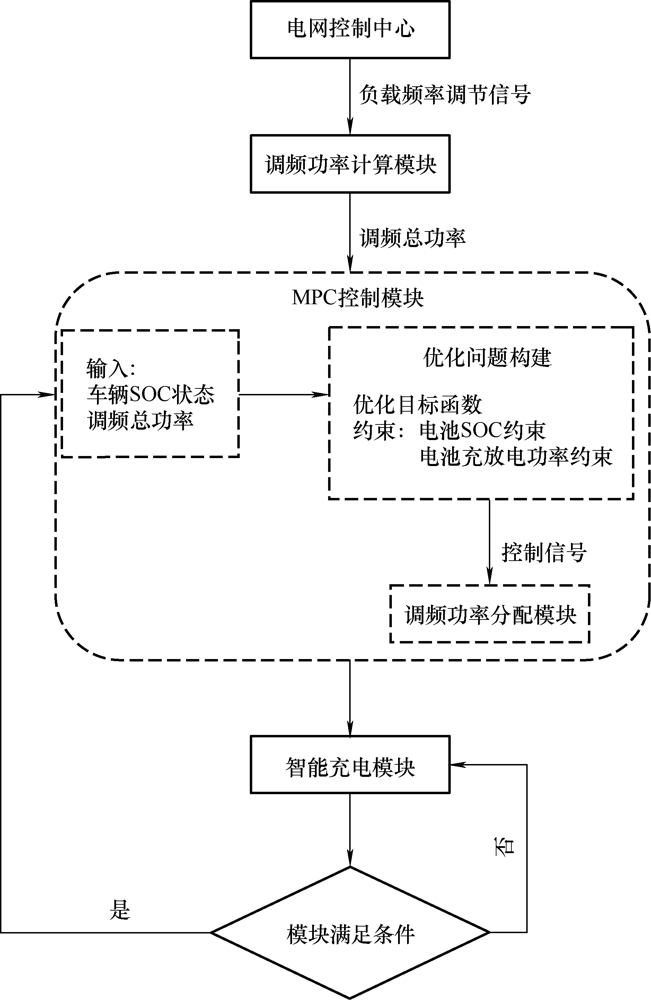
图2 为本文所提出的主动抑制电池老化的优化控制原理图,该原理框架主要包含四个模块:判断模块、调频功率计算模块、MPC控制模块和电动汽车智能充电模块。其中,电动汽车参与V2G服务判断模块负责收集电动汽车集中管理器中各电动汽车实时的SOC值,基于此初步选择参与调频服务的电动汽车,并将控制信号发送到各电动汽车,判断选择条件如下
(1) ${{\lambda }_{n}}=\left\{ \begin{align} & 1\text{ }\mathrm{SO}{{\mathrm{C}}_{\min }}\le \mathrm{SO}{{\mathrm{C}}_{n}}(t)\le \mathrm{SO}{{\mathrm{C}}_{\max }} \\ & 0\text{ } \\ & \text{0}\le \text{SO}{{\text{C}}_{n}}(t)\le \mathrm{SO}{{\mathrm{C}}_{\min }}\ \mathrm{SO}{{\mathrm{C}}_{\max }}\le \text{SO}{{\text{C}}_{n}}(t)\le 1 \\ \end{align} \right.$
式中,${{\lambda }_{n}}$为控制信号,其取值决定第$n$辆EV是否具有资格参与V2G调频服务。${{\lambda }_{n}}=1$表示第$n$辆EV具有资格,${{\lambda }_{n}}=0$则表示第$n$辆EV不具有资格。t 表示时刻,$\text{SO}{{\text{C}}_{n}}(t)$表示第$n$辆EV在t 时刻的SOC值,$\text{SO}{{\text{C}}_{\min }}\text{ }\text{SO}{{\text{C}}_{\max }}$分别表示电动汽车电池允许达到的最小和最大SOC值。
图2
调频功率计算模块将电网控制中心传递的负荷频率控制信号转化为调频功率需求信号,并传递到MPC控制模块,MPC控制模块则基于该调频功率需求信号,并依据采集的电动汽车SOC信息,以电池老化最小和调频功率需求信号跟踪效果最好为优化目标,优化参与V2G调频的各电动汽车充放电功率,进而将功率控制信号发送到电动汽车智能充电模块。其中控制器对调频功率需求信号跟踪效果基于误差$\Psi $评价,表达式如下
(2) $\Psi =\frac{1}{w}\sqrt{\sum\limits_{k=1}^{w}{[(\sum\limits_{i=1}^{N}{{{P}_{E{{V}_{i,k}}}}-{{P}_{op{{t}_{k}}}})/{{P}_{op{{t}_{k}}}}{{]}^{2}}}}}\times 100%$
式中,$w={{T}_{total}}/\Delta t$,${{T}_{total}}$为调频总时长,$\Delta t$为采样时间间隔,$\Psi $越趋近于0,表明跟踪效果越好。N 为参与调频的车辆数,下标i 代表车辆编号,${{P}_{E{{V}_{i,k}}}}$为第i 辆车在第k 个采样时段的充放电功率,${{P}_{op{{t}_{k}}}}$为第k 个采样时段电网需求调频功率。
基于该控制信号,智能充电桩对参与V2G调频的电动汽车充放电功率进行实时控制,从而实现在维持电力系统频率稳定的同时抑制电池老化。
3 优化控制器开发
3.1 电池模型
3.1.1 电池充放电模型
本文应用电池等效内阻模型来描述其充放电特性,表达式[29 ] 如下所示
(3) ${{I}_{i}}(t)=\frac{{{U}_{O{{C}_{i}}}}(t)-{{U}_{{{t}_{i}}}}(t)}{{{R}_{i}}}$
(4) ${{P}_{E{{V}_{i}}}}(t)={{U}_{{{t}_{i}}}}(t){{I}_{i}}(t)$
(5) ${{I}_{i}}(t)=\frac{{{U}_{O{{C}_{i}}}}(t)-\sqrt{{{U}^{2}}_{O{{C}_{i}}}(t)-4{{R}_{i}}{{P}_{E{{V}_{i}}}}(t)}}{2{{R}_{i}}}$
式中,${{I}_{i}}(t)$表示$t$时刻第$i$辆车的电池电流,${{R}_{i}}$表示第$i$辆车的电池内阻,${{U}_{O{{C}_{i}}}}(t)$表示t 时刻第i 辆车的电池开路电压,${{U}_{{{t}_{i}}}}(t)$表示t 时刻第i 辆车的电池路端电压,${{P}_{E{{V}_{i}}}}(t)$表示t 时刻第i 辆车电池侧的充放电率,充电为正,放电为负。
电池SOC定义为电池剩余容量与额定容量的比值[30 ] ,表达式如下所示
(6) ${{Z}_{i}}(t)=\frac{{{Q}_{i}}(t)}{{{Q}_{no{{m}_{i}}}}}$
式中,${{Z}_{i}}(t)$表示$t$时刻第$i$辆车的电池SOC,${{Q}_{i}}(t)$表示$t$时刻第$i$辆车的电池可用容量,${{Q}_{no{{m}_{i}}}}$表示第$i$辆车的电池额定容量。基于式(5)进一步对时间求导可得
(7) ${{Z}_{i}}(t)=-\int{\frac{{{U}_{O{{C}_{i}}}}(t)-\sqrt{{{U}^{2}}_{O{{C}_{i}}}(t)-4{{R}_{i}}{{P}_{E{{V}_{i}}}}(t)}}{2{{R}_{i}}{{Q}_{no{{m}_{i}}}}}}\mathrm{d}t$
(8) $\left\{ \begin{align} & {{Z}_{i,{{t}_{k+1}}}}={{Z}_{i,{{t}_{k}}}}-\frac{{{U}_{O{{C}_{i,{{t}_{k}}}}}}-\sqrt{{{U}^{2}}_{O{{C}_{i,{{t}_{k}}}}}-4{{R}_{i}}{{P}_{E{{V}_{i,{{t}_{k}}}}}}}}{2{{R}_{i}}{{Q}_{no{{m}_{i}}}}}\Delta t \\ & \Delta Z_{i}^{k}={{Z}_{i,{{t}_{k+1}}}}-{{Z}_{i,{{t}_{k}}}} \\ \end{align} \right.$
式中,下标${{t}_{k}}$表示第$k$个时刻,则${{t}_{k+1}}={{t}_{k}}+\Delta t$。$\text{ }\!\!\Delta\!\!\text{ }Z_{i}^{k}$为第$k$个时段SOC的变化量。
3.1.2 电池容量衰退模型
对于石墨负极锂离子电池,其性能衰退主要是由于固液界面膜(Solid electrolyte interface,SEI)生长和活性物质损失导致。SEI膜生长主要是由于电解液在电极表面的副反应引发,而活性物质损失则主要为锂离子嵌入嵌出电极诱发的力学应力所导致的活性物质破裂与脱离[30 -31 ] 。本文将通过优化电动汽车电流以最大限度减小电池容量衰退。为了简化模型,本文运用电池活性物质损失模型来描述电池老化。
根据文献[31 ],恒温条件下的电池活性物质损失模型为
(9) ${{Q}_{A{{M}_{i}}}}={{\Phi }_{(T)}}\int{{{Z}_{i}}(t)\left| {{I}_{i}}(t) \right|\mathrm{d}t}$
(10) ${{\Phi }_{(T)}}={{k}_{AM}}\exp \left( -\frac{{{E}_{AM}}}{RT} \right)$
式中,${{\Phi }_{(T)}}$为温度影响因子;${{k}_{AM}}$为活性物质损失指数因子;${{E}_{AM}}$为活性物质活化能;$T$为环境温度。式(9)表明,电池无论是充电还是放电都会造成其容量衰退。
第$k$个$\Delta T$时段内电池的容量衰减量为
(11) $\Delta {{Q}_{A{{M}_{i}},k}}={{\Phi }_{(T)}}\int_{{{t}_{k}}}^{{{t}_{k+1}}}{{{Z}_{i}}(t)\left| {{I}_{i}}(t) \right|\mathrm{d}t}$
(12) ${{I}_{i}}(t)=-{{Q}_{no{{m}_{i}}}}\frac{\mathrm{d}{{Z}_{i}}(t)}{\mathrm{d}t}$
(13) $\Delta {{Q}_{A{{M}_{i,k}}}}={{\Phi }_{(T)}}{{Q}_{no{{m}_{i}}}}\int_{{{Z}_{i,{{t}_{k}}}}}^{{{Z}_{i,{{t}_{k+1}}}}}{{{Z}_{i}}(t)\left| \mathrm{d}z \right|}$
(14) $\Delta {{Q}_{A{{M}_{i,k}}}}={{\Phi }_{(T)}}{{Q}_{no{{m}_{i}}}}\left| \Delta Z_{i}^{k} \right|\frac{{{Z}_{i,{{t}_{k}}}}+{{Z}_{i,{{t}_{k+1}}}}}{2}$
3.2 约束条件
(1) 电池SOC约束,即每辆参与调频的电动汽车电池SOC在调频时间内不会低于最小SOC值,也不会高于最大SOC值。
(15) $\left\{ \begin{align} & {{Z}_{\min }}\le {{Z}_{i}}(t)\le {{Z}_{\max }}\ \ \ \ \text{ }i=1,2,\cdots,N \\ & {{Z}_{i,{{t}_{k+1}}}}={{Z}_{i,{{t}_{k}}}}-\frac{{{U}_{O{{C}_{i,{{t}_{k}}}}}}-\sqrt{{{U}^{2}}_{O{{C}_{i,{{t}_{k}}}}}-4{{R}_{i}}{{P}_{E{{V}_{i,{{t}_{k}}}}}}}}{2{{R}_{i}}{{Q}_{no{{m}_{i}}}}}\cdot \Delta t\ \ \ i=1,2,\cdots,Nk=1,2,\cdots,M\text{ } \\ \end{align} \right.$
(2) 电池充放电功率的约束,即每辆参与调频的电动汽车的充放电功率不会低于最小放电功率,也不会高于最大充电功率。
(16) ${{P}_{\min }}\le {{P}_{E{{V}_{i,{{t}_{k}}}}}}\le {{P}_{\max }}\text{ }i=1,2,\cdots,N\ \ \ k=1,2,\cdots,M $
3.3 目标函数
为了使参与V2G调频的电动汽车在未来$M$个时间段内的电池老化最小,同时保证其良好的调频功率跟踪效果,构建目标函数
(17) ${{J}^{\text{MD}}}=\text{ }\sum\limits_{k=\text{1}}^{M}{\text{(}}\alpha (\sum\limits_{i=1}^{N}{\Delta {{Q}_{A{{M}_{i,k}}}}})+\beta (\sum\limits_{i=1}^{N}{{{P}_{E{{V}_{i,k}}}}-{{P}_{opt}}_{k})}\text{)}$
式中,$\alpha $和$\beta $为惩罚因子。通过调整$\alpha $和$\beta $值即可控制电池老化抑制率以及车辆总充放电功率对电网需求功率的跟踪效果。
3.4 MPC控制模型
电动汽车参与V2G调频过程中,抑制前$M$个时间段内的电池老化的优化模型构建如下
(18) $\left\{ \begin{align} & \text{min }{{J}^{\text{MD}}}=\text{ } \\ & \sum\limits_{k=\text{1}}^{M}{\text{(}\alpha \text{(}}\sum\limits_{i=1}^{N}{\Delta {{Q}_{A{{M}_{i,k}}}}}+\beta (\sum\limits_{i=1}^{N}{{{P}_{E{{V}_{i,k}}}}-{{P}_{opt}}_{k})}\text{)} \\ & \text{s}\text{.t}\text{. } \\ & {{Z}_{\min }}\le {{Z}_{i}}(t)\le {{Z}_{\max }}\text{ }i=1,2,\cdots,N\ \ k=1,2,\cdots,M \\ & \\ & {{P}_{\min }}\le {{P}_{E{{V}_{i,{{t}_{k}}}}}}\le {{P}_{\max }}\text{ }i=1,2,\cdots,N\ \ k=\text{1,2},\cdots \text{,}M \\ \end{align} \right.$
4 仿真与结果分析
4.1 仿真试验设置
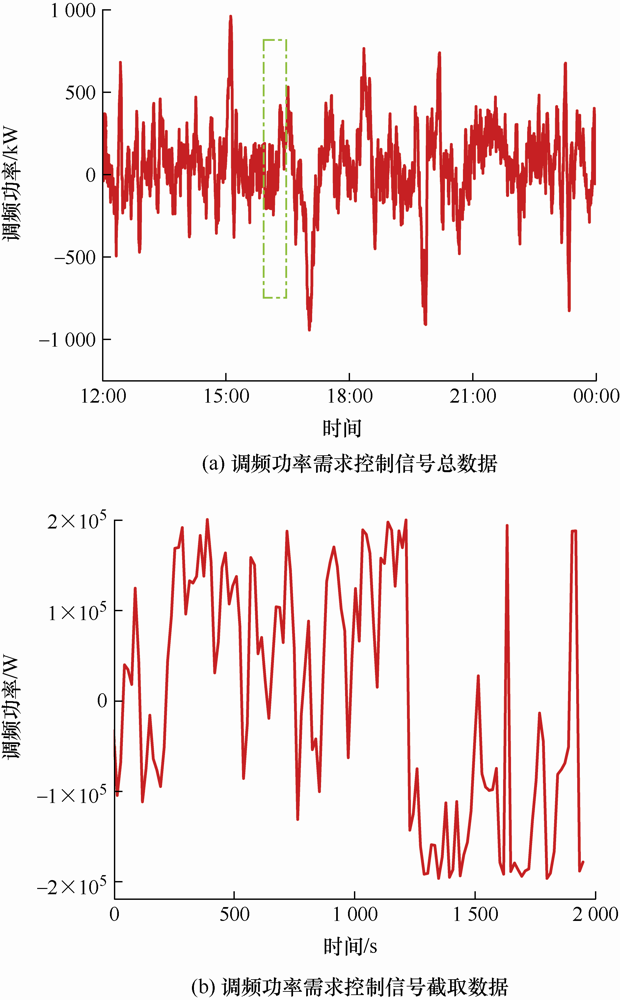
本节中将对本文所提出的主动抑制电池老化的V2G调频策略进行仿真试验。图3 为调频功率需求控制信号图。电力系统调频功率需求控制信号选取自美国PJM电力市场2022年2月12日当日12 h时长的数据,如图3 a所示。图3 b从图3 a截取部分数据,总时长为1 950 s,作为本文的主要仿真试验数据,其采样时间间隔为15 s。试验选取10辆三种不同类型的电动汽车参与调频服务,包括NIO EC6、BYD han 以及Tesla model S,三种车型对应的电池容量分别为214.29 A·h、135 A·h、211.44 A·h,试验中,车辆电池初始SOC值在约束范围内由低到高进行设置。无特殊说明,本文电池SOH(State of health)均定义为92.9%,即电池容量衰减了7.1%。
图3
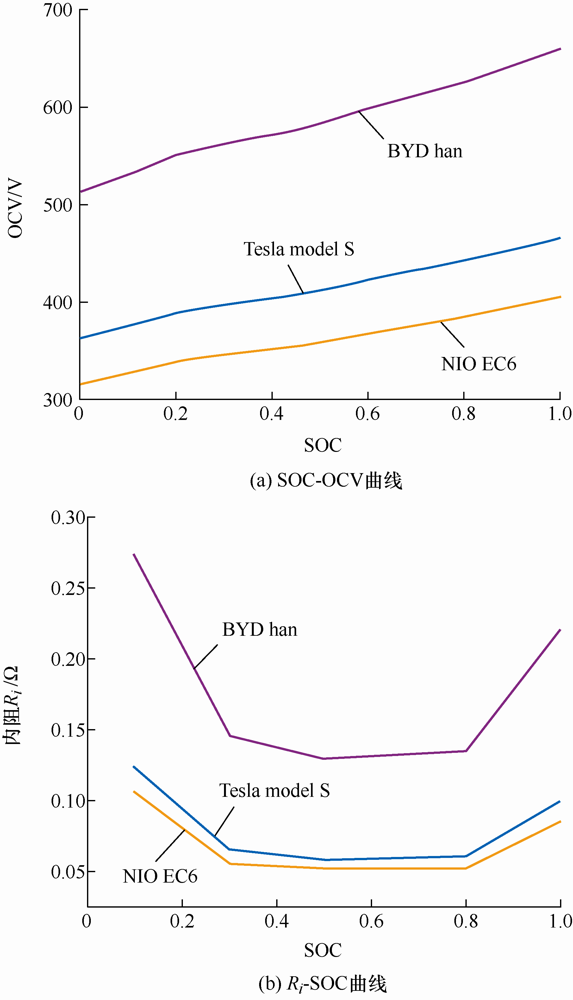
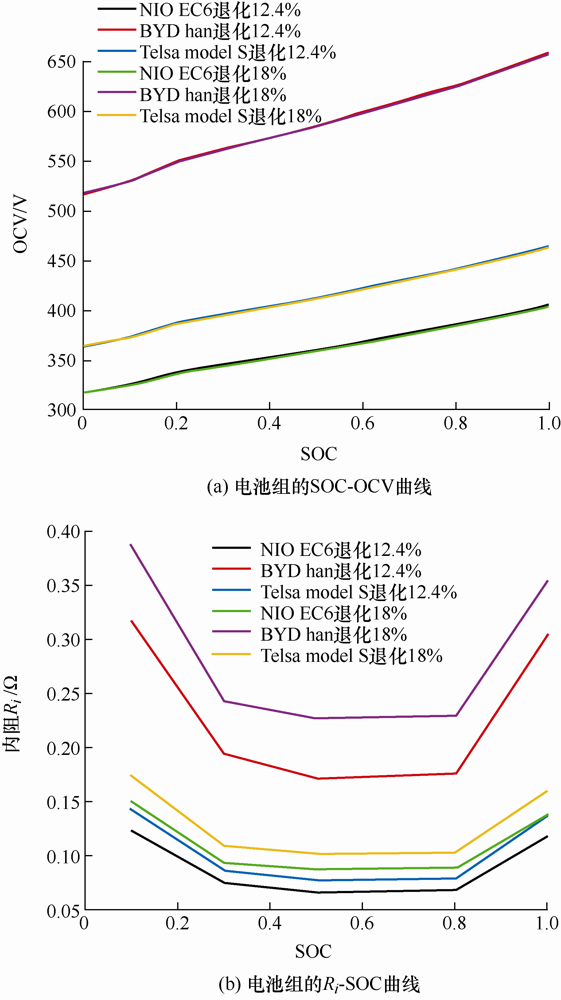
为简化计算流程,本文假设三种类型的电动汽车的电池包均采用Li(NiCoAl)O2 单体电池,该电池单体额定容量和额定电压分别为3.0 A·h和3.6 V。该电池的大量详细老化试验结果可参考文献[30 ]。在本研究中,对单体电池的开路电压(Open circuit voltage,OCV)和内阻(Internal resistance,IR)Ri 分别进行成比例放大以得到相应车辆电池组的对应参数。该电池组初始容量衰退7.1%后的SOC-OCV与Ri -SOC曲线如图4 所示。
图4
图4
电池组初始容量衰退7.1%后的SOC-OCV与Ri -SOC曲线图
电池老化模型式(7)中的参数参考文献[31 ]进行设置,其中${{k}_{AM}}=1.368\text{ l/(A}\cdot \text{h)}$和${{E}_{AM}}=39\ 500\text{ J/mol}$。电池包的温度假设为25 ℃,因此$T=298.15\text{ K}$。其他相关参数设置如表1 所示。本文采用功率平均分配策略作为基准优化控制策略来验证所开发模型的高性能。
4.2 仿真与结果分析
4.2.1 M =20以及M =30的仿真结果
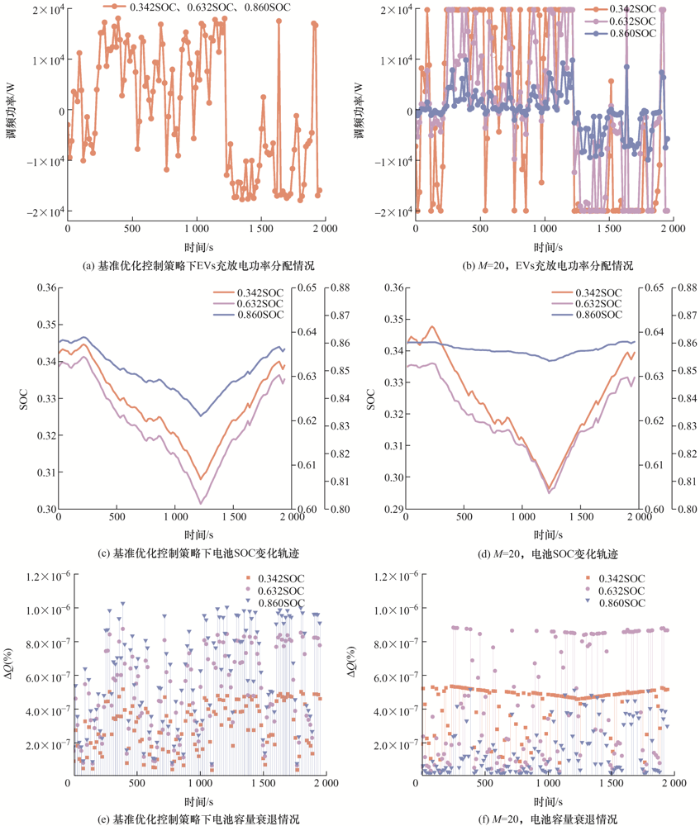
图5 为采用基准优化控制策略以及M =20条件下的电动汽车V2G调频控制策略仿真结果,其中选择三种车型初始SOC差异较大的调频结果进行比较。图5 a为采用基准优化控制策略电动汽车的充放电功率分配情况,图5 b为采用主动抑制电池老化优化控制策略电池的充放电功率分配情况。可以看出,与功率平均分配策略相比,优化后的功率分配策略中每一时段电池的充放电功率大小与其SOC值成负相关关系,即初始SOC值为0.342的电池充放电功率较大,而初始SOC值为0.860的电池充放电率反而较小。
图5
图5
采用基准优化控制策略以及M =20,V2G调频控制策略优化仿真结果
图5 c为采用基准优化控制策略电动汽车的SOC变化趋势,图5 d为调频功率优化后的电池SOC变化轨迹,其中SOC初始值为0.342的轨迹曲线斜率最大,这表明此时该电池总是以最大充放电功率去响应调频信号。而SOC初始值为0.860的电池SOC曲线变化较为平缓,即在仿真时间内该车辆电池都是以较小的充放电功率去响应调频信号。值得注意的是,3辆电动汽车参与调频的电池初始SOC值和截止SOC值相差很小,不到1%,这与文献[32 ]中所展示的结果一致,即在1 h模拟时间内,SOC偏差保持在一个非常窄的SOC范围内,最大偏差不超过1%。图5 e为采用功率平均分配策略时电动汽车的电池容量衰退情况。结果表明,当充放电功率相同时,电池SOC值越大,其容量衰退越快,这与式(14)所表达的结果一致。图5 f为调频策略优化后的车辆电池容量衰退情况。
可以看出,与功率平均分配策略相比,功率优化分配策略条件下,电池SOC值较大的电动汽车因充放电功率明显减少导致其电池容量衰退明显降低,且优化结果表明,本文所提出的V2G调频功率优化控制策略可将电池的总体老化降低22.15%。
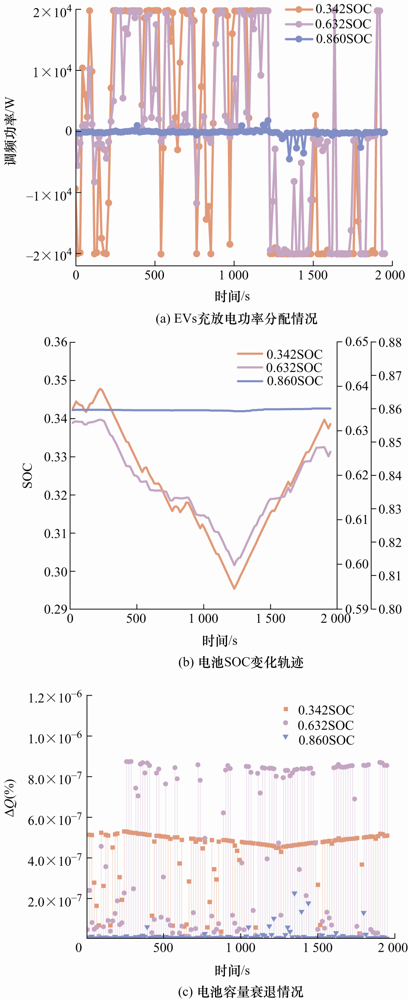
图6 为M =30条件下的车辆参与V2G调频功率优化仿真结果。图6 a为采用主动抑制电池老化优化控制策略电池的充放电功率分配情况。可以看出,初始SOC值为0.860的电动汽车在大多数时段所分配到的充放电功率很小。与M =20的仿真结果相比,该电动汽车的充放电功率明显减小,而其他两辆电动汽车的充放电功率有略微增加。图6 b为调频功率优化后的电池SOC变化轨迹。可以看出,初始SOC值为0.860的电动汽车的SOC曲线因充放电功率再次减小而变得更为平缓,近乎一条水平线,而其他两辆电动汽车因充放电功率变化极小导致其电池SOC变化很小。图6 c为调频策略优化后的车辆电池容量衰退情况,相比于M =20,SOC较大的电动汽车的电池容量衰减有了极为明显的减小,SOC较小的两辆电动汽车电池容量衰减变化极小。结果表明,前瞻时段M =30时,与功率平均分配策略相比,电池的总体老化降低了22.34%。与M =20的仿真结果相比,优化控制器主动抑制电池老化能力则提升0.19%。
图6
4.2.2 SOC变化分析
表2 为所选取的10辆电动汽车参与V2G调频的SOC的初始值、最终值以及变化范围。从表2 可以看出,在不同的调频策略下,电动汽车电池SOC的最终值与初始值的最大偏差分别为0.24%、0.51%、0.70%,即电动汽车在短时间内参与V2G调频服务所导致的SOC偏差是很小的,并不会对车主的出行造成影响。
此外,SOC偏差较小表明电动汽车向电网净供能较小,而电力市场中电价除在用电高峰溢价较大,其余大部分时段电价波动较小[33 -34 ] ,考虑电池老化成本,短时间内电动汽车参与V2G调频获利的可能性极小[13 -14 ] ,这是本文不考虑市场电价,着重于抑制V2G调频老化电池的主要原因。
4.2.3 不同前瞻时段M 的控制器性能比较
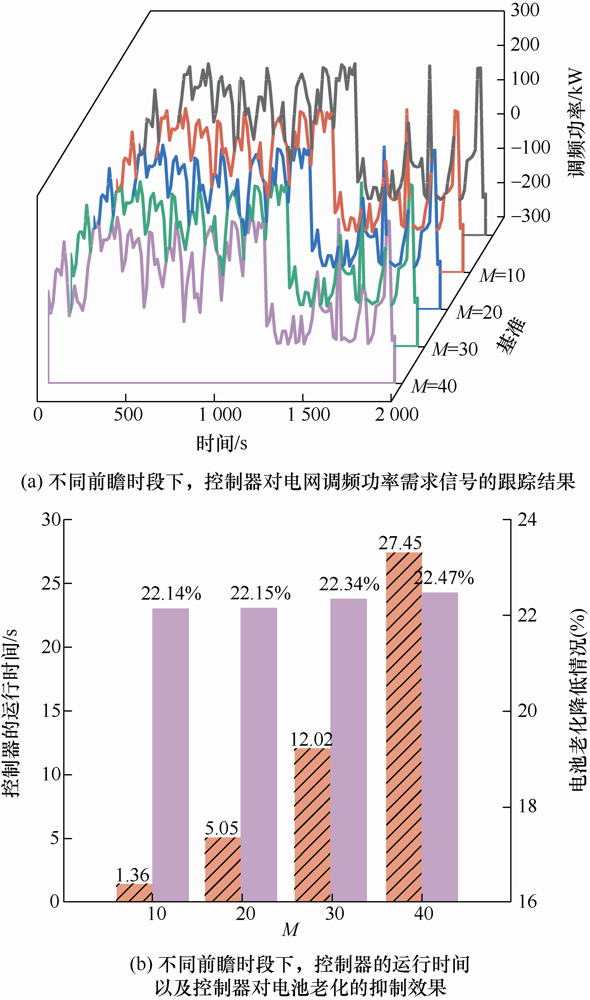
图7 为M 分别取10、20、30以及40时控制器的性能结果。图7 a为不同前瞻时段下,控制器对电网调频功率需求信号的跟踪结果。
图7
图7
M 分别取10、20、30以及40时控制器的性能结果
可以看出,在4种不同前瞻时段下,控制器对电网调频功率需求信号跟踪效果均较好,其跟踪误差$\Psi $分别为0.986%、0.953%、0.891%以及0.775%。且随着控制时段M 的增加,跟踪效果有略微提升的趋势。图7 b为不同前瞻时段下,控制器的运行时间以及控制器对电池老化的抑制效果对比。可以看出,控制器的运行时间随着M 的增加呈指数型增长。当M =10时,程序运行时间仅为1.36 s,但相比之下,该策略抑制电池老化效果最差;而当M =40时,虽然该策略抑制电池容量衰退情况最好,与功率平均分配策略相比,电池的总体老化降低高达22.47%,但是其控制器运行时间长达27.45 s,已经远远超过本试验设置的采样时间15 s。相比于M =20的仿真结果,虽然M =30时的控制器运行时间有所增加,但仍小于采样时间15 s,且其抑制电池老化的效果也有所提升。因此在满足采样时间情况下,考虑V2G各参与者的利益以及控制器的控制性能,可将前瞻时段M 取值设置为30。实际过程中则可根据硬性条件确定合理的M 值。
4.2.4 不同电池SOH的调频结果比较
为研究参与V2G调频对不同SOH条件下电池的性能衰退,本文构建另外两种不同SOH条件的电池组,其单体电池同样为Li(NiCoAl)O2 电池,电池组的开路电压及内阻大小可由同等健康状态下的单体电池的对应参数成比例缩放得到。图8 所示为对应的电池组额定OCV-SOC(图8 a)和Ri - SOC(图8 b) 曲线。可以看出,OCV-SOC曲线随着电池老化变化很小,而内阻Ri 随着电池老化而不断增加。其他试验参数设置同第3.1节。
图8
图8
不同SOH条件下电池组额定OCV-SOC和Ri -SOC曲线图
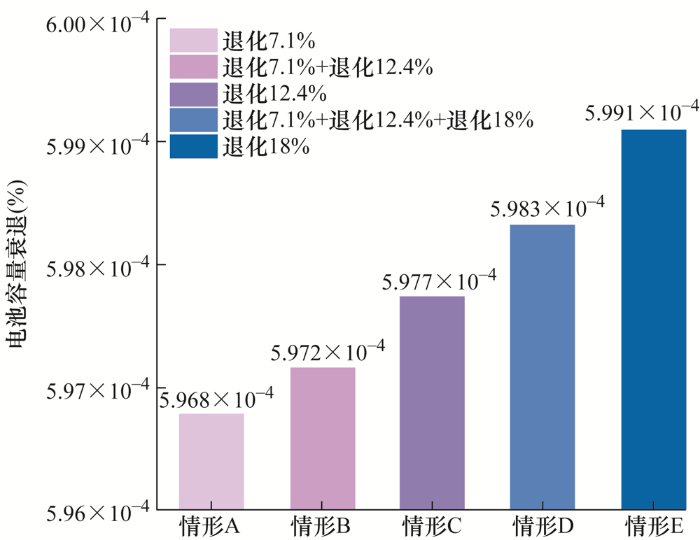
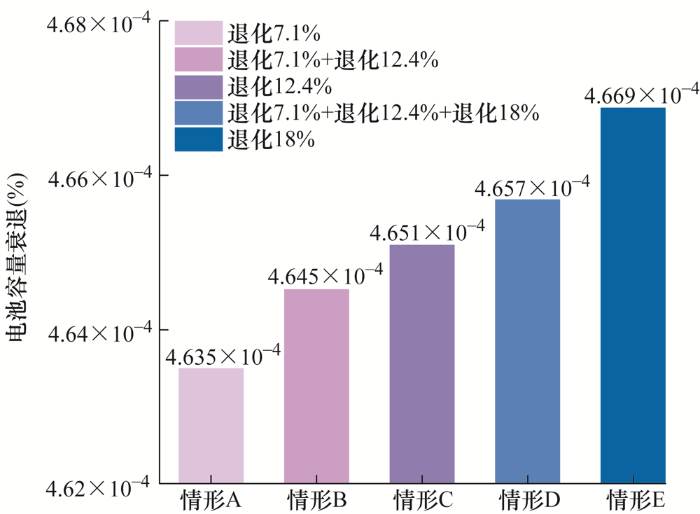
图9 为在平均分配策略下,不同情形下的电池参与V2G调频的容量衰退情况,包括A、B、C、D、E共5个情形。其中,情形A为各辆车的电池SOH均为92.9%,情形B为NIO EC6及Tesla model S的电池SOH为92.9%,而BYD han的电池SOH为87.6%,情形C为各辆车电池均SOH为87.6%,情况D为NIO EC6、BYD han及Tesla model S的电池SOH分别为92.9%、87.6%及82%,情况E为各辆车电池的SOH均为82%。结果表明,参与V2G调频的电池容量衰减程度与其初始SOH成正相关关系,即情形A中电池老化程度最轻,而情形E中电池老化程度最严重。图10 为基于优化调频策略且前瞻时段M =30时,不同情形下的电池参与V2G调频的容量衰退情况。此时,与情形A相比,情形B、C、D和E的电池老化分别增加0.22%、0.34%、0.47%和0.73%。显然,随着电池初始SOH降低,电池参与V2G调频过程中的容量衰减逐渐增加,即低SOH电池加速了其性能的退化过程。与功率平均分配策略相比,情形A、B、C、D以及E的老化分别减少了22.34%、22.21%、22.19%、22.17%和22.07%。可以看出,所开发的控制器对不同健康状态的电池参与V2G调频均起到了较好的抑制老化作用,抑制效果最低为22.07%。
图9
图9
平均分配策略下,不同情形下的电池参与V2G调频的容量衰退情况
图10
图10
M =30,不同情形下的电池参与V2G调频的容量衰退情况
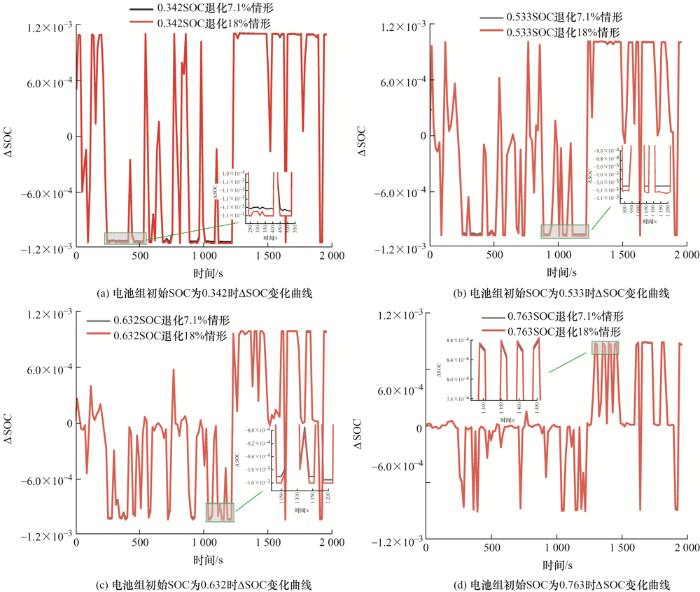
图11 对电池老化会加速其性能退化的原因做出了解释。图11 为基于V2G调频优化控制策略(M =30),不同初始SOH条件下的车辆电池组ΔSOC的变化曲线。从图11 可以看出,任意时刻,电池组初始SOC相同情况下,电池容量衰减为18%的电池组的SOC变化量总是大于电池容量减为7.1%的电池组的SOC变化量。结合式(13)可知,该现象是导致电池老化增加的主要原因。而该现象主要是由于电池容量的衰退以及内阻变大所导致的,如式(8)及图8 所示。因此电池性能的衰退会加剧V2G调频过程中电池的老化。
图11
图11
M =30,不同初始SOH条件下的车辆电池组ΔSOC的变化曲线
5 结论
基于当前的电池价格,研究如何抑制V2G调频过程中的电池老化具有重要意义。因此,本文通过引入基于机理的电池老化模型,建立了以抑制电池老化为目标的优化模型,并基于模型预测控制理论,开发了一种全新的优化控制器,实现了对电动汽车充放电功率的实时、高效控制,进而研究了前瞻时间长度不同时各电动汽车充放电功率分配情况、SOC变化趋势、电池容量衰减程度、程序的运行时间以及对调频信号的跟踪效果。本文比较了V2G调频过程中不同健康状态条件下的电池容量衰退效率。试验结果表明,当采用基准优化控制策略时,V2G调频对SOC值较小的电池造成的电池容量衰退最小,而当采用以抑制电池老化为目的的优化控制策略时,V2G更倾向于让SOC值较大的电池以较小的充放电功率响应调频信号。基于所开发的优化控制策略下,电动汽车电池SOC的最终值与初始值最大偏差未超过1%,即电动汽车在短时间内参与V2G辅助服务所导致的SOC偏差是极小的,并不会影响车主的出行。当前瞻时段为30时,控制器综合性能最好,可将电池老化降低高达22.34%。
参考文献
View Option
[1]
BYRNE J RICH D . Energy and environment [M]. New York : Routledge , 2021 .
[本文引用: 1]
[2]
ULLAH K HAFEEZ G KHAN I , et al . A multi-objective energy optimization in smart grid with high penetration of renewable energy sources
[J]. Applied Energy , 2021 , 299 :117104 .
DOI:10.1016/j.apenergy.2021.117104
URL
[本文引用: 1]
[3]
COLAK M BALCI S . Intelligent techniques to connect renewable energy sources to the grid:A review
[C]// 2021 9th International Conference on Smart Grid (icSmartGrid). IEEE , 2021 :179 -185 .
[本文引用: 1]
[4]
AKHTAR I KIRMANI S JAMEEL M . Reliability assessment of power system considering the impact of renewable energy sources integration into grid with advanced intelligent strategies
[J]. IEEE Access , 2021 , 9 :32485 -32497 .
DOI:10.1109/ACCESS.2021.3060892
URL
[本文引用: 1]
[5]
NUNNA H K BATTULA S DOOLLA S , et al . Energy management in smart distribution systems with vehicle-to-grid integrated microgrids
[J]. IEEE Transactions on Smart Grid , 2016 , 9 (5 ):4004 -4016 .
DOI:10.1109/TSG.2016.2646779
URL
[本文引用: 1]
[6]
ROTERING N ILIC M . Optimal charge control of plug-in hybrid electric vehicles in deregulated electricity markets
[J]. IEEE Transactions on Power Systems , 2010 , 26 (3 ):1021 -1029 .
DOI:10.1109/TPWRS.2010.2086083
URL
[本文引用: 1]
[7]
BUŠIĆ A HASHMI M U MEYN S . Distributed control of a fleet of batteries
[C]// 2017 American Control Conference (ACC). IEEE , 2017 :3406 -3411 .
[本文引用: 1]
[8]
HAMID Q R BARRIA J A . Congestion avoidance for recharging electric vehicles using smoothed particle hydrodynamics
[J]. IEEE Transactions on Power Systems , 2015 , 31 (2 ):1014 -1024 .
DOI:10.1109/TPWRS.2015.2412653
URL
[本文引用: 1]
[9]
JAFARI M GAUCHIA A ZHAO S , et al . Electric vehicle battery cycle aging evaluation in real-world daily driving and vehicle-to-grid services
[J]. IEEE Transactions on Transportation Electrification , 2017 , 4 (1 ):122 -134 .
DOI:10.1109/TTE.2017.2764320
URL
[本文引用: 1]
[10]
BISHOP J D K AXON C J BONILLA D , et al . Evaluating the impact of V2G services on the degradation of batteries in PHEV and EV
[J]. Applied Energy , 2013 , 111 :206 -218 .
DOI:10.1016/j.apenergy.2013.04.094
URL
[本文引用: 1]
[11]
THINGVAD A CALEARO L ANDERSEN P B , et al . Empirical capacity measurements of electric vehicles subject to battery degradation from V2G services
[J]. IEEE Transactions on Vehicular Technology , 2021 , 70 (8 ):7547 -7557 .
DOI:10.1109/TVT.2021.3093161
URL
[本文引用: 1]
[12]
ZHENG Y SHAO Z LEI X , et al . The economic analysis of electric vehicle aggregators participating in energy and regulation markets considering battery degradation
[J]. Journal of Energy Storage , 2022 , 45 :103770 .
DOI:10.1016/j.est.2021.103770
URL
[本文引用: 1]
[13]
GOUGH R DICKERSON C ROWLEY P , et al . Vehicle-to-grid feasibility:A techno-economic analysis of EV-based energy storage
[J]. Applied Energy , 2017 , 192 :12 -23 .
DOI:10.1016/j.apenergy.2017.01.102
URL
[本文引用: 2]
[14]
LUNZ B WALZ H SAUER D U . Optimizing vehicle-to-grid charging strategies using genetic algorithms under the consideration of battery aging
[C]// 2011 IEEE Vehicle Power and Propulsion Conference. IEEE , 2011 :1 -7 .
[本文引用: 2]
[15]
ZHANG Z TIAN R . Studying battery range and range anxiety for electric vehicles based on real travel demands
[C]// Proceedings of the Human Factors and Ergonomics Society Annual Meeting,Sage CA:Los Angeles , CA : SAGE Publications , 2021 , 65 (1 ):332 -336 .
[本文引用: 1]
[16]
ELDESOKY A LOGAN E R LOULI A J , et al . Impact of graphite materials on the lifetime of NMC811/graphite pouch cells:Part II. Long-term cycling,stack pressure growth,isothermal microcalorimetry,and lifetime projection
[J]. Journal of The Electrochemical Society , 2022 , 169 (1 ):010501 .
DOI:10.1149/1945-7111/ac42f1
URL
[本文引用: 1]
[17]
ATTIA P M GROVER A JIN N , et al . Closed-loop optimization of fast-charging protocols for batteries with machine learning
[J]. Nature , 2020 , 578 :397 -402 .
DOI:10.1038/s41586-020-1994-5
URL
[本文引用: 1]
[18]
HUANG J W LIU Y H WANG S C , et al . Fuzzy-control-based five-step Li-ion battery charger
[C]// 2009 International Conference on Power Electronics and Drive Systems (PEDS). IEEE , 2009 :1547 -1551 .
[本文引用: 1]
[20]
FORTENBACHER P MATHIEU J L ANDERSSON G . Modeling and optimal operation of distributed battery storage in low voltage grids
[J]. IEEE Transactions on Power Systems , 2017 , 32 (6 ):4340 -4350 .
DOI:10.1109/TPWRS.2017.2682339
URL
[本文引用: 1]
[21]
PATSIOS C WU B CHATZINIKOLAOU E , et al . An integrated approach for the analysis and control of grid connected energy storage systems
[J]. Journal of Energy Storage , 2016 , 5 :48 -61 .
DOI:10.1016/j.est.2015.11.011
URL
[本文引用: 1]
[22]
UDDIN K JACKSON T WIDANAGE W D , et al . On the possibility of extending the lifetime of lithium-ion batteries through optimal V2G facilitated by an integrated vehicle and smart-grid system
[J]. Energy , 2017 , 133 :710 -722 .
DOI:10.1016/j.energy.2017.04.116
URL
[本文引用: 1]
[23]
LI S LI J SU C , et al . Optimization of bi-directional V2G behavior with active battery anti-aging scheduling
[J]. IEEE Access , 2020 , 8 :11186 -11196 .
DOI:10.1109/ACCESS.2020.2964699
URL
[本文引用: 1]
[24]
BUŠIĆ A HASHMI M U MEYN S . Distributed control of a fleet of batteries
[C]// 2017 American Control Conference (ACC). IEEE , 2017 :3406 -3411 .
[本文引用: 1]
[25]
RAJAMAND S . Feedback-based control structure for frequency/voltage regulation using the state of electrical vehicle charge station and point estimation method
[J]. Sustainable Energy Technologies and Assessments , 2022 , 51 :101922 .
DOI:10.1016/j.seta.2021.101922
URL
[本文引用: 1]
[26]
KAUR K KUMAR N SINGH M . Coordinated power control of electric vehicles for grid frequency support:MILP-based hierarchical control design
[J]. IEEE Transactions on Smart Grid , 2018 , 10 (3 ):3364 -3373 .
DOI:10.1109/TSG.2018.2825322
URL
[本文引用: 1]
[27]
PENG C ZOU J LIAN L . Dispatching strategies of electric vehicles participating in frequency regulation on power grid:A review
[J]. Renewable and Sustainable Energy Reviews , 2017 , 68 :147 -152 .
DOI:10.1016/j.rser.2016.09.133
URL
[本文引用: 1]
[28]
REHMAN U U . A robust vehicle to grid aggregation framework for electric vehicles charging cost minimization and for smart grid regulation
[J]. International Journal of Electrical Power & Energy Systems , 2022 , 140 :108090 .
DOI:10.1016/j.ijepes.2022.108090
URL
[本文引用: 1]
[29]
CHEN Z ZHANG H XIONG R , et al . Energy management strategy of connected hybrid electric vehicles considering electricity and oil price fluctuations:A case study of ten typical cities in China
[J]. Journal of Energy Storage , 2021 , 36 :102347 .
DOI:10.1016/j.est.2021.102347
URL
[本文引用: 1]
[30]
ZHANG Y XIONG R HE H , et al . State of charge-dependent aging mechanisms in graphite/Li(NiCoAl)O2 cells:Capacity loss modeling and remaining useful life prediction
[J]. Applied Energy , 2019 , 255 :113818 .
DOI:10.1016/j.apenergy.2019.113818
URL
[本文引用: 3]
[31]
JIN X VORA A HOSHING V , et al . Physically-based reduced-order capacity loss model for graphite anodes in Li-ion battery cells
[J]. Journal of Power Sources , 2017 , 342 :750 -761 .
DOI:10.1016/j.jpowsour.2016.12.099
URL
[本文引用: 3]
[32]
HAN S HAN S . Economic feasibility of V2G frequency regulation in consideration of battery wear
[J]. Energies , 2013 , 6 (2 ):748 -765 .
DOI:10.3390/en6020748
URL
[本文引用: 1]
[33]
BELLO A RENESES J MUÑOZ A , et al . Probabilistic forecasting of hourly electricity prices in the medium-term using spatial interpolation techniques
[J]. International Journal of Forecasting , 2016 , 32 (3 ):966 -980 .
DOI:10.1016/j.ijforecast.2015.06.002
URL
[本文引用: 1]
[34]
HUANG C J SHEN Y CHEN Y H , et al . A novel hybrid deep neural network model for short-term electricity price forecasting
[J]. International Journal of Energy Research , 2021 , 45 (2 ):2511 -2532 .
DOI:10.1002/er.5945
URL
[本文引用: 1]
1
2021
... 随着能源和环境问题日益突出[1 ] ,水电、风电、光伏等可再生能源作为清洁能源的代表,对电网的渗透规模不断扩大[2 -3 ] .然而,可再生能源具有波动性大和间歇性强等特点,这给电力系统的频率稳定带来了巨大压力[4 ] .传统机组爬坡率低、响应速度慢,因此无法及时调节可再生能源不确定性对电力系统频率扰动的影响.随着电动汽车的普及,越来越多的电动汽车可作为移动储能系统和调峰装置接入电网[5 -6 ] ,其所发挥的削峰填谷、频率调节等功能可大大提高电力系统运行的可靠性和经济性[7 -8 ] .为此,V2G(Vehicle-to-grid)技术引起了国内外学者的广泛关注. ...
A multi-objective energy optimization in smart grid with high penetration of renewable energy sources
1
2021
... 随着能源和环境问题日益突出[1 ] ,水电、风电、光伏等可再生能源作为清洁能源的代表,对电网的渗透规模不断扩大[2 -3 ] .然而,可再生能源具有波动性大和间歇性强等特点,这给电力系统的频率稳定带来了巨大压力[4 ] .传统机组爬坡率低、响应速度慢,因此无法及时调节可再生能源不确定性对电力系统频率扰动的影响.随着电动汽车的普及,越来越多的电动汽车可作为移动储能系统和调峰装置接入电网[5 -6 ] ,其所发挥的削峰填谷、频率调节等功能可大大提高电力系统运行的可靠性和经济性[7 -8 ] .为此,V2G(Vehicle-to-grid)技术引起了国内外学者的广泛关注. ...
Intelligent techniques to connect renewable energy sources to the grid:A review
1
2021
... 随着能源和环境问题日益突出[1 ] ,水电、风电、光伏等可再生能源作为清洁能源的代表,对电网的渗透规模不断扩大[2 -3 ] .然而,可再生能源具有波动性大和间歇性强等特点,这给电力系统的频率稳定带来了巨大压力[4 ] .传统机组爬坡率低、响应速度慢,因此无法及时调节可再生能源不确定性对电力系统频率扰动的影响.随着电动汽车的普及,越来越多的电动汽车可作为移动储能系统和调峰装置接入电网[5 -6 ] ,其所发挥的削峰填谷、频率调节等功能可大大提高电力系统运行的可靠性和经济性[7 -8 ] .为此,V2G(Vehicle-to-grid)技术引起了国内外学者的广泛关注. ...
Reliability assessment of power system considering the impact of renewable energy sources integration into grid with advanced intelligent strategies
1
2021
... 随着能源和环境问题日益突出[1 ] ,水电、风电、光伏等可再生能源作为清洁能源的代表,对电网的渗透规模不断扩大[2 -3 ] .然而,可再生能源具有波动性大和间歇性强等特点,这给电力系统的频率稳定带来了巨大压力[4 ] .传统机组爬坡率低、响应速度慢,因此无法及时调节可再生能源不确定性对电力系统频率扰动的影响.随着电动汽车的普及,越来越多的电动汽车可作为移动储能系统和调峰装置接入电网[5 -6 ] ,其所发挥的削峰填谷、频率调节等功能可大大提高电力系统运行的可靠性和经济性[7 -8 ] .为此,V2G(Vehicle-to-grid)技术引起了国内外学者的广泛关注. ...
Energy management in smart distribution systems with vehicle-to-grid integrated microgrids
1
2016
... 随着能源和环境问题日益突出[1 ] ,水电、风电、光伏等可再生能源作为清洁能源的代表,对电网的渗透规模不断扩大[2 -3 ] .然而,可再生能源具有波动性大和间歇性强等特点,这给电力系统的频率稳定带来了巨大压力[4 ] .传统机组爬坡率低、响应速度慢,因此无法及时调节可再生能源不确定性对电力系统频率扰动的影响.随着电动汽车的普及,越来越多的电动汽车可作为移动储能系统和调峰装置接入电网[5 -6 ] ,其所发挥的削峰填谷、频率调节等功能可大大提高电力系统运行的可靠性和经济性[7 -8 ] .为此,V2G(Vehicle-to-grid)技术引起了国内外学者的广泛关注. ...
Optimal charge control of plug-in hybrid electric vehicles in deregulated electricity markets
1
2010
... 随着能源和环境问题日益突出[1 ] ,水电、风电、光伏等可再生能源作为清洁能源的代表,对电网的渗透规模不断扩大[2 -3 ] .然而,可再生能源具有波动性大和间歇性强等特点,这给电力系统的频率稳定带来了巨大压力[4 ] .传统机组爬坡率低、响应速度慢,因此无法及时调节可再生能源不确定性对电力系统频率扰动的影响.随着电动汽车的普及,越来越多的电动汽车可作为移动储能系统和调峰装置接入电网[5 -6 ] ,其所发挥的削峰填谷、频率调节等功能可大大提高电力系统运行的可靠性和经济性[7 -8 ] .为此,V2G(Vehicle-to-grid)技术引起了国内外学者的广泛关注. ...
Distributed control of a fleet of batteries
1
2017
... 随着能源和环境问题日益突出[1 ] ,水电、风电、光伏等可再生能源作为清洁能源的代表,对电网的渗透规模不断扩大[2 -3 ] .然而,可再生能源具有波动性大和间歇性强等特点,这给电力系统的频率稳定带来了巨大压力[4 ] .传统机组爬坡率低、响应速度慢,因此无法及时调节可再生能源不确定性对电力系统频率扰动的影响.随着电动汽车的普及,越来越多的电动汽车可作为移动储能系统和调峰装置接入电网[5 -6 ] ,其所发挥的削峰填谷、频率调节等功能可大大提高电力系统运行的可靠性和经济性[7 -8 ] .为此,V2G(Vehicle-to-grid)技术引起了国内外学者的广泛关注. ...
Congestion avoidance for recharging electric vehicles using smoothed particle hydrodynamics
1
2015
... 随着能源和环境问题日益突出[1 ] ,水电、风电、光伏等可再生能源作为清洁能源的代表,对电网的渗透规模不断扩大[2 -3 ] .然而,可再生能源具有波动性大和间歇性强等特点,这给电力系统的频率稳定带来了巨大压力[4 ] .传统机组爬坡率低、响应速度慢,因此无法及时调节可再生能源不确定性对电力系统频率扰动的影响.随着电动汽车的普及,越来越多的电动汽车可作为移动储能系统和调峰装置接入电网[5 -6 ] ,其所发挥的削峰填谷、频率调节等功能可大大提高电力系统运行的可靠性和经济性[7 -8 ] .为此,V2G(Vehicle-to-grid)技术引起了国内外学者的广泛关注. ...
Electric vehicle battery cycle aging evaluation in real-world daily driving and vehicle-to-grid services
1
2017
... 车辆参与V2G服务意味着电池需要依据电网需求进行频繁充放电,这不可避免地加剧了电池的老化速度.JAFARI等[9 ] 发现电动汽车若每天执行V2G服务,则会显著缩短电池寿命.BISHOP等[10 ] 发现在不同的电池容量、充电方式和放电深度下,V2G服务对动力电池退化影响程度是不同的,其中电动汽车电池组的退化对充电方式以及单个电池的放电深度最为敏感.THINGVAD等[11 ] 研究了电动汽车长期执行V2G服务对电池容量衰退的影响,发现电池可用容量两年后平均降低了10%,五年后降低了17.8%.电池老化加剧会导致其维修保养成本的提升,从而降低V2G所带来的服务效益.ZHENG等[12 ] 发现在当前电池成本下,电动汽车提供V2G服务,车主极难从中获取利润.GOUGH等[13 ] 发现V2G服务可获得的利润无法弥补电动汽车参与辅助服务所造成的电池老化成本损失.LUNZ等[14 ] 发现V2G在电力市场能源交换所带来的收益与电池老化成本相比是极小的.此外,电池容量衰退还会造成车辆续航里程下降,引发用户“里程焦虑”[15 ] .为此,研究如何抑制车辆参与V2G服务所引起的电池老化,从而延长电池寿命,具有重要意义. ...
Evaluating the impact of V2G services on the degradation of batteries in PHEV and EV
1
2013
... 车辆参与V2G服务意味着电池需要依据电网需求进行频繁充放电,这不可避免地加剧了电池的老化速度.JAFARI等[9 ] 发现电动汽车若每天执行V2G服务,则会显著缩短电池寿命.BISHOP等[10 ] 发现在不同的电池容量、充电方式和放电深度下,V2G服务对动力电池退化影响程度是不同的,其中电动汽车电池组的退化对充电方式以及单个电池的放电深度最为敏感.THINGVAD等[11 ] 研究了电动汽车长期执行V2G服务对电池容量衰退的影响,发现电池可用容量两年后平均降低了10%,五年后降低了17.8%.电池老化加剧会导致其维修保养成本的提升,从而降低V2G所带来的服务效益.ZHENG等[12 ] 发现在当前电池成本下,电动汽车提供V2G服务,车主极难从中获取利润.GOUGH等[13 ] 发现V2G服务可获得的利润无法弥补电动汽车参与辅助服务所造成的电池老化成本损失.LUNZ等[14 ] 发现V2G在电力市场能源交换所带来的收益与电池老化成本相比是极小的.此外,电池容量衰退还会造成车辆续航里程下降,引发用户“里程焦虑”[15 ] .为此,研究如何抑制车辆参与V2G服务所引起的电池老化,从而延长电池寿命,具有重要意义. ...
Empirical capacity measurements of electric vehicles subject to battery degradation from V2G services
1
2021
... 车辆参与V2G服务意味着电池需要依据电网需求进行频繁充放电,这不可避免地加剧了电池的老化速度.JAFARI等[9 ] 发现电动汽车若每天执行V2G服务,则会显著缩短电池寿命.BISHOP等[10 ] 发现在不同的电池容量、充电方式和放电深度下,V2G服务对动力电池退化影响程度是不同的,其中电动汽车电池组的退化对充电方式以及单个电池的放电深度最为敏感.THINGVAD等[11 ] 研究了电动汽车长期执行V2G服务对电池容量衰退的影响,发现电池可用容量两年后平均降低了10%,五年后降低了17.8%.电池老化加剧会导致其维修保养成本的提升,从而降低V2G所带来的服务效益.ZHENG等[12 ] 发现在当前电池成本下,电动汽车提供V2G服务,车主极难从中获取利润.GOUGH等[13 ] 发现V2G服务可获得的利润无法弥补电动汽车参与辅助服务所造成的电池老化成本损失.LUNZ等[14 ] 发现V2G在电力市场能源交换所带来的收益与电池老化成本相比是极小的.此外,电池容量衰退还会造成车辆续航里程下降,引发用户“里程焦虑”[15 ] .为此,研究如何抑制车辆参与V2G服务所引起的电池老化,从而延长电池寿命,具有重要意义. ...
The economic analysis of electric vehicle aggregators participating in energy and regulation markets considering battery degradation
1
2022
... 车辆参与V2G服务意味着电池需要依据电网需求进行频繁充放电,这不可避免地加剧了电池的老化速度.JAFARI等[9 ] 发现电动汽车若每天执行V2G服务,则会显著缩短电池寿命.BISHOP等[10 ] 发现在不同的电池容量、充电方式和放电深度下,V2G服务对动力电池退化影响程度是不同的,其中电动汽车电池组的退化对充电方式以及单个电池的放电深度最为敏感.THINGVAD等[11 ] 研究了电动汽车长期执行V2G服务对电池容量衰退的影响,发现电池可用容量两年后平均降低了10%,五年后降低了17.8%.电池老化加剧会导致其维修保养成本的提升,从而降低V2G所带来的服务效益.ZHENG等[12 ] 发现在当前电池成本下,电动汽车提供V2G服务,车主极难从中获取利润.GOUGH等[13 ] 发现V2G服务可获得的利润无法弥补电动汽车参与辅助服务所造成的电池老化成本损失.LUNZ等[14 ] 发现V2G在电力市场能源交换所带来的收益与电池老化成本相比是极小的.此外,电池容量衰退还会造成车辆续航里程下降,引发用户“里程焦虑”[15 ] .为此,研究如何抑制车辆参与V2G服务所引起的电池老化,从而延长电池寿命,具有重要意义. ...
Vehicle-to-grid feasibility:A techno-economic analysis of EV-based energy storage
2
2017
... 车辆参与V2G服务意味着电池需要依据电网需求进行频繁充放电,这不可避免地加剧了电池的老化速度.JAFARI等[9 ] 发现电动汽车若每天执行V2G服务,则会显著缩短电池寿命.BISHOP等[10 ] 发现在不同的电池容量、充电方式和放电深度下,V2G服务对动力电池退化影响程度是不同的,其中电动汽车电池组的退化对充电方式以及单个电池的放电深度最为敏感.THINGVAD等[11 ] 研究了电动汽车长期执行V2G服务对电池容量衰退的影响,发现电池可用容量两年后平均降低了10%,五年后降低了17.8%.电池老化加剧会导致其维修保养成本的提升,从而降低V2G所带来的服务效益.ZHENG等[12 ] 发现在当前电池成本下,电动汽车提供V2G服务,车主极难从中获取利润.GOUGH等[13 ] 发现V2G服务可获得的利润无法弥补电动汽车参与辅助服务所造成的电池老化成本损失.LUNZ等[14 ] 发现V2G在电力市场能源交换所带来的收益与电池老化成本相比是极小的.此外,电池容量衰退还会造成车辆续航里程下降,引发用户“里程焦虑”[15 ] .为此,研究如何抑制车辆参与V2G服务所引起的电池老化,从而延长电池寿命,具有重要意义. ...
... 此外,SOC偏差较小表明电动汽车向电网净供能较小,而电力市场中电价除在用电高峰溢价较大,其余大部分时段电价波动较小[33 -34 ] ,考虑电池老化成本,短时间内电动汽车参与V2G调频获利的可能性极小[13 -14 ] ,这是本文不考虑市场电价,着重于抑制V2G调频老化电池的主要原因. ...
Optimizing vehicle-to-grid charging strategies using genetic algorithms under the consideration of battery aging
2
2011
... 车辆参与V2G服务意味着电池需要依据电网需求进行频繁充放电,这不可避免地加剧了电池的老化速度.JAFARI等[9 ] 发现电动汽车若每天执行V2G服务,则会显著缩短电池寿命.BISHOP等[10 ] 发现在不同的电池容量、充电方式和放电深度下,V2G服务对动力电池退化影响程度是不同的,其中电动汽车电池组的退化对充电方式以及单个电池的放电深度最为敏感.THINGVAD等[11 ] 研究了电动汽车长期执行V2G服务对电池容量衰退的影响,发现电池可用容量两年后平均降低了10%,五年后降低了17.8%.电池老化加剧会导致其维修保养成本的提升,从而降低V2G所带来的服务效益.ZHENG等[12 ] 发现在当前电池成本下,电动汽车提供V2G服务,车主极难从中获取利润.GOUGH等[13 ] 发现V2G服务可获得的利润无法弥补电动汽车参与辅助服务所造成的电池老化成本损失.LUNZ等[14 ] 发现V2G在电力市场能源交换所带来的收益与电池老化成本相比是极小的.此外,电池容量衰退还会造成车辆续航里程下降,引发用户“里程焦虑”[15 ] .为此,研究如何抑制车辆参与V2G服务所引起的电池老化,从而延长电池寿命,具有重要意义. ...
... 此外,SOC偏差较小表明电动汽车向电网净供能较小,而电力市场中电价除在用电高峰溢价较大,其余大部分时段电价波动较小[33 -34 ] ,考虑电池老化成本,短时间内电动汽车参与V2G调频获利的可能性极小[13 -14 ] ,这是本文不考虑市场电价,着重于抑制V2G调频老化电池的主要原因. ...
Studying battery range and range anxiety for electric vehicles based on real travel demands
1
2021
... 车辆参与V2G服务意味着电池需要依据电网需求进行频繁充放电,这不可避免地加剧了电池的老化速度.JAFARI等[9 ] 发现电动汽车若每天执行V2G服务,则会显著缩短电池寿命.BISHOP等[10 ] 发现在不同的电池容量、充电方式和放电深度下,V2G服务对动力电池退化影响程度是不同的,其中电动汽车电池组的退化对充电方式以及单个电池的放电深度最为敏感.THINGVAD等[11 ] 研究了电动汽车长期执行V2G服务对电池容量衰退的影响,发现电池可用容量两年后平均降低了10%,五年后降低了17.8%.电池老化加剧会导致其维修保养成本的提升,从而降低V2G所带来的服务效益.ZHENG等[12 ] 发现在当前电池成本下,电动汽车提供V2G服务,车主极难从中获取利润.GOUGH等[13 ] 发现V2G服务可获得的利润无法弥补电动汽车参与辅助服务所造成的电池老化成本损失.LUNZ等[14 ] 发现V2G在电力市场能源交换所带来的收益与电池老化成本相比是极小的.此外,电池容量衰退还会造成车辆续航里程下降,引发用户“里程焦虑”[15 ] .为此,研究如何抑制车辆参与V2G服务所引起的电池老化,从而延长电池寿命,具有重要意义. ...
Impact of graphite materials on the lifetime of NMC811/graphite pouch cells:Part II. Long-term cycling,stack pressure growth,isothermal microcalorimetry,and lifetime projection
1
2022
... 目前,研究人员主要通过以下几个方面来延长电池寿命.第一,研发具有超长电池寿命的下一代电池技术.如ELDESOKY等[16 ] 开发的最新NMC811/Graphite电池在室温条件下工作寿命可长达数十年.第二,通过优化电池充电策略延长电池寿命.如ATTIA等[17 ] 开发了一种机器学习方法,通过优化电池充电协议,最大化电池循环寿命,同时还可以缓解电动汽车用户的续航焦虑.HUANG等[18 ] 基于模糊控制的充电协议设计了一种先进的电池充电器,有效缩短了充电时间,同时还提高了电池循环寿命和充电效率.第三,基于当前电池技术开发先进的V2G优化控制模型,以抑制电池老化.RENIERS等[19 ] 基于锂电池老化物理模型来计算能源交易收入并测量电池老化,从而在能源交易市场中弥补了技术保真度和经济调度之间的差距.数据分析表明,与传统启发式退化建模方法相比,该方法可以增加20%的收入,同时减少30%的电池老化.FORTENBACHER等[20 ] 提出了一种用于分布式电池存储的新型两阶段集中式MPC方案,该方案由调度实体和实时控制实体组成,研究发现,在实时控制阶段使用详细的电池模型,可以将电网调度对电池的损耗降低30%.PATSIOS等[21 ] 提出了一种集成的电-热-化学建模方法,并构建了一种从电池到电网的电网储能系统的集成建模框架.仿真发现其可将电力系统调度对电池的损耗减少两倍.UDDIN等[22 ] 构建了一种完整的电池退化模型,该模型综合考虑了电池所有的老化行为,结果表明,智能电网可将电动汽车电池组容量衰减最多减少9.1%.LI等[23 ] 提出了一种主动抑制电池老化的调度系统,采用雨流循环计数法量化电池老化,以电池老化最小化为优化目标之一,发现通过优化参与调度车辆规模以及各辆车充放电时间可以使电池充放电周期最小.综上可见,当前大部分研究聚焦于V2G在削峰填谷与能源交易市场电量调度过程中减少电池老化,但如何抑制V2G调频服务中的电池老化却鲜有研究. ...
Closed-loop optimization of fast-charging protocols for batteries with machine learning
1
2020
... 目前,研究人员主要通过以下几个方面来延长电池寿命.第一,研发具有超长电池寿命的下一代电池技术.如ELDESOKY等[16 ] 开发的最新NMC811/Graphite电池在室温条件下工作寿命可长达数十年.第二,通过优化电池充电策略延长电池寿命.如ATTIA等[17 ] 开发了一种机器学习方法,通过优化电池充电协议,最大化电池循环寿命,同时还可以缓解电动汽车用户的续航焦虑.HUANG等[18 ] 基于模糊控制的充电协议设计了一种先进的电池充电器,有效缩短了充电时间,同时还提高了电池循环寿命和充电效率.第三,基于当前电池技术开发先进的V2G优化控制模型,以抑制电池老化.RENIERS等[19 ] 基于锂电池老化物理模型来计算能源交易收入并测量电池老化,从而在能源交易市场中弥补了技术保真度和经济调度之间的差距.数据分析表明,与传统启发式退化建模方法相比,该方法可以增加20%的收入,同时减少30%的电池老化.FORTENBACHER等[20 ] 提出了一种用于分布式电池存储的新型两阶段集中式MPC方案,该方案由调度实体和实时控制实体组成,研究发现,在实时控制阶段使用详细的电池模型,可以将电网调度对电池的损耗降低30%.PATSIOS等[21 ] 提出了一种集成的电-热-化学建模方法,并构建了一种从电池到电网的电网储能系统的集成建模框架.仿真发现其可将电力系统调度对电池的损耗减少两倍.UDDIN等[22 ] 构建了一种完整的电池退化模型,该模型综合考虑了电池所有的老化行为,结果表明,智能电网可将电动汽车电池组容量衰减最多减少9.1%.LI等[23 ] 提出了一种主动抑制电池老化的调度系统,采用雨流循环计数法量化电池老化,以电池老化最小化为优化目标之一,发现通过优化参与调度车辆规模以及各辆车充放电时间可以使电池充放电周期最小.综上可见,当前大部分研究聚焦于V2G在削峰填谷与能源交易市场电量调度过程中减少电池老化,但如何抑制V2G调频服务中的电池老化却鲜有研究. ...
Fuzzy-control-based five-step Li-ion battery charger
1
2009
... 目前,研究人员主要通过以下几个方面来延长电池寿命.第一,研发具有超长电池寿命的下一代电池技术.如ELDESOKY等[16 ] 开发的最新NMC811/Graphite电池在室温条件下工作寿命可长达数十年.第二,通过优化电池充电策略延长电池寿命.如ATTIA等[17 ] 开发了一种机器学习方法,通过优化电池充电协议,最大化电池循环寿命,同时还可以缓解电动汽车用户的续航焦虑.HUANG等[18 ] 基于模糊控制的充电协议设计了一种先进的电池充电器,有效缩短了充电时间,同时还提高了电池循环寿命和充电效率.第三,基于当前电池技术开发先进的V2G优化控制模型,以抑制电池老化.RENIERS等[19 ] 基于锂电池老化物理模型来计算能源交易收入并测量电池老化,从而在能源交易市场中弥补了技术保真度和经济调度之间的差距.数据分析表明,与传统启发式退化建模方法相比,该方法可以增加20%的收入,同时减少30%的电池老化.FORTENBACHER等[20 ] 提出了一种用于分布式电池存储的新型两阶段集中式MPC方案,该方案由调度实体和实时控制实体组成,研究发现,在实时控制阶段使用详细的电池模型,可以将电网调度对电池的损耗降低30%.PATSIOS等[21 ] 提出了一种集成的电-热-化学建模方法,并构建了一种从电池到电网的电网储能系统的集成建模框架.仿真发现其可将电力系统调度对电池的损耗减少两倍.UDDIN等[22 ] 构建了一种完整的电池退化模型,该模型综合考虑了电池所有的老化行为,结果表明,智能电网可将电动汽车电池组容量衰减最多减少9.1%.LI等[23 ] 提出了一种主动抑制电池老化的调度系统,采用雨流循环计数法量化电池老化,以电池老化最小化为优化目标之一,发现通过优化参与调度车辆规模以及各辆车充放电时间可以使电池充放电周期最小.综上可见,当前大部分研究聚焦于V2G在削峰填谷与能源交易市场电量调度过程中减少电池老化,但如何抑制V2G调频服务中的电池老化却鲜有研究. ...
Unlocking extra value from grid batteries using advanced models
1
2021
... 目前,研究人员主要通过以下几个方面来延长电池寿命.第一,研发具有超长电池寿命的下一代电池技术.如ELDESOKY等[16 ] 开发的最新NMC811/Graphite电池在室温条件下工作寿命可长达数十年.第二,通过优化电池充电策略延长电池寿命.如ATTIA等[17 ] 开发了一种机器学习方法,通过优化电池充电协议,最大化电池循环寿命,同时还可以缓解电动汽车用户的续航焦虑.HUANG等[18 ] 基于模糊控制的充电协议设计了一种先进的电池充电器,有效缩短了充电时间,同时还提高了电池循环寿命和充电效率.第三,基于当前电池技术开发先进的V2G优化控制模型,以抑制电池老化.RENIERS等[19 ] 基于锂电池老化物理模型来计算能源交易收入并测量电池老化,从而在能源交易市场中弥补了技术保真度和经济调度之间的差距.数据分析表明,与传统启发式退化建模方法相比,该方法可以增加20%的收入,同时减少30%的电池老化.FORTENBACHER等[20 ] 提出了一种用于分布式电池存储的新型两阶段集中式MPC方案,该方案由调度实体和实时控制实体组成,研究发现,在实时控制阶段使用详细的电池模型,可以将电网调度对电池的损耗降低30%.PATSIOS等[21 ] 提出了一种集成的电-热-化学建模方法,并构建了一种从电池到电网的电网储能系统的集成建模框架.仿真发现其可将电力系统调度对电池的损耗减少两倍.UDDIN等[22 ] 构建了一种完整的电池退化模型,该模型综合考虑了电池所有的老化行为,结果表明,智能电网可将电动汽车电池组容量衰减最多减少9.1%.LI等[23 ] 提出了一种主动抑制电池老化的调度系统,采用雨流循环计数法量化电池老化,以电池老化最小化为优化目标之一,发现通过优化参与调度车辆规模以及各辆车充放电时间可以使电池充放电周期最小.综上可见,当前大部分研究聚焦于V2G在削峰填谷与能源交易市场电量调度过程中减少电池老化,但如何抑制V2G调频服务中的电池老化却鲜有研究. ...
Modeling and optimal operation of distributed battery storage in low voltage grids
1
2017
... 目前,研究人员主要通过以下几个方面来延长电池寿命.第一,研发具有超长电池寿命的下一代电池技术.如ELDESOKY等[16 ] 开发的最新NMC811/Graphite电池在室温条件下工作寿命可长达数十年.第二,通过优化电池充电策略延长电池寿命.如ATTIA等[17 ] 开发了一种机器学习方法,通过优化电池充电协议,最大化电池循环寿命,同时还可以缓解电动汽车用户的续航焦虑.HUANG等[18 ] 基于模糊控制的充电协议设计了一种先进的电池充电器,有效缩短了充电时间,同时还提高了电池循环寿命和充电效率.第三,基于当前电池技术开发先进的V2G优化控制模型,以抑制电池老化.RENIERS等[19 ] 基于锂电池老化物理模型来计算能源交易收入并测量电池老化,从而在能源交易市场中弥补了技术保真度和经济调度之间的差距.数据分析表明,与传统启发式退化建模方法相比,该方法可以增加20%的收入,同时减少30%的电池老化.FORTENBACHER等[20 ] 提出了一种用于分布式电池存储的新型两阶段集中式MPC方案,该方案由调度实体和实时控制实体组成,研究发现,在实时控制阶段使用详细的电池模型,可以将电网调度对电池的损耗降低30%.PATSIOS等[21 ] 提出了一种集成的电-热-化学建模方法,并构建了一种从电池到电网的电网储能系统的集成建模框架.仿真发现其可将电力系统调度对电池的损耗减少两倍.UDDIN等[22 ] 构建了一种完整的电池退化模型,该模型综合考虑了电池所有的老化行为,结果表明,智能电网可将电动汽车电池组容量衰减最多减少9.1%.LI等[23 ] 提出了一种主动抑制电池老化的调度系统,采用雨流循环计数法量化电池老化,以电池老化最小化为优化目标之一,发现通过优化参与调度车辆规模以及各辆车充放电时间可以使电池充放电周期最小.综上可见,当前大部分研究聚焦于V2G在削峰填谷与能源交易市场电量调度过程中减少电池老化,但如何抑制V2G调频服务中的电池老化却鲜有研究. ...
An integrated approach for the analysis and control of grid connected energy storage systems
1
2016
... 目前,研究人员主要通过以下几个方面来延长电池寿命.第一,研发具有超长电池寿命的下一代电池技术.如ELDESOKY等[16 ] 开发的最新NMC811/Graphite电池在室温条件下工作寿命可长达数十年.第二,通过优化电池充电策略延长电池寿命.如ATTIA等[17 ] 开发了一种机器学习方法,通过优化电池充电协议,最大化电池循环寿命,同时还可以缓解电动汽车用户的续航焦虑.HUANG等[18 ] 基于模糊控制的充电协议设计了一种先进的电池充电器,有效缩短了充电时间,同时还提高了电池循环寿命和充电效率.第三,基于当前电池技术开发先进的V2G优化控制模型,以抑制电池老化.RENIERS等[19 ] 基于锂电池老化物理模型来计算能源交易收入并测量电池老化,从而在能源交易市场中弥补了技术保真度和经济调度之间的差距.数据分析表明,与传统启发式退化建模方法相比,该方法可以增加20%的收入,同时减少30%的电池老化.FORTENBACHER等[20 ] 提出了一种用于分布式电池存储的新型两阶段集中式MPC方案,该方案由调度实体和实时控制实体组成,研究发现,在实时控制阶段使用详细的电池模型,可以将电网调度对电池的损耗降低30%.PATSIOS等[21 ] 提出了一种集成的电-热-化学建模方法,并构建了一种从电池到电网的电网储能系统的集成建模框架.仿真发现其可将电力系统调度对电池的损耗减少两倍.UDDIN等[22 ] 构建了一种完整的电池退化模型,该模型综合考虑了电池所有的老化行为,结果表明,智能电网可将电动汽车电池组容量衰减最多减少9.1%.LI等[23 ] 提出了一种主动抑制电池老化的调度系统,采用雨流循环计数法量化电池老化,以电池老化最小化为优化目标之一,发现通过优化参与调度车辆规模以及各辆车充放电时间可以使电池充放电周期最小.综上可见,当前大部分研究聚焦于V2G在削峰填谷与能源交易市场电量调度过程中减少电池老化,但如何抑制V2G调频服务中的电池老化却鲜有研究. ...
On the possibility of extending the lifetime of lithium-ion batteries through optimal V2G facilitated by an integrated vehicle and smart-grid system
1
2017
... 目前,研究人员主要通过以下几个方面来延长电池寿命.第一,研发具有超长电池寿命的下一代电池技术.如ELDESOKY等[16 ] 开发的最新NMC811/Graphite电池在室温条件下工作寿命可长达数十年.第二,通过优化电池充电策略延长电池寿命.如ATTIA等[17 ] 开发了一种机器学习方法,通过优化电池充电协议,最大化电池循环寿命,同时还可以缓解电动汽车用户的续航焦虑.HUANG等[18 ] 基于模糊控制的充电协议设计了一种先进的电池充电器,有效缩短了充电时间,同时还提高了电池循环寿命和充电效率.第三,基于当前电池技术开发先进的V2G优化控制模型,以抑制电池老化.RENIERS等[19 ] 基于锂电池老化物理模型来计算能源交易收入并测量电池老化,从而在能源交易市场中弥补了技术保真度和经济调度之间的差距.数据分析表明,与传统启发式退化建模方法相比,该方法可以增加20%的收入,同时减少30%的电池老化.FORTENBACHER等[20 ] 提出了一种用于分布式电池存储的新型两阶段集中式MPC方案,该方案由调度实体和实时控制实体组成,研究发现,在实时控制阶段使用详细的电池模型,可以将电网调度对电池的损耗降低30%.PATSIOS等[21 ] 提出了一种集成的电-热-化学建模方法,并构建了一种从电池到电网的电网储能系统的集成建模框架.仿真发现其可将电力系统调度对电池的损耗减少两倍.UDDIN等[22 ] 构建了一种完整的电池退化模型,该模型综合考虑了电池所有的老化行为,结果表明,智能电网可将电动汽车电池组容量衰减最多减少9.1%.LI等[23 ] 提出了一种主动抑制电池老化的调度系统,采用雨流循环计数法量化电池老化,以电池老化最小化为优化目标之一,发现通过优化参与调度车辆规模以及各辆车充放电时间可以使电池充放电周期最小.综上可见,当前大部分研究聚焦于V2G在削峰填谷与能源交易市场电量调度过程中减少电池老化,但如何抑制V2G调频服务中的电池老化却鲜有研究. ...
Optimization of bi-directional V2G behavior with active battery anti-aging scheduling
1
2020
... 目前,研究人员主要通过以下几个方面来延长电池寿命.第一,研发具有超长电池寿命的下一代电池技术.如ELDESOKY等[16 ] 开发的最新NMC811/Graphite电池在室温条件下工作寿命可长达数十年.第二,通过优化电池充电策略延长电池寿命.如ATTIA等[17 ] 开发了一种机器学习方法,通过优化电池充电协议,最大化电池循环寿命,同时还可以缓解电动汽车用户的续航焦虑.HUANG等[18 ] 基于模糊控制的充电协议设计了一种先进的电池充电器,有效缩短了充电时间,同时还提高了电池循环寿命和充电效率.第三,基于当前电池技术开发先进的V2G优化控制模型,以抑制电池老化.RENIERS等[19 ] 基于锂电池老化物理模型来计算能源交易收入并测量电池老化,从而在能源交易市场中弥补了技术保真度和经济调度之间的差距.数据分析表明,与传统启发式退化建模方法相比,该方法可以增加20%的收入,同时减少30%的电池老化.FORTENBACHER等[20 ] 提出了一种用于分布式电池存储的新型两阶段集中式MPC方案,该方案由调度实体和实时控制实体组成,研究发现,在实时控制阶段使用详细的电池模型,可以将电网调度对电池的损耗降低30%.PATSIOS等[21 ] 提出了一种集成的电-热-化学建模方法,并构建了一种从电池到电网的电网储能系统的集成建模框架.仿真发现其可将电力系统调度对电池的损耗减少两倍.UDDIN等[22 ] 构建了一种完整的电池退化模型,该模型综合考虑了电池所有的老化行为,结果表明,智能电网可将电动汽车电池组容量衰减最多减少9.1%.LI等[23 ] 提出了一种主动抑制电池老化的调度系统,采用雨流循环计数法量化电池老化,以电池老化最小化为优化目标之一,发现通过优化参与调度车辆规模以及各辆车充放电时间可以使电池充放电周期最小.综上可见,当前大部分研究聚焦于V2G在削峰填谷与能源交易市场电量调度过程中减少电池老化,但如何抑制V2G调频服务中的电池老化却鲜有研究. ...
Distributed control of a fleet of batteries
1
2017
... 当前有关V2G调频的研究主要集中在如何有效跟踪电网频率信号,忽略了V2G调频对电池老化的影响.BUŠIĆ等[24 ] 在满足电池约束界限情况下,为跟踪电网端调频功率需求信号,引入分布式随机控制构架,并为不同类型的电池定义不同的随机决策规则,以优化单个电池的静置时间和充电状态.RAJAMAND[25 ] 发现将电动汽车的荷电状态(State of charge,SOC)反馈到控制结构中,可以很好地改善微电网频率/电压调节.KAUR等[26 ] 针对电动汽车参与次级频率控制,提出了一种双层分级控制方案,以电动汽车车主使用需求为约束条件,结果显示,该方案减小了电网频率偏差.PENG等[27 ] 提出了一种智能充电算法,可以根据频率偏差信号协调电动汽车充放电,该算法可以改善低压配电网的负载系数和电压水平.REHMAN[28 ] 提出了一种最优分层双向聚合算法,通过优化电动汽车充放电功率,预测电力需求,并在智能电网中执行日前负载调度来实现为电网提供电压和频率调节服务.因此,研究如何抑制V2G调频过程中的电池老化,将对V2G调频的经济效益产生重要影响. ...
Feedback-based control structure for frequency/voltage regulation using the state of electrical vehicle charge station and point estimation method
1
2022
... 当前有关V2G调频的研究主要集中在如何有效跟踪电网频率信号,忽略了V2G调频对电池老化的影响.BUŠIĆ等[24 ] 在满足电池约束界限情况下,为跟踪电网端调频功率需求信号,引入分布式随机控制构架,并为不同类型的电池定义不同的随机决策规则,以优化单个电池的静置时间和充电状态.RAJAMAND[25 ] 发现将电动汽车的荷电状态(State of charge,SOC)反馈到控制结构中,可以很好地改善微电网频率/电压调节.KAUR等[26 ] 针对电动汽车参与次级频率控制,提出了一种双层分级控制方案,以电动汽车车主使用需求为约束条件,结果显示,该方案减小了电网频率偏差.PENG等[27 ] 提出了一种智能充电算法,可以根据频率偏差信号协调电动汽车充放电,该算法可以改善低压配电网的负载系数和电压水平.REHMAN[28 ] 提出了一种最优分层双向聚合算法,通过优化电动汽车充放电功率,预测电力需求,并在智能电网中执行日前负载调度来实现为电网提供电压和频率调节服务.因此,研究如何抑制V2G调频过程中的电池老化,将对V2G调频的经济效益产生重要影响. ...
Coordinated power control of electric vehicles for grid frequency support:MILP-based hierarchical control design
1
2018
... 当前有关V2G调频的研究主要集中在如何有效跟踪电网频率信号,忽略了V2G调频对电池老化的影响.BUŠIĆ等[24 ] 在满足电池约束界限情况下,为跟踪电网端调频功率需求信号,引入分布式随机控制构架,并为不同类型的电池定义不同的随机决策规则,以优化单个电池的静置时间和充电状态.RAJAMAND[25 ] 发现将电动汽车的荷电状态(State of charge,SOC)反馈到控制结构中,可以很好地改善微电网频率/电压调节.KAUR等[26 ] 针对电动汽车参与次级频率控制,提出了一种双层分级控制方案,以电动汽车车主使用需求为约束条件,结果显示,该方案减小了电网频率偏差.PENG等[27 ] 提出了一种智能充电算法,可以根据频率偏差信号协调电动汽车充放电,该算法可以改善低压配电网的负载系数和电压水平.REHMAN[28 ] 提出了一种最优分层双向聚合算法,通过优化电动汽车充放电功率,预测电力需求,并在智能电网中执行日前负载调度来实现为电网提供电压和频率调节服务.因此,研究如何抑制V2G调频过程中的电池老化,将对V2G调频的经济效益产生重要影响. ...
Dispatching strategies of electric vehicles participating in frequency regulation on power grid:A review
1
2017
... 当前有关V2G调频的研究主要集中在如何有效跟踪电网频率信号,忽略了V2G调频对电池老化的影响.BUŠIĆ等[24 ] 在满足电池约束界限情况下,为跟踪电网端调频功率需求信号,引入分布式随机控制构架,并为不同类型的电池定义不同的随机决策规则,以优化单个电池的静置时间和充电状态.RAJAMAND[25 ] 发现将电动汽车的荷电状态(State of charge,SOC)反馈到控制结构中,可以很好地改善微电网频率/电压调节.KAUR等[26 ] 针对电动汽车参与次级频率控制,提出了一种双层分级控制方案,以电动汽车车主使用需求为约束条件,结果显示,该方案减小了电网频率偏差.PENG等[27 ] 提出了一种智能充电算法,可以根据频率偏差信号协调电动汽车充放电,该算法可以改善低压配电网的负载系数和电压水平.REHMAN[28 ] 提出了一种最优分层双向聚合算法,通过优化电动汽车充放电功率,预测电力需求,并在智能电网中执行日前负载调度来实现为电网提供电压和频率调节服务.因此,研究如何抑制V2G调频过程中的电池老化,将对V2G调频的经济效益产生重要影响. ...
A robust vehicle to grid aggregation framework for electric vehicles charging cost minimization and for smart grid regulation
1
2022
... 当前有关V2G调频的研究主要集中在如何有效跟踪电网频率信号,忽略了V2G调频对电池老化的影响.BUŠIĆ等[24 ] 在满足电池约束界限情况下,为跟踪电网端调频功率需求信号,引入分布式随机控制构架,并为不同类型的电池定义不同的随机决策规则,以优化单个电池的静置时间和充电状态.RAJAMAND[25 ] 发现将电动汽车的荷电状态(State of charge,SOC)反馈到控制结构中,可以很好地改善微电网频率/电压调节.KAUR等[26 ] 针对电动汽车参与次级频率控制,提出了一种双层分级控制方案,以电动汽车车主使用需求为约束条件,结果显示,该方案减小了电网频率偏差.PENG等[27 ] 提出了一种智能充电算法,可以根据频率偏差信号协调电动汽车充放电,该算法可以改善低压配电网的负载系数和电压水平.REHMAN[28 ] 提出了一种最优分层双向聚合算法,通过优化电动汽车充放电功率,预测电力需求,并在智能电网中执行日前负载调度来实现为电网提供电压和频率调节服务.因此,研究如何抑制V2G调频过程中的电池老化,将对V2G调频的经济效益产生重要影响. ...
Energy management strategy of connected hybrid electric vehicles considering electricity and oil price fluctuations:A case study of ten typical cities in China
1
2021
... 本文应用电池等效内阻模型来描述其充放电特性,表达式[29 ] 如下所示 ...
State of charge-dependent aging mechanisms in graphite/Li(NiCoAl)O2 cells:Capacity loss modeling and remaining useful life prediction
3
2019
... 电池SOC定义为电池剩余容量与额定容量的比值[30 ] ,表达式如下所示 ...
... 对于石墨负极锂离子电池,其性能衰退主要是由于固液界面膜(Solid electrolyte interface,SEI)生长和活性物质损失导致.SEI膜生长主要是由于电解液在电极表面的副反应引发,而活性物质损失则主要为锂离子嵌入嵌出电极诱发的力学应力所导致的活性物质破裂与脱离[30 -31 ] .本文将通过优化电动汽车电流以最大限度减小电池容量衰退.为了简化模型,本文运用电池活性物质损失模型来描述电池老化. ...
... 为简化计算流程,本文假设三种类型的电动汽车的电池包均采用Li(NiCoAl)O2 单体电池,该电池单体额定容量和额定电压分别为3.0 A·h和3.6 V.该电池的大量详细老化试验结果可参考文献[30 ].在本研究中,对单体电池的开路电压(Open circuit voltage,OCV)和内阻(Internal resistance,IR)Ri 分别进行成比例放大以得到相应车辆电池组的对应参数.该电池组初始容量衰退7.1%后的SOC-OCV与Ri -SOC曲线如图4 所示. ...
Physically-based reduced-order capacity loss model for graphite anodes in Li-ion battery cells
3
2017
... 对于石墨负极锂离子电池,其性能衰退主要是由于固液界面膜(Solid electrolyte interface,SEI)生长和活性物质损失导致.SEI膜生长主要是由于电解液在电极表面的副反应引发,而活性物质损失则主要为锂离子嵌入嵌出电极诱发的力学应力所导致的活性物质破裂与脱离[30 -31 ] .本文将通过优化电动汽车电流以最大限度减小电池容量衰退.为了简化模型,本文运用电池活性物质损失模型来描述电池老化. ...
... 根据文献[31 ],恒温条件下的电池活性物质损失模型为 ...
... 电池老化模型式(7)中的参数参考文献[31 ]进行设置,其中${{k}_{AM}}=1.368\text{ l/(A}\cdot \text{h)}$和${{E}_{AM}}=39\ 500\text{ J/mol}$.电池包的温度假设为25 ℃,因此$T=298.15\text{ K}$.其他相关参数设置如表1 所示.本文采用功率平均分配策略作为基准优化控制策略来验证所开发模型的高性能. ...
Economic feasibility of V2G frequency regulation in consideration of battery wear
1
2013
... 图5 c为采用基准优化控制策略电动汽车的SOC变化趋势,图5 d为调频功率优化后的电池SOC变化轨迹,其中SOC初始值为0.342的轨迹曲线斜率最大,这表明此时该电池总是以最大充放电功率去响应调频信号.而SOC初始值为0.860的电池SOC曲线变化较为平缓,即在仿真时间内该车辆电池都是以较小的充放电功率去响应调频信号.值得注意的是,3辆电动汽车参与调频的电池初始SOC值和截止SOC值相差很小,不到1%,这与文献[32 ]中所展示的结果一致,即在1 h模拟时间内,SOC偏差保持在一个非常窄的SOC范围内,最大偏差不超过1%.图5 e为采用功率平均分配策略时电动汽车的电池容量衰退情况.结果表明,当充放电功率相同时,电池SOC值越大,其容量衰退越快,这与式(14)所表达的结果一致.图5 f为调频策略优化后的车辆电池容量衰退情况. ...
Probabilistic forecasting of hourly electricity prices in the medium-term using spatial interpolation techniques
1
2016
... 此外,SOC偏差较小表明电动汽车向电网净供能较小,而电力市场中电价除在用电高峰溢价较大,其余大部分时段电价波动较小[33 -34 ] ,考虑电池老化成本,短时间内电动汽车参与V2G调频获利的可能性极小[13 -14 ] ,这是本文不考虑市场电价,着重于抑制V2G调频老化电池的主要原因. ...
A novel hybrid deep neural network model for short-term electricity price forecasting
1
2021
... 此外,SOC偏差较小表明电动汽车向电网净供能较小,而电力市场中电价除在用电高峰溢价较大,其余大部分时段电价波动较小[33 -34 ] ,考虑电池老化成本,短时间内电动汽车参与V2G调频获利的可能性极小[13 -14 ] ,这是本文不考虑市场电价,着重于抑制V2G调频老化电池的主要原因. ...