1 引言
卫星电源系统是产生、存储、变换和分配电能的系统,是卫星的重要组成单元,目前90%以上的航天器采用了太阳能电池阵/蓄电池(SA/B)电源系统。电源控制器(Power Control Unit,PCU)用来控制太阳能电池阵产生的能量的分配,以及蓄电池的充放电,可使航天器在整个在轨运行期间将功率母线电压稳定在规定范围内。目前我国研制的PCU母线电压有28V、42V和100V三种等级[1]。
当卫星进入阴影区不能从太阳能电池阵得到功率或在光照区太阳能电池阵提供的功率不足时,为保证母线电压稳定,蓄电池向母线提供电能,在此过程中蓄电池放电调节器(Battery Charge Regulator,BDR)起主要作用。需要研究一款高效率、兼顾动态和稳态性能的DC-DC模块作为BDR,使得蓄电池经BDR放电时,仍能维持较好的母线性能[2]。
由于太阳能电池的输出特性具有较强的非线性特征,将最大功率点跟踪(Maximum Power Point Tracking,MPPT)技术与顺序开关分流调节拓扑(Sequential Switch Shunt Regulator,S3R)或顺序开关串联分流拓扑(Sequential Switch Series Shunt Regulator,S4R)相结合形成的S3MPR和S4MPR[3]可以实时调整太阳能电池阵的工作点,使之始终工作在最大功率点附近,有利于最大限度利用太阳能电池阵的输出功率。由于母线电压始终保持在太阳能电池阵的最大功率点电压上,因此该电压将随着太阳能电池阵的温度和光照情况而变化。为了获得稳定的直流母线,在S3MPR或S4MPR调节器后面需串联一级高效率、高功率密度的DC-DC变换器[4]。
选择BDR拓扑和S3MPR或S4MPR后级串联的DC-DC变换器拓扑,主要考虑效率、复杂性、稳定性和升压特性等因素,非隔离型Weinberg变换器(Non-isolated Weinberg Converter,NIWC)能很好地满足这些需求。目前在欧洲和美国,NIWC已经在卫星中成功应用,如Olympus、Inmarsat11、Eurostar 3000、SpaceBus4000和BepiColombo等,国内目前还处于研究和试验阶段[4]。本文分析了NIWC的工作原理,建立其小信号数学模型并对系统稳定性进行分析,进而提出主电路参数和控制环路的设计方法,并进行仿真及实验验证。
2 NIWC的原理分析
2.1 工作状态分析
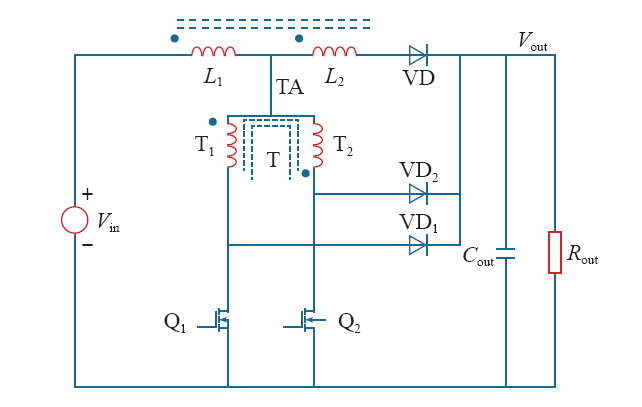
图1为NIWC的电路拓扑。忽略漏电感和磁化电感的影响,非隔离Weinberg变换器理想工作时有两种工作状态:
图1
(1)Q1或Q2导通,使得VD2或VD1导通,VD关断。
(2)Q1和Q2均关断,VD导通。
通过产生的PWM波控制Q1和Q2的导通与关断,从而实现输出电压的控制。Q1和Q2交替导通,一个开关周期内有两次MOSFET开通关断,即等效PWM频率是实际频率的两倍。因此在不增加开关损耗的情况下,增加了变换器的带宽,同时有效地减少了磁心元件和滤波器元件的尺寸,提高了功率密度。
2.2 稳态直流增益
两种工作状态时,输出电流都受到耦合电感或变压器的限制,因此输出电流连续[5],由此可得Weinberg电路的电压增益为
式中,D = tON/TSWITCHING,TSWITCHING是实际开关周期的一半。
NIWC的输出电流连续且纹波很小的特点使得该拓扑便于电流型控制,且易于进行多模块并联以扩展功率。
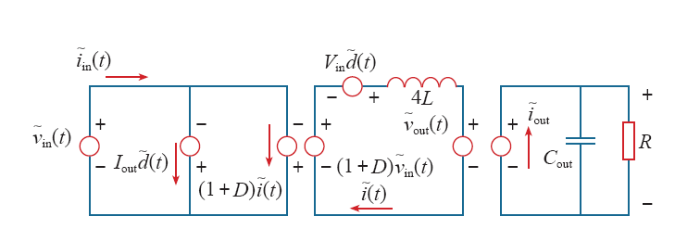
2.3 小信号模型
图2
由图2可得NIWC电压控制方式的传递函数为
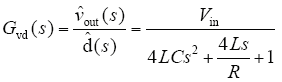
从式(2)的传递函数可知,NIWC的理想化模型为二阶,便于控制系统设计。
3 NIWC系统设计
3.1 主电路参数设计
本文设计的DC-DC变换器的参数如下:母线电压42V;输入电压25~35V;输出功率300W;开关频率100kHz;输出电流纹波10%;母线电压纹波1%。根据以上指标,对主电路参数进行优化设计。
(1)耦合电感设计。输出电流纹波由耦合电感的大小决定,即
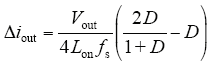
其中,fs为等效开关频率。
由式(3)可知,当D = 0.414时输出电流扰动最大。由于本文占空比D的范围为0.2~0.68,因此电感值L需使D = 0.414时的输出电流纹波满足10%的要求。经过计算可得Lon = 12.6μH,留有一定裕度,取耦合电感Lon = 20μH。
(2)滤波电容设计。为保证Weinberg电路的输出电压纹波大小符合技术指标,需要在输出端加上输出滤波电容。输出滤波电容的设计准则为
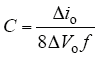
经计算可得C = 1.06μF,留有一定裕度,取输出滤波电容C = 10μF。
3.2 补偿网络设计
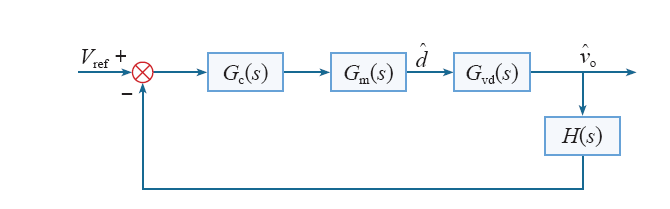
要使输出电压在输入电压波动和负载变化情况下经过暂态调节后保持稳定,需要对系统进行闭环设计,最简单的方法是电压单环补偿[7]。
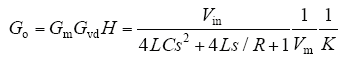
图3
式中,Vm为PWM调制器中锯齿波的幅值;K为反馈分压系数,这里分别取3V和8.3。代入相应参数,可以画出原始回路增益函数Go(s)的Bode图,如图4所示。
图4
图4
原始回路增益函数Go(s)的Bode图
Fig.4
The Bode graphs of original loop gain function Go(s)
图5
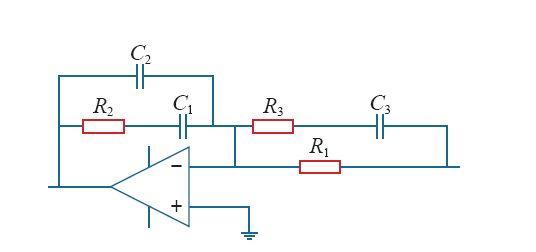
图5中,有源超前—滞后补偿问题的传递函数为
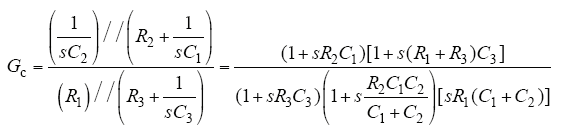
此有源超前—滞后补偿网络有两个零点、三个极点,分别对其进行设计,可得R1 = 3.92kΩ,R2 = 10kΩ,R3 = 54.4kΩ,C1 = 5.7nF,C2 = 0.8pF,C3 = 14.5nF。代入相应参数,可以得到补偿网络Gc(s)的传递函数。
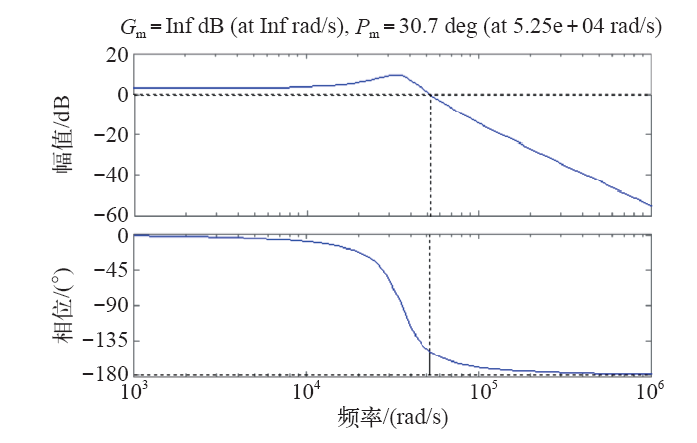
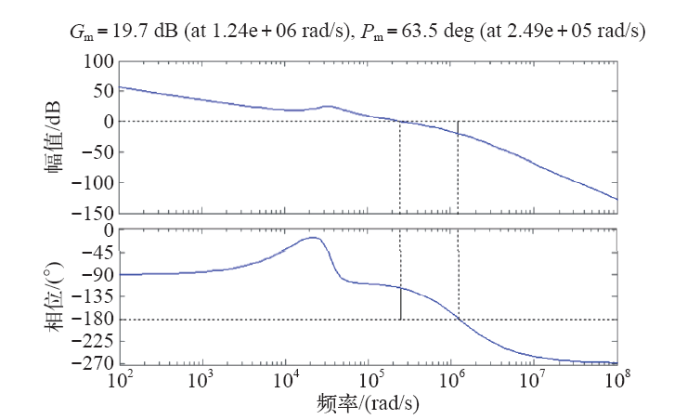
经补偿后的回路增益函数G(s)的Bode图如图6所示。可以看出,G(s)在低频段有较高增益,同时以-20dB/dec斜率下降,保证系统拥有较好的稳态精度;幅频特性在40kHz处以-20dB/dec穿过零分贝线,相位裕度为63.5°,幅值裕度为19.7dB,保证系统具有较高的稳定裕度。
图6
4 仿真与实验验证
图7
图8
图8
输入、输出电压仿真波形
Fig.8
The simulation waveforms of input voltage and output voltage
图9
图9
输出电流及输出电压纹波仿真波形
Fig.9
The simulation waveforms of output current and output voltage ripple
图10
图11
图12
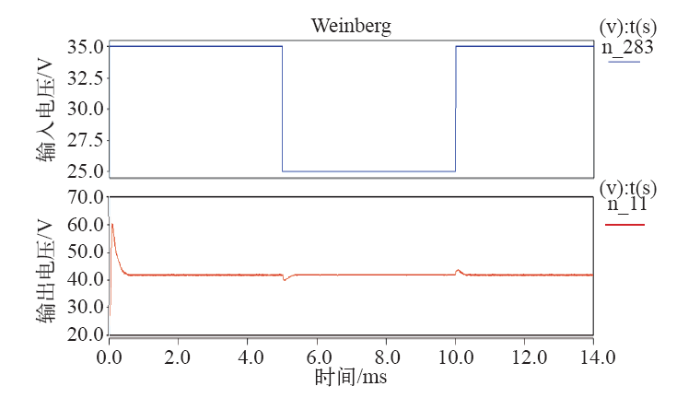
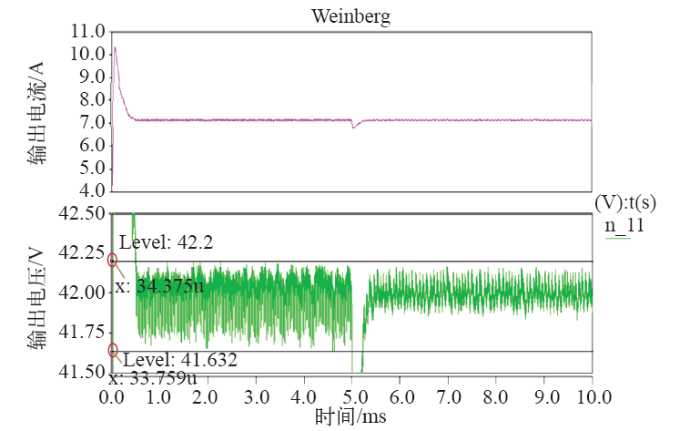
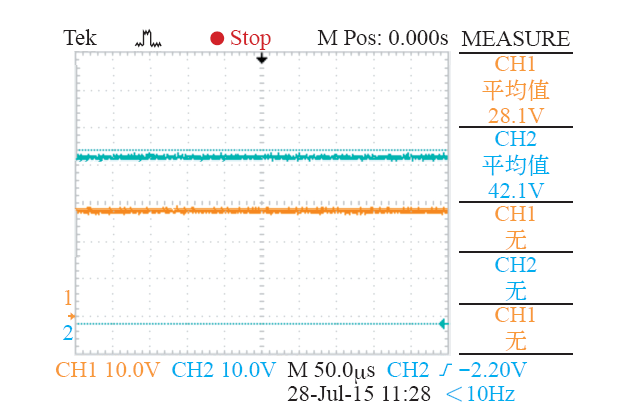
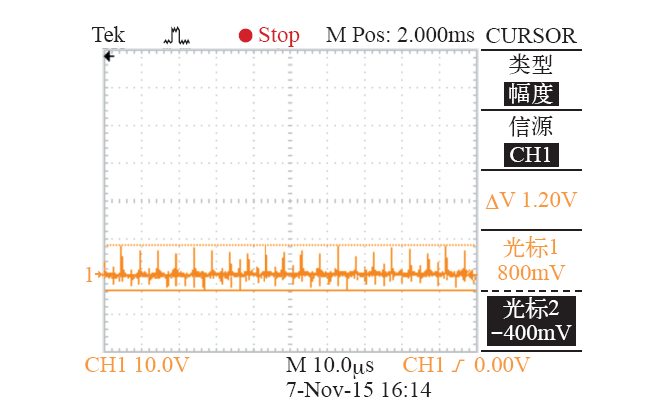
仿真和实验结果说明,输出电流为7A即额定负载下,输入电压在较大范围内突变时,输出电压可以快速进行调整,实现42V的稳态输出,且输出电压纹波基本在1%范围内。说明此系统主电路参数设计合理,且闭环控制系统具有良好的稳定性和快速性。
5 结束语
本文根据DC-DC变换器分析的基本原理,对非隔离型Weinberg变换器建立了小信号模型,分析了传递函数,设计了补偿网络,搭建了仿真电路与实验平台。仿真和实验结果表明,该变换器不但能实现升压功能,还具有高功率密度、高效率、输出电流连续等优点,对此变换器的研究为航天电源系统中的BDR电路和S3MPR或S4MPR后级变换器的研制提供了理论基础。
参考文献
空间电源功率调节技术综述
[J].
Review on power conditioning unit for spacecraft
[J].
High-efficiency Weinberg converter for battery discharging in aerospace applications
[C].
采用MPPT技术的国外深空探测器电源系统综述
[J].
Overview of space power syster design using MPPT for deep space spacecraft
[J].
一种新的航天器电源系统拓扑
[J].
A novel topology of spacecraft electric power system
[J].
A high power, high frequency, DC to DC converter for space applications
[C].
基于非隔离型Weinberg变换器多模块并联系统的建模与控制环路设计
[J].
Modeling and design of control loops for parallel non-isolated Weinberg converter system
[J].