1 引言
三相PWM整流桥通过桥臂中的6个半导体全控开关管的开通与关断实现其整流功能,与传统二极管整流器相比,PWM整流器具有很好的网侧电流和直流侧电压控制性能以及能量双向流动能力;但是开关管的开关损耗是整流桥重要的损耗来源。为了提高三相PWM整流器的效率,在保持系统高控制性能的同时,降低开关损耗是研究的重要方向。
2 三相PWM整流器数学模型[3,4,5]
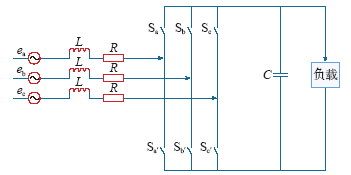
三相PWM整流器主回路包含网侧三相电源、线路等效电感和等效电阻、整流桥、直流侧电容以及负载。其主回路电路图如图1所示。
图1
所以可以得到整流器主回路数学公式
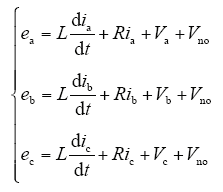
式中,ea、eb、ec为网侧三相电源电压;L、R分别为网侧线路等效电感和等效电阻;Va、Vb、Vc分别为整流桥等效电压。
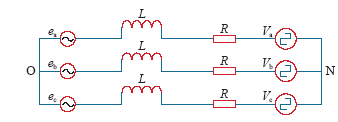
由于电网电源一般为三相正弦对称且稳定,所以可以将整流器主回路三相等效成如图2所示的等效电路图,其中将整流器桥直接等效为整流桥电源,由此推导得出整流器主回路的数学公式。
图2
将式(1)的三相电压和电流量改写成复矢量形式,得到
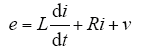
式中,v = Va,b,c + Vno。
根据复功率定义[1]和功率与电流、电压的关系,经坐标系转换,可以得到
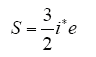
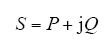
式中,i*代表电流复矢量的共轭值。
3 传统模型预测控制
3.1 模型预测控制框图
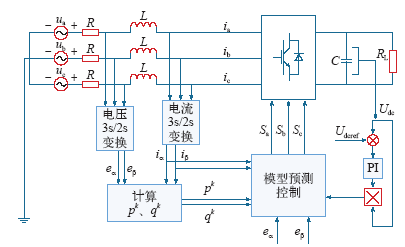
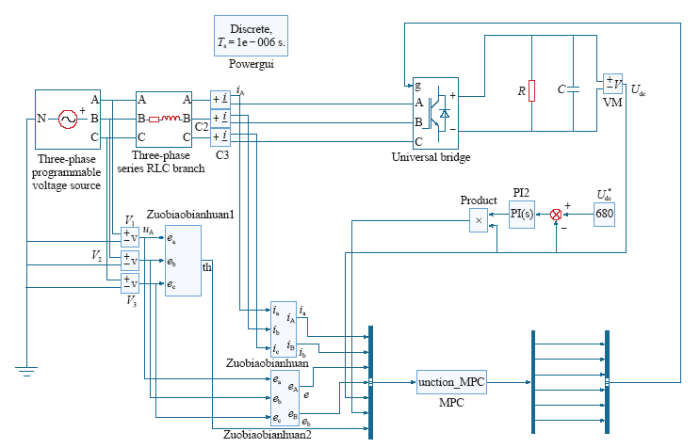
基于模型预测控制的PWM整流器控制系统框图如图3所示。
图3
显然,通过对交流侧电网电压及电流和当前时刻直流侧电压的检测,可以得到当前时刻的电压、电流以及功率值,并可依据现有的PWM整流器模型和已经确定的当前时刻有功功率和无功功率预测当前时刻施加不同开关矢量对下一时刻的有功功率与无功功率的影响,再通过目标函数的评价,就可以得出当前时刻应该施加的最优作用开关矢量。
3.2 单矢量模型预测控制原理[9]
根据PWM整流器的旋转坐标系下的数学模型,则可以得到
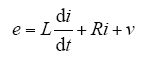
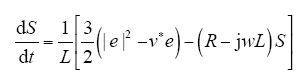
假设当前时刻为k时刻,对于单一矢量作用后的整流器有功功率和无功功率,通过模型预测方法可以得出现在所施加的开关矢量对有功功率和无功功率的影响
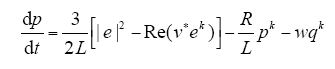
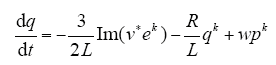
则可以推导出第一个矢量作用完毕,k + 1时刻的复功率预测值
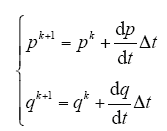
根据目标函数
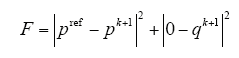
显然可以判定,当前k时刻施加的开关矢量(选出的开关矢量为6个非零矢量和零矢量中的任意一个)。
3.3 双矢量模型预测控制原理[10]
相比于单矢量模型预测的方法,双矢量模型预测控制方法由于其在每一个PWM周期内可以作用两个开关矢量,所以在相同的采样频率下双矢量模型预测方法的开关频率因为高于单矢量控制,其效果明显优于单矢量控制;而在相同的开关频率下,其采样频率要低于单矢量模型预测方法。不仅如此双矢量模型预测控制选择开关矢量作用时间上有更好的灵活性,所以其控制效果理论上要优于单矢量控制。
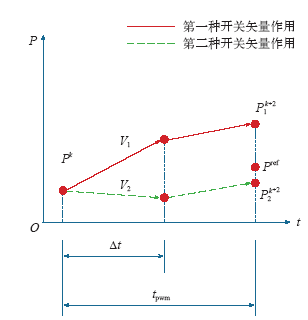
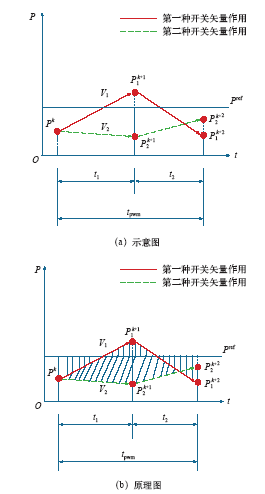
如图4所示,基于双矢量模型预测控制在一个PWM周期内作用两个开关矢量(这两个开关矢量分别是6个非零矢量和零矢量中的一个开关矢量),假设第一个矢量作用完毕是k + 1时刻,第二个矢量作用完毕是k + 2时刻,第一个矢量作用时间为Δt,且其对有功功率的影响为dp1/dt,第二个矢量对有功功率的影响为dp2/dt,可以得出
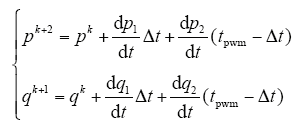
图4
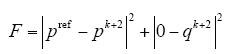
显然通过目标函数衡量两矢量作用完后对有功功率和无功功率的影响进行评价,可以在k + 2时刻获得良好的控制效果,如图3所示,选择第二种开关矢量进行作用。
4 改进模型预测控制
4.1 改进双矢量模型预测控制
4.1.1 改进双矢量模型预测控制原理
传统双矢量模型预测控制方法的目标函数针对的是一个PWM周期末k + 2时刻有功功率和无功功率值偏差值优化。但第一个矢量作用后的k + 1时刻的有功功率及无功功率偏差值失控的话,控制效果则依然会不佳,这就是为什么在同样开关频率下,传统双矢量模型预测控制THD比单矢量还差的原因,因为单矢量模型预测控制不存在失控的k + 1时刻。
本文所提出的改进方法有如下两点:
(1)首先把双矢量控制的k + 1时刻的功率偏差与k + 2时刻功率偏差值和作为优化目标,从而消除了双矢量控制的失控时刻。
(2)改进不仅仅考虑对k + 1和k + 2这两个时刻的功率偏差值的优化,也考虑将从k时刻到k + 2时刻这一段时间的每一个时刻的偏差的积分值进行优化,该积分值几何上等于也就是考虑将无功功率和有功功率参考值与实际值的差对应的面积大小。要使其在k到k + 2时刻之间所有时刻积分值最小,也就是使得参考值和实际值差围成的面积最小。为了减少积分计算工作量,本文提出了一种使k + 1时刻和k + 2时刻偏差值符号相反的方法来确保在偏差大小差不多的情况下偏差与时间轴围成的面积更小,从而可以降低整个PWM周期的误差积分值,降低网侧电流THD数值。
图5
图5
双矢量MPC与改进双矢量MPC有功功率控制原理示意图
Fig.5
Double vector MPC and improved double vector MPC active control schematic
由图5b可以推出,同时考虑k + 1和k + 2时刻有功功率和无功功率偏差的目标函数F1为
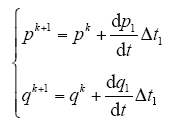
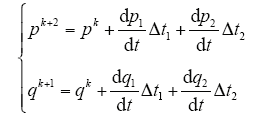
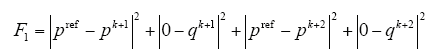
由式(15)可知,该目标函数不仅将k + 2时刻的有功功率和无功功率效果进行衡量,而且将k + 1时刻的有功功率和无功功率进行评估,通过该目标函数可以很好地选出在k + 1与k + 2时刻同时对电压、电流波形影响最小的开关矢量,这样在各种情况下就不会出现k + 1时刻控制效果劣于单矢量控制方法的现象。
为了进一步降低整个周期期间的偏差积分值,也就是降低偏差面积,需要在k + 1和k + 2时刻偏差目标函数的基础上,加上偏差的正负检测项F2,其为
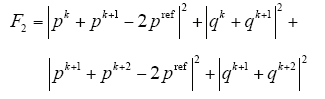
综合考虑F1和F2的影响,因为k + 1和k + 2时刻的偏差F1对面积的影响更直接,将F1加权系数设为1,F2加权系数设为1/2,所以最终的目标函数为
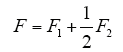
4.1.2 开关矢量及其作用时间
根据两个开关矢量分别在6个非零矢量及一个零矢量中选择(两个零矢量按一个有效零矢量计算),则理论上共计49种组合,但是只有42种有效组合,另外7种组合与这42种组合有重复情况出现。由于在目标函数中对控制稳态效果影响较大的是F1部分,所以在计算矢量作用时间时以F1为准进行计算。
显然,根据式(11)和式(15),可以计算
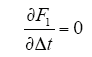
得到第一个矢量最优的作用时间(第二个矢量作用时间为tpwm - Δt)
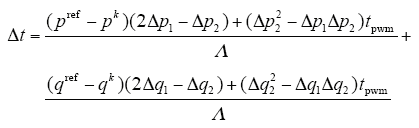
其中
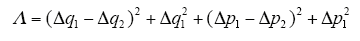
4.2 改进单矢量模型预测控制原理
为了验证前节改进算法对其他模型预测控制算法也具有改进潜力,本节将前述的改进算法应用于传统单矢量模型预测控制算法,其原理是使k时刻和k + 1时刻有功和无功功率给定值与实际预测值的偏差数值的符号相反,而传统方法不考虑k时刻和k + 1时刻偏差的符号变号,仅考虑在每个时刻偏差最小。如前面双矢量模型预测控制改进算法类似,改进算法通过安排前后时刻偏差变号,与不变号相比,可以确保在每个时刻的偏差大小差不多的情况下,偏差与横坐标围成的面积更小,从而可以降低整个PWM周期的误差积分值,降低网侧电流THD数值。
根据单矢量模型预测控制改进算法原理,将式(16)和式(17)目标函数改进为
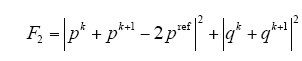
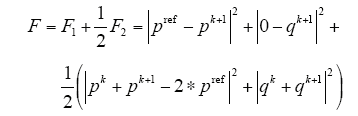
由于单矢量模型预测控制在一个PWM周期内只作用一个开关矢量,所以其不需要再单独计算矢量作用时间。
4.3 零矢量的选择
假若预测控制选择开关矢量的结果里有一个为零矢量,另外一个为非零矢量,则根据非零矢量选择零矢量为“000”还是“111”状态,若非零矢量中“1”状态较多,则选择“111”为有效零矢量,若“0”状态较多,则选取“000”为有效零矢量。
5 仿真结果分析
本文对SVPWM控制方法和传统的单矢量、双矢量模型预测控制进行了仿真。仿真中,PWM整流器各个参数为:交流侧电网电压e = 380V;电感参数为L = 10mH;电阻值为R = 0.3Ω;直流侧电压给定为U*dc = 680V,电压给定突变时U*dc = 685V,Rroad = 97Ω,直流侧电容值为C = 840μF。内环阶跃响应信号:模型预测控制为10 000W,SVPWM控制方法由于内环为电流环,所以根据电流功率对应关系给阶跃信号为14A。其中SVPWM控制方法的内环参数为P = 10,I = 1,此时开关频率设定为2kHz。模型预测控制的仿真图如图6所示。
图6
5.1 动态性能指标对比
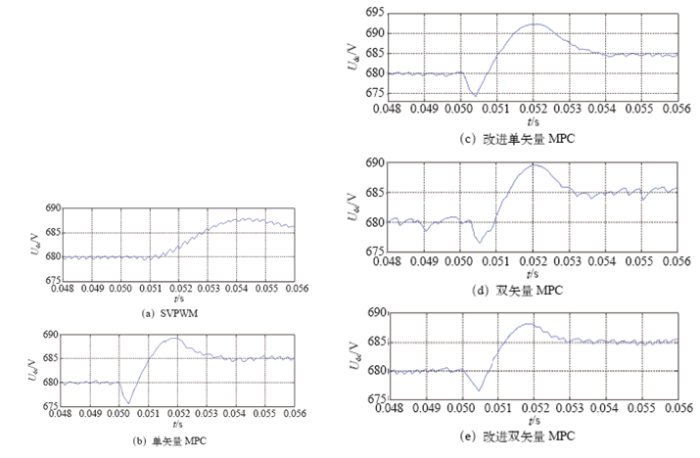
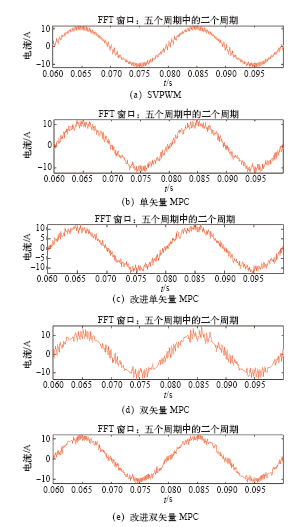
为了验证改进双矢量模型预测控制的动态性能,观察了系统的两种动态响应:电压外环给定突变以及内环的阶跃响应。根据以上仿真数据进行仿真的动态性能波形如图7所示。
图7
图7显示了电压给定突变时直流侧母线电压的变化,显然2kHz开关频率时SVPWM控制方法的快速性能最差,而单、双矢量模型预测控制与改进的单、双矢量模型预测控制都几乎在0.005 3s时达到稳定,但其中单矢量模型预测控制的电压超调量大于双矢量模型预测控制与改进双矢量模型预测控制,改进双矢量模型预测控制的快速性同时优于另外两种模型预测控制方法,其超调量在模型预测控制中也是最少的,改进单矢量模型控制的动态性能没有太大变化,验证了改进模型预测控制的动态性能优于另外3种控制算法。
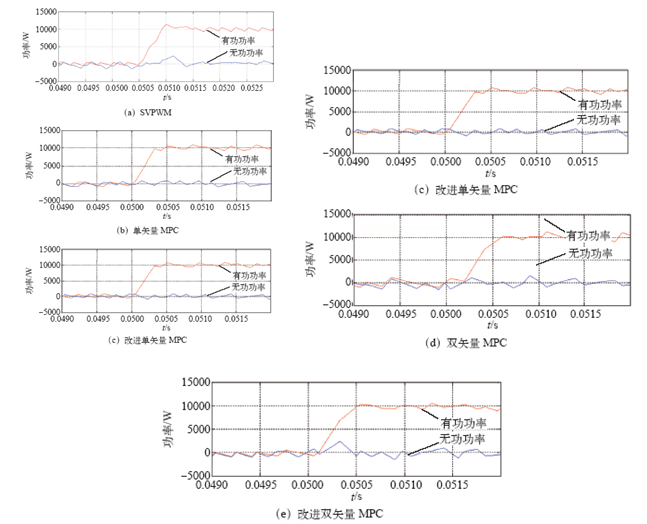
图8显示的是内环阶跃响应,显然SVPWM控制方法的快速性能依然较差,单矢量模型预测控制虽然比双矢量模型预测控制方法与改进的控制方法早达到稳定状态,但是其反应时间几乎相同都是约为0.000 35s,而改进双矢量模型预测控制方法的稳态功率波动是最优的。
图8
5.2 稳态性能指标对比
图9
图9
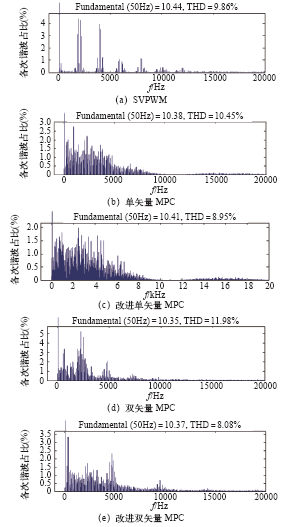
网侧电流FFT分析电流信号图
Fig.9
The grid current fft analysis of current signal diagram
图10
表 各种控制方法THD对比
Tab
| 控制方法 | Tpwm/s | THD(%) |
|---|---|---|
| SVPWM | 0.000 5 | 9.86 |
| 传统单矢量MPC | 0.000 091 | 10.45 |
| 改进单矢量MPC | 0.000 092 | 8.95 |
| 传统双矢量MPC | 0.000 21 | 11.98 |
| 改进双矢量MPC | 0.000 211 | 8.08 |
此外,从SVPWM控制方法的频谱分析显示其谐波主要存在于开关频率或者倍频于开关频率附近,所以其THD主要由于开关频率造成,而模型预测方法主要是集中于低频段,尤其是改进后的双矢量控制方法将频谱向高频挪移,得到了较优的控制效果,该改进方法可望推广到其他模型预测控制算法以改进网侧电流THD性能。
6 结论
通过与传统单、双矢量模型预测控制及SVPWM控制方法的数据对比发现,改进单、双矢量MPC控制方法在相同的开关频率下的动态响应明显优于SVPWM,且稳态波动小于未改进之前的单、双矢量模型预测方法,其稳态 THD指标明显优于另外3种控制方法,所以改进双矢量模型预测方法的动态性能和稳态性能都是最优的,改进单矢量模型预测方法其次,仿真结果充分验证了本文提出的改进方法在双矢量和单矢量模型预测控制算法上的可行性以及其优良的网侧电流THD性能。
参考文献
基于新型开关表的PWM整流器直接功率控制
[J].
Direct power control of PWM rectifier based on new switch table
[J].
Deadbeat direct power control of three-phase pulse-width modulation rectifiers
[J].
A novel three-vectors-based predictive direct power control of doubly fed induction generator for wind energy applications
[C].
Model predictive control—a simple and powerful method to control power converters
[J].
Low complexity model predictive power control-double vector based approach
[J].