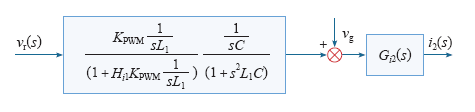1 引言
近年来,为解决能源危机和环境污染等问题,许多发达国家致力于开发利用广泛分布且污染小的风能和太阳能等可再生能源。基于交流母线方式的RE-DPGS是可再生能源单元和储能单元通过电力电子变换器接入交流母线,并经过电力变压器馈入大电网,这种结构的系统容量相对较小、可靠性高[1,2]。并网逆变器对RE-DPGS的安全、稳定和高质量运行具有十分重要的作用。并网逆变器通常采用PWM调制策略,输出电压存在大量的开关谐波,为了抑制并网电流中的开关谐波,采用体积更小、成本更低的LCL滤波器[3,4,5]。相对于两级式光伏并网逆变器,单级式具有结构简单、体积小、成本低、效率高的特点[6,7]。本文针对单级式光伏并网LCL型逆变器研究其控制方法。并网中电流跟踪控制采用两相旋转坐标系下的PI控制实现[8],这种控制需要多次坐标变换,控制参量解耦,算法相对复杂。无差拍控制算法在并网逆变器中应用较广[9],其动态跟踪性能较好,但控制精度依赖系统参数,除了对控制量进行预测外,还要对系统参数进行在线估算,增加了算法的复杂程度。电压源型逆变器(Voltage Source Inverter,VSI)在两相静止坐标系下完全解耦,采用PR调节器可独立控制坐标轴交流分量,实现特定频率交流量的无静差控制[3]。因此本文在设计逆变器输出电路LCL型滤波器的基础上,探讨有源阻尼、电压前馈、准PR调节综合控制法提高逆变器并网性能与并网质量,重点研究准PR调节器比例放大系数对系统稳定性及动态响应性能的影响。
2 并网系统结构及控制原理
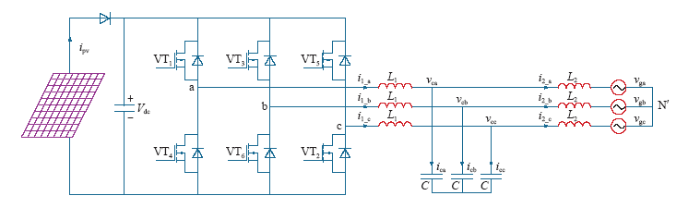
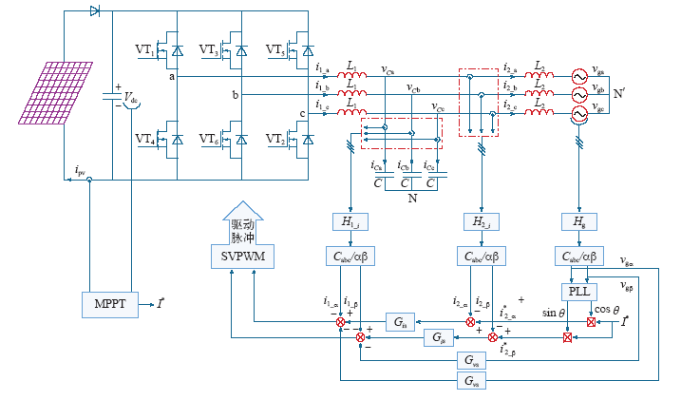
三相单级式LCL型光伏并网逆变器电路结构如图1所示。光伏并网发电系统利用光伏电池将太阳能转化为电能,经过防反充二极管,直接通过并网逆变器将电能供给电力系统。图中,ipv为光伏电池阵列输出电流;Vdc为逆变器直流侧储能电容电压;i1_a、i1_b、i1_c为LCL滤波器电感L1上的电流;vCa、vCb、vCc为电容上的电压;i2_a、i2_b、i2_c为电感L2上的电流;vg为并网交流母线电压。图2为基于单级式LCL型逆变器的并网控制原理图。系统主要由光伏阵列、DC/AC逆变器、并网滤波器、控制单元组成。并网发电系统控制原理为:为提高光照利用率,需要调整光伏电池阵列工作在最大功率点,采集光伏阵列输出的电压、电流,通过MPPT算法调整并网逆变器输出指令电流,实时动态搜索最大功率点。控制逆变器输出电流跟踪并网指令电流,实现经LCL滤波器的并网电流与电网电压同频同相,并网功率因数为1。
图1
图1
三相单级式LCL 型光伏逆变器电路结构
Fig.1
Structure of single-stage PV three-phase inverter with LCL filter
图2
图2
三相单级式LCL 型逆变器光伏并网控制原理图
Fig.2
Diagram of PV grid-connected control principles of single-stage three-phase inverter with LCL filter
3 LCL滤波器设计
3.1 电容C的选取
选取滤波电容C需要考虑电容引入的无功功率,电容容量越大,引入的无功功率越大,流过电感L1和开关管VT的导通损耗会增加。一般采用滤波电容C引入的无功功率与并网逆变器输出额定有功功率之比λc小于5%来确定滤波电容最大值[10],即
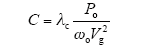
式中,Po为逆变器输出额定功率;Vg电网电压有效值;ωo电网基波角频率。
3.2 电感L = L1 + L2的选取
输出滤波电感大小影响电感电流的纹波,选择电感应使电流纹波一般小于额定电流的15%~20%,这里按三相L型逆变器设计滤波电感最小值,选取额定电流的20%。设逆变器额定输出相电压为Vin,额定输出相电流为In,电感电流纹波为ΔiLmax,逆变器直流输入母线电压为Vdc,电网相电压有效值为E,开关频率为fk,基波频率为fo。额定电流计算公式为
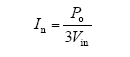
式(3)为输出线电流纹波与两桥臂回路间滤波电感即2倍L的关系,D为一个开关周期内的平均占空比,且
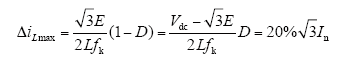
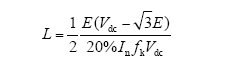
3.3 电感L1、L2的选取
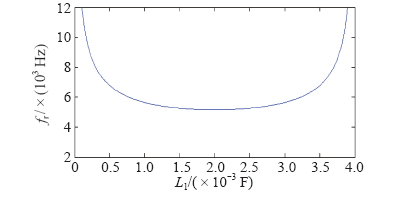
如果电感L1值太大,将使系统的动态响应变慢,L1值太小则会增加输出的脉动,增大损耗。以避免在较低和较高频率段的谐振问题,LCL滤波器固有谐振频率的范围应该在10倍的基波频率与1/2开关频率之间,即10fo<fr<0.5fk。谐振频率表达式为
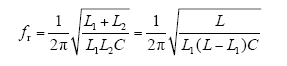
其中,L = L1 + L2,且L1>L2,图3为以L1为自变量的关于谐振频率的函数波形。
图3
L确定后,L1在取值范围内的中部较大区域,fr变化率较小,但在取值范围端部fr变化率较大。在满足10fo<fr<0.5fk条件下,选取fr小于一定变化率,可确定L1的取值范围,这里选取L/2<L1<4L/5。
4 并网控制系统设计
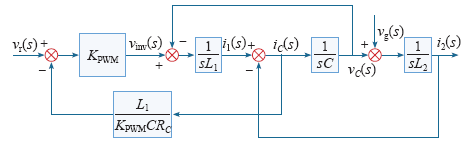
4.1 电容电流反馈有源阻尼设计
LCL 滤波器能够很好地满足谐波衰减的要求,但它是一个无阻尼三阶系统,容易发生谐振,在谐振频率处会有一个很高的谐振尖峰,一方面会导致大量谐波电流注入电网,另一方面谐振频率附近容抗高,对控制系统的相位影响较大,严重时可导致系统运行不稳定。对于小功率系统往往采用增加无源阻尼的方式,可以在LCL滤波器中的电容并联电阻,并入电阻的LCL滤波器控制框图如图4所示。
图4
图4
并网逆变器LCL 滤波电容并联电阻无源阻尼结构图
Fig.4
Structure of capacity with parallel resistance for passive damping in LCL filter of grid-connected inverter
电容无并联电阻时LCL传递函数为
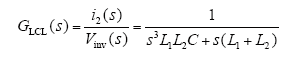
电容并联电阻时LCL传递函数为
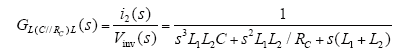
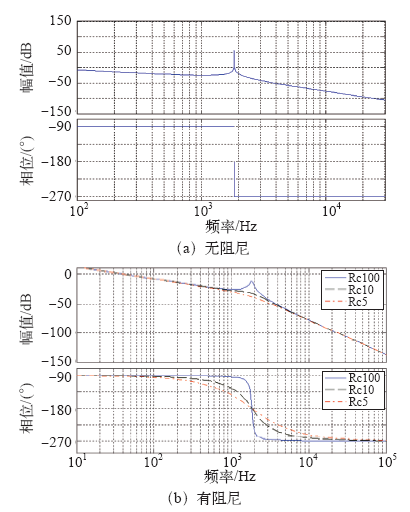
图5分别为LCL无阻尼、有阻尼及不同阻尼系数(并联电阻越大,阻尼系数越小)时的幅值、相角频率特性的伯德图。
图5
图5
LCL 型并网逆变器无阻尼与有阻尼伯德图
Fig.5
BODE of LCL grid-connected inverter with nondamping and damping
图6
图6
无源阻尼等效为电容电流比例反馈结构图
Fig.6
Structure of capacitor current proportional feedback equivalent topassivedamping
4.2 并网电压前馈设计
并网逆变器在电网公共节点(PCC)附近都会接有非线性设备,这些设备运行中会产生谐波电流,电流流经线路阻抗,造成PCC处电网电压波形畸变,若在控制电路中不加以补偿将导致并网逆变器输出并网电流畸变,同时根据不同控制方法电网电压基波分量也会成为扰动量影响并网电流,产生幅值、相位误差[12]。本文采用准PR电流跟踪控制算法,需要对电网电压扰动进行补偿,在可测量扰动电网电压与控制量误差测量点之间加入校正控制器,这种前馈控制可有效抑制并网电压谐波分量,减小与指令电流幅值、相位稳态误差。
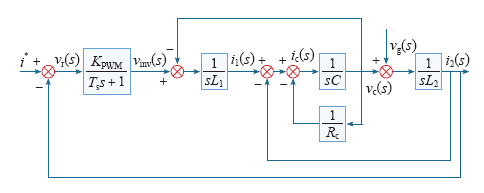
图7
图7
有源阻尼LCL 型逆变器传递函数框图
Fig.7
Diagram of transfer function of inverter with active damping of LCL
图8
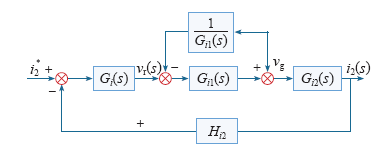
其中,Hi1 = L1/(KPWMCRC),若Gi1 =( KPWM/L1Cs2)/[(1 + Hi1KPWM/sL1)(1 + s2L1C)],则闭环传递函数为
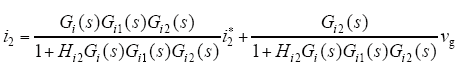
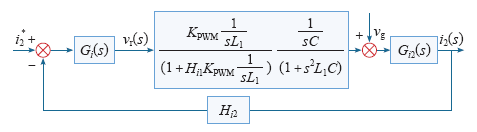
系统开环传递函数为Go = Hi2Gi(s)Gi1(s)Gi2(s)。
i2由i2*和vg两分量决定,由于在fo附近Go>>1,则
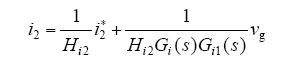
式中,Hi2为比例反馈系数,在电流跟踪控制中输出电流应与指令电流同频同相位,而指令电流的频率、相位是通过锁相环技术跟踪电网电压基频的频率与相位;vg/[Hi2(s)Gi(s)Gi1(s)]分量的相位、频率由vg/[Gi(s)Gi1(s)]决定,因此该分量影响电流跟踪精度。通过变量前馈控制消除电网电压对输出电流的影响。这样前馈函数为1/Gi1,如图9所示。
图9
4.3 准PR电流调节器设计
PR调节器可有效提高基波增益实现对交流信号的无静差控制,用于并网变换器控制系统中,可在两相静止坐标系下对电流进行调节,避免了复杂的坐标变换和分量间的解耦问题。为提高调节器对电网电压频率波动的适应性,这里采用准PR控制方法[13]。控制表达式为
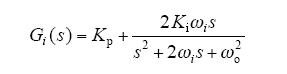
式中,Kp为比例系数;Ki为谐振系数;ωo = 2πfo为基波角频率;ωi为-3dB的谐振带宽。光伏电站允许的电网频率波动范围49.5~50.2Hz,允许最大偏差为Δf = 0.5Hz,PR调节器为适应电网频率在规定范围内波动,需要在电网频率波动范围内增益足够大。选取ωi = 2πΔf,这里取ωi = 5rad/s。可见准PR控制器是对一定带宽谐振频率的正弦量进行幅值积分,其对数频率特性曲线如图10所示。带宽谐振频率之外等同于比例环节。
系统开环传递函数为
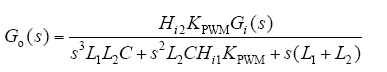
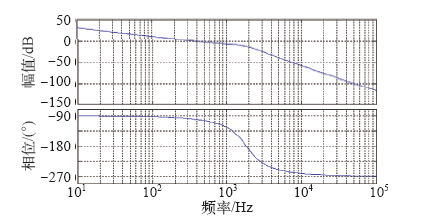
其中,Hi1 = L1/(KPWMCRC),补偿前Gi(s) = 1,其伯德图如图11所示。
图11
图11
电流补偿前系统开环传递函数伯德图
Fig.11
Diagram of BODE of open loop transfer function before adding current control
准PR控制器在谐振带宽的低、高频段等效为比例调节器,则系统高频段等效开环传递函数为
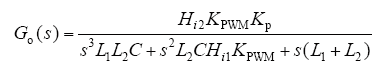
因为10fo<fr<0.5fk,电流补偿后系统截止频率fc应在fo<fc<fr范围内。系统截止频率fc,幅值、相位裕度,开环增益影响系统跟踪速度、抗干扰能力和稳态误差。若开环增益变低,则截止频率fc减小,系统幅值、相位裕度变高;开环增益变高,则截止频率fc增大,系统幅值、相位裕度变低,可见准PR调节器比例系数决定幅值、相位裕度、开环增益和fc的大小。
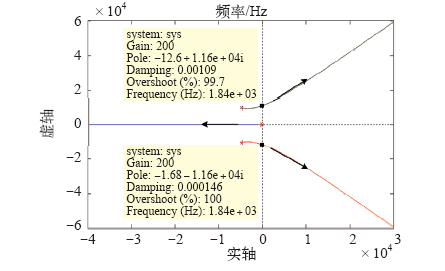
系统闭环特征函数为1+Go(s),由劳斯判据确定调节器增益稳定范围为0<Kp<(L1+L2)Hi1/L1Hi2。图12所示为系统高频段开环传递函数零、极点分布与根轨迹。由图可确定系统稳定的增益Kp的变化范围,以及闭环主导极点,满足系统动态性能指标。
图12
图12
闭环系统高频段调节器增益根轨迹图
Fig.12
Root locus diagram of regulator gain in the high frequency band of the closed loop system
谐振系数Ki是以fo为中心的带宽谐振频率的开环增益,该值将影响基频信号跟踪稳态误差。一般可选取Ki>Kp。
5 仿真结果与分析
设置单级式LCL光伏并网系统仿真参数,模拟光伏电池经串并联组成光伏阵列组件,在光照强度1 000W/m2、温度25℃时,最大输出功率为1kW,最大功率点输出电压为100V,模拟交流电网电压55V,基波频率50Hz,逆变器开关频率20kHz,逆变器侧电感L1 = 2 400μH,网侧电感L2 = 600μH,滤波电容C = 10μF。
图13
图13
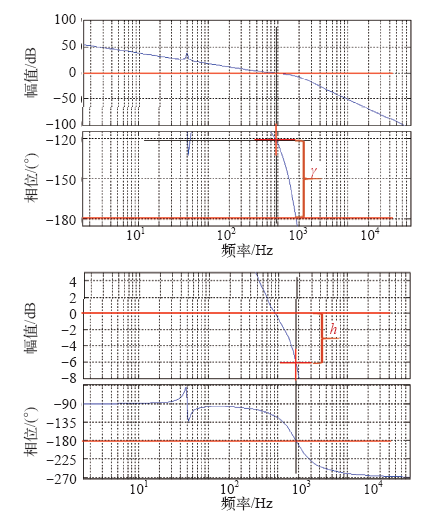
加入电流调节器的系统相位、幅值裕度伯德图
Fig.13
BODE of phase angle and amplitude margin of system with current regulator
图14
图14
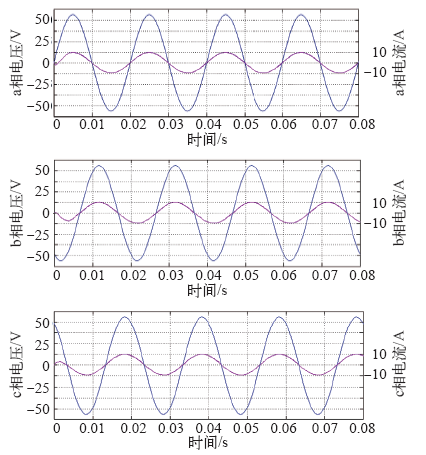
有功功率并网三相电压电流波形图
Fig.14
Waveforms of three-phase active power gridconnected voltage and current
图15
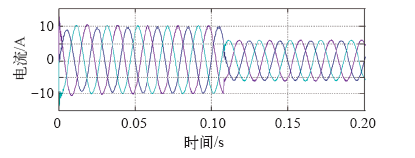
图15
光伏能源功率波动电流动态响应波形
Fig.15
Grid-connected current dynamic responding under PV power fluctuation
图16
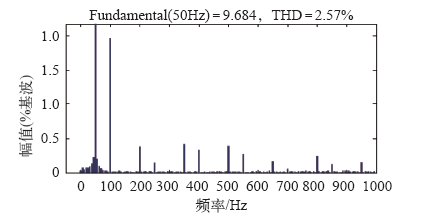
图16
LCL 型并网逆变器准PR 控制并网电流谐波分析结果
Fig.16
Harmonic analysis result of grid-connected current of LCL inverter with quasi-PR control
6 结束语
本文分析了三相LCL型光伏并网逆变器的工作原理并研究了LCL滤波器参数设计方法;分析了电容电流比例反馈实现有源阻尼抑制谐振尖峰;分析了电网电压对并网电流的影响及采用前馈控制方法加以消除;准PR调节器比例系数影响系统截止频率和低频段幅值增益,通过分析高频段传递函数,利用劳斯稳定性判据及根轨迹法确定比例系数取值范围,根据伯德图确定系统满足一定相位、幅值裕度的准PR比例参数,最后根据系统设计参数搭建仿真模型,仿真结果表明系统稳态性能和动态响应性能较好,并网电流谐波含量低,实现以单位功率因数并网。
参考文献
Design, analysis, and real-time testing of a controller for multi-bus micro-grid system
[J].
Micro-grid autonomous operation during and subsequent to islanding process
[J].
A new feedback method for PR current control of LCL filter-based grid-connected inverter
[J].
Explicit model-predictive control of a PWM inverter with a LCL filter[]
Design of LCL filters of active-front-end two-level voltage-source converters
[J].
Modeling guidelines and a benchmark for power system simulation studies of three-phase single-stage photovoltaic systems
[J].
两级式三相光伏并网发电系统仿真研究
[J].
Simulation research of two-stage three-phase PV grid-connected system
[J].
基于PI控制的三相光伏并网逆变器电流控制器设计
[J].
Design of the PI current controller of three-phase photovoltaic grid-connected inverter
[J].
基于电流无差拍控制的三相光伏并网逆变器的研究
[J].
Study on three-phase photovoltaic grid-connected inverter based on current deadbeat control
[J].
Design and control of an LCL-filter-based three-phase active recitifer
[J].
Generalized design of high performance shunt active power filter with output LCL filter
[J].
Suppression of line voltage related distortion in current controlled grid connected inverters
[J].
A closed-loop selective harmonic compensation for active filter
[J].