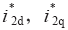1 引言
为此,本文研究了一种电网电压前馈控制策略[9],在PI控制的基础上采样电网电压,根据逆变器数学模型推导得到前馈传递函数,并将前馈信号叠加到并网逆变器的调制波中,消除电网电压的影响,从而实现并网电流谐波及不平衡分量的抑制。电网电压前馈控制具有以下优点:只需引入前馈传递函数即可实现并网电流不平衡和谐波分量的抑制,控制器结构相对简单;不影响逆变器并网电流环路增益,能够保持系统良好的动态和稳态性能。
2 非理想电网电压对并网电流影响分析
2.1 并网逆变器的数学模型
本节主要在不考虑功率管开关所产生的高次谐波的情况下,建立微电网逆变器针对基波的状态平均模型[10],能清晰地反映出逆变器各个物理量之间的关系和系统的工作原理。
在分析微电网逆变器模型之前,作如下假设:
(1)系统中开关管为理想开关,不考虑死区时间带来的影响。
(2)输出滤波器中的电感和电容皆为理想元件,且各相参数完全相同。
(3)逆变器输出端电压为三相平衡电压,为理想正弦波。
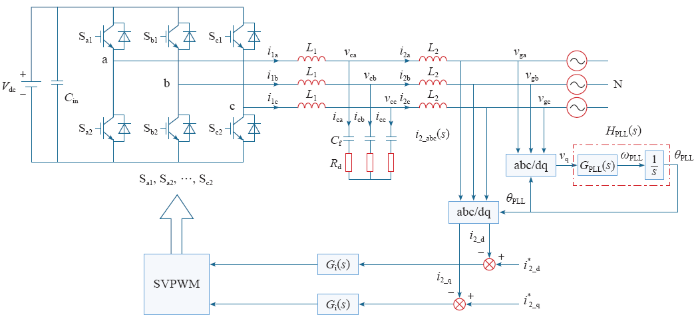
如图1所示,逆变器采用三相全桥结构,输出滤波采用LCL结构,采用电容支路串联电阻的无源阻尼方法来抑制谐振峰。其中,Cin为直流端电容,L1为逆变器侧电感,Cf为滤波电容,L2为网侧电感,Rd为阻尼电阻,vgabc为电网电压。
图1
图1
并网逆变器结构及控制框图
Fig.1
Structure and control chart of the grid-connected inverter
逆变器工作时,采用网侧电感电流反馈的闭环控制,电流调节器为PI控制器。参考图1三相LCL逆变器结构,应用Clark 变换和Park变换可以得到dq坐标系下并网逆变器的数学模型为
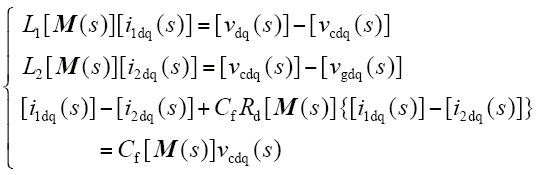
其中,[vdq(s)] = [vd(s) vq(s)]T,[vcdq(s)] = [vcd(s) vcq(s)]T,
[vgdq(s)] = [vgd(s) vgq(s)]T, [i1dq(s)] = [i1d(s) i1q(s)]T, [i2dq(s)] = [i2d(t) i2q(s)]T;ω为电网基波角频率; 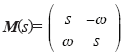
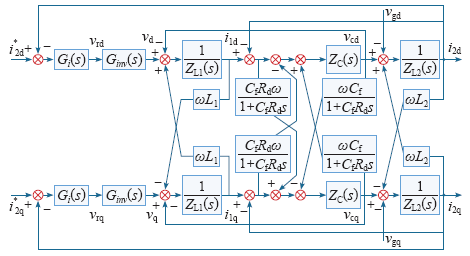
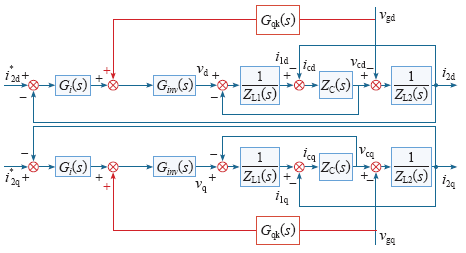
根据式(1),可以绘出三相LCL并网逆变器在dq同步旋转坐标系下的控制框图,如图2所示。可以看出,同步旋转坐标系下,d轴与q轴间存在四组耦合量,分别为逆变器侧电感电流、电容支路电流、电容支路电压及网侧电感电流。dq轴耦合量大小相等,方向相反。为实现有功与无功的独立控制,需在dq轴下进行解耦。
图2
图2
dq坐标系下三相LCL并网逆变器控制框图
Fig.2
Control diagram of the three phase LCL-type grid-connected inverter with the d-q coordinate system
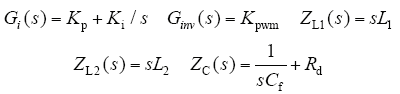
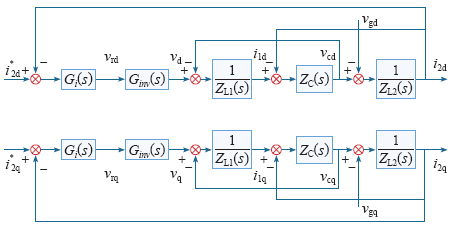
Kpwm为调制比,由于本文为空间矢量调制,(Space Vector Pulse Width Modulation,SVPWM)调制过程中引入了直流电压的前馈环节,所以Kpwm为1。
图3
图3
dq坐标系下三相LCL并网逆变器解耦后控制框图
Fig.3
Control diagram of the decoupled three phase LCL-type grid-connected inverter with the d-q coordinate system
2.2 电网电压对电流的影响原因分析
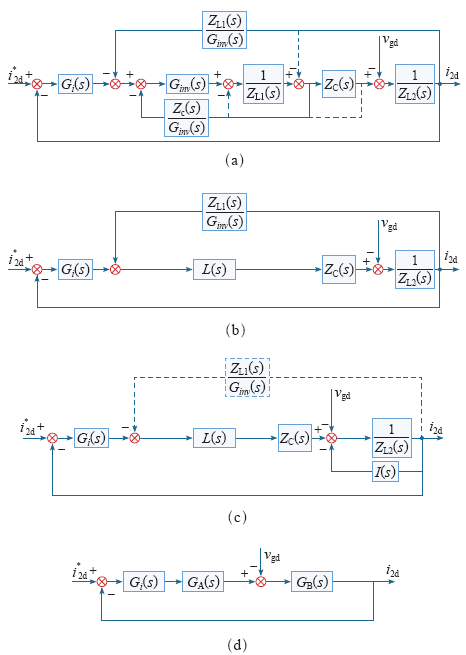
为分析并网电流的影响因素,需对其表达式进行求解。解耦后d轴模型与q轴模型完全对称,现以d轴为例进行分析。逆变器模型较为复杂,需对其进行等效变换,变换过程如图4所示。图中虚线表示变换前模型,实线表示变换后模型。
图4
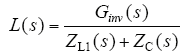
图4c中将并网电流反馈支路的反馈量叠加点由电流调节器输出端移至ZC(s)输出端,其中,I(s)表达式为
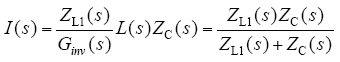
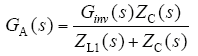
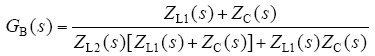
以上等效变化将框图进行最简化,根据简化后框图(如图4d所示),可以求出d轴并网电流表达式
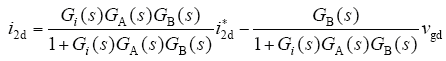
与d轴完全对称的q轴并网电流表达式形式与d轴表达式完全相同,下面给出并网电流dq轴总体表达式
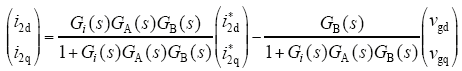
由上式可以看出,三相LCL并网逆变器并网电流由两部分组成:一部分为并网电流给定值i2dq[1];另一部分为电网电压扰动分量i2dq[2]。其中,并网电流给定值i2dq[1]根据三相并网逆变器功率值直接给出,i2d[1]即d轴并网电流给定值由有功功率值给出,i2q[1]即q轴并网电流给定值由无功功率值给出;电网电压扰动分量i2dq[2]由电网电压决定,其值与电网电压成正比。
三相并网逆变器在理想电网电压下并网时,由于电网电压值只含有基波正序分量,相应的在并网电流中产生的扰动是三相平衡且不含有谐波的。非理想电网条件下,电网电压存在三相不平衡和含有谐波两种情况,此时,电网电压可以分解成基波正序分量、基波负序分量和谐波分量,相应地在并网电流中产生的扰动也含有正负序分量和谐波分量,造成三相并网电流的不平衡及含有谐波,并网电流质量变差。
3 电网电压前馈数学模型推导
3.1 电网电压前馈控制推导
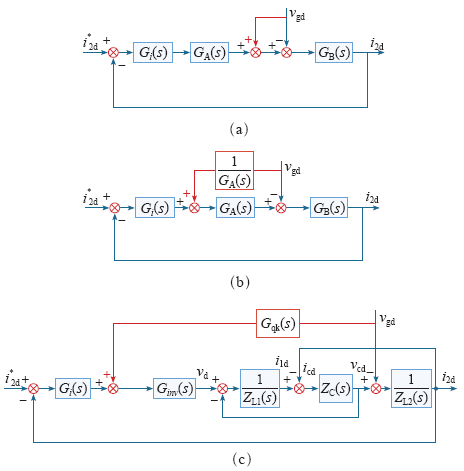
根据上节分析,并网电流中含有电网电压扰动分量,为抑制这一扰动影响,采用电网电压前馈控制。电网电压前馈控制的基本思想是:对并网电流的电网电压扰动源直接进行采样,增加前馈支路消除扰动源影响。下面对电网电压前馈控制进行详细分析。
图5
图5
电网电压前馈控制推导过程
Fig.5
The derivation of the feedback control scheme of the grid voltage
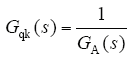
代入GA(s)表达式(5),得到
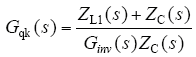
q轴电网电压前馈函数推导过程与d轴类似,前馈函数完全相同,这里不再赘述。
为验证电网电压前馈策略的正确性,对加入前馈支路后的并网电流控制框图进行分析。未加入前馈支路前,三相LCL并网逆变器并网电流表达式如式(8)所示,由两部分组成:一部分为并网电流给定值i2dq[1];另一部分为电网电压扰动分量i2dq[2]。加入前馈支路后,并网电流表达式增加一部分,即为电网电压前馈分量i2dq[3]
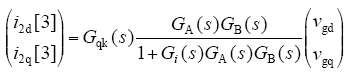
代入式(9)可得
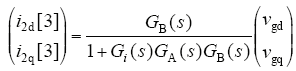
可以看出,加入电网电压前馈支路后,电网电压前馈分量i2dq[3]与电网电压扰动分量i2dq[2]大小相同,方向相反,即为
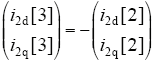
此时并网电流表达式为
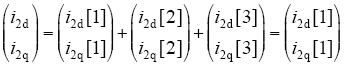
电网电压前馈下并网电流表达式中只含有并网电流给定分量,电网电压扰动分量与电网电压前馈分量相互抵消,电网电压前馈策略有效。
图6给出同步旋转坐标系下电网电压前馈控制策略dq轴总控制框图,电网电压经过前馈函数后加入PI控制器输出端,与电网电压扰动分量相抵消。
图6
图6
电网电压前馈控制框图
Fig.6
Control diagram of the feedback control scheme of the grid voltage
3.2 电网电压前馈函数分析
将逆变器侧电感感值,滤波电容支路阻抗值和逆变桥传递函数带入式(10),可以得到电网电压前馈函数具体形式为
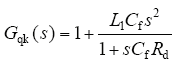
无源阻尼控制时前馈函数由两部分组成,分别为比例项和分子为二阶,分母为一阶的表达式项,以下统称为比例项和第二项。下面对前馈函数进行详细分析。
电网电压谐波频率变化时,前馈函数比例项大小恒定,第二项大小随着电网电压谐波频率的变化而改变。因此,电网电压谐波频率变换时,两项分量占总前馈量的份额会有所不同。为方便描述,以下表中系统参数为例进行定量分析。
表 三相LCL逆变器系统参数
Tab.
| 参 数 | 数 值 | 参 数 | 数 值 |
|---|---|---|---|
| 额定功率/kW | 15 | 开关频率/kHz | 20 |
| 直流母线电压/V | 700 | 电网电压/V | 220 |
| 滤波电容/μH | 6.8 | 逆变器侧电感/mH | 1.5 |
| 阻尼电阻/Ω | 1.7 | 网侧电感/mH | 0.2 |
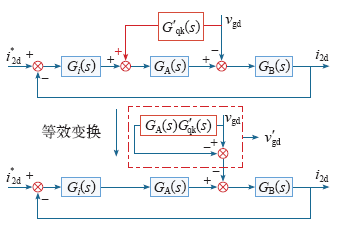
从等效电网电压扰动量的角度来说明各项作用。以d轴为例,图7给出了等效电网电压扰动量求解过程,虚线框中为电网电压等效扰动量 
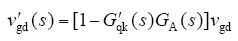
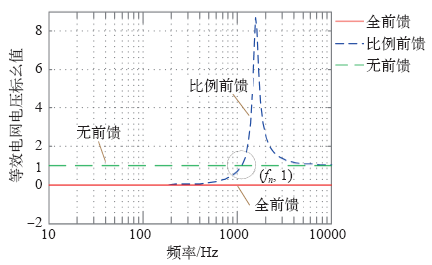
无前馈时, 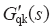
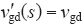
全前馈时, 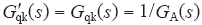
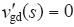
图7
图7
电网电压等效扰动分量求解
Fig.7
The solution procedure of the equivalent perturbance component in the grid voltage
比例前馈时,G′qk(s) = 1,此时等效电网电压扰动量
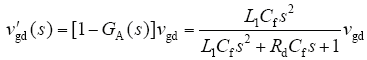
q轴等效电网电压扰动量求解过程与d轴相似。为了更直观分析,以电网电压d轴量、q轴量为基准,绘出三种情况下等效电网电压扰动量 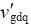
图8
图8
等效电网电压扰动量对比图
Fig.8
The contrast diagram of the equivalent perturbance component in the grid voltage
由以上分析可知,低频段电网电压前馈函数可以近似为比例前馈;频率升高时,比例前馈不能完全消除电网电压扰动分量,此时需要引入电网电压全前馈。
4 实验验证
为验证三相LCL并网逆变器控制策略有效性,本文通过搭建一台三相LCL并网逆变器进行实验,实验平台参数与前表相同。实验中使用可编程交流源来模拟畸变电网条件。
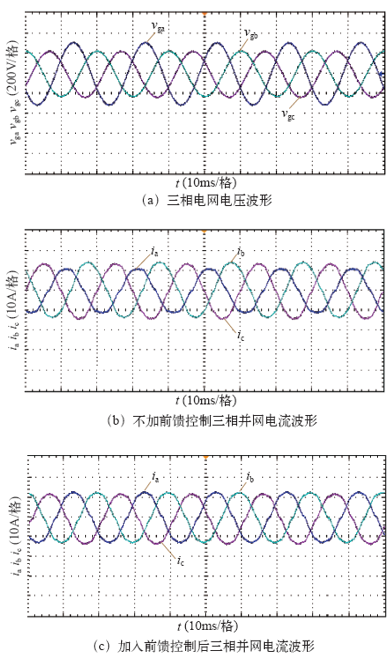
以三相功率6kW为例,分别在普通单电流环不加入前馈控制和加入电网电压前馈控制两种方法下进行实验,对比实验结果。模拟B、C相电压降低情况,A、B和C三相电网电压有效值分别为220V、160V和160V。图9所示为B相降落情况下实验波形。图9a所示为三相不平衡电网电压波形,B相降低。图9b所示为不加入前馈控制时三相并网电流波形,可以明显看出,三相电流出现不平衡,根据示波器计算,A相电流有效值为8.0A,B相电流有效值为9.86A,C相电流有效值为9.81A。图9 c所示为加入前馈控制后三相并网电流波形,根据示波器计算,A相电流有效值为9.21A,B相电流有效值为9.21A,C相电流有效值为9.17A,对其进行FFT分析,可得并网电流THD为3.79%,加入前馈控制后波形质量良好且三相基本平衡。
图9
图9
B相C相电压降低时三相电压电流实验波形
Fig.9
Experimental Waveforms of the three phase voltage and current with the voltage of BC-phase falling
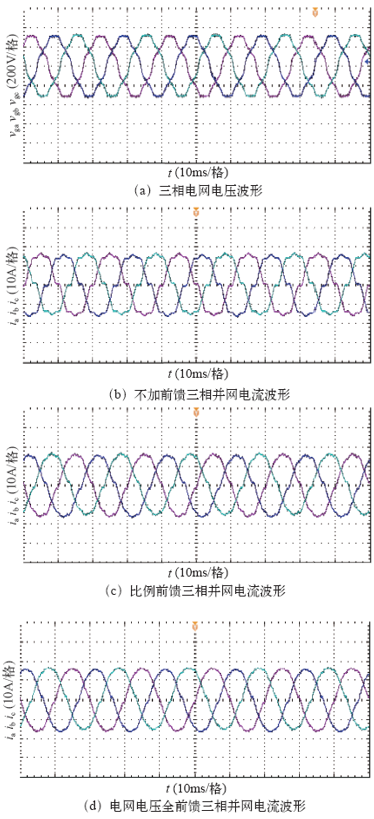
以三相功率7.5kW为例,考虑实际中电网常见谐波次数,三相电网电压中注入5次谐波含量5%,7次谐波含量5%,11次谐波含量2%,13次谐波含量2%,电网电压总谐波畸变率为7.62%。实验波形如图10所示。图10a所示为注入谐波之后的三相电网电压波形,电压畸变严重。图10b所示为采用单电流环PI控制不加入前馈时三相并网电流波形,三相电流明显发生畸变,对其进行FFT分析,可得并网电流总谐波畸变率达10.64%;图10c所示为加入电网电压比例前馈控制后三相并网电流波形,与不加入前馈控制时相比明显得到改善,此时并网电流THD为5.67%;图10d所示为加入电网电压全前馈控制后三相并网电流波形,波形得到进一步改善,质量较好,FFT分析得到并网电流THD为4.30%。
图10
图10
电网电压含谐波时实验波形
Fig.10
Experimental Waveforms of the voltage and current with harmonics in the grid voltage
5 结论
本文对基于电网电压前馈的三相并网逆变器电流控制方法进行了研究,获得以下成果:
(1)推导出三相LCL并网逆变器在同步旋转dq坐标系下逆变器数学模型。根据数学模型求解出并网电流表达式,分析了电网电压对并网电流的影响。
(2)为抑制并网电流不平衡与谐波分量,提出一种电网电压前馈控制,与电流环PI控制相结合,文中详细分析了电网电压前馈控制原理,得到前馈函数并对其进行了分析。
(3)搭建三相LCL并网逆变器实验平台,在电网电压不平衡和含谐波条件下进行实验,并网电流质量良好,验证了电网电压前馈控制的有效性。
参考文献
High-quality power generation through distributed control of a power park microgrid
[J].
IEEE Standard 1547
[S].
IEEE Standard 929
[S].
Improvement of grid-connected inverter systems with PR controllers under the unbalanced and distorted grid voltage
[C].
Full feedforward of grid voltage for grid-connected inverter with LCL filter to suppress current distortion due to grid voltage Harmonics
[J].