电气工程学报, 2015, 10(10): 15-20 doi:

理论研究

具有自适应学习的开环PD型迭代学习控制算法研究

郝晓弘, 周勃

兰州理工大学电气工程与信息工程学院 兰州 730050

Research on Open-Loop PD-Type Iterative Learning Control with Adaptive Learning

Hao Xiaohong, Zhou Bo

Lanzhou University of Technology Lanzhou 730050 China

责任编辑: 杨晓花

收稿日期: 2015-07-9   网络出版日期: 2015-10-25

基金资助: 国家自然科学基金资助项目.  61263008

Editor: Yang Xiaohua

Received: 2015-07-9   Online: 2015-10-25

作者简介 About authors

郝晓弘, 男 1960年生,教授,博士生导师,研究方向为复杂系统的控制、网络控制、智能控制理论与应用。

周勃, 男 1989年生,硕士研究生,研究方向为电力系统及其自动化、电能质量分析。

摘要

针对常见的PD型迭代学习控制算法收敛速度慢、收敛精度低的问题,提出了一种具有自适应学习的开环PD型迭代学习控制算法。该算法融合自适应学习和开环PD型学习律,采用自适应因子来优化学习率,通过数学方法证明了其收敛性,并通过仿真验证了算法的有效性。

关键词： 非线性系统 ; 迭代学习控制 ; PD型学习率 ; 自适应学习

Abstract

A kind of open-loop PD-type iterative learning control adaptive learning algorithm is put forward to against PD type iterative learning control algorithm convergence slow and low convergence accuracy problem in the paper. The algorithm integrates adaptive learning and open-loop PD-type learning law, the adaptive factor is used to optimize the learning rate and its convergence is proved through mathematic method. The simulation validates the validity of the algorithm.

Keywords： Nonlinear system ; iterative learning control ; PD type learning algorithm ; adaptive learning algorithm

PDF (3269KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

郝晓弘, 周勃. 具有自适应学习的开环PD型迭代学习控制算法研究. 电气工程学报[J], 2015, 10(10): 15-20 doi:

Hao Xiaohong. Research on Open-Loop PD-Type Iterative Learning Control with Adaptive Learning. Journal of Electrical Engineering[J], 2015, 10(10): 15-20 doi:

1 引言

迭代学习控制最先由日本学者Uchiyama提出,而Arimoto[1]在1990年提出了具体的学习算法,进一步推广了迭代学习控制的思想。迭代学习控制[2-3]适用于一类具备重复运行特性的被控目标, 其任务是寻找控制输入, 使得被控系统的实际输出轨迹在有限时间区间上沿整个期望输出轨迹实现误差为零的完全跟踪, 并且整个控制过程要求快速完成迭代学习及其适应性和有效性,因此得到了越来越多科研人员的重视。文献[4]讨论迭代初态与期望初态存在固定偏移情形下的迭代学习控制问题,并提出了带有反馈辅助项的PD型迭代学习控制算法;文献[5]提出了一类含控制时滞的非线性时变系统在任意初值下采用开环PD型迭代学习控制算法的收敛条件;文献[6]提出了一种带遗忘因子的PD型迭代学习控制算法;文献[7]提出了一种具有初态学习能力的闭环PD型控制算法,解决了闭环PD迭代学习的初态问题,并且放宽了收敛条件;文献[8]提出了一种采用RBF补偿的迭代学习控制方法;文献[9,10]将迭代学习控制理论与非线性时变系统相结合,提出了一种同时应用比例条件与微分作用的开闭环PD迭代学习控制律;文献[11,12]将迭代学习控制在其他方面的应用做了一定的总结。

本文研究针对一种具有重复运行特性的非线性系统,在任意初值条件下,采用具有自适应学习方式的开环PD型迭代学习律,并给出了该算法的收敛条件,证明了算法的收敛性。最后进行了仿真,验证了所得结论的可行性,并最终达到减小误差、加快系统收敛的目的。

2 问题描述

考虑如下形式的重复运行非线性系统

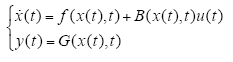
式中,时间变量t ∈ [0,T],状态向量x(t) ∈ Rn,输出向量yk(t) ∈ Rm,控制变量uk(t) ∈ Rr;f (x(t),t) : Rn× [0,T]→Rn;B(x(t),t) : Rn×[0,T]→Rn;G(x(t),t) : Rn×[0,T]→Rm;G(x(t),t) : Rn×[0,T]→Rm,关于x,t可微。

第k次运行时,系统的动态方程为

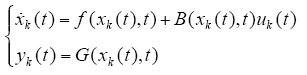
系统的输出误差为

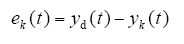
采用具有自适应学习的开环PD型迭代学习率

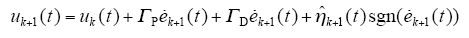
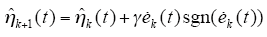
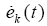
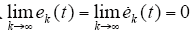
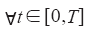
其中, 。如果ΓP、ΓD、γ均大于零,则ek(t)、 对于任意k ∈ R+都有界,且 , 。

初始状态学习律为

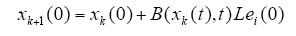
3 基本数学知识

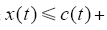
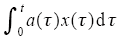
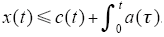
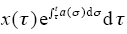
引理1[2] 设x(t)、c(t)、a(t)是[0,T]上的实值连续函数,且a(t) ∈ [0,T]在上非负,如果 ,其中,t ∈ [0,T],则 ,其中,t ∈ [0,T]。

引理2[3] 假定算子Q : Cr[0,T]→Cr[0,T]满足下列条件

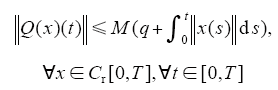
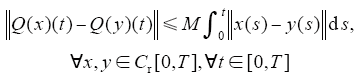
其中,M、q为非负常数,则有如下结论：

（1） y ∈ Cr[0,T],存在唯一的 x ∈ Cr[0,T],使得x(t) + Qx(t) = y(t),t ∈ [0,T]。

（2）定义算子Q : Cr[0,T]→Cr[0,T]为 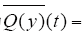Q(x)(t), y ∈ Cr[0,T]。

其中, x ∈ Cr[0,T]是由结论（1）定义的唯一解。则存在M1>0,使得。

引理3[3] 设常数序列{bk}k≥0(bk≥0),收敛到零算子Q : Cr[0,T]→Cr[0,T]满足

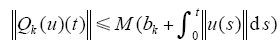
其中,M≥1为常数,Cr[0,T]的r维向量取最大值范数,设P(t)为r×r维连续函数矩阵,令

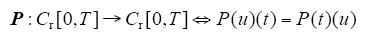
若P的谱半径小于1,则

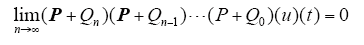
对于t一致成立。

4 收敛性证明

定理：对于式（1）描述的系统,在t ∈ [0,T]满足如下条件：

（1）f (t,x(t))关于x(t)满足Lipschitz条件,即对于x1(t),x2(t) ∈ R,t ∈ [0,T],存在Kf,使得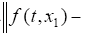

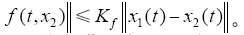
（2）期望轨迹yd在t ∈ [0,T]上连续。

（3）存在唯一理想的控制c,使得系统的状态和输出为期望值。

（4）G(t,x(t))关于x(t)的导数Gx(t,x(t))存在,G(t,x(t))关于x(t)满足全局一致Lipschitz条件,且g(t,x(t))有界。

（5）I + Gx(t,x(t))B(t)L(t)≤1,x(t) ∈ Rn,t ∈ [0,T],∀t ∈ [0,T],其逆矩阵必定存在。

设采用迭代学习律（4）所示的开环PD型迭代学习律,对于任意给定的初始控制u0(t),及每次运行的初始状态x0(t),由此得到的序列{xk(t)}k≥0,{yk(t)}k≥0,{uk(t)}k≥0对t一致收敛到xd(t)、yd(t)、ud(t)的充分条件为谱半径

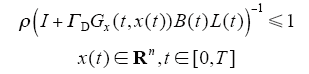
其必要条件为

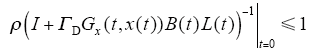
若ΓD、Gx(t,x(t))、B(t)为常数,则ρ(I + ΓDGx(t,x(t)) B(t)L(t)) - 1<1是系统收敛的充分必要条件,则当k→∞时,yk(t)一致收敛于yd(t)。

证明[13]：

设存在满足条件（1）~（5）的输入非线性系统,则

（1）充分性。不妨令

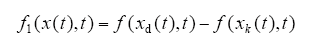
且设

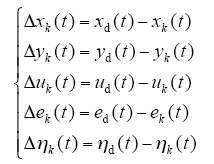
则由式（6）、学习律及输出误差可以得到

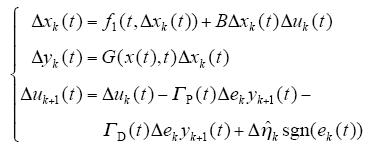
由式（7）,可得

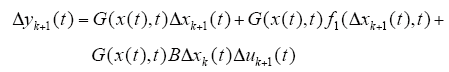
于是,由条件（4）、条件（5）有

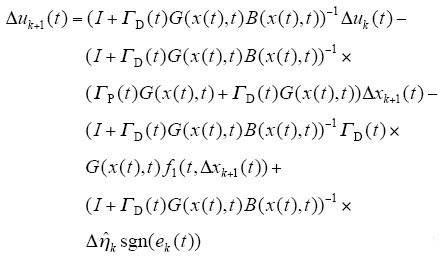
定义算子Q : Cr[0,T]→Cr[0,T]为

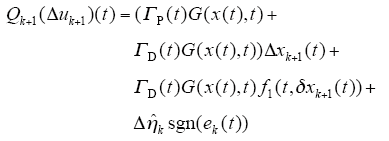
其中,Δxk为式（7）中第一个方程式当Δu(t)给定时的解。

由式（8）、式（9）可得

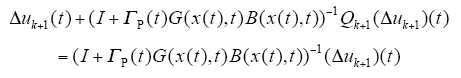
下面对Qk+1进行估计,若Δxk为式（9）当Δu(t)给定时的解,则

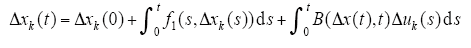
两边取范数,则

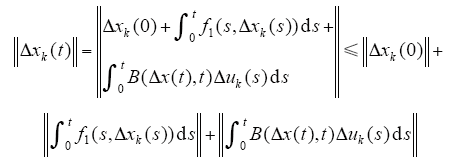
由已知条件和Bellman-Gronwell引理可知,存在K1,使得

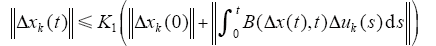
由已知条件和式（9）可知,存在常数K2≥1,使得

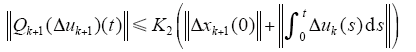
设w、v ∈ Cr[0,T],则

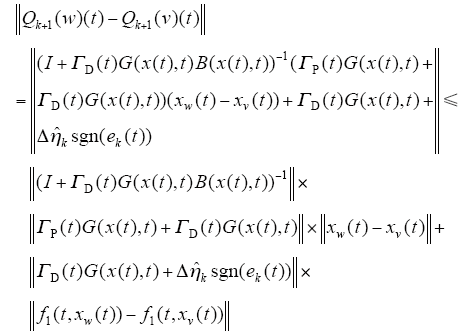
其中,Cr[0,T]分别为系统方程式（1）在初态控制取w、v时的解,故有

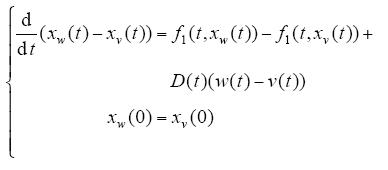
由上式可得

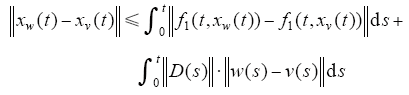
由已知条件及Bellman-Gronwell引理可知,存在K3>0,使得

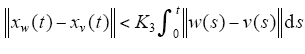
由式（12）、式（14）可知,存在K4>0,使得

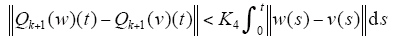
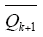
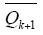
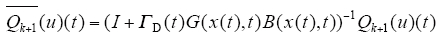
由式（11）、式（13）可知,Qk+1满足引理的两个条件,则存在算子 ,定义 = Cr[0,T]→ Cr[0,T]。

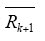
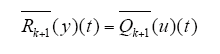
根据引理2,存在算子 = Cr[0,T]→Cr[0,T],使得

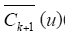
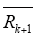
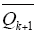
其中,u满足u(t) + (u)(t) = y(t),即存在算子 ,使得 (δuk + 1)(t)可用δuk + 1表示。

定义算子P : Cr[0,T]→Cr[0,T]为

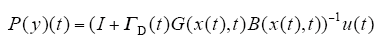
定义算子Rk + 1 = Cr[0,T]→Cr[0,T],使得

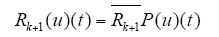
则由以上定义的算子可将式（10）写为

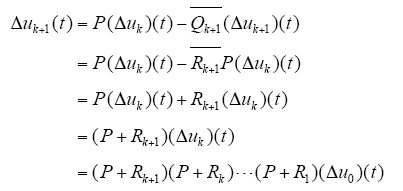
由引理2,可知存在常数Ks≥1,满足

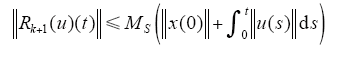
同理,有

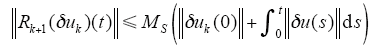
由式（16）~式（18）及引理1可知,若P的谱半径满足

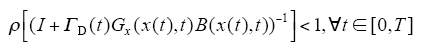
则δuk(t)→0对于一切t成立,由式（3）可知{uk(t)}k≥0

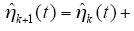
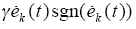
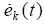
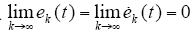
对t一致地收敛到ud(t)。根据式（3）、式（6）、式（7）及Bellman-Gronwell引理,有 ,ΓP、ΓD、γ均大于零,则ek(t)、 对于任意k ∈ R+都有界,且 ,∀t ∈ [0,T],则可知{xk(t)}k≥0、{yk(t)}k≥0对t一致地收敛到xd(t)、yd(t),则充分性证明完毕。

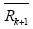
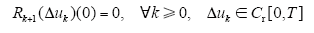
（2）必要性。取Δxk+1(0) = 0,∀k≥0,由式（12）、式（13）及算子Rk+1、 的定义得

故由上式和式（17）可得

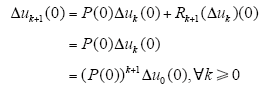
ρ[(I + ΓD(t)G(x(t),t)) - 1]≥1, 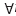t ∈ [0,T],则存在δu0(0) ≠ 0,δuk+1 = (P(0))k+1δu0(0)不趋于0,故只有当ρ[(I + ΓD(t)G(x(t),t)) - 1]<1,δuk+1(0)→0。必要性证明完毕。

5 仿真实例

考虑以下非线性系统

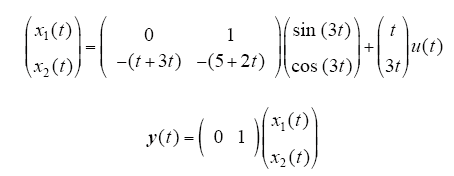
采用式（4）的开环PD型学习律,学习增益矩阵为

仿真结果如图1、图2所示。

图1

新窗口打开| 下载原图ZIP| 生成PPT

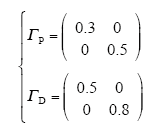
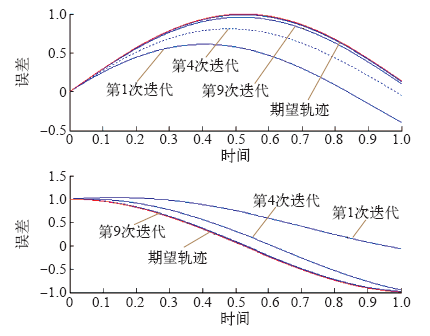
图1   开环PD型实际输出结果与期望轨迹

Fig.1   The actual output and desired trajectory curve of the open-loop PD type iterative learning control algorithmwith adaptive learning


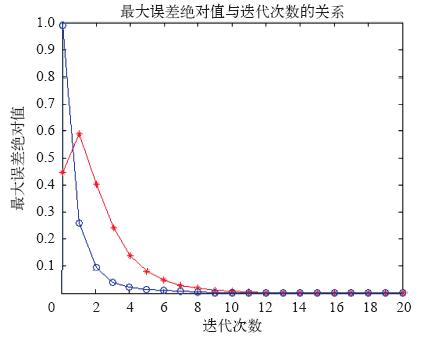
图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   开环PD型学习率跟踪轨迹误差

Fig.2   The maximum absolute error of the open-loop PD type iterative learning control algorithm with adaptive learning


图1所示为系统在学习控制律（4）的作用下,第1、4、9次的实际输出与期望输出之间的关系。图2所示为开环PD型学习率跟踪轨迹误差曲线。由图2可知,在控制系统经过9次迭代后,就能很好地跟踪期望轨迹,并且达到了较高的跟踪进度,控制系统的收敛速度比较快。

仿真结果表明,对于非线性系统,采用带自适应的开环PD型迭代学习控制方法,经过9级学习后就能够很好地跟踪期望轨迹。

6 结束语

在迭代学习控制理论研究中,一般的PD方法收敛速度已不再满足人们的要求。针对常见的非线性控制系统,本文提出了一种具有自适应学习的开环PD型迭代学习控制算法研究,提出了具有自适应控制的PD型迭代学习控制律,达到了减小收敛误差、提高系统收敛速度的目的。最后应用仿真实例,表明了方法的有效性。

参考文献

Arimoto S .

Learning control theory for robotic motion

[J]. International Journal of Adaptive Control and Signal Processing, 1990,4(6):543-564.

DOI:10.1177/2055668318793585      URL     PMID:31191950      [本文引用: 2]

The objective of this article is to introduce the robotic platform KIINCE and its emphasis on the potential of kinetic objectives for studying and training human walking and standing. The device is motivated by the need to characterize and train lower limb muscle coordination to address balance deficits in impaired walking and standing.

孙明轩, 黄宝建 . 迭代学习控制[M]. 北京: 国防工业出版社, 1999.

[本文引用: 3]

林辉, 王林 . 迭代学习控制理论[M]. 西安: 西北工业大学出版社, 1998.

[本文引用: 4]

孙明轩 .

反馈辅助PD型迭代学习控制:初值问题及修正策略

[J]. 自动化学报, 2015,41(1):157-164.

DOI:10.16383/j.aas.2015.c140133      URL     [本文引用: 2]

This paper addresses the problem of iterative learning control for systems in the presence of a fixed initial shift. A feedback-aided PD-type learning algorithm is proposed, and the convergence analysis indicates that such a learning algorithm can ensure that the tracking error achieves asymptotic convergence with respect to time, as the iteration approaches infinity. Furthermore, the initial rectifying and terminal converging strategies are adopted respectively to form learning algorithms for eliminating the effect of the fixed initial shift. It is shown that the system output converges to the desired trajectory over a pre-specified time interval no matter what value the fixed initial shift takes. Numerical results are presented to demonstrate the effectiveness of the proposed learning algorithms.

Sun Mingxuan, Bi Hongbo, Zhou Guoliang , et al.

Feedback-aided PD-type iterative learning control: initial condition problem and rectifying strategies

[J]. ACTA AUTOMATICA SINICA, 2015,41(1):157-164.

DOI:10.16383/j.aas.2015.c140133      URL     [本文引用: 2]

This paper addresses the problem of iterative learning control for systems in the presence of a fixed initial shift. A feedback-aided PD-type learning algorithm is proposed, and the convergence analysis indicates that such a learning algorithm can ensure that the tracking error achieves asymptotic convergence with respect to time, as the iteration approaches infinity. Furthermore, the initial rectifying and terminal converging strategies are adopted respectively to form learning algorithms for eliminating the effect of the fixed initial shift. It is shown that the system output converges to the desired trajectory over a pre-specified time interval no matter what value the fixed initial shift takes. Numerical results are presented to demonstrate the effectiveness of the proposed learning algorithms.

孙瑜, 李志安 .

一类含控制时滞非线性系统在任意初值下的开环PD型迭代学习控制

[J]. 测控技术, 2009,28(8):51-57.

[本文引用: 1]

Sun Yu, Li Zhian .

Open-loop PD-type iterative learning control for a class of nonlinear systems with control delay and arbitrary initial value

[J]. Measurement and Control Technology, 2009,28(5):51-57.

[本文引用: 1]

杨红 .

带遗忘因子的PD型迭代学习控制算法研究

[J]. 暨南大学学报(自然科学版), 2013,34(1):27-30.

[本文引用: 2]

Yang Hong .

PD-type iterative learning control algorithm research with forgetting factor

[J]. Journal of Jinan University (Natural Science, 2013,34(1):27-30.

[本文引用: 2]

曹伟, 戴学丰 .

具有初态学习的闭环PD型迭代学习控制

[J]. 武汉理工大学学报, 2010,32(2):98-102.

[本文引用: 2]

Cao Wei, Dai Xuefeng .

Closed-loop PD-type iterative learning control with initial state learning

[J]. Journal of Wuhan University of Technology, 2010,32(2):98-102.

[本文引用: 2]

武瑞兵 .

采用RBF网络补偿的直线电动机迭代学习控制

[J]. 电气应用, 2015,34(8):57-59.

[本文引用: 2]

Wu Ruibing .

A linear motor iterative learning control based on RBF network compensation

[J]. Electric Control, 2015,34(8):57-59.

[本文引用: 2]

杨晓峰, 樊晓平, 杨胜跃 , 等.

非线性系统开闭环PD型迭代学习控制及其在机器人中的应用

[J]. 长沙铁道学院学报, 2002,20(1):78-84.

[本文引用: 2]

Yang Xiaofeng, Fan Xiaoping, Yang Shengyue , et al.

Open-closed loop PD-type iterative learning control for nonlinear system and its application in robot

[J]. Journal of Changsha Railway University, 2002,20(1):78-84.

[本文引用: 2]

Feng Z F, Zhang Z J, Pi D Y.

Open-closed-loop PD-type iterative learning controller for nonlinear controller for nonlinear systems and its convergence

[C]. Congress on Intelligent Control and Automation, 2004: 1241-1245.

[本文引用: 2]

吴敬兵, 罗安 , 等.

混合有源电力滤波器的新型电流迭代学习控制

[J]. 电工技术学报, 2012,27(8):133-140.

URL     [本文引用: 2]

混合有源电力滤波器可以动态抑制电网谐波电流和补偿容性无功功率, 改善电网电能质量。针对传统PI型迭代学习控制算法在并联有源电力滤波器应用中的不足, 算法收敛性严重依赖于学习控制的初始输入, 迭代学习控制器的参数是定常值, 会影响有源滤波系统的控制性能。本文提出一种新型PI迭代学习控制算法, 将其应用于混合有源电力滤波器系统的电流反馈控制中, 得到了应用迭代算法的收敛性条件, 并采用一种改进的Ziegler-Nichols方法对控制器参数进行了优化, 以提高系统的控制精度。为了提高系统的动态响应性能, 提出一种谐波电流误差的反馈-前馈控制策略, 其中电流误差信号的D型前馈控制环节用于实现滤波器系统的电流快速补偿, 同时利用一个三层BP神经网络对前馈控制增益进行优化。仿真和实验结果证明了该迭代算法及控制策略的可行性与有效性。

Wu Jingbing, Luo An , et al.

A novel iterative learning control for current tracking of hybrid active power filter

[J]. Transaction of China Electrotechnical Society, 2012,27(8):133-140.

URL     [本文引用: 2]

混合有源电力滤波器可以动态抑制电网谐波电流和补偿容性无功功率, 改善电网电能质量。针对传统PI型迭代学习控制算法在并联有源电力滤波器应用中的不足, 算法收敛性严重依赖于学习控制的初始输入, 迭代学习控制器的参数是定常值, 会影响有源滤波系统的控制性能。本文提出一种新型PI迭代学习控制算法, 将其应用于混合有源电力滤波器系统的电流反馈控制中, 得到了应用迭代算法的收敛性条件, 并采用一种改进的Ziegler-Nichols方法对控制器参数进行了优化, 以提高系统的控制精度。为了提高系统的动态响应性能, 提出一种谐波电流误差的反馈-前馈控制策略, 其中电流误差信号的D型前馈控制环节用于实现滤波器系统的电流快速补偿, 同时利用一个三层BP神经网络对前馈控制增益进行优化。仿真和实验结果证明了该迭代算法及控制策略的可行性与有效性。

杨俊友, 刘永恒 .

基于迭代学习与小波滤波器的永磁直线伺服系统扰动抑制

[J]. 电工技术学报, 2013,28(3):87-92.

URL     [本文引用: 1]

针对迭代学习控制(ILC)算法抑制永磁直线同步电机(PMLSM)周期性扰动时存在非周期分量影响问题, 提出一种迭代学习控制算法与小波滤波器相结合的扰动抑制方法。通过重构输入误差信号, 剔除非周期分量, 从而使设计的PMLSM伺服系统迭代学习控制器快速收敛, 减少了迭代次数。提出通过实验确定ILC中L形滤波器参数的方法。实验结果表明, 与不带小波滤波器及传统PID比较, 所提出的控制方法能够使系统的跟踪效果更好, 且保证了在较少迭代次数下, 被控系统的输出轨迹能精确地收敛到期望轨迹。

Yang Junyou, Liu Yongheng .

Disturbance rejection for PMLSM based on iterative learning control and wavelet filter

[J]. Transaction of China Electrotechnical Society, 2013,28(3):87-92.

URL     [本文引用: 1]

针对迭代学习控制(ILC)算法抑制永磁直线同步电机(PMLSM)周期性扰动时存在非周期分量影响问题, 提出一种迭代学习控制算法与小波滤波器相结合的扰动抑制方法。通过重构输入误差信号, 剔除非周期分量, 从而使设计的PMLSM伺服系统迭代学习控制器快速收敛, 减少了迭代次数。提出通过实验确定ILC中L形滤波器参数的方法。实验结果表明, 与不带小波滤波器及传统PID比较, 所提出的控制方法能够使系统的跟踪效果更好, 且保证了在较少迭代次数下, 被控系统的输出轨迹能精确地收敛到期望轨迹。

惠阿丽, 郑建明, 孙瑜 .

非线性系统闭环PD型迭代学习收敛性分析

[J]. 广东工业大学学报, 2006,23(2):42-47.

Hui Ali, Zhen Jianming, Sun Yu .

A closed-loop PD-type iterative learning control scheme for nonlinear systems and its convergence

[J]. Journal of Guangdong University of Technology, 2006,23(2):42-47.