近年来铁路行业发展迅速，已成为主要能耗阵地。随着“双碳”目标的提出，可再生能源的发展持续向好。为减少碳排放，在电气化铁路牵引领域引入新能源成为推动铁路低碳绿色发展的迫切需要。

电气化列车在运行中，除了从牵引网大量用能外，还会产生大量再生制动能量，目前从牵引变电站返送回电网的再生制动能量是返送正计或返送不计费的^[1]，因此提高再生制动能量的利用率有助于降低列车的用能成本。目前针对再生制动能量回收利用最有效的方法就是加入储能装置^[2-3]。考虑列车再生制动能量同时具有功率大和能量大的特点，本文采用由全钒氧化还原液流电池(钒电池)和超级电容组成的混合储能系统来参与列车的调度运行。混合储能的接入既能回收列车再生制动能量，又能用于平衡系统内的源-车功率供需不平衡，从而促进新能源的消纳^[4]。

关于含新能源的牵引供电系统优化运行研究，文献[5-6]开展含光伏的牵引供电混合储能系统的容量规划研究，论证了光伏和储能在铁路行业中的潜力和适用性。文献[7]提出计及光伏和储能接入的牵引供电系统能量管理策略，采用日前联合调控、日内滚动调节的方式优化控制铁路用能，有效降低系统运行成本。文献[8-9]以含光伏混合储能系统的牵引变电站日运行成本最低为目标，建立了计及系统电能质量指标的日前能量优化与调度模型，通过CPLEX求解器进行求解，验证了所提模型的有效性。文献[10]建立包括风电、光伏、混合储能在内的铁路系统运行调度模型，以系统的运营成本最小为目标，使用差分进化算法进行求解，得到新能源和储能的最优出力情况。上述研究仅考虑高铁系统的运行成本，未考虑新能源储能系统给高铁系统带来的收益问题，也没有考虑高铁系统参与碳排放交易所获得的收益，其投资参考价值不太符合未来中国低碳发展进程。此外上述研究仅采用常规的确定性优化方法进行求解，得到的高铁系统优化运行方案取决于新能源预测的精度，未考虑新能源的不确定性对系统调度运行的影响。

综上，本文提出一种高铁新能源混合储能系统低碳经济优化运行模型。随着中国碳排放权交易市场的建立，高铁系统引入新能源混合储能系统可以通过碳排放交易获得收益，该模型在求解混合储能系统接入最优容量时，将碳收益纳入其中，采用拉丁超立方机会约束规划法来处理新能源的不确定性，并提出一种混合储能系统能量管理策略，以钒电池停止充放电阈值与储能容量配置参数为优化变量，以新能源混合储能系统全寿命周期内为高铁系统带来的总净收益最大为优化目标，采用基于柯西变异的自适应粒子群算法对模型进行求解，通过分析与对比，验证所提方案和算法的有效性和优越性。

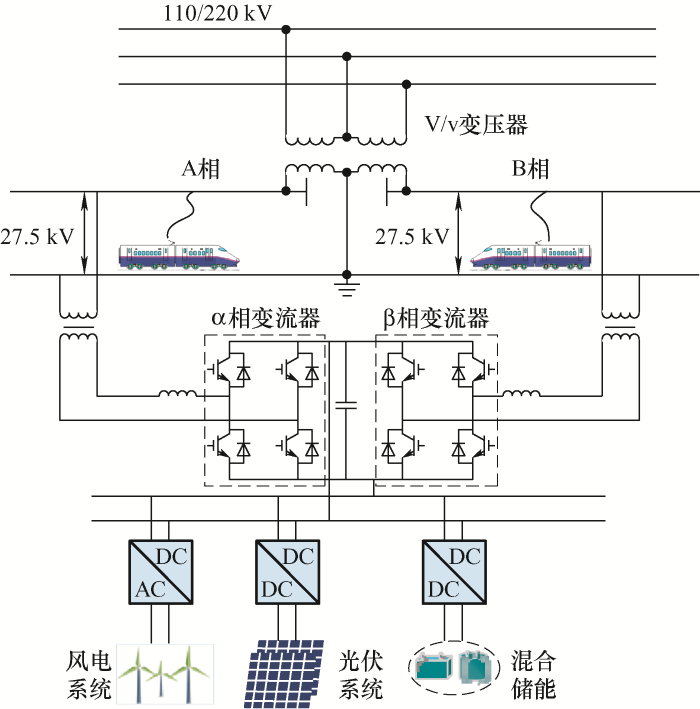
本文将涵盖风电、光伏、混合储能系统的分布式互补能源系统接入高铁牵引供电系统^[4,11]，如图1所示。系统通过V/v牵引变压器将110/220 kV三相交流电转变为27.5 kV单相交流电，为列车提供电能。新能源和混合储能系统通过相应变流器接入两相供电臂的背靠背变流器的直流母线侧，可同时向两侧母线供电，混合储能系统既能回收列车再生制动能量和新能源发电系统的多余能量，也能将自身存储的能量释放出来用于供给列车牵引负荷。

相比于一般能源，新能源具有明显的随机性、不确定性等特征。故对新能源的出力进行随机模拟，其过程如下所示

式中，P_wt(t)、P_pv(t)为t时刻风电、光伏的实际功率；wt(t)、pv(t)为风电、光伏的预测功率；u_wt、u_pv为风电、光伏的预测误差。

根据现有的新能源预测技术^[12]和中心极限定理可知，新能源的预测误差服从如下正态分布

式中，V_wt、V_pv为风电、光伏系统的装机容量；正态分布的均值μ=0，σ_wt、σ_pv为正态分布的标准差。

风电、光伏实际功率应满足出力约束为

钒电池和超级电容从开始时刻到t时刻累计的充放电电量为

则钒电池和超级电容在t时刻的荷电状态 (State of charge, SOC)为

式中，SOC_ba(0)是钒电池开始时刻的SOC；SOC_sc(0)是超级电容开始时刻的SOC；T为系统运行周期；E_ba和E_sc分别为钒电池和超级电容的额定容量；X_ba和Y_ba是钒电池的充放电状态；X_sc和Y_sc是超级电容的充放电状态；P_bach和P_badis是钒电池的充放电功率；P_scch和P_scdis是超级电容的充放电功率；η_ba、η_sc是钒电池和超级电容的充放电效率。

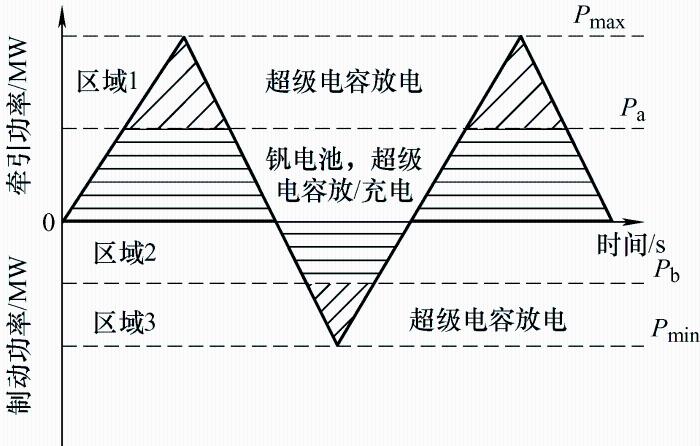
当新能源发电功率大于牵引负荷时，利用储能装置回收未消纳的新能源发电量和列车再生制动能量，所使用的储能装置进入充电阶段；当新能源功率小于牵引负荷时，除了列车从外部电网购电，储能设备也将回收的能量释放出来，以减少列车用电成本并降低碳排放，此时储能装置进入放电阶段。为充分发挥两种储能各自的优势，本文采用基于钒电池停止充放电阈值的能量管理策略，可根据牵引变电站负荷和新能源实际功率之差来确定钒电池的停止充放电阈值。图2为牵引负荷与新能源实际功率差值示意图。图2中P_max和P_min分别为牵引负荷与新能源实际功率差值的最大与最小值，即

式中，P_load(t)为t时段高铁牵引变电站负荷功率，当其大于零时表示列车牵引用电，小于零则表示列车产生的再生制动能量。

P_a和P_b为钒电池的停止放电和充电阈值，将图2分为3个区域。区域1和3为峰谷区间，此部分功率较大，考虑钒电池为能量型储能^[13]，很难快速跟踪到功率较大区域，故此部分完全由超级电容进行响应，发挥其大功率、充放电速率快、循环寿命长的优势；区域2为功率较小部分，借助钒电池大容量的特点让其优先工作，同时由超级电容进行功率补充，以此减少电池的循环次数，延长使用寿命。

以新能源混合储能系统全寿命周期内为高铁系统带来的总净收益最大为优化目标，目标函数为

式中，I_i为高铁系统第i项收益；C_j为第j项成本。

(1) 电度电费收益

式中，Y为新能源储能系统全寿命周期；r为折现率；c_e为电度电价；ΔE_s为高铁接入新能源储能系统后每天节省的电能。

(2) 基本电费收益

式中，c_o为基本电价；ΔE_max为新能源混合储能系统为牵引负荷带来的最大功率削减量。基本电费按牵引变压器容量计算收费，因为牵引变压器容量与牵引负荷最大功率需量成正相关，故本文按牵引负荷最大功率需量方式计算基本电费。

(3) 回收残值收益

式中，C₁为混合储能系统初始投资成本；σ为回收残值率，一般取3%~5%，本文取4%。新能源储能系统在寿命终期可通过回收利用产生收益。

(4) 碳收益。为响应双碳目标，考虑将碳收益纳入到高铁系统优化运行模型中，进一步调动铁路行业的减碳积极性。高铁系统购电时，上级电网的电能主要由火力发电产生，故会产生一定量的碳排放。考虑将铁路行业参与碳交易市场，碳交易机制会根据历史铁路牵引负荷为铁路公司分配碳排放配额，在国内，目前有两种主要的碳交易配额分配方法，一种是历史法，另一种是基准线法。本文采用基准线法来分配碳排放额。当高铁加入新能源储能系统后，会有效降低列车购电量，从而降低系统产生的碳排放量，此时可将节省的碳排放配额在碳交易市场中进行交易，产生碳收益。通过这种碳排放交易机制，企业可以控制碳排放并获得经济激励，从而促进清洁能源的发展。新能源储能系统全寿命周期内为高铁系统带来的碳收益为

式中，a为高铁系统从上级电网购电的单位电量碳排放配额，它取决于上级电网的基准线排放因子；δ为碳交易价格。

(5) 初始投资成本

式中，c_bw和c_sw为钒电池和超级电容单位功率成本；W_ba和W_sc为钒电池和超级电容的额定功率；c_be和c_se为钒电池和超级电容单位容量成本；E_ba和E_sc为钒电池和超级电容的额定容量；c_wt和c_pv为风电和光伏单位容量投资成本。

(6) 运维成本

式中，c_beo和c_seo为钒电池和超级电容单位容量运维成本；c_bwo和c_swo为钒电池和超级电容每年单位功率运维成本；c_wto和c_pvo为风电和光伏运维成本系数；E_B和E_P为钒电池和超级电容一天的总充放电电量；E_wt和E_pv为每日风电和光伏发电的总电量。

(7) 储能替换成本

式中，q_ba和q_sc分别为钒电池和超级电容的替换次数；c_ber和c_ser为钒电池和超级电容单位容量替换成本。当储能系统达到循环寿命次数需要更换时，一般只需更换内部电池，其他设备不更换。

(8) 报废处置成本

式中，c_bwp为钒电池单位功率报废成本；c_bep为钒电池单位容量报废成本；c_swp为超级电容单位功率报废成本；c_sep为超级电容单位容量报废成本。

为了计算全寿命周期内两种类型储能的替换次数，可通过储能的实际充放电电量与额定容量的比值来得出^[14]。储能系统日等效循环次数L₁、L₂为

式中，L_ba和L_sc为两者的循环使用寿命。

(1) 功率平衡约束

(2) 钒电池约束

式中，SOCmax ba和SOCmin ba为钒电池荷电状态的上下界；考虑到钒电池不会同时处在充电或放电阶段，因此增加了充放电状态约束；同时为避免钒电池过充或过放，还增加了充放电功率约束与SOC约束。

钒电池的额定功率应满足停止充放电阈值的最大值，考虑钒电池的充放电效率可得

根据储能系统的数学模型及SOC约束可得钒电池的额定容量约束范围为

当式(27)取等号且SOC_ba(0)取式(28)时，此时配置的钒电池额定容量最小。

(3) 超级电容器约束。与钒电池类似，超级电容也具有SOC、充放电状态、充放电功率约束如下

超级电容的额定功率应满足牵引负荷与新能源实际功率差值的最大值，可得

根据储能系统的数学模型及SOC约束可得超级电容的额定容量约束范围为

(4) 钒电池停止充放电阈值约束

机会约束规划法^[15]能很好地处理含有随机变量的问题，是以概率的形式满足约束条件，允许系统运行结果在一定程度上不满足约束条件，但约束条件成立的概率不小于预设的置信率。一般机会约束规划模型为

式中，x为决策向量；ξ为随机向量；f为目标函数；Pr为约束条件成立的概率；α为置信率。

本文采用拉丁超立方随机机会约束规划法来解决新能源的不确定性对高铁系统优化运行的影响。首先采用式(1)~(7)对新能源出力进行随机模拟，并采用拉丁超立方采样方法对新能源预测误差进行随机分层抽样得到新能源实际出力。由于新能源出力具有随机性，故式(23)的功率平衡将不再适用。基于上述方法将含随机变量的功率平衡约束进行一定次数的随机模拟，使模拟出的结果在一定的置信率下成立。可得机会约束规划模型为

本文采用基于柯西变异的自适应粒子群算法对上述模型进行求解。关于对常规粒子群算法(Particle swarm optimization, PSO)的介绍，文献[16]已做详述，本文不再赘述。假设粒子种群数为N，维度j=1,2,···,d，则第i个粒子在j维的初始位置和速度为

整个粒子群的速度和位置更新公式为

式中，ω为惯性权重因子，其大小影响粒子的搜索能力；c₁、c₂为学习因子，其大小分别影响粒子的自我学习能力和社会学习能力；r₁、r₂为服从U(0,1)的随机数；pk ij为粒子个体在j维下的最优值；pk gj为群体在j维下的最优值；k为迭代次数。考虑到常规粒子群算法存在收敛速度慢、求解精度不高、搜索范围不广、易陷入局部最优的缺陷，故从两个方面进行改进以提高其优越性。

首先，该算法的ω和c₁, c₂一般为某一固定值，这就限制了算法的遍历性，易陷入局部最优，因此进行以下改进使其可以自适应调整搜索范围，提高其求解精度。

式中，ω_max、ω_min为ω的上下限；τ的取值由经验决定，一般τ在20~55取值；c_1max、c_1min为c₁的上下限；c_2max、c_2min为c₂的上下限；k_max为算法总迭代次数。迭代前期，ω较大且c₁较大，c₂较小，使粒子自我学习能力较强，社会学习能力较弱，有利于增强粒子前期的全局搜索能力，防止出现早熟收敛问题。随着迭代次数的增加，ω、c₁逐渐减小，c₂逐渐增大，粒子局部搜索能力逐渐增强，便于算法的收敛。

此外考虑引入变异策略，许多学者在粒子群算法中引入不同的变异算子以提高其运算性能，引入的变异算子主要包括高斯变异和柯西变异。已知柯西分布比正态分布变异尺度更大^[17]，故在式(37)中，考虑引入柯西变异作为控制变异步长的参数以此增加种群的多样性，提高算法的搜索精度。柯西分布的概率密度函数为

式中，γ为尺度参数；x₀为位置参数；当x₀=0，γ=1时，式(40)变为标准柯西分布，记为C(0,1)。由于柯西分布在峰值处分布较小，在两侧分布较长，故粒子群在变异后可以在较短时间内跳出局部最优位置，搜索其他邻域区间。因此可将式(37)更新为

式中，φ为柯西变异强度，本文取0.8。

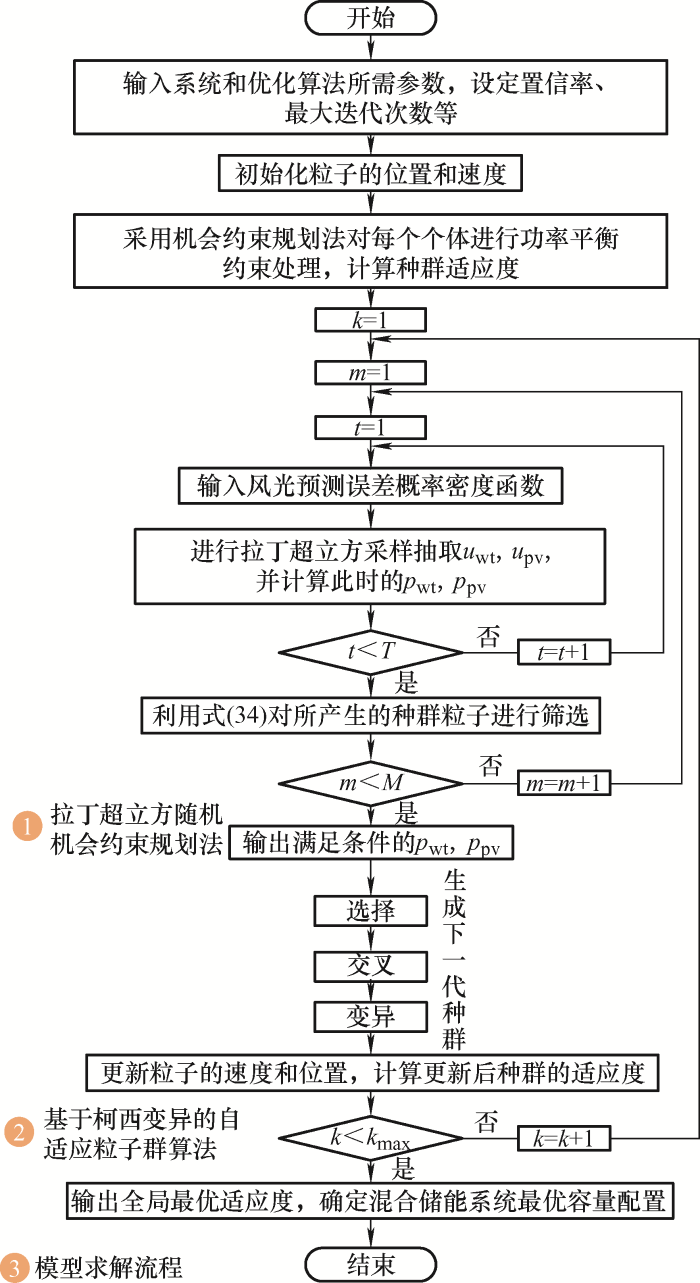
本文将拉丁超立方机会约束规划法与基于柯西变异的自适应粒子群算法相结合来求解高铁新能源混合储能系统优化运行模型。过程如图3所示。

首先采用式(1)~(7)进行新能源出力的随机模拟，然后进行拉丁超立方采样得到高铁系统一天的新能源出力值，此时记为一次随机模拟。设置随机模拟次数m=1,2,…,M，利用式(34)对所产生的粒子进行筛选，使种群在随机模拟M次过程中，粒子的功率平衡约束条件成立的概率不小于预设的置信率，计算种群最优适应度，即新能源混合储能系统全寿命周期内为高铁系统带来的净收益，继续对粒子进行选择、交叉、变异，生成新的种群，计算新的适应度函数，直至达到最大迭代次数，输出全局最优适应度，并确定混合储能系统最优容量配置。

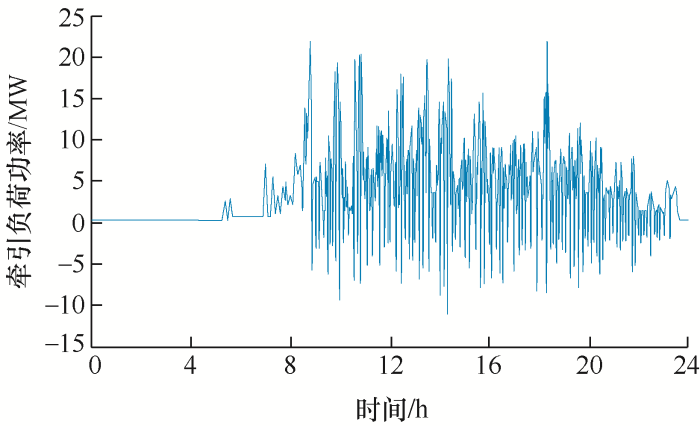
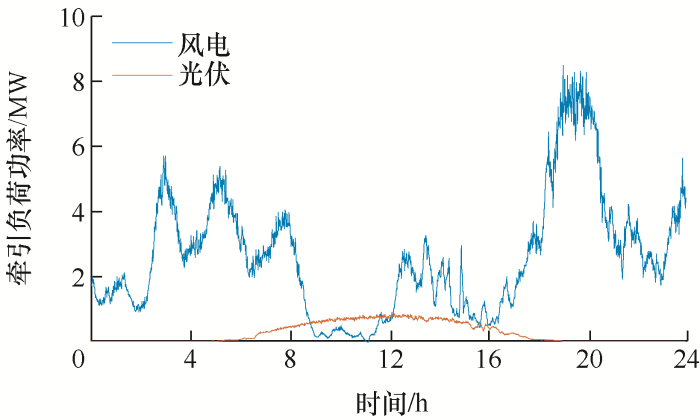
本文以国内某高铁牵引变电站为例，对高铁系统中新能源混合储能系统接入后经济性运行进行优化研究。牵引变电站日负荷实测曲线如图4所示。考虑在牵引变电站及其附近安装风电和光伏发电系统，其装机容量分别为10 MW和1 MW，风电和光伏典型日出力预测曲线如图5所示。各曲线中的单位采样时间为1 min，总时长为1天。

高铁向配电网购电电费执行两部制电价，分为电度电费和基本电费。高铁系统接入的新能源储能系统全寿命周期为20年，折现率为8%。碳交易价格为50元/t，电网的基准线排放因子^[18]为0.482 kg/(kW·h)。置信率α=95%，ω_max、ω_min分别设置为0.9和0.4，c_1max、c_1min分别设置为2.5和0.5，c_2max、c_2min分别为2.5和0.5，算法最大迭代次数k_max为1 500次，随机模拟次数M取1 000次。所建立模型中使用的储能设备及其他设备的各项参数^[19⇓-21]如表1、表2所示。

本文对以下两种方案进行研究分析：方案一：高铁系统仅采用混合储能系统；方案二：高铁系统采用新能源混合储能系统。其仿真结果如表3所示。

由表3可知，高铁系统仅采用混合储能系统产生了碳收益，混合储能可以回收列车的再生制动能量来削减牵引负荷峰值，从而减少列车购电量，降低碳排放量，由此产生碳收益和电度电费收益。通过对牵引负荷峰值的削减，降低了牵引变压器容量，产生基本电费收益。由于混合储能系统全寿命周期成本大于其对高铁产生的收益，故总净收益为负。考虑将新能源混合储能系统接入牵引供电系统来参与列车优化运行，对比仅采用混合储能系统场景，所产生的碳收益、电度电费收益和基本电费收益都大幅度增加，可知高铁系统加入新能源混合储能系统，可更有效削减牵引负荷峰值，降低碳排放。全寿命周期下新能源混合储能系统成本远小于其对高铁系统产生的经济收益，明显增加系统总净收益。

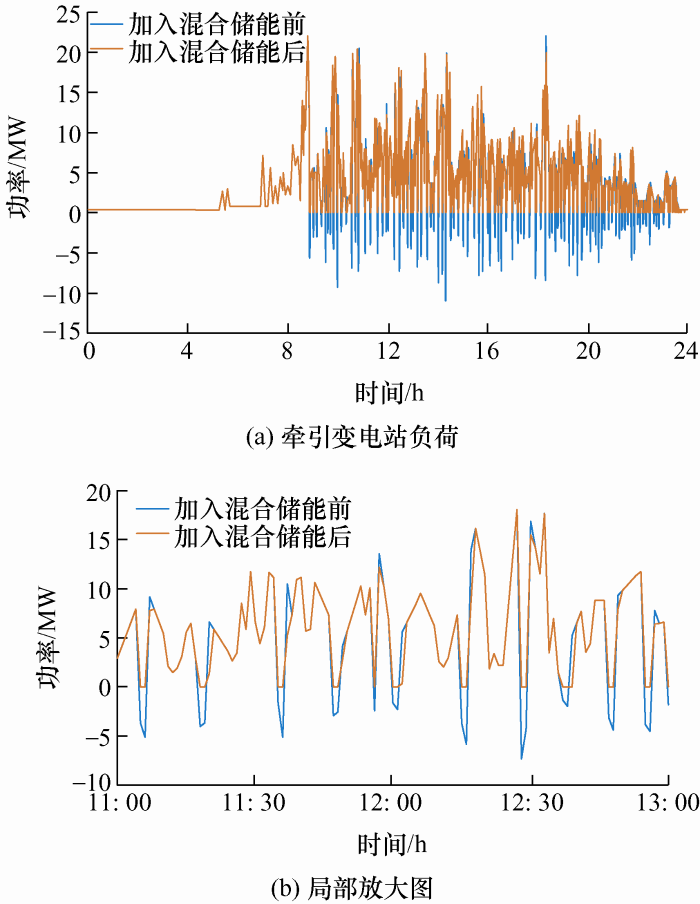
图6为高铁系统加入混合储能前后牵引负荷的日变化情况，为了便于分析，将其中11：00—13：00的曲线部分进行放大。从图6可以看出，由于混合储能的作用，高铁的再生制动能量得到有效回收，同时实现对牵引负荷峰值的削减，起到了“削峰填谷”的作用。

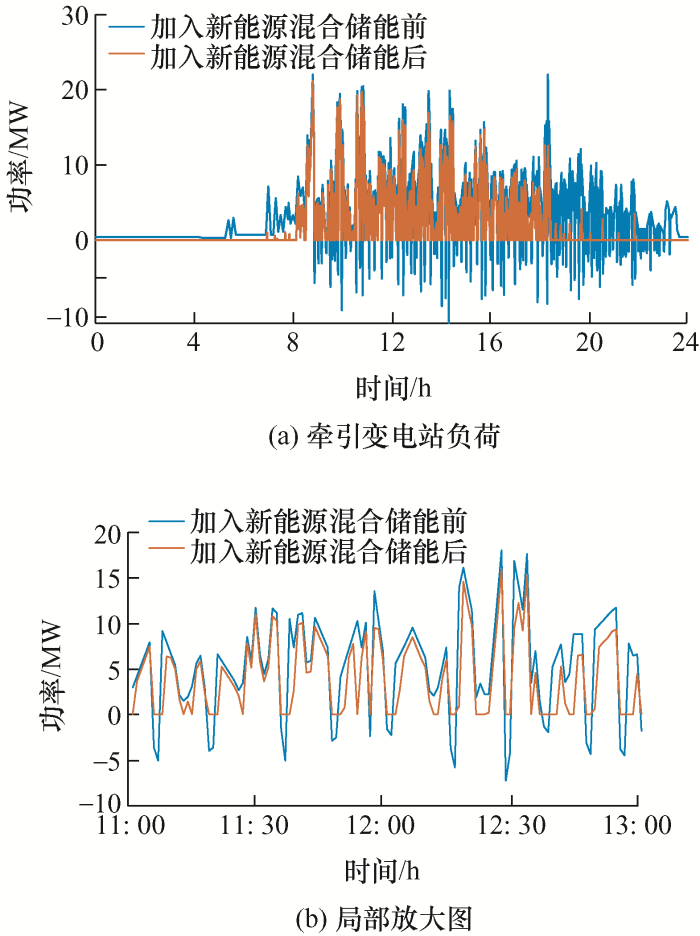
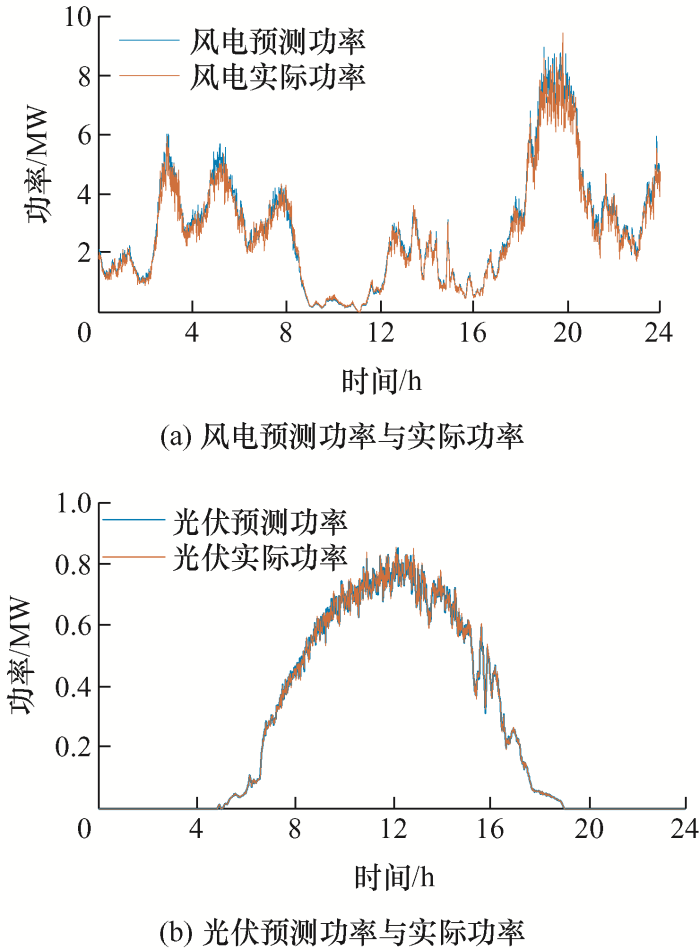
图7为高铁系统加入新能源混合储能系统前后牵引负荷的日变化情况。由图7可知，由于新能源系统的加入，列车牵引负荷削减效果显著提升，且在19：00—24：00列车牵引用电主要来自新能源混合储能系统，大大降低了列车购电量和牵引变压器容量，有效减少碳排放量。图8为新能源混合储能系统在全寿命周期内为高铁系统带来的总净收益最大时，风电、光伏一天的实际功率与预测功率情况。

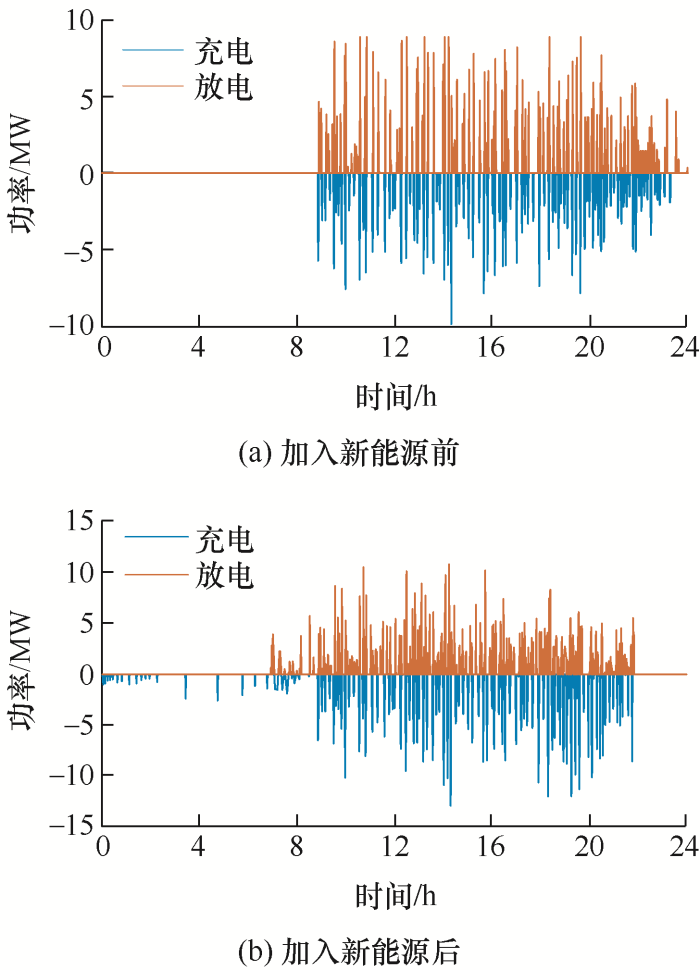
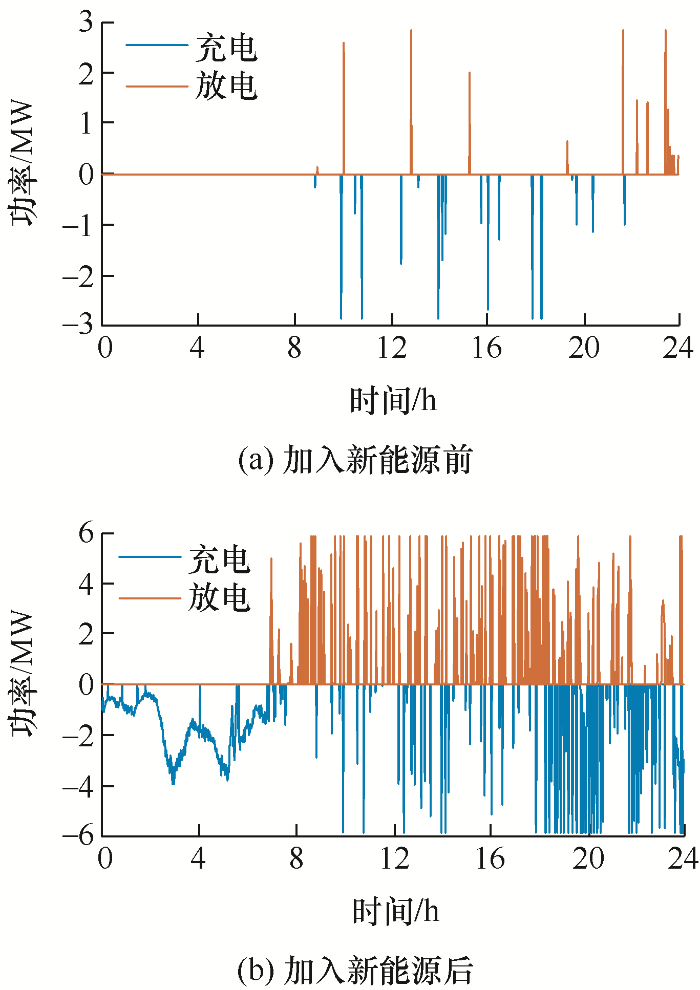
图9、10分别为高铁系统加入新能源前后超级电容和钒电池的日充放电功率。加入新能源后两者的充放电频率明显高于加入前，这是因为储能装置不仅要回收高铁的再生制动能量，还要储存未消纳的新能源发电量，当列车牵引运行时，储能装置再将储存的能量释放出来，且相比于钒电池，超级电容的充放电功率较大，充放电频率较高。

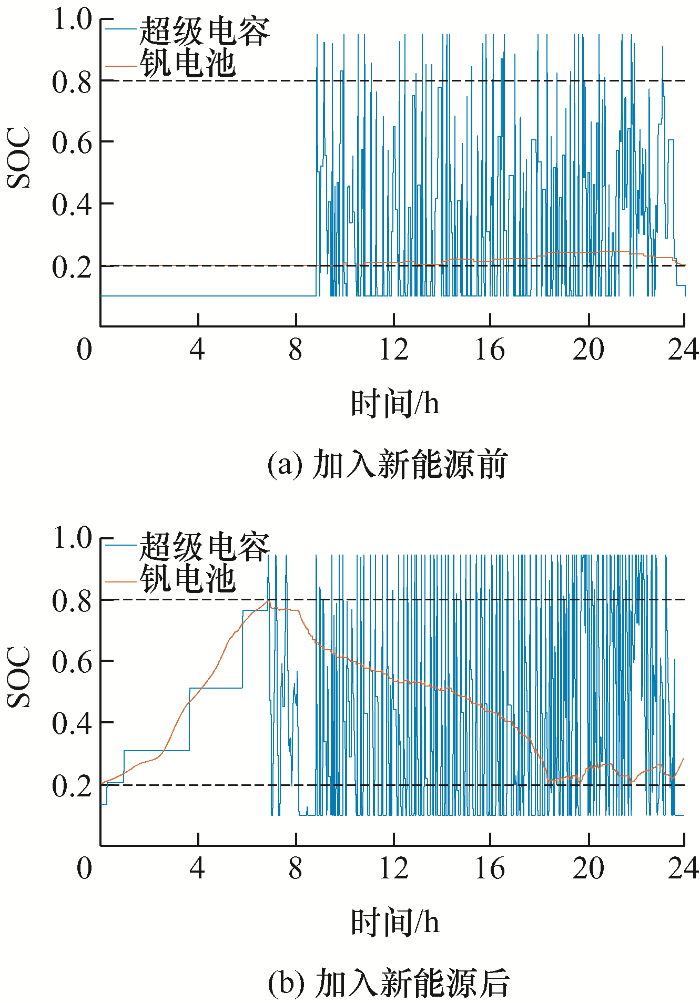
根据储能替换次数计算方法可得高铁系统加入新能源前后，超级电容日等效循环次数分别为102.94次和163.49次，钒电池日等效循环次数分别为0.17次和2.32次；全寿命周期内超级电容不进行更换，钒电池的更换次数分别为0次和1次。图11为加入新能源前后超级电容和钒电池的SOC。从图11可以看出，加入新能源前后钒电池的SOC均维持在0.2~0.8，超级电容的SOC均维持在0.1~0.95，且超级电容的SOC波动频率均高于钒电池。由此可见，超级电容具有快速充放电特性且循环寿命长，可以协助减少钒电池的循环使用次数，延长其使用寿命，符合本文设定的能量管理策略要求。

随着“双碳”目标的提出，中国政府出台各种政策措施来鼓励和推动清洁能源的发展。国家能源局发布《新型电力系统发展蓝皮书》，制定了新型电力系统“三步走”发展路径，未来的电力系统将逐渐以新能源为主体。随着新能源并网容量的增加，传统的火电机组占比逐渐减少，则电网主要碳排放源的碳排放量总占比逐渐降低，故高铁系统上级电网的基准线排放因子逐渐降低。

外部电网发电侧新能源并网容量占比将持续增加，根据《新型电力系统发展蓝皮书》在2035年将初步形成以新能源为主体的新型电力系统，此时预测的电网的基准线排放因子^[22]为0.443 8 kg/(kW·h)。假设高铁外部电网采用2035年的新型电力系统，并对上述两种方案进行仿真研究，如表4所示。

由仿真结果可知，高铁系统外部电网采用2035年的新型电力系统，两种方案下，高铁系统的电度电费收益和基本电费收益不变，而碳收益有所下降，全寿命周期内高铁系统的总净收益随之下降。高铁系统的主要成本来源于向外部电网购电电费。高铁加入一定容量的新能源是为了减少列车的购电量，而储能系统是为了回收列车的再生制动能量和未消纳的新能源发电量，并在列车牵引时释放，同样为了减少列车购电，此外牵引负荷的峰值也得到了削减，故高铁系统产生了电度电费收益和基本电费收益。而电度电费和基本电费收益是基于铁路现行电费政策提出的，铁路电价基本保持稳定，与外部电网发电侧新能源占比无关。但是，高铁系统的碳排放配额取决于上级电网的基准线排放因子，通过加入新能源储能系统可减少列车购电量，从而节省了碳排放配额，为高铁系统带来碳收益。随着外部电网发电侧新能源装机容量的增加，其基准线排放因子随之减少，则为高铁系统分配的碳排放配额也随之降低，则高铁系统的碳收益随之减少，其总净收益跟着减少。可见，随着新型电力系统的发展，铁路公司参与碳交易市场获得的碳收益逐渐减少，在一定程度上削弱了铁路行业的减碳积极性。

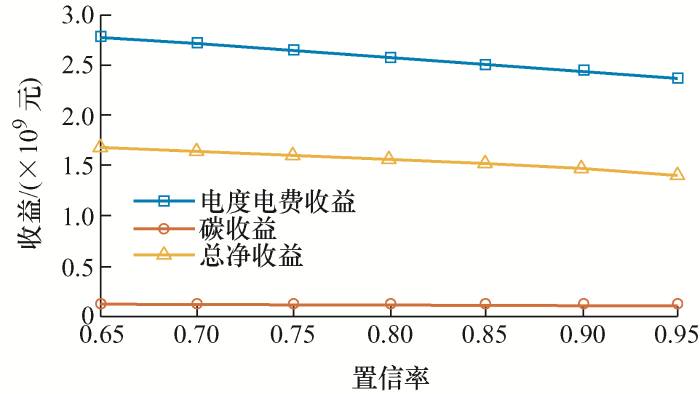
置信率的高低反映高铁系统应对新能源不确定性风险的能力。置信率越高，系统约束条件执行越严格，当置信率为1时，意味着新能源的所有不确定出力情况都满足系统功率平衡约束条件。图12为不同置信率对高铁系统经济收益的影响。由图12可知，随着置信率增大，电度电费收益和碳收益随之变小，因为随着置信率增大，新能源预测误差集区间范围变大，新能源不确定性引起的功率缺失主要由外部电网补充，高铁的购电量也随之增大，则电度电费收益随之减少，所产生的碳排放量随之增加，碳收益也因此减少，故新能源混合储能系统在全寿命周期内为高铁系统带来的总净收益也随之减少。

为了验证所提算法的有效性和优越性，将本文所采用的基于柯西变异的自适应粒子群算法(CMAPSO)与传统粒子群算法和文献[3]所提惯性权重自适应变化粒子群算法(AIWPSO)进行对比，各方案算法均以新能源混合储能系统在全寿命周期内为高铁系统带来的净收益最大为优化目标。传统粒子群算法中惯性权重ω=1，学习因子c₁=c₂=2。表5给出了三种算法的结果比较。从对比结果看出，CMAPSO算法的最优值优于其他两种，可见其寻优能力表现更强，通过对比平均值和方差也可以看出CMAPSO算法的寻优精度更高且更加稳定。

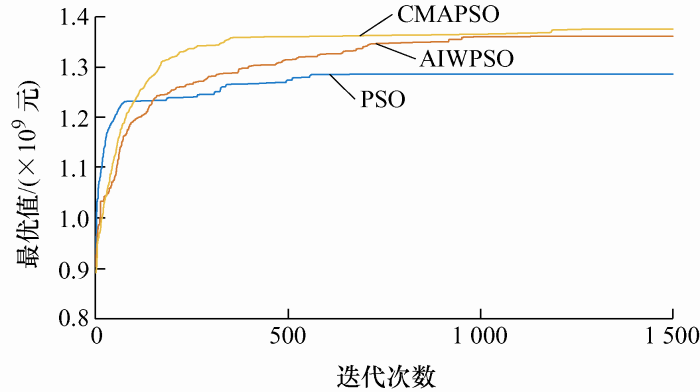
三种算法的收敛曲线如图13所示。从图13可看出传统PSO的收敛速度更快，但在第560代左右趋于稳定，意味着传统PSO易陷入局部最优。CMAPSO算法比AIWPSO算法收敛速度更快且在第1 200代趋于稳定，这表明相较于其他两种算法，CMAPSO算法搜索范围更广，更易跳出局部最优，表现出更好的全局搜索能力和较快的收敛速度。

本文考虑新能源的不确定性并引入碳收益，综合考虑新能源混合储能系统在全寿命周期内为高铁系统带来的各项收益和成本，提出一种高铁新能源混合储能系统低碳经济优化运行模型，结论如下所述。

(1) 基于本文设定的能量管理策略，在由钒电池和超级电容组成的混合储能系统最优配置下，新能源混合储能系统在全寿命周期内为高铁系统带来的碳收益为9.5×10⁷元，总净收益为1.37×10⁹元，具有良好的低碳经济效益。

(2) 仅用混合储能接入牵引供电系统的方案与新能源混合储能接入方案比较分析，可知高铁系统加入一定量的新能源系统能更大幅度削减牵引负荷峰值，从而大大降低碳排放量，明显增加系统总收益。

(3) 采用拉丁超立方机会约束规划法处理新能源出力的不确定性，通过设置不同置信率来反映新能源不确定性对高铁系统经济收益的影响。随着置信率增大，电度电费收益随之减少，所产生的碳排放量随之增加，碳收益因此减少，高铁系统的总净收益也随之减少。

(4) 与传统粒子群算法和现有的惯性权重自适应变化粒子群算法进行对比，验证本文所采用的基于柯西变异的自适应粒子群算法的有效性和优越性。