基于改进飞蛾扑火优化算法的并网复合装置滑模变控制器参数优化

doi:10.11985/2023.04.031

基于改进飞蛾扑火优化算法的并网复合装置滑模变控制器参数优化

刘家军, 林皓琨^,, 苗淼^,, 刘立鹏^,

西安理工大学电气工程学院西安 710054

Parameter Optimization of Sliding Mode Variable Controller for Grid Connected Compound Device Based on Improved Moth-flame Optimization Algorithm

LIU Jiajun, LIN Haokun^,, MIAO Miao^,, LIU Lipeng^,

School of Electrical Engineering, Xi’an University of Technology, Xi’an 710054

通讯作者: 林皓琨，女，1995年生，博士研究生。主要研究方向为人工智能在电力系统中的应用。E-mail：705271400@qq.com

收稿日期: 2022-12-2 修回日期: 2023-04-20

Received: 2022-12-2 Revised: 2023-04-20

作者简介 About authors

刘家军，1967年生，博士，教授。主要研究方向为电器及其控制、人工智能在电力系统中的应用等。E-mail：liujiajun-88@163.com

苗淼，女，1998年生，硕士研究生。主要研究方向为电力系统运行与控制。E-mail：1552202598@qq.com

刘立鹏，男，1998年生，硕士研究生。主要研究方向为电力系统运行与控制。E-mail：24027934405@qq.com

摘要

针对背靠背MMC-HVDC并网复合装置滑模变控制参数整定困难的问题，提出一种基于改进飞蛾扑火优化算法的控制器优化方法。引入佳点集初始化，在初始化种群时增加变量取值的多样性，加快算法收敛速度，减少计算量；结合Lévy飞行更新机制，避免算法陷入局部最优。通过8个标准测试函数测试所提改进飞蛾扑火算法的性能，并与多个常见群智能优化算法进行对比，验证所提算法的优越性。研究实现Python-PSCAD联合仿真方法，以综合ITAE指标为目标函数，对滑模变控制器进行参数优化。仿真结果表明，经改进飞蛾扑火算法优化的控制器参数可以使并网复合装置具有更好的动态性能。

关键词： 背靠背MMC-HVDC; 并网复合装置; 飞蛾扑火优化算法; Python-PSCAD联合仿真

Abstract

Aiming at the problem of difficult parameter tuning of sliding mode variable control for back-to-back MMC-HVDC grid connected composite device, a controller optimization method based on improved moth-flame optimization algorithm is proposed. Good point set initialization is introduced to increase the diversity of variable values when initializing the population, speed up the convergence speed of the algorithm and reduce the amount of calculation. Combined with Lévy flight update mechanism, the algorithm can avoid falling into local optimization. The performance of the proposed improved moth-flame optimization algorithm is tested by 8 standard test functions, and compared with several common swarm intelligence optimization algorithms to verify the superiority of the proposed algorithm. The Python-PSCAD joint simulation method is studied and realized. Taking the comprehensive ITAE index as the objective function, the parameters of the sliding mode variable controller are optimized. The simulation results show that the controller parameters optimized by the improved moth-flame optimization algorithm can make the grid connected composite device have better dynamic performance.

Keywords： Back-to-back MMC-HVDC; grid connected composite device; moth-flame optimization algorithm; Python-PSCAD joint simulation

PDF (522KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

刘家军, 林皓琨, 苗淼, 刘立鹏. 基于改进飞蛾扑火优化算法的并网复合装置滑模变控制器参数优化[J]. 电气工程学报, 2023, 18(4): 288-299 doi:10.11985/2023.04.031

LIU Jiajun, LIN Haokun, MIAO Miao, LIU Lipeng. Parameter Optimization of Sliding Mode Variable Controller for Grid Connected Compound Device Based on Improved Moth-flame Optimization Algorithm[J]. Chinese Journal of Electrical Engineering, 2023, 18(4): 288-299 doi:10.11985/2023.04.031

1 引言

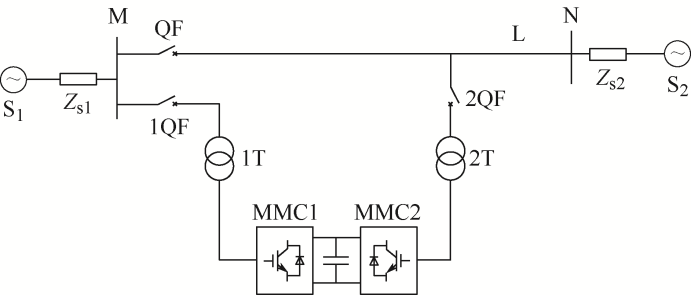
随着互联电网向智能化、自动化发展，可靠、有效的新型并网方式的研究至关重要^[1]。有学者提出基于背靠背VSC-HVDC的并网复合装置，通过在待并列两侧系统间传递有功和无功功率，调节待并列两侧的频率和电压，实现电网间的同期并列，该方法改变了传统同期并列方法完全依靠人工操作、操作涉及面广且难度较大、并网速度慢、成功率低的现状^[2⇓-4]。文献[5]研究了并网复合系统的解列和并网功能的综合控制策略，提高了电网自动化程度。文献[6]提出了一种并网系统转换为UPFC的方法，并分析了转化过程中对并网系统的影响。针对并网装置转换为UPFC的过程中出现功率和电压长时间波动问题，文献[7]提出了一种基于功率传递方式实现电网并网与UPFC功能相结合的控制策略。文献[8]通过建立并网装置转换为静止同步串联补偿器后复合系统的等效模型，验证了不同故障情况下静止同步串联补偿器的限流能力。文献[9]研究了低惯量电力系统中并网复合装置控制稳定性的问题，为低惯量电力系统平滑并网提供了新的思路。文献[10]为抑制背靠背MMC-HVDC并网复合系统功率传递过程中的联络线波动，将阻抗分析法与现有控制策略结合，以提高并网稳定性。上述文献提出了基于背靠背MMC-HVDC并网复合装置的概念，对并网复合装置的控制策略做了一定的研究，但未考虑控制器参数手动调节参数的复杂性和不确定性问题。

基于背靠背MMC-HVDC的并网复合装置具有复杂的拓扑结构和多环节的控制策略，因此一个性能良好的控制系统必不可少^[11-12]。滑模变控制以其响应速度快、鲁棒性强、结构简单等优点^[13]被应用于并网复合装置的控制系统中，但滑模变控制参数整定时常采用经验试凑法，这不仅无法充分发挥控制器的控制性能，而且十分耗费研究者的精力和时间。因此，有必要利用智能优化算法对控制器参数进行优化。

为了保证优化效果，本文利用全局搜索与局部搜索兼顾的飞蛾扑火优化算法(Moth-flame optimization，MFO)进行基于背靠背MMC-HVDC并网复合装置的滑模变控制器参数优化。文献[14]提出飞蛾扑火优化算法，并在29个基准和7个实际工程问题上与其他著名的自然启发算法进行了比较，验证其优越性。文献[15]针对风力发电机组PI控制参数整定难的问题，利用飞蛾扑火优化算法对控制器参数进行优化，试验证明参数优化后的PI控制器控制效果得到明显改善。文献[16]提出基于飞蛾扑火优化算法的多运行方式PSS参数协调优化方法，仿真算例结果表明，应用该方法后有效提高了系统的动态稳定性。文献[17]针对电力系统最优潮流问题，提出采用MFO算法的最优化求解方案，算例结果表明，采用MFO算法求解最优潮流问题具有收敛速度更快、搜索精度更高、鲁棒性强等优点。根据上述研究成果，传统MFO算法存在着两大问题：一是算法后期收敛速度慢。考虑到传统MFO算法的螺旋式飞行搜索和位置更新机制虽对全局搜索能力和局部搜索能力有一定的平衡作用，在优化前期，该算法可快速接近相对最优解，但是在经过一定迭代次数之后，螺旋式飞行搜索会将飞蛾局限在某较小的区域中，该搜索方式仅会对当前位置做一些较小的更新，导致算法后期的收敛速度变慢。二是早熟收敛。MFO不具备跳出局部最优的机制，一旦陷入局部最优，就难以跳出，导致发生早熟收敛现象。同时MFO算法的火焰自适应熄灭机制虽增强了局部寻优能力，但在一定程度上减少了种群多样性，也会导致早熟收敛现象。

针对MFO算法的不足，本文将佳点集初始化和Lévy飞行机制与飞蛾扑火优化算法结合，在加快收敛速度的同时提高算法的全局寻优能力，即使算法暂时陷入局部最优，也可通过Lévy飞行跳出，并以Automation Library为纽带，实现Python-PSCAD联合仿真，验证所提方法能够有效改善并网复合装置滑模变控制器的控制性能。

2 并网复合装置滑模变控制器设计

2.1 电流内环滑模变结构控制器设计

滑模变结构控制最突出的优势是系统的运行只受滑模面参数影响，不受系统原参数影响，从而使系统在一定条件下具有比鲁棒性更加优越的完全自适应性^[18-19]。并网复合装置拓扑如图1所示，将背靠背MMC-HVDC并网复合装置投入待并列的两系统之间，将高频侧系统的有功功率通过控制策略向低频侧系统快速传递，从而减少两侧频率差；同时，装置向电压较低并列点注入容性无功，即减少无功负荷；向电压较高并列点吸收无功，即增大无功负荷，以调整并列点的电压幅值与相角，通过功率传递满足并网条件，实现快速并网。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 背靠背MMC-HVDC并网复合装置拓扑图

MMC在dq坐标轴下的动态方程为

(1)

\{\begin{matrix} L \frac{d i_{d}}{d t} + R i_{d} = u_{d} - v_{d} + ω L i_{q} \\ L \frac{d i_{q}}{d t} + R i_{q} = u_{q} - v_{q} + ω L i_{d} \end{matrix}

式中， $i_{d}$ 、 $i_{q}$ 是MMC交流侧电流分别在d、q轴上的分量； $u_{d}$ 、 $u_{q}$ 为MMC交流侧接入端电压分别在d、q轴上的分量； $v_{d}$ 、 $v_{q}$ 表示MMC桥臂中点的基波电压在d、q轴上的分量。式(1)可转换为

(2)

\{\begin{matrix} {\dot{i}}_{d} = - \frac{R}{L} i_{d} + ω i_{q} + \frac{1}{L} u_{d} - \frac{1}{L} v_{d} \\ {\dot{i}}_{q} = - \frac{R}{L} i_{q} - ω i_{d} + \frac{1}{L} u_{q} - \frac{1}{L} v_{q} \end{matrix}

滑模面和趋近律的选择作为滑模变控制器设计的重中之重，其选取直接影响到滑模变控制器的控制性能。考虑到积分可消除系统的静态误差，因此本文选取积分滑模面，如式(3)所示

(3)

\{\begin{matrix} s_{1} = e_{1} + k_{s 1} \int_{0}^{t} e_{1} d t \\ s_{2} = e_{2} + k_{s 2} \int_{0}^{t} e_{2} d t \end{matrix}

式中， $e_{1}$ 和 $e_{2}$ 为控制误差， $e_{1} = i_{d} - i_{d r e f}$ ， $e_{2} = i_{q} - i_{q r e f}$ ， $i_{d}$ 和 $i_{q}$ 分别为电流在d、q轴上的分量，i_d_ref和i_q_ref分别为电流在d轴和q轴上的参考值； $s_{1}$ 和 $s_{2}$ 表示滑模面； $k_{s 1}$ 和 $k_{s 2}$ 为滑模面控制参数，通过调节该参数可以获得更好的稳态性能。

当系统处于稳态时，系统状态是运行在滑模面上的。但系统在进入稳态前，必须施加一控制作用使系统向滑模面趋近。

选取指数趋近律，如式(4)所示

(4)

\dot{s} = - ε sgn (s) - k s ε > 0 k > 0

式中， $s$ 为切换函数； $\dot{s} = - k s$ 是指数趋近项，其解为 $s = s (0) e x p (- k t)$ ， $k$ 为趋近速度。 $\dot{s} = - ε sgn (s)$ 是等速趋近项， $ε$ 为到达速度， $sgn (s)$ 为符号函数，如式(5)所示

(5)

sgn (s) = \{\begin{matrix} 1 s > 0 \\ 0 s = 0 \\ - 1 s < 0 \end{matrix}

指数趋近律中同时包含指数趋近项和等速趋近项，这样使得系统能很快地趋近切换面。

将 ${|x|}^{2}$ 引入式(4)的等速趋近项，并与式(3)联立可得

(6)

\{\begin{matrix} {\dot{s}}_{1} = {\dot{i}}_{d} - {\dot{i}}_{d r e f} + k_{s 1} (i_{d} - i_{d r e f}) = \\ - ε_{1} {|x_{1}|}^{2} sgn (s_{1}) - k_{1} s_{1} \\ {\dot{s}}_{2} = {\dot{i}}_{q} - {\dot{i}}_{q r e f} + k_{s 2} (i_{q} - i_{q r e f}) = \\ - ε_{2} {|x_{2}|}^{2} sgn (s_{2}) - k_{2} s_{2} \end{matrix}

式中， $x$ 为系统的状态变量，本文选用控制误差。

控制之初 $- ε {|x|}^{2} sgn (s)$ 与 $- k s$ 共同作用，趋近速度较快。随着状态变量x与滑模面距离的逐渐缩小， $- ε {|x|}^{2} sgn (s)$ 与 $- k s$ 均趋于零，最终稳定在滑模面上。该趋近律可根据状态变量与滑模面之间的距离调整趋近速度，在削弱抖振的同时达到稳定运行状态。

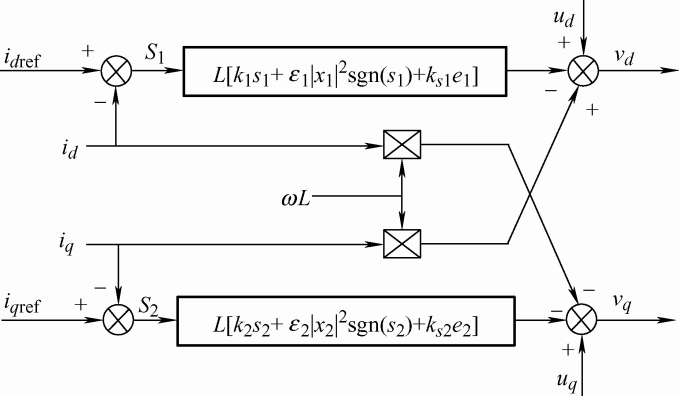
由式(1)可知，MMC变换器交流侧电流 $i_{d}$ 、 $i_{q}$ 受控制量 $u_{d}$ 、 $u_{q}$ ，电网电动势 $v_{d}$ 、 $v_{q}$ 以及交叉耦合项 $ω L i_{q}$ 、 $ω L i_{d}$ 影响，因此需要采用前馈解耦控制。将式(6)代入式(2)，可得并网复合装置电流内环滑模变结构控制律，如式(7)所示。并网复合装置电流内环滑模变结构控制框图如图2所示。

(7)

\{\begin{matrix} \begin{array}{l} u_{d} = R i_{d} - ω L i_{q} + v_{d} - \\ L [k_{1} s_{1} + ε_{1} {|x_{1}|}^{2} sgn (s_{1}) + k_{s 1} e_{1}] \end{array} \\ \begin{array}{l} u_{q} = R i_{q} + ω L i_{d} + v_{q} - \\ L [k_{2} s_{2} + ε_{2} {|x_{2}|}^{2} sgn (s_{2}) + k_{s 2} e_{2}] \end{array} \end{matrix}

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 电流内环滑模变控制策略结构框图

2.2 电压外环滑模变结构控制器设计

MMC每个桥臂是由多个子模块级联组成，其直流侧电容电压是由子模块电容电压支撑，由能量守恒定律可得

(8)

\frac{3}{2} (u_{d} i_{d} + u_{q} i_{q}) = u_{d c} i_{d c} = C_{e q} u_{d c} \frac{d u_{d c}}{d t}

式中， $i_{d c}$ 为逆变器直流侧电流； $C_{e q}$ 为直流侧等效电容值。对于三相平衡电网，有 $u_{q} = 0$ ，故MMC直流侧动态方程为

(9)

\frac{d u_{d c}}{d t} = \frac{3 u_{d} i_{d}}{2 C_{e q} u_{d c}}

直流侧直流电压指令值 $u_{d c r e f}$ 与实际的直流电压 $u_{d c}$ 的误差为 $e_{3}$ ， $e_{3} = u_{d c r e f}$ 。

考虑到电压外环控制器的控制目标是维持直流侧电压的稳定，因此该控制器的设计要求是保证直流侧电压的控制具有较强的抗干扰能力，微分作用能够消除扰动对系统的影响，能够较好地消除抖振。因此选取一阶滑模为

(10)

s_{3} = e_{3} + β \frac{d e_{3}}{d t}

式中， $β$ 为微分项系数。将式(9)代入式(10)可得

(11)

\begin{matrix} s_{3} = (u_{d c r e f} - u_{d c}) + β ({\dot{u}}_{d c r e f} - \frac{d u_{d c}}{d t}) = \\ (u_{d c r e f} - u_{d c}) + β ({\dot{u}}_{d c r e f} - \frac{3 u_{d} i_{d}}{2 C_{e q} u_{d c}}) = \\ (u_{d c r e f} - u_{d c}) - \frac{3 β u_{d} i_{d}}{2 C_{e q} u_{d c}} \end{matrix}

令 $s_{3} = 0$ ，可得

(12)

i_{d r e f} = \frac{2 C_{e q} u_{d c}}{3 β u_{d}} (u_{d c r e f} - u_{d c})

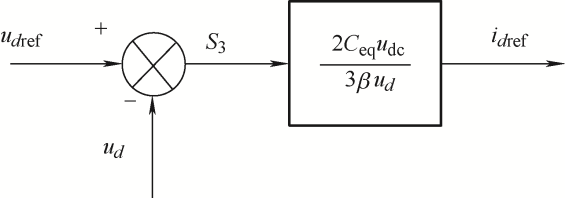
由式(12)便可得到内环控制器的参考有功电流i_d_ref。电压外环滑模变结构控制框图如图3所示。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 电压外环滑模变控制策略结构框图

当系统的状态轨迹到达滑模面后，因为实际切换装置会存在延时现象，很难完全沿着预设的滑模面向平衡点滑动，而是遵循着在切换面的两侧反复切换的原则运动，这便是系统的抖振现象。抖振在影响系统控制精度的同时还会影响器件的使用寿命，但抖振是滑模变控制中固有的，无法将其彻底消除，只能尽可能削弱^[20]。抖振的大小受滑模变控制器参数直接影响，因此找寻滑模变控制器的最优参数，可有效提高系统控制性能。

3 改进的飞蛾扑火优化算法

3.1 算法原理

该算法衍生于以螺旋趋近的方式趋近光源的飞蛾扑火现象，飞蛾是不断搜索找寻最优值的个体，而火焰则是飞蛾寻优过程中获得的最优位置。每个飞蛾在相对应的火焰周围寻优，并在找到更好解的情况下更新火焰位置，从而保证寻优过程中最优解的保留^[21]。

MFO算法可表示为三元组寻优问题

(13)

\{\begin{cases} M F O = (I, P, T) \\ I : f \to \{M, O M\} \\ P : M \to M^{'} \\ T : M \to \{true, false\} \end{cases}

式中， $M$ 为飞蛾位置，即待优化变量； $O M$ 为 $M$ 中飞蛾对应的适应度值； $f$ 为适应度函数； $P$ 为飞蛾围绕火焰进行螺旋式位置更新机制； $M^{'}$ 为更新后的飞蛾位置； $T$ 为迭代判断函数，其为真则停止迭代，否则继续迭代寻优。

P函数可以表示为

(14)

M_{i} = S (M_{i}, F_{j})

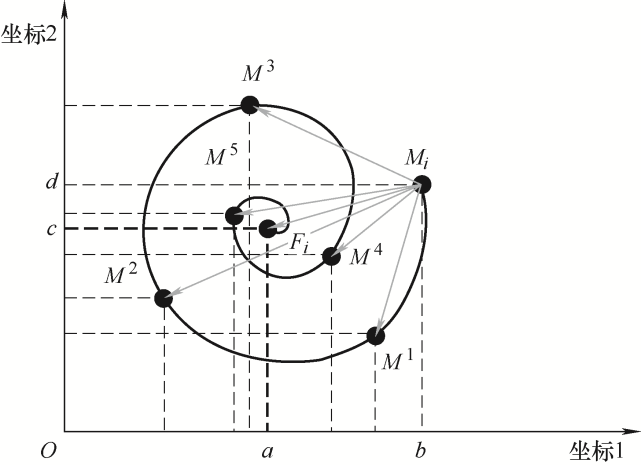
式中，S是螺旋函数；M_i表示第 $i$ 只飞蛾；F_j表示第j个火焰。

(15)

S (M_{i}, F_{j}) = D_{i} e x p (b t) \cos (2 π t) + F_{j}

式中， $t$ 为位移变量，在[-1，1]区间内随机生成；b为螺旋函数的形状常数； $D_{i}$ 表示第 $i$ 只飞蛾与第 $j$ 个火焰之间的距离，可以表示为

(16)

D_{i} = |F_{j} - M_{i}|

式中， $M_{i}$ 表示第 $i$ 只飞蛾； $F_{j}$ 表示第 $j$ 个火焰； $D_{i}$ 表示第 $i$ 只飞蛾与第 $j$ 个火焰之间的距离。

飞蛾围绕火焰利用对数螺线函数更新位置的模型如图4所示，为便于分析，图4中只显示了一只飞蛾在一个维度时的模型，可以此类比至多只飞蛾和多个维度的情况。图4中$M_i$为飞蛾初始位置，在其飞行时，可能飞行至$M^1$、$M^2$、$M^3$、$M^4$、$M^5$等位置。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 飞蛾位置更新机制

若每次迭代都有n只飞蛾，则飞蛾会侧重于全局寻优而影响局部寻优的精度，并且排序在最后的火焰寻优价值也较低。研究者提出火焰自熄灭机制，随着算法迭代次数的增加，逐渐抛弃适应度差的火焰，火焰熄灭式可以表示为

(17)

F_{\min} = r o u n d (N - k \times \frac{N - 1}{T})

式中， $N$ 为种群个数； $k$ 为当前迭代次数； $T$ 为总迭代次数。

传统MFO算法用随机取值的方式设置飞蛾初始位置，但该方式无法使飞蛾初始位置均匀分布在允许范围内。利用佳点集初始化^[22-23]来代替随机滑模变参数飞蛾初始位置的产生方式，可以使飞蛾种群初始位置分布得更加均匀。

佳点的构造不受空间维数的影响，能够较好地解决高维空间求解问题。因此，应用佳点集初始化方法对飞蛾初始位置进行设置，能得到一个相对较好的初始飞蛾种群。佳点集初始化的具体表达式为

(18)

P_{n} (k) = \{(\{r^{1} k\}, \dots, \{r^{i} k\}, \dots, \dots, \{r^{t} k\}) k = 1, 2, \dots, n\}

式中， $r^{i} = \{2 \cos (2 π i / p)\} ， 1 \leq i \leq t$ ；P是满足 $p \geq 2 t + 3$ 的最小素数。

基于Lévy飞行的滑模变参数飞蛾路径优化^[24-25]将Lévy飞行机制与经典MFO算法结合，能够增加种群多样性和扩大搜索范围，即使算法暂时陷入局部最优，也可通过Lévy飞行跳出。Lévy飞行位置更新式为

(19)

\begin{matrix} x_{i}^{t + 1} = x_{i}^{t} + α \oplus L e v y (λ) & i = 1, 2, \dots, n \end{matrix}

式中， $x_{i}^{t}$ 表示 $x_{i}$ 第 $t$ 代位置； $\oplus$ 为点对点乘法； $α$ 表示步长控制量； $L e v y (λ)$ 为随机搜索路径，并且满足

(20)

\begin{matrix} L e v y ～ u = t^{- λ} & 1 < λ \leq 3 \end{matrix}

因此，Lévy飞行跳跃路径更新机制为

(21)

\{\begin{cases} s = \frac{μ}{{|v|}^{\frac{1}{β}}} \\ μ ～ N (0, σ_{μ}^{2}) \\ v ～ N (0, σ_{v}^{2}) \\ σ_{μ} = {[\frac{Γ (1 + β) \sin (\frac{β π}{2})}{Γ (\frac{1 + β}{2}) 2^{(\frac{β π}{2})} β}]}^{\frac{1}{β}} \\ σ_{v} = 1 \end{cases}

式中， $s$ 为随机步长； $β = λ - 1$ ； $μ$ ， $v$ 服从正态分布。

为了提高滑膜变结构控制器的性能，将电流内环滑模变结构控制参数和电压外环滑模变结构控制参数作为改进后的MFO算法寻优对象，并通过以下步骤实现控制器参数优化。

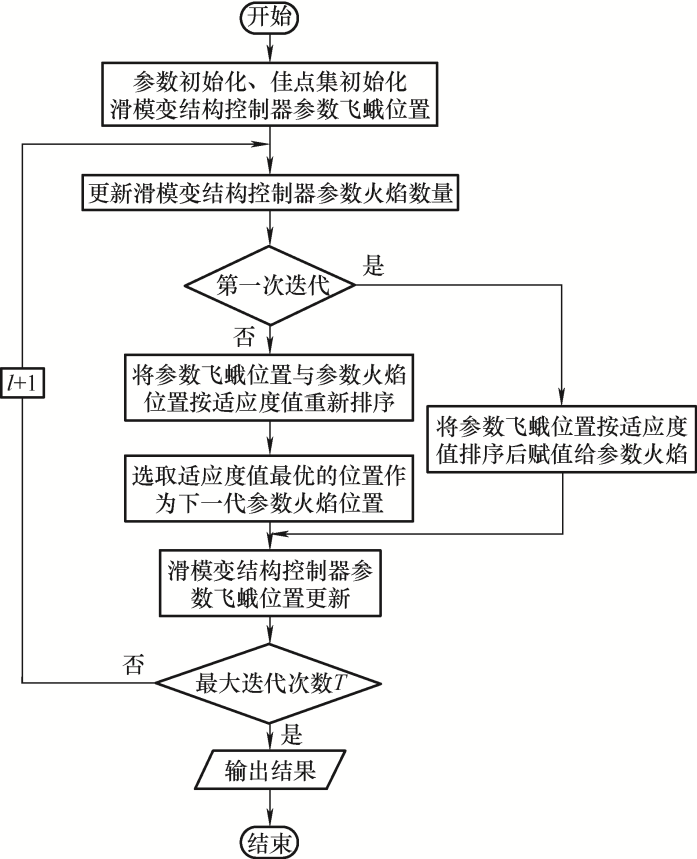
(1) 对参数进行初始化定义，并根据佳点集初始化方法，即式(18)生成滑模变结构控制器参数飞蛾初始位置。

(2) 使用式(17)更新滑模变结构控制器参数火焰数量。

(3) 判断是否为第一次迭代，若是则根据目标函数计算每个滑模变结构控制器参数飞蛾个体的适应度值，按照适应度值对滑模变结构控制器参数飞蛾排序，把滑模变结构控制器参数飞蛾的适应度值赋给对应的滑模变结构控制器参数火焰，得到第一代滑模变结构控制器参数火焰的位置；若不是第一次迭代，将滑模变结构控制器参数飞蛾位置与滑模变结构控制器参数火焰位置按照适应度值排序，将适应度值最优的位置赋给滑模变结构控制器参数火焰，成为下一代滑模变结构控制器参数火焰的位置。

(4) 将Lévy飞行与自适应惯性权重加入滑模变结构控制器参数飞蛾更新位置机制。

(5) 判断是否满足迭代停止条件，若未满足则返回步骤(2)，若满足则执行步骤(6)。

(6) 输出寻优后的数值，即为控制器的最佳参数。

上述步骤即可实现基于改进飞蛾扑火优化算法的并网复合装置滑模变控制器参数优化，其流程如图5所示。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 改进MFO算法优化滑模变控制参数流程图

3.2 算法测试

为了更加全面和客观地对改进的飞蛾扑火优化算法进行性能测试，选取8个不同的测试函数进行测试，其中表1为8个不同的测试函数，表2为函数测试的结果。

表1 测试函数

测试函数	$f_{\min} (x)$
$f_{1} (x) = \sum_{i = 1}^{n} x_{i}^{2}$	0
$f_{2} (x) = \sum_{i = 1}^{n} \|x_{i}\| + \prod_{i = 1}^{n} \|x_{i}\|$	0
$f_{3} (x) = \sum_{i = 1}^{n} {(\sum_{j = 1}^{i} x_{j})}^{2}$	0
$f_{4} (x) = \max_{i} \{\|x_{i}\|, 1 \leq i \leq D\}$	0
$f_{5} (x) = \sum_{i = 1}^{n} x_{i} \sin (x_{i}) + 0.1 x_{i}$	0
$f_{6} (x) = \sum_{i = 1}^{n} [x_{i}^{2} - 10 \cos (2 π x_{i}) + 10]$	0
$f_{7} (x) = - 20 e x p (- 0.2 \sqrt{\frac{1}{n} \sum_{i = 1}^{n} x_{i}^{2}} - \exp (\sqrt{\frac{1}{n} \sum_{i = 1}^{n} \cos 2 π x_{i}})) + 20 + e$	0
$f_{8} (x) = \frac{1}{4 000} \sum_{i = 1}^{n} (x_{i}^{2}) - \prod_{i = 1}^{n} \cos (\frac{x_{i}}{\sqrt{i}}) + 1$	0

新窗口打开| 下载CSV

表1中， $f_{1}$ ~ $f_{4}$ 为单峰测试函数； $f_{5}$ ~ $f_{6}$ 为多峰测试函数，将粒子群算法(Particle swarm optimization，PSO)、MFO以及改进MFO三种群优化算法进行测试函数仿真对比，验证所提改进MFO的性能。设置所有算法种群为30，最大迭代次数为1 000，维度为10。由表2可明显看出，改进MFO的寻优能力明显优于MFO和PSO。

表2 测试结果

测试函数	算法	平均值	方差
$f_{1}$	PSO	2.642 245	0.144 362
	MFO	7.92×10^-30	1.49×10^-59
	改进MFO	1.10×10^-189	0
$f_{2}$	PSO	1.098 57	0.028 251
	MFO	1.333 333	3.80×10^-38
	改进MFO	4.50×10^-103	1.00×10^-208
$f_{3}$	PSO	19.212 38	88.857 96
	MFO	1.34×10^-6	2.13×10^-14
	改进MFO	2.80×10^-151	0
$f_{4}$	PSO	0.907 91	0.150 335
	MFO	2.852 998	5.537 056
	改进MFO	2.87×10^-88	2.80×10^-178
$f_{5}$	PSO	70.704 18	0.876 751
	MFO	12.259 06	4.81×10^-24
	改进MFO	3.60×10^-101	9.50×10^-212
$f_{6}$	PSO	26.165 55	110.614 7
	MFO	21.626 07	24.748 14
	改进MFO	0	0
$f_{7}$	PSO	1.565 486	0.038 066
	MFO	4.91×10^-15	0
	改进MFO	8.88×10^-16	0
$f_{8}$	PSO	0.829 78	0.009 495
	MFO	0.159 074	0.000 667
	改进MFO	0	0

新窗口打开| 下载CSV

4 仿真验证

4.1 Python-PSCAD联合仿真

目前在PSCAD平台上搭建的控制器进行参数优化主要通过PSCAD与Matlabll接口实现，但PSCAD与Matlab互联时无法后台运行，利用Python-PSCAD联合仿真即可解决该问题。Automation Library是Python与PSCAD联合仿真的纽带，Automation Library由Python开发，支持PSCAD 4.6.1及以上版本，用于与PSCAD接口。此库接口允许用户从自定义脚本调用PSCAD函数，可通过Python语言对PSCAD实现启动PSCAD、加载工作区、项目和库、运行模拟、更改工作区和项目设置、更改组件参数等功能。

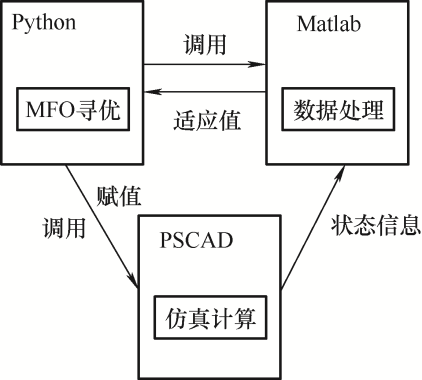
利用Python进行飞蛾扑火算法寻优，在数据处理部分，利用Python调用Matlab引擎进行适应度计算，而计算所需的状态信息则由Python利用Automation Library与PSCAD联合仿真获得，联合仿真结构图如图6所示。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 联合仿真结构图

4.2 评估指标

采用综合ITAE指标作为衡量滑模变控制器控制性能好坏的标准，综合ITAE指标相比于ITAE指标增加了对调节时间和超调量的指标，避免优化算法过度重视ITAE指标而忽略调节时间和超调量等重要指标的问题，修改后的综合ITAE指标描述为

(22)

J_{s y n_I T A E} = \int_{t}^{T} t |e (t)| d t + ω_{1} t_{c} + ω_{2} δ (σ)

式中，t_c为控制器调节时间； $δ (σ)$ 为超调量； $ω_{1}$ 、 $ω_{2}$ 分别为调节时间以及超调量的权重系数。

考虑并网复合装置在功率传递过程中的动态特性，故设置目标函数为

(23)$\begin{array}{c} Q_{f}(X)=\omega_{\mathrm{Dc}} \int_{t}^{T} t \bullet\left|e_{\mathrm{DC}}(t)\right| \mathrm{d} t+\omega_{11} t_{\mathrm{c} 1}+\omega_{21} \delta(\sigma)_{1}+ \\ \omega_{\mathrm{P}} \int_{t}^{T} t \bullet\left|e_{\mathrm{p}}(t)\right| \mathrm{d} t+\omega_{12} t_{\mathrm{c} 2}+\omega_{22} \delta(\sigma)_{2}+ \\ \omega_{Q_{1}} \int_{t}^{T} t \bullet\left|e_{Q_{1}}(t)\right| \mathrm{d} t+\omega_{13} t_{\mathrm{c} 3}+\omega_{23} \delta(\sigma)_{3}+ \\ \omega_{Q_{2}} \int_{t}^{T} t \cdot\left|e_{Q_{2}}(t)\right| \mathrm{d} t+\omega_{14} \delta(\sigma)+\omega_{24} \delta(\sigma)_{4} \end{array}$

式中， $ω_{D C}$ 、 $ω_{P}$ 、 $ω_{Q_{1}}$ 、 $ω_{Q_{2}}$ 分别为直流电压DC、有功功率P、MM1的无功功率和MM2的无功功率的综合ITAE评估指标的权重系数。

4.3 仿真验证模型

在PSCAD/EMTDC仿真软件中搭建41电平的背靠背MMC-HVDC并网复合装置的仿真模型，用以验证和分析飞蛾扑火算法在滑模变控制参数优化过程中的有效性。两侧待并列系统设为水轮机模型，机组额定容量为120 MV·A，发电机出口电压13.8 kV，变压器变比13.8/230 kV；两侧系统的负荷分别为S₁=70+j62 MV·A，S₂=10+j20 MV·A。试验的详细仿真参数如表3所示。

表3 仿真参数

参数	数值
系统电压/kV	220
直流侧电压额定值/kV	40
MMC容量/(MV·A)	40
桥臂模块数	40
子模块电容值/mF	10
桥臂电抗器电感值/mH	10

新窗口打开| 下载CSV

本文以有功功率、无功功率和直流侧电压的综合ITAE值组成目标函数作为评价指标，着重对MMC1与MMC2的电流内环滑模变控制参数、MMC2的电压外环滑模变控制参数进行优化，其余参数设为定值。

将本文所述的改进飞蛾扑火算法应用于并网复合装置控制参数优化。在1台8 G内存，2.4 GHz主频的计算机上实现Python与PSCAD之间的联合运行。算法种群数量设置为30，最大迭代次数设置为100。

用传统MFO和所提改进MFO算法对并网复合装置的滑模变控制器参数进行优化，并与优化前的控制性能进行对比，表4展示了优化前后的评价指标。

表4 优化前后评价指标对比

算法	综合ITAE值
优化前	0.442 789
MFO	0.366 769
改进MFO	0.358 213

新窗口打开| 下载CSV

通过表4的综合ITAE指标可看出，MFO算法及改进MFO算法均可对控制参数进行优化，使控制性能提高，而且本文提出的基于改进飞蛾扑火优化算法的并网复合装置滑模变控制参数优化方法的优化程度明显高于传统MFO算法。

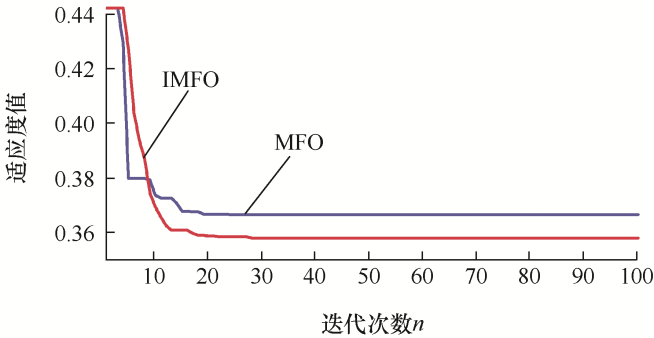
图7为控制器参数优化迭代过程中的收敛曲线，可看出在寻优初期，MFO的寻优速度暂时领先于IMFO。迭代10次之后，在达到相同的寻优精度时，IMFO的收敛速度明显快于MFO，且IMFO的寻优精度也高于MFO。综上所述，在背靠背MMC-HVDC并网复合系统的滑模变结构控制器参数优化过程中，IMFO较MFO的优化效果更突出。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 参数优化收敛曲线

仅用综合ITAE指标验证控制效果较为片面，本节以直流侧电压和MMC1侧的有功功率、无功功率以及MMC2侧的无功功率的波形图来对比优化前后的参数控制效果。

图8、9为直流侧电压波形及其局部放大图。由图8可以明显看出未经参数优化、经MFO参数优化后以及经改进MFO参数优化后的功率传递过程中的直流侧电压波动。未经参数优化时，功率传递过程中滑模变控制下的直流侧电压波动约0.2 kV，而经过MFO和改进MFO优化的直流侧电压波动约0.04 kV，说明经控制器参数优化后的直流侧电压波动幅值明显减小，提高了系统稳定性。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 直流侧电压波形

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 直流侧电压局部放大波形1

此外，优化前后直流侧电压波动及响应速度情况如表5所示。

表5 优化前后直流侧电压波动及响应速度

算法	直流侧电压波动/kV	响应速度/s
优化前	0.20	0.7
MFO	0.04	0.6
改进MFO	0.04	0.2

新窗口打开| 下载CSV

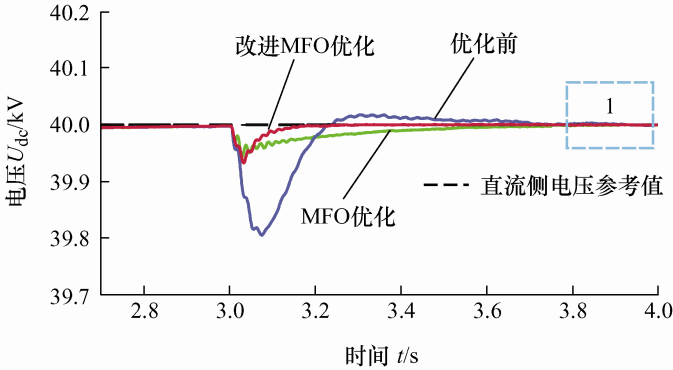
由表5可以看出，未经参数优化的直流侧电压需要0.7 s才能回归稳态，经MFO算法寻优后的直流侧电压需要0.6 s回归稳态，经改进MFO算法寻优后的直流侧电压的响应速度最低，仅需要0.2 s即可回归稳态。上述数据可有效说明控制器参数优化后的直流侧电压响应速度明显加快。

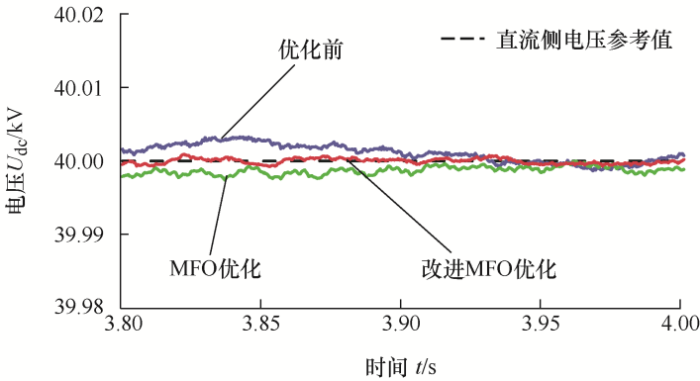
为进一步分析参数优化对系统稳态性能的影响，选取3.8~4 s之间的直流侧电压波形如图9所示，可见未经参数优化的直流侧电压和经MFO优化后的直流侧电压波形在稳态有一定的稳态误差，而经改进MFO优化后的电压波形具有良好的稳态性能，无明显稳态误差。综上所述，经MFO及改进MFO参数优化的系统直流侧电压较未经参数优化的系统直流侧电压具有更小的波动、更快的响应速度以及更小的稳态误差，且经改进MFO参数优化后的动、静态性能较MFO更佳。

功率传递过程中的有功功率波形如图10所示，为观察波形，将图10进行局部放大如图11所示，由图11a可明显看出未经参数优化、经MFO优化后以及改进MFO优化后的功率传递过程中有功功率的响应速度及超调情况，具体数据如表6所示。

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 有功功率波形

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 有功功率局部放大波形

表6 优化前后有功功率的响应速度及超调情况

算法	响应速度/s	超调情况/MW
优化前	0.14	0.094
MFO	0.09	0.037
改进MFO	0.08	0.021

新窗口打开| 下载CSV

由表6可知，未经参数优化时，有功功率传递时约有0.094 MW的超调量，且有功功率需要0.14 s才能回归稳态。而经参数优化的有功功率超调量为0.037 MW，有功功率响应速度为0.09 s；经改进MFO参数优化的有功功率响应速度为0.08 s。图11b反映了有功功率的静态特性，可见三种情况下有功功率的静态性能无明显区别。综上所述，经MFO及改进MFO参数优化的有功功率较未经参数优化的有功功率具有更小的超调、更快的响应速度，且经改进MFO参数优化后的动态性能较MFO更佳。

图12为功率传递过程中的MMC1的无功功率波形，为观察波形，将图12进行局部放大如图13所示，由图13a可明显看出未经参数优化、经MFO优化后以及改进MFO优化后的功率传递过程中MMC1的无功功率的响应速度及超调情况。具体情况如表7所示，几种情况下均无明显超调情况。

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12 MMC1无功功率波形

图13

新窗口打开| 下载原图ZIP| 生成PPT

图13 MMC1无功功率局部放大波形

表7 优化前后MMC1无功功率的响应速度及超调情况

算法	响应速度/s	超调情况/MVar
优化前	0.08	0.120
MFO	0.13	0.075
改进MFO	0.07	0.024

新窗口打开| 下载CSV

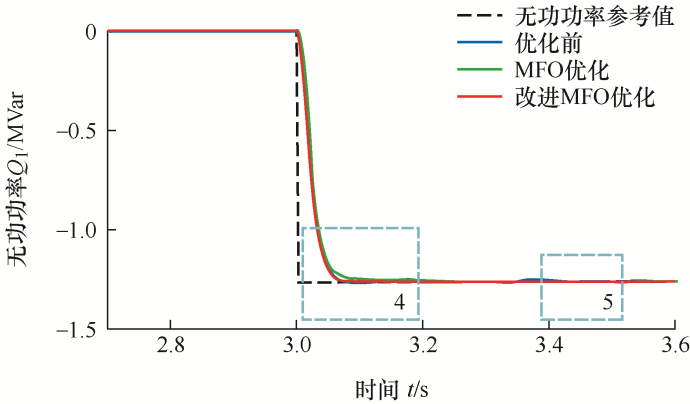
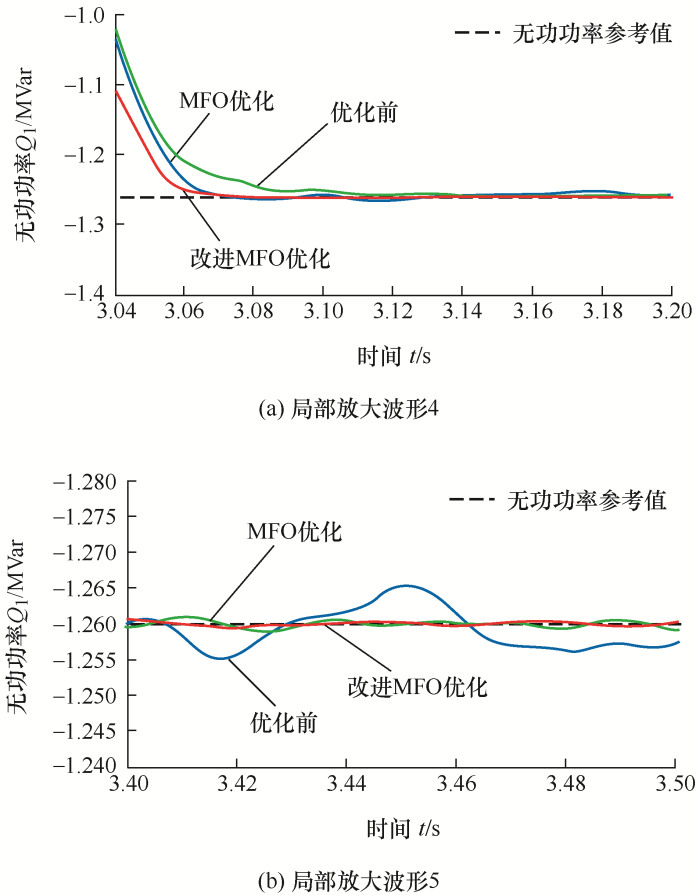
然而，从图13b来看，未经参数优化的无功功率静态性能较差，在无功功率已回归稳态后，仍存在幅值约为0.01 MVar的波动，而经MFO参数优化后的无功功率静态性能良好。经改进MFO参数优化后的响应速度为0.07 s。此外，经改进MFO参数优化后的无功功率静态性能较经MFO参数优化后的无功功率静态性能更优。

综上所述，经改进MFO参数优化后的系统无功功率较未经参数优化的系统无功功率具有更快的响应速度及更好的静态稳定性。

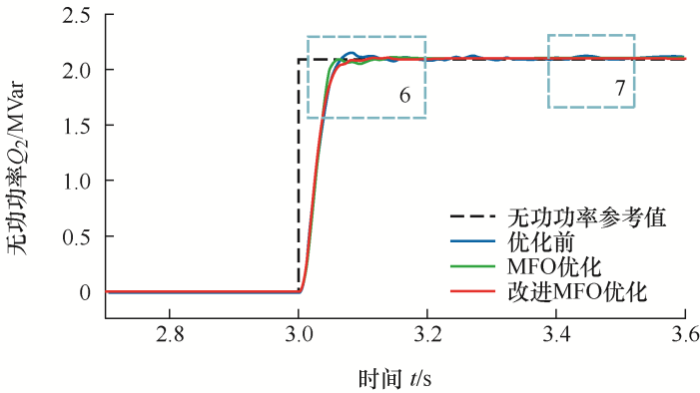
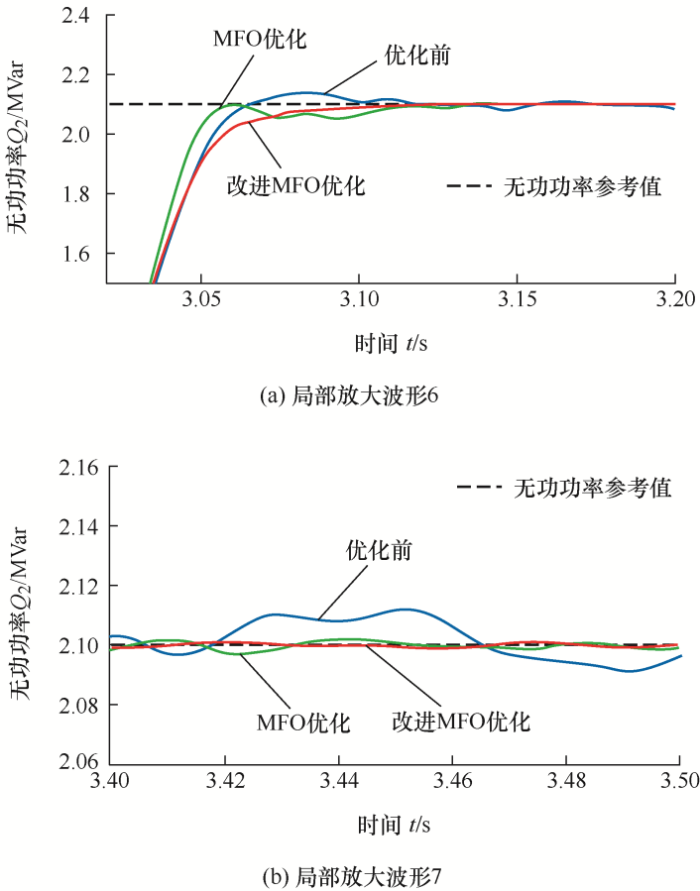
图14为功率传递过程中的MMC2的无功功率波形，局部放大如图15所示。具体数据如表8所示。可以明显看出经改进MFO算法优化的控制器可以得到最佳的动态性能。

图14

新窗口打开| 下载原图ZIP| 生成PPT

图14 MMC2无功功率波形

图15

新窗口打开| 下载原图ZIP| 生成PPT

图15 MMC2无功功率局部放大波形

表8 优化前后MMC2无功功率的响应速度及超调情况

算法	响应速度/s	超调情况/MVar
优化前	0.14	0.47
MFO	0.13	0.49
改进MFO	0.11	0.11

新窗口打开| 下载CSV

图14b可反映无功功率的静态特性，未经参数优化的无功功率静态性能较差，在无功功率已回归稳态后，仍存在幅值约为0.02 MVar的波动，而经参数优化后的无功功率静态性能良好，且根据波形看出经改进MFO参数优化后的无功功率静态性能较将经MFO参数优化后的无功功率静态性能更优。综上所述，经MFO及改进MFO参数优化的无功功率较未经参数优化的无功功率具有更小的超调、更快的响应速度，且经改进MFO参数优化后的动、静态性能较MFO更佳。

综合上述分析，对背靠背MMC-HVDC并网复合装置滑模变控制器进行参数优化可进一步抑制功率传递过程中直流侧电压的波动，同时提高系统的动、静态性能。根据对比可知，相对于传统MFO算法对并网复合装置直流侧电压波动的抑制以及系统动、静态性能的提高，改进MFO算法优化后的参数对并网复合装置直流侧电压波动的抑制以及系统动、静态性能的提高更具有优越性。

5 结论

为解决背靠背MMC-HVDC并网复合装置滑模变控制参数整定困难的问题，本文提出了一种改进飞蛾扑火优化算法，通过优化控制器参数以充分发挥控制器的性能。主要得出以下结论。

(1) 针对飞蛾扑火优化算法全局搜索能力差和容易早熟收敛的问题，本文将佳点集初始化种群和Lévy飞行更新机制与飞蛾扑火优化算法结合，其与原始飞蛾扑火算法相比，收敛速度得到了提升，并改善了算法陷入局部最优的问题。

(2) 针对Matlab-PSCAD联合仿真参数优化方法无法后台运行的问题，提出了基于Automation Library的Python-PSCAD联合仿真方法，以综合ITAE指标为目标函数，实现了原始MFO算法和改进MFO算法应用于背靠背MMC-HVDC并网复合装置滑模变控制器参数的优化。仿真结果表明，控制器参数整定问题得到了解决，同时控制器的性能也得到了有效提升，从而提高了系统的动态和静态性能。

(3) 本文通过仿真分析验证了所提控制器参数优化算法的有效性，可为实际工程控制器参数的调制提供一定的理论依据。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

张兴, 李明, 郭梓暄, 等.

新能源并网逆变器控制策略研究综述与展望

[J]. 全球能源互联网. 2021, 4(5):506-515.