1 引言
近年来,风电并网的容量日益增大,风力发电的出力功率因风速、风向等诸多因素具有不确定性,大规模的风电并网可能对电力系统的稳定运行造成重大影响[1 ] 。因此,提高风电功率预测的准确度,对电力系统的安全、稳定、经济运行具有重要的指导意义。
当前,风电功率的预测按照时间长短可分为超短期预测、短期预测、中长期预测[2 ] ,其中,超短期预测是实时调度及保证风电并网稳定运行的重点工作。风电预测的方法主要有人工神经网络[3 ] 、时间序列法[4 ] 、空间相关性法[5 ] 、极限学习机[6 ] 和最小二乘支持向量机(Least square support vector machine, LSSVM)[7 ] 等。神经网络有较强的信息提取能力和非线性拟合能力,因此在风电功率预测中有着重要的应用[8 ] 。LSSVM相比人工神经网络法有很强的泛化能力,但参数的选择会影响预测效果,若选取不合适将造成较大的预测误差[9 ] 。文献[10 ]运用改进的蚁群算法对LSSVM参数进行优化,利用LSSVM模型分别对风速和风功率进行预测。上述研究中,尽管风电功率预测精度有了较大提升,但是若神经网络等超参数选择不合适将造成收敛速度变慢等问题。
深度学习因具有较强的特征提取能力而得到快速发展。长短时记忆网络(Long short-term memory, LSTM)[11 ] 具有学习长期依赖的能力,适合处理风电功率等非线性序列,文献[12 ]将注意力机制加入LSTM,提高了预测精度。但是LSTM也存在超参数不易确定的问题,不准确的参数设置对预测精度影响很大。因此,采用智能优化算法进行超参数寻优是一种较好的方法。由于风能具有不稳定性和波动性,单一的回归预测模型不能满足高精度要求。因此,需要对原始功率数据进行分解处理,获得较规律的特征。经验模态分解(Empirical mode decomposition, EMD)针对非线性序列的处理具有较好的效果[13 ] 。但是,EMD分解后的各分量可能出现模态混淆的现象[14 ] 。因此,文献[15 ]提出了集成经验模态分解(Ensemble empirical mode decomposition, EEMD)和LSSVM功率预测模型,EEMD分解能避免EMD分解产生的模态混淆现象,但是如果添加的噪声不合适,可能会使计算规模变大,影响功率预测的准确度。自适应噪声完全集合经验模态分解(Complete ensemble empirical mode decomposition with adaptive noise analysis, CEEMDAN)通过加入自适应白噪声能够减少模态混淆的现象,与EEMD方法相比,能够大大减少迭代次数,提高了重构准确度,具有较好的收敛特性。如果对每一个分量都分别直接预测,可能使计算规模变大、预测速度变慢[16 ] ,通过合并样本熵值相近的量可以降低计算规模。
鉴于以上研究,本文提出了改进飞蛾扑火算法(Moth-flame optimization,MFO)优化Attention- LSTM的超短期风电功率预测模型。首先,通过CEEMDAN算法将原始数据分解成不同的模态分量,通过计算样本熵合并相近的IMF分量来降低计算规模。然后,通过对飞蛾扑火算法进行改进,用改进的MFO算法对Attention-LSTM的超参数进行优化。最后,用改进MFO优化Attention-LSTM对合并后的各新分量分别进行预测,将各个分量的单独预测结果进行叠加,可以得到最终的超短期功率预测结果。预测结果表明,该方法相比单一LSSVM、LSTM、Attention-LSTM、MFO-Attention-LSTM等模型具有更好的预测效果,提升了功率预测的准确度。
2 风电功率时间序列的预处理
2.1 风电功率数据特性
当风力发电系统中检测到风向时,相对应的控制系统对涡轮机进行控制以适应不同的风速和风向,风能通过动力系统将动能输送到发电系统,经转换后的电能进行并网。由于风能的自然特性,风速是不断变化的,风力机输出功率也随之不断变化,因此风电功率时间序列具有波动性和不确定性。风电功率与风速关系如下所示
(1) P = 1 2 ρ S V 3 C P
式中,P 为风力机输出功率;ρ 为空气密度;S 为风轮扫掠面积;V 是风速;CP 为风能利用系数。
针对风电功率的波动性和不确定性问题,需要对原始序列进行分解以获得较规律的特征。自适应噪声完全集合经验模态分解(CEEMDAN)通过加入自适应白噪声能够减少EMD分解的模态混淆现象,克服EEMD使计算规模变大的问题,能够大大减少迭代次数,提高重构准确度,具有较好的收敛特性。样本熵是常用来衡量原始时间序列的复杂度。原始序列越复杂,样本熵值就越高[17 ] 。如果对每一个子分量都分别直接预测,可能使计算规模变大、预测速度变慢。因此,将熵值相近的序列合并,可以降低计算规模,提高预测速度。
2.2 风电功率时间序列分解算法
CEEMDAN是对EEMD算法的改进[18 ] ,克服了EEMD产生重构误差的问题,使风电功率原始数据的分解更加完整,更适合非线性信号的分析[19 ] 。CEEMDAN方法分解数据的具体过程如下所示。
步骤1:将信号x (n )中添加I 次均值为0的白噪声,共构造I 次待分解序列
(2) x i ( n ) = x ( n ) + β ω i ( n ) i = 1 , ⋯ , I
式中,β 为白噪声权值系数;ωi (n )为第i 次处理时产生的白噪声。
步骤2:先对上述序列进行EMD分解,分解后得到第一个分量IMF 1 (n )和第一阶段的剩余信号
(3) I M F 1 ( n ) = 1 I ∑ i = 1 I I M F 1 i ( n )
(4) r 1 ( n ) = x ( n ) − I M F 1 ( n )
式中,IMF 1 (n )表示CEEMDAN分解得到的第一个模态分量;I 表示一共I 次待分解序列;r 1 (n )表示第一次分解后的剩余信号。
步骤3:设Ek (·)为模态算子,对r 1 (n )+γ 1 E 1 (ωi (n ))进行分解,则CEEMDAN的第二模态分量为
(5) I M F 2 ( n ) = 1 I ∑ i = 1 I E 1 { r 1 ( n ) + β 1 E 1 [ ω i ( n ) ] }
式中,β 1 为白噪声权值系数;ωi (n )为第i 次处理时产生的白噪声;r 1 (n )为第一阶段剩余信号;E 1 为模态算子;I 表示分解序列次数。剩余信号表示为
(6) r 2 ( n ) = r 1 ( n ) − I M F ( n )
(7) r k ( n ) = r k − 1 ( n ) − I M F k ( n )
(8) I M F ( k + 1 ) ( n ) = 1 I ∑ i = 1 I E 1 { r k ( n ) + β k E k [ ω i ( n ) ] }
步骤5:重复上述步骤,直到满足CEEMDAN停止条件,最后数据分解为
(9) x ( n ) = ∑ k = 1 K I M F k ( n ) + R ( n )
2.3 样本熵
对于N 个样本的时间序列,组成m 维向量序列X (1),X (2),…,X (N-m+ 1),其中Xm (i )= [x (i ),x (i+ 1),…,x (i+m- 1)],定义序列中绝对值相差最大的距离为dm (X (i ),X (j ))<r ,给定相似容限r ,对每一个i 值统计dm (X (i ),X (j ))<r 的数目,其与距离总数的比值为Bm (r )。
(10) S a m p E n ( m , r ) = lim N → ∞ − ln B m + 1 ( r ) B m ( r )
(11) S a m p E n ( N , m , r ) = − ln B m + 1 ( r ) B m ( r )
3 Attention-LSTM和改进MFO算法
长短期记忆网络[20 ] (LSTM)是对传统循环神经网络(Recurrent neural network, RNN)的改进,具有学习长期依赖的能力,适合处理风电功率预测和负荷预测等动态非线性数据。由于风电数据具有间断性、不确定性等特点,本文将Attention机制用于计算LSTM神经网络的隐层状态的不同权重,以选择性地关注不同时刻输入对风电功率预测的影响,从而改善功率预测效果。针对LSTM模型超参数目标函数表达式未知、超参数众多、迭代搜索复杂等问题,提出改进的MFO算法优化LSTM模型,得到最优的超参数组合。
3.1 LSTM神经网络
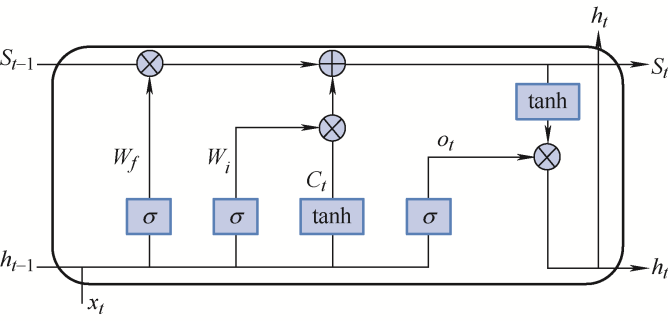
LSTM引入遗忘门、输入门和输出门三个门来解决RNN存在的梯度不合理问题,其结构如图1 所示。这些门使LSTM在进行反向传播中能有一个更稳定的误差,使风电功率预测模型可以在多个时间步上继续学习,减小风电功率预测的误差,提高风电功率预测的精度。
(12) h t = f h t − 1 , X t
(13) i t = σ W i × h t − 1 , X t + b i
(14) f t = σ W f × h t − 1 , X t + b f
(15) o t = σ W o × h t − 1 , X t + b o
(16) C t = tanh W c × h t − 1 , X t + b c
(17) S t = f t × S t − 1 + i t × C t
(18) h t = o t × tanh S t
式中,W 和b 是LSTM单元的参数;St 是当前单元状态;Ct 是新单元状态St 的候选值;ot 表示输出门;ft 表示遗忘门;it 表示输入门。
图1
3.2 Attention机制
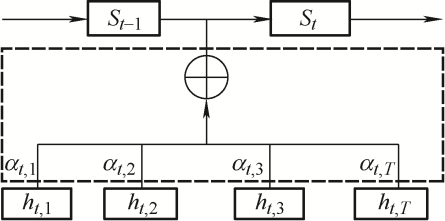
Attention机制是一种模拟人脑注意力的模型,根据风电功率数据输入的每一项特征对输出风电功率预测值的影响来为神经网络中的隐层状态赋予不同的权重。主要原理是通过保持LSTM层对输入序列建模时每一步的中间输出结果,并将它们与输出风电功率的值联系起来,从而训练模型选择性地关注输入功率数据,为相关性更高的功率输入向量赋予更高的权重,具体原理如图2 所示。
图2
在t 时刻得到LSTM层的隐层状态为[ht , 1 ,ht , 2 ,⋯,ht , i ht , T αt , i t 时刻隐层状态hi 对当前输出的注意力权重,本文选择点乘形式计算注意力权重,如下所示
(19) e t , i = S t − 1 T × h t , i
(20) α t , i = exp e t , i ∑ k = 1 T exp e t , k
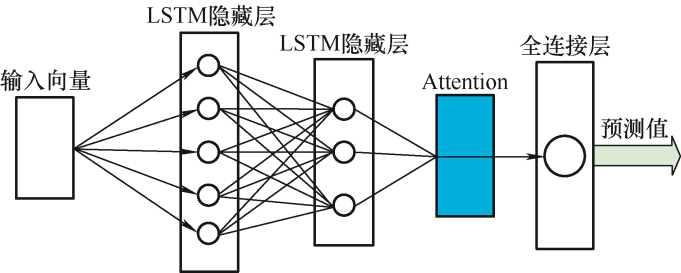
本文将Attention机制用于计算LSTM神经网络隐层状态的不同权重,结合注意力权重和LSTM神经网络实现超短期风电功率预测。输入向量由输入层进入LSTM隐藏层进行训练,经训练后的向量进入注意力机制层,通过该层进行权重计算,得到的新向量进入全连接层,经过训练输出风电功率最终预测值。Attention-LSTM预测模型如图3 所示。
图3
3.3 标准飞蛾扑火算法(MFO)
MFO算法优化问题的待求解是飞蛾的位置,将飞蛾群按适应度排列后作为火焰,飞蛾根据螺旋函数不断向火焰运动,寻优过程中火焰数量不断减少,直到适应度值符合要求则停止[21 ] 。算法原理如下所示。
飞蛾种群由矩阵M
(21) O M = O M 1 . . . O M n
MFO算法要求每只飞蛾有与其对应的火焰来更新其位置,对全局搜索能力有较大提升。飞蛾位置用矩阵F
(22) O F = O F 1 . . . O F n
(23) M i = S ( M i , F j )
式中,M i i 只飞蛾;F j j 个火焰;S 为螺旋函数。S 的计算式如下所示
(24) S M i , F j = D i ⋅ e b t ⋅ cos 2 π t + F j
式中,D i j 和飞蛾i 之间的距离;b 为螺旋常数;t 为[-1,1]区间中的随机数。Di 的计算式如下
(25) D i = F j − M i
(26) F lame . no = r o u n d N − k · N − 1 T
式中,N 表示飞蛾种群数;k 表示迭代次数;T 表示总迭代次数。
3.4 改进MFO算法
在求解复杂的多峰值函数过程中,传统的飞蛾扑火算法在飞蛾飞向火焰的过程中容易使飞蛾错过全局的最优点,仍存在收敛精度不够、收敛速度慢、陷入局部最优等缺点。因此,本文通过加入混沌映射、自适应权值、柯西变异对传统MFO算法进行改进。
3.4.1 Chebyshev混沌映射
混沌优化是利用混沌映射产生的混沌序列,具有内部随机性和遍历、均匀性等特点。通过混沌映射可以得到分布均匀及多样化的初始种群,因此可以提高算法寻优的能力,有利于克服局部最优问题,找到全局最优解。
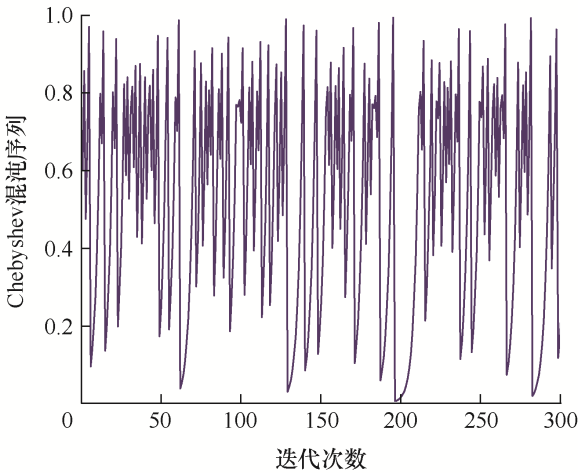
Chebyshev混沌映射的混沌序列拥有较好的内部随机特性,而且零均值白噪声统计和遍历统计特性一致。定义如下
(27) x n + 1 = cos [ k cos − 1 ( x n ) ] x n ∈ − 1 , 1
式中,k 为控制参数;x 0 为初值。其迭代过程如图4 所示。
图4
采用式(28)将Chebyshev映射产生的变量映射到飞蛾个体上,实现飞蛾种群的初始化。
(28) x = x l b + x l b − x u b x k + 1
式中,xlb 、xub 分别为每个个体在每个维度的上限和下限;x 为映射后个体。
3.4.2 Sigmoid函数的惯性权重
传统的飞蛾扑火算法在飞蛾飞向火焰的过程中容易使飞蛾错过全局的最优点,有一定的缺点。本文借鉴粒子群算法的改进,引入自适应权值的方法,其自适应权值从1到0非线性减小,可以提高算法后期的寻找最优解能力,避免错过最优解。本文引入基于Sigmoid函数的惯性权值,表达式如下
(29) ω = 1 − 1+exp − l T − 1
引入惯性权值后的飞蛾相对火焰位置更新策略表达式如下
(30) S M i , F j = D i ⋅ e b t ⋅ cos 2 π t + ω F j
惯性权值ω ω ω
3.4.3 柯西变异
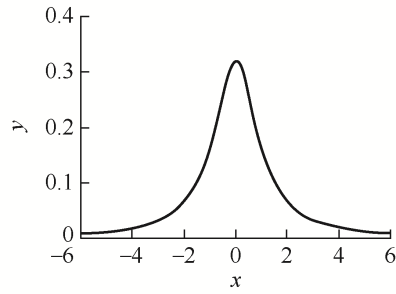
(31) y = 1 π t t 2 + x 2 − ∞ < x < + ∞
式中,t 为比例参数且大于0。其函数图像如图5 所示。
图5
柯西分布使其产生与原点相距很远的随机数,通过柯西变异,飞蛾个体能快速逃离局部极值。每次计算迭代中由柯西分布产生柯西变异矩阵,变异公式如下
(32) S M i , F j = β × C 1 , 0 × D i e b t ⋅ cos 2 π t + F j
式中,C (1,0)表示柯西分布;Fj 为待变异飞蛾的位置;β 影响柯西变异的范围。更新公式如下
(33) β = α M b − N b
式中,Mb 表示解空间的上限;Nb 表示解空间的下限;α 是不断更新的参数。通过柯西变异提高了种群搜索的多样性。
3.5 算法性能测试
为验证改进MFO算法的寻优能力,选用表1 所示的四种函数作为对比不同算法寻优性能的测试函数。
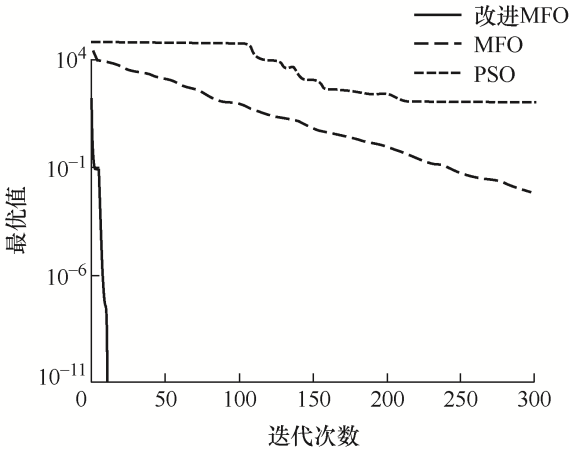
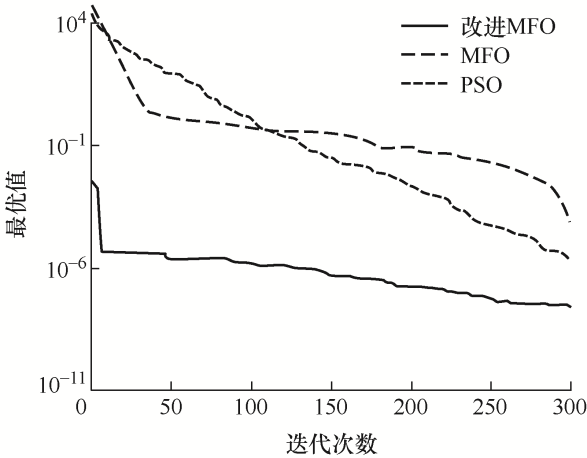
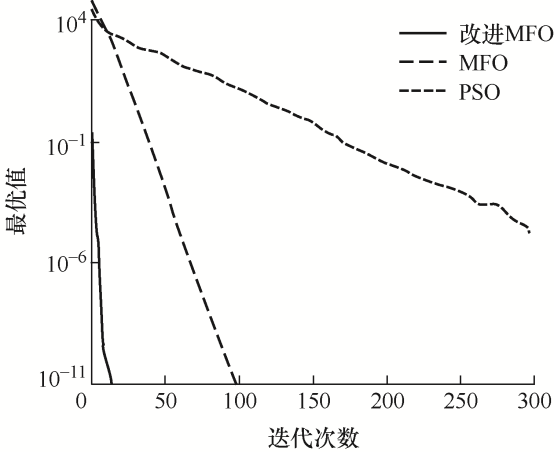
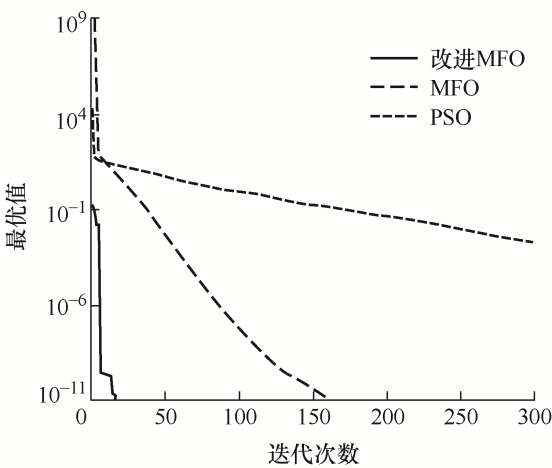
将改进的MFO算法和原始MFO、PSO算法进行寻优性能比较,寻优过程如图6 ~9 所示,寻优结果如表2 所示。
图6
图7
图8
图9
f 1 和f 3 函数仅有全局最小点,改进MFO算法相比其他算法有较高的收敛精度和速度。f 2 和f 4 函数具有多个极小值,可以看出改进MFO算法能跳出局部最优,收敛到全局最小值。
通过以上比较试验可以看出,加入混沌映射、柯西变异和惯性权重对于改善飞蛾扑火算法的寻优能力和收敛速度具有十分明显的作用,而且和其他算法相比,对于不同测试函数,改进后的飞蛾扑火算法都具有较强的适应能力。
4 基于改进MFO优化Attention- LSTM的模型建立
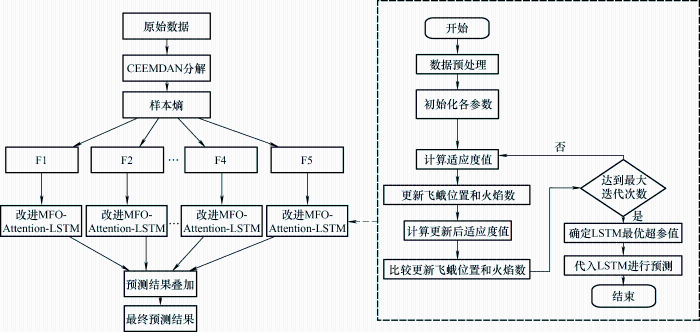
风电功率具有不确定性、波动性等特征。本文建立一种基于改进MFO优化Attention-LSTM的风电功率超短期预测模型,以提高风电功率预测的准确度,组合模型建模过程如图10 所示,具体步骤如下所示。
步骤1:数据预处理:对风电功率数据预处理,去掉其中的异常值。
步骤2:初始化各参数,包括超参数寻优范围、设置控制变量维度d 、搜索规模n 、最高迭代次数T 、螺旋常数b 等参数。
步骤3:将LSTM中的超参数第一隐含层单元数、第二隐含层单元数、学习率作为优化对象。
步骤4:通过式(23)更新飞蛾与火焰的相对位置。计算飞蛾适应度值并与上次迭代过程的值作对比。若高出原值,则保存新值为最优适应值;否则保留原值继续迭代。
步骤5:达到迭代条件后,停止搜索,输出最优的超参数。否则返回步骤4重新计算。
步骤6:采用CEEMDAN方法将原始风电功率数据进行分解得到各IMF分量和残余量R (n )。
步骤7:计算各分解得到的各分量的样本熵值,将样本熵值近似的分量进行相加,得到新分量。
步骤8:针对每个子分量分别建立改进MFO- Attention-LSTM预测模型,得到各自的预测值。
步骤9:将各分量的风电功率预测结果线性叠加,得到超短期风电功率预测的最终结果。
图10
图10
改进MFO优化Attention-LSTM预测流程
5 实例仿真分析
5.1 模型的评价标准
为对预测结果进行科学准确评价,本文选取平均绝对百分比误差(Mean absolute percentage error, MAPE)和均方根误差(Root mean square error, RMSE)进行评估。
(34) M A P E = 1 n ∑ i = 1 n y i − y ^ i y i × 100 %
(35) R M S E = ∑ i = 1 n ( y i − y ^ i ) 2 n
5.2 数据选择与处理
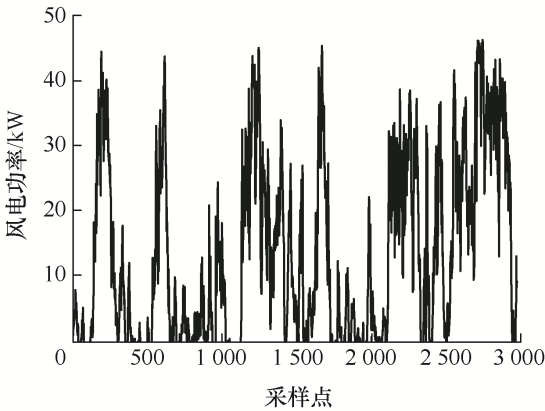
本文以锦州某风电场24台2 kW风机总功率从2020年12月1日至31日共31天的2 976组数据进行建模仿真分析,原始数据采样间隔为15 min。将前26天的2 496组数据作为训练样本,后5天的480组数据作为测试样本。本文对风电功率采用提前15 min的单步预测,采用迭代式预测,即将前一刻预测数据作为历史值进行下一次预测。原始数据时间序列如图11 所示。由图11 可知,风机最高功率与最低功率变化幅度较大,体现了风电功率的不稳定性和波动性。
图11
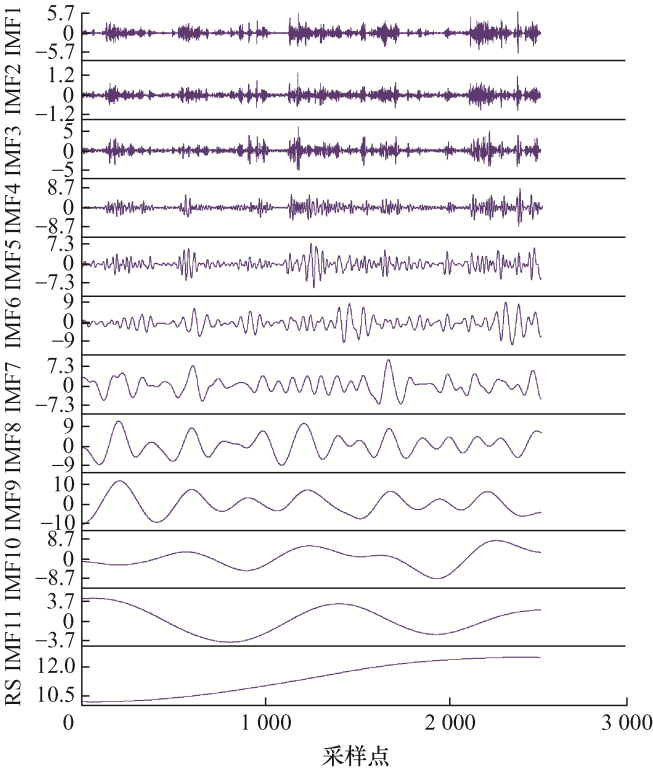
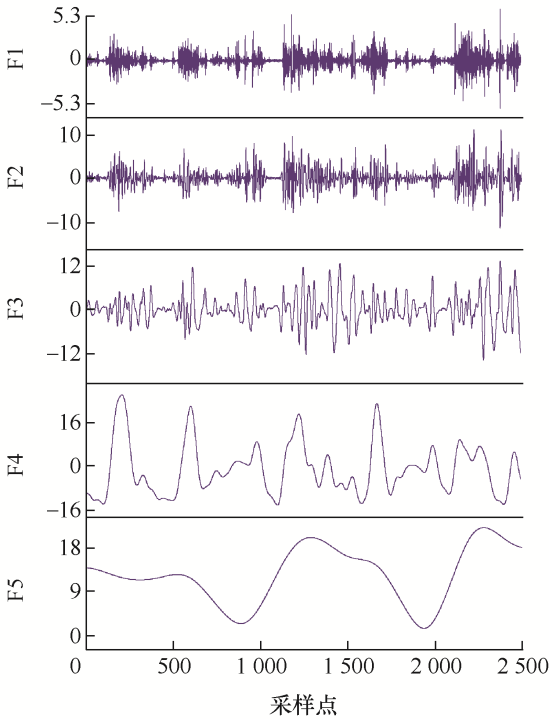
首先对训练集 2 496 组功率原始数据进行CEEMDAN分解,结果如图12 所示。
图12
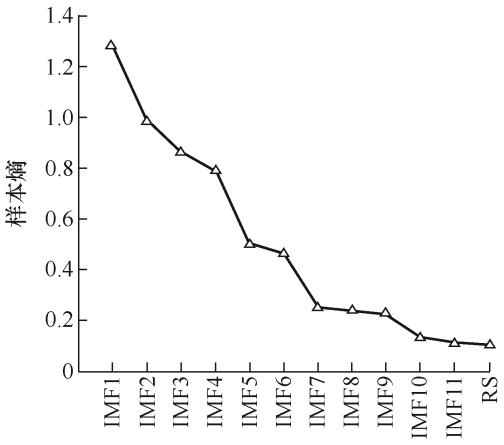
然后计算各分量的样本熵,由式(10)、(11)可以看出,样本熵值受m 、r 大小的影响。由研究结果可知[22 ] ,m= 1或2,r =0.1Sd ~0.25Sd 时得到的样本熵较合理且经过多次试验,本文中取m =2,r =0.2Sd 。CEEMDAN分解的各分量样本熵如图13 所示。
图13
由图13 可以看出,各分量的样本熵值随着各个IMF分量频率的下降而不断降低,说明样本的复杂度不断减小,证明样本熵值有效。
单独对每个IMF分量进行预测,会使计算规模变大,为了降低计算规模,将熵值相近的分量进行合并,产生新的序列,针对每一个新序列,分别采用改进MFO-Attention-LSTM模型进行仿真预测,降低非平稳性对预测结果产生的影响。各IMF分量合并重组后的新序列结果如表3 所示,合并后的新分量如图14 所示。
图14
5.3 改进MFO-Attention-LSTM模型超参数优化结果
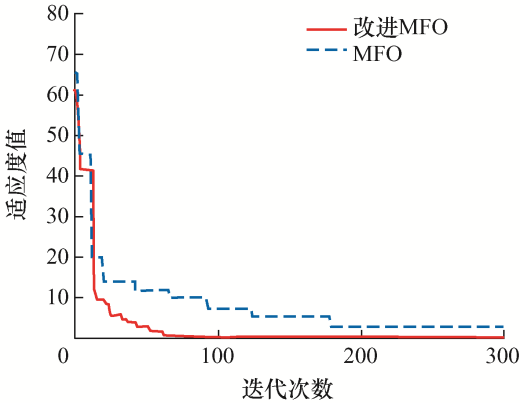
针对风电功率预测,本文将MFO-LSTM和改进MFO-LSTM模型的输入层个数设置为1,随着隐藏层数目的增多,模型的拟合能力提高,但是模型复杂度和训练时间也将增加,本文设置隐藏层个数为2,根据历史功率数据预测下一步的风电功率,因此设输出层个数为1。飞蛾种群规模设置为50,控制变量维度d 为3,最大迭代次数为300。学习率的搜索范围为[0.000 1,0.01],第一隐藏层神经元个数n 1 和第二隐藏层神经元个数n 2 的搜索范围为[0,100]。经过多次试验,将LSTM网络的n 1 设置为20,n 2 设置为10,学习率为0.001。MFO算法和改进MFO算法寻优过程飞蛾个体适应度变化曲线如图15 所示。
图15
由图15 可知,改进MFO算法比MFO算法更易找到最优解,并且适应度值更小,说明改进MFO算法具有更好的寻优性能。
MFO算法寻找的最优LSTM参数为n 1 =40,n 2 =75,学习率为2.313×10-3 ;改进MFO算法寻找的最优参数为n 1 =15,n 2 =10,学习率为1.622×10-3 。
5.4 预测结果分析
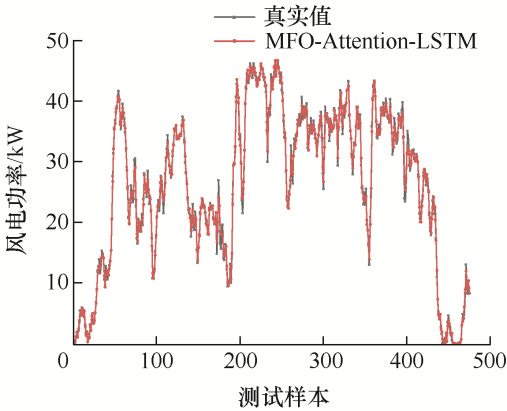
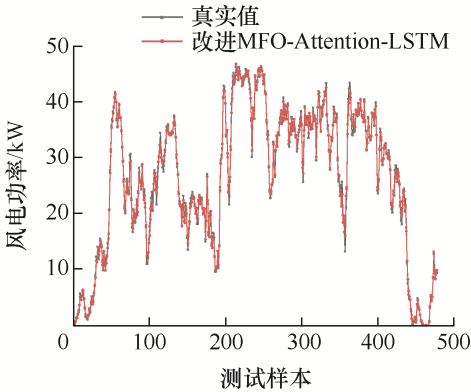
标准的MFO算法优化Attention-LSTM模型和改进MFO优化Attention-LSTM模型的功率预测结果分别如图16 、17 所示。
图16
图16
MFO优化Attention-LSTM预测结果
图17
图17
改进MFO优化Attention-LSTM预测结果
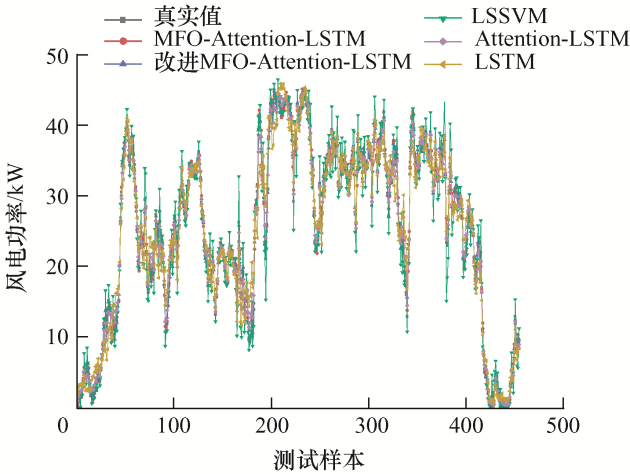
为了进一步验证改进MFO-Attention-LSTM算法的准确性,本文还采用单一LSSVM算法、LSTM算法和Attention-LSTM算法,来对风电功率进行超短期对比预测。不同模型测试样本预测结果如图18 所示。
图18
由图16 、17 可知,改进MFO-Attention-LSTM算法的预测曲线拟合程度更高,预测精度更是高于MFO-Attention-LSTM算法。由图18 可以看出,单一的LSSVM模型拟合情况最差,改进MFO- Attention-LSTM的预测曲线拟合程度高于其他四种,说明本文所提模型预测效果较好。各模型的误差结果如表4 所示。MAPE的值在10%以下则认为模型预测准确度较高。
由表4 可知,LSTM模型比单一的LSSVM模型的MAPE值降低了4.10%,RMSE的值也下降1.404。加入Attention机制的LSTM预测模型比LSTM模型的MAPE值降低2.51%,RMSE值降低0.912,引入MFO优化算法的Attention-LSTM模型比Attention-LSTM模型的MAPE值降低了2.89%,RMSE值降低了0.517,说明加入Attention机制和MFO优化算法使预测精度都有了提升。本文提出的改进MFO-Attention-LSTM算法的MAPE的值比其他四种模型分别降低了12.16%、8.06%、5.55%、2.66%,且均方根误差(RMSE)值分别降低2.998、1.594、0.682、0.165,预测精度有了很大提高,能够更好地应用于风力机发电功率预测,对风电并网运行具有一定的指导意义。
6 结论
(1) 针对风电功率的不确定性,研究CEEMDAN分解技术、样本熵理论。CEEMDAN分解有效解决了模态混叠现象,提高了预测精度;样本熵法可以合并相似分量,大大降低计算规模,提高预测速度。
(2) 鉴于MFO算法存在收敛速度慢,易陷入局部最优的问题,通过加入混沌映射和柯西变异、惯性权重对MFO算法进行改进,显著提高了算法的收敛能力,并且可以克服局部最优的缺点,最后通过和传统算法进行对比论证了该算法的优越性。
(3) 将Attention机制用于计算LSTM神经网络的隐层状态的不同权重,Attention-LSTM模型中,结合注意力权重和LSTM神经网络实现超短期风电功率预测。
(4) 本文方法较单一的LSSVM、LSTM、Attention-LSTM、MFO-Attention-LSTM算法具有更高的预测精度,具有一定的理论研究和工程实践意义。
参考文献
View Option
[1]
林卫星 , 文劲宇 , 艾小猛 , 等 . 风电功率波动特性的概率分布研究
[J]. 中国电机工程学报 , 2012 , 32 (1 ):38 -46 .
[本文引用: 1]
LIN Weixing WEN Jinyu AI Xiaomeng et al. Research on probability distribution of wind power fluctuation characteristics
[J]. Proceedings of the CSEE , 2012 , 32 (1 ):38 -46 .
[本文引用: 1]
[2]
姜贵敏 , 陈志军 , 李笑竹 , 等 . 基于EEMD-ACS-LSSVM的短期风电功率预测
[J]. 太阳能学报 , 2020 , 41 (5 ):77 -84 .
[本文引用: 1]
JIANG Guimin CHEN Zhijun LI Xiaozhu et al. Short-term wind power forecast based on EEMD-ACS-LSSVM
[J]. Acta Energiae Solaris Sinica , 2020 , 41 (5 ):77 -84 .
[本文引用: 1]
[3]
孙改平 , 蒋传文 . 基于两级级联聚类的神经网络风电功率预测
[J]. 太阳能学报 , 2021 , 42 (3 ):56 -62 .
[本文引用: 1]
SUN Gaiping JIANG Chuanwen Neural network wind power prediction based on two-level cascade clustering
[J]. Acta Energiae Solaris Sinica , 2021 , 42 (3 ):56 -62 .
[本文引用: 1]
[4]
黎静华 , 黄玉金 , 黄乾 . 基于改进混沌时间序列的风电功率区间预测方法
[J]. 电力自动化设备 , 2019 , 39 (5 ):53 -60 ,68.
[本文引用: 1]
LI Jinghua HUANG Yujin HUANG Qian Wind power interval forecasting method based onimproved chaotic time series
[J]. Electric Power Automation Equipment , 2019 , 39 (5 ):53 -60 ,68.
[本文引用: 1]
[5]
胡帅 , 向月 , 沈晓东 , 等 . 计及气象因素和风速空间相关性的风电功率预测模型
[J]. 电力系统自动化 , 2021 , 45 (7 ):28 -36 .
[本文引用: 1]
HU Shuai XIANG Yue SHEN Xiaodong et al. Wind power prediction model considering meteorological factor and spatial correlation of wind speed
[J]. Automation of Electric Power Systems , 2021 , 45 (7 ):28 -36 .
[本文引用: 1]
[6]
杨锡运 , 邢国通 , 马雪 , 等 . 一种核极限学习机分位数回归模型及风电功率区间预测
[J]. 太阳能学报 , 2020 , 41 (11 ):300 -306 .
[本文引用: 1]
YANG Xiyun XING Guotong MA Xue et al. A quantile regression model of nuclear extreme learning machine and interval prediction of wind power
[J]. Acta Energiae Solaris Sinica , 2020 , 41 (11 ):300 -306 .
[本文引用: 1]
[7]
向玲 , 邓泽奇 . 基于改进经验小波变换和最小二乘支持向量机的短期风速预测
[J]. 太阳能学报 , 2021 , 42 (2 ):97 -103 .
[本文引用: 1]
XIANG Ling DENG Zeqi Short-term wind speed prediction based on improved empirical wavelet transform and least square support vector machine
[J]. Acta Energiae Solaris Sinica , 2021 , 42 (2 ):97 -103 .
[本文引用: 1]
[9]
谢国民 , 倪乐水 , 曹媛 . 基于VSRP与β-GWO-SVM的变压器故障辨识方法
[J]. 高电压技术 , 2021 , 47 (10 ):3635 -3641 .
[本文引用: 1]
XIE Guomin NI Leshui CAO Yuan Transformer fault identification method based on VSRP and β-GWO-SVM
[J]. High Voltage Engineering , 2021 , 47 (10 ):3635 -3641 .
[本文引用: 1]
[10]
LI Yanan YANG Peng WANG Huajun Short-term wind speed forecasting based on improved ant colony algorithm for LSSVM
[J]. Cluster Computing , 2019 , 22 (5 ):11575 -11581 .
DOI:10.1007/s10586-017-1422-2
[本文引用: 1]
[11]
王炜 , 刘宏伟 , 陈永杰 , 等 . 基于LSTM循环神经网络的风力发电预测
[J]. 可再生能源 , 2020 , 38 (9 ):1187 -1191 .
[本文引用: 1]
WANG Wei LIU Hongwei CHEN Yongjie et al. Wind power generation forecast based on LSTM recurrent neural network
[J]. Renewable Energy , 2020 , 38 (9 ):1187 -1191 .
[本文引用: 1]
[12]
钱勇生 , 邵洁 , 季欣欣 , 等 . 基于LSTM-Attention网络的短期风电功率预测
[J]. 电机与控制应用 , 2019 , 46 (9 ):95 -100 .
[本文引用: 1]
QIAN Yongsheng SHAO Jie JI Xinxin et al. Short-term wind power prediction based on LSTM-Attention network
[J]. Electric Machines and Control Application , 2019 , 46 (9 ):95 -100 .
[本文引用: 1]
[13]
赵倩 , 黄景涛 . 基于EMD-SA-SVR的超短期风电功率预测研究
[J]. 电力系统保护与控制 , 2020 , 48 (4 ):89 -96 .
[本文引用: 1]
ZHAO Qian HUANG Jingtao Research on ultra-short-term wind power prediction based on EMD-SA-SVR
[J]. Power System Protection and Control , 2020 , 48 (4 ):89 -96 .
[本文引用: 1]
[14]
文孝强 , 许洋 . 基于EMD分解的风力机功率特性分析与预测建模
[J]. 太阳能学报 , 2021 , 42 (11 ):293 -298 .
[本文引用: 1]
WEN Xiaoqiang XU Yang Analysis and prediction modeling of wind turbine power characteristics based on EMD decomposition
[J]. Acta Energiae Solaris Sinica , 2021 , 42 (11 ):293 -298 .
[本文引用: 1]
[15]
程启明 , 陈路 , 程尹曼 , 等 . 基于EEMD和LS-SVM模型的风电功率短期预测方法
[J]. 电力自动化设备 , 2018 , 38 (5 ):27 -35 .
[本文引用: 1]
CHENG Qiming CHEN Lu CHENG Yinman et al. Short-term wind power forecasting method based on EEMD and LS-SVM model
[J]. Electric Power Automation Equipment , 2018 , 38 (5 ):27 -35 .
[本文引用: 1]
[16]
YEH J R SHIEH J S HUANG N E Complementary ensemble empirical mode decomposition:A novel noise enhanced data analysis method
[J]. Advances in Adaptive Data Analysis , 2010 , 2 (2 ):135 -156 .
DOI:10.1142/S1793536910000422
URL
[本文引用: 1]
The phenomenon of mode-mixing caused by intermittence signals is an annoying problem in Empirical Mode Decomposition (EMD) method. The noise assisted method of Ensemble EMD (EEMD) has not only effectively resolved this problem but also generated a new one, which tolerates the residue noise in the signal reconstruction. Of course, the relative magnitude of the residue noise could be reduced with large enough ensemble, it would be too time consuming to implement. An improved algorithm of noise enhanced data analysis method is suggested in this paper. In this approach, the residue of added white noises can be extracted from the mixtures of data and white noises via pairs of complementary ensemble IMFs with positive and negative added white noises. Though this new approach yields IMF with the similar RMS noise as EEMD, it effectively eliminated residue noise in the IMFs. Numerical experiments were conducted to demonstrate the new approach and also illustrate the problems of mode splitting and translation.
[17]
杨森 , 刘三明 , 王致杰 . 基于GRU-XGBoost的风电场功率短期预测
[J]. 仪表技术 , 2020 (1 ):17 -21 .
[本文引用: 1]
YANG Sen LIU Sanming WANG Zhijie Short-term prediction of wind farm power based on GRU-XGBoost
[J]. Instrumentation Technology , 2020 (1 ):17 -21 .
[本文引用: 1]
[18]
张学清 , 梁军 , 张熙 , 等 . 基于样本熵和极端学习机的超短期风电功率组合预测模型
[J]. 中国电机工程学报 , 2013 , 33 (25 ):33 -40 .
[本文引用: 1]
ZHANG Xueqing LIANG Jun ZHANG Xi et al. Ultra-short-term wind power combined forecasting model based on sample entropy and extreme learning machine
[J]. Proceedings of the CSEE , 2013 , 33 (25 ):33 -40 .
[本文引用: 1]
[19]
魏乐 , 李思莹 . 基于MEEMD-LSSVM的风电功率超短期预测研究
[J]. 智慧电力 , 2020 , 48 (5 ):21 -26 .
[本文引用: 1]
WEI Le LI Siying Research on ultra-short-term prediction of wind power based on MEEMD-LSSVM
[J]. Smart Power , 2020 , 48 (5 ):21 -26 .
[本文引用: 1]
[20]
潘晓杰 , 张立伟 , 张文朝 , 等 . 基于飞蛾扑火优化算法的多运行方式电力系统稳定器参数协调优化方法
[J]. 电网技术 , 2020 , 44 (8 ):3038 -3046 .
[本文引用: 1]
PAN Xiaojie ZHANG Liwei ZHANG Wenchao et al. Coordinated optimization method of multi-operation power system stabilizer parameters based on moth fire suppression optimization algorithm
[J]. Power System Technology , 2020 , 44 (8 ):3038 -3046 .
[本文引用: 1]
[21]
LIN T K LEE D Y Composite multiscale cross-sample entropy analysis for long-term structural health monitoring of residential buildings
[J]. Entropy , 2020 , 23 (1 ):60 .
DOI:10.3390/e23010060
URL
[本文引用: 1]
This study proposesd a novel, entropy-based structural health monitoring (SHM) system for measuring microvibration signals generated by actual buildings. A structural health diagnosis interface was established for demonstration purposes. To enhance the reliability and accuracy of entropy evaluation at various scales, composite multiscale cross-sample entropy (CMSCE) was adopted to increase the number of coarse-grained time series. The degree of similarity and asynchrony between ambient vibration signals measured on adjacent floors was used as an in-dicator for structural health assessment. A residential building that has been monitored since 1994 was selected for long-term monitoring. The accumulated database, including both the earthquake and ambient vibrations in each seismic event, provided the possibility to evaluate the practicability of the CMSCE-based method. Entropy curves obtained for each of the years, as well as the stable trend of the corresponding damage index (DI) graphs, demonstrated the relia-bility of the proposed SHM system. Moreover, two large earthquake events that occurred near the monitoring site were analyzed. The results revealed that the entropy values may have been slightly increased after the earthquakes. Positive DI values were obtained for higher floors, which could provide an early warning of structural instability. The proposed SHM system is highly stable and practical.
[22]
刘强 , 胡志强 , 周宇 , 等 . 基于CEEMD和随机森林算法的短期风电功率预测
[J]. 智慧电力 , 2019 , 47 (6 ):71 -76 ,94.
[本文引用: 1]
LIU Qiang HU Zhiqiang ZHOU Yu et al. Short-term wind power prediction based on CEEMD and random forest algorithm
[J]. Smart Power , 2019 , 47 (6 ):71 -76 ,94.
[本文引用: 1]
风电功率波动特性的概率分布研究
1
2012
... 近年来,风电并网的容量日益增大,风力发电的出力功率因风速、风向等诸多因素具有不确定性,大规模的风电并网可能对电力系统的稳定运行造成重大影响[1 ] .因此,提高风电功率预测的准确度,对电力系统的安全、稳定、经济运行具有重要的指导意义. ...
Research on probability distribution of wind power fluctuation characteristics
1
2012
... 近年来,风电并网的容量日益增大,风力发电的出力功率因风速、风向等诸多因素具有不确定性,大规模的风电并网可能对电力系统的稳定运行造成重大影响[1 ] .因此,提高风电功率预测的准确度,对电力系统的安全、稳定、经济运行具有重要的指导意义. ...
基于EEMD-ACS-LSSVM的短期风电功率预测
1
2020
... 当前,风电功率的预测按照时间长短可分为超短期预测、短期预测、中长期预测[2 ] ,其中,超短期预测是实时调度及保证风电并网稳定运行的重点工作.风电预测的方法主要有人工神经网络[3 ] 、时间序列法[4 ] 、空间相关性法[5 ] 、极限学习机[6 ] 和最小二乘支持向量机(Least square support vector machine, LSSVM)[7 ] 等.神经网络有较强的信息提取能力和非线性拟合能力,因此在风电功率预测中有着重要的应用[8 ] .LSSVM相比人工神经网络法有很强的泛化能力,但参数的选择会影响预测效果,若选取不合适将造成较大的预测误差[9 ] .文献[10 ]运用改进的蚁群算法对LSSVM参数进行优化,利用LSSVM模型分别对风速和风功率进行预测.上述研究中,尽管风电功率预测精度有了较大提升,但是若神经网络等超参数选择不合适将造成收敛速度变慢等问题. ...
Short-term wind power forecast based on EEMD-ACS-LSSVM
1
2020
... 当前,风电功率的预测按照时间长短可分为超短期预测、短期预测、中长期预测[2 ] ,其中,超短期预测是实时调度及保证风电并网稳定运行的重点工作.风电预测的方法主要有人工神经网络[3 ] 、时间序列法[4 ] 、空间相关性法[5 ] 、极限学习机[6 ] 和最小二乘支持向量机(Least square support vector machine, LSSVM)[7 ] 等.神经网络有较强的信息提取能力和非线性拟合能力,因此在风电功率预测中有着重要的应用[8 ] .LSSVM相比人工神经网络法有很强的泛化能力,但参数的选择会影响预测效果,若选取不合适将造成较大的预测误差[9 ] .文献[10 ]运用改进的蚁群算法对LSSVM参数进行优化,利用LSSVM模型分别对风速和风功率进行预测.上述研究中,尽管风电功率预测精度有了较大提升,但是若神经网络等超参数选择不合适将造成收敛速度变慢等问题. ...
基于两级级联聚类的神经网络风电功率预测
1
2021
... 当前,风电功率的预测按照时间长短可分为超短期预测、短期预测、中长期预测[2 ] ,其中,超短期预测是实时调度及保证风电并网稳定运行的重点工作.风电预测的方法主要有人工神经网络[3 ] 、时间序列法[4 ] 、空间相关性法[5 ] 、极限学习机[6 ] 和最小二乘支持向量机(Least square support vector machine, LSSVM)[7 ] 等.神经网络有较强的信息提取能力和非线性拟合能力,因此在风电功率预测中有着重要的应用[8 ] .LSSVM相比人工神经网络法有很强的泛化能力,但参数的选择会影响预测效果,若选取不合适将造成较大的预测误差[9 ] .文献[10 ]运用改进的蚁群算法对LSSVM参数进行优化,利用LSSVM模型分别对风速和风功率进行预测.上述研究中,尽管风电功率预测精度有了较大提升,但是若神经网络等超参数选择不合适将造成收敛速度变慢等问题. ...
Neural network wind power prediction based on two-level cascade clustering
1
2021
... 当前,风电功率的预测按照时间长短可分为超短期预测、短期预测、中长期预测[2 ] ,其中,超短期预测是实时调度及保证风电并网稳定运行的重点工作.风电预测的方法主要有人工神经网络[3 ] 、时间序列法[4 ] 、空间相关性法[5 ] 、极限学习机[6 ] 和最小二乘支持向量机(Least square support vector machine, LSSVM)[7 ] 等.神经网络有较强的信息提取能力和非线性拟合能力,因此在风电功率预测中有着重要的应用[8 ] .LSSVM相比人工神经网络法有很强的泛化能力,但参数的选择会影响预测效果,若选取不合适将造成较大的预测误差[9 ] .文献[10 ]运用改进的蚁群算法对LSSVM参数进行优化,利用LSSVM模型分别对风速和风功率进行预测.上述研究中,尽管风电功率预测精度有了较大提升,但是若神经网络等超参数选择不合适将造成收敛速度变慢等问题. ...
基于改进混沌时间序列的风电功率区间预测方法
1
2019
... 当前,风电功率的预测按照时间长短可分为超短期预测、短期预测、中长期预测[2 ] ,其中,超短期预测是实时调度及保证风电并网稳定运行的重点工作.风电预测的方法主要有人工神经网络[3 ] 、时间序列法[4 ] 、空间相关性法[5 ] 、极限学习机[6 ] 和最小二乘支持向量机(Least square support vector machine, LSSVM)[7 ] 等.神经网络有较强的信息提取能力和非线性拟合能力,因此在风电功率预测中有着重要的应用[8 ] .LSSVM相比人工神经网络法有很强的泛化能力,但参数的选择会影响预测效果,若选取不合适将造成较大的预测误差[9 ] .文献[10 ]运用改进的蚁群算法对LSSVM参数进行优化,利用LSSVM模型分别对风速和风功率进行预测.上述研究中,尽管风电功率预测精度有了较大提升,但是若神经网络等超参数选择不合适将造成收敛速度变慢等问题. ...
Wind power interval forecasting method based onimproved chaotic time series
1
2019
... 当前,风电功率的预测按照时间长短可分为超短期预测、短期预测、中长期预测[2 ] ,其中,超短期预测是实时调度及保证风电并网稳定运行的重点工作.风电预测的方法主要有人工神经网络[3 ] 、时间序列法[4 ] 、空间相关性法[5 ] 、极限学习机[6 ] 和最小二乘支持向量机(Least square support vector machine, LSSVM)[7 ] 等.神经网络有较强的信息提取能力和非线性拟合能力,因此在风电功率预测中有着重要的应用[8 ] .LSSVM相比人工神经网络法有很强的泛化能力,但参数的选择会影响预测效果,若选取不合适将造成较大的预测误差[9 ] .文献[10 ]运用改进的蚁群算法对LSSVM参数进行优化,利用LSSVM模型分别对风速和风功率进行预测.上述研究中,尽管风电功率预测精度有了较大提升,但是若神经网络等超参数选择不合适将造成收敛速度变慢等问题. ...
计及气象因素和风速空间相关性的风电功率预测模型
1
2021
... 当前,风电功率的预测按照时间长短可分为超短期预测、短期预测、中长期预测[2 ] ,其中,超短期预测是实时调度及保证风电并网稳定运行的重点工作.风电预测的方法主要有人工神经网络[3 ] 、时间序列法[4 ] 、空间相关性法[5 ] 、极限学习机[6 ] 和最小二乘支持向量机(Least square support vector machine, LSSVM)[7 ] 等.神经网络有较强的信息提取能力和非线性拟合能力,因此在风电功率预测中有着重要的应用[8 ] .LSSVM相比人工神经网络法有很强的泛化能力,但参数的选择会影响预测效果,若选取不合适将造成较大的预测误差[9 ] .文献[10 ]运用改进的蚁群算法对LSSVM参数进行优化,利用LSSVM模型分别对风速和风功率进行预测.上述研究中,尽管风电功率预测精度有了较大提升,但是若神经网络等超参数选择不合适将造成收敛速度变慢等问题. ...
Wind power prediction model considering meteorological factor and spatial correlation of wind speed
1
2021
... 当前,风电功率的预测按照时间长短可分为超短期预测、短期预测、中长期预测[2 ] ,其中,超短期预测是实时调度及保证风电并网稳定运行的重点工作.风电预测的方法主要有人工神经网络[3 ] 、时间序列法[4 ] 、空间相关性法[5 ] 、极限学习机[6 ] 和最小二乘支持向量机(Least square support vector machine, LSSVM)[7 ] 等.神经网络有较强的信息提取能力和非线性拟合能力,因此在风电功率预测中有着重要的应用[8 ] .LSSVM相比人工神经网络法有很强的泛化能力,但参数的选择会影响预测效果,若选取不合适将造成较大的预测误差[9 ] .文献[10 ]运用改进的蚁群算法对LSSVM参数进行优化,利用LSSVM模型分别对风速和风功率进行预测.上述研究中,尽管风电功率预测精度有了较大提升,但是若神经网络等超参数选择不合适将造成收敛速度变慢等问题. ...
一种核极限学习机分位数回归模型及风电功率区间预测
1
2020
... 当前,风电功率的预测按照时间长短可分为超短期预测、短期预测、中长期预测[2 ] ,其中,超短期预测是实时调度及保证风电并网稳定运行的重点工作.风电预测的方法主要有人工神经网络[3 ] 、时间序列法[4 ] 、空间相关性法[5 ] 、极限学习机[6 ] 和最小二乘支持向量机(Least square support vector machine, LSSVM)[7 ] 等.神经网络有较强的信息提取能力和非线性拟合能力,因此在风电功率预测中有着重要的应用[8 ] .LSSVM相比人工神经网络法有很强的泛化能力,但参数的选择会影响预测效果,若选取不合适将造成较大的预测误差[9 ] .文献[10 ]运用改进的蚁群算法对LSSVM参数进行优化,利用LSSVM模型分别对风速和风功率进行预测.上述研究中,尽管风电功率预测精度有了较大提升,但是若神经网络等超参数选择不合适将造成收敛速度变慢等问题. ...
A quantile regression model of nuclear extreme learning machine and interval prediction of wind power
1
2020
... 当前,风电功率的预测按照时间长短可分为超短期预测、短期预测、中长期预测[2 ] ,其中,超短期预测是实时调度及保证风电并网稳定运行的重点工作.风电预测的方法主要有人工神经网络[3 ] 、时间序列法[4 ] 、空间相关性法[5 ] 、极限学习机[6 ] 和最小二乘支持向量机(Least square support vector machine, LSSVM)[7 ] 等.神经网络有较强的信息提取能力和非线性拟合能力,因此在风电功率预测中有着重要的应用[8 ] .LSSVM相比人工神经网络法有很强的泛化能力,但参数的选择会影响预测效果,若选取不合适将造成较大的预测误差[9 ] .文献[10 ]运用改进的蚁群算法对LSSVM参数进行优化,利用LSSVM模型分别对风速和风功率进行预测.上述研究中,尽管风电功率预测精度有了较大提升,但是若神经网络等超参数选择不合适将造成收敛速度变慢等问题. ...
基于改进经验小波变换和最小二乘支持向量机的短期风速预测
1
2021
... 当前,风电功率的预测按照时间长短可分为超短期预测、短期预测、中长期预测[2 ] ,其中,超短期预测是实时调度及保证风电并网稳定运行的重点工作.风电预测的方法主要有人工神经网络[3 ] 、时间序列法[4 ] 、空间相关性法[5 ] 、极限学习机[6 ] 和最小二乘支持向量机(Least square support vector machine, LSSVM)[7 ] 等.神经网络有较强的信息提取能力和非线性拟合能力,因此在风电功率预测中有着重要的应用[8 ] .LSSVM相比人工神经网络法有很强的泛化能力,但参数的选择会影响预测效果,若选取不合适将造成较大的预测误差[9 ] .文献[10 ]运用改进的蚁群算法对LSSVM参数进行优化,利用LSSVM模型分别对风速和风功率进行预测.上述研究中,尽管风电功率预测精度有了较大提升,但是若神经网络等超参数选择不合适将造成收敛速度变慢等问题. ...
Short-term wind speed prediction based on improved empirical wavelet transform and least square support vector machine
1
2021
... 当前,风电功率的预测按照时间长短可分为超短期预测、短期预测、中长期预测[2 ] ,其中,超短期预测是实时调度及保证风电并网稳定运行的重点工作.风电预测的方法主要有人工神经网络[3 ] 、时间序列法[4 ] 、空间相关性法[5 ] 、极限学习机[6 ] 和最小二乘支持向量机(Least square support vector machine, LSSVM)[7 ] 等.神经网络有较强的信息提取能力和非线性拟合能力,因此在风电功率预测中有着重要的应用[8 ] .LSSVM相比人工神经网络法有很强的泛化能力,但参数的选择会影响预测效果,若选取不合适将造成较大的预测误差[9 ] .文献[10 ]运用改进的蚁群算法对LSSVM参数进行优化,利用LSSVM模型分别对风速和风功率进行预测.上述研究中,尽管风电功率预测精度有了较大提升,但是若神经网络等超参数选择不合适将造成收敛速度变慢等问题. ...
Short-term wind power prediction based on EEMD-LASSO-QRNN model
1
2021
... 当前,风电功率的预测按照时间长短可分为超短期预测、短期预测、中长期预测[2 ] ,其中,超短期预测是实时调度及保证风电并网稳定运行的重点工作.风电预测的方法主要有人工神经网络[3 ] 、时间序列法[4 ] 、空间相关性法[5 ] 、极限学习机[6 ] 和最小二乘支持向量机(Least square support vector machine, LSSVM)[7 ] 等.神经网络有较强的信息提取能力和非线性拟合能力,因此在风电功率预测中有着重要的应用[8 ] .LSSVM相比人工神经网络法有很强的泛化能力,但参数的选择会影响预测效果,若选取不合适将造成较大的预测误差[9 ] .文献[10 ]运用改进的蚁群算法对LSSVM参数进行优化,利用LSSVM模型分别对风速和风功率进行预测.上述研究中,尽管风电功率预测精度有了较大提升,但是若神经网络等超参数选择不合适将造成收敛速度变慢等问题. ...
基于VSRP与β-GWO-SVM的变压器故障辨识方法
1
2021
... 当前,风电功率的预测按照时间长短可分为超短期预测、短期预测、中长期预测[2 ] ,其中,超短期预测是实时调度及保证风电并网稳定运行的重点工作.风电预测的方法主要有人工神经网络[3 ] 、时间序列法[4 ] 、空间相关性法[5 ] 、极限学习机[6 ] 和最小二乘支持向量机(Least square support vector machine, LSSVM)[7 ] 等.神经网络有较强的信息提取能力和非线性拟合能力,因此在风电功率预测中有着重要的应用[8 ] .LSSVM相比人工神经网络法有很强的泛化能力,但参数的选择会影响预测效果,若选取不合适将造成较大的预测误差[9 ] .文献[10 ]运用改进的蚁群算法对LSSVM参数进行优化,利用LSSVM模型分别对风速和风功率进行预测.上述研究中,尽管风电功率预测精度有了较大提升,但是若神经网络等超参数选择不合适将造成收敛速度变慢等问题. ...
Transformer fault identification method based on VSRP and β-GWO-SVM
1
2021
... 当前,风电功率的预测按照时间长短可分为超短期预测、短期预测、中长期预测[2 ] ,其中,超短期预测是实时调度及保证风电并网稳定运行的重点工作.风电预测的方法主要有人工神经网络[3 ] 、时间序列法[4 ] 、空间相关性法[5 ] 、极限学习机[6 ] 和最小二乘支持向量机(Least square support vector machine, LSSVM)[7 ] 等.神经网络有较强的信息提取能力和非线性拟合能力,因此在风电功率预测中有着重要的应用[8 ] .LSSVM相比人工神经网络法有很强的泛化能力,但参数的选择会影响预测效果,若选取不合适将造成较大的预测误差[9 ] .文献[10 ]运用改进的蚁群算法对LSSVM参数进行优化,利用LSSVM模型分别对风速和风功率进行预测.上述研究中,尽管风电功率预测精度有了较大提升,但是若神经网络等超参数选择不合适将造成收敛速度变慢等问题. ...
Short-term wind speed forecasting based on improved ant colony algorithm for LSSVM
1
2019
... 当前,风电功率的预测按照时间长短可分为超短期预测、短期预测、中长期预测[2 ] ,其中,超短期预测是实时调度及保证风电并网稳定运行的重点工作.风电预测的方法主要有人工神经网络[3 ] 、时间序列法[4 ] 、空间相关性法[5 ] 、极限学习机[6 ] 和最小二乘支持向量机(Least square support vector machine, LSSVM)[7 ] 等.神经网络有较强的信息提取能力和非线性拟合能力,因此在风电功率预测中有着重要的应用[8 ] .LSSVM相比人工神经网络法有很强的泛化能力,但参数的选择会影响预测效果,若选取不合适将造成较大的预测误差[9 ] .文献[10 ]运用改进的蚁群算法对LSSVM参数进行优化,利用LSSVM模型分别对风速和风功率进行预测.上述研究中,尽管风电功率预测精度有了较大提升,但是若神经网络等超参数选择不合适将造成收敛速度变慢等问题. ...
基于LSTM循环神经网络的风力发电预测
1
2020
... 深度学习因具有较强的特征提取能力而得到快速发展.长短时记忆网络(Long short-term memory, LSTM)[11 ] 具有学习长期依赖的能力,适合处理风电功率等非线性序列,文献[12 ]将注意力机制加入LSTM,提高了预测精度.但是LSTM也存在超参数不易确定的问题,不准确的参数设置对预测精度影响很大.因此,采用智能优化算法进行超参数寻优是一种较好的方法.由于风能具有不稳定性和波动性,单一的回归预测模型不能满足高精度要求.因此,需要对原始功率数据进行分解处理,获得较规律的特征.经验模态分解(Empirical mode decomposition, EMD)针对非线性序列的处理具有较好的效果[13 ] .但是,EMD分解后的各分量可能出现模态混淆的现象[14 ] .因此,文献[15 ]提出了集成经验模态分解(Ensemble empirical mode decomposition, EEMD)和LSSVM功率预测模型,EEMD分解能避免EMD分解产生的模态混淆现象,但是如果添加的噪声不合适,可能会使计算规模变大,影响功率预测的准确度.自适应噪声完全集合经验模态分解(Complete ensemble empirical mode decomposition with adaptive noise analysis, CEEMDAN)通过加入自适应白噪声能够减少模态混淆的现象,与EEMD方法相比,能够大大减少迭代次数,提高了重构准确度,具有较好的收敛特性.如果对每一个分量都分别直接预测,可能使计算规模变大、预测速度变慢[16 ] ,通过合并样本熵值相近的量可以降低计算规模. ...
Wind power generation forecast based on LSTM recurrent neural network
1
2020
... 深度学习因具有较强的特征提取能力而得到快速发展.长短时记忆网络(Long short-term memory, LSTM)[11 ] 具有学习长期依赖的能力,适合处理风电功率等非线性序列,文献[12 ]将注意力机制加入LSTM,提高了预测精度.但是LSTM也存在超参数不易确定的问题,不准确的参数设置对预测精度影响很大.因此,采用智能优化算法进行超参数寻优是一种较好的方法.由于风能具有不稳定性和波动性,单一的回归预测模型不能满足高精度要求.因此,需要对原始功率数据进行分解处理,获得较规律的特征.经验模态分解(Empirical mode decomposition, EMD)针对非线性序列的处理具有较好的效果[13 ] .但是,EMD分解后的各分量可能出现模态混淆的现象[14 ] .因此,文献[15 ]提出了集成经验模态分解(Ensemble empirical mode decomposition, EEMD)和LSSVM功率预测模型,EEMD分解能避免EMD分解产生的模态混淆现象,但是如果添加的噪声不合适,可能会使计算规模变大,影响功率预测的准确度.自适应噪声完全集合经验模态分解(Complete ensemble empirical mode decomposition with adaptive noise analysis, CEEMDAN)通过加入自适应白噪声能够减少模态混淆的现象,与EEMD方法相比,能够大大减少迭代次数,提高了重构准确度,具有较好的收敛特性.如果对每一个分量都分别直接预测,可能使计算规模变大、预测速度变慢[16 ] ,通过合并样本熵值相近的量可以降低计算规模. ...
基于LSTM-Attention网络的短期风电功率预测
1
2019
... 深度学习因具有较强的特征提取能力而得到快速发展.长短时记忆网络(Long short-term memory, LSTM)[11 ] 具有学习长期依赖的能力,适合处理风电功率等非线性序列,文献[12 ]将注意力机制加入LSTM,提高了预测精度.但是LSTM也存在超参数不易确定的问题,不准确的参数设置对预测精度影响很大.因此,采用智能优化算法进行超参数寻优是一种较好的方法.由于风能具有不稳定性和波动性,单一的回归预测模型不能满足高精度要求.因此,需要对原始功率数据进行分解处理,获得较规律的特征.经验模态分解(Empirical mode decomposition, EMD)针对非线性序列的处理具有较好的效果[13 ] .但是,EMD分解后的各分量可能出现模态混淆的现象[14 ] .因此,文献[15 ]提出了集成经验模态分解(Ensemble empirical mode decomposition, EEMD)和LSSVM功率预测模型,EEMD分解能避免EMD分解产生的模态混淆现象,但是如果添加的噪声不合适,可能会使计算规模变大,影响功率预测的准确度.自适应噪声完全集合经验模态分解(Complete ensemble empirical mode decomposition with adaptive noise analysis, CEEMDAN)通过加入自适应白噪声能够减少模态混淆的现象,与EEMD方法相比,能够大大减少迭代次数,提高了重构准确度,具有较好的收敛特性.如果对每一个分量都分别直接预测,可能使计算规模变大、预测速度变慢[16 ] ,通过合并样本熵值相近的量可以降低计算规模. ...
Short-term wind power prediction based on LSTM-Attention network
1
2019
... 深度学习因具有较强的特征提取能力而得到快速发展.长短时记忆网络(Long short-term memory, LSTM)[11 ] 具有学习长期依赖的能力,适合处理风电功率等非线性序列,文献[12 ]将注意力机制加入LSTM,提高了预测精度.但是LSTM也存在超参数不易确定的问题,不准确的参数设置对预测精度影响很大.因此,采用智能优化算法进行超参数寻优是一种较好的方法.由于风能具有不稳定性和波动性,单一的回归预测模型不能满足高精度要求.因此,需要对原始功率数据进行分解处理,获得较规律的特征.经验模态分解(Empirical mode decomposition, EMD)针对非线性序列的处理具有较好的效果[13 ] .但是,EMD分解后的各分量可能出现模态混淆的现象[14 ] .因此,文献[15 ]提出了集成经验模态分解(Ensemble empirical mode decomposition, EEMD)和LSSVM功率预测模型,EEMD分解能避免EMD分解产生的模态混淆现象,但是如果添加的噪声不合适,可能会使计算规模变大,影响功率预测的准确度.自适应噪声完全集合经验模态分解(Complete ensemble empirical mode decomposition with adaptive noise analysis, CEEMDAN)通过加入自适应白噪声能够减少模态混淆的现象,与EEMD方法相比,能够大大减少迭代次数,提高了重构准确度,具有较好的收敛特性.如果对每一个分量都分别直接预测,可能使计算规模变大、预测速度变慢[16 ] ,通过合并样本熵值相近的量可以降低计算规模. ...
基于EMD-SA-SVR的超短期风电功率预测研究
1
2020
... 深度学习因具有较强的特征提取能力而得到快速发展.长短时记忆网络(Long short-term memory, LSTM)[11 ] 具有学习长期依赖的能力,适合处理风电功率等非线性序列,文献[12 ]将注意力机制加入LSTM,提高了预测精度.但是LSTM也存在超参数不易确定的问题,不准确的参数设置对预测精度影响很大.因此,采用智能优化算法进行超参数寻优是一种较好的方法.由于风能具有不稳定性和波动性,单一的回归预测模型不能满足高精度要求.因此,需要对原始功率数据进行分解处理,获得较规律的特征.经验模态分解(Empirical mode decomposition, EMD)针对非线性序列的处理具有较好的效果[13 ] .但是,EMD分解后的各分量可能出现模态混淆的现象[14 ] .因此,文献[15 ]提出了集成经验模态分解(Ensemble empirical mode decomposition, EEMD)和LSSVM功率预测模型,EEMD分解能避免EMD分解产生的模态混淆现象,但是如果添加的噪声不合适,可能会使计算规模变大,影响功率预测的准确度.自适应噪声完全集合经验模态分解(Complete ensemble empirical mode decomposition with adaptive noise analysis, CEEMDAN)通过加入自适应白噪声能够减少模态混淆的现象,与EEMD方法相比,能够大大减少迭代次数,提高了重构准确度,具有较好的收敛特性.如果对每一个分量都分别直接预测,可能使计算规模变大、预测速度变慢[16 ] ,通过合并样本熵值相近的量可以降低计算规模. ...
Research on ultra-short-term wind power prediction based on EMD-SA-SVR
1
2020
... 深度学习因具有较强的特征提取能力而得到快速发展.长短时记忆网络(Long short-term memory, LSTM)[11 ] 具有学习长期依赖的能力,适合处理风电功率等非线性序列,文献[12 ]将注意力机制加入LSTM,提高了预测精度.但是LSTM也存在超参数不易确定的问题,不准确的参数设置对预测精度影响很大.因此,采用智能优化算法进行超参数寻优是一种较好的方法.由于风能具有不稳定性和波动性,单一的回归预测模型不能满足高精度要求.因此,需要对原始功率数据进行分解处理,获得较规律的特征.经验模态分解(Empirical mode decomposition, EMD)针对非线性序列的处理具有较好的效果[13 ] .但是,EMD分解后的各分量可能出现模态混淆的现象[14 ] .因此,文献[15 ]提出了集成经验模态分解(Ensemble empirical mode decomposition, EEMD)和LSSVM功率预测模型,EEMD分解能避免EMD分解产生的模态混淆现象,但是如果添加的噪声不合适,可能会使计算规模变大,影响功率预测的准确度.自适应噪声完全集合经验模态分解(Complete ensemble empirical mode decomposition with adaptive noise analysis, CEEMDAN)通过加入自适应白噪声能够减少模态混淆的现象,与EEMD方法相比,能够大大减少迭代次数,提高了重构准确度,具有较好的收敛特性.如果对每一个分量都分别直接预测,可能使计算规模变大、预测速度变慢[16 ] ,通过合并样本熵值相近的量可以降低计算规模. ...
基于EMD分解的风力机功率特性分析与预测建模
1
2021
... 深度学习因具有较强的特征提取能力而得到快速发展.长短时记忆网络(Long short-term memory, LSTM)[11 ] 具有学习长期依赖的能力,适合处理风电功率等非线性序列,文献[12 ]将注意力机制加入LSTM,提高了预测精度.但是LSTM也存在超参数不易确定的问题,不准确的参数设置对预测精度影响很大.因此,采用智能优化算法进行超参数寻优是一种较好的方法.由于风能具有不稳定性和波动性,单一的回归预测模型不能满足高精度要求.因此,需要对原始功率数据进行分解处理,获得较规律的特征.经验模态分解(Empirical mode decomposition, EMD)针对非线性序列的处理具有较好的效果[13 ] .但是,EMD分解后的各分量可能出现模态混淆的现象[14 ] .因此,文献[15 ]提出了集成经验模态分解(Ensemble empirical mode decomposition, EEMD)和LSSVM功率预测模型,EEMD分解能避免EMD分解产生的模态混淆现象,但是如果添加的噪声不合适,可能会使计算规模变大,影响功率预测的准确度.自适应噪声完全集合经验模态分解(Complete ensemble empirical mode decomposition with adaptive noise analysis, CEEMDAN)通过加入自适应白噪声能够减少模态混淆的现象,与EEMD方法相比,能够大大减少迭代次数,提高了重构准确度,具有较好的收敛特性.如果对每一个分量都分别直接预测,可能使计算规模变大、预测速度变慢[16 ] ,通过合并样本熵值相近的量可以降低计算规模. ...
Analysis and prediction modeling of wind turbine power characteristics based on EMD decomposition
1
2021
... 深度学习因具有较强的特征提取能力而得到快速发展.长短时记忆网络(Long short-term memory, LSTM)[11 ] 具有学习长期依赖的能力,适合处理风电功率等非线性序列,文献[12 ]将注意力机制加入LSTM,提高了预测精度.但是LSTM也存在超参数不易确定的问题,不准确的参数设置对预测精度影响很大.因此,采用智能优化算法进行超参数寻优是一种较好的方法.由于风能具有不稳定性和波动性,单一的回归预测模型不能满足高精度要求.因此,需要对原始功率数据进行分解处理,获得较规律的特征.经验模态分解(Empirical mode decomposition, EMD)针对非线性序列的处理具有较好的效果[13 ] .但是,EMD分解后的各分量可能出现模态混淆的现象[14 ] .因此,文献[15 ]提出了集成经验模态分解(Ensemble empirical mode decomposition, EEMD)和LSSVM功率预测模型,EEMD分解能避免EMD分解产生的模态混淆现象,但是如果添加的噪声不合适,可能会使计算规模变大,影响功率预测的准确度.自适应噪声完全集合经验模态分解(Complete ensemble empirical mode decomposition with adaptive noise analysis, CEEMDAN)通过加入自适应白噪声能够减少模态混淆的现象,与EEMD方法相比,能够大大减少迭代次数,提高了重构准确度,具有较好的收敛特性.如果对每一个分量都分别直接预测,可能使计算规模变大、预测速度变慢[16 ] ,通过合并样本熵值相近的量可以降低计算规模. ...
基于EEMD和LS-SVM模型的风电功率短期预测方法
1
2018
... 深度学习因具有较强的特征提取能力而得到快速发展.长短时记忆网络(Long short-term memory, LSTM)[11 ] 具有学习长期依赖的能力,适合处理风电功率等非线性序列,文献[12 ]将注意力机制加入LSTM,提高了预测精度.但是LSTM也存在超参数不易确定的问题,不准确的参数设置对预测精度影响很大.因此,采用智能优化算法进行超参数寻优是一种较好的方法.由于风能具有不稳定性和波动性,单一的回归预测模型不能满足高精度要求.因此,需要对原始功率数据进行分解处理,获得较规律的特征.经验模态分解(Empirical mode decomposition, EMD)针对非线性序列的处理具有较好的效果[13 ] .但是,EMD分解后的各分量可能出现模态混淆的现象[14 ] .因此,文献[15 ]提出了集成经验模态分解(Ensemble empirical mode decomposition, EEMD)和LSSVM功率预测模型,EEMD分解能避免EMD分解产生的模态混淆现象,但是如果添加的噪声不合适,可能会使计算规模变大,影响功率预测的准确度.自适应噪声完全集合经验模态分解(Complete ensemble empirical mode decomposition with adaptive noise analysis, CEEMDAN)通过加入自适应白噪声能够减少模态混淆的现象,与EEMD方法相比,能够大大减少迭代次数,提高了重构准确度,具有较好的收敛特性.如果对每一个分量都分别直接预测,可能使计算规模变大、预测速度变慢[16 ] ,通过合并样本熵值相近的量可以降低计算规模. ...
Short-term wind power forecasting method based on EEMD and LS-SVM model
1
2018
... 深度学习因具有较强的特征提取能力而得到快速发展.长短时记忆网络(Long short-term memory, LSTM)[11 ] 具有学习长期依赖的能力,适合处理风电功率等非线性序列,文献[12 ]将注意力机制加入LSTM,提高了预测精度.但是LSTM也存在超参数不易确定的问题,不准确的参数设置对预测精度影响很大.因此,采用智能优化算法进行超参数寻优是一种较好的方法.由于风能具有不稳定性和波动性,单一的回归预测模型不能满足高精度要求.因此,需要对原始功率数据进行分解处理,获得较规律的特征.经验模态分解(Empirical mode decomposition, EMD)针对非线性序列的处理具有较好的效果[13 ] .但是,EMD分解后的各分量可能出现模态混淆的现象[14 ] .因此,文献[15 ]提出了集成经验模态分解(Ensemble empirical mode decomposition, EEMD)和LSSVM功率预测模型,EEMD分解能避免EMD分解产生的模态混淆现象,但是如果添加的噪声不合适,可能会使计算规模变大,影响功率预测的准确度.自适应噪声完全集合经验模态分解(Complete ensemble empirical mode decomposition with adaptive noise analysis, CEEMDAN)通过加入自适应白噪声能够减少模态混淆的现象,与EEMD方法相比,能够大大减少迭代次数,提高了重构准确度,具有较好的收敛特性.如果对每一个分量都分别直接预测,可能使计算规模变大、预测速度变慢[16 ] ,通过合并样本熵值相近的量可以降低计算规模. ...
Complementary ensemble empirical mode decomposition:A novel noise enhanced data analysis method
1
2010
... 深度学习因具有较强的特征提取能力而得到快速发展.长短时记忆网络(Long short-term memory, LSTM)[11 ] 具有学习长期依赖的能力,适合处理风电功率等非线性序列,文献[12 ]将注意力机制加入LSTM,提高了预测精度.但是LSTM也存在超参数不易确定的问题,不准确的参数设置对预测精度影响很大.因此,采用智能优化算法进行超参数寻优是一种较好的方法.由于风能具有不稳定性和波动性,单一的回归预测模型不能满足高精度要求.因此,需要对原始功率数据进行分解处理,获得较规律的特征.经验模态分解(Empirical mode decomposition, EMD)针对非线性序列的处理具有较好的效果[13 ] .但是,EMD分解后的各分量可能出现模态混淆的现象[14 ] .因此,文献[15 ]提出了集成经验模态分解(Ensemble empirical mode decomposition, EEMD)和LSSVM功率预测模型,EEMD分解能避免EMD分解产生的模态混淆现象,但是如果添加的噪声不合适,可能会使计算规模变大,影响功率预测的准确度.自适应噪声完全集合经验模态分解(Complete ensemble empirical mode decomposition with adaptive noise analysis, CEEMDAN)通过加入自适应白噪声能够减少模态混淆的现象,与EEMD方法相比,能够大大减少迭代次数,提高了重构准确度,具有较好的收敛特性.如果对每一个分量都分别直接预测,可能使计算规模变大、预测速度变慢[16 ] ,通过合并样本熵值相近的量可以降低计算规模. ...
基于GRU-XGBoost的风电场功率短期预测
1
2020
... 针对风电功率的波动性和不确定性问题,需要对原始序列进行分解以获得较规律的特征.自适应噪声完全集合经验模态分解(CEEMDAN)通过加入自适应白噪声能够减少EMD分解的模态混淆现象,克服EEMD使计算规模变大的问题,能够大大减少迭代次数,提高重构准确度,具有较好的收敛特性.样本熵是常用来衡量原始时间序列的复杂度.原始序列越复杂,样本熵值就越高[17 ] .如果对每一个子分量都分别直接预测,可能使计算规模变大、预测速度变慢.因此,将熵值相近的序列合并,可以降低计算规模,提高预测速度. ...
Short-term prediction of wind farm power based on GRU-XGBoost
1
2020
... 针对风电功率的波动性和不确定性问题,需要对原始序列进行分解以获得较规律的特征.自适应噪声完全集合经验模态分解(CEEMDAN)通过加入自适应白噪声能够减少EMD分解的模态混淆现象,克服EEMD使计算规模变大的问题,能够大大减少迭代次数,提高重构准确度,具有较好的收敛特性.样本熵是常用来衡量原始时间序列的复杂度.原始序列越复杂,样本熵值就越高[17 ] .如果对每一个子分量都分别直接预测,可能使计算规模变大、预测速度变慢.因此,将熵值相近的序列合并,可以降低计算规模,提高预测速度. ...
基于样本熵和极端学习机的超短期风电功率组合预测模型
1
2013
... CEEMDAN是对EEMD算法的改进[18 ] ,克服了EEMD产生重构误差的问题,使风电功率原始数据的分解更加完整,更适合非线性信号的分析[19 ] .CEEMDAN方法分解数据的具体过程如下所示. ...
Ultra-short-term wind power combined forecasting model based on sample entropy and extreme learning machine
1
2013
... CEEMDAN是对EEMD算法的改进[18 ] ,克服了EEMD产生重构误差的问题,使风电功率原始数据的分解更加完整,更适合非线性信号的分析[19 ] .CEEMDAN方法分解数据的具体过程如下所示. ...
基于MEEMD-LSSVM的风电功率超短期预测研究
1
2020
... CEEMDAN是对EEMD算法的改进[18 ] ,克服了EEMD产生重构误差的问题,使风电功率原始数据的分解更加完整,更适合非线性信号的分析[19 ] .CEEMDAN方法分解数据的具体过程如下所示. ...
Research on ultra-short-term prediction of wind power based on MEEMD-LSSVM
1
2020
... CEEMDAN是对EEMD算法的改进[18 ] ,克服了EEMD产生重构误差的问题,使风电功率原始数据的分解更加完整,更适合非线性信号的分析[19 ] .CEEMDAN方法分解数据的具体过程如下所示. ...
基于飞蛾扑火优化算法的多运行方式电力系统稳定器参数协调优化方法
1
2020
... 长短期记忆网络[20 ] (LSTM)是对传统循环神经网络(Recurrent neural network, RNN)的改进,具有学习长期依赖的能力,适合处理风电功率预测和负荷预测等动态非线性数据.由于风电数据具有间断性、不确定性等特点,本文将Attention机制用于计算LSTM神经网络的隐层状态的不同权重,以选择性地关注不同时刻输入对风电功率预测的影响,从而改善功率预测效果.针对LSTM模型超参数目标函数表达式未知、超参数众多、迭代搜索复杂等问题,提出改进的MFO算法优化LSTM模型,得到最优的超参数组合. ...
Coordinated optimization method of multi-operation power system stabilizer parameters based on moth fire suppression optimization algorithm
1
2020
... 长短期记忆网络[20 ] (LSTM)是对传统循环神经网络(Recurrent neural network, RNN)的改进,具有学习长期依赖的能力,适合处理风电功率预测和负荷预测等动态非线性数据.由于风电数据具有间断性、不确定性等特点,本文将Attention机制用于计算LSTM神经网络的隐层状态的不同权重,以选择性地关注不同时刻输入对风电功率预测的影响,从而改善功率预测效果.针对LSTM模型超参数目标函数表达式未知、超参数众多、迭代搜索复杂等问题,提出改进的MFO算法优化LSTM模型,得到最优的超参数组合. ...
Composite multiscale cross-sample entropy analysis for long-term structural health monitoring of residential buildings
1
2020
... MFO算法优化问题的待求解是飞蛾的位置,将飞蛾群按适应度排列后作为火焰,飞蛾根据螺旋函数不断向火焰运动,寻优过程中火焰数量不断减少,直到适应度值符合要求则停止[21 ] .算法原理如下所示. ...
基于CEEMD和随机森林算法的短期风电功率预测
1
2019
... 然后计算各分量的样本熵,由式(10)、(11)可以看出,样本熵值受m 、r 大小的影响.由研究结果可知[22 ] ,m= 1或2,r =0.1Sd ~0.25Sd 时得到的样本熵较合理且经过多次试验,本文中取m =2,r =0.2Sd .CEEMDAN分解的各分量样本熵如图13 所示. ...
Short-term wind power prediction based on CEEMD and random forest algorithm
1
2019
... 然后计算各分量的样本熵,由式(10)、(11)可以看出,样本熵值受m 、r 大小的影响.由研究结果可知[22 ] ,m= 1或2,r =0.1Sd ~0.25Sd 时得到的样本熵较合理且经过多次试验,本文中取m =2,r =0.2Sd .CEEMDAN分解的各分量样本熵如图13 所示. ...