零相位滑动平均滤波器锁相环在LCL型逆变器中的应用*

doi:10.11985/2023.01.007

零相位滑动平均滤波器锁相环在LCL型逆变器中的应用^*

周立^,, 刘一鸣^,, 刘金澍^,, 李京明^,

辽宁工程技术大学电气与控制工程学院葫芦岛 125105

Application of Zero Phase Moving Average Filter in LCL Inverter

ZHOU Li^,, LIU Yiming^,, LIU Jinshu^,, LI Jingming^,

Faculty of Electrical and Control Engineering, Liaoning Technical University, Huludao 125105

通讯作者: 刘一鸣，男，1997年生，博士研究生。主要研究方向为电力电子电力传动技术与应用、人工智能与深度学习。E-mail：934680047@qq.com

收稿日期: 2021-06-10 修回日期: 2021-11-16

基金资助:

*国家自然科学基金资助项目. 51177067

Received: 2021-06-10 Revised: 2021-11-16

作者简介 About authors

周立，男，1963年生，高级工程师。主要研究方向为电力电子电力传动技术与应用。E-mail：834661681@qq.com

刘金澍，男，1997年生，硕士研究生。主要研究方向为电力电子电力传动技术与应用。E-mail：347308979@qq.com

李京明，男，1994年生，硕士研究生。主要研究方向为电力电子与电力传动。E-mail：541660964@qq.com

摘要

在并网控制过程中，锁相技术是并网逆变器与电网同步的关键，提出以二阶广义积分(Second-order generalized integrator，SOGI)和滑动平均滤波算法(Moving average filter，MAF)为基础的零相位滑动平均滤波器二阶广义积分锁相环(Zero-phase moving average filter-second-order generalized integrator-phase-locked loop，ZPMAF-SOGI-PLL)。通过改进SOGI结构和MAF算法得到ZPMAF-SOGI-PLL，在并网逆变器控制的环节中使用了ZPMAF-SOGI-PLL方法进行锁相，进而使锁相环在不理想情况下能快速、稳定、准确地从电网中获取电压正负序分量、频率、相位等参数，并通过现代控制理论分析了该方法的稳定性。通过电网电压不平衡和含有高次谐波工况下的仿真和试验结果表明，所提方法可使LCL并网逆变器准确检测正负序分量，且并网电流的谐波含量在两种具体的工况下分别降低到1.89%和2.71%，使LCL型并网逆变器运行更稳定。

关键词： LCL型并网逆变器 ; 二阶广义积分器 ; 锁相环 ; 零相位滑动平均滤波

Abstract

In the process of grid-connected control, phase-locked technology is the key to the synchronization of grid-connected inverter and power grid. A zero-phase moving average filter second-order generalized integrator phase locked loop(ZPMAF-SOGI-PLL) based on second-order generalized integrator(SOGI) and moving average filter algorithm(MAF) is proposed. By improving the SOGI structure and MAF algorithm, it can be solved that the phase-locked loop can quickly, stably and accurately obtain the positive and negative sequence component voltage, frequency, phase and other parameters from the power grid under unsatisfactory conditions. The stability of this method is analyzed by modern control theory, and the SOGI-PLL method is used for phase locking in the link of grid-connected inverter control. The simulation and experimental results under unbalanced grid voltage and high-order harmonic conditions show that the proposed method enables the LCL grid-connected inverter to accurately detect the positive and negative sequence components, so that the harmonic content of the grid-connected current is reduced to 1.89% and 2.71% under the two conditions, respectively, and the operation of the LCL grid-connected inverter is more stable.

Keywords： LCL grid-connected inverter ; second-order generalized integrator ; phase-locked loop ; zero-phase sliding average filter

PDF (867KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

周立, 刘一鸣, 刘金澍, 李京明. 零相位滑动平均滤波器锁相环在LCL型逆变器中的应用^*. 电气工程学报[J], 2023, 18(1): 68-84 doi:10.11985/2023.01.007

ZHOU Li, LIU Yiming, LIU Jinshu, LI Jingming. Application of Zero Phase Moving Average Filter in LCL Inverter. Chinese Journal of Electrical Engineering[J], 2023, 18(1): 68-84 doi:10.11985/2023.01.007

1 引言

并网逆变器需要获得高质量的电能来输送到电网，因此，在并网过程中常使用锁相环进行控制。锁相环是一种广泛应用于并网逆变器中检测频率和电网电压相位的一种方法，它能够很好地控制电能传输^[1-2]。实际上，电网中总存在一些不理想的情况，包括电网电压不平衡、失真和频率变化。电压的不平衡和谐波干扰会使得到的电流质量效果较差。近十年来，锁相环(Phase-locked loop，PLL)技术已被广泛应用于电网同步和监控中。逆变器与电网相连时，两者同步最为重要^[3]。

同步旋转坐标系锁相环(Synchronous-reference frame phase-locked loop，SRF-PLL)常用来提取电网中的相位、频率，但在电网电压不平衡、谐波污染等状态下，SRF-PLL的检测能力不准确且存在较大误差^[4-5]。文献[6]采用改进型锁相环SRF-PLL，虽然在电网出现故障的情况下锁相的准确性得到了提升，但是不能削弱电网中负序分量。解耦双同步旋转坐标系的锁相环(Decoupled double synchronous referonce-frame phase-locked loop，DDSRF-PLL)能够削弱电网中负序分量的影响，但其抑制谐波能力较差^[7]。双二阶广义积分器锁相环(Double second-order generalized integrator phase-locked loop，DSOGI-PLL)可在电网电压含负序分量或谐波含量较低的情况下锁相结果准确，误差小，但在谐波严重污染且三相不平衡强度较大的情况下，提取相位、频率的性能远远小于DDSRF-PLL。运用解耦算法的解耦双同步旋转坐标系锁相环(DDSRF-PLL)获得正负序分量是较为容易的^[8]，但是当电网电压含有高次谐波且电压不平衡时，检测的信号存在较大的误差，且运算速度和动态响应速度较慢。

为了解决上述问题，本文提出了一种改进型二阶广义积分锁相环，将滑动平均滤波器的一种改进算法零相位滑动平均滤波器(Zero-phase moving average filter，ZPMAF)和一阶低通滤波器(Low pass filter，LPF)应用于DSOGI-PLL中，使该锁相环可以在电网电压同时包含负序分量和直流分量时，对同步的电压信号进行精确检测，具有良好的动态响应性能。利用改进型DSOGI-PLL可实现对电网电压、相位、频率的精确跟踪，在电网电压不平衡、含有高次谐波的工况下运行稳定^[9]。

2 SOGI原理

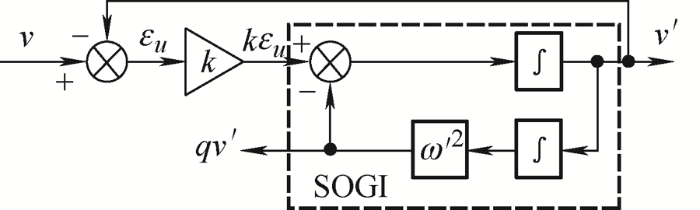
SOGI-PLL首先需要相应的数学模型，SOGI是在SRF-PLL的原理上改进的，如图1所示，SOGI为虚线框内部分。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 传统二阶广义积分器结构图

根据图1可知，${v}'$和$q{v}'$是两个输出信号，${v}'$的相位要超前于$q{v}'$，SOGI的传递函数为

(1)${{D}_{1}}(s)=\frac{{v}'(s)}{v(s)}=\frac{ks}{{{s}^{2}}+ks+{{\omega }^{\prime 2}}}$

(2)${{Q}_{1}}(s)=\frac{q{v}'(s)}{v(s)}=\frac{k{{\omega }^{\prime 2}}}{{{s}^{2}}+ks+{{\omega }^{\prime 2}}}$

式中，v为信号输入的正弦电压；k为阻尼系数。当系统的中心频率${\omega }'$与输入频率ω大小相等时，${v}'$和$q{v}'$幅值相等，并且${v}'$的相位、幅值等于$v$。

D₁(s)和Q₁(s)的伯德图如图2所示。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 D₁(s)和Q₁(s)的伯德图

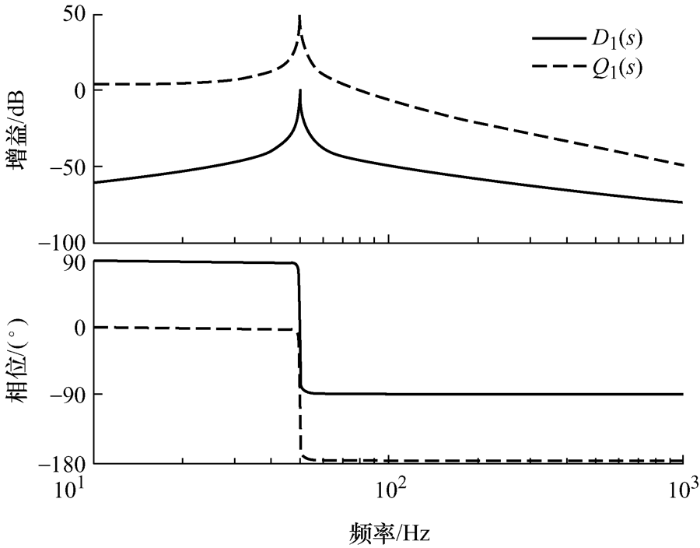
(3)${{D}_{1}}(s)={{A}_{0}}\frac{\frac{{{\omega }'}}{{{Q}_{D1}}}s}{{{s}^{2}}+\frac{{{\omega }'}}{{{Q}_{D1}}}s+{{{{\omega }'}}^{2}}}$

式中，A₀为D₁(s)的增益；Q_D₁为品质因数。

(4)${{Q}_{D1}}=\frac{{{\omega }'}}{k}$

由式(4)可知，当k一定时，D₁(s)的品质因数和${\omega }'$成正比关系，所以Q_D₁与输入信号的频率也有关，进而影响动态特性^[10]。根据图2可知，Q₁(s)在低频段幅值较低，不能滤除掉qv的直流分量，且相角裕度比较低，所以传统SOGI对直流分量抑制能力比较弱，针对此问题，本文提出了一种改进型SOGI-PLL方法。

3 改进的SOGI-PLL

3.1 改进型SOGI

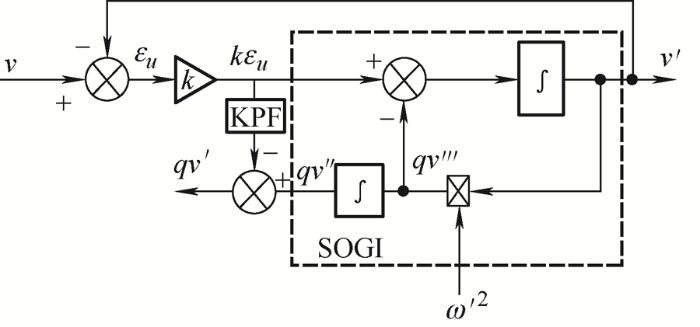
通过第2节式(4)对传统SOGI-PLL进行频域特性分析可知，传统SOGI-PLL对直流分量抑制能力比较弱，所以在高频段不能抑制高次谐波，根据以上分析对传统SOGI-PLL进行改进，如图3所示，在虚线框中进行了改进，通过分离${{{\omega }'}^{2}}$和在$q{v}'$后引入反馈来抑制直流分量，低通滤波器LPF的作用是滤掉高次谐波。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 改进型SOGI结构图

LPF的传递函数为

(5)${{G}_{\text{LPF}}}(s)=\frac{1}{1+\tau s}$

式中，τ 为LPF阻尼系数，根据图3可得D₂(s)和Q₂(s)的传递函数为

(6)${{D}_{2}}(s)=\frac{{v}'(s)}{v(s)}=\frac{k{\omega }'s}{{{s}^{2}}+k{\omega }'s+{{{{\omega }'}}^{2}}}$

(7)${{Q}_{2}}(s)=\frac{q{v}'(s)}{v(s)}=\frac{-k\left( \tau {\omega }'s-{{s}^{2}} \right)}{\left( {{s}^{2}}+k{\omega }'s+{{{{\omega }'}}^{2}} \right)(1+\tau s)}$

由式(6)得到D₂(s)的品质因数为

(8)${{Q}_{D2}}=\frac{1}{k}$

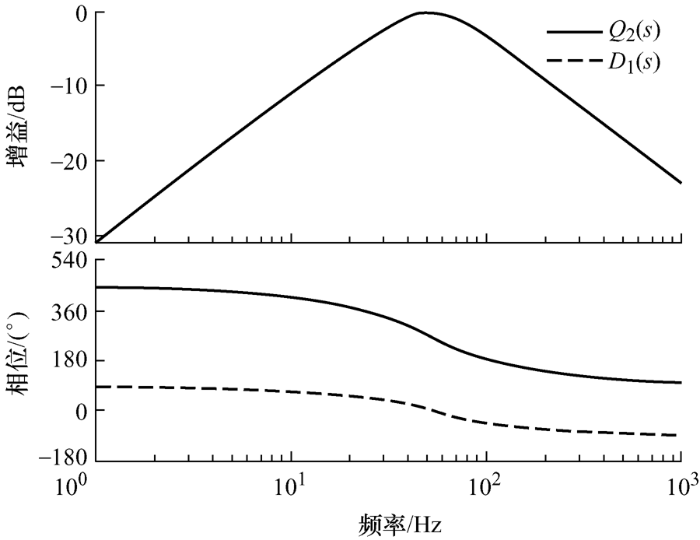
由式(8)可知，频率${\omega }'$对改进后SOGI的品质因数影响较低。将式(8)与式(4)进行比较，得出结果Q_D₂<Q_D₁，说明改进后的SOGI通频带宽比较宽，所以在锁相锁频的过程中更容易使系统保持稳定。为了进一步证明改进型SOGI和传统SOGI之间存在的差异，由图2和图4可以看出传统SOGI的带宽十分窄，对频率的依赖很强，而改进的SOGI对频率依赖要小。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 D₂(s)与Q₂(s)的伯德图

根据现代控制理论，高频段应满足频率自适应性，进而才能提高抗干扰能力。所以改进后的SOGI不仅能有效地抑制输入信号的直流分量，而且还能有效地抑制高频分量^[11-12]。并且由于LPF的加入，使锁相环的相角裕度增大，在基频上没有明显的延迟，所以锁相环的性能得到了提升^[13]。

3.2 改进型ZPMAF-SOGI-PLL结构

在电网发生故障时，如果存在谐波干扰，则必须先将谐波成分排除掉，才能得到电网电压基波正序分量。MAF在一定条件下可用作理想低通滤波器，可将MAF的输出信号表示为^[14]

(9)$\bar{x}\text{(}t)=\frac{1}{{{T}_{w}}}\int_{\ t-{{T}_{w}}}^{\ t}{x\text{(}\tau )d\tau }$

式中，x(τ)为输入信号；T_w为窗口宽度。

对输出MAF从t-T_w时刻到t时刻对x(τ)进行积分，得到MAF的传递函数可表示为

(10)${{G}_{MAF}}\text{(}s)=\frac{\bar{x}\text{(}s)}{x\text{(}s)}=\frac{1-exp(-{{T}_{w}}s)}{{{T}_{w}}s}$

式中，$exp(-{{T}_{w}}s)\approx \frac{1-{{T}_{w}}s/2}{1+{{T}_{w}}s/2}$，即G_MAF可简化为

(11)${{G}_{MAF}}\text{(}s)\approx \frac{1}{1+{{T}_{w}}s/2}$

将$s=j{{\omega }_{M}}$代入式(11)，得到幅相频特性为

(12)$\left| {{G}_{MAF}}\text{(}j{{\omega }_{M}}) \right|=\frac{\sqrt{2}}{{{\omega }_{M}}{{T}_{w}}}\sqrt{1-\cos \text{(}{{\omega }_{M}}{{T}_{w}})}$

(13)$\phi \left[ {{G}_{MAF}}\text{(}j{{\omega }_{M}}) \right]=-\frac{{{\omega }_{M}}{{T}_{w}}}{2}$

T_w是MAF设计中最重要的一个参数，对T_w进行设置时必须在MAF的动态响应速度和滤波性能之间进行设置。通常以滤除电网中所包含的最低次主要谐波频率作为T_w的选择原则。文献[7]为了消除不平衡电网电压产生的基波负序分量，将T_w设置为电网基频周期T的一半，即T/2，这虽然增强了MAF的滤波能力，但降低了其动态响应速度，故提出了一种ZPMAF算法，G_ZPMAF为改进型MAF的一种表达形式，其表达式为

(14)${{G}_{\text{ZPMAF}}}(s)=\frac{2(\pi s+{{\omega }_{c}})}{2{{\omega }_{c}}+s{{T}_{w}}}$

式中，T_w是窗口宽度；ω_c为截止频率。

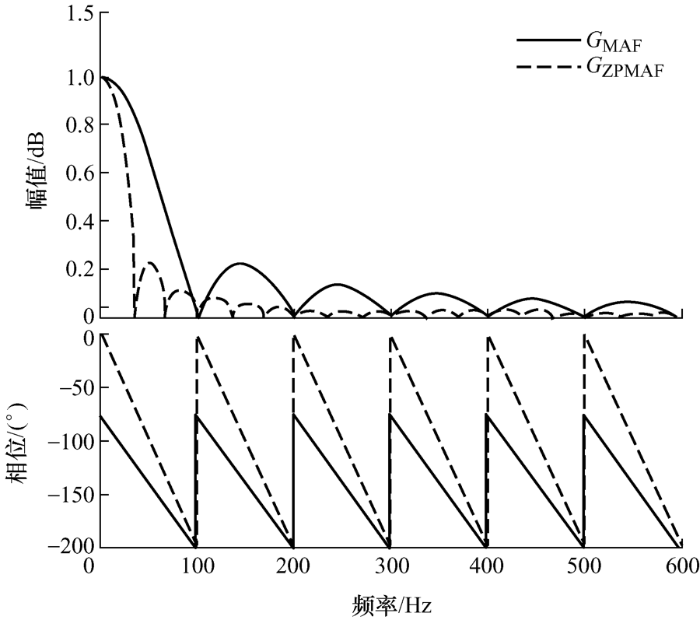
根据式(11)和式(14)画出频率特性图，如图5所示，根据图5可知，ZPMAF的响应更快，稳定性更好。把MAF应用到SOGI-PLL中，当电网电压含有谐波时，可以滤除谐波，还可以有效地提取正、负序分量^[15]。将SOGI-PLL提取的频率ω₀反馈到MAF中，还可以使SOGI-PLL具有频率自适应的功能。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 MAF与ZPMAF的伯德图

从电网电压中提取到的电压正序分量计算公式为

(15)$\nu_\alpha^+=\nu_\alpha^\prime-q\nu_\beta^\prime$

(16)$v_{\mathrm{ }\!\!\beta\!\!\text{ }}^{+}=q{{{v}'}_{\mathrm{ }\!\!\alpha\!\!\text{ }}}+{{{v}'}_{\mathrm{ }\!\!\beta\!\!\text{ }}}$

式中，$\nu_\alpha^\prime$和$\nu_\beta^\prime$为正交基波信号，关系如图6所示。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 改进型SOGI-PLL结构图

综合以上分析，将改进型SOGI-PLL应用到LCL并网逆变器控制侧，改进型SOGI-PLL在三相电压不平衡和含有高次谐波情况下锁相结果比传统的SOGI-PLL更加准确。

4 系统控制策略

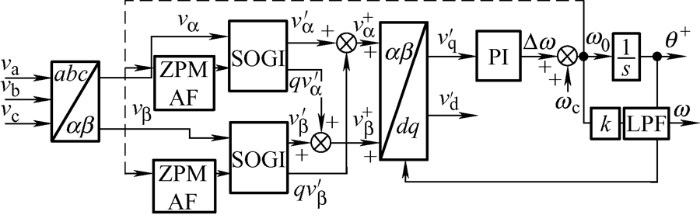
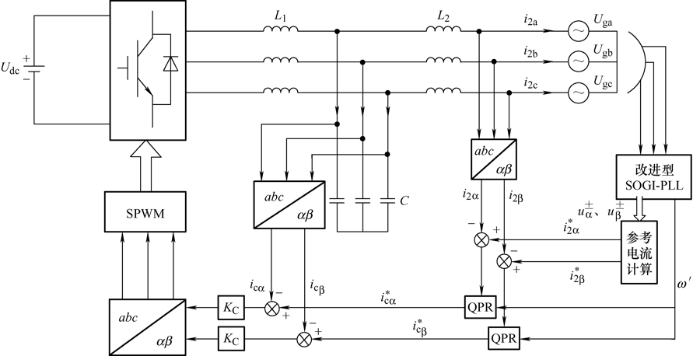
LCL型并网逆变器经常在dq和αβ坐标系中用到准比例谐振(Quasi-proportional resonance，QPR)电流控制的方法^[16-17]。如图7所示，在QPR控制策略中，使用改进SOGI-PLL提取电压的正序和负序分量，借助PLL快速准确地检测电网相位。将QPR控制器用作并网电流外环控制器^[18]，其传递函数如下

(17)${{G}_{QPR}}\text{(}s)={{K}_{P}}+\frac{2{{K}_{R}}{{\omega }_{c}}s}{{{s}^{2}}+2{{\omega }_{c}}s+{{\omega }_{0}}^{2}}$

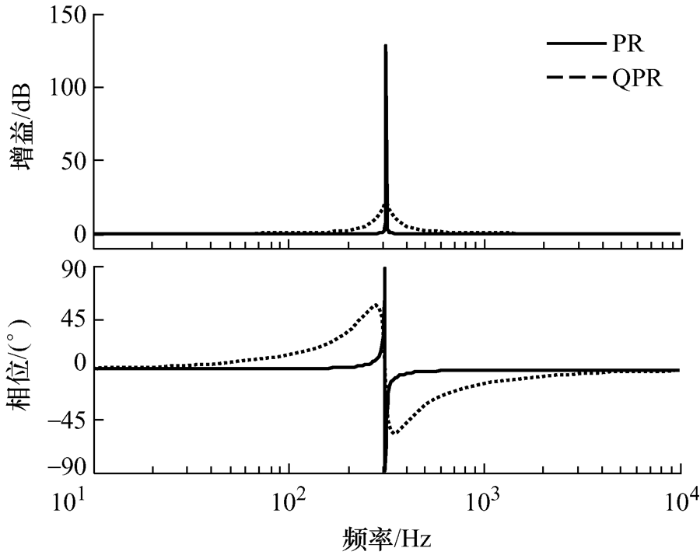
式中，ω_c为截止频率；K_P是比例系数；K_R是谐振系数，将QPR的控制方法与传统的比例谐振(Proportional resonance，PR)控制^[19]进行比较，得到伯德图如图8所示。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 电流控制的结构图

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 QPR和PR控制器的伯德图

如图8所示，QPR控制器很好地解决了PR控制在基波频率下增益无穷大和增益带宽不足的问题。所以QPR控制不但可以实现对谐振频率信号的无静差跟踪控制，而且可以有效地抑制电网谐波，提高系统运行稳定性。

5 Simulink仿真和试验验证

根据图7，利用Matlab/Simulink搭建改进型SOGI-PLL在三相电压不平衡、电网电压中注入高次谐波工况下的仿真模型，搭建成功后与文献[1]提到的改进SRF-PLL进行对比。模型中主要参数如表1所示。

表1 仿真参数

序号	参数	数值
1	直流源电压U_dc/V	500
2	电网电压U_g/V	311
3	滤波电容C/μF	8
4	逆变侧滤波电感L₁/mH	3
5	网侧电感L₂/mH	2
6	开关频率f_s/kHz	10
7	额定频率f_n/Hz	50
8	额定有功功率P_n/kW	20
9	谐振频率ω₀/(rad/s)	314
10	截止频率ω_c/(rad/s)	5
11	比例调节系数K_p	12.732
12	积分调节系数K_i	6.366
13	改进型SOGI的LPF阻尼系数τ	0.707
14	QPR控制器比例系数K_P	15
15	QPR控制器谐振系数K_R	100

新窗口打开| 下载CSV

5.1 三相电压不平衡

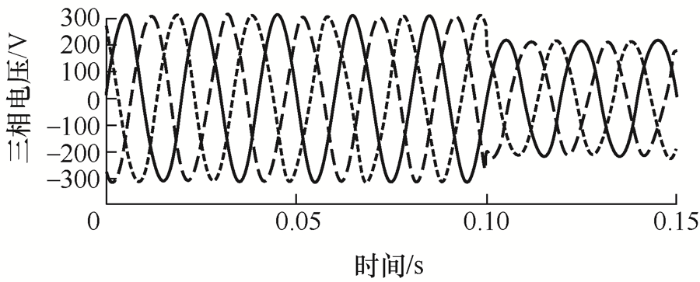
在电网中，三相电压不平衡是一种常见的故障，一旦发生故障，图9是A、B、C三相电压依次在0.1 s处下降70%的仿真波形。文献[1]提到的改进型SRF-PLL相位向上移动，且频率不稳定。改进型SOGI-PLL能有效检测三相电网电压不平衡时的正序分量，并且可以在电网电压不平衡的情况下精确获得相位和频率。由图6可知电网电压相位v_α⁺和v_β⁺通过帕克变换得到v_d、v_q，再经过PI等环节得到θ⁺，根据式(15)、式(16)和图10，对改进型SOGI-PLL和改进型SRF-PLL正序分量分析，通过图9可以看到，改进型SRF-PLL电压相位向上移动而改进型SOGI-PLL没有向上移动，向上移动会影响θ⁺的准确输出，说明改进SOGI-PLL可以解决电网电压相位瞬时增大或减小的问题。相比于SRF-PLL，改进型SOGI-PLL谐波含量为1.89%，而SRF-PLL谐波含量26.51%，通过图10对改进型SOGI-PLL和改进型SRF-PLL的THD和并网电流进行分析可知，改进SOGI-PLL谐波含量低，可以有效提高并网的稳定性。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 三相电压不平衡工况

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 三相电压不平衡工况

5.2 电网电压中注入高次谐波

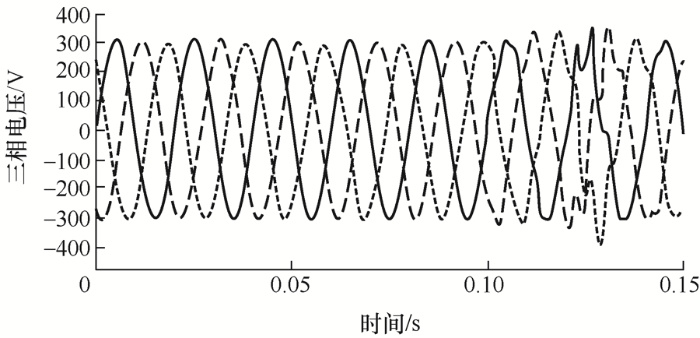
为了验证改进型SOGI-PLL的抗谐波能力，图11为A、B、C三相中注入幅值为30的25次、29次和33次谐波，图12显示了系统的仿真波形。仿真证明，文献[1]提到的改进型SRF-PLL不能准确地检测到需要的正序基本成分且存在谐波含量较大的问题。改进型SOGI-PLL能准确地检测到需要的正序基本成分，检测到的锁相频率稳定且超调小，改进后的SOGI-PLL与SRF-PLL的并网逆变电流谐波含量相差2.81%，说明改进型SOGI-PLL可以有效抑制高次谐波。

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 三相电压注入高次谐波工况

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12 注入谐波的仿真

5.3 试验验证

在理论和仿真验证的基础上，搭建了一台功率为100 W的试验样机，如图13所示，采用电网模拟器对电网电压信号进模拟，其采样频率为12.5 kHz。

图13

新窗口打开| 下载原图ZIP| 生成PPT

图13 试验平台照片

采用STM32F103对改进型SOGI-PLL算法分别在电压跌落幅度为70%的情况下和A、B、C三相中注入幅值为30的高次谐波的工况下进行试验。

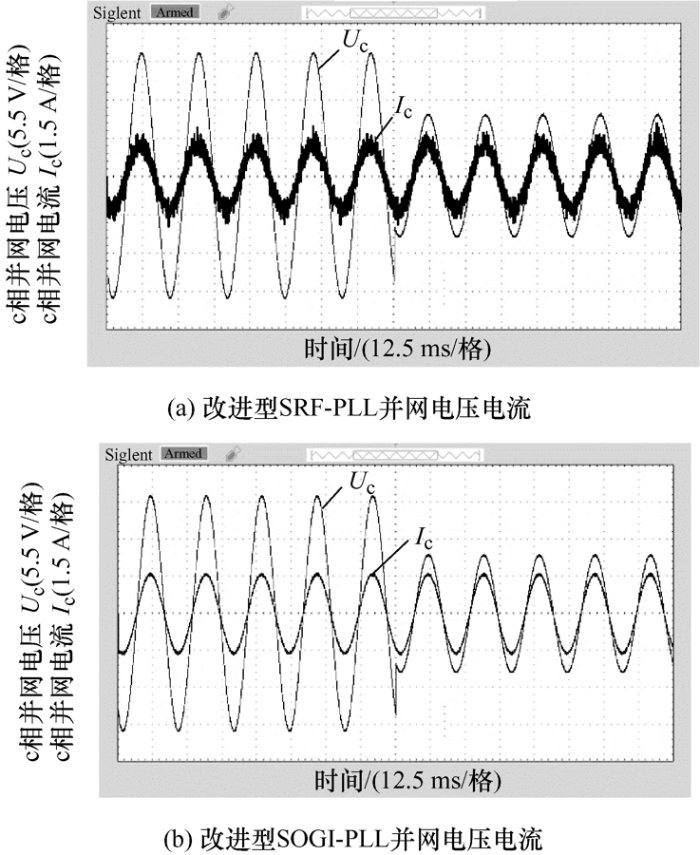
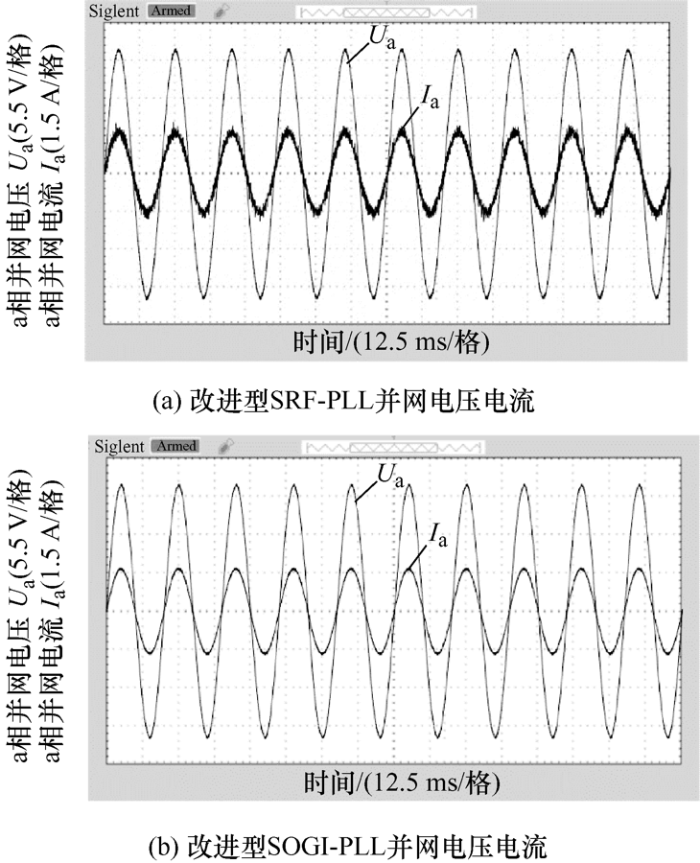
由图14、图15可见，通过三相电压的不平衡试验和三相电压注入谐波试验的结果可知，改进型SRF-PLL并网电流的谐波含量比改进型SOGI-PLL并网电流的谐波含量要高。所得到的试验结果与仿真结果基本保持一致，验证了本文提出的改进型SOGI-PLL能够使LCL并网逆变器输出稳定可靠的电流进行准确并网，进而说明了电网正序分量同步方法的正确性和有效性。

图14

新窗口打开| 下载原图ZIP| 生成PPT

图14 三相电压的不平衡试验

图15

新窗口打开| 下载原图ZIP| 生成PPT

图15 三相电压注入谐波试验

6 结论

本文提出了一种零相位滑动平均滤波器二阶广义积分锁相环(Zero-phase moving average filter second-order generalized integrator phase locked loop，ZPMAF-SOGI-PLL)，通过仿真和试验证明该锁相环在并网逆变过程中的可行性。

(1) 通过不平衡电压与高次谐波试验说明了该锁相环在实际应用中具有可实施性，并在并网逆变器的控制系统中通过了验证。

(2) 提出改进型SOGI-PLL方法能够将重要的参数在非理想条件下准确无误差地检测出相位、频率和正负序分量等参数。

(3) 通过这些参数使逆变器输出的电流谐波含量在三相电压不平衡的情况下从4.25%降低至1.89%，在含有高次谐波的情况下从5.52%降低至2.71%，进而使LCL型并网逆变器更加稳定、安全地运行。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

GOLESTAN

, EBRAHIMZADEH

, WEN

et al.

dq-frame impedance modeling of three-phase grid-tied voltage source converters equipped with advanced PLLs

[J]. IEEE Transactions on Power Electronics, 2021, 36(3):3524-3539.

DOI:10.1109/TPEL.63 URL [本文引用: 4]

[2]

张烨, 田慕琴, 宋建成,

等.

弱电网下计及锁相环影响的并网逆变器输出阻抗重塑

[J]. 高电压技术, 2021, 47(11):4033-4044.