基于残差观测器的智能电网虚假数据攻击检测研究*

doi:10.11985/2023.01.012

基于残差观测器的智能电网虚假数据攻击检测研究^*

张明月^,¹, 王新宇^,²^,³

1.燕山大学建筑工程与力学学院秦皇岛 066004

2.燕山大学电气工程学院秦皇岛 066004

3.燕山大学电力电子节能与传动控制河北省重点实验室秦皇岛 066004

Detection of False Data Attack in Smart Grid Based on Residual Observer

ZHANG Mingyue^,¹, WANG Xinyu^,²^,³

1. School of Civil Engineering and Mechanics, Yanshan University, Qinhuangdao 066004

2. Institute of Electrical Engineering, Yanshan University, Qinhuangdao 066004

3. Key Lab of Power Electronics for Energy Conservation & Motor Drive of Hebei Province,Yanshan University, Qinhuangdao 066004

通讯作者: 王新宇，男，博士，讲师。主要研究方向为电气控制、信息物理安全。E-mail：wxyzmya@ysu.edu.cn

收稿日期: 2022-01-17 修回日期: 2022-03-2

基金资助:

*国家自然科学基金青年科学基金.  62103357
河北省自然科学基金青年.  F2021203043
河北省教育厅自然科学基金青年.  QN2021139
江苏省配电网智能技术与装备协同创新中心开放基金.  XTCX202203

Received: 2022-01-17 Revised: 2022-03-2

作者简介 About authors

张明月，女，硕士，讲师。主要研究方向为电气控制、数字信号处理。E-mail：zhangmingyue91@ysu.edu.cn

摘要

信息物理系统的深度融合实现了智能电网系统的高效运行，但也使其面临潜在的信息物理攻击安全威胁。攻击者通过注入虚假数据可以实现测量输出无变化，进而欺骗传统基于Kalman的卡方检测方法。考虑虚假数据攻击对系统内部状态变化的影响，提出了基于内部状态变化的神经网络观测器虚假数据攻击检测方法。基于建立的智能电网物理动态模型，分析了虚假数据攻击的隐蔽特性。进而考虑虚假数据攻击对系统内部状态变化的影响，提出基于神经网络观测器的状态残差检测方法。此外，考虑扰动对检测阈值的影响，设计自适应阈值替代传统的经验阈值从而缩短虚假数据攻击检测时间。最后，在IEEE三电机六总线验证了所提基于神经网络观测器的状态残差攻击检测方法的优越性。

关键词： 智能电网 ; 虚假数据攻击 ; 神经网络观测器 ; 自适应阈值 ; 攻击检测

Abstract

The deep integration of cyber-physical systems enables efficient operation of smart grid systems while also exposing them to security threats posed by cyber-physical attacks. By injecting false data, attackers can achieve no change in measurement output and thus deceive the traditional detection methods based on chi-square. By considering the impact of false data attack on the internal state change of the system, a detection method against false data attack based on neural network observer is proposed. Based on the established smart grid physical dynamics model, the stealthy characteristics of the false data attack are analyzed. Considering the impact of the false data attack on the internal state change of the system, the state residual detection method based on the neural network observer is proposed. In addition, considering the impact of perturbation on the threshold, adaptive thresholds are designed to replace the traditional empirical thresholds for cutting the false data attack detection time. Finally, the superiority of the proposed state residual attack detection method based on neural network observer is verified in IEEE 3-generator 6-bus grid system.

Keywords： Smart grid ; false data attack ; neural network observer ; adaptive threshold ; attack detection

PDF (354KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

张明月, 王新宇. 基于残差观测器的智能电网虚假数据攻击检测研究^*. 电气工程学报[J], 2023, 18(1): 111-117 doi:10.11985/2023.01.012

ZHANG Mingyue, WANG Xinyu. Detection of False Data Attack in Smart Grid Based on Residual Observer. Chinese Journal of Electrical Engineering[J], 2023, 18(1): 111-117 doi:10.11985/2023.01.012

1 引言

智能电网作为国家基础设施，其安全性直接影响国家经济以及国民生活。尤其在“十四五”期间面对新能源大规模的接入，重点要确保能源转型过程中智能电网系统的安全稳定运行^[1⇓⇓-4]。然而，系统的信息-物理融合特性使其面临潜在的信息安全风险，尤其是具有信息-物理协同能力的虚假数据攻击^[5⇓-7]。这类攻击可以通过注入虚假数据到信息网以掩盖物理系统的内部动态变化，进而造成级联故障引发大面积停电^[8⇓-10]。例如，2018年，俄罗斯和伊朗基础电力网络攻击事件导致全球20万台路由器遭受影响。2019年，委内瑞拉电力系统网络攻击事件波及全国23个州。因此，迫切需要一种针对虚假数据攻击的检测机制来确保能源转型过程中智能电网系统的安全稳定运行。

在2009年，LIU等^[11⇓-13]设计了具有隐蔽特性的虚假数据攻击，并揭示了其可以欺骗传统基于测量输出的电网安全机制。为了确保智能电网的安全运行，学者们从多方面开展了对恶意攻击的检测研究。结合系统负荷预测，文献[14]提出了基于无迹卡尔曼滤波的虚假数据攻击检测方法。此外，文献[15]考虑电网系统模型未知的情况下，给出了基于数据递归的无迹卡尔曼攻击检测策略。进一步考虑噪声特性影响，文献[16]提出了基于欧几里得的虚假数据攻击检测方法。基于输出测量数据的改善，以上检测方法可以有效地检测注入到系统中虚假数据攻击，但是缺乏进一步对虚假数据攻击下系统内部状态变化的研究。此外，以上检测方法中检测阈值均为先验阈值，其取值会影响攻击检测性能，例如取值过大会导致攻击的漏检等问题。

本文提出了基于神经网络观测器的攻击检测方法，主要贡献如下所述。

(1) 考虑虚假数据攻击可以欺骗传统基于Kalman的卡方检测方法，本文通过设计神经网络观测器，可以获得虚假数据攻击下内部状态的实际变化，进而给出基于状态残差的检测逻辑。

(2) 考虑先验阈值对攻击检测性能的影响，本文设计了自适应阈值来替代传统的先验阈值，可以提高虚假数据攻击的检测性能。最后，通过在IEEE三电机六总线上仿真验证所提攻击检测方法的优越性。

本文的逻辑结构如下：第2节给出了电网线性模型和虚假数据攻击特性；第3节中提出了基于内部状态残差变化的神经网络观测器检测方法，以及自适应阈值设计；第4节中仿真验证了本文所提攻击检测方法的优越性；最后，第5节给出本文结论和工作展望。

2 电网模型和问题描述

2.1 智能电网模型

考虑到智能电网的复杂性，在系统中所有部分均可能受到恶意攻击，为简化研究程度，本文研究对象为智能电网的电机侧。考虑电网系统内部状态变化，建立第$i(i=1,2,\cdots,n)$个发电机动力学方程如下^[17]

(1)$\left\{ \begin{align} & {{{\dot{\delta }}}_{i}}={{\omega }_{i}} \\ & {{{\dot{\omega }}}_{i}}=-\frac{{{D}_{i}}}{{{J}_{i}}}{{\omega }_{i}}+\frac{1}{{{J}_{i}}}({{P}_{{{M}_{i}}}}-{{P}_{{{E}_{i}}}}) \\\end{align} \right.$

式中，${{\delta }_{i}}$为功率角；${{\omega }_{i}}$是角速度；${{J}_{i}}$表示转动惯量；${{D}_{i}}$为阻尼系数；${{P}_{{{M}_{i}}}}$为机械功率输入；${{P}_{{{E}_{i}}}}$为输出有功功率。

基于式(1)可以得到如下电网模型

(2)$\begin{array}{c}x(\dot{t})=\boldsymbol{A} x(t)+\boldsymbol{B} u(t)+\omega(t) \\x(t)=\left(\begin{array}{c}\delta(t) \\\omega(t)\end{array}\right) \quad u(t)=\left(P_{M}-P_{E}\right) \\\boldsymbol{A}=\left(\begin{array}{cc}0 & I \\0 & -\frac{D}{J}\end{array}\right) \quad \delta(t)=\left[\delta_{1}(t), \cdots, \delta_{n}(t)\right]^{\mathrm{T}} \\\boldsymbol{B}=\left[\begin{array}{c}0 \\\frac{1}{J}\end{array}\right) \quad \omega(t)=\left[\omega_{1}(t), \cdots, \omega_{n}(t)\right]^{\mathrm{T}} \\D=\operatorname{diag}\left[D_{1}, \cdots, D_{n}\right] \quad J=\operatorname{diag}\left[J_{1}, \cdots, J_{n}\right] \\P_{M}=\left[P_{M_{1}}, \cdots, P_{M_{n}}\right] \quad P_{E}=\left[P_{E_{1}}, \cdots, P_{E_{n}}\right]\end{array}$

式中，ω(t)为系统扰动且范数有界。

2.2 攻击特性描述

电网中的安全机制是通过输出残差与先验阈值的比较来判断系统是否遭受到外部攻击，其检测表达式如下^[18-19]

(3)$\left\{ \begin{align} & \begin{matrix} \left\| r \right\|=\left\| z-H(\widehat{x}) \right\|<\tau & \\\end{matrix} \\ & \begin{matrix} \left\| r \right\|=\left\| z-H(\widehat{x}) \right\|\ge \tau & \\\end{matrix} \\\end{align} \right.$

式中，r是测量残差；z是测量输出；H是雅可比矩阵；τ是先验阈值。

为了欺骗基于卡方的攻击检测机制，攻击者设计了虚假数据$a={{\left[ {{a}_{1}},{{a}_{2}},\cdots,{{a}_{m}} \right]}^{\mathrm{T}}}$，满足$a=Hc$时，可以实现测量残差无变化，即

(4)$\begin{matrix} \left\| r \right\|=\left\| {{z}_{bad}}-H{{x}_{bad}} \right\|=\left\| z+a-H(\widehat{x}+c) \right\|= \\ \left\| z-H\widehat{x}+a-Hc \right\|<\tau \\\end{matrix}$

综上可知，虚假数据攻击对现有基于Kalman的输出估计检测方法具有欺骗特性，即攻击者可以通过注入一组虚假数据实现测量残差的无变化，进而掩盖对系统内部状态的改变。因此，虚假数据攻击的检测给智能电网的安全机制带来了巨大挑战。

2.3 问题描述

考虑电网系统存在虚假数据攻击f(t)，电网的系统模型表达式为

(5)$\left\{ \begin{align} & x(\dot{t})=Ax(t)+Bu(t)+w(t)+Ff(t) \\ & y(t)=Cx(t) \\\end{align} \right.$

式中，F是攻击选择矩阵；f(t)是虚假数据攻击向量；$w(t)$代表扰动。

本文通过设计神经网络观测器来对智能电网系统中的内部状态进行观测，进而实现对虚假数据注入攻击的残差检测。

3 虚假数据攻击检测方法

3.1 观测器设计

设计神经网络观测器之前，给出以下假设和引理。

引理3.1^[20]：给定任意$\varepsilon >0$，对于任意的L₂型函数$f:{{\left[ 0,1 \right]}^{n}}\to {{R}^{m}}$，存在一个RBF网络可在任意ε平方误差精度内逼近函数f。

基于引理3.1，本文采用如下RBF神经网络在线逼近虚假数据攻击，其形式如下

(6)$f(t)={{W}^{*\mathrm{T}}}\delta (x,u)+\varepsilon $

式中，$\left[ x,u \right]$代表神经网络的输入；${{W}^{*}}={{\left[ W_{1}^{*},W_{2}^{*},\cdots,W_{n}^{*} \right]}^{\mathrm{T}}}$是理想神经网络权值；${{W}^{*}}=\arg \underset{W\in {{\Omega }_{w}}}{\mathop{\min }}\,\left[ \underset{X\in {{A}_{d}}}{\mathop{\sup }}\,\left| f(x,u,W)-\left. f(x,u,t) \right| \right. \right]$；W是实际权值向量。

综上，设计神经网络观测器形式如下

(7)$\left\{ \begin{align} & \dot{\hat{x}}(t)=A\hat{x}(t)+Bu(t)+F\hat{f}(t)+K(y(t)-\hat{y}(t))+s(t) \\ & \hat{y}(t)=C\hat{x}(t) \\\end{align} \right.$

式中，K是观测器增益；v为对扰动和不确定性的补偿项；$\hat{x}(t)$为估计值；$\hat{y}(t)$为估计输出；$s(t)=\frac{\alpha \hat{y}(t)}{\left| \hat{y}(t) \right|}$是扰动的补偿项。其中，$\hat{W}$为神经网络权值估计值。因此，利用RBF神经网络在线估计$\hat{f}(t)$为

(8)$\hat{f}(t)={{\hat{W}}^{\mathrm{T}}}\delta (\hat{x},u)$

由式(5)和式(7)得到动态误差方程如下

(9)$\left\{ \begin{align} & {{e}_{x}}(t)=x(t)-\hat{x}(t) \\ & {{e}_{y}}(t)=y(t)-\hat{y}(t) \\ & {{e}_{f}}(t)=f(t)-\hat{f}(t) \\\end{align} \right.$

将式(5)~(8)代入式(9)并求导得

(10)$\left\{ \begin{align} & {{{\dot{e}}}_{x}}(t)=(A-KC){{e}_{x}}+w(t)+F{{e}_{f}}(u,t)-s(t) \\ & {{e}_{y}}(t)=C{{e}_{x}}(t) \\ & {{e}_{f}}(t)=({{W}^{\ *\mathrm{T}}})\widetilde{\delta }+\varepsilon -{{\widetilde{W}}^{T}}\delta (\widehat{x},u) \\\end{align} \right.$

为确保设计式(10)中神经网络观测器误差稳定，给出如下定理。

定理3.1^[20]：在假设3.1条件下，存在正定矩阵$P>0$，正定矩阵T、K满足以下

(11)$\left( \begin{matrix} \Omega +{{C}^{\mathrm{T}}}C & P & PF \\ * & -{{\gamma }^{2}}{{I}_{\text{w}}} & 0 \\ * & 0 & -{{\gamma }^{2}}{{I}_{\text{t}}} \\\end{matrix} \right)<0$

(12)$\Omega ={{(A-KC)}^{\mathrm{T}}}P+P(A-KC)$

(13)$TC={{F}^{\mathrm{T}}}P$

设计神经网络攻击的自适应估计率为

(14)$\overset{\centerdot }{\mathop{\widehat{W}}}\,=\Lambda \delta \left( \widehat{x},u \right)e_{y}^{\mathrm{T}}{{T}^{\mathrm{T}}}$

则状态误差e_x最终有界。

3.2 自适应阈值设计

考虑外部扰动对检测阈值的影响，本节提出自适应阈值的设计来替代现有电网安全机制中的先验阈值，进而提高虚假数据攻击的检测性能。

考虑系统不存在攻击的检测函数表示为

(15)$\rho (x,\hat{x})=\frac{\left\| {{x}^{w}}+{{x}^{e}} \right\|}{\left\| x \right\|\centerdot \left\| {\hat{x}} \right\|}$

式中，${{x}^{w}}$代表噪声；${{x}^{e}}$代表估计误差。

由式(15)可以得到

(16)$\rho (x,\hat{x})\le \frac{\left\| {{x}^{w}} \right\|+\left\| {{x}^{e}} \right\|}{\left\| x \right\|\centerdot \left\| {\hat{x}} \right\|}=\frac{J_{th}^{w}+J_{th}^{e}}{\left\| x \right\|\centerdot \left\| {\hat{x}} \right\|}$

式中，$J_{th}^{e}=\left\| Hx-H\hat{x} \right\|=\left\| HR \right\|$。

综上，自适应阈值计算表达式为

(17)$\Psi =\underset{{{x}^{w}},{{x}^{e}}}{\mathop{\sup }}\,\left\| \rho (x,\hat{x}) \right\|$

基于神经网络观测器，可以得到状态残差表示为

(18)$R=\hat{x}(t)-x(t)$

基于式(17)和式(18)，给出攻击检测逻辑决策为

(19)$\left\{ \begin{align} & \begin{matrix} \left| R \right|<\Psi & \\\end{matrix} \\ & \begin{matrix} \left| R \right|\ge \Psi & \\\end{matrix} \\\end{align} \right.$

基于以上逻辑检测决策，给出对应攻击检测算法如表1所示。

表1 基于残差观测器的攻击检测算法

算法3-1: 基于残差观测器的攻击检测算法
1. 输入一个大型电网包含N个电网子区域； 2. 建造式(7)所示残差观测器； 3. 计算对应状态残差R和自适应阈值Ψ； 4. for 所有检测电网区域 if \|R\|<Ψ then 无攻击； else 有攻击注入； end if 5. end for 6. 输出检测结果：攻击的子区域。

新窗口打开| 下载CSV

3.3 检测性能分析指标

为了评价攻击检测性能，本文引入攻击检测率P_D和误报率P_F两个变量，表达式如下^[21]

(20)$\left\{ \begin{align} & {{P}_{D}}\left( l/h,p \right)=1-\theta \left( \frac{l-p}{h} \right)+\theta \left( \frac{-l-p}{h} \right) \\ & {{P}_{D}}\left( l/h,p \right)=1-\chi {{P}_{F}}\left( l \right) \\\end{align} \right.$

式中，$h,p\in R$为系统注入攻击的强度变量；χ为虚报和漏报的比例系数；l为检测阈值。

4 仿真结果分析

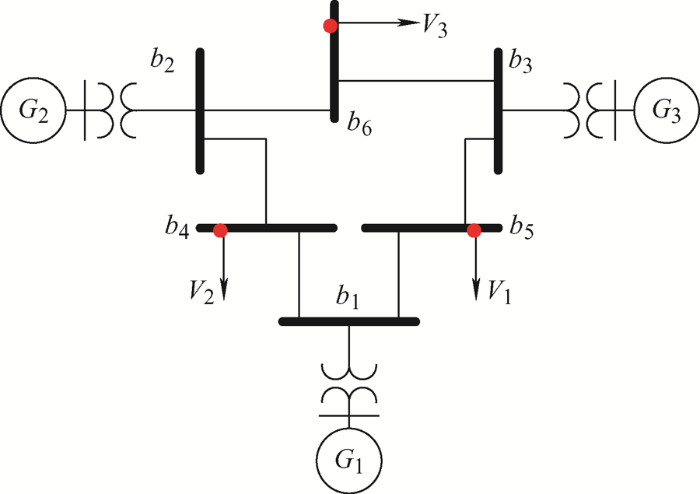
在如图1所示的IEEE三电机六总线上验证所提攻击检测方法的性能，其中部分相关系统参数可参考文献[10]。首先通过与传统卡方检测方法的对比，验证所提检测方法的有效性。然后，通过与欧式检测方法对比可知，所提检测方法可以快速检测入侵的虚假数据攻击，提高了攻击的检测率。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 IEEE三电机六总线电网系统

4.1 攻击检测方法有效性分析

假设电网系统正常运行，攻击者在t=8 s时注入虚假数据攻击，其中的虚假数据攻击模型为

(21)${{z}_{bad}}_{{}}=H{{x}_{bad}}_{{}}+\Gamma {{y}_{k}}{{^{{}}}^{{}}}{{^{{}}}^{{}}}{{^{{}}}^{{}}}k\in T$

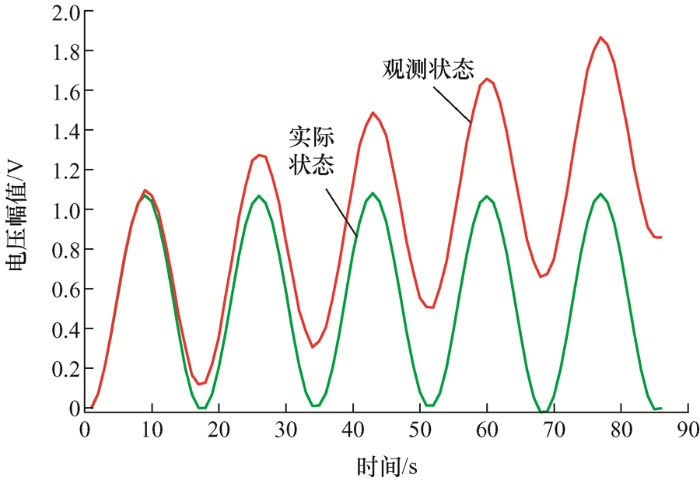
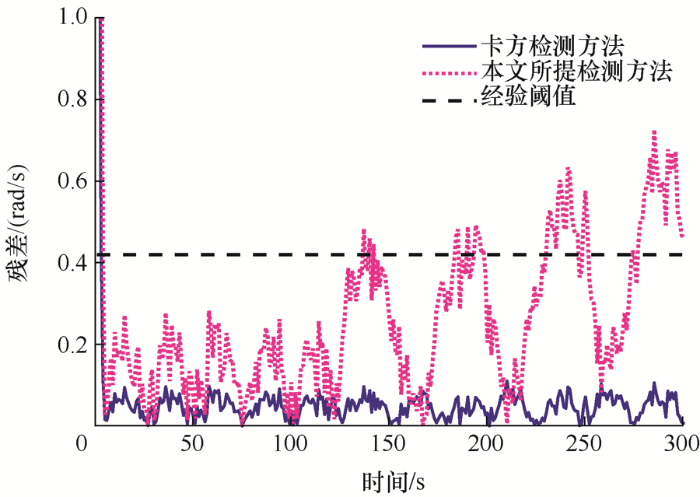
式中，$\Gamma =diag\left( {{\gamma }_{1}},\cdots,{{\gamma }_{n}} \right)$代表传感器选择矩阵；${{y}_{k}}$是攻击向量序列；${{x}_{bad}}$表示被攻击后系统的状态；${{z}_{bad}}$代表被攻击后系统的量测输出。

基于检测算法1，得到注入攻击后卡方检测系统状态变化(图2)和检测结果(图3)，可以发现攻击者成功改变了系统状态变化而未触发系统报警。基于本文所提的攻击检测方法，可以得到攻击检测结果如图3所示。由于$\left| R \right|\ge \Psi $，可以成功检测到入侵的虚假数据攻击。与传统的卡方检测方法对比，本文所提检测方法可以有效检测入侵的虚假数据攻击。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 虚假数据攻击下系统状态电压变化

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 本文检测方法与卡方检测的攻击检测对比

4.2 攻击检测性能对比分析

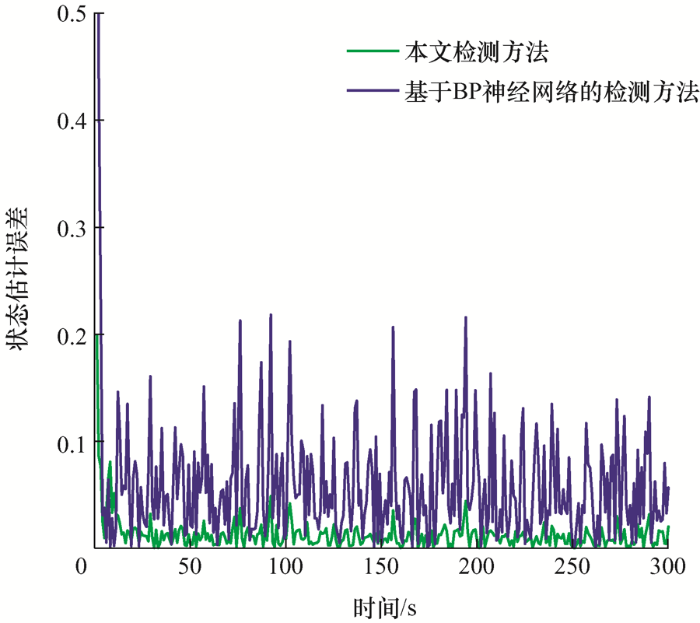
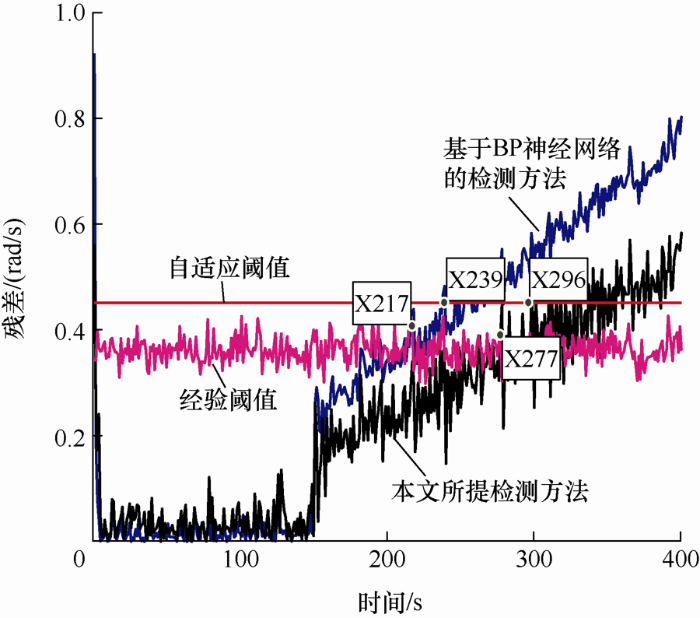
在t=200 s攻击入侵情况下，分别采用基于BP神经网络和本文算法1检测虚假数据攻击，如图4和图5所示。基于图4的对比结果可以发现，本文所提的检测方法比基于BP神经网络方法得到的状态估计误差更小，进而获得更准确的估计状态。此外，在同一检测阈值的情况下，本文所提检测方法可以更快地检测到注入的虚假数据。图5中检测结果表明自适应阈值替代传统先验阈值后进一步缩短攻击检测时间，提高攻击检测性能。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 本文方法与BP神经网络的状态估计误差分析

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 本文方法与BP神经网络的攻击检测分析

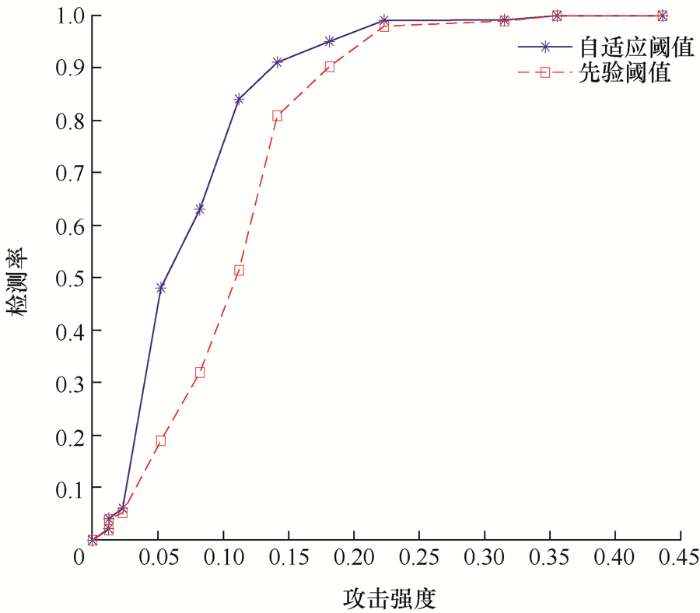
图6揭示了检测率P_D取决于检测阈值的选取值，即检测阈值越小，检测率越高。在自适应阈值替代先验阈值情况下，可以进一步缩短攻击检测时间，提高攻击的检测率。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 检测率分析

5 结论

本文提出基于神经网络观测器的虚假数据攻击检测方法，主要工作总结如下所述。

(1) 考虑虚假数据攻击对内部状态的影响，提出基于内部状态差变化的神经网络观测器残差检测方法，解决了虚假数据攻击欺骗传统基于Kalman的卡方检测方法问题。

(2) 基于状态估计误差和外部扰动的范数上界，设计自适应阈值替代传统的先验阈值，缩短了虚假数据攻击的检测时间。

最后，在IEEE三电机六总线上验证对比了所提攻击检测方法性能的优越性。未来工作中，本文还需要进一步考虑建模时电网模型不确定性对攻击检测的影响，以及针对不同类别的虚假数据攻击的检测与防御研究。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

中华人民共和国国务院新闻办公室.

新时代的中国能源发展

[N]. 人民日报,2020-12-22(010).