电气工程学报, 2022, 17(4): 11-19 doi: 10.11985/2022.04.003

特邀专栏：电化学储能系统安全管理与运维

基于改进最小二乘支持向量机的锂离子电池健康状态快速估计方法*

徐彬翔,1,2, 郑林锋,1,2, 黄乙恒1,2, 肖志能1,2, 王新月1,2

1.暨南大学国际能源学院 珠海 519070

2.暨南大学轨道交通研究院 珠海 519070

Fast Estimating the State of Health of Lithium-ion Batteries Based on Improved Least Squares Support Vector Machine

XU Binxiang,1,2, ZHENG Linfeng,1,2, HUANG Yiheng1,2, XIAO Zhineng1,2, WANG Xinyue1,2

1. International Energy College, Jinan University, Zhuhai 519070

2. Institute of Rail Transportation, Jinan University, Zhuhai 519070

通讯作者: 郑林锋，男，1989年生，博士，副教授。主要研究方向为动力/储能电池在新能源汽车和电网储能系统中的应用。E-mail：lfzheng@jnu.edu.cn

收稿日期: 2022-08-24   修回日期: 2022-10-9  

基金资助: *广东省科技创新战略专项资金(“攀登计划”专项资金).  pdjh2021b0056
广东省基础与应用基础研究基金.  2019A1515012210
广州市科技计划.  202201010601

Received: 2022-08-24   Revised: 2022-10-9  

作者简介 About authors

徐彬翔，男，2001年生，硕士研究生。主要研究方向为电池管理系统。E-mail：binxiangxu@163.com

摘要

锂离子电池健康状态(State of health, SOH)是电池系统安全管理与运维的主要参数之一，准确快速的SOH估计对提高电池应用的安全性有着重要意义。针对目前存在的电池SOH估计速度与精度难以兼顾的问题，提出一种基于改进最小二乘支持向量机(Improved least squares support vector machine, ILS-SVM)的SOH快速准确估计方法。通过对LS-SVM算法设定合适的临界系数，舍弃部分支持向量，削弱边界样本对算法的影响，从而提高了算法的鲁棒性与运行速度，形成改进的LS-SVM算法。通过分析电池电压特性，选取特征电压数据区间进行估计，有效避免电池的完全充放电测量，提高SOH的估计效率。验证结果表明，所提出的电池SOH估计方法估计精度较高，大部分估计误差小于1%，且所提算法相比于改进之前的算法，运行速度提升最高可达20%。

关键词： 锂离子电池 ; 健康状态估算 ; 最小二乘支持向量机 ; 数据驱动

Abstract

State of health(SOH) is one of the core parameters for the safe management and operation of battery systems. Accurate and rapid estimation of SOH is of great significance to the safe utilization of batteries. To address the issue that conventional SOH estimation algorithms are difficult to involve both high running speed and high accuracy, a fast estimation method of battery SOH using an improved least squares support vector machine(ILS-SVM) is proposed. The robustness and running speed of the algorithm can be effectively improved by setting appropriate critical parameters, which discards some support vectors and weakens the influence of boundary samples on the algorithm. The ILS-SVM is then employed to fast estimate SOH of different battery data sets. By analyzing the operation data of batteries, a specific voltage data interval is used for data preprocessing to avoid the complete charging and discharging measurement of the battery, thus improving the efficiency of battery SOH estimation. The verified results show that accurate estimates can be achieved, and most of estimation errors of battery SOH are less than 1%. Compared with the original LS-SVM algorithm, the running speed of the ILS-SVM can be improved by up to 20%.

Keywords： Lithium-ion battery ; SOH estimation ; least squares support vector machine(LS-SVM) ; data driven

PDF (36463KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

徐彬翔, 郑林锋, 黄乙恒, 肖志能, 王新月. 基于改进最小二乘支持向量机的锂离子电池健康状态快速估计方法*. 电气工程学报[J], 2022, 17(4): 11-19 doi:10.11985/2022.04.003

XU Binxiang, ZHENG Linfeng, HUANG Yiheng, XIAO Zhineng, WANG Xinyue. Fast Estimating the State of Health of Lithium-ion Batteries Based on Improved Least Squares Support Vector Machine. Chinese Journal of Electrical Engineering[J], 2022, 17(4): 11-19 doi:10.11985/2022.04.003

1 引言

锂离子电池具有能量密度高、循环寿命长、自放电率低、污染较小等优点[1]，被广泛应用于电网储能、新能源汽车[2]及航天航空等领域。锂离子电池健康状态(State of health, SOH)是反映电池衰退老化程度的重要指标。随着电池使用次数的增加，电池的最大可用容量降低，SOH降低，剩余使用寿命减少。一般来说，电池SOH下降到80%，则其达到电动汽车退役标准[3]。锂离子电池SOH的准确快速估计对于电池系统的科学安全使用有着重要的意义。

不同于电池外部特性如电压电流的直接测量，电池SOH的估计需要经过一系列参数的测量与转换，且其内部电化学反应复杂、其外特性易受不同工况的影响，准确快速地估计电池SOH极具挑战性。近年来，国内外研究学者对电池SOH的估计做了大量的研究，SOH估计方法主要可以分为两类：基于电池模型的方法[4⇓⇓⇓⇓⇓⇓⇓-12]和基于数据驱动的方法[13⇓⇓⇓⇓⇓-19]。

基于电池模型的方法主要采用等效电路模型[4⇓⇓⇓-8]或电化学模型[9⇓⇓-12]。文献[4]选用一阶RC等效电路模型，利用电池欧姆内阻、极化内阻与极化电容共3个模型参数进行评估，提高估计精度。文献[5]通过构建非线性的等效电路电池模型，利用卡尔曼滤波算法在线辨识电池内阻，得到内阻自适应的电池模型。文献[6]采用改进的自适应无迹卡尔曼滤波算法，建立电池状态空间模型，实时估计电池模型中的欧姆电阻，提高电池模型估计精度，从而准确估算电池SOH。文献[7]基于Thevenin等效电路模型的欧姆内阻、极化内阻和极化电容构建HI，引入灰色神经网络模型估计电池SOH。文献[8]采用复杂非线性最小二乘算法，将电池阻抗数据用于拟合等效电路模型，并通过观测模型参数变化，检测电池SOH。等效电路模型结构简单、计算量小，可以利用优化算法进行长期实时的估计，但鲁棒性较差，不同工况条件下容易产生估计误差。电化学模型根据电池的电化学反应机理，建立动力学系统模型，精度较高，但参数辨识困难。文献[9]利用溶剂扩散和电解质界面相应参数的变化，通过映射函数拟合试验数据，实现SOH估计。文献[10]考虑锂离子电池寿命衰退期副反应，基于ECM(Equivalent circuit model)模型与电化学模型，借助平衡电势量化容量衰减来实现SOH的估计。文献[11]提出一种改进的基于单粒子锂电池模型的降阶电化学模型，包括了电解质-相电位差的解析表达式，并考虑了未建模动态因素的影响，通过估计电池内阻增值实现SOH估计。文献[12]利用温度依赖的电化学模型和增强单粒子模型，建立自适应互联观测器，估计电池阳极扩散系数和SEI层离子电导率，进而估计出电池SOH。基于电池模型方法在模型的建立过程中，需要充分考虑SOH与电池内部参数的相关性，利用电池衰退过程中模型参数的变化来实现对SOH的估计，其复杂性相对较高。

基于数据驱动的SOH估计方法不需要深入了解电池的工作机理和特性，通过提取与电池老化相关的特征参数，收集老化数据，利用机器学习或深度学习算法建立与SOH的非线性映射关系，进行SOH测算。文献[13]在动态工况下构建表征电池衰减的健康指标，引入极限学习机离线训练电池全生命周期的衰退模型，通过该模型对电池SOH进行估计。文献[14]对电压、电流和电荷电容的测量数据进行深度学习，利用深度卷积神经网络进行电池容量预测。文献[15]通过提取电池恒流充电时的电压、电流以及温度曲线，作为估计的健康特征，通过相关向量机构建模型实现SOH估计。文献[16]采用遗忘因子算法对等效电路模型进行参数识别，利用支持向量机(Support vector machine, SVM)算法对电池健康状态进行估计。另外，文献[17]针对电池实际运行工况，提出一种可适用于非恒流的不稳定工况的电池特征提取方案，并开发了基于多维特征和混合聚类算法的健康状态综合评分体系，对电池健康状态进行准确评估。文献[18]从恒流充电的老化试验中提取健康特征，基于双高斯过程回归模型分析电池容量电阻变化的不一致性，从而估计SOH。文献[19]通过提取增量容量分析后的峰值和位置作为HF，利用高斯过程回归建立SOH模型，并优化超参数进行电池容量预测。基于数据驱动的SOH估计方法适应性较强，实现过程较简单，并能通过优化算法减小模型复杂度提高运算速度，但需要足够的样本量训练模型以提高估计精度。

在数据驱动方法中，以卷积神经网络为代表的深度学习虽然可以通过参数共享减小网络的训练参数，但是通常计算量较大，对硬件、模型设计等要求较高[20]。高斯过程回归类方法较为常用，但本文中电池端电压的特征数据较多，在高维空间的预测表现较差[21]。相关向量机类方法虽然拥有简洁的核函数，但在训练样本较多时，模型通常较复杂，存在训练速度较慢的问题[22]。SVM通过非线性映射，将问题转化为带不等式约束的凸二次规划问题，具有学习速度快、泛化能力好的特点，能够较好地解决小样本、非线性、高维数和局部极小点等问题[23]。但由于SVM通过二次规划来求解支持向量，当样本规模较大时，矩阵阶数增加，二次规划的计算量将严重降低计算效率。最小二乘支持向量机(Least squares support vector machine, LS-SVM)是一种基于统计理论的改进型SVM算法，具有较强的非线性映射能力，能够将二次优化问题的解转化为线性方程组的求解，从而弥补SVM对于大规模样本的弊端，降低算法复杂度。因此，本文采用LS-SVM方法进行动力电池SOH的快速估计研究。由于LS-SVM将支持向量机的不等式约束改为等式约束，失去了对松弛向量的约束性，致使LS-SVM缺失稀疏性[24]。当样本模型较大时，可能造成支持向量数量的大幅度增加。另外，随着样本数量的增加，普通线性方程组的求解也将变得复杂。

为了进一步实现对动力电池SOH的快速估计，本文在传统LS-SVM基础上，设置临界参数ac，以降低算法复杂度，减小支持向量数量，同时削弱边界样本对整体模型的影响，提高算法鲁棒性与运行速度，实现对数据的快速处理，并通过试验验证了算法的可行性和准确性。

2 电池SOH与数据处理

电池的健康状态(SOH)表征电池的老化程度，伴随着电池充放电次数的增加，电池内部欧姆电阻增大，实际容量逐渐减小。通常情况下，电池SOH小于80%即达到新能源汽车的退役标准。目前，电池SOH尚未有统一的定义，可以用不同的电池老化参数来表征SOH，比如电池实际容量、内阻、功率等，其中，常用容量比来定义电池SOH[25]，用式(1)表示为

$\mathrm{SO}{{\mathrm{H}}_{i}}=\frac{{{C}_{i}}}{{{C}_{0}}}$

式中，$\mathrm{SO}{{\mathrm{H}}_{i}}$为第i周期的SOH值，${{C}_{i}}$为第i周期电池容量，${{C}_{0}}$为电池初始容量。

本文采用斯坦福大学-MIT和美国NASA公开的电池测试数据集[26-27]进行算法的开发与验证。斯坦福-MIT数据集所用电池为磷酸铁锂电池，在30 ℃的强制对流温箱中进行试验。电池的标称容量为1.1 A·h，标称电压为3.3 V，上、下限截止电压分别为3.6 V和2.0 V。对电池采用两步快速充电策略进行充电，即先对电池进行恒流充电，当电池SOC达到规定值时，切换电池恒流充电倍率，当SOC达到80%时，进行恒流恒压充电至充电结束；放电操作以4C倍率进行。NASA数据集所使用的电池为LG Chem 18650圆柱形电池，在24 ℃、4 ℃进行试验。电池额定容量为2.1 A·h，常规工作电压范围为3.2~4.2 V。对B1、B2、B3、B4四节锂离子电池进行循环恒流恒压充放电，以1.5 A的恒定电流模式进行充电，直到电池电压达到4.2 V，然后在恒定电压模式下继续充电，直到充电电流降至20 mA，再在2 A的恒流水平下进行放电，直到电池电压分别降至2.5 V，从而得到不同老化程度的电池电压、电流、容量和温度等数据。

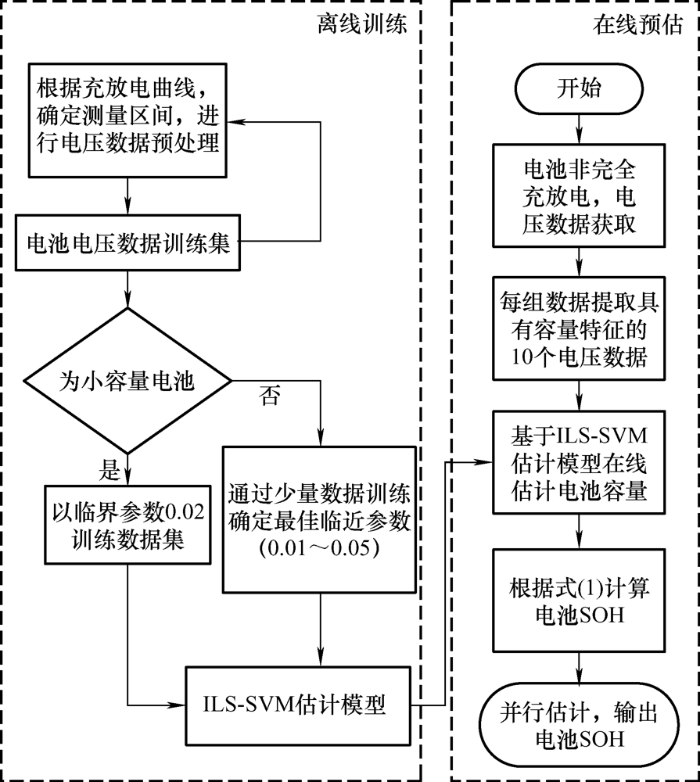
为实现对锂电池SOH快速估计，即减少电池充放电测量时间，避免锂电池的完全充放电；本文拟通过测量一段时间内的电池充放电数据，然后对数据进行预处理，通过改进LS-SVM算法，建立ILS-SVM(Improved least squares support vector machine)模型，实现对锂电池SOH的快速准确估计。本文所提方法示意图如图1所示。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   基于ILS-SVM估计电池SOH示意图


本文所提ILS-SVM电池SOH估计方法主要分为两步：① 离线训练阶段，通过电池电压数据等确定测量区间，进行预处理，以避免电池完全充放电；并通过临界参数，对传统模型进行改进，建立ILS-SVM估计模型；② 在线预估阶段，提取送检电池电压特征数据，通过ILS-SVM模型，估计出电池容量，进而计算并输出电池SOH。

对于斯坦福-MIT数据集，数据采集过程中，电池循环充放电至电池SOH衰减到80%，期间每隔100 ms取样一次电池端电压温度等数据，测算出电池容量，得到相关数据。恒流充电过程中，电池端电压呈现出非线性衰减特性，不同容量电池衰减速率存在差异。经过对斯坦福-MIT数据集电压数据的分析发现，电池充电电压3.5~3.6 V区间不同容量电池差异较大，能较好地与锂离子电池容量衰减特性建立联系。故本文选择此段电压区间，进行数据预处理，形成数据集。以下为具体操作步骤。

取电池恒流充电的电压数据，以电池端电压3.5 V电压为基准电压，每隔100 ms记录一次，记录不少于30次，得到Cell1、Cell2、Cell3三节电池不同充放电循环的电压训练数据集。部分数据集如表1所示，其中电压1为基准电压，电压2为经过100 ms后测得电压值，电压3为经过200 ms后测得电压值，以此类推。

表1   斯坦福-MIT数据集部分电压数据

电池实际容量
/(A·h)		电压1/V电压2/V电压3/V电压4/V
Cell11.089 83.5003.5043.5073.512
Cell10.981 73.5003.5083.5163.523
Cell10.869 03.5003.5213.5383.551
Cell21.054 43.5003.5053.5103.515
Cell21.016 73.5003.5063.5123.517
Cell20.845 03.5003.5293.5483.561
Cell31.074 23.5003.5053.5093.513
Cell30.957 93.5003.5143.5243.532
Cell30.890 33.5003.5213.5353.547

新窗口打开| 下载CSV


由表1可知，不同容量电池在同一基准电压下的充电电压存在差异，容量大的电池端电压上升速度更慢，且随着取样次数和时间的增加，差异表现更明显。为综合考虑估计精度与速度，取基准电压后10次的电压数据(包括基准电压)作为一组数据集。最终，以3节电池恒流充电电端电压3.5~3.6 V区间数据为参考，整理数据，得到3组电池数据集，合并成总的数据集。

在NASA数据集中，对充电电池端电压数据进行类似的预处理。通过数据分析，以3.7 V为参考电压，10个电压输入量及1个电池容量形成一个数据集，合并3节电池数据成总的数据集。将总的数据集按3∶1的比例随机划分为训练集和测试集，分别用于模型的训练、预测。

3 ILS-SVM算法

支持向量机对小样本的统计问题有很好的学习能力。相比于标准支持向量机，最小二乘支持向量机具有更快的收敛速度，更适合对海量数据的处理[28]。

设输入训练样本集为

$\left\{ {{x}_{1}},{{y}_{1}};{{x}_{2}},{{y}_{2}};\ldots ;{{x}_{n}},{{y}_{n}} \right\}$

高维线性映射函数为

$f\left( x \right)={{w}^{\mathrm{T}}}\varphi \left( x \right)+b$

式中，$f\left( x \right)$为映射输出值，$\varphi \left( x \right)$为非线性映射函数，$w$为权值，b为偏值。

根据结构风险最小化原则，并引入间隔概念，LSSVM回归预测问题可表示为

$\left\{ \begin{matrix} \mathrm{min}\ P\left( w,e \right)=\frac{1}{2}{{w}^{\mathrm{T}}}w+\frac{1}{2}\gamma \underset{i=1}{\overset{n}{\mathop \sum }}\,e_{i}^{2}\ \ \ \ \ \ \ \ \\ \mathrm{s}.\mathrm{t}.\ {{y}_{i}}={{w}^{\mathrm{T}}}\varphi \left( {{x}_{i}} \right)+b+{{e}_{i}}\ \ \ \ i=1,2,\cdots,n \\ \end{matrix} \right.$

式中，${{e}_{i}}$为训练误差，$\gamma $为正规化因子，$e={{\left( {{e}_{1}},{{e}_{2}},\ldots,{{e}_{n}} \right)}^{\mathrm{T}}}$为预测误差。

利用拉格朗日法求解式(3)，优化问题转化为求解线性方程

$L\left( w,b,e,\alpha \right)=\frac{1}{2}{{w}^{\mathrm{T}}}w+\frac{1}{2}\gamma \underset{i=1}{\overset{n}{\mathop \sum }}\,e_{i}^{2}-\underset{i=1}{\overset{n}{\mathop \sum }}\,{{\alpha }_{i}}(w\varphi \left( x \right)+b+{{e}_{i}}-{{y}_{i}})$

式中，$\alpha =({{\alpha }_{1}},{{\alpha }_{2}},\ldots,{{\alpha }_{i}})$。对式(4)求偏导可得

$\left\{ \begin{matrix} \frac{\partial L}{\partial w}=0\ \ \ \ \ \\ \frac{\partial L}{\partial b}=0\ \ \ \ \ \ \\ \frac{\partial L}{\partial {{e}_{i}}}=0\ \ \ \ \ \\ \frac{\partial L}{\partial {{\alpha }_{i}}}=0\ \ \ \ \ \\ i=1,2,\cdots,n \\ \end{matrix} \right.\Rightarrow \left\{ \begin{matrix} w=\underset{i=1}{\overset{n}{\mathop \sum }}\,{{\alpha }_{i}}\varphi \left( x \right)\ \ \ \ \ \ \ \ \ \ \\ \underset{i=1}{\overset{n}{\mathop \sum }}\,{{\alpha }_{i}}=0\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ \alpha =\gamma {{e}_{i}}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ b={{y}_{i}}-{{w}^{\mathrm{T}}}\varphi \left( {{x}_{i}} \right)-{{e}_{i}} \\ \end{matrix} \right.$

进一步求解可得非线性映射模型

$y\left( x \right)=\underset{i=1}{\overset{n}{\mathop \sum }}\,{{\alpha }_{i}}K\left( x,{{x}_{i}} \right)+b$

式中，$K\left( x,{{x}_{i}} \right)$为核函数。本文选取径向基函数为核函数，即

$K\left( x,{{x}_{i}} \right)=\text{exp}\left( -\frac{|{{\left| x-{{x}_{i}}| \right|}^{2}}}{2{{\gamma }^{2}}} \right)$

传统LS-SVM方法不仅需要保存模型参数$\left[ b~{{\alpha }_{1}}~{{\alpha }_{2}}~{{\alpha }_{3}}\ldots ~{{\alpha }_{n}} \right]~$，还需要保存支持向量集，计算量大且需要大量的变量存储空间，特别是对于输入维数较多、对象又较复杂的情况。通过定义临界系数${{\alpha }_{c}}$对求解式(4)得到的系统${{\alpha }_{i}}$进行改进，若$\left| {{\alpha }_{i}} \right|<{{\alpha }_{c}}$，则令${{\alpha }_{i}}=0$。${{\alpha }_{c}}$的取值由工程需要而定，${{\alpha }_{c}}$越小，模型预测精度越高，但模型复杂度越高，计算量越大[29]。

通过设置合适的${{\alpha }_{c}}$可以削弱边界样本对整体模型的影响，同时保留对模型参数更加重要的主体样本，在模型的复杂性和学习能力之间寻求最佳折衷，获得更好的泛化能力。与LS-SVM相比，ILS-SVM算法能大幅度减小支持向量的数量，从而降低模型复杂度，节省变量存储空间，缩短运算时间。另外，通过对边界值的处理，能够减小电池充放电时的局部异常电压电流数据对整体模型精度的影响，降低模型对异常值的敏感度，提高鲁棒性。

为了验证ILS-SVM算法相对于传统的LS-SVM和SVM算法的优势，对算法检测速度和精度进行对比试验。根据单一变量原则，所测检测算法数据集均取自上文斯坦福-MIT数据集，共300组，其中200组用于模型训练，100组用于数据测试。试验均采取5折交叉验证防止过拟合，在配置为i5-8265U CPU、8 GB RAM的计算机上运行算法，所得运行时间均取3次测试平均值。ILS-SVM临界参数${{\alpha }_{c}}$取不同值，试验结果如表2所示。

表2   改进算法与原算法的对比

算法方均根误差
(RMSE)(%)		运行时间/s
训练集测试集
SVM0.591.150.151
LS-SVM0.771.110.123


ILS-SVM
${{\alpha }_{c}}$=0.010.581.120.109
${{\alpha }_{c}}$=0.020.560.840.103
${{\alpha }_{c}}$=0.030.621.090.97
${{\alpha }_{c}}$=0.040.791.530.95
${{\alpha }_{c}}$=0.050.981.970.093

新窗口打开| 下载CSV


分析试验结果可知，SVM算法虽能保证估计的准确性，但运行时间较长；ILS-SVM算法的${{\alpha }_{c}}$取值越大，舍弃的支持向量越多，算法复杂性越低，算法运行时间越短。当${{\alpha }_{c}}$取值适当时，能够降低算法对局部异常值的敏感度，从而增强鲁棒性，减小方均根误差。由表3可知，当${{\alpha }_{c}}$=0.02时，能在保证算法估计精度的同时，提高算法运行速度，故下文选取临界参数${{\alpha }_{c}}$=0.02进行相关试验。

表3   斯坦福-MIT数据集电池SOH估计结果分析

电池
编号		方均根误差(%)总运行时间/s
ILS-SVMLS-SVM提升量ILS-SVMLS-SVM提升量(%)
Cell10.184 12.579 192.860.1970.22813.596
Cell20.143 91.110 087.830.2060.24415.574
Cell30.430 50.874 850.790.2010.24718.623

新窗口打开| 下载CSV


4 模型训练

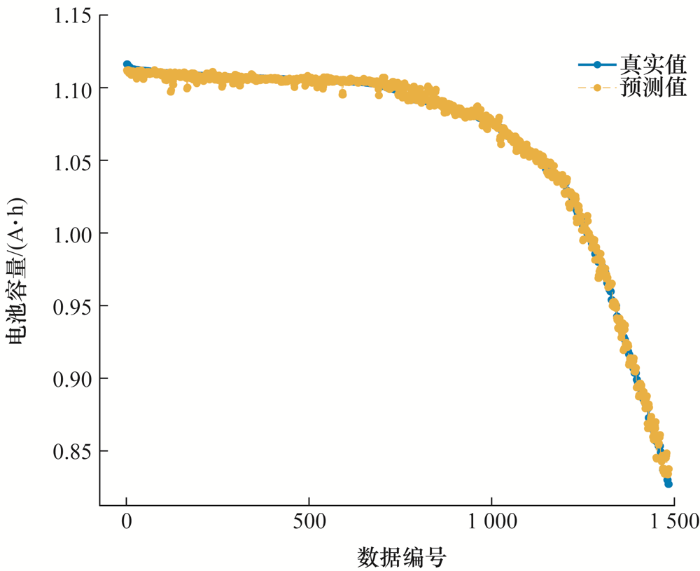
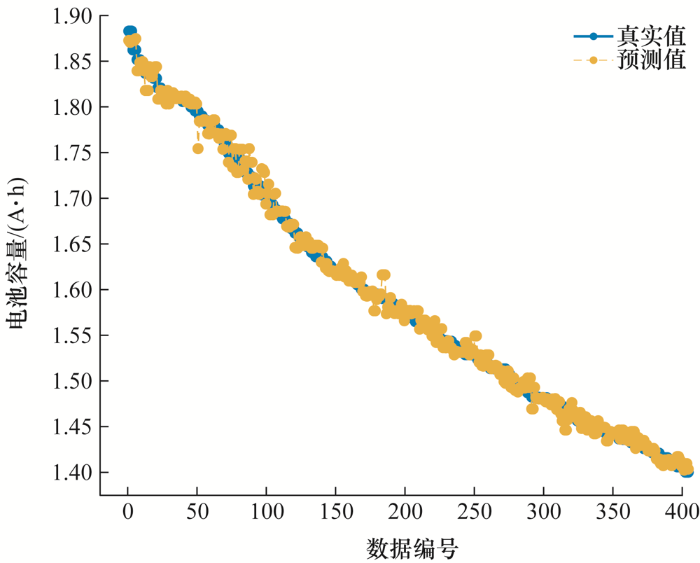
模型训练过程中，取临界系数${{\alpha }_{c}}$为0.02，并使用交叉验证将数据集分成5折，防止过拟合。通过以上操作，得到基于ILS-SVM的电池SOH估计模型。从斯坦福-MIT数据集和NASA数据集抽取约50%数据集作为训练集，余下50%数据集作为验证集。模型训练结果如图2和图3所示。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   斯坦福-MIT数据集ILS-SVM模型训练


图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   NASA数据集ILS-SVM模型训练


由图2、图3可知，预测值与真实值保持较高一致性，虽然存在个别偏离点，但模型整体预测精度高。斯坦福-MIT数据集的预测结果方均根误差为0.46%，NASA数据集的预测结果方均根误差为1.36%，均可实现对电池实际容量的准确预测。不同种类电池充电曲线有较大差别，但从模型训练过程来看，临界参数${{\alpha }_{c}}$=0.02时，结果较理想，鲁棒性较好。预测的实际容量值代入式(1)可得到电池的SOH。

5 SOH估计验证与分析

5.1 斯坦福-MIT数据集验证

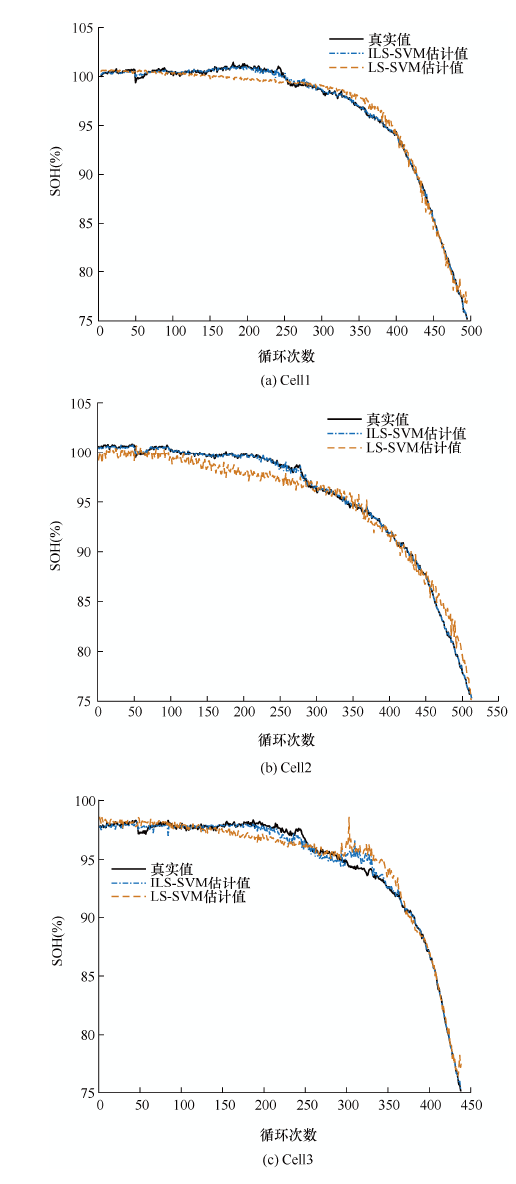
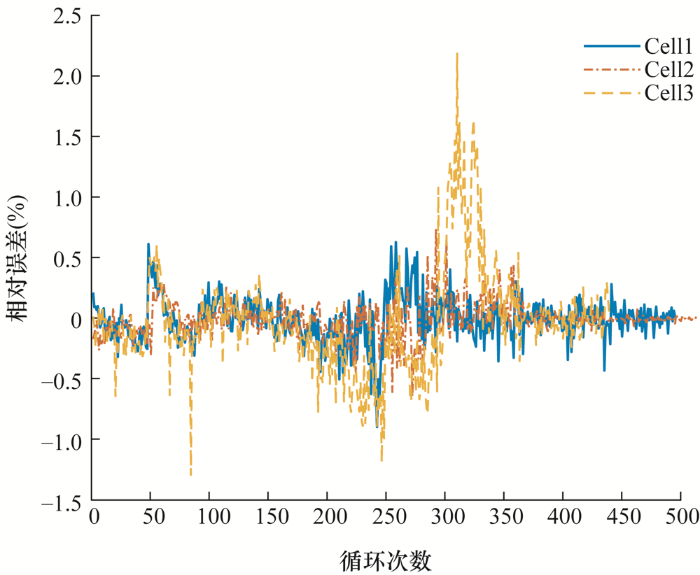
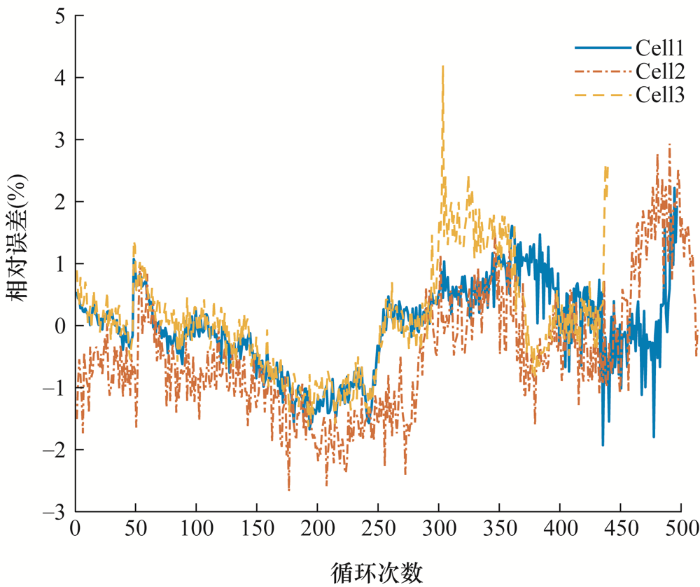
根据已有ILS-SVM模型，对斯坦福-MIT数据集中不同老化程度的Cell1、Cell2、Cell3等三节电池进行SOH估计，计算机配置为i5-8265U CPU、8 GB RAM，估计结果如图4所示，估计结果与误差分析如图5、图6和表3所示。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   斯坦福-MIT数据集电池Cell1、Cell2、Cell3估计结果


图5

新窗口打开| 下载原图ZIP| 生成PPT

图5   斯坦福-MIT数据集ILS-SVM算法估计结果误差分析


图6

新窗口打开| 下载原图ZIP| 生成PPT

图6   斯坦福-MIT数据集LS-SVM算法估计结果误差分析


由图4、图5和图6对比结果可知，ILS-SVM算法相比LS-SVM算法估计准确度有较大提升。通过分析表3可知，ILS-SVM算法估计准确度提升量超过50%，运行时间提升量在10%~20%之间。

在进行不同电池编号的数据预测时，预测精度和速度提升量存在一定的差异。原因是同一型号不同编号的电池存在不一致性，使用同一模型进行预测存在差异。由表3结果可知，该差异对改进算法的提升效果影响不大，估计精度与速度平均提升量依然较大。由图4可知，对于大部分电池充电循环中出现的非连续的跳变点，模型也能较准确预测。原因是电池循环充放电过程中，SOH出现跳变时，相应输入变量，即电池端电压数据也随之改变。模型通过电池此时的端电压数据，也能较为准确地追踪到电池的SOH。

由ILS-SVM算法在估计精度、运行时间上的提升量，数据预处理操作解决的电池完全充放电问题，本文所提方法具有较高的工程实用价值。

5.2 NASA数据集验证

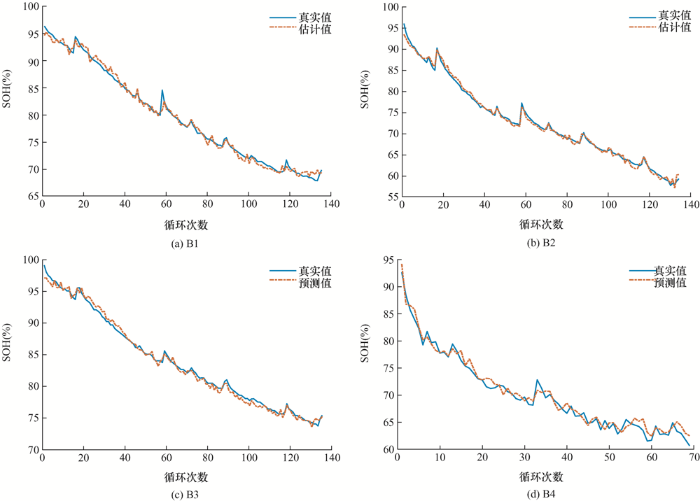
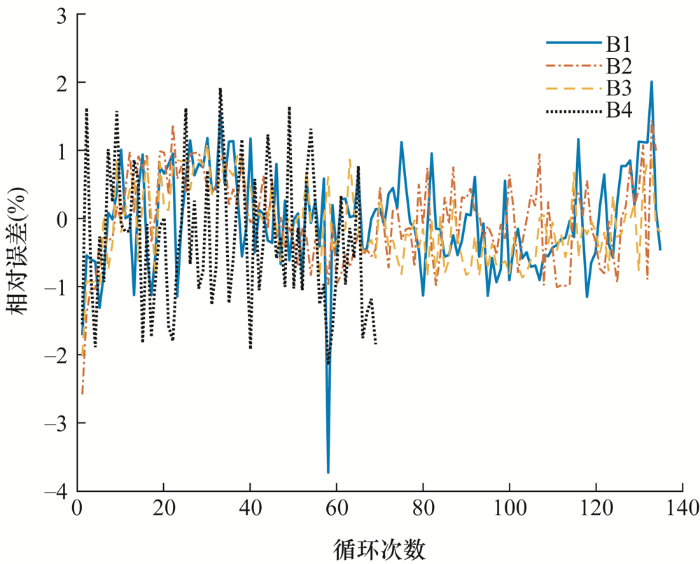
根据已有ILS-SVM模型，对NASA数据集中不同老化程度的B1、B2、B3、B4四节电池进行SOH估计。其中，B1、B2、B3为环境温度24 ℃时的测试电池，B4为环境温度4 ℃时的测试电池。估计结果如图7所示，估计结果与误差分析如图8和表4所示。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7   NASA数据集电池B1、B2、B3、B4估计结果


图8

新窗口打开| 下载原图ZIP| 生成PPT

图8   NASA数据集ILS-SVM算法估计结果误差分析


表4   电池SOH估计结果分析

电池
编号		最大误差
(ME)(%)		方均根误差
(RMSE)(%)		总运行时间/s
B13.727 30.745 20.179
B22.578 80.644 10.176
B32.019 40.574 10.154
B42.145 51.082 40.089

新窗口打开| 下载CSV


由图8可知，电池SOH估计值与真实值的拟合程度高，在曲线两端也能跟踪真实值的变化，能够对不同老化程度的电池进行SOH估计。由表4进一步分析可得，对于常温电池B1、B2、B3的预测，大部分样本估计误差稳定在1%以内，方均根误差保持在0.5%~0.8%之间，估计精度高，且总运行时间较短。对于低温电池B4的SOH预测，虽然预测精度有所降低，但大部分样本估计误差也能稳定在2%以内，方均根误差保持在1.1%以内，算法预测精度依然较高。

虽然斯坦福-MIT数据集与NASA数据集电池衰退曲线差异较大，但本文提出的基于ILS-SVM算法的SOH估算精度都较高，说明了该算法具有较好的鲁棒性。

6 结论

为实现对锂离子电池SOH的快速准确估算，本文提出一种基于ILS-SVM算法的电池SOH快速估算方法，并通过不同的电池测试数据集验证了其有效性。为避免采集电池数据时对电池进行完全充放电，本文对斯坦福-MIT数据集和NASA数据集中不同老化的电池电压数据进行分析，提取表征锂离子电池容量衰减差异性的主要电压区间，进行分段预处理，形成试验数据集，并用于模型训练与验证。在传统LS-SVM算法的基础上，通过设定临界系数${{\alpha }_{c}}$改进传统算法，以降低算法复杂度、提高模型鲁棒性。验证试验结果表明，选取适当的临界系数${{\alpha }_{c}}$，相比于传统的LS-SVM算法，ILS-SVM算法能够提高运行速度与估计精度。利用训练后的模型对多个电池的不同老化状态进行SOH估计，结果表明，该方法具有较高的估计精度，大部分样本估计误差稳定在1%以内，且能够在短时间内实现电池SOH的估计，有效避免对电池进行完全充放电检测，提高了SOH的估计效率。

参考文献

缪平, 姚祯, LEMMON J, 等.

电池储能技术研究进展及展望

[J]. 储能科学与技术, 2020, 9(3):670-678.

[本文引用: 1]

MIAO Ping, YAO Zhen, LEMMON J, et al.

Current situations and prospects of energy storage batteries

[J]. Energy Storage Science and Technology, 2020, 9(3):670-678.

[本文引用: 1]

欧阳明高.

能源革命与新能源智能汽车

[J]. 中国工业和信息化, 2019(11):21-24.

[本文引用: 1]

OUYANG Minggao.

Energy revolution and new energy intelligent vehicles

[J]. China Industry and Information Technology, 2019(11):21-24.

[本文引用: 1]

LIN C P, CABRERA J, YANG F, et al.

Battery state of health modeling and remaining useful life prediction through time series model

[J]. Applied Energy, 2020, 275:115338.

DOI:10.1016/j.apenergy.2020.115338      URL     [本文引用: 1]

陈猛, 乌江, 焦朝勇, 等.

锂离子电池健康状态多因子在线估计方法

[J]. 西安交通大学学报, 2020, 54(1):169-175.

[本文引用: 3]

CHEN Meng, WU Jiang, JIAO Chaoyong, et al.

Multi-factor online estimation method for health status of lithium-ion battery

[J]. Journal of Xi’an Jiaotong University, 2020, 54(1):169-175.

[本文引用: 3]

戴海峰, 魏学哲, 孙泽昌.

基于等效电路的内阻自适应锂离子电池模型

[J]. 同济大学学报, 2010, 38(1):98-102.

[本文引用: 3]

DAI Haifeng, WEI Xuezhe, SUN Zechang.

An inner resistance adaptive model based on equivalent circuit of lithium-ion batteries

[J]. Journal of Tongji University, 2010, 38(1):98-102.

[本文引用: 3]

魏克新, 陈峭岩.

基于自适应无迹卡尔曼滤波算法的锂离子动力电池状态估计

[J]. 中国电机工程学报, 2014, 34(3):445-452.

[本文引用: 3]

WEI Kexin, CHEN Qiaoyan.

States estimation of Li-ion power batteries based on adaptive unscented Kalman filters

[J]. Proceedings of the CSEE, 2014, 34(3):445-452.

[本文引用: 3]

韦海燕, 陈孝杰, 吕治强, 等.

灰色神经网络模型在线估算锂离子电池SOH

[J]. 电网技术, 2017, 41(12):4038-4044.

[本文引用: 3]

WEI Haiyan, CHEN Xiaojie, LÜ Zhiqiang, et al.

Online estimation of lithium-ion battery state of health using grey neural network

[J]. Power System Technology, 2017, 41(12):4038-4044.

[本文引用: 3]

SIHVO J, ROINILA T, STROE D I.

SOH analysis of Li-ion battery based on ECM parameters and broadband impedance measurements

[C]// IECON2020:The 46th Annual Conference of the IEEE Industrial Electronics Society, 2020:1923-1928.

[本文引用: 3]

SANKARASUBRAMANIAN S, KRISHNAMURTHY B.

A capacity fade model for lithium-ion batteries including diffusion and kinetics

[J]. Electrochimica Acta, 2012, 70:248-254.

DOI:10.1016/j.electacta.2012.03.063      URL     [本文引用: 3]

GAO Y Z, ZHANG X, YANG J, et al.

Estimation of state-of-charge and state-of-health for lithium-ion degraded battery considering side reactions

[J]. Journal of the Electrochemical Society, 2018, 165(16):A4018-A4026.

DOI:10.1149/2.0981816jes      URL     [本文引用: 3]

LOTFI N, LI J, LANDERS R G, et al.

Li-ion battery state of health estimation based on an improved single particle model

[C]// 2017 American Contrl. Conference, 2017:86-91.

[本文引用: 3]

ALLAM A, ONORI S.

Online capacity estimation for lithium-ion battery cells via an electrochemical model-based adaptive interconnected observer

[J]. IEEE Transactions on Control Systems Technology, 2021, 29(4):1639-1651.

[本文引用: 3]

潘海鸿, 吕治强, 付兵, 等.

采用极限学习机实现锂离子电池健康状态在线估算

[J]. 汽车工程, 2017, 39(12):1375-1381,1396.

[本文引用: 2]

PAN Haihong, LÜ Zhiqiang, FU Bing, et al.

Online estimation of lithium battery’s state of health using extreme learning machine

[J]. Automotive Engineering, 2017, 39(12):1375-1381,1396.

[本文引用: 2]

SHEN S, SADOUGHI M, CHEN X, et al.

A deep learning method for online capacity estimation of lithium-ion batteries

[J]. The Journal of Energy Storage, 2019, 25:100817.

DOI:10.1016/j.est.2019.100817      URL     [本文引用: 2]

GUO P, CHENG Z, YANG L.

A data-driven remaining capacity estimation approach for lithium-ion batteries based on charging health feature extraction

[J]. Journal of Power Sources, 2019, 412:442-450.

DOI:10.1016/j.jpowsour.2018.11.072      URL     [本文引用: 2]

SHU X, LI G, SHEN J, et al.

An adaptive fusion estimation algorithm for state of charge of lithium-ion batteries considering wide operating temperature and degradation

[J]. Journal of Power Sources, 2020, 462:228132.

DOI:10.1016/j.jpowsour.2020.228132      URL     [本文引用: 2]

贾俊, 胡晓松, 邓忠伟, 等.

数据驱动的锂离子电池健康状态综合评分及异常电池筛选

[J]. 机械工程学报, 2021, 57(14):141-149,159.

DOI:10.3901/JME.2021.14.141      [本文引用: 2]

锂离子电池是电动汽车和储能系统最重要的组成部分，其故障预测和健康管理对于运行维护至关重要。数据驱动的方法较基于模型的方法更适合大规模工程应用，针对实际应用中工况复杂和数据质量较差的场景，提出数据驱动的健康状态综合评分及异常筛选算法，具有较强的适应性。首先，针对电池实际运行工况提出一种新的特征提取方案，可适用于非恒流的不稳定工况。开发了基于多维特征和混合聚类算法的健康状态综合评分体系，该方案采用无监督学习的算法框架，对可提取特征的数量和质量要求不高，无需进行事先的模型训练和复杂的超参数调整。然后，在麻省理工学院和斯坦福大学提供的公开数据集进行了算法验证，基于电池生命周期各阶段特征集进行健康度等级预测，并应用于健康度高低分选，均能达到92%以上的准确率。在某用户侧储能电站实现了该算法的应用，采用早期运行数据即可快速筛选异常电池，有利于尽早维护，提高电池系统的安全性和经济性。

JIA Jun, HU Xiaosong, DENG Zhongwei, et al.

Data-driven comprehensive evaluation of lithium-ion battery state of health and abnormal battery screening

[J]. Journal of Mechanical Engineering, 2021, 57(14):141-149,159.

DOI:10.3901/JME.2021.14.141      [本文引用: 2]

Lithium-ion batteries are the most important part of electric vehicles and energy storage systems, and their health management and fault identification are critical to operation and maintenance. The data-driven method is more suitable for large-scale engineering applications than the model-based method. Aiming at scenarios with complex working conditions and poor data quality in practical applications, a data-driven comprehensive evaluation of lithium-ion battery state of health and abnormal battery screening algorithm are proposed. First, a novel feature extraction scheme is proposed for the actual operating conditions of batteries, which can be applied to unstable working conditions with non-constant current. A comprehensive state of health scoring system based on multi-dimensional features and hybrid clustering algorithms is developed. This scheme is an algorithm framework for unsupervised learning, which does not require high quantity and quality of extractable features, without prior model training and complicated hyper parameter adjustment. Then, the algorithm is verified at the public data set of Massachusetts Institute of Technology and Stanford. Based on the feature set of each stage of the battery life cycle, the health level prediction can be achieved, and the accuracy is more than 92% when applied to classify the health level. Finally, the proposed algorithm is implemented in a user-side energy storage power station. Early operation data can be used to quickly screen abnormal batteries, which is beneficial to early maintenance, and improve the safety and economy of the battery system.

HU X, CHE Y, LIN X, et al.

Health prognosis for electric vehicle battery packs:A data-driven approach

[J]. IEEE/ASME Transactions on Mechatronics, 2020, 25(6):2622-2632.

DOI:10.1109/TMECH.2020.2986364      URL     [本文引用: 2]

WANG Z P, MA J, ZHANG L.

State-of-health estimation for lithium-ion batteries based on the multi-island genetic algorithm and the Gaussian process regression

[J]. IEEE Access, 2017, 5:21286-21295.

DOI:10.1109/ACCESS.2017.2759094      URL     [本文引用: 2]

KATTERNBORN T, LEITLOFF J, SCHIEFER F, et al.

Review on convolutional neural networks (CNN) in vegetation remote sensing

[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2021, 173:24-49.

DOI:10.1016/j.isprsjprs.2020.12.010      URL     [本文引用: 1]

LI Y, LIU K L, FOLEY A M, et al.

Data-driven health estimation and lifetime prediction of lithium-ion batteries:A review

[J]. Renewable and Sustainable Energy Reviews, 2019, 113:109254.

DOI:10.1016/j.rser.2019.109254      URL     [本文引用: 1]

LEI Y G, LI N P, GUO L, et al.

Machinery health prognostics:A systematic review from data acquisition to RUL prediction

[J]. Mechanical Systems and Signal Processing, 2018, 104:799-834.

DOI:10.1016/j.ymssp.2017.11.016      URL     [本文引用: 1]

叶美盈, 汪晓东, 张浩然.

基于在线最小二乘支持向量机回归的混沌时间序列预测

[J]. 物理学报, 2005, 54(6):2568-2573.

[本文引用: 1]

YE Meiying, WANG Xiaodong, ZHANG Haoran, et al.

Chaotic time series prediction based on online least squares support vector machine regression

[J]. Acta Physica Sinica, 2005, 54(6):2568-2573.

DOI:10.7498/aps.54.2568      URL     [本文引用: 1]

ZHAO Y P, WANG J J, LI X Y, et al.

Extended least squares support vector machine with applications to fault diagnosis of aircraft engine

[J]. ISA Transactions, 2020, 97:189-201.

DOI:10.1016/j.isatra.2019.08.036      URL     [本文引用: 1]

YANG D, ZHANG X, PAN R, et al.

A novel Gaussian process regression model for state-of-health estimation of lithium-ion battery using charging curve

[J]. Journal of Power Sources, 2018, 384:387-395.

DOI:10.1016/j.jpowsour.2018.03.015      URL     [本文引用: 1]

SEVERSON K A, ATTIA P M, JIN N, et al.

Data-driven prediction of battery cycle life before capacity degradation

[J]. Nature Energy, 2019, 4:383-391.

DOI:10.1038/s41560-019-0356-8      [本文引用: 1]

Accurately predicting the lifetime of complex, nonlinear systems such as lithium-ion batteries is critical for accelerating technology development. However, diverse aging mechanisms, significant device variability and dynamic operating conditions have remained major challenges. We generate a comprehensive dataset consisting of 124 commercial lithium iron phosphate/graphite cells cycled under fast-charging conditions, with widely varying cycle lives ranging from 150 to 2,300 cycles. Using discharge voltage curves from early cycles yet to exhibit capacity degradation, we apply machine-learning tools to both predict and classify cells by cycle life. Our best models achieve 9.1% test error for quantitatively predicting cycle life using the first 100 cycles (exhibiting a median increase of 0.2% from initial capacity) and 4.9% test error using the first 5 cycles for classifying cycle life into two groups. This work highlights the promise of combining deliberate data generation with data-driven modelling to predict the behaviour of complex dynamical systems.

BOLE B, KULKARNI C S, DAIGLE M.

Adaptation of an electrochemistry-based Li-ion battery model to account for deterioration observed under randomized use

[C]// Annual Conference of the Prognostics and Health Management Society, 2014, 6(1):2490.

[本文引用: 1]

阎威武, 邵惠鹤.

支持向量机和最小二乘支持向量机的比较及应用研究

[J]. 控制与决策, 2003(3):358-360.

[本文引用: 1]

YAN Weiwu, SHAO Huihe.

Application of support vector machines and least squares support vector machines to heart disease diagnoses

[J]. Control and Decision, 2003(3):358-360.

[本文引用: 1]

顾燕萍, 赵文杰, 吴占松.

最小二乘支持向量机的算法研究

[J]. 清华大学学报, 2010, 50(7):1063-1066,1071.

[本文引用: 1]

GU Yanping, ZHAO Wenjie, WU Zhansong.

Least squares support vector machine algorithm

[J]. Journal of Tsinghua University, 2010, 50(7):1063-1066,1071.

[本文引用: 1]

/

〈 〉