1 引言
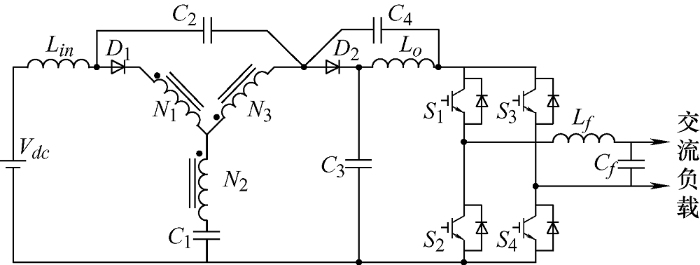
近年来,为了满足一些特殊的应用需求,逆变器的拓扑结构变得越来越复杂。其中,以Z源逆变器为代表的阻抗源逆变器能够解决传统电压源型逆变器和电流源型逆变器许多固有的缺点,例如负载电压或电流调节范围有限,需要引入死区时间或重叠时间导致输出波形畸变等[1 ⇓ -3 ] 。随后,国内外学者相继提出了一些改进的阻抗源逆变器拓扑结构。其中,准Z源逆变器[4 -5 ] 是将电源放置在电感支路构造而来的,具备连续的输入电流,减小启动冲击电流的能力。国内外学者提出一系列新型拓扑以改善Z源逆变器的升压性能,包括改进型开关电感型Quasi-Z源逆变器[6 ] 、级联Z源逆变器[7 ] 等。上述拓扑通过级联阻抗网络的方式提高了升压性能,然而在实际工程实施中,级联数的增加使得逆变器设计趋于复杂化,同时附加的寄生参数导致升压性能下降,降低能量交换效率。为此,相继出现了trans-Z源逆变器[8 ] 、Γ-Z源逆变器[9 ] 和Y源逆变器[10 ] 等耦合电感型阻抗源逆变器拓扑结构。通过调整耦合电感的匝数比,逆变器可以在较低的直通占空比下实现较高的电压增益。其中,Y源逆变器结合了trans-Z源和Γ-Z源逆变器的升压特点,利用三端耦合电感传递能量,具有更高的匝数比设计自由度,更加显著地体现含有耦合电感的阻抗源网络的优势。文献[11 ]提出了一种高升压比Y源逆变器(High step-up Y-source inverter,HS-YSI),拓扑结构如图1 所示。
图1
目前,针对电子器件应力分析方法研究较少,文献[12 ]通过相位分析及理论计算可以详细推导出其逆变器桥臂电压、电流应力;文献[13 ]通过搭建仿真模型的方法给出晶闸管所承受电压应力,但是不能给出具体表达式,不具有普遍性;文献[14 ]应用指数电压源模型,推导出精确的晶闸管开通电流应力,但存在计算量较大、适用性不强等缺点。针对逆变器使用最多的是传统分析方法[15 -16 ] ,传统方法在分析过程中需要将每个开关周期分为几个模态,如果变换器中电容和电感选取足够大时,可以假设电容两端的电压和流过电感的电流恒定不变。然而,电容电流和电感电压在每个模态是不同的,因此必须采用不同的状态变量进行表示。然后,将推导的电容电流和电感电压表达式分别在一个开关周期内进行安秒和伏秒的积分求和,从而获得由电容电压和电感电流表示的表达式,用于计算变换器中所有器件的电压、电流应力。
然而,在分析多状态变量、多模态电路(例如阻抗源逆变器)时,传统分析方法显得较为复杂。以HS-YSI为例,其工作状态可分为直通状态和非直通状态。根据二极管的运行条件,每一个工作状态又分为若干个子模态。同时,又因为其独特的耦合电感结构使得不同状态变量之间相互耦合,因此在对每个子模态的分析过程中,至少需要列写27个方程来获得流过电容C 1 ~C 4 的电流表达式和电感Lin 、LM 和Lo 的电压表达式。最后,对上述电容电流和电感电压表达式列写一个开关周期内的积分和表达式,得到7个线性方程。虽然传统方法获得的电路参数较为全面,但求解这7个线性方程的过程较为繁琐且容易出错,往往需要借助计算机求解。为了简化多状态变量、多模态电路复杂的分析过程,在不影响计算结果的情况下,本文提出了一种基于无源器件消除的器件应力简化分析方法。
本文首先使用传统方法阐述了HS-YSI电路中电压、电流应力的计算过程;然后,详细分析了无源器件消除法的原理,并对比分析了两种方法的优缺点和适用范围;最后,通过搭建HS-YSI的试验样机验证所提方法的正确性。
2 传统方法分析HS-YSI电路
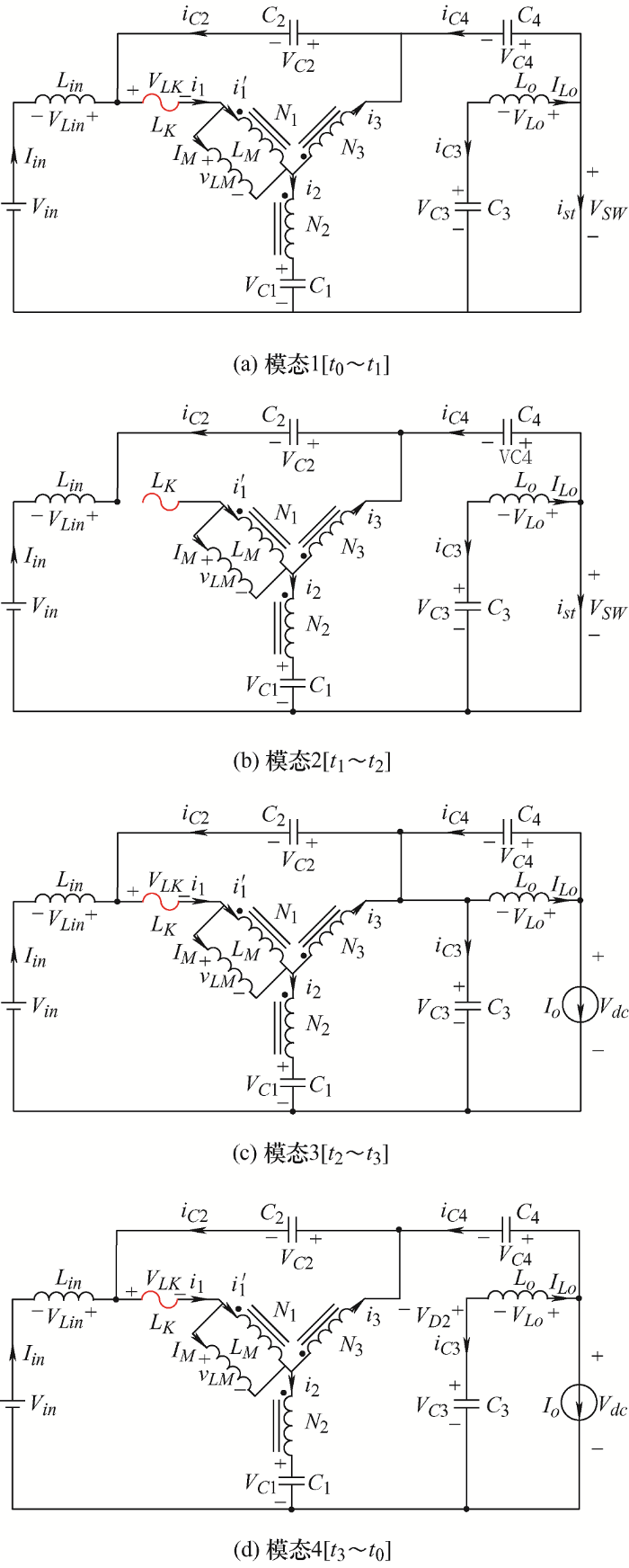
HS-YSI在每个开关周期内可以分为4个工作模态,如图2 所示。其中,逆变桥和交流负载被等效为开关SW 和一个电流源Io 并联的形式。假定电容C 1 ~C 4 以及三个电感Lin 、Lo 和LM 都选取足够大,由前面的分析可以认为,它们对应的电压和电流在整个开关周期内恒定。为简化电路分析,三端耦合电感的励磁电感可以等效成LM 与一次绕组并联,因此LM 并不是一个实际的电感。此外,三端耦合电感漏感都被等效为与N 1 串联的漏感LK 。
图2
图2 a为模态1,逆变桥中同一桥臂的两个开关管导通,逆变器进入直通状态。此时,D 1 继续导通,D 2 则保持关断。当通过绕组N 1 的电流降到零后,D 1 结束导通。然后,逆变器进入如图2 b所示的模态2,二极管D 1 和D 2 反偏,电感Lin 、Lo 和LM 被充电,而电容C 1 和C 4 处于放电状态。模态2是直通状态中持续时间最长的状态,在桥臂的一个开关管关断后结束。此时逆变器将进入如图2 c所示的非直通状态下的模态3,二极管D 1 和D 2 全部导通。由于D 2 的导通,使得C 3 和C 4 串联后钳位住直流链上的电压。因此,消除了从直通状态到非直通状态过程中直流链的电压尖峰。然而,当二极管D 2 停止导通后,逆变器进入了如图2 d所示的非直通状态下的模态4。
2.1 电流分析
由于漏感的影响,HS-YSI需要经历如图2 a所示的工作状态。由于模态1持续的时间要显著小于其他三个状态,电感和电容上的能量在模态1中几乎不发生改变,因此该模态下的数学分析可以忽略。
电流分析从模态2开始,该模态下二极管D 1 、D 2 反偏,开关SW 导通,可以得到相应的电容电流表达式,即
(1) ${{i}_{C1}}={{i}_{2}}=-{{i}_{3}}$
(2) ${{i}_{C2}}=-{{I}_{in}}$
(3) ${{i}_{C3}}=-{{I}_{Lo}}$
(4) ${{i}_{C4}}=-\left( {{I}_{in}}+{{i}_{3}} \right)$
(5) ${{N}_{1}}{{{i}'}_{1}}+\left( {{N}_{3}}-{{N}_{2}} \right){{i}_{3}}=0$
(6) ${{{i}'}_{1}}=-{{I}_{M}}$
式(5)、(6)表示耦合电感中的电流关系。将它们代入式(1)和式(4)可以得到流过电容C 1 和C 4 的电流为
(7) ${{i}_{C1}}=-\frac{{{N}_{1}}}{{{N}_{3}}-{{N}_{2}}}{{I}_{M}}$
(8) ${{i}_{C4}}=-{{I}_{in}}-\frac{{{N}_{1}}}{{{N}_{3}}-{{N}_{2}}}{{I}_{M}}$
模态3时,二极管D 1 、D 2 导通,开关SW 关断。流过电容的电流发生改变,i 2 和iC 2 线性增加,然而iC 3 和iC 4 在t 2 时刻发生突变,即
(9) ${{i}_{C3}}\left( {{t}_{2}} \right)={{I}_{in}}-{{I}_{o}}+\frac{{{N}_{1}}}{{{N}_{3}}-{{N}_{2}}}{{I}_{M}}$
(10) ${{i}_{C4}}\left( {{t}_{2}} \right)={{I}_{Lo}}-{{I}_{o}}$
当电路工作状态切换到如图2 d所示的模态4时,电容电流会再次发生改变,相应的表达式为
(11) ${{i}_{C3}}=-{{I}_{Lo}}$
(12) ${{i}_{C4}}={{I}_{Lo}}-{{I}_{o}}$
(13) ${{i}_{C1}}={{i}_{2}}$
(14) ${{i}_{1}}={{I}_{in}}+{{i}_{C2}}$
(15) ${{i}_{3}}={{I}_{o}}-{{I}_{Lo}}+{{i}_{C2}}$
(16) ${{i}_{2}}={{I}_{in}}+{{I}_{Lo}}-{{I}_{o}}$
(17) $N_{1} i_{1}^{\prime}+N_{2} i_{2}+N_{3} i_{3}=0$
(18) $i_{1}=i_{1}^{\prime}+I_{M}$
其中,式(17)、(18)表示耦合电感的电流关系,通过式(11)~(18)可以推导出流过电容C 1 和C 2 的电流为
(19) ${{i}_{C1}}={{I}_{in}}+{{I}_{Lo}}-{{I}_{o}}$
(20) ${{i}_{C2}}=\frac{\left( {{N}_{3}}-{{N}_{2}} \right)\left( {{I}_{in}}+{{I}_{Lo}}-{{I}_{o}} \right)+{{N}_{1}}{{I}_{M}}}{{{N}_{3}}+{{N}_{1}}}-{{I}_{in}}$
接下来,对电容C 1 、C 2 、C 3 和C 4 列写一个开关周期内积分和表达式
(21) $\begin{matrix} \int_{{{t}_{1}}}^{{{t}_{2}}}{{{i}_{Cx}}}dt+\int_{{{t}_{2}}}^{{{t}_{3}}}{{{i}_{Cx}}}dt+\int_{{{t}_{3}}}^{{{t}_{0}}}{{{i}_{Cx}}}dt= \\ \int_{0}^{dT}{{{i}_{Cx}}}dt+\int_{dT}^{\left( \alpha +d \right)T}{{{i}_{Cx}}}dt+\int_{\left( \alpha +d \right)T}^{T}{{{i}_{Cx}}}dt=0 \\ \end{matrix}$
式中,α =(t 3 -t 2 )/T 为比例系数;x =1、2、3和4为电容的下标。
最后,可以推导出阻抗网络中所有元件流过的电流表达式为
(22) $\alpha =\frac{2}{1+K}\left( 1-d \right)$
(23) ${{I}_{Lo}}={{I}_{in}}$
(24) ${{I}_{M}}=\frac{({{N}_{1}}+{{N}_{3}})}{{{N}_{1}}}{{I}_{in}}$
(25) ${{I}_{o}}=\frac{1-(2+K)d}{1-d}{{I}_{in}}$
式中,K =(N 1 +N 3 )/(N 3 -N 2 );d 为直通占空比。
传统电流分析方法借助KCL列出所有电容电流表达式,而模态3和模态4也要重复上述过程,因此会推导出12个电容电流表达式。此外,为了建立电容电流与输入电流Iin 、输出电感电流ILo 和励磁电流IM 之间的关系,必须引入三个模态下的6个耦合电感电流表达式。利用在一个开关周期内电容电流积分和为零的特性,进而得到4个积分和表达式。因此,仅仅对电流分析就得使用22个表达式,计算过程比较繁琐。
2.2 电压分析
电压分析时,模态1和模态2的等效电路相同,开关SW 开通,耦合电感N 2 和N 3 被电容C 1 和C 4 的电压钳位。相应的电压表达式为
(26) ${{v}_{LM}}=\left( {{V}_{C1}}+{{V}_{C4}} \right)\frac{{{N}_{1}}}{{{N}_{3}}-{{N}_{2}}}$
(27) ${{v}_{Lo}}=-{{V}_{C3}}$
(28) ${{v}_{Lin}}=-\left( {{V}_{in}}+{{V}_{C2}}+{{V}_{C4}} \right)$
式中,VC 1 、VC 2 、VC 3 和VC 4 分别为电容C 1 、C 2 、C 3 和C 4 上的电压;vLM 、vLo 和vLin 分别为电感LM 、Lo 和Lin 上的电压。
t 2 时开关SW 关断,电路进入如图2 c所示的非直通状态,流过漏感LK 的电流线性增加,耦合电感N 2 和N 3 被电容C 1 和C 3 的电压钳位。相关的电感电压表达式为
(29) ${{v}_{LM}}=\left( {{V}_{C1}}-{{V}_{C3}} \right)\frac{{{N}_{1}}}{{{N}_{3}}-{{N}_{2}}}$
(30) ${{v}_{Lo}}={{V}_{C4}}$
(31) ${{v}_{Lin}}={{V}_{C3}}-{{V}_{C2}}-{{V}_{in}}$
(32) ${{v}_{LK}}=-\left( {{V}_{C1}}-{{V}_{C3}} \right)\frac{{{N}_{1}}+{{N}_{3}}}{{{N}_{3}}-{{N}_{2}}}-{{V}_{C2}}$
此外,由于流过漏感LK 的电流在t 2 时刻从0开始线性增加,在t 3 时刻,其电流表达式为
(33) ${{i}_{1}}\left( {{t}_{3}} \right)=0+\frac{1}{{{L}_{K}}}\int_{dT}^{\left( d+\alpha \right)T}{{{v}_{LK}}}dt$
结合式(14)、(20)和式(22)~(25)可以推导出漏感LK 的电压表达式为
(34) ${{v}_{LK}}=\frac{{{\left( 1+K \right)}^{2}}}{2{{\left( 1-d \right)}^{2}}KT}{{I}_{in}}{{L}_{K}}$
当电路进入模态4时,耦合电感N 2 、N 3 和漏感LK 由电容C 2 的电压钳位。各个电感电压为
(35) ${{v}_{LM}}=\left( {{V}_{C1}}-{{V}_{C3}}+{{v}_{D2}} \right)\frac{{{N}_{1}}}{{{N}_{3}}-{{N}_{2}}}$
(36) ${{v}_{Lo}}={{V}_{C4}}-{{v}_{D2}}$
(37) ${{v}_{Lin}}={{V}_{C3}}-{{V}_{C2}}-{{V}_{in}}-{{v}_{D2}}$
(38) $\begin{matrix} {{v}_{LK}}=-{{V}_{C2}}\frac{{{L}_{K}}}{{{L}_{K}}+\left( 1+\frac{{{N}_{3}}}{{{N}_{1}}} \right){{L}_{M}}}= \\ -\left( {{V}_{C1}}-{{V}_{C3}}+{{v}_{D2}} \right)\frac{{{N}_{1}}+{{N}_{3}}}{{{N}_{3}}-{{N}_{2}}}-{{V}_{C2}} \\ \end{matrix}$
由于LK $\ll $ M ,模态4时,LK 两端电压接近于0。将式(32)和式(34)代入式(38),可以推导出二极管的反向偏置电压为
(39) ${{v}_{D2}}=\frac{{{\left( 1+K \right)}^{2}}}{2{{\left( 1-d \right)}^{2}}{{K}^{2}}T}{{I}_{in}}{{L}_{K}}$
通过代入数值运算,可以证明vD 2 很小,为简化运算,可以忽略vD 2 的大小,因此认为模态3和模态4下的电感电压一致是合理的。此外,根据式(38)可以进一步推导出
(40) $\left( {{V}_{C3}}-{{V}_{C1}} \right)\frac{{{N}_{1}}+{{N}_{3}}}{{{N}_{3}}-{{N}_{2}}}-{{V}_{C2}}={{v}_{D2}}\frac{{{N}_{1}}+{{N}_{3}}}{{{N}_{3}}-{{N}_{2}}}\approx 0$
最后,对电感LM 、Lo 和Lin 应列写一个开关周期内积分和表达式,有
(41) $\int_{{{t}_{0}}}^{{{t}_{2}}}{{{v}_{Lx}}}dt+\int_{{{t}_{2}}}^{{{t}_{0}}}{{{v}_{Lx}}}dt=\int_{0}^{dT}{{{v}_{Lx}}}dt+\int_{dT}^{T}{{{v}_{Lx}}}dt=0$
式中,Lx 代表LM 、Lo 和Lin 。最后,可以得到4个电容两端电压的表达式为
(42) ${{V}_{C1}}=(1-2d)B{{V}_{in}}$
(43) ${{V}_{C2}}=dKB{{V}_{in}}$
(44) ${{V}_{C3}}=(1-d)B{{V}_{in}}$
(45) ${{V}_{C4}}=dB{{V}_{in}}$
式中,B =[1-(2+K )d ]为HS-YSI的升压比。
(46) ${{V}_{dc}}=B{{V}_{in}}$
(47) ${{\hat{v}}_{o}}=BM{{V}_{in}}$
传统的电压分析方法需要借助KVL方程列写所有的电感电压表达式,因此,在3个模态下总计需要列写9个电压方程。利用在一个开关周期内电感电压积分和为零的特性,可以得到3个积分和表达式。所以,共需要12个表达式分析HS-YSI的电压。
根据上面的电流和电压分析过程,总计需要34个表达式来求解HS-YSI电路的状态变量,其中包含7个线性方程。然而,求解这7个线性方程较为复杂,往往需要借助计算机编程求解。甚至,为了获得电容电流和电感电压的积分表达式,必须知道所有无功器件在各个模态下的状态。因此,传统电力电子电路分析方法十分复杂,尤其应用在像HS-YSI含有多个电感和电容支路的阻抗源逆变器的电路中。
3 无源器件消除法分析HS-YSI电路
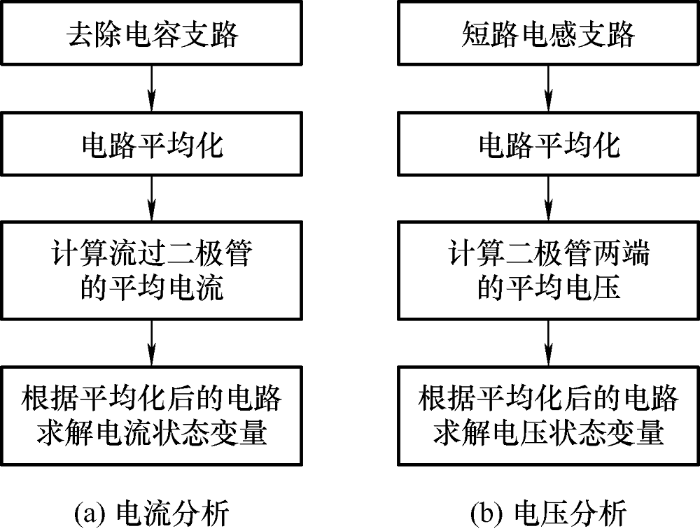
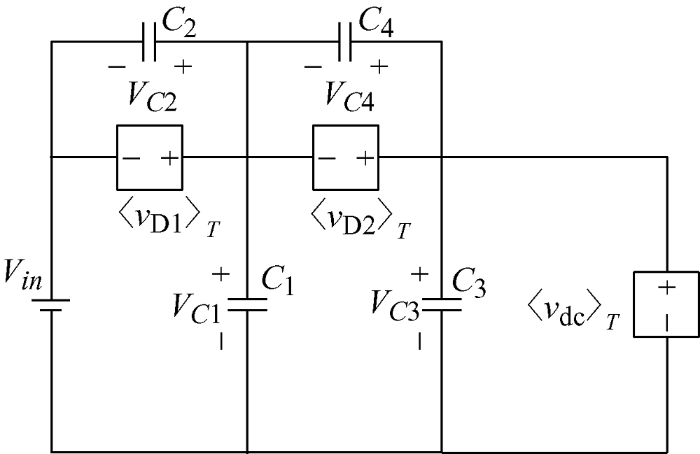
为了简化传统分析方法繁复的计算过程,本文提出了一种新型电力电子电路分析方法,在仅仅关系系统参数的情况下,可以通过消除不影响分析结果的无源元件,进而简化计算量。图3 为所提的基于无源器件消除的电力电子电路分析方法的实施流程。考虑到电路稳态时,待求的状态变量在一个开关周期内可以认为是常量,因此将电路平均化之后这些状态变量可以直接用等效后的物理量表示。电流分析时,如果平均化流过电容支路的电流,由于电容能量不会发生突变,电容支路中流过的开关平均电流一定是零,因此在平均化后的电路中可以将电容支路视为断路。对电压分析来说,如果对电感支路的两端电压进行平均化,则电感支路的开关平均电压必然为零,因此可以认为在平均化后的电路中将电感支路短路。因此,应用新型的电路分析方法,电路中所需要分析的各个状态变量之间的耦合关系被极大地简化了。另一方面,所提方法中不需要列写复杂的积分和表达式,也不必去求解相应的多元线性方程组,这为工程计算带来了极大的便利性。
图3
下面将所提方法用于图1 所示的HS-YSI电路分析中以更好地阐述其分析过程。
3.1 电流分析
根据能量平衡原理,流过HS-YSI中电容的电流在一个开关周期为零,即
(48) ${{\left\langle {{i}_{C\text{1}}} \right\rangle }_{T}}={{\left\langle {{i}_{C\text{2}}} \right\rangle }_{T}}={{\left\langle {{i}_{C\text{3}}} \right\rangle }_{T}}={{\left\langle {{i}_{C\text{4}}} \right\rangle }_{T}}=0$
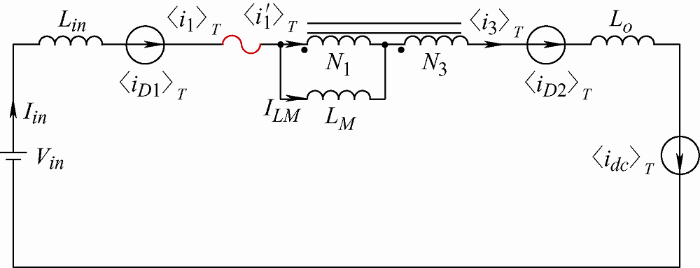
式中,${{\left\langle x \right\rangle }_{T}}$ T 内的平均量。因此,电容C 1 、C 2 、C 3 和C 4 将不影响其他元件的平均电流。也就是说,任何与这些电容串联的支路在分析平均电流时可以移除,从而得到图4 所示的等效平均电流电路。由KCL可得
(49) ${{\left\langle {{i}_{D1}} \right\rangle }_{T}}={{\left\langle {{i}_{1}} \right\rangle }_{T}}={{\left\langle {{i}_{3}} \right\rangle }_{T}}={{\left\langle {{i}_{D2}} \right\rangle }_{T}}={{\left\langle {{i}_{dc}} \right\rangle }_{T}}={{I}_{in}}$
(50) ${{I}_{Lo}}={{I}_{in}}$
(51) $\left\langle i_{1}\right\rangle_{T}=\left\langle i_{1}^{\prime}\right\rangle_{T}+I_{M}$
图4
尽管在图4 所示的等效平均电路中,绕组N 2 由于与电容C 2 串联被一起移除了,但是绕组N 1 和N 3 依然可以满足耦合电感电流关系,即
(52) ${{N}_{1}}{{\left\langle {{{{i}'}}_{1}} \right\rangle }_{T}}+{{N}_{3}}{{\left\langle {{i}_{3}} \right\rangle }_{T}}=0$
(53) ${{N}_{1}}({{\left\langle {{i}_{1}} \right\rangle }_{T}}-{{I}_{M}})+{{N}_{3}}{{\left\langle {{i}_{3}} \right\rangle }_{T}}=0$
(54) ${{I}_{M}}=\frac{({{N}_{1}}+{{N}_{3}})}{{{N}_{1}}}{{I}_{in}}$
由第2节分析可知,由于模态1持续时间很短可以忽略,因此直通时间仅为图2 b所示的模态2持续的时间。从而,耦合电感电流表达式为
(55) ${{N}_{1}}{{{i}'}_{1}}+({{N}_{3}}-{{N}_{2}}){{i}_{3}}=0$
(56) ${{{i}'}_{1}}=-{{I}_{M}}$
(57) ${{i}_{dc}}={{I}_{Lo}}+{{I}_{in}}+{{i}_{3}}$
由图2 c和图2 d可知,在非直通状态下,流过直流链的电流等于负载电流,即
(58) ${{i}_{dc}}={{I}_{o}}$
(59) ${{\left\langle {{i}_{dc}} \right\rangle }_{T}}=d({{I}_{Lo}}+{{I}_{in}}+\frac{{{N}_{1}}}{{{N}_{3}}-{{N}_{2}}}{{I}_{M}})+(1-d){{I}_{o}}$
将式(49)、(50)和(53)代入式(59),可得
(60) ${{I}_{o}}=\frac{1-(2+K)d}{(1-d)}{{I}_{in}}$
明显地,式(50)、(54)和(60)分别与式(23)~(25)相同,证明了所提方法的正确性。因为仅使用了7个表达式(式(49)~(52)、式(54)、(59)和(60)),很大程度上简化了分析过程并避免了求解复杂的多元线性方程。
3.2 电压分析
与电流分析类似,HS-YSI中所有电感的电压在一个开关周期为零,即
(61) ${{\left\langle {{v}_{{{L}_{in}}}} \right\rangle }_{T}}={{\left\langle {{v}_{{{L}_{1}}}} \right\rangle }_{T}}={{\left\langle {{v}_{{{L}_{2}}}} \right\rangle }_{T}}={{\left\langle {{v}_{{{L}_{3}}}} \right\rangle }_{T}}={{\left\langle {{v}_{{{L}_{O}}}} \right\rangle }_{T}}=0$
由于电感Lin 、L 1 、L 2 、L 3 和Lo 不影响其他元件的平均电压,因此电感支路可以作短路处理,从而得到图5 所示的等效平均电压电路。电压分析同样从模态2开始,二极管D 1 电压为电容C 2 、绕组N 1 和N 3 电压之和。此外,绕组N 1 和N 3 的电压与VC 1 和VC 4 有关。结合耦合绕组的电压关系,直通状态下二极管D 1 和D 2 两端的电压为
(62) ${{v}_{D\text{1}}}={{V}_{C2}}+K({{V}_{C1}}+{{V}_{C4}})$
(63) ${{v}_{D2}}={{V}_{C3}}+{{V}_{C4}}$
图5
如图2 c和图2 d所示,非直通状态下二极管D 1 始终导通,二极管D 2 反向电压始终等于零或接近零,因此二极管D 1 和D 2 两端的平均电压为
(64) ${{\left\langle {{v}_{D\text{1}}} \right\rangle }_{T}}=d[{{V}_{C2}}+K({{V}_{C1}}+{{V}_{C4}})]$
(65) ${{\left\langle {{v}_{D2}} \right\rangle }_{T}}=d({{V}_{C3}}+{{V}_{C4}})$
(66) ${{V}_{C1}}={{\left\langle {{v}_{D1}} \right\rangle }_{T}}+{{V}_{in}}$
(67) ${{V}_{C2}}={{\left\langle {{v}_{D1}} \right\rangle }_{T}}$
(68) ${{V}_{C3}}={{V}_{C1}}\text{+}{{\left\langle {{v}_{D2}} \right\rangle }_{T}}$
(69) ${{V}_{C4}}={{\left\langle {{v}_{D2}} \right\rangle }_{T}}$
将式(64)、(65)代入式(66)~(69)可得
(70) ${{V}_{C1}}=(1-2d)B{{V}_{in}}$
(71) ${{V}_{C2}}=dKB{{V}_{in}}$
(72) ${{V}_{C3}}=(1-d)B{{V}_{in}}$
(73) ${{V}_{C4}}=dB{{V}_{in}}$
可以看出,式(70)~(73)与传统分析方法所得到的式(42)~(45)为相同的表达式。将已求得的电容电压代入式(62)和式(63),可以得到二极管电压表达式
(74) ${{V}_{D1}}=KB{{V}_{in}}$
(75) ${{V}_{D2}}=B{{V}_{in}}$
根据图3 可知,逆变桥等效开关电压vSW 在直通状态和非直通状态下分别为0和Vdc 。因此,开关的平均电压为
(76) ${{\left\langle {{v}_{SW}} \right\rangle }_{T}}=(1-d){{V}_{dc}}$
(77) ${{\left\langle {{v}_{SW}} \right\rangle }_{T}}={{V}_{C3}}$
(78) ${{V}_{dc}}=\frac{1}{1-(2+K)d}{{V}_{in}}=B{{V}_{in}}$
(79) ${{V}_{sw}}\text{=(1}-d\text{)}B{{V}_{in}}$
显然,所提方法算出的直流链电压表达式也与传统方法一致。当采用本文所提方法分析HS-YSI这种具有耦合电感的拓扑时存在很大的优势,较传统方法所需方程数减少一半左右。这是因为新型方法不仅不需要计算流过每个电容的电流和每个电感两端承受的电压,而且只需要计算不同模态下二极管的电流和电压。事实上,耦合电感型阻抗源逆变器只有较少数量的二极管,而且工程上一般忽略其关断电流和导通压降,因此分析二极管无疑比直接分析无源器件简单很多。
基于无源器件消除的器件应力分析方法忽略了开关周期内的细节,部分物理量不能求解,无法确定电路中各个模态下电流电压的具体波形,这不利于电路细节的分析和设计。因此新方法在拓扑原理研究的先期验证阶段以及工程实际中对电路状态量的快速计算时能够取得事半功倍的效果,而电路设计时更应该依赖于传统电路分析方法。
4 试验结果
为验证上述理论分析方法的正确性,搭建了由TMS320F28335所控制的200 W逆变器试验样机,其试验参数如表1 所示。
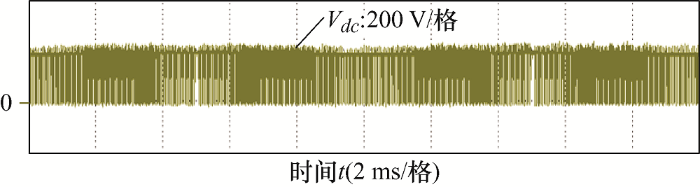
图6 为HS-YSI的直流链电压试验波形。从图6 可以看到HS-YSI直流链电压最高值在200 V左右,与理论电压非常接近,而且直流链上几乎不存在电压尖峰。
图6
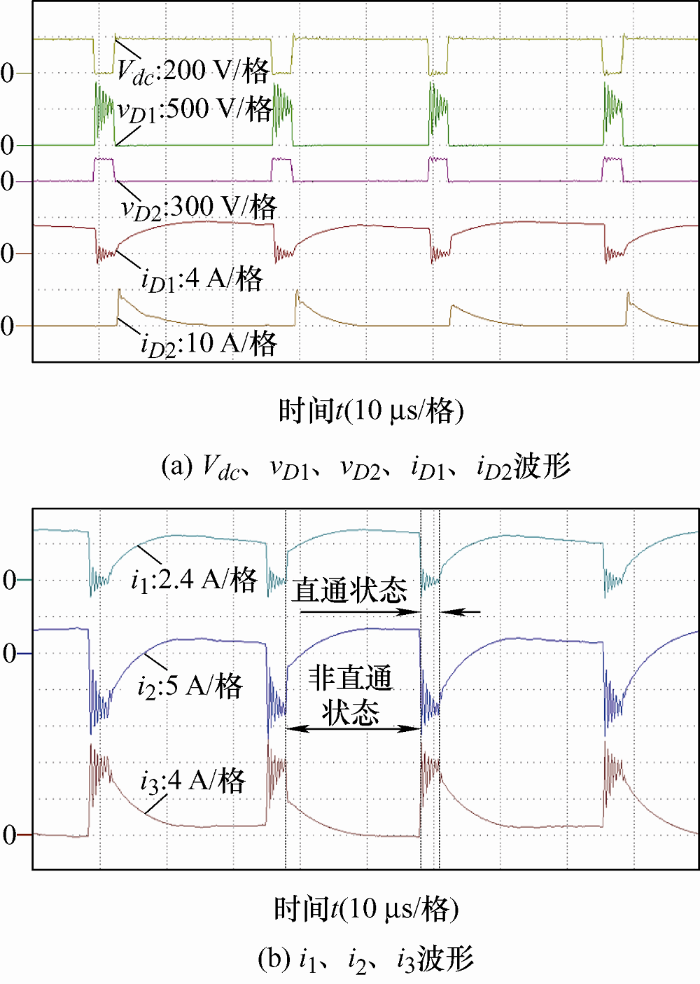
图7 a为直流链电压和二极管电压电路波形。直通状态进入非直通状态时,流过二极管D 1 和线圈N 1 的电流iD 1 是缓慢变化的,因此几乎不产生电压尖峰,其直流链电压的稳定值为194 V。图7 b为流过线圈N 1 、N 2 和N 3 的电流,可以看到三者均在电路由直通状态进入非直通状态时变化较慢,没有电流谐振。
图7
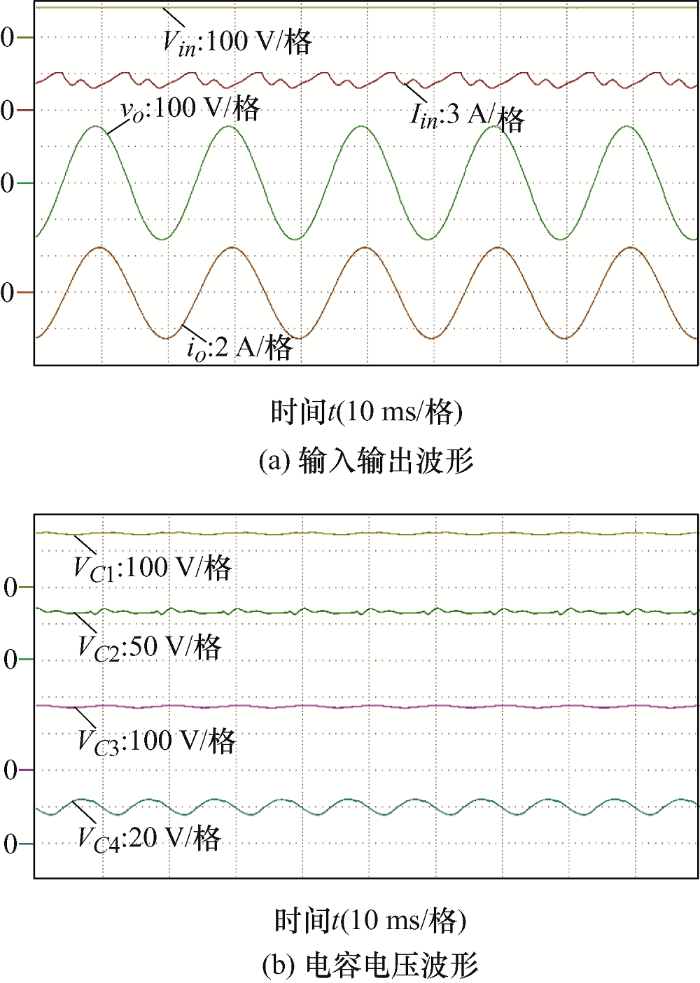
图8 为HS-YSI的输入输出以及电容电压波形。HS-YSI输出电压峰值为155 V,相比理论电压160 V稍低,主要是由耦合电感寄生参数导致直通占空比丢失引起的。电容C 1 、C 2 、C 3 和C 4 的电压分别为150 V、69 V、176 V和20 V,这与理论公式所计算出来的结果VC 1 =152 V、VC 2 =72 V、VC 3 =176 V、VC 4 =24 V相符,验证了理论分析的正确性。
图8
5 结论
传统器件应力分析方法分析含有多个电感和电容的耦合电感型阻抗源逆变器时,计算过程冗长且容易出错,为了简化电路分析,提出一种基于无源器件消除的器件应力简化分析方法。作为例子,详细对比了传统方法和新型方法分析复杂的HS-YSI电路,得到以下结论。
(1) 新型方法首先使用安秒和伏秒平衡原则建立变换器的简化等效平均电路,只需要计算不同模态下二极管的电流和电压,从而更容易推导出其他器件电流、电压的表达式。
(2) 新型方法尤其适用于像耦合电感型阻抗源逆变器这种具有多个电感、电容的逆变器拓扑,新型方法在不影响计算结果的情况下,较传统方法所需方程数减少一半左右,大幅度简化了分析过程的复杂性。
参考文献
View Option
[2]
黄瑞哲 , 陈道炼 , 许志龙 . 新颖的单相电压型准Z源逆变器
[J]. 电工技术学报 , 2015 , 30 (16 ):33 -41 .
[本文引用: 1]
HUANG Ruizhe CHEN Daolian XU Zhilong . A novel single phase voltage mode quasi-Z-source inverter
[J]. Transactions of China Electrotechnical Society , 2015 , 30 (16 ):33 -41 .
[本文引用: 1]
[3]
刘贇 , 丁新平 , 赵德林 , 等 . 新型倍压-Z源逆变器
[J]. 太阳能学报 , 2021 , 42 (8 ):133 -139 .
[本文引用: 1]
LIU Yun DING Xinping ZHAO Delin , et al . Novel Z-source inverter with voltage multiplier unit
[J]. Acta Energiae Solaris Sinica , 2021 , 42 (8 ):133 -139 .
[本文引用: 1]
[4]
王树文 , 单硕硕 , 张洋 , 等 . 改进型准Z源逆变器
[J]. 电力自动化设备 , 2016 , 36 (9 ):142 -150 .
[本文引用: 1]
WANG Shuwen SHAN Shuoshuo ZHANG Yang , et al . Improved quasi-Z-source inverter
[J]. Electric Power Automation Equipment , 2016 , 36 (9 ):142 -150 .
[本文引用: 1]
[5]
YANG L Q QIU D ZHANG B , et al . High-performance quasi-Z-source inverter with low capacitor voltage stress and small inductance
[J]. IET Power Electronics , 2015 , 8 (6 ):1061 -1067 .
DOI:10.1049/iet-pel.2014.0372
URL
[本文引用: 1]
[6]
刘孝辉 , 郑建勇 , 尤鋆 , 等 . 开关电感型Quasi-Z源逆变器
[J]. 电力自动化设备 , 2011 , 31 (9 ):65 -68 ,99.
[本文引用: 1]
LIU Xiaohui ZHENG Jianyong YOU Jun , et al . Switched inductor Quasi-Z source inverters
[J]. Electric Power Automation Equipment , 2011 , 31 (9 ):65 -68 ,99.
[本文引用: 1]
[7]
贺昱曜 , 冯伟 , 宋石磊 . Z源级联三电平中点钳位逆变器
[J]. 电网技术 , 2012 , 36 (4 ):219 -224 .
[本文引用: 1]
HE Yuyao FENG Wei SONG Shilei . A cascaded Z-source three-level neutral point clamped inverter
[J]. Power System Technology , 2012 , 36 (4 ):219 -224 .
[本文引用: 1]
[10]
SIWAKOTI Y P LOH P C BLAABJERG F , et al . Y-source impedance network
[J]. IEEE Transactions on Power Electronics , 2014 , 29 (7 ):3250 -3254 .
DOI:10.1109/TPEL.2013.2296517
URL
[本文引用: 1]
[11]
LIU H P ZHOU Zichao LIU Kuan , et al . High step-up Y-source inverter with reduced DC-link voltage spikes
[J]. IEEE Transactions on Power Electronics , 2019 , 34 (6 ):5487 -5499 .
DOI:10.1109/TPEL.2018.2866635
URL
[本文引用: 1]
[12]
李佳逸 , 雷勇 , 李媛 , 等 . 单相准Z源逆变器二倍频纹波的抑制及应力分析
[J]. 电力系统保护与控制 , 2018 , 46 (9 ):25 -33 .
[本文引用: 1]
LI Jiayi LEI Yong LI Yuan , et al . Suppression and stress analysis of double-line frequency ripple of single-phase quasi Z source inverter
[J]. Power System Protection and Control , 2018 , 46 (9 ):25 -33 .
[本文引用: 1]
[13]
李江涛 , 顾悦 , 任子媛 , 等 . 高压大功率晶闸管阀关断的电应力分析
[J]. 高压电器 , 2018 , 54 (7 ):206 -210 .
[本文引用: 1]
LI Jiangtao GU Yue REN Ziyuan , et al . Analysis on the turn-off electrical stress of high voltage power thyristor valve
[J]. High Voltage Apparatus , 2018 , 54 (7 ):206 -210 .
[本文引用: 1]
[14]
仲崇山 , 杨仁刚 , 李成榕 . 动态均压缓冲电路引起的晶闸管电流应力计算方法
[J]. 电网技术 , 2011 , 35 (3 ):124 -128 .
[本文引用: 1]
ZHONG Chongshan YANG Rengang LI Chengron . An approach to calculate current stress caused by dynamic voltage-sharing snubber circuit during thyristor turning-on process
[J]. Power System Technology , 2011 , 35 (3 ):124 -128 .
[本文引用: 1]
[15]
葛学健 , 孙跃 , 唐春森 , 等 . 用于动态无线供电系统的双输出逆变器
[J]. 电工技术学报 , 2020 , 35 (4 ):786 -798 .
[本文引用: 1]
GE Xuejian SUN Yue TANG Chunsen , et al . Dual-output inverter for dynamic wireless power transfer system
[J]. Transactions of China Electrotechnical Society , 2020 , 35 (4 ):786 -798 .
[本文引用: 1]
[16]
马雨辉 , 皇甫宜耿 , 徐良材 , 等 . 一种基于开关电容倍压单元的新型浮地并联高增益变换器
[J]. 电气工程学报 , 2021 , 16 (2 ):181 -189 .
[本文引用: 1]
MA Yuhui HUANGFU Yigeng XU Liangcai , et al . A novel floating parallel high-gain converter based on switched capacitor voltage doubler
[J]. Journal of Electrical Engineering , 2021 , 16 (2 ):181 -189 .
[本文引用: 1]
Z-source inverter
1
2003
... 近年来,为了满足一些特殊的应用需求,逆变器的拓扑结构变得越来越复杂.其中,以Z源逆变器为代表的阻抗源逆变器能够解决传统电压源型逆变器和电流源型逆变器许多固有的缺点,例如负载电压或电流调节范围有限,需要引入死区时间或重叠时间导致输出波形畸变等[1 ⇓ -3 ] .随后,国内外学者相继提出了一些改进的阻抗源逆变器拓扑结构.其中,准Z源逆变器[4 -5 ] 是将电源放置在电感支路构造而来的,具备连续的输入电流,减小启动冲击电流的能力.国内外学者提出一系列新型拓扑以改善Z源逆变器的升压性能,包括改进型开关电感型Quasi-Z源逆变器[6 ] 、级联Z源逆变器[7 ] 等.上述拓扑通过级联阻抗网络的方式提高了升压性能,然而在实际工程实施中,级联数的增加使得逆变器设计趋于复杂化,同时附加的寄生参数导致升压性能下降,降低能量交换效率.为此,相继出现了trans-Z源逆变器[8 ] 、Γ-Z源逆变器[9 ] 和Y源逆变器[10 ] 等耦合电感型阻抗源逆变器拓扑结构.通过调整耦合电感的匝数比,逆变器可以在较低的直通占空比下实现较高的电压增益.其中,Y源逆变器结合了trans-Z源和Γ-Z源逆变器的升压特点,利用三端耦合电感传递能量,具有更高的匝数比设计自由度,更加显著地体现含有耦合电感的阻抗源网络的优势.文献[11 ]提出了一种高升压比Y源逆变器(High step-up Y-source inverter,HS-YSI),拓扑结构如图1 所示. ...
新颖的单相电压型准Z源逆变器
1
2015
... 近年来,为了满足一些特殊的应用需求,逆变器的拓扑结构变得越来越复杂.其中,以Z源逆变器为代表的阻抗源逆变器能够解决传统电压源型逆变器和电流源型逆变器许多固有的缺点,例如负载电压或电流调节范围有限,需要引入死区时间或重叠时间导致输出波形畸变等[1 ⇓ -3 ] .随后,国内外学者相继提出了一些改进的阻抗源逆变器拓扑结构.其中,准Z源逆变器[4 -5 ] 是将电源放置在电感支路构造而来的,具备连续的输入电流,减小启动冲击电流的能力.国内外学者提出一系列新型拓扑以改善Z源逆变器的升压性能,包括改进型开关电感型Quasi-Z源逆变器[6 ] 、级联Z源逆变器[7 ] 等.上述拓扑通过级联阻抗网络的方式提高了升压性能,然而在实际工程实施中,级联数的增加使得逆变器设计趋于复杂化,同时附加的寄生参数导致升压性能下降,降低能量交换效率.为此,相继出现了trans-Z源逆变器[8 ] 、Γ-Z源逆变器[9 ] 和Y源逆变器[10 ] 等耦合电感型阻抗源逆变器拓扑结构.通过调整耦合电感的匝数比,逆变器可以在较低的直通占空比下实现较高的电压增益.其中,Y源逆变器结合了trans-Z源和Γ-Z源逆变器的升压特点,利用三端耦合电感传递能量,具有更高的匝数比设计自由度,更加显著地体现含有耦合电感的阻抗源网络的优势.文献[11 ]提出了一种高升压比Y源逆变器(High step-up Y-source inverter,HS-YSI),拓扑结构如图1 所示. ...
A novel single phase voltage mode quasi-Z-source inverter
1
2015
... 近年来,为了满足一些特殊的应用需求,逆变器的拓扑结构变得越来越复杂.其中,以Z源逆变器为代表的阻抗源逆变器能够解决传统电压源型逆变器和电流源型逆变器许多固有的缺点,例如负载电压或电流调节范围有限,需要引入死区时间或重叠时间导致输出波形畸变等[1 ⇓ -3 ] .随后,国内外学者相继提出了一些改进的阻抗源逆变器拓扑结构.其中,准Z源逆变器[4 -5 ] 是将电源放置在电感支路构造而来的,具备连续的输入电流,减小启动冲击电流的能力.国内外学者提出一系列新型拓扑以改善Z源逆变器的升压性能,包括改进型开关电感型Quasi-Z源逆变器[6 ] 、级联Z源逆变器[7 ] 等.上述拓扑通过级联阻抗网络的方式提高了升压性能,然而在实际工程实施中,级联数的增加使得逆变器设计趋于复杂化,同时附加的寄生参数导致升压性能下降,降低能量交换效率.为此,相继出现了trans-Z源逆变器[8 ] 、Γ-Z源逆变器[9 ] 和Y源逆变器[10 ] 等耦合电感型阻抗源逆变器拓扑结构.通过调整耦合电感的匝数比,逆变器可以在较低的直通占空比下实现较高的电压增益.其中,Y源逆变器结合了trans-Z源和Γ-Z源逆变器的升压特点,利用三端耦合电感传递能量,具有更高的匝数比设计自由度,更加显著地体现含有耦合电感的阻抗源网络的优势.文献[11 ]提出了一种高升压比Y源逆变器(High step-up Y-source inverter,HS-YSI),拓扑结构如图1 所示. ...
新型倍压-Z源逆变器
1
2021
... 近年来,为了满足一些特殊的应用需求,逆变器的拓扑结构变得越来越复杂.其中,以Z源逆变器为代表的阻抗源逆变器能够解决传统电压源型逆变器和电流源型逆变器许多固有的缺点,例如负载电压或电流调节范围有限,需要引入死区时间或重叠时间导致输出波形畸变等[1 ⇓ -3 ] .随后,国内外学者相继提出了一些改进的阻抗源逆变器拓扑结构.其中,准Z源逆变器[4 -5 ] 是将电源放置在电感支路构造而来的,具备连续的输入电流,减小启动冲击电流的能力.国内外学者提出一系列新型拓扑以改善Z源逆变器的升压性能,包括改进型开关电感型Quasi-Z源逆变器[6 ] 、级联Z源逆变器[7 ] 等.上述拓扑通过级联阻抗网络的方式提高了升压性能,然而在实际工程实施中,级联数的增加使得逆变器设计趋于复杂化,同时附加的寄生参数导致升压性能下降,降低能量交换效率.为此,相继出现了trans-Z源逆变器[8 ] 、Γ-Z源逆变器[9 ] 和Y源逆变器[10 ] 等耦合电感型阻抗源逆变器拓扑结构.通过调整耦合电感的匝数比,逆变器可以在较低的直通占空比下实现较高的电压增益.其中,Y源逆变器结合了trans-Z源和Γ-Z源逆变器的升压特点,利用三端耦合电感传递能量,具有更高的匝数比设计自由度,更加显著地体现含有耦合电感的阻抗源网络的优势.文献[11 ]提出了一种高升压比Y源逆变器(High step-up Y-source inverter,HS-YSI),拓扑结构如图1 所示. ...
Novel Z-source inverter with voltage multiplier unit
1
2021
... 近年来,为了满足一些特殊的应用需求,逆变器的拓扑结构变得越来越复杂.其中,以Z源逆变器为代表的阻抗源逆变器能够解决传统电压源型逆变器和电流源型逆变器许多固有的缺点,例如负载电压或电流调节范围有限,需要引入死区时间或重叠时间导致输出波形畸变等[1 ⇓ -3 ] .随后,国内外学者相继提出了一些改进的阻抗源逆变器拓扑结构.其中,准Z源逆变器[4 -5 ] 是将电源放置在电感支路构造而来的,具备连续的输入电流,减小启动冲击电流的能力.国内外学者提出一系列新型拓扑以改善Z源逆变器的升压性能,包括改进型开关电感型Quasi-Z源逆变器[6 ] 、级联Z源逆变器[7 ] 等.上述拓扑通过级联阻抗网络的方式提高了升压性能,然而在实际工程实施中,级联数的增加使得逆变器设计趋于复杂化,同时附加的寄生参数导致升压性能下降,降低能量交换效率.为此,相继出现了trans-Z源逆变器[8 ] 、Γ-Z源逆变器[9 ] 和Y源逆变器[10 ] 等耦合电感型阻抗源逆变器拓扑结构.通过调整耦合电感的匝数比,逆变器可以在较低的直通占空比下实现较高的电压增益.其中,Y源逆变器结合了trans-Z源和Γ-Z源逆变器的升压特点,利用三端耦合电感传递能量,具有更高的匝数比设计自由度,更加显著地体现含有耦合电感的阻抗源网络的优势.文献[11 ]提出了一种高升压比Y源逆变器(High step-up Y-source inverter,HS-YSI),拓扑结构如图1 所示. ...
改进型准Z源逆变器
1
2016
... 近年来,为了满足一些特殊的应用需求,逆变器的拓扑结构变得越来越复杂.其中,以Z源逆变器为代表的阻抗源逆变器能够解决传统电压源型逆变器和电流源型逆变器许多固有的缺点,例如负载电压或电流调节范围有限,需要引入死区时间或重叠时间导致输出波形畸变等[1 ⇓ -3 ] .随后,国内外学者相继提出了一些改进的阻抗源逆变器拓扑结构.其中,准Z源逆变器[4 -5 ] 是将电源放置在电感支路构造而来的,具备连续的输入电流,减小启动冲击电流的能力.国内外学者提出一系列新型拓扑以改善Z源逆变器的升压性能,包括改进型开关电感型Quasi-Z源逆变器[6 ] 、级联Z源逆变器[7 ] 等.上述拓扑通过级联阻抗网络的方式提高了升压性能,然而在实际工程实施中,级联数的增加使得逆变器设计趋于复杂化,同时附加的寄生参数导致升压性能下降,降低能量交换效率.为此,相继出现了trans-Z源逆变器[8 ] 、Γ-Z源逆变器[9 ] 和Y源逆变器[10 ] 等耦合电感型阻抗源逆变器拓扑结构.通过调整耦合电感的匝数比,逆变器可以在较低的直通占空比下实现较高的电压增益.其中,Y源逆变器结合了trans-Z源和Γ-Z源逆变器的升压特点,利用三端耦合电感传递能量,具有更高的匝数比设计自由度,更加显著地体现含有耦合电感的阻抗源网络的优势.文献[11 ]提出了一种高升压比Y源逆变器(High step-up Y-source inverter,HS-YSI),拓扑结构如图1 所示. ...
Improved quasi-Z-source inverter
1
2016
... 近年来,为了满足一些特殊的应用需求,逆变器的拓扑结构变得越来越复杂.其中,以Z源逆变器为代表的阻抗源逆变器能够解决传统电压源型逆变器和电流源型逆变器许多固有的缺点,例如负载电压或电流调节范围有限,需要引入死区时间或重叠时间导致输出波形畸变等[1 ⇓ -3 ] .随后,国内外学者相继提出了一些改进的阻抗源逆变器拓扑结构.其中,准Z源逆变器[4 -5 ] 是将电源放置在电感支路构造而来的,具备连续的输入电流,减小启动冲击电流的能力.国内外学者提出一系列新型拓扑以改善Z源逆变器的升压性能,包括改进型开关电感型Quasi-Z源逆变器[6 ] 、级联Z源逆变器[7 ] 等.上述拓扑通过级联阻抗网络的方式提高了升压性能,然而在实际工程实施中,级联数的增加使得逆变器设计趋于复杂化,同时附加的寄生参数导致升压性能下降,降低能量交换效率.为此,相继出现了trans-Z源逆变器[8 ] 、Γ-Z源逆变器[9 ] 和Y源逆变器[10 ] 等耦合电感型阻抗源逆变器拓扑结构.通过调整耦合电感的匝数比,逆变器可以在较低的直通占空比下实现较高的电压增益.其中,Y源逆变器结合了trans-Z源和Γ-Z源逆变器的升压特点,利用三端耦合电感传递能量,具有更高的匝数比设计自由度,更加显著地体现含有耦合电感的阻抗源网络的优势.文献[11 ]提出了一种高升压比Y源逆变器(High step-up Y-source inverter,HS-YSI),拓扑结构如图1 所示. ...
High-performance quasi-Z-source inverter with low capacitor voltage stress and small inductance
1
2015
... 近年来,为了满足一些特殊的应用需求,逆变器的拓扑结构变得越来越复杂.其中,以Z源逆变器为代表的阻抗源逆变器能够解决传统电压源型逆变器和电流源型逆变器许多固有的缺点,例如负载电压或电流调节范围有限,需要引入死区时间或重叠时间导致输出波形畸变等[1 ⇓ -3 ] .随后,国内外学者相继提出了一些改进的阻抗源逆变器拓扑结构.其中,准Z源逆变器[4 -5 ] 是将电源放置在电感支路构造而来的,具备连续的输入电流,减小启动冲击电流的能力.国内外学者提出一系列新型拓扑以改善Z源逆变器的升压性能,包括改进型开关电感型Quasi-Z源逆变器[6 ] 、级联Z源逆变器[7 ] 等.上述拓扑通过级联阻抗网络的方式提高了升压性能,然而在实际工程实施中,级联数的增加使得逆变器设计趋于复杂化,同时附加的寄生参数导致升压性能下降,降低能量交换效率.为此,相继出现了trans-Z源逆变器[8 ] 、Γ-Z源逆变器[9 ] 和Y源逆变器[10 ] 等耦合电感型阻抗源逆变器拓扑结构.通过调整耦合电感的匝数比,逆变器可以在较低的直通占空比下实现较高的电压增益.其中,Y源逆变器结合了trans-Z源和Γ-Z源逆变器的升压特点,利用三端耦合电感传递能量,具有更高的匝数比设计自由度,更加显著地体现含有耦合电感的阻抗源网络的优势.文献[11 ]提出了一种高升压比Y源逆变器(High step-up Y-source inverter,HS-YSI),拓扑结构如图1 所示. ...
开关电感型Quasi-Z源逆变器
1
2011
... 近年来,为了满足一些特殊的应用需求,逆变器的拓扑结构变得越来越复杂.其中,以Z源逆变器为代表的阻抗源逆变器能够解决传统电压源型逆变器和电流源型逆变器许多固有的缺点,例如负载电压或电流调节范围有限,需要引入死区时间或重叠时间导致输出波形畸变等[1 ⇓ -3 ] .随后,国内外学者相继提出了一些改进的阻抗源逆变器拓扑结构.其中,准Z源逆变器[4 -5 ] 是将电源放置在电感支路构造而来的,具备连续的输入电流,减小启动冲击电流的能力.国内外学者提出一系列新型拓扑以改善Z源逆变器的升压性能,包括改进型开关电感型Quasi-Z源逆变器[6 ] 、级联Z源逆变器[7 ] 等.上述拓扑通过级联阻抗网络的方式提高了升压性能,然而在实际工程实施中,级联数的增加使得逆变器设计趋于复杂化,同时附加的寄生参数导致升压性能下降,降低能量交换效率.为此,相继出现了trans-Z源逆变器[8 ] 、Γ-Z源逆变器[9 ] 和Y源逆变器[10 ] 等耦合电感型阻抗源逆变器拓扑结构.通过调整耦合电感的匝数比,逆变器可以在较低的直通占空比下实现较高的电压增益.其中,Y源逆变器结合了trans-Z源和Γ-Z源逆变器的升压特点,利用三端耦合电感传递能量,具有更高的匝数比设计自由度,更加显著地体现含有耦合电感的阻抗源网络的优势.文献[11 ]提出了一种高升压比Y源逆变器(High step-up Y-source inverter,HS-YSI),拓扑结构如图1 所示. ...
Switched inductor Quasi-Z source inverters
1
2011
... 近年来,为了满足一些特殊的应用需求,逆变器的拓扑结构变得越来越复杂.其中,以Z源逆变器为代表的阻抗源逆变器能够解决传统电压源型逆变器和电流源型逆变器许多固有的缺点,例如负载电压或电流调节范围有限,需要引入死区时间或重叠时间导致输出波形畸变等[1 ⇓ -3 ] .随后,国内外学者相继提出了一些改进的阻抗源逆变器拓扑结构.其中,准Z源逆变器[4 -5 ] 是将电源放置在电感支路构造而来的,具备连续的输入电流,减小启动冲击电流的能力.国内外学者提出一系列新型拓扑以改善Z源逆变器的升压性能,包括改进型开关电感型Quasi-Z源逆变器[6 ] 、级联Z源逆变器[7 ] 等.上述拓扑通过级联阻抗网络的方式提高了升压性能,然而在实际工程实施中,级联数的增加使得逆变器设计趋于复杂化,同时附加的寄生参数导致升压性能下降,降低能量交换效率.为此,相继出现了trans-Z源逆变器[8 ] 、Γ-Z源逆变器[9 ] 和Y源逆变器[10 ] 等耦合电感型阻抗源逆变器拓扑结构.通过调整耦合电感的匝数比,逆变器可以在较低的直通占空比下实现较高的电压增益.其中,Y源逆变器结合了trans-Z源和Γ-Z源逆变器的升压特点,利用三端耦合电感传递能量,具有更高的匝数比设计自由度,更加显著地体现含有耦合电感的阻抗源网络的优势.文献[11 ]提出了一种高升压比Y源逆变器(High step-up Y-source inverter,HS-YSI),拓扑结构如图1 所示. ...
Z源级联三电平中点钳位逆变器
1
2012
... 近年来,为了满足一些特殊的应用需求,逆变器的拓扑结构变得越来越复杂.其中,以Z源逆变器为代表的阻抗源逆变器能够解决传统电压源型逆变器和电流源型逆变器许多固有的缺点,例如负载电压或电流调节范围有限,需要引入死区时间或重叠时间导致输出波形畸变等[1 ⇓ -3 ] .随后,国内外学者相继提出了一些改进的阻抗源逆变器拓扑结构.其中,准Z源逆变器[4 -5 ] 是将电源放置在电感支路构造而来的,具备连续的输入电流,减小启动冲击电流的能力.国内外学者提出一系列新型拓扑以改善Z源逆变器的升压性能,包括改进型开关电感型Quasi-Z源逆变器[6 ] 、级联Z源逆变器[7 ] 等.上述拓扑通过级联阻抗网络的方式提高了升压性能,然而在实际工程实施中,级联数的增加使得逆变器设计趋于复杂化,同时附加的寄生参数导致升压性能下降,降低能量交换效率.为此,相继出现了trans-Z源逆变器[8 ] 、Γ-Z源逆变器[9 ] 和Y源逆变器[10 ] 等耦合电感型阻抗源逆变器拓扑结构.通过调整耦合电感的匝数比,逆变器可以在较低的直通占空比下实现较高的电压增益.其中,Y源逆变器结合了trans-Z源和Γ-Z源逆变器的升压特点,利用三端耦合电感传递能量,具有更高的匝数比设计自由度,更加显著地体现含有耦合电感的阻抗源网络的优势.文献[11 ]提出了一种高升压比Y源逆变器(High step-up Y-source inverter,HS-YSI),拓扑结构如图1 所示. ...
A cascaded Z-source three-level neutral point clamped inverter
1
2012
... 近年来,为了满足一些特殊的应用需求,逆变器的拓扑结构变得越来越复杂.其中,以Z源逆变器为代表的阻抗源逆变器能够解决传统电压源型逆变器和电流源型逆变器许多固有的缺点,例如负载电压或电流调节范围有限,需要引入死区时间或重叠时间导致输出波形畸变等[1 ⇓ -3 ] .随后,国内外学者相继提出了一些改进的阻抗源逆变器拓扑结构.其中,准Z源逆变器[4 -5 ] 是将电源放置在电感支路构造而来的,具备连续的输入电流,减小启动冲击电流的能力.国内外学者提出一系列新型拓扑以改善Z源逆变器的升压性能,包括改进型开关电感型Quasi-Z源逆变器[6 ] 、级联Z源逆变器[7 ] 等.上述拓扑通过级联阻抗网络的方式提高了升压性能,然而在实际工程实施中,级联数的增加使得逆变器设计趋于复杂化,同时附加的寄生参数导致升压性能下降,降低能量交换效率.为此,相继出现了trans-Z源逆变器[8 ] 、Γ-Z源逆变器[9 ] 和Y源逆变器[10 ] 等耦合电感型阻抗源逆变器拓扑结构.通过调整耦合电感的匝数比,逆变器可以在较低的直通占空比下实现较高的电压增益.其中,Y源逆变器结合了trans-Z源和Γ-Z源逆变器的升压特点,利用三端耦合电感传递能量,具有更高的匝数比设计自由度,更加显著地体现含有耦合电感的阻抗源网络的优势.文献[11 ]提出了一种高升压比Y源逆变器(High step-up Y-source inverter,HS-YSI),拓扑结构如图1 所示. ...
Trans-Z-source inverter
1
2011
... 近年来,为了满足一些特殊的应用需求,逆变器的拓扑结构变得越来越复杂.其中,以Z源逆变器为代表的阻抗源逆变器能够解决传统电压源型逆变器和电流源型逆变器许多固有的缺点,例如负载电压或电流调节范围有限,需要引入死区时间或重叠时间导致输出波形畸变等[1 ⇓ -3 ] .随后,国内外学者相继提出了一些改进的阻抗源逆变器拓扑结构.其中,准Z源逆变器[4 -5 ] 是将电源放置在电感支路构造而来的,具备连续的输入电流,减小启动冲击电流的能力.国内外学者提出一系列新型拓扑以改善Z源逆变器的升压性能,包括改进型开关电感型Quasi-Z源逆变器[6 ] 、级联Z源逆变器[7 ] 等.上述拓扑通过级联阻抗网络的方式提高了升压性能,然而在实际工程实施中,级联数的增加使得逆变器设计趋于复杂化,同时附加的寄生参数导致升压性能下降,降低能量交换效率.为此,相继出现了trans-Z源逆变器[8 ] 、Γ-Z源逆变器[9 ] 和Y源逆变器[10 ] 等耦合电感型阻抗源逆变器拓扑结构.通过调整耦合电感的匝数比,逆变器可以在较低的直通占空比下实现较高的电压增益.其中,Y源逆变器结合了trans-Z源和Γ-Z源逆变器的升压特点,利用三端耦合电感传递能量,具有更高的匝数比设计自由度,更加显著地体现含有耦合电感的阻抗源网络的优势.文献[11 ]提出了一种高升压比Y源逆变器(High step-up Y-source inverter,HS-YSI),拓扑结构如图1 所示. ...
Г-Z-source inverters
1
2013
... 近年来,为了满足一些特殊的应用需求,逆变器的拓扑结构变得越来越复杂.其中,以Z源逆变器为代表的阻抗源逆变器能够解决传统电压源型逆变器和电流源型逆变器许多固有的缺点,例如负载电压或电流调节范围有限,需要引入死区时间或重叠时间导致输出波形畸变等[1 ⇓ -3 ] .随后,国内外学者相继提出了一些改进的阻抗源逆变器拓扑结构.其中,准Z源逆变器[4 -5 ] 是将电源放置在电感支路构造而来的,具备连续的输入电流,减小启动冲击电流的能力.国内外学者提出一系列新型拓扑以改善Z源逆变器的升压性能,包括改进型开关电感型Quasi-Z源逆变器[6 ] 、级联Z源逆变器[7 ] 等.上述拓扑通过级联阻抗网络的方式提高了升压性能,然而在实际工程实施中,级联数的增加使得逆变器设计趋于复杂化,同时附加的寄生参数导致升压性能下降,降低能量交换效率.为此,相继出现了trans-Z源逆变器[8 ] 、Γ-Z源逆变器[9 ] 和Y源逆变器[10 ] 等耦合电感型阻抗源逆变器拓扑结构.通过调整耦合电感的匝数比,逆变器可以在较低的直通占空比下实现较高的电压增益.其中,Y源逆变器结合了trans-Z源和Γ-Z源逆变器的升压特点,利用三端耦合电感传递能量,具有更高的匝数比设计自由度,更加显著地体现含有耦合电感的阻抗源网络的优势.文献[11 ]提出了一种高升压比Y源逆变器(High step-up Y-source inverter,HS-YSI),拓扑结构如图1 所示. ...
Y-source impedance network
1
2014
... 近年来,为了满足一些特殊的应用需求,逆变器的拓扑结构变得越来越复杂.其中,以Z源逆变器为代表的阻抗源逆变器能够解决传统电压源型逆变器和电流源型逆变器许多固有的缺点,例如负载电压或电流调节范围有限,需要引入死区时间或重叠时间导致输出波形畸变等[1 ⇓ -3 ] .随后,国内外学者相继提出了一些改进的阻抗源逆变器拓扑结构.其中,准Z源逆变器[4 -5 ] 是将电源放置在电感支路构造而来的,具备连续的输入电流,减小启动冲击电流的能力.国内外学者提出一系列新型拓扑以改善Z源逆变器的升压性能,包括改进型开关电感型Quasi-Z源逆变器[6 ] 、级联Z源逆变器[7 ] 等.上述拓扑通过级联阻抗网络的方式提高了升压性能,然而在实际工程实施中,级联数的增加使得逆变器设计趋于复杂化,同时附加的寄生参数导致升压性能下降,降低能量交换效率.为此,相继出现了trans-Z源逆变器[8 ] 、Γ-Z源逆变器[9 ] 和Y源逆变器[10 ] 等耦合电感型阻抗源逆变器拓扑结构.通过调整耦合电感的匝数比,逆变器可以在较低的直通占空比下实现较高的电压增益.其中,Y源逆变器结合了trans-Z源和Γ-Z源逆变器的升压特点,利用三端耦合电感传递能量,具有更高的匝数比设计自由度,更加显著地体现含有耦合电感的阻抗源网络的优势.文献[11 ]提出了一种高升压比Y源逆变器(High step-up Y-source inverter,HS-YSI),拓扑结构如图1 所示. ...
High step-up Y-source inverter with reduced DC-link voltage spikes
1
2019
... 近年来,为了满足一些特殊的应用需求,逆变器的拓扑结构变得越来越复杂.其中,以Z源逆变器为代表的阻抗源逆变器能够解决传统电压源型逆变器和电流源型逆变器许多固有的缺点,例如负载电压或电流调节范围有限,需要引入死区时间或重叠时间导致输出波形畸变等[1 ⇓ -3 ] .随后,国内外学者相继提出了一些改进的阻抗源逆变器拓扑结构.其中,准Z源逆变器[4 -5 ] 是将电源放置在电感支路构造而来的,具备连续的输入电流,减小启动冲击电流的能力.国内外学者提出一系列新型拓扑以改善Z源逆变器的升压性能,包括改进型开关电感型Quasi-Z源逆变器[6 ] 、级联Z源逆变器[7 ] 等.上述拓扑通过级联阻抗网络的方式提高了升压性能,然而在实际工程实施中,级联数的增加使得逆变器设计趋于复杂化,同时附加的寄生参数导致升压性能下降,降低能量交换效率.为此,相继出现了trans-Z源逆变器[8 ] 、Γ-Z源逆变器[9 ] 和Y源逆变器[10 ] 等耦合电感型阻抗源逆变器拓扑结构.通过调整耦合电感的匝数比,逆变器可以在较低的直通占空比下实现较高的电压增益.其中,Y源逆变器结合了trans-Z源和Γ-Z源逆变器的升压特点,利用三端耦合电感传递能量,具有更高的匝数比设计自由度,更加显著地体现含有耦合电感的阻抗源网络的优势.文献[11 ]提出了一种高升压比Y源逆变器(High step-up Y-source inverter,HS-YSI),拓扑结构如图1 所示. ...
单相准Z源逆变器二倍频纹波的抑制及应力分析
1
2018
... 目前,针对电子器件应力分析方法研究较少,文献[12 ]通过相位分析及理论计算可以详细推导出其逆变器桥臂电压、电流应力;文献[13 ]通过搭建仿真模型的方法给出晶闸管所承受电压应力,但是不能给出具体表达式,不具有普遍性;文献[14 ]应用指数电压源模型,推导出精确的晶闸管开通电流应力,但存在计算量较大、适用性不强等缺点.针对逆变器使用最多的是传统分析方法[15 -16 ] ,传统方法在分析过程中需要将每个开关周期分为几个模态,如果变换器中电容和电感选取足够大时,可以假设电容两端的电压和流过电感的电流恒定不变.然而,电容电流和电感电压在每个模态是不同的,因此必须采用不同的状态变量进行表示.然后,将推导的电容电流和电感电压表达式分别在一个开关周期内进行安秒和伏秒的积分求和,从而获得由电容电压和电感电流表示的表达式,用于计算变换器中所有器件的电压、电流应力. ...
Suppression and stress analysis of double-line frequency ripple of single-phase quasi Z source inverter
1
2018
... 目前,针对电子器件应力分析方法研究较少,文献[12 ]通过相位分析及理论计算可以详细推导出其逆变器桥臂电压、电流应力;文献[13 ]通过搭建仿真模型的方法给出晶闸管所承受电压应力,但是不能给出具体表达式,不具有普遍性;文献[14 ]应用指数电压源模型,推导出精确的晶闸管开通电流应力,但存在计算量较大、适用性不强等缺点.针对逆变器使用最多的是传统分析方法[15 -16 ] ,传统方法在分析过程中需要将每个开关周期分为几个模态,如果变换器中电容和电感选取足够大时,可以假设电容两端的电压和流过电感的电流恒定不变.然而,电容电流和电感电压在每个模态是不同的,因此必须采用不同的状态变量进行表示.然后,将推导的电容电流和电感电压表达式分别在一个开关周期内进行安秒和伏秒的积分求和,从而获得由电容电压和电感电流表示的表达式,用于计算变换器中所有器件的电压、电流应力. ...
高压大功率晶闸管阀关断的电应力分析
1
2018
... 目前,针对电子器件应力分析方法研究较少,文献[12 ]通过相位分析及理论计算可以详细推导出其逆变器桥臂电压、电流应力;文献[13 ]通过搭建仿真模型的方法给出晶闸管所承受电压应力,但是不能给出具体表达式,不具有普遍性;文献[14 ]应用指数电压源模型,推导出精确的晶闸管开通电流应力,但存在计算量较大、适用性不强等缺点.针对逆变器使用最多的是传统分析方法[15 -16 ] ,传统方法在分析过程中需要将每个开关周期分为几个模态,如果变换器中电容和电感选取足够大时,可以假设电容两端的电压和流过电感的电流恒定不变.然而,电容电流和电感电压在每个模态是不同的,因此必须采用不同的状态变量进行表示.然后,将推导的电容电流和电感电压表达式分别在一个开关周期内进行安秒和伏秒的积分求和,从而获得由电容电压和电感电流表示的表达式,用于计算变换器中所有器件的电压、电流应力. ...
Analysis on the turn-off electrical stress of high voltage power thyristor valve
1
2018
... 目前,针对电子器件应力分析方法研究较少,文献[12 ]通过相位分析及理论计算可以详细推导出其逆变器桥臂电压、电流应力;文献[13 ]通过搭建仿真模型的方法给出晶闸管所承受电压应力,但是不能给出具体表达式,不具有普遍性;文献[14 ]应用指数电压源模型,推导出精确的晶闸管开通电流应力,但存在计算量较大、适用性不强等缺点.针对逆变器使用最多的是传统分析方法[15 -16 ] ,传统方法在分析过程中需要将每个开关周期分为几个模态,如果变换器中电容和电感选取足够大时,可以假设电容两端的电压和流过电感的电流恒定不变.然而,电容电流和电感电压在每个模态是不同的,因此必须采用不同的状态变量进行表示.然后,将推导的电容电流和电感电压表达式分别在一个开关周期内进行安秒和伏秒的积分求和,从而获得由电容电压和电感电流表示的表达式,用于计算变换器中所有器件的电压、电流应力. ...
动态均压缓冲电路引起的晶闸管电流应力计算方法
1
2011
... 目前,针对电子器件应力分析方法研究较少,文献[12 ]通过相位分析及理论计算可以详细推导出其逆变器桥臂电压、电流应力;文献[13 ]通过搭建仿真模型的方法给出晶闸管所承受电压应力,但是不能给出具体表达式,不具有普遍性;文献[14 ]应用指数电压源模型,推导出精确的晶闸管开通电流应力,但存在计算量较大、适用性不强等缺点.针对逆变器使用最多的是传统分析方法[15 -16 ] ,传统方法在分析过程中需要将每个开关周期分为几个模态,如果变换器中电容和电感选取足够大时,可以假设电容两端的电压和流过电感的电流恒定不变.然而,电容电流和电感电压在每个模态是不同的,因此必须采用不同的状态变量进行表示.然后,将推导的电容电流和电感电压表达式分别在一个开关周期内进行安秒和伏秒的积分求和,从而获得由电容电压和电感电流表示的表达式,用于计算变换器中所有器件的电压、电流应力. ...
An approach to calculate current stress caused by dynamic voltage-sharing snubber circuit during thyristor turning-on process
1
2011
... 目前,针对电子器件应力分析方法研究较少,文献[12 ]通过相位分析及理论计算可以详细推导出其逆变器桥臂电压、电流应力;文献[13 ]通过搭建仿真模型的方法给出晶闸管所承受电压应力,但是不能给出具体表达式,不具有普遍性;文献[14 ]应用指数电压源模型,推导出精确的晶闸管开通电流应力,但存在计算量较大、适用性不强等缺点.针对逆变器使用最多的是传统分析方法[15 -16 ] ,传统方法在分析过程中需要将每个开关周期分为几个模态,如果变换器中电容和电感选取足够大时,可以假设电容两端的电压和流过电感的电流恒定不变.然而,电容电流和电感电压在每个模态是不同的,因此必须采用不同的状态变量进行表示.然后,将推导的电容电流和电感电压表达式分别在一个开关周期内进行安秒和伏秒的积分求和,从而获得由电容电压和电感电流表示的表达式,用于计算变换器中所有器件的电压、电流应力. ...
用于动态无线供电系统的双输出逆变器
1
2020
... 目前,针对电子器件应力分析方法研究较少,文献[12 ]通过相位分析及理论计算可以详细推导出其逆变器桥臂电压、电流应力;文献[13 ]通过搭建仿真模型的方法给出晶闸管所承受电压应力,但是不能给出具体表达式,不具有普遍性;文献[14 ]应用指数电压源模型,推导出精确的晶闸管开通电流应力,但存在计算量较大、适用性不强等缺点.针对逆变器使用最多的是传统分析方法[15 -16 ] ,传统方法在分析过程中需要将每个开关周期分为几个模态,如果变换器中电容和电感选取足够大时,可以假设电容两端的电压和流过电感的电流恒定不变.然而,电容电流和电感电压在每个模态是不同的,因此必须采用不同的状态变量进行表示.然后,将推导的电容电流和电感电压表达式分别在一个开关周期内进行安秒和伏秒的积分求和,从而获得由电容电压和电感电流表示的表达式,用于计算变换器中所有器件的电压、电流应力. ...
Dual-output inverter for dynamic wireless power transfer system
1
2020
... 目前,针对电子器件应力分析方法研究较少,文献[12 ]通过相位分析及理论计算可以详细推导出其逆变器桥臂电压、电流应力;文献[13 ]通过搭建仿真模型的方法给出晶闸管所承受电压应力,但是不能给出具体表达式,不具有普遍性;文献[14 ]应用指数电压源模型,推导出精确的晶闸管开通电流应力,但存在计算量较大、适用性不强等缺点.针对逆变器使用最多的是传统分析方法[15 -16 ] ,传统方法在分析过程中需要将每个开关周期分为几个模态,如果变换器中电容和电感选取足够大时,可以假设电容两端的电压和流过电感的电流恒定不变.然而,电容电流和电感电压在每个模态是不同的,因此必须采用不同的状态变量进行表示.然后,将推导的电容电流和电感电压表达式分别在一个开关周期内进行安秒和伏秒的积分求和,从而获得由电容电压和电感电流表示的表达式,用于计算变换器中所有器件的电压、电流应力. ...
一种基于开关电容倍压单元的新型浮地并联高增益变换器
1
2021
... 目前,针对电子器件应力分析方法研究较少,文献[12 ]通过相位分析及理论计算可以详细推导出其逆变器桥臂电压、电流应力;文献[13 ]通过搭建仿真模型的方法给出晶闸管所承受电压应力,但是不能给出具体表达式,不具有普遍性;文献[14 ]应用指数电压源模型,推导出精确的晶闸管开通电流应力,但存在计算量较大、适用性不强等缺点.针对逆变器使用最多的是传统分析方法[15 -16 ] ,传统方法在分析过程中需要将每个开关周期分为几个模态,如果变换器中电容和电感选取足够大时,可以假设电容两端的电压和流过电感的电流恒定不变.然而,电容电流和电感电压在每个模态是不同的,因此必须采用不同的状态变量进行表示.然后,将推导的电容电流和电感电压表达式分别在一个开关周期内进行安秒和伏秒的积分求和,从而获得由电容电压和电感电流表示的表达式,用于计算变换器中所有器件的电压、电流应力. ...
A novel floating parallel high-gain converter based on switched capacitor voltage doubler
1
2021
... 目前,针对电子器件应力分析方法研究较少,文献[12 ]通过相位分析及理论计算可以详细推导出其逆变器桥臂电压、电流应力;文献[13 ]通过搭建仿真模型的方法给出晶闸管所承受电压应力,但是不能给出具体表达式,不具有普遍性;文献[14 ]应用指数电压源模型,推导出精确的晶闸管开通电流应力,但存在计算量较大、适用性不强等缺点.针对逆变器使用最多的是传统分析方法[15 -16 ] ,传统方法在分析过程中需要将每个开关周期分为几个模态,如果变换器中电容和电感选取足够大时,可以假设电容两端的电压和流过电感的电流恒定不变.然而,电容电流和电感电压在每个模态是不同的,因此必须采用不同的状态变量进行表示.然后,将推导的电容电流和电感电压表达式分别在一个开关周期内进行安秒和伏秒的积分求和,从而获得由电容电压和电感电流表示的表达式,用于计算变换器中所有器件的电压、电流应力. ...