基于长短期记忆网络的电网同调机群快速辨识

doi:10.11985/2022.02.023

基于长短期记忆网络的电网同调机群快速辨识

毛煜^,¹^,², 尚海昆^,¹, 于卓琦^,¹

1.东北电力大学电气工程学院吉林 132012

2.国网浙江省电力有限公司杭州市富阳区供电公司杭州 311400

A Fast Prediction Method of Coherent Generators Based on Long Short-term Memory Network

MAO Yu^,¹^,², SHANG Haikun^,¹, YU Zhuoqi^,¹

1. School of Electrical Engineering, Northeast Electric Power University, Jilin 132012

2. State Grid Zhejiang Hangzhou Fuyang Power Supply Company Co., Ltd., Hangzhou 311400

收稿日期: 2021-07-17 修回日期: 2022-02-18

Received: 2021-07-17 Revised: 2022-02-18

作者简介 About authors

毛煜,男,1995年生,硕士研究生。主要研究方向为电力系统优化。E-mail： maoyu2565@163.com

尚海昆,男,1984年生,副教授。主要研究方向为变压器振动信号。E-mail： shikey007@sina.com

于卓琦,男,1995年生,硕士。主要研究方向为电力设备智能运维。E-mail： 2639579599@qq.com

摘要

基于长短期记忆网络(Long short-term memory,LSTM)提出了一种电网同调机群的快速辨识方法。首先针对两机振荡模型,挖掘相量平面内电压相量轨迹的分类特性,为机组的同调性辨识提供了依据;其次,基于短时响应数据,利用LSTM分别对机端电压实、虚部时序轨迹进行预测,并依据复合而成的相量轨迹判断机组的分群情况;最后,利用扩展等面积法则(Extended equal area criterion,EEAC)对上述分群情况进行验证,进而给出同调机群的最终辨识结果。IEEE-39节点系统算例验证了方法的有效性,具有较好的工程应用价值。

关键词： 同调机群辨识 ; 电压相量轨迹 ; 长短期记忆网络(LSTM) ; 扩展等面积法则(EEAC)

Abstract

Based on the long short-term memory network(LSTM), a fast prediction method of coherent generators is proposed. Firstly, the classification characteristics of bus voltage phase trajectories are extracted to provide a new way for the identification of generator coherency. Secondly, based on the short-term response data, the real and imaginary parts of the generator terminal voltage phase are predicted respectively by using LSTM, and the coherent generators are identified based on the fitted voltage phase trajectories. Finally, the extended equal area criterion(EEAC) is used to further verify the coherency of the identified generator groups. The proposed method is validated used in the IEEE-39 bus system, and the simulation results show that the method has the advantages of higher engineering practice value.

Keywords： Coherent generator identification ; voltage phase trajectory ; long short-term memory network(LSTM) ; extended equal area criteria(EEAC)

PDF (446KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

毛煜, 尚海昆, 于卓琦. 基于长短期记忆网络的电网同调机群快速辨识. 电气工程学报[J], 2022, 17(2): 201-207 doi:10.11985/2022.02.023

MAO Yu, SHANG Haikun, YU Zhuoqi. A Fast Prediction Method of Coherent Generators Based on Long Short-term Memory Network. Chinese Journal of Electrical Engineering[J], 2022, 17(2): 201-207 doi:10.11985/2022.02.023

1 引言

随着我国电网架构逐步完善,系统规模逐步扩大,以及随之而来的新能源占比不断攀升,导致电力系统运行方式愈发复杂多变^[1]。传统故障态的监测与应急处理方式难以满足大电网运行的时效与精度要求,为电网的安全稳定运行带来诸多不确定因素。因此深入对电力系统暂态稳定的研究具有重要意义^[2]。

合理的暂态安全稳定控制措施是电力系统二、三道防线的核心内容,其中,同调机群快速辨识是电力系统暂态稳定控制的先决条件^[3-4]。同调机群划分的实质是同步机组动态响应行为的相似性。目前针对此方向的研究主要分为以下三类。

(1) 针对受扰机组的功角曲线进行数学分析,从而实现同调机群的快速辨识,文献[5]综合时域、频域、小波分析三种方法研究机组功角轨迹的波动特性,进而辨识同调机群;文献[6]用发电机转子角之差在时间域内的最大值来反映同调程度。该类方法以海量样本为决策基础,其灵活性与泛化能力难以满足复杂大电网需求。

(2) 基于状态矩阵判别同调机群,通过构建非线性点处线性化后的模型获得状态矩阵,从而间接判断目标系统同趋性^[7⇓-9]。该类方法利用电力系统静态稳定分析方法分析暂态问题,其结果准确性势必会出现偏差。

(3) 人工智能方法,文献[10]主要通过构建发电机状态参数(发电机功角以及动能)同发电机组同趋性的映射关系;文献[11]基于发电机端口能量吸收/输出状态判断机组运行状态。该类方法指标的构建需要精准反映机群同趋性的划分标准,因此其模型泛化能力较弱。

近年来广域测量系统(Wide area measurement system,WAMS)和通信技术的快速发展,给电网同调机群的快速辨识提供了新的思路,通过相量测量单元(Phasor measurement unit,PMU)实时获取机端电气量,基于特征提取技术辨识同调性,方法优势在于不受模型参数影响^[12-13]。

电网受扰后系统内各机组的机端电压会随之跌落并开始波动,钳制了发电机功率输出能力,系统失稳导致功角曲线发散。由此可知,受扰后的电压时序轨迹中蕴藏着丰富的时空关联知识,利用电压时序轨迹信息挖掘机组同调特性是一种崭新视角^[14-15]。本文基于广域量测系统采集机端电气量,继而转为电压复空间内的相量轨迹;为保证轨迹预测准确性,提升辨识结果精度,引入长短期记忆网络(Long short-term memory network,LSTM)^[16]分别对电压实部、虚部进行预测,得到未来一定时段内的电压相量轨迹;最终结合扩展等面积定则(Extended equal area criteria,EEAC)给出同调机群预测及验证方案。

2 同调机群辨识原理

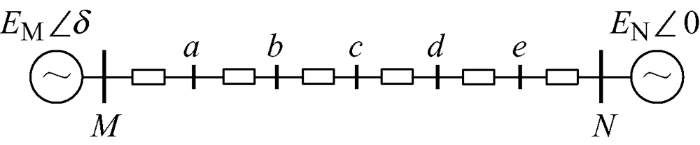
以图1所示的等值两机系统为例,分析系统发生失步振荡时的节点电压相量轨迹变化情况,图1中a、b、c、d、e分别为联络线上的阻抗等分点。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 电力系统的两机模型

位于电压复平面内的点,其电压幅值V、相角θ与实部Re、虚部Im的对应关系如式(1)、(2)所示

(1)$ V=\sqrt{\operatorname{Re}^{2}+\operatorname{Im}^{2}}$

(2)

θ=arctan(Im/Re)

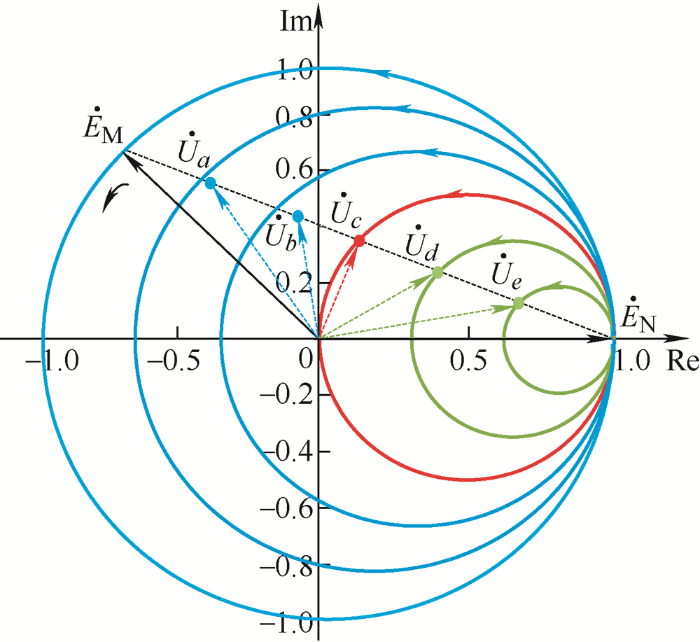
为简单起见,参照文献[14],假设系统两电势的幅值相等,此时失步振荡中心恰好落在联络线中点c处。构造横坐标为电压实部,纵坐标为虚部的电压相量平面,当M侧电源功角δ在0°~360°内变化,各节点在相量平面内的轨迹为半径不同的圆,如图2所示。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 节点电压相量轨迹

位于失步振荡中心左侧的节点a、b,其轨迹介于M和c的轨迹之间,在振荡过程中轨迹会越过虚轴,对应电压相角会单调递增至180°;位于失步振荡中心右侧的节点d、e,其轨迹介于N和c的轨迹之间,振荡过程中轨迹不会越过虚轴,对应电压相角不会超过90°。因此,对于失步振荡中心同一侧的节点,其电压相量的变化轨迹具有相似性,可将其视为同类节点。

若将上述两机模型联络线上各节点视为不同机组的并网接入点^[15],当系统发生失步振荡,通常以失步联络线相位差大于180°为判据,此时机端电压相角已超过180°。由图2可知,当a、b节点相量轨迹抵达实轴时,电压相角恰为180°,说明接入点的轨迹分类特性可用于表征发电机群的同调性。

3 同调机群辨识方法

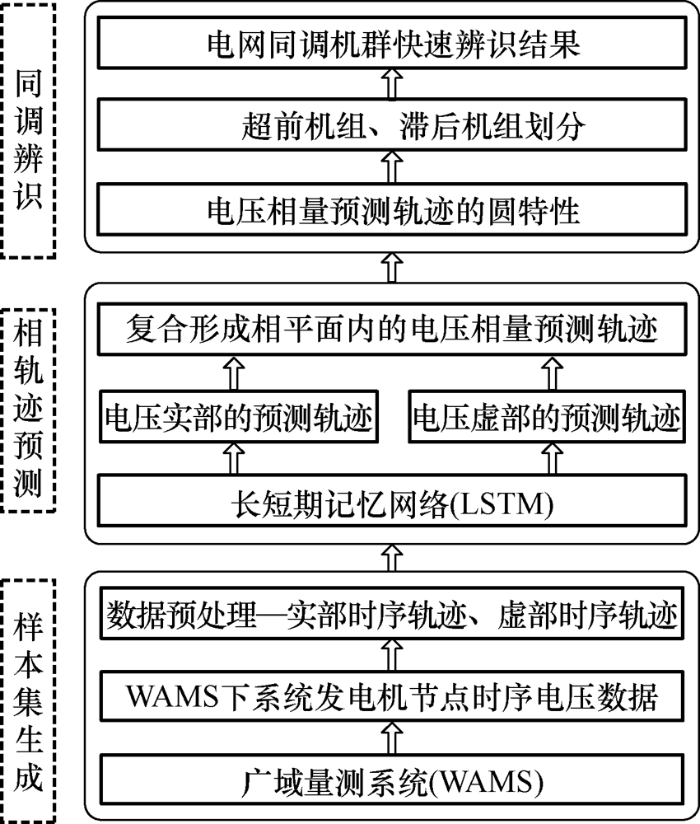
随着电网规模逐渐增大,动态特性日趋复杂,致使传统同调机群辨识方法在时效性与精度的判断上存在一定误差,亟需新方法提升机群同调辨识的准确性。近年来人工智能技术已同电力系统深度融合,在如今相量量测装置已大面积推广应用的背景下,本文基于LSTM技术,结合电相量轨迹的相关理论知识,提出了同调机群快速辨识的方法框架,如图3所示。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 电力系统同调机群辨识体系

该方法首先基于PMU实时采集电网运行状态数据,并对实时量测的节点电压数据进行统一处理,转换为电压实部、虚部随时间时序变化的动态轨迹;然后,基于LSTM分别对两类时序轨迹进行预测,进而复合形成相量平面内的电压相量轨迹;最后,根据机端电压的相量轨迹判断发电机分群情况,给出同调机群的在线辨识结果。

3.1 基于LSTM的电压相量轨迹预测

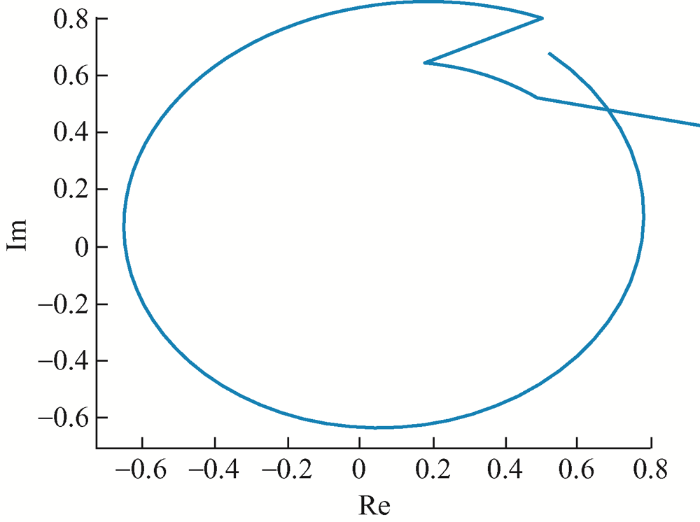
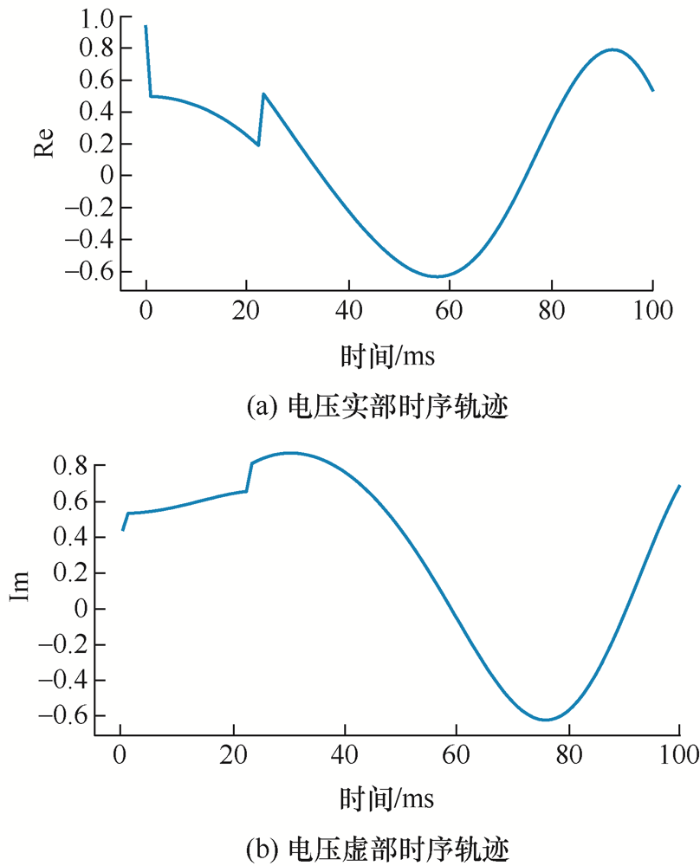
图4为IEEE-39节点系统某一故障形态下1号发电机节点电压相轨迹图,故障于0 s时刻发生,于0.22 s清除,故障清除后机端电压的相量轨迹波动相对平滑,数据间具有较强的关联关系。为深度挖掘这种关联关系,完成高精度的时序轨迹预测,本文选用擅长时序轨迹预测的LSTM加以实现。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 相平面内电压相轨迹曲线

因电压相量轨迹的横纵坐标分别为电压实、虚部,电压相平面隐含了时间属性,给时序轨迹的预测带来难度。本文将电压相量轨迹进行合理拆分,分别得到电压实、虚部随时间时序变化的运动轨迹,如图5a、5b所示。待预测完成后,再将电压实、虚部进行复合,即可得到相平面内的时序轨迹。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 电压时序轨迹

作为循环神经网络的改进版,LSTM考虑时间因素的影响,结合其“门”结构强化对长期信息的记忆功能,可有效解决“梯度消失”问题。凭借其卓越的非线性拟合能力可以实现对复杂数据的预测问题,针对现今互联电网中多源信息交互的量测信息,可以有效记忆反映电网轨迹波动规律的特征信息,充分挖掘量测数据间潜藏的关联关系,因此通过LSTM技术提高电网同调机群快速辨识的精度实属必然。

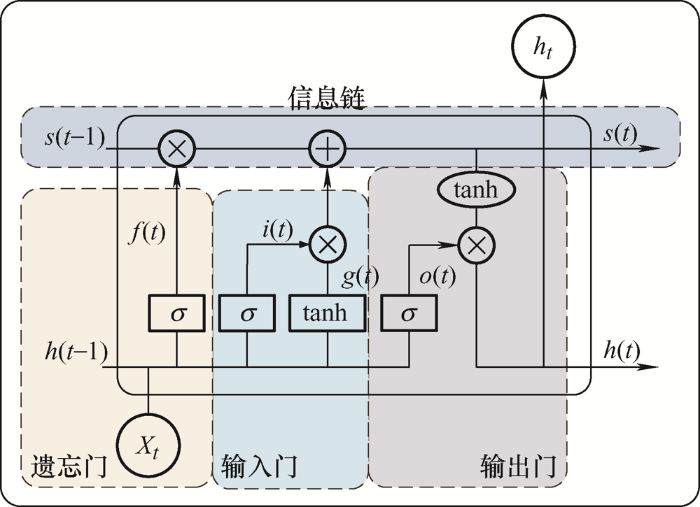
LSTM由输入层、输出层、隐含层三部分组成。同传统循环神经网络所不同,LSTM内部增添了具有长期记忆功能的LSTM单元。图6所示为LSTM的记忆单元,其内包含输入门(Input gate)、输出门(Output gate)、遗忘门(Forget gate)三个门控制器,用以实现对冗余信息的剔除以及对有用信息的留存记忆功能。同时LSTM的记忆单元内增添了用来记忆信息的信息链,其学习记忆的信息通过信息链进行传递迭代。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 LSTM记忆单元内部示意图

其中,LSTM记忆单元中的信息保存与遗忘通过上述门控装置中的tanh以及sigmoid激活函数实现,具体如下：任意时刻中,门控装置会接收输入信息X_t以及上一时刻隐含层的输出信息h(t-1)两类信息,除此之外,三个门控装置还会接收来自记忆单元的状态信息即S(t-1)。各门接收上述信息后通过门内激活函数实现信息的遗忘与记忆功能。由图6可以看出,信息链的更新主要由遗忘门与输入门决定,并最终同输出门共同决定记忆单元的输出h(t),上述过程中的变量计算如下所示

(3)$ i(t)=\sigma\left(\boldsymbol{W}_{i x} x(t)+\boldsymbol{W}_{i h} h(t-1)\right)+\boldsymbol{b}_{i}$

(4)$ f(t)=\sigma\left(\boldsymbol{W}_{f x} x(t)+\boldsymbol{W}_{f h} h(t-1)\right)+\boldsymbol{b}_{f}$

(5)$ o(t)=\sigma\left(\boldsymbol{W}_{o x} x(t)+\boldsymbol{W}_{o h} h(t-1)\right)+\boldsymbol{b}_{o}$

(6)$ s(t)=g(t) \times i(t)+s(t-1) \times f(t)$

式中,W_ix、W_fx、W_ox代表同输入状态信息间的连接权重矩阵;W_ih、W_fh、W_oh代表同上一时刻记忆单元输出信息间的权重矩阵;b_i、b_f、b_o代表偏置向量。其中δ为记忆单元的激活函数,一般为tanh函数亦或是sigmoid函数。激活函数具体如下式所示

(7)$ \sigma=\operatorname{sigmiod}=\frac{1}{1+\exp (-x)}$

(8)$ \tanh =\frac{\exp (x)-\exp (-x)}{\exp (x)+\exp (-x)}$

式(3)代表输入门的相关计算公式,输入门主要通过激活函数决定输入信息的去留;式(4)代表遗忘门的相关计算公式,遗忘门主要提出当前输入信息以及之前隐含层输出信息中的冗余信息;式(5)代表输出门相关的计算公式,输出门主要将有用的信息输出并进行下一次迭代功能。

综上所述,针对现今互联大电网高维时变数据而言,LSTM可以深度挖掘数据中的深层关联关系,对输入信息进行自主学习并选择性记忆,从而提高轨迹的预测精度。

3.2 同调机群快速辨识及验证方法

为提高轨迹预测精度,有必要对故障清除后的受扰轨迹加以利用,因此本文提出基于拟合窗口的同调机群预测及验证方法。

在拟合窗口内提取响应轨迹信息,依据LSTM实时预测的电压相量轨迹与实轴负半轴有无交点来辨识机组的同调性。若机组的预测轨迹与实轴负半轴无交点,则认为与选取的参考机组(相角最为滞后)同调程度强,将其划入滞后群,记为A;否则认为该两机组的同调程度弱,将该机组划入超前群,记为S。

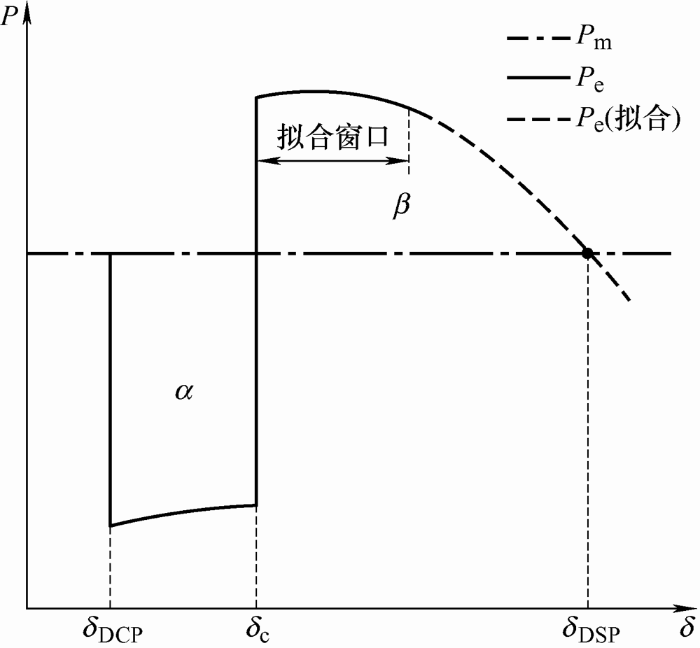
为确保分群结果的准确性,本文进一步利用EEAC^[17]验证所辨识出机群的同调性,S和A的等值功-角轨迹如图7所示。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 P-δ等值曲线

图7中δ_DCP和δ_c分别为在动态中心点(Dynamic center point,DCP)处和故障清除时刻的等值功角;P_m和P_e分别为等值机械功率和电磁功率。因故障清除后P_e类似正弦曲线,故在拟合窗口内可参考如式(9)的函数形式预测P_e后续一段轨迹(图7中虚线)。

(9)$P_{\mathrm{e}}=A_{1}+A_{2} \sin \left(\delta+A_{3}\right)$

δ_DSP为功-角轨迹到达动态鞍点(Dynamic saddle point,DSP)时刻的等值功角,进而可依据等面积法则计算系统的暂态稳定裕度η=α/β,其中α为加速面积,β为最大减速面积。经EEAC验证后最终辨识结果如表1所示。

表1 同调辨识结果

暂态稳定裕度	同调辨识结果
η≥1	S和A具有强同调性
η<1	S和A分为两群

新窗口打开| 下载CSV

4 仿真结果分析

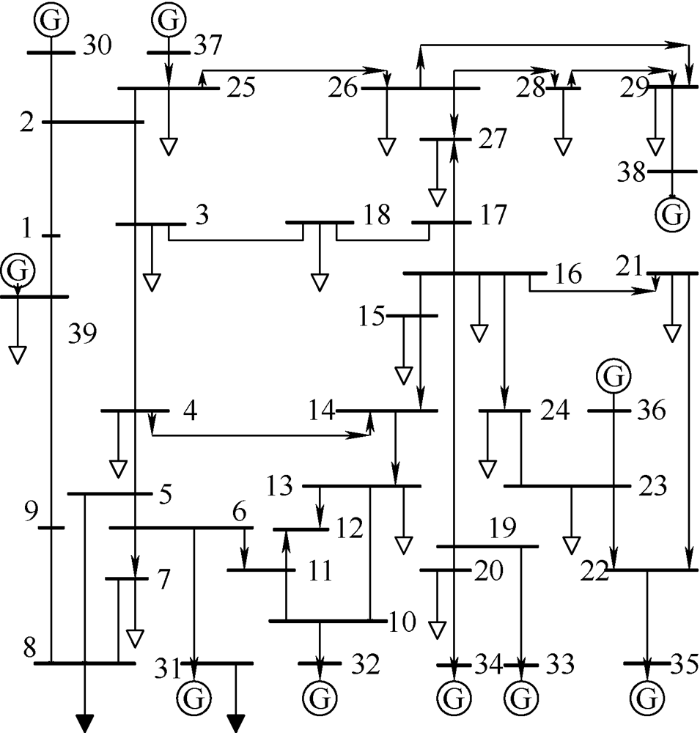
采用如图8所示的IEEE-39节点系统算例对所提方法进行分析验证,用仿真数据模拟广域量测系统的实时量测数据。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 IEEE-39节点系统

系统电压相量部分预测轨迹在Windows系统环境下完成,采用Python3.7计算平台,通过Keras深度学习库加以实现。LSTM神经元参数设置如表2所示。

表2 神经元参数表

神经元参数	描述
激活函数	sigmoid
权值初始化	正态
损失函数	方均根误差函数
优化算法	RMSProp
Batchsize	15

新窗口打开| 下载CSV

为使预测结果的精度得以保证,经过反复试验,本文LSTM采用方均根误差作为损失函数,通过实验总结设置batchsize大小为15,继而根据RMSprop优化算法不断优化LSTM预测结果的精度。考虑到WAMS的采样周期,本文设置预测网络的步长timestep为1(对应时间间隔为0.01 s)。

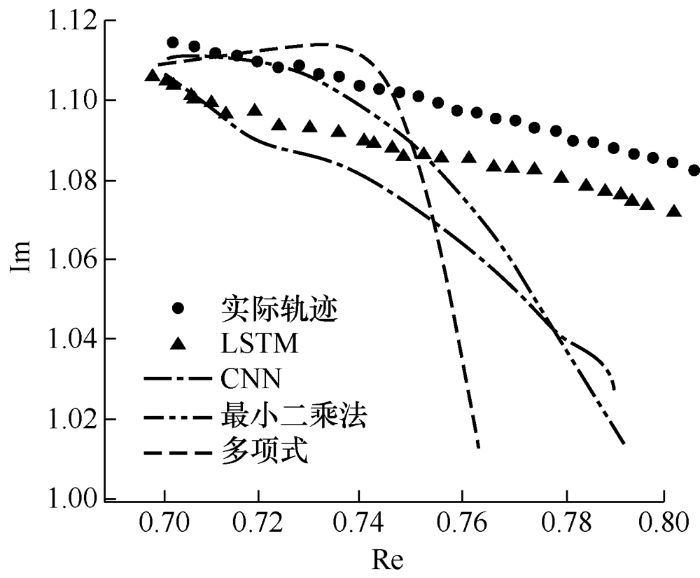
通过故障位置以及故障清除时刻的不同组合方式共生成12 000个样本,从中随机选取10 000个作为LSTM训练样本,剩余2 000个作为测试样本。选取某一样本为例,38号机组的电压相量部分预测轨迹如图9所示。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 预测结果

由图9不难看出,通过LSTM方法拟合机端电压相量轨迹与实际量测曲线基本吻合,二者在故障切除后较长时间段内同样基本吻合,而其余预测方式均存在不同程度的偏差。

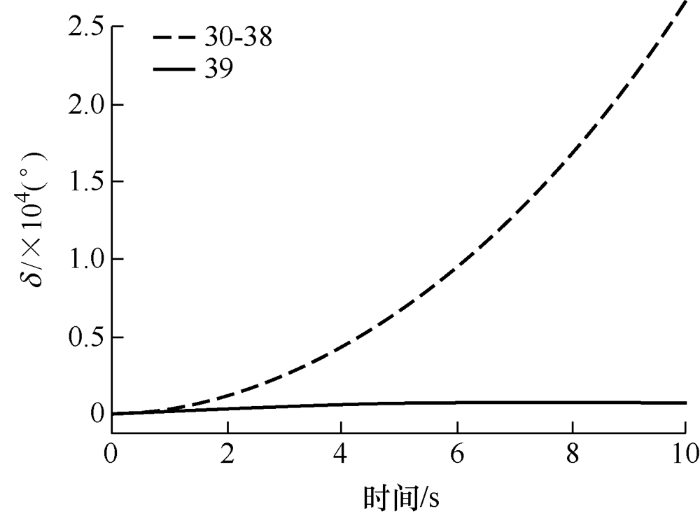
大量仿真表明,系统失稳模式大多为两群摇摆,而多群失稳也往往由两群失稳发展而来^[18],因此本文对两群失稳模式进行研究。设定t=0时线路Bus14-Bus15的20%处发生三相短路故障,0.23 s后切除故障线路。系统呈现两群摇摆模式,39号机组为滞后机组,其余机组为超前机组,机组功角轨迹如图10所示。

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 机组功角曲线

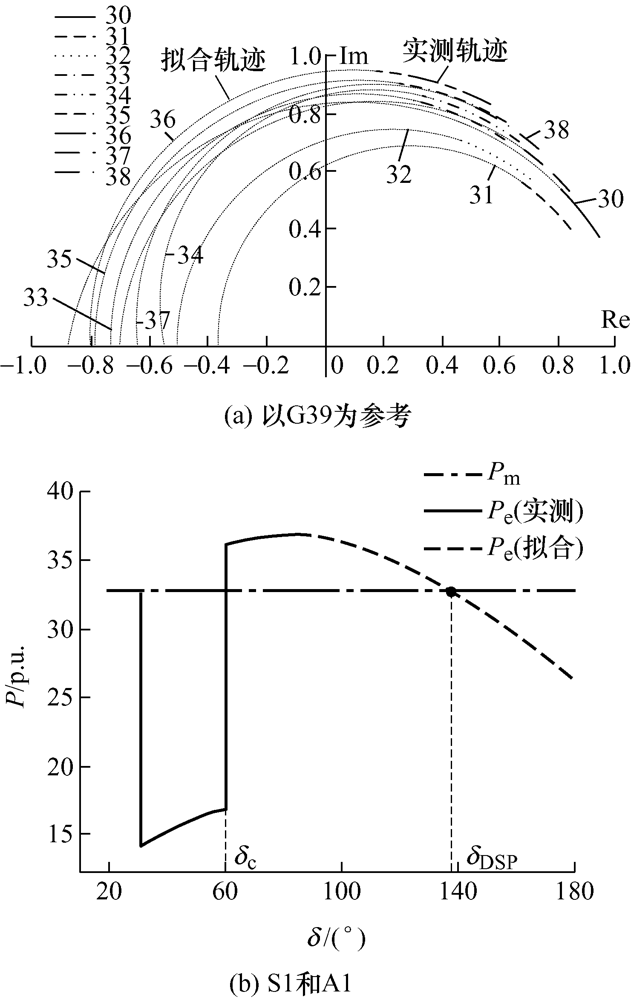
利用故障清除后5个时刻的量测数据预测各机端后续电压相量轨迹,如图11a所示。

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 仿真结果曲线

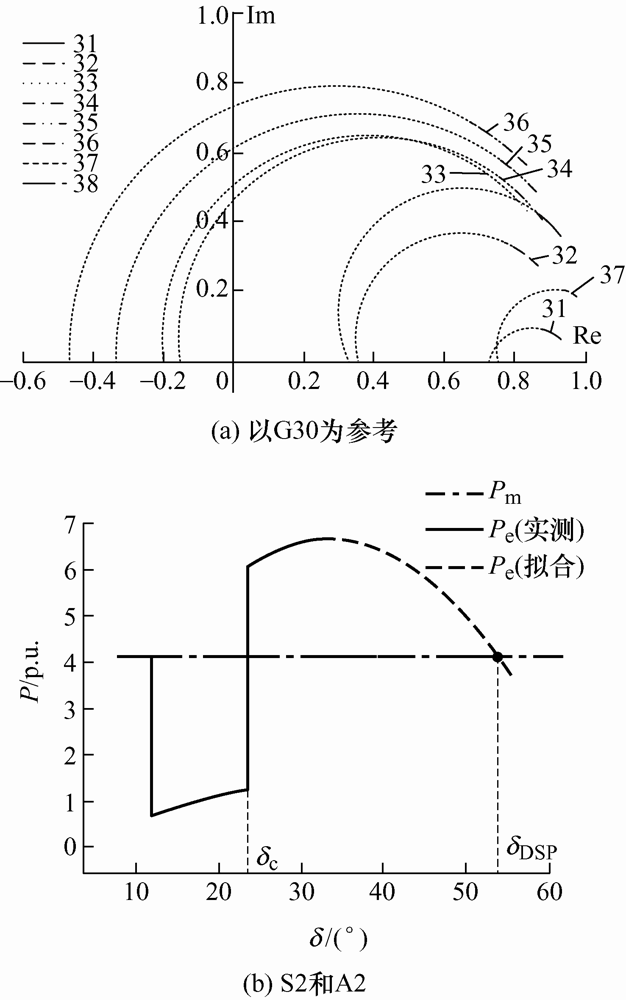
由图11a可将机组分为S₁(G30-G38)和A₁(G39)两群,图11b为上述两群的等值功-角轨迹,通过计算可得η=0.86<1,说明该两群同调性较弱。进一步对超前机群S₁内机组同调性进行辨识,各机端电压相量轨迹及等值功-角轨迹如图12所示。

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12 仿真结果曲线

由于η=1.93>1,说明S₂(G31, G32, G37, G38)和A₂(G33-G36)可视为同一群,因此最终预测39号机组和剩余机组分为两群。不断往后滑动拟合窗口,同调预测结果均为超前群S₁和滞后群A₁,当t=0.32 s时可认为辨识完成。而上述两群的实测等值功-角轨迹在t=0.81 s时越过DSP,继而最终确认S₁和A₁分为两群,该对比说明本文方法因其基于短时量测轨迹而具有预测性质,同调辨识耗时较短。

5 结论

针对同调机群在线预测问题,结合电压相量轨迹和LSTM,提出了基于短时电压相量轨迹的同调机群快速辨识方法,有以下结论。

(1) 在振荡过程中,基于节点电压相量轨迹几何特征提取轨迹的分类特性,为同调机群的辨识提供了新的途径。

(2) 通过LSTM可实现机端电压相量轨迹的快速预测,与其他机器学习算法相比较,具有更好的拟合精度。

(3) 给出了同调机群快速辨识方法,仅利用短时量测即可辨识出机组的同调性,不受网络结构和模型参数的限制,有效提高了方法的时效性。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

李明节, 陈国平, 董存, 等.

新能源电力系统电力电量平衡问题研究

[J]. 电网技术, 2019, 43(11):3979-3986.