电气工程学报, 2021, 16(4): 127-134 doi: 10.11985/2021.04.016

电力电子与电力传动

三电平UPQC的变阻尼无源混合控制策略*

夏亮,1, 王久和1, 陈美锋,2, 刘金昌,1

1.北京信息科技大学自动化学院 北京 100192

2.西安航空职业技术学院自动化工程学院 西安 710089

Passivity-based Hybrid Control Strategy with Variable Damping for Three Level UPQC

XIA Liang,1, WANG Jiuhe1, CHEN Meifeng,2, LIU Jinchang,1

1. School of Automation, Beijing Information Science and Technology University, Beijing 100192

2. School of Automation Engineering, Xi’an Aeronautical Polytechnic Institute, Xi’an 710089

收稿日期: 2021-03-26   修回日期: 2021-11-10  

基金资助: * 国家自然科学基金.  51777012
北京市自然科学基金-教委联合.  KZ201911232045

Received: 2021-03-26   Revised: 2021-11-10  

作者简介 About authors

夏亮,男,1996年生,硕士研究生。主要研究方向为电能质量控制。E-mail： 932115152@qq.com

陈美锋,男,1992年生,硕士。主要研究方向为电能质量控制。E-mail： 953666784@qq.com

刘金昌,男,1996年生,硕士研究生。主要研究方向为电能质量控制。E-mail： 2250073040@qq.com

摘要

为改善统一电能质量调节器(Unified power quality conditioner, UPQC)的谐波补偿性能,基于UPQC的端口受控的耗散哈密顿(Port-controlled Hamiltonian with dissipation, PCHD)数学模型,利用该模型和UPQC的无源性,设计变阻尼无源控制器,电流内环采用变阻尼无源控制,电压外环采用变积分系数的非线性自抗扰-PI(Active disturbance rejection-proportional integral, ADR-PI)控制。与传统的PI恒阻尼无源控制策略相比,采用的变阻尼无源混合控制策略补偿后的负载电压和电网电流总谐波畸变率更低。最后,在Matlab/Simulink 仿真平台上搭建了TNPC-UPQC的变阻尼无源混合控制系统的仿真模型,对UPQC的谐波补偿性能进行了仿真研究。仿真结果表明,采用的变阻尼无源混合控制策略是可行的。

关键词： 统一电能质量调节器 ; PCHD模型 ; 变阻尼 ; 非线性自抗扰-PI控制 ; 无源控制

Abstract

In order to improve the compensation performance of unified power quality conditioner (UPQC) for harmonic, based on the port-controlled Hamiltonian with dissipation (PCHD) mathematical model of UPQC, a passivity-based with variable damping controller is designed by using the model and the passivity of UPQC, the inner current loop adopts variable damping passivity-based control, and the outer voltage loop adopts variable integral coefficient nonlinear active disturbance rejection-proportional integral (ADR-PI) control. Compared with the traditional PI constant damping passivity-based control strategy, the total harmonic distortion rate of load voltage and grid current compensated by the variable damping passivity-based hybrid control strategy is lower. Finally, the simulation model of the T-type neutral point clamped UPQC passivity-based with variable damping hybrid control system is built on the Matlab/Simulink simulation platform, and the compensation performance of harmonic of UPQC is simulated. The simulation results show that the passivity-based with variable damping hybrid control strategy is feasible.

Keywords： UPQC ; PCHD model ; variable damping ; nonlinear ADR-PI control ; passivity-based control

PDF (2495KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

夏亮, 王久和, 陈美锋, 刘金昌. 三电平UPQC的变阻尼无源混合控制策略*. 电气工程学报[J], 2021, 16(4): 127-134 doi:10.11985/2021.04.016

XIA Liang, WANG Jiuhe, CHEN Meifeng, LIU Jinchang. Passivity-based Hybrid Control Strategy with Variable Damping for Three Level UPQC. Journal of Electrical Engineering[J], 2021, 16(4): 127-134 doi:10.11985/2021.04.016

1 引言

近些年来,由于非线性电力电子负载和设备在工业和住宅中的使用日益广泛,电能质量问题已经成为导致电压和电流产生谐波的主要问题之一[1]。此外,各种网络故障和电容器组的切换也会产生电能质量问题,例如电压暂降/暂升、电压不平衡、电压中断、电流谐波、电流相位超前与滞后等。电能质量问题的提出由来已久,人们对电能质量的要求也越来越高,如何改善电能质量成为目前研究的热点问题之一。在电力系统中,一些设备的运行使得电网中电压和电流波形畸变严重,谐波水平不断上升。为改善配电网的电能质量,许多种类的调节器应运而生,包括无功补偿器、静止同步补偿器、动态电压恢复器、有源电力滤波器、统一电能质量调节器(Unified power quality conditioner, UPQC)等[2]。UPQC是一种用户电力装置,是解决这些电能质量问题的可行方案之一[3,4]。

UPQC由串联逆变器、并联逆变器等组合而成,其控制策略分为直接控制策略和间接控制策略,还可细分为无源控制、滑模控制、模糊控制等。无源控制策略属于间接控制策略中的非线性控制策略,它通过寻找与被控状态变量或由状态变量表征的被控量相关的能量存储函数,同时确定与系统期望平衡点相对应的能量存储函数,然后基于系统的模型和无源性设计相应的控制器,控制器结构简单、易于实现[5,6]。

文献[7]采用滑模PI控制策略,在一定程度上提高了直流电压控制的稳态精度和响应速度,但是控制参数过多,整定复杂。文献[8]采用模糊PI自适应控制方法,设计了相应的控制器,与PI控制相比,直流侧电压更稳定,但是控制系统的设计方法是凭经验进行,缺少理论依据,系统的稳定性不能保证。文献[9]介绍了一种基于极限环振荡器频率锁定环的无功功率补偿控制算法,并且采用了Jaya优化算法,优化后的值用于调整PI控制器的增益,改善了UPQC在负载不平衡、无功补偿等方面的补偿性能,但是采用的方法控制复杂、计算量大。文献[10]同样利用了Jaya算法实现PI参数的优化,特别的是设置了两个独立的目标函数分别对串联和并联逆变器进行控制,通过与传统粒子群优化、基于教学学习优化算法的固定PI增益优化方法作比较,证明了基于Jaya的自整定PI控制器的优越性,提高了光伏UPQC的性能,但是计算复杂,可能陷入局部最优。由于传统PI控制以不变的模式和参数来处理多变的动态过程,难以解决平稳性、快速性和准确性之间的矛盾,恒阻尼无源控制具有全局稳定性,无奇异点,但阻尼的注入值恒定不变,不能很好地处理稳态误差和电流畸变率之间的矛盾,因此本文将ADR-PI控制和变阻尼无源控制结合起来应用在UPQC中,仿真结果证实了与传统PI恒阻尼无源控制相比,所提控制方法在谐波补偿方面取得的控制效果更好。

2 T-NPC型UPQC的拓扑结构和PCHD数学模型

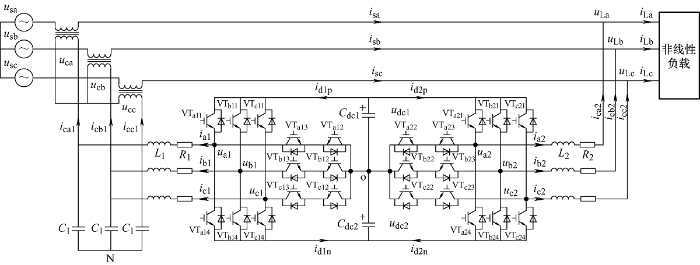
三电平UPQC的逆变器包括中点钳位(Neutral point clamped, NPC)型逆变器和T型中点钳位(T-type neutral point clamped, T-NPC)型逆变器。由于T-NPC型逆变器与NPC相比,损耗和体积更小、效率更高、成本更低[11],因此本文将T-NPC型三电平逆变器应用在UPQC的主电路中。TNPC-UPQC主电路主要包含串联环节、并联环节和直流储能环节。串联环节包含串联逆变器和变压器,接入电网与非线性负载之间,而并联环节主要由并联逆变器组成,接在负载侧,两者功能相对独立。一般将电容作为串联环节和并联环节共用的直流储能环节。UPQC的串联环节相当于受控电压源,补偿的是电网电压,最终使负载获得正弦交流电压;其并联环节相当于受控电流源,补偿的是负载电流,最终使电网获得正弦交流电流。TNPC-UPQC的电路拓扑结构如图1所示。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   T-NPC型UPQC的电路拓扑结构


无源控制器的设计可基于欧拉-拉格朗日(Euler-Lagrange, EL)模型和端口受控哈密顿(Port-controued Hamiltonian with dissipation, PCHD)模型,由于前者只能进行阻尼注入,而后者既能进行阻尼注入,又能进行能量成型,因此建立PCHD模型。无源控制器主要控制的是UPQC的交流电流,因此在三相静止abc坐标系下建立以交流电流为状态变量的PCHD数学模型。同时,假设UPQC的开关器件无损耗,电感和电容均为线性元件且电感磁路无饱和,可以得到

$\left\{ \begin{array}{l} {L_1}\frac{{{\rm{d}}{i_{a1}}}}{{dt}} + {R_1}{i_{a1}} - {u_{a1}} = - {u_{ca}}\\ {L_1}\frac{{{\rm{d}}{i_{b1}}}}{{dt}} + {R_1}{i_{b1}} - {u_{b1}} = - {u_{cb}}\\ {L_1}\frac{{{\rm{d}}{i_{c1}}}}{{dt}} + {R_1}{i_{c1}} - {u_{c1}} = - {u_{cc}}\\ {L_2}\frac{{{\rm{d}}{i_{a2}}}}{{dt}} + {R_2}{i_{a2}} - {u_{a2}} = - {u_{La}}\\ {L_2}\frac{{{\rm{d}}{i_{b2}}}}{{dt}} + {R_2}{i_{b2}} - {u_{b2}} = - {u_{Lb}}\\ {L_2}\frac{{{\rm{d}}{i_{c2}}}}{{dt}} + {R_2}{i_{c2}} - {u_{c2}} = - {u_{Lc}} \end{array} \right.$

为了简化分析,利用正交变换矩阵

${M_{abc/dq0}} = \sqrt {\frac{2}{3}} \left[ {\begin{array}{*{20}{c}}{\cos \omega t}&{\cos (\omega t - \frac{{2\pi }}{3})}&{\cos (\omega t + \frac{{2\pi }}{3})}\\{\sin \omega t}&{\sin (\omega t - \frac{{2\pi }}{3})}&{\sin (\omega t + \frac{{2\pi }}{3})}\\{\frac{1}{{\sqrt 2 }}}&{\frac{1}{{\sqrt 2 }}}&{\frac{1}{{\sqrt 2 }}}\end{array}} \right]$

将式(1)变换到两相同步旋转dq0坐标系下, 可得

$\left\{ \begin{array}{l}{L_1}\frac{{{\rm{d}}{i_{d1}}}}{{dt}} = \omega {L_1}{i_{q1}} - {R_1}{i_{d1}} + {u_{d1}} - {u_{cd}}\\{L_1}\frac{{{\rm{d}}{i_{q1}}}}{{dt}} = - \omega {L_1}{i_{d1}} - {R_1}{i_{q1}} + {u_{q1}} - {u_{cq}}\\{L_2}\frac{{{\rm{d}}{i_{d2}}}}{{dt}} = \omega {L_2}{i_{q2}} - {R_2}{i_{d2}} + {u_{d2}} - {u_{Ld}}\\{L_2}\frac{{{\rm{d}}{i_{q2}}}}{{dt}} = - \omega {L_2}{i_{d2}} - {R_2}{i_{q2}} + {u_{q2}} - {u_{Lq}}\end{array} \right.$

为简化计算,选择电感磁链为状态变量,即

$x = {\left[ {{x_1},{x_2},{x_3},{x_4}} \right]^T} = {\left[ {{L_1}{i_{d1}},{L_1}{i_{q1}},{L_2}{i_{d2}},{L_2}{i_{q2}}} \right]^T}$

设能量存储函数为

$H(x) = \frac{{x_1^2}}{{2{L_1}}} + \frac{{x_2^2}}{{2{L_1}}} + \frac{{x_3^2}}{{2{L_2}}} + \frac{{x_4^2}}{{2{L_2}}} = \frac{1}{2}{x^T}Dx$

式中,$D = diag\left\{ {\frac{1}{{{L_1}}},\frac{1}{{{L_1}}},\frac{1}{{{L_2}}},\frac{1}{{{L_2}}}} \right\}$,H(x)是哈密顿函数,为正定的能量函数。

根据式(3)可得PCHD模型为

$\dot x = (J - R)\frac{{\partial H(x)}}{{\partial x}} + u$

式中,J为互联反对称矩阵,即$J = - {J^T}$;R为半正定对称矩阵,是系统的耗散矩阵;u为系统的输 入,且

$J = \left[ {\begin{array}{*{20}{c}}0&{\omega {L_1}}&0&0\\{ - \omega {L_1}}&0&0&0\\0&0&0&{\omega {L_2}}\\0&0&{ - \omega {L_2}}&0\end{array}} \right] R = diag\left\{ {{R_1},{R_1},{R_2},{R_2}} \right\} u = \left[ {\begin{array}{*{20}{c}}{{u_{d1}} - {u_{cd}}}\\{{u_{q1}} - {u_{cq}}}\\{{u_{d2}} - {u_{Ld}}}\\{{u_{q2}} - {u_{Lq}}}\end{array}} \right]$

3 无源混合控制器的设计

3.1 无源控制器

由于不含有内部能量源,且满足无源性的定义,因此UPQC为无源系统,可采用阻尼注入设计无源控制器。无源控制器的设计如下。

系统的期望平衡点为

${x_r} = {\left[ {{x_{1r}},{x_{2r}},{x_{3r}},{x_{4r}}} \right]^T} = {\left[ {{L_1}{i_{d1r}},{L_1}{i_{q1r}},{L_2}{i_{d2r}},{L_2}{i_{q2r}}} \right]^T}$

根据UPQC所需的补偿电压ucar、ucbr、uccr (由电压补偿量检测电路给出),将其变换为ucdr、ucqr,最终得到id1r、iq1r、id2r、iq2r。

对于id1r、iq1r,有

$\left\{ \begin{array}{l}{C_1}\frac{{d{u_{ca}}}}{{dt}} = {i_{a1}} - {i_{ca1}}\\{C_1}\frac{{d{u_{cb}}}}{{dt}} = {i_{b1}} - {i_{cb1}}\\{C_1}\frac{{d{u_{cc}}}}{{dt}} = {i_{c1}} - {i_{cc1}}\end{array} \right.$

根据式(2),将其变换至dq0坐标系下,得到

$\left\{ \begin{array}{l}{i_{cd1}} = {i_{d1}} + \omega {C_1}{u_{cq}} - {C_1}\frac{{d{u_{cd}}}}{{dt}}\\{i_{cq1}} = {i_{q1}} - \omega {C_1}{u_{cd}} - {C_1}\frac{{d{u_{cq}}}}{{dt}}\end{array} \right.$

将式(9)中的电压项和电流项替换为期望补偿值,整理得

$\left\{ \begin{array}{l}{i_{d1r}} = {i_{cd1r}} - \omega {C_1}{u_{cqr}} + {C_1}\frac{{d{u_{cdr}}}}{{dt}}\\{i_{q1r}} = {i_{cq1r}} + \omega {C_1}{u_{cdr}} + {C_1}\frac{{d{u_{cqr}}}}{{dt}}\end{array} \right.$

对于id2r、iq2r,根据电流补偿电路给出的期望ica2r=ia2r、icb2r=ib2r、icc2r=ic2r,将其变换至dq0坐标系下可得id2r、iq2r。

采用互联和阻尼分配无源控制(Interconnection and damping assignment passivity-based control, IDA-PBC)设计方法Ⅱ[3],根据能量存储函数式(5),取成型后的能量存储函数为

${H_d}(x) = \frac{1}{2}{x_e}^TD{x_e}$

式中,${x_e} = x - {x_r}$,令阻尼注入矩阵Ra=diag{ra1, ra1, ra2, ra2},则Rd = R + Ra;为简化控制器的设计,取Ja = 0,则

$u = - \left[ {{R_a}Dx + (J - {R_d})D{x_r}} \right]$

根据式(12)可得

$\left\{ \begin{array}{l}{u_{d1}} = {u_{cd}} - {R_{a1}}{i_{d1}} - \omega {L_1}{i_{q1r}} + ({R_1} + {R_{a1}}){i_{d1r}}\\{u_{q1}} = {u_{cq}} - {R_{a1}}{i_{q1}} + \omega {L_1}{i_{d1r}} + ({R_1} + {R_{a1}}){i_{q1r}}\\{u_{d2}} = {u_{Ld}} - {R_{a2}}{i_{d2}} - \omega {L_2}{i_{q2r}} + ({R_2} + {R_{a2}}){i_{d2r}}\\{u_{q2}} = {u_{Lq}} - {R_{a2}}{i_{q2}} + \omega {L_2}{i_{d2r}} + ({R_2} + {R_{a2}}){i_{q2r}}\end{array} \right.$

式(13)虽然不是开关函数,但是可作为逆变器输出电压在d、q轴上的分量,因为ud1=Sd1×udc,uq1=Sq1×udc,ud2=Sd2×udc,uq2=Sq2×udc,可由此获得SVPWM调制模块的输入信号。其中,式(13)前两项为串联逆变器的控制律,后两项为并联逆变器的控制律。

3.2 电压外环的控制

通常情况下,UPQC的电压外环采用PI控制,但PI控制难于保证控制系统具有较好的动态性能以及大范围工作的稳定性[12]。因此,需要对PI控制进行改进,电压外环采用自抗扰比例积分控制策略,采用这种控制策略可使系统动态性能变好。本文采用变积分系数非线性ADR-PI控制器,其积分系数随误差大小而变。控制器的表达式如下

$\left\{ \begin{array}{l}\Delta {u_{dc}} = {u_{dcr}} - {u_{dc}}\\\dot \eta = \Delta {u_{dc}}\\\Delta {i_d} = {k_p}\Delta {u_{dc}} + fal(\Delta {u_{dc}},\alpha,\delta ){k_i}\eta \end{array} \right.$

式中,Δudc为电压跟踪误差;η为其积分信号;udcr为直流侧期望电压;udc为直流侧实际电压;Δid为控制器的输出;kp为控制器的比例系数。非线性误差反馈函数fal(Δudc, α, δ)与ki的乘积构成随电压 跟踪误差大小可变的积分系数,fal(Δudc, α, δ)的表达式为

$fal(\Delta {u_{dc}},\alpha,\delta ) = \left\{ \begin{array}{l}\frac{{\Delta {u_{dc}}}}{{{\delta ^{1 - \alpha }}}}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left| {\Delta {u_{dc}}} \right| \le \delta \\{\left| {\Delta {u_{dc}}} \right|^\alpha }{\mathop{\rm sgn}} (\Delta {u_{dc}})\;\;\;\;\left| {\Delta {u_{dc}}} \right| > \delta \end{array} \right.$

式中,α为非线性函数的可调参数;δ为滤波因子,表示fal函数线性段的长度,是用来界定大、小误差的;sgn(·)为符号函数。一般取α<1,此时非线性函数fal(Δudc, α, δ)体现出“小误差,大增益;大误差,小增益”。参数α和δ的取值可参考文献[12]。

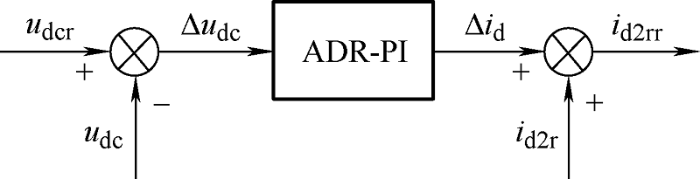
考虑到直流电压udc受id2r的控制,同时为了节约成本、简化控制,对UPQC中的并联逆变器进行适当的控制来调节直流侧母线电压。将电压跟踪误差Δudc输送到ADR-PI控制器中并输出电流修正信号Δid,将该信号与id2r叠加,即可得到新的补偿电流期望值id2rr。${u_{dc}} > \sqrt 6 {u_{Lr}}$,uLr为期望负载相电压的有效值,udcr的值应在仿真前设定。直流电压控制方案如图2所示。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   id2rr的获得


3.3 电流内环的控制

UPQC的电流内环采用变阻尼无源控制策略。阻尼注入参数的取值影响控制器的性能,若阻尼注入过小,稳态误差大,稳定性能较差;若阻尼注入过大,稳态误差小,稳定性能好,但电流畸变率过大[13]。采用二阶跟踪微分器(Second order tracking differentiator, SOTD)可以实现变阻尼的注入,变阻尼注入是在系统启动开始时加入较大阻尼,加快系统反应速度;当快接近稳定平衡点时,加入较小的阻尼,使得在平衡点处稳定性能好[14]。本文采用非线性饱和函数sinsgn构成二阶跟踪微分器：输入s(t),输出x1和x2,其中x1跟踪s(t),从而x2作为s(t)的“近似微分”。

二阶跟踪微分器的方程为

$\left\{ \begin{array}{l}{{\dot x}_1} = {x_2}\\{{\dot x}_2} = - \beta {\sin _{{\mathop{\rm sgn}} }}({x_1} - s(t) + \frac{{{x_2}\left| {{x_2}} \right|}}{{2\beta }},\varepsilon )\end{array} \right.$
${\sin _{{\mathop{\rm sgn}} }}(A,\varepsilon ) = \left\{ {\begin{array}{*{20}{c}}{\sin \frac{{\pi A}}{{2\varepsilon }}\;\;}&{\left| A \right| \le \varepsilon \;\;\;\;\varepsilon > 0}\\{{\mathop{\rm sgn}} (A)\;}&{\left| A \right| > \varepsilon \;\;\;\;\;\;\;\;\;\;\;}\end{array}} \right.$

式中,$A = {x_1} - s(t) + \frac{{{x_2}\left| {{x_2}} \right|}}{{2\beta }}$,参数β和ε的取值可参考文献[6]。

为实现变阻尼注入,可以把跟踪微分器的输出倒用,则阻尼注入值由式(16)和式(17)确定

$y = {n_1} - ({n_1} - {n_2}){x_1}$

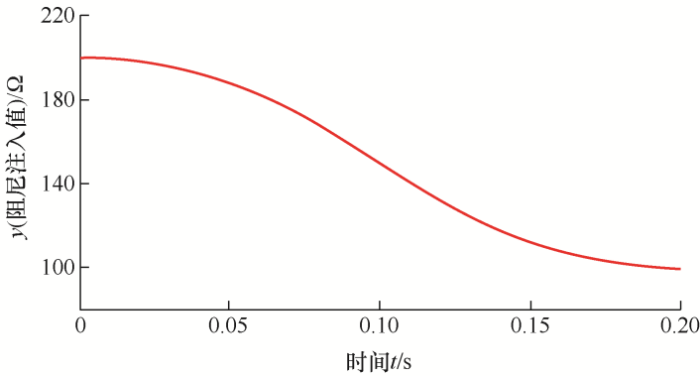
式中,n1是启动开始时希望加入的较大阻尼值;n2是接近稳态时希望加入的较小阻尼值,即n1>n2>0;y为阻尼输出,其输出值作为式(13)中的阻尼注入rak(k=1, 2)。ra1为串联逆变器的注入阻尼,ra2为并联逆变器的注入阻尼。令n1=200,n2=100,SOTD的输入信号s(t)设置为初值为1,终值为0的单位阶跃信号,则阻尼注入值的变化图如图3所示。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   阻尼注入值变化图


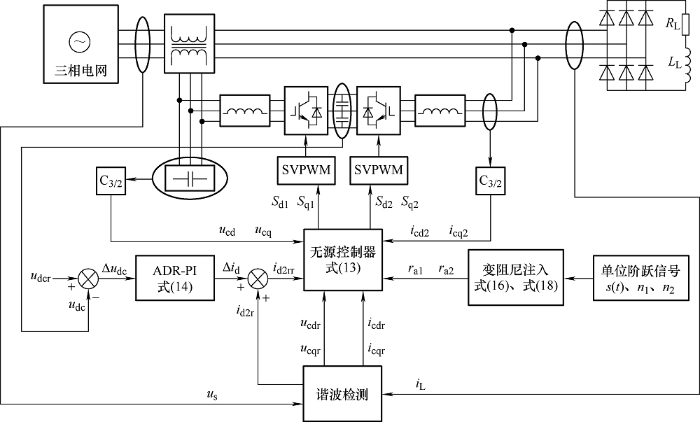
本文TNPC-UPQC的变阻尼无源混合控制原理如图4所示。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   变阻尼无源混合控制原理图


4 仿真结果

为验证本文所设计的变阻尼无源混合控制器的可行性,在Matlab/Simulink仿真平台上搭建仿真模型并进行仿真分析。常用的补偿量检测方法有自适应检测方法、基于小波变换的检测方法、基于瞬时无功功率理论的检测方法等。本文采用文献[15]中的基于电网工频时钟的dq0检测法对电网电压和负载电流进行检测,这种方法通过外加与电网工频同步的时钟和正余弦发生器,获得dq0变换矩阵所需的正余弦信号,并设置其与相电压同步旋转,代替了锁相环,避免了因其引起的检测误差。

电网电压为三相工频交流电压,非线性负载为三相二极管全桥整流电路,直流侧电压udcr的值设置为800 V,在0~0.2 s向电网中注入幅值为基波幅值10%的五次谐波和5%的七次谐波,用来模拟被谐波污染的电网。对于仿真模型进行时长0.2 s的仿真,仿真参数如表1所示。

表1   仿真参数

参数数值
串联侧电容C1/μF6.8
电感L1/mH0.5
内阻R1/Ω0.01
kp10.5
ki10.5
并联侧电感L2/mH1
内阻R2/Ω0.2
kp21
ki20.1
负载侧电阻RL/Ω10
电感LL/mH5
ADR-PIα0.5
δ0.1
SOTDβ100
ε0.001
n1200
n2100

新窗口打开| 下载CSV


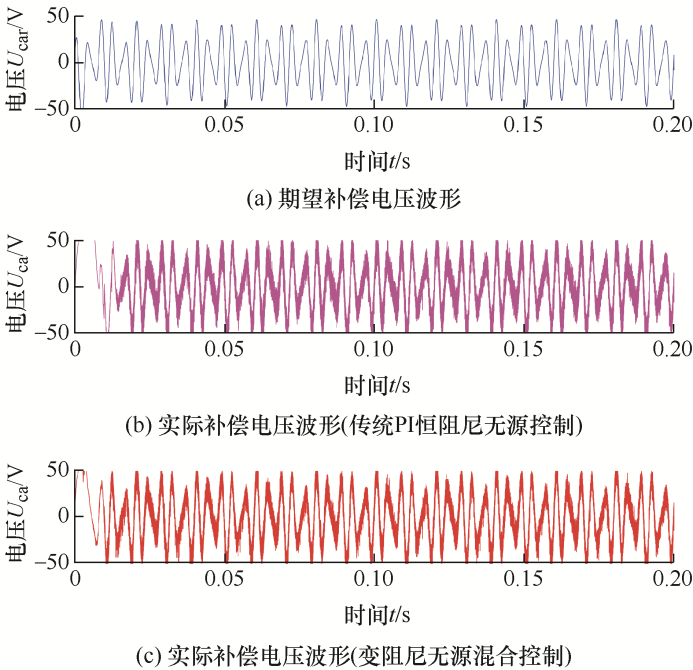
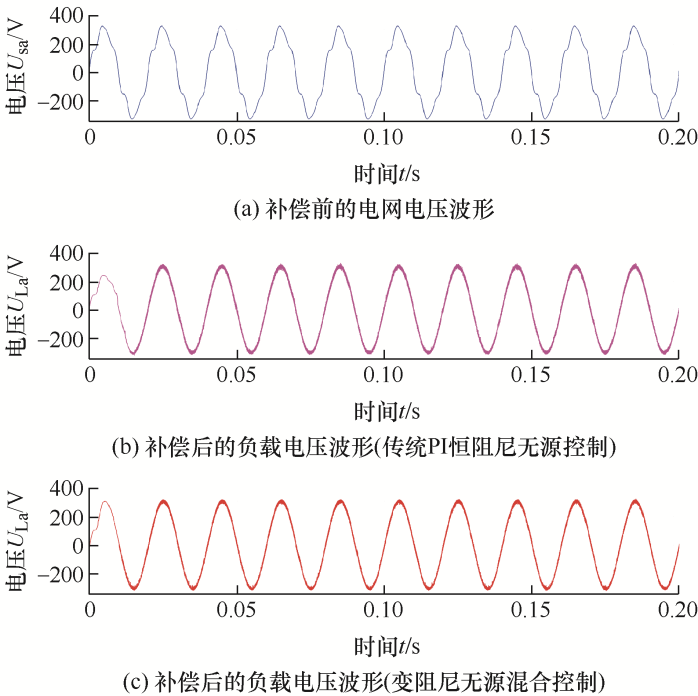
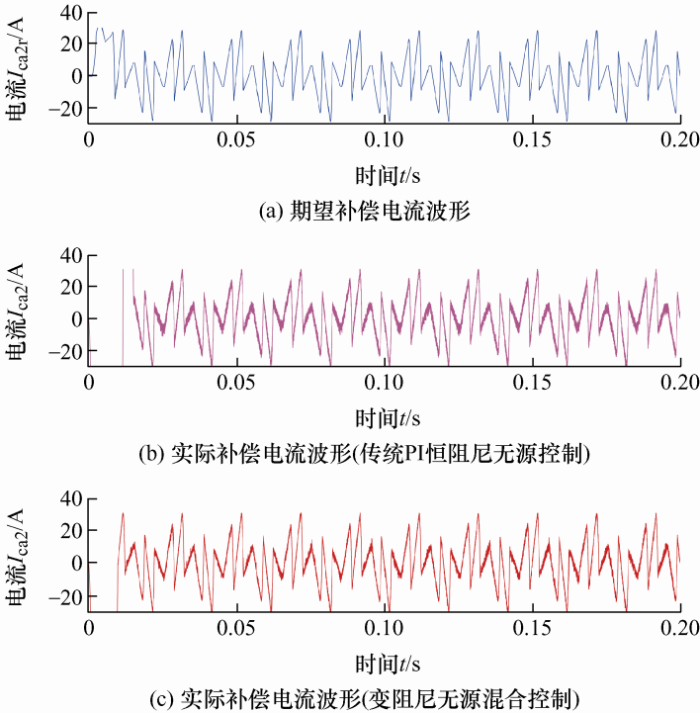
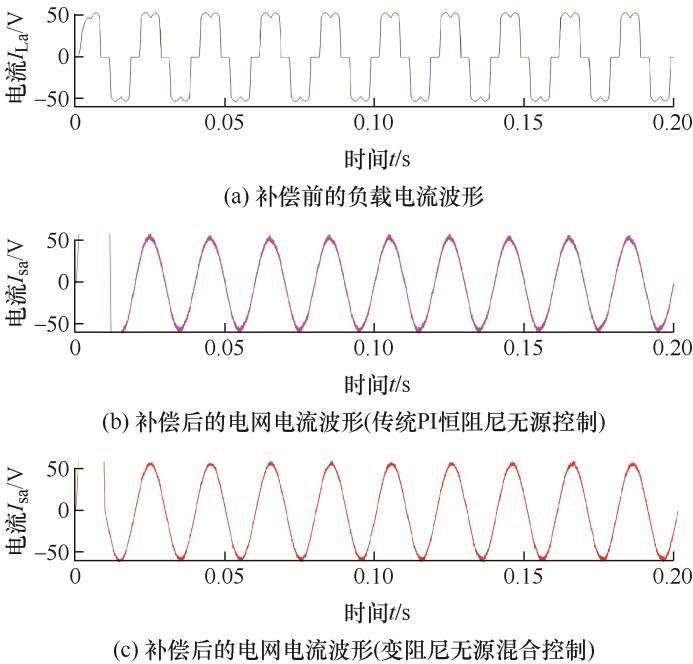
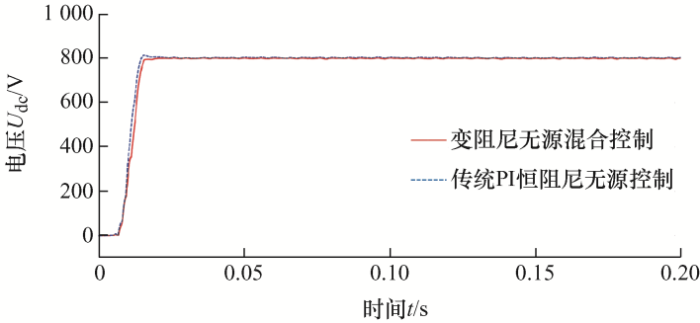
由于系统三相对称,仅给出A相的仿真结果。图5a~5c由上至下分别为A相期望补偿电压、实际补偿电压波形(传统PI恒阻尼无源控制)和实际补偿电压波形(变阻尼无源混合控制);图6a~6c由上至下分别为补偿前电网侧A相电压波形、补偿后负载A相电压波形(传统PI恒阻尼无源控制)、补偿后负载侧A相电压波形(变阻尼无源混合控制);图7a~7c由上至下分别为A相期望补偿电流、实际补偿电流波形(传统PI恒阻尼无源控制)和实际补偿电流波形(变阻尼无源混合控制);图8a~8c由上至下分别为补偿前负载侧A相电流波形、补偿后电网侧A相电流波形(传统PI恒阻尼无源控制)、补偿后电网侧A相电流波形(变阻尼无源混合控制);图9为两种控制方法下的直流侧电容电压波形对比。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5   A相期望补偿电压和实际补偿电压波形


图6

新窗口打开| 下载原图ZIP| 生成PPT

图6   A相补偿前的电网电压和补偿后的负载电压波形


图7

新窗口打开| 下载原图ZIP| 生成PPT

图7   A相期望补偿电流和实际补偿电流波形


图8

新窗口打开| 下载原图ZIP| 生成PPT

图8   A相补偿前的负载电流和补偿后的电网电流波形


图9

新窗口打开| 下载原图ZIP| 生成PPT

图9   两种控制方法下的直流侧电容电压波形对比


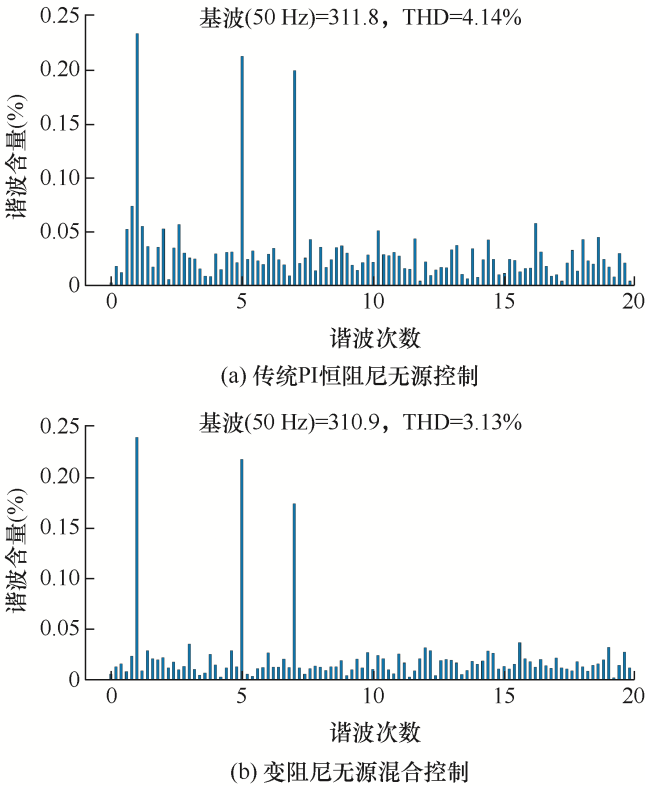
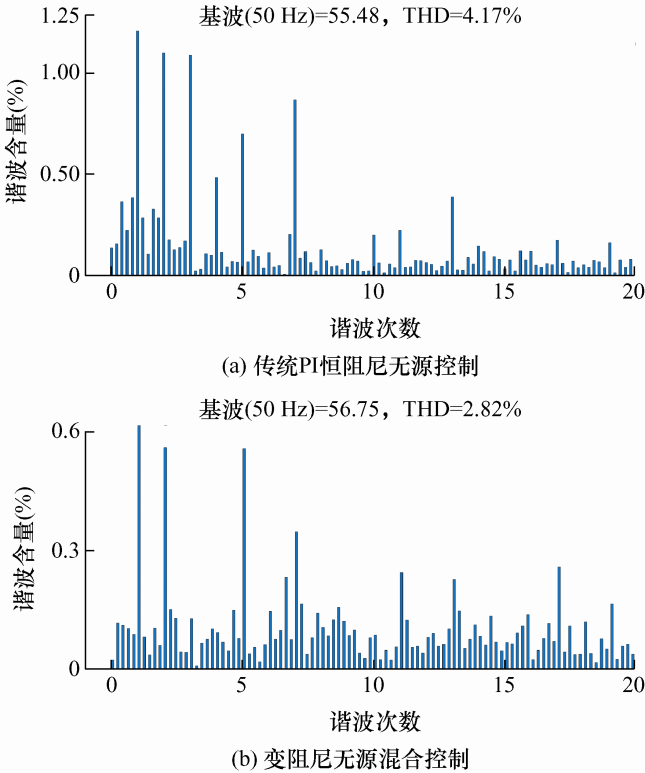
对以上结果进行谐波分析,采用传统PI恒阻尼无源控制和本文的控制方法补偿后的负载电压THD分别如图10a、10b所示,而采用传统PI恒阻尼无源控制和本文的控制方法补偿后的电网电流THD分别如图11a、11b所示。

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10   补偿后的负载电压THD波形图


图11

新窗口打开| 下载原图ZIP| 生成PPT

图11   补偿后的电网电流THD波形图


根据以上仿真结果可以看出,与传统PI恒阻尼无源控制方法相比,本文采用方法补偿后的负载电压和电网电流的波形更加接近期望波形。另外,当采用传统PI恒阻尼无源控制方法时,负载侧A相电压THD为4.14%,而采用本文方法时,相应的THD为3.13%;当采用传统PI恒阻尼无源控制方法时,电网侧A相电流THD为4.17%,而采用本文方法时,相应的THD为2.82%。因此,本文采用的控制策略对于负载电压和电网电流的谐波补偿效果好于传统PI恒阻尼无源控制。

5 结论

本文基于UPQC的无源性,建立了TNPC-UPQC的PCHD模型,设计了变阻尼无源控制器,并且在Matlab/Simulink仿真平台上搭建了TNPC-UPQC的变阻尼无源混合控制系统的仿真模型,对TNPC-UPQC的谐波补偿性能进行了仿真研究。由仿真结果得出以下结论。

(1) 与传统PI恒阻尼无源控制相比,采用本文的控制策略,当电网电压包含谐波时,负载侧电压波形接近正弦波。

(2) 对于非线性负载注入电网的谐波电流,补偿之后,电网侧的电流也接近正弦波。

仿真结果表明本文采用的变阻尼无源混合控制策略是可行的,并且补偿效果好于传统PI恒阻尼无源控制。

参考文献

肖湘宁. 电能质量分析与控制[M]. 北京: 中国电力出版社, 2016.

[本文引用: 1]

XIAO Xiangning. Power quality analysis and control[M]. Beijing: China Electric Power Press, 2016.

[本文引用: 1]

李勋.

统一电能质量调节器(UPQC)的分析与控制

[D]. 武汉:华中科技大学, 2006.

[本文引用: 1]

LI Xun.

Analysis and control of UPQC

[D]. Wuhan:Huazhong University of Science and Technology, 2006.

[本文引用: 1]

王久和. 统一电能质量调节器及其无源控制[M]. 北京: 机械工业出版社, 2018.

[本文引用: 2]

WANG Jiuhe. Unified power quality conditioner and its passivity-based control[M]. Beijing: China Machine Press, 2018.

[本文引用: 2]

倪福银, 李正明.

统一电能质量调节器的研究发展综述

[J]. 电力系统保护与控制, 2020, 48(20):177-187.

[本文引用: 1]

NI Fuyin, LI Zhengming.

Review of research and development of unified power quality conditioner

[J]. Power System Protection and Control, 2020, 48(20):177-187.

[本文引用: 1]

王久和. 无源控制理论及其应用[M]. 北京: 电子工业出版社, 2010.

[本文引用: 1]

WANG Jiuhe. Passivity-based control theory and its application[M]. Beijing: Electronic Industry Press, 2010.

[本文引用: 1]

王久和. 先进非线性控制理论及其应用[M]. 北京: 科学出版社, 2012.

[本文引用: 2]

WANG Jiuhe. Advanced nonlinear control theory and its application[M]. Beijing: Science Press, 2012.

[本文引用: 2]

李兰芳, 徐晓刚, 吴国兵, 等.

并联型APF直流侧电压的滑模PI控制策略研究

[J]. 电力系统保护与控制, 2017, 45(5):32-37.

[本文引用: 1]

LI Lanfang, XU Xiaogang, WU Guobing, et al.

Study on sliding mode PI control strategy of DC-link voltage of shunt active power filter

[J]. Power System Protection and Control, 2017, 45(5):32-37.

[本文引用: 1]

李少波, 陈寅龙, 孙采鹰.

有源电力滤波器直流侧电压模糊PI自适应控制

[J]. 电工技术, 2018(18):69-72.

[本文引用: 1]

LI Shaobo, CHEN Yinlong, SUN Caiying.

Fuzzy PI adaptive control for DC voltage of active power filter

[J]. Electric Engineering, 2018(18):69-72.

[本文引用: 1]

ARYA S R, ALAM S J, RAY P.

Control algorithm based on limit cycle oscillator-FLL for UPQC-S with optimized PI gains

[J]. CSEE Journal of Power and Energy Systems, 2020, 6(3):649-661.

[本文引用: 1]

DASH S K, RAY P K.

Power quality improvement utilizing PV fed unified power quality conditioner based on UV-PI and PR-R controller

[J]. CPSS Transactions on Power Electronics and Applications, 2018, 3(3):243-253.

DOI:10.24295/CPSSTPEA      URL     [本文引用: 1]

郑成才, 王久和, 慕小斌.

PCHD模型的TNPC-UPQC无源混合控制

[J]. 辽宁工程技术大学学报, 2018, 37(1):179-185.

[本文引用: 1]

ZHENG Chengcai, WANG Jiuhe, MU Xiaobin.

TNPC-UPQC passivity-based hybrid control of PCHD model

[J]. Journal of Liaoning Technical University, 2018, 37(1):179-185.

[本文引用: 1]

张晓华, 郭源博, 周鑫, 等.

PWM整流器的欠驱动特性与非线性控制

[J]. 中国电机工程学报, 2011, 31(33):85-92.

[本文引用: 2]

ZHANG Xiaohua, GUO Yuanbo, ZHOU Xin, et al.

Underactuated characteristics and nonlinear control of PWM rectifier

[J]. Proceedings of the CSEE, 2011, 31(33):85-92.

[本文引用: 2]

夏培容, 尹怡欣, 王久和, 等.

基于变阻尼的电压型PWM整流器无源控制研究

[J]. 北京信息科技大学学报, 2009, 24(4):30-34.

[本文引用: 1]

XIA Peirong, YIN Yixin, WANG Jiuhe, et al.

Research on passivity-based control of voltage source PWM rectifier based on variable damping

[J]. Journal of Beijing Information Science and Technology University, 2009, 24(4):30-34.

[本文引用: 1]

尹忠刚, 丁虎晨, 钟彦儒, 等.

基于PCHD模型的感应电机变阻尼无源性控制策略

[J]. 电工技术学报, 2014, 29(8):70-80.

[本文引用: 1]

YIN Zhonggang, DING Huchen, ZHONG Yanru, et al.

Variable damping passivity-based control strategy of induction motor based on PCHD model

[J]. Transactions of China Electrotechnical Society, 2014, 29(8):70-80.

[本文引用: 1]

ZHENG Chengcai, WANG Jiuhe.

The method of harmonic compensation of UPQC based on Euler-Lagrange model

[C]// 2016 IEEE 8th International Power Electronics and Motion Control Conference (IPEMC-ECCE Asia),Hefei,China,22-26 May 2016,IEEE Conference Publications, 2016:142-146.

[本文引用: 1]

/

〈 〉