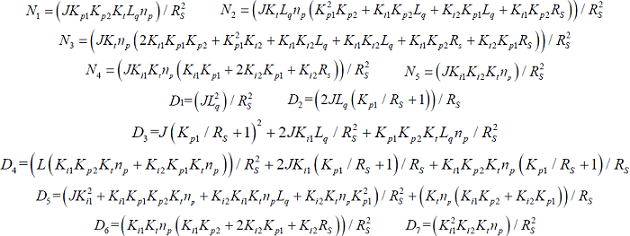电气工程学报, 2021, 16(4): 120-126 doi: 10.11985/2021.04.015

特邀专栏：高性能永磁电机驱动与控制

基于高频方波电压注入法和改进龙伯格观测器的永磁同步电机转速估计的研究*

巫庆辉,1, 黄成鑫,1, 侯元祥,2

1.辽宁工程技术大学电气与控制工程学院 葫芦岛 125105

2.渤海大学工学院 锦州 121013

Sensorless FOC of PMSM Based on High Frequency Square-wave Voltage Injection and Improved Luenberger Position Observer

WU Qinghui,1, HUANG Chengxin,1, HOU Yuanxiang,2

1. Faculty of Electrical and Control Engineering, Liaoning Technical University, Huludao 125105

2. College of Engineering, Bohai University, Jinzhou 121013

收稿日期: 2021-07-5   修回日期: 2021-10-30  

基金资助: * 辽宁省教育厅重点攻关资助项目.  LZ2020001

Received: 2021-07-5   Revised: 2021-10-30  

作者简介 About authors

巫庆辉,男,1974年生,博士,教授。主要研究方向为电力电子与电力传动。E-mail： qinghuiwu@qq.com

黄成鑫,男,1998年生,硕士研究生。主要研究方向为电力电子与电力传动。E-mail： 1204391187@qq.com

侯元祥,男,1995年生,硕士研究生。主要研究方向为电力电子与电力传动。E-mail： 1451582076@qq.com

摘要

针对传统矢量控制方法难以获得精确的转子位置和转速的问题,提出一种基于高频方波注入法和改进龙伯格观测器的永磁同步电机的转速研究方法。因高阶系统稳定性较差,微机控制难度较高,并且由于高阶的传递函数中参数对电机参数和控制器参数的依赖性较大,因此很难对于永磁同步电机具有通用的控制性能。为解决上述问题,将龙伯格观测器中的电磁转矩前馈项替换为一个由速度指令组成的二阶系统,并用最小二乘法得到该二阶系统。仿真结果表明,改进方案在负载扰动下具有更好的跟踪精度和鲁棒性。

关键词： 永磁同步电机 ; 无传感器控制 ; 方波电压注入法 ; 龙伯格观测器 ; 最小二乘法

Abstract

Aiming at the problem that the traditional vector control method is difficult to obtain accurate rotor position and speed, a speed research method of permanent magnet synchronous motor based on high frequency square wave injection method and improved Luenberger observer is proposed. Because of the poor stability of the high-order system, the microcomputer control is difficult. Besides, the parameters in the high-order transfer function are highly dependent on the motor parameters and controller parameters, it is difficult to have general control performance for permanent magnet synchronous motor. In order to solve these problems, the electromagnetic torque feedforward term in the Luenberger observer is replaced by a second-order system composed of speed commands, and the second-order system is obtained by the least square method. Simulation results show that the improved scheme has better tracking accuracy and robustness under load disturbance.

Keywords： PMSM ; sensorless control ; square-wave voltage ; Luenberger observer ; least square method

PDF (661KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

巫庆辉, 黄成鑫, 侯元祥. 基于高频方波电压注入法和改进龙伯格观测器的永磁同步电机转速估计的研究*. 电气工程学报[J], 2021, 16(4): 120-126 doi:10.11985/2021.04.015

WU Qinghui, HUANG Chengxin, HOU Yuanxiang. Sensorless FOC of PMSM Based on High Frequency Square-wave Voltage Injection and Improved Luenberger Position Observer. Journal of Electrical Engineering[J], 2021, 16(4): 120-126 doi:10.11985/2021.04.015

1 引言

永磁同步电动机(Permanent magnet synchronous motor,PMSM)由于其高效率、高功率密度和无直流磁场等优点,近年来被广泛应用于交流传动领域[1]。特别是随着高精度伺服控制和电动汽车领域的高速发展,对永磁同步电机的磁场定向控制提出了更高的要求。矢量控制的核心是如何获得精确的转子位置和转速。目前已有许多无传感器技术用于估计转子的位置和速度。

多年前,基于高频正弦信号注入的无位置传感器控制方法开辟了永磁同步电机无位置传感器控制的新领域[2,3,4]。在零频或低频情况下,转子的位置可以通过注入旋转高频电压或脉动高频电压,并使用跟踪算法或外差法获得[5]。但是当采用旋转或脉动的高频电压注入方法时,需要使用低通滤波器(Low pass filter, LPF)If来获得误差信号,这些低通滤波器由于其固有的时延而降低了无位置传感器的控制性能[6]。近十年来,基于方波信号注入的方法得到了发展,该方法不需要LPFs,而是通常使用一个龙伯格位置观测器来收敛估计误差,将电流控制器的带宽提高到250 Hz,速度控制器的带宽提高到50 Hz[7]。通常,龙伯格位置观测器采用电磁转矩前馈来提高转子位置跟踪性能。通过仿真试验,研究发现观测器的稳定性取决于负载转矩的预测精度,当负载扰动频繁变化时,传统的方法无法快速跟踪转子位置[8]。

基于以上研究成果和存在的问题,本文对龙伯格位置观测器进行了改进。首先,分析了永磁同步电机的矢量控制和方波高频电压注入法的原理[9];然后,利用矢量控制中的速度指令构造了一个新的二阶系统。作为一个新的前馈控制参数,前馈项不再受负载的影响。仿真结果表明,改进的转子位置观测器在负载扰动下具有较好的性能。

2 永磁同步电机矢量控制系统

矢量控制(Field-oriented control,FOC)采用空间矢量表示定子电流。它将三相定子电流(A, B, C)转换为两相时变系统(α, β)。从该时变系统通过旋转变换得到一个双坐标时不变系统(d, q)。这两个组成部分相互垂直,相互独立。这样,它们可以分开调节,类似于直流电机的双闭环控制系统。

永磁同步电机在电源频率和实际转子坐标系(d-q坐标系)下的电压方程的矩阵形式为

$\left[ {\begin{array}{*{20}{c}} {ud}\\ {uq} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{R_S}}&{ - \omega rLq}\\ {\omega rLd}&{{R_S}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {id}\\ {iq} \end{array}} \right] + \frac{d}{{dt}}\left[ {\begin{array}{*{20}{c}} {Ld}&0\\ 0&{Lq} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {id}\\ {iq} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} 0\\ {\omega r{\psi _f}} \end{array}} \right]$

式中,${u_d}$和${u_q}$为d-q轴电压;$id$和$iq$为d-q轴电流;$Ld$和$Lq$为d-q轴电感;RS为定子电阻;$\omega r$为转子电角速度;${\psi _f}$为永磁体磁通[10,11]。由此可得电磁 转矩

$Te{\rm{ = }}np\left[ {iq{\psi _f} + \left( {Ld - Lq} \right)idiq} \right]$

忽略阻尼力矩和扭转弹性力矩,力学方程为

$\frac{{np}}{J}\frac{{d\left( {np\omega r} \right)}}{{dt}} = Te - TL$

式中,$Te$为电磁转矩;$TL$为负载转矩;$np$为磁极对数;J为转子转动惯量[12,13]。

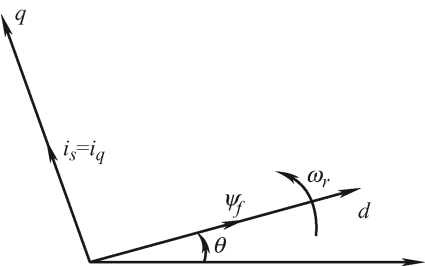
由式(1)、式(2)可知,电磁转矩依赖于直轴电流id和交轴电流iq[10]。对于表面式永磁同步电机(Surface permanent magnet synchronous motor, SPMSM),因为$Ld$和$Lq$相等,$Te$只与iq有关。FOC通常采用最大转矩电流比(Maximum torque per ampere,MTPA)控制方法($id = 0$)。因此,定子电流is为全转矩电流。矢量图如图1所示。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   最大转矩电流比控制矢量图


实现矢量控制最主要是要得到转子电角度$\theta$与机械转速ωm,在具有编码器的应用场景中,可直接通过编码器得到,对于无传感器的系统,通常需要利用电机的电流以及反电势信息,采用观测器的方法进行位置估算。

3 高频方波注入法原理

一般情况下,高频注入信号的频率远高于电机运行的基频[14],幅值较低。因此,当将方波电压注入估计转子参考系d-q轴时,感应高频电流与电压的关系可以描述为

$\frac{d}{{dt}}\left[ {\begin{array}{*{20}{c}}{id}\\{iq}\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}{1/Ld}&0\\0&{1/Lq}\end{array}} \right]\left[ {\begin{array}{*{20}{c}}{ud}\\{uq}\end{array}} \right]$

因此,感应高频电流可以推导如下

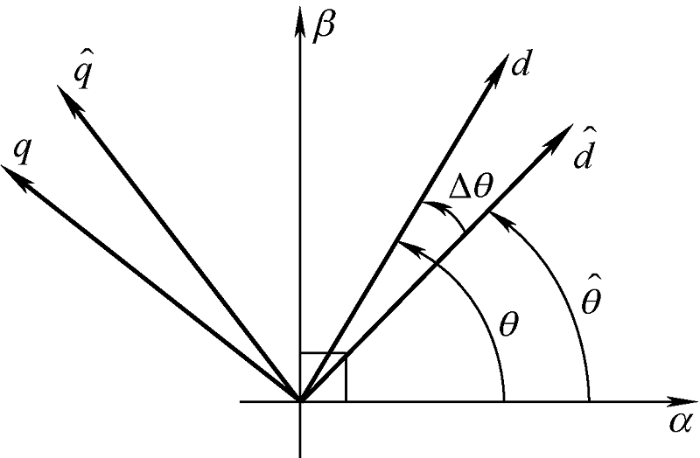
$\frac{d}{{dt}}\left[ {\begin{array}{*{20}{c}} {{i_d}}\\ {{i_q}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {1/{L_d}}&0\\ 0&{1/{L_q}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\cos \Delta \theta }&{\sin \Delta \theta }\\ { - \sin \Delta \theta }&{\cos \Delta \theta } \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {u_d^'}\\ {u_q^'} \end{array}} \right]$

式中,$u_d^'$和$u_q^'$为向估计$\mathord{\buildrel{\lower3pt\hbox{$^$}} \over d} - \mathord{\buildrel{\lower3pt\hbox{$^$}} \over q}$坐标系注入的高频电压;Δθ为估计转子参考系与实际转子参考系的角度差$\left( {\Delta \theta = \mathord{\buildrel{\lower3pt\hbox{$^$}} \over \theta } - \theta } \right)$,如图2所示。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   转子参考系和估计转子参考系电压平面


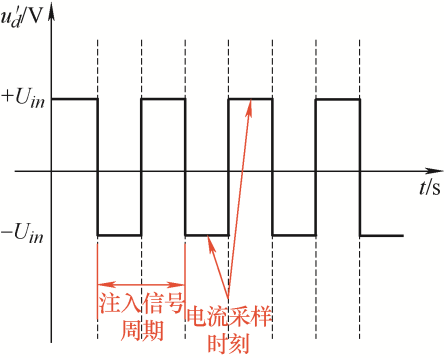
为了不影响电机的输出转矩,高频信号通常只注入估计的d轴。方波型注入电压示意图如图3所示,其中$Uin$为注入电压幅值。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   方波注入信号示意图


当转子位置的估计误差$\left( {\Delta \theta = \mathord{\buildrel{\lower3pt\hbox{$^$}} \over \theta } - \theta } \right)$足够小时,式(5)变化为

$\frac{d}{{dt}}\left[ {\begin{array}{*{20}{c}} {{i_d}}\\ {iq} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {1/{L_d}}&0\\ 0&{1/{L_q}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} { \pm {U_{in}}}\\ 0 \end{array}} \right]$

在两相时变系统(α, β)中对电流进行采样,式(6)通过反派克变换为

$\frac{d}{{dt}}\left[ {\begin{array}{*{20}{c}} {i\alpha }\\ {i\beta } \end{array}} \right] = \frac{{ \pm Uin}}{{Ld}}\left[{\begin{array}{*{20}{c}} {\cos \mathord{\buildrel{\lower3pt\hbox{^}} \over \theta } }\\ {\sin \mathord{\buildrel{\lower3pt\hbox{^}} \over \theta } } \end{array}} \right]$

为便于微机控制,采样周期设为T。这里“$\Delta i\alpha,\Delta i\beta$”表示采样瞬间的当前值与之前值的差值,可以表示为

$\left[ {\begin{array}{*{20}{c}} {\Delta i\alpha }\\ {\Delta i\beta } \end{array}} \right]{\rm{ = }}\frac{{ \pm {U_{in}}}}{{Ld}}\left[ {\begin{array}{*{20}{c}} {\cos \mathord{\buildrel{\lower3pt\hbox{^}} \over \theta } }\\ {\sin \mathord{\buildrel{\lower3pt\hbox{^}} \over \theta } } \end{array}} \right]$

因此,转子位置可以通过atan2函数得到

$\mathord{\buildrel{\lower3pt\hbox{^}} \over \theta } {\rm{ = atan}}2\left( {\Delta i\alpha,\Delta i\beta } \right)$

由式(8)可以看出,采样周期越短,得到的角度$\mathord{\buildrel{\lower3pt\hbox{^}} \over \theta}$越接近真实值。需要注意的是,式(4)~(9)的推导是基于高频信号的,因此,在实际应用中,需要通过高通/带通滤波器获得α-β轴上的高频电流分量。由于滤波器产生的采样噪声和高频噪声放大效应,式(9)得到的角度$\mathord{\buildrel{\lower3pt\hbox{^}} \over \theta}$不能直接用于FOC,通常需要设计一个位置观测器。

4 龙伯格位置观测器的设计与改进

龙伯格观测器属于全状态观测器,通过输出y和输入u实现对系统状态的观测。永磁同步电机的力学方程如式(3)所示,其状态空间方程式为

$\left\{ \begin{array}{l} \left[ {\begin{array}{*{20}{c}} {\theta '}\\ {{{\omega '}_m}} \end{array}} \right]{\rm{ = }}\left[ {\begin{array}{*{20}{c}} 0&{np}\\ 0&0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} \theta \\ {\omega m} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} 0\\ {\frac{1}{J}} \end{array}} \right]Te - \left[ {\begin{array}{*{20}{c}} 0\\ {\frac{1}{J}} \end{array}} \right]TL\\ y = \left[ {\begin{array}{*{20}{c}} 1&0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} \theta \\ {\omega m} \end{array}} \right] \end{array} \right.$

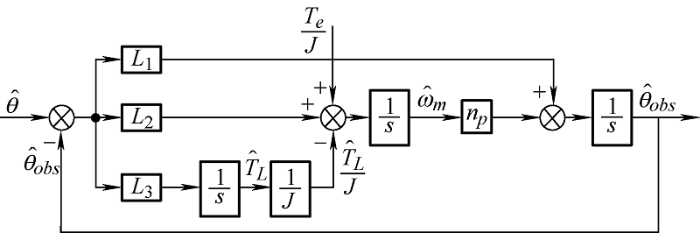
由于负载转矩TL不可测量,为了提高观测器的稳态性能,增加积分环节对TL进行估计,最终使观测器的角度误差趋于零。龙伯格观测器可以设计 如下

$\left\{ \begin{array}{l} \left[ {\begin{array}{*{20}{c}} {{{\hat \theta '}_{obs}}}\\ {{{\hat \omega '}_m}}\\ {{{\hat T'}_L}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {0{\rm{ }}{n_p}{\rm{ }}0}\\ {0{\rm{ }}0{\rm{ }} - \frac{1}{J}}\\ {0{\rm{ }}0{\rm{ }}0} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\hat \theta }\\ {{{\hat \omega }_m}}\\ {{{\hat T}_L}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} 0\\ {\frac{1}{J}}\\ 0 \end{array}} \right]{T_e} + \left[ {\begin{array}{*{20}{c}} {{L_1}}\\ {{L_2}}\\ {{L_3}} \end{array}} \right]\left( {\hat \theta - {{\hat \theta }_{obs}}} \right)\\ \hat y = \left[ {1{\rm{ }}0} \right]\left[ {\begin{array}{*{20}{c}} {\hat \theta }\\ {{{\hat \omega }_m}} \end{array}} \right] \end{array} \right.$

程序框图如图4所示。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   龙伯格观测器结构框图


图4中,$\mathord{\buildrel{\lower3pt\hbox{$^$}} \over \theta}$角度由式(8)和式(9)得出;${L_1}、{L_2}、{L_3}$为观测器的增益;${\hat \omega _m}$为估计机械角速度;${\hat \theta _{obs}}$为估计电角度;${\hat T_L}$为估计的负载转矩。在${L_1}、{L_2}、{L_3}$的作用下,位置观测的稳态误差可以趋近于零。此 外,采用${T_e}$作为前馈控制可以实现无延迟的角度跟踪,提高观测器的性能。

仿真和试验表明,由于观测器不能实时跟踪${T_L}$、${T_e}$作为前馈控制,在负载波动较大时,会出现缓慢的角收敛甚至误差发散现象。增加$L_3}$系数会得到更好的效果,但不能保证观测器的稳定性。

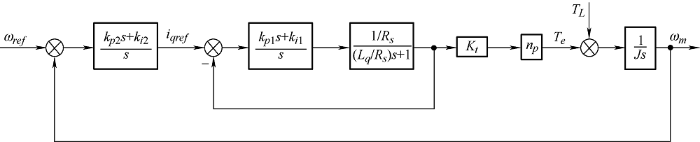
针对传统观测器易受TL影响的缺点,本文提出了一种改进的方法。当采用${i_d} = 0$的FOC模式时,整个矢量控制系统的传递函数方框如图5所示。 图5中,np=2表示电机的磁极对数,从图5可以看出,永磁同步电机输出转矩的变化可以归结为两个方面：转速命令${\omega _{ref}}$和TL的扰动。由于已知${\omega _{ref}}$,可以分别提取${\omega _{ref}}$和TL的传递函数进行前馈,避免负载扰动对龙伯格观测器的不利影响。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5   FOC传递函数框图


图5中${\omega _{ref}}$为速度指令,$kp_1、kp_2、ki_1、ki_2$分别为电流环和速度环PI控制器的比例系数和积分系数;${K_t}$为转矩系数[15]。据传递函数框图化简运算得到${T_e}$和${\omega _{ref}}$的闭环传递函数如下

$\frac{{Te\left( s \right)}}{{\omega ref\left( s \right)}} = \frac{{{N_1}{s^5} + {N_2}{s^4} + {N_3}{s^3} + {N_4}{s^2} + {N_5}s}}{{{D_1}{s^6} + {D_2}{s^5} + {D_3}{s^4} + {D_4}{s^3} + {D_5}{s^2} + {D_6}s + {D_7}}}$

其中

式(12)为六阶6极点5零点系统,阶数较高,不易由微机控制,传递函数参数严重依赖于电机参数和控制器参数,不具有通用性。因此对于该高阶模型进行降阶为二阶模型[12],本文采用二阶系统代替式(12)所示系统,二阶系统的基本模型如式(13)所示,模型参数的整定计算采用最小二乘系统辨识方法实现,减少观测器对模型的依赖性。此外,最小二乘系统辨识方法是基于离散系统的,易于在微机控制系统中应用。降阶后的二阶z域传递函数标准型为

$G\left( {{z^{ - 1}}} \right) = \frac{{{b_1}{z^{ - 1}} + {b_2}{z^{ - 2}}}}{{1 + {a_1}{z^{ - 1}} + {a_2}{z^{ - 2}}}}$

式中,${a_1}、{a_2}、{b_1}、{b_2}$为待识别参数。式(13)可写成差分方程,排序为最小二乘法的基本公式

$z\left( k \right) = \left[ {\begin{array}{*{20}{c}}{ - z\left( {k - 1} \right)}&{ - z\left( {k - 2} \right)}&{u\left( {k - 1} \right)}&{u\left( {k - 2} \right)}\end{array}} \right]\left[ {\begin{array}{*{20}{c}}{a1}\\{a2}\\{b1}\\{b2}\end{array}} \right] + v\left( k \right)$

式中,$v\left( k \right)$是白噪声;$u\left( k \right)$是一个伪随机序列 组成的速度命令,数据长度为N,通过式(14)可以 得到N个方程,最后也可以得到待确定的系数${a_1}、{a_2}、{b_1}、{b_2}$。

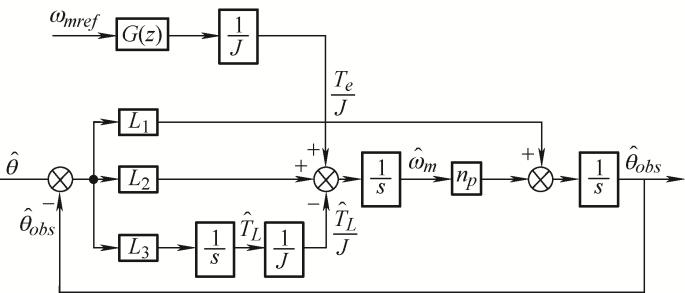
综上所述,改进后的龙伯格位置观测器结构图如图6所示。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6   改进后的龙伯格观测器结构示意图


5 仿真与结果分析

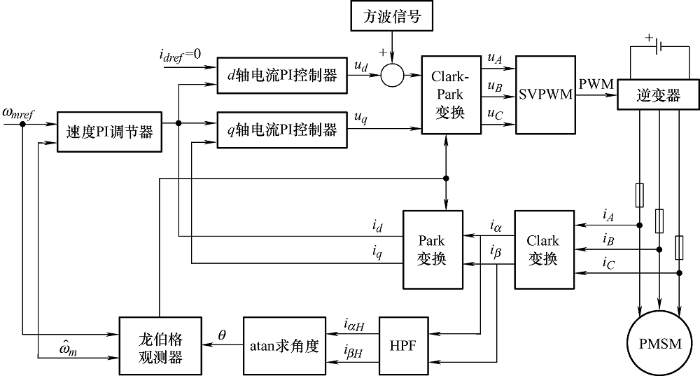
为了验证上述算法的可行性,在Matlab中进行了仿真。整个系统的结构图如图7所示。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7   无传感器FOC系统结构图


仿真所用的永磁同步电机参数如表1所示。

表1   仿真用永磁同步电机参数

参数数值
额定线电压/V24
额定电流/A5
额定功率/W200
定子绕组/Ω1.45
d轴电感/mH4.15
q轴电感/mH16.74
磁极对数2
转动惯量/(kg·m2)0.01
永磁体磁链/Wb0.504

新窗口打开| 下载CSV


5.1 前馈控制参数识别

在本文试验中,PI控制器的参数为$K{i_1} = {\rm{1}}{\rm{.0}}$和$K{p_{\rm{2}}} = {\rm{1}}.0$,$K{i_2} = 23.0$,将参数代入式(12), 可得式(15)。利用第3节的方法,用最小二乘法对式(15)的阶数进行降阶,待定参数${a_1}、{a_2}、{b_1}、{b_2}$通过Matlab编写最小二乘法代码,实现参数整定,其中$u\left( k \right)$为转速指令构成的离散数据点,$z\left( k \right)$为电磁转矩${T_e}$构成的离散数据点,代入数据计算转换后得到离散域的二阶简化模型,如式(16)所示

$\frac{{Te\left( s \right)}}{{\omega ref\left( s \right)}} = \frac{{2.407{e^{ - 4}}{s^5} + 0.069{s^4} + 1.509{s^3} + 0.826{s^2} + 0.11s}}{{1.330{e^{ - 6}}{s^6} + 7.086{e^{ - 4}}{s^5} + 0.114{s^4} + 7.004{s^3} + 140.969{s^2} + 82.629s + 11.026}}$
$G\left( z \right) = \frac{{Te\left( z \right)}}{{\omega ref\left( z \right)}} = \frac{{0.160\;\;07z - 0.160\;\;11}}{{{z^2} - 1.779\;\;05z + 0.791\;\;33}}$

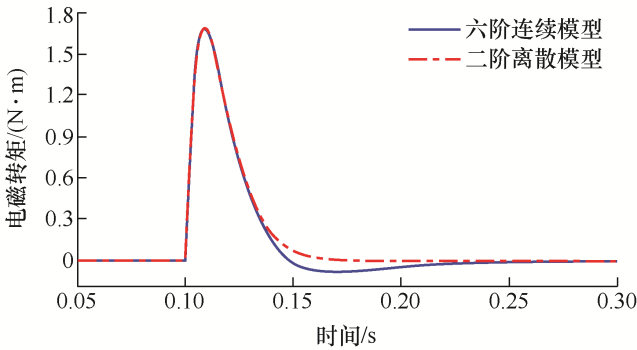
图8为采用速度步进命令时的仿真结果对比。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8   原模型和简化模型的阶跃响应


可以看出,虽然模型的阶数降低了,但是主要的动态信息仍然保留,离散域的二阶模型在微机控制系统中很容易实现。

5.2 仿真试验和结果分析

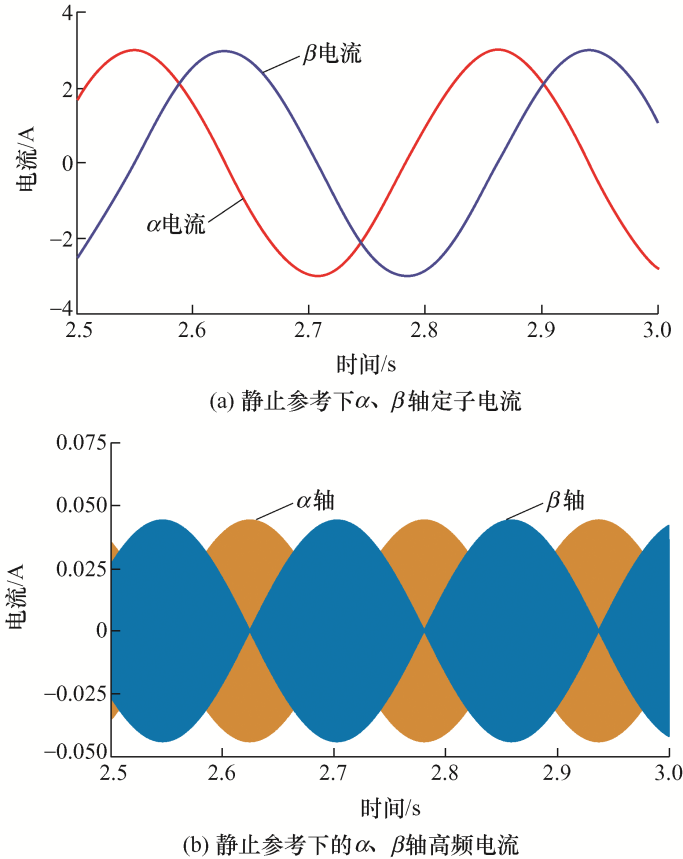
离散系统的仿真进行了采样时间为0.001 s,d轴注入信号的频率是5 kHz,振幅是4 V,二阶巴特沃斯高通滤波器的截止频率是1 kHz,用于过滤电流信号。电机稳定后,在向d轴注入高频电压后 图9a为α、β轴电流波形,图9b为α、β轴经过高通滤波后的电流波形。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9   α、β轴电流波形


由于高频方波信号的注入,在α、β轴的电流波形中存在大量的高次谐波。通过提取高频信号,可以通过式(8)和式(9)得到永磁同步电机转子位置 信息。

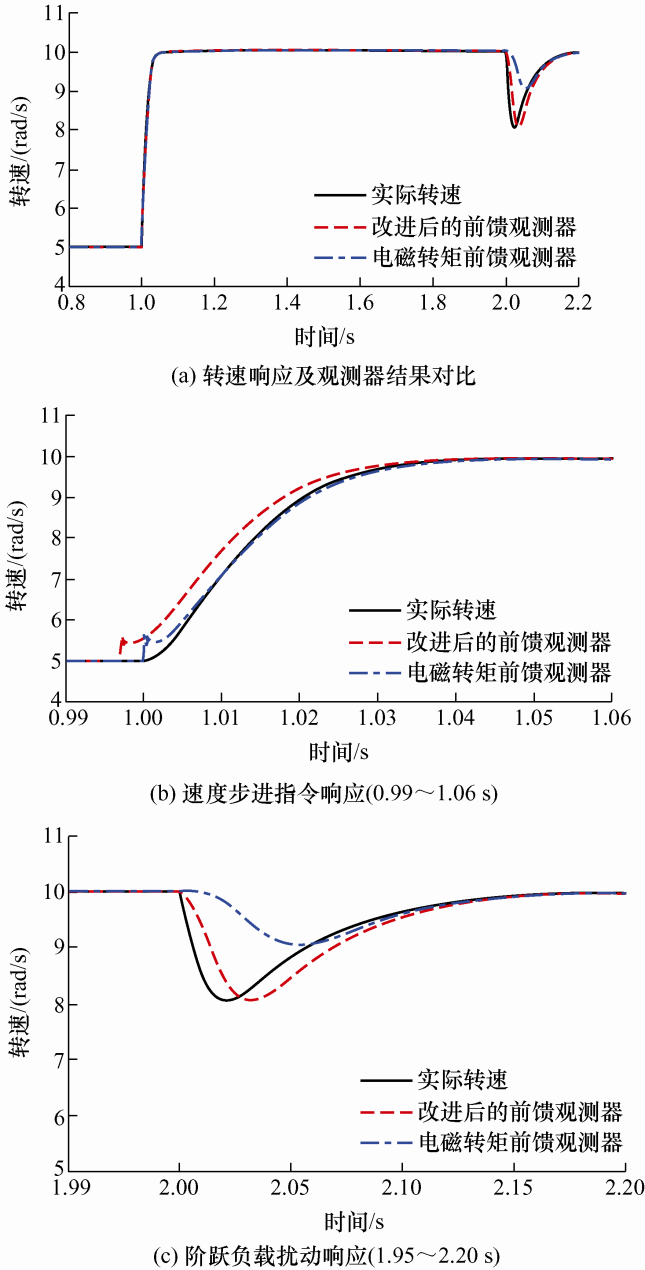
为了进一步验证本文提出的改进方法的效果和观测器的动态性能,在仿真过程中加入了速度指令和负载扰动。仿真过程如下：电机空载起动,期望转速为5 rad/s,电机稳定后,1 s处增加10 rad/s阶跃速度指令,2 s处增加3 N •m阶跃负载扰动。图10为传统观测器和改进观测器对电机转速的观测结果对比,实线是电机的实际速度。

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10   不同情况下转速对比


根据图6,位置信息直接由速度信息积分而来,因此速度的跟踪性能间接反映了位置的估计效果。为了更直观地比较,将速度命令的跟踪时间和误差的标准差作为观测器性能的评价标准,结果如表2所示。

表2   观测器的性能比较

名称速度阶跃指令
响应时间/ms		误差标准差
传统观测器35.525.696
改进后的观测器35.774.510

新窗口打开| 下载CSV


从图10和表2可以看出,改进的龙伯格观测器在速度指令阶跃扰动下的跟踪效果与传统观测器基本相同,基本可以实现对电机转速的无延时跟踪。由于改进龙伯格观测器的前馈项不受负载转矩影响,负载的抗扰性显著提高。在试验的第2 s时,速度的跟踪效果明显优于常规观测器。在整个试验过程中,速度跟踪误差的标准差为4.510,降低了约20%。

6 结论

(1) 本文对永磁同步电机无传感器FOC系统中的转子位置观测器进行了改进。利用速度指令构造的离散二阶系统作为位置观测器的前馈,解决了传统位置观测器易受负载扰动的问题。

(2) 利用最小二乘法辨识二阶系统的参数,该方法不依赖于永磁同步电机的模型和控制器参数,方便应用于DSP控制系统。

(3) 仿真结果表明,改进后的观测器具有更好的跟踪效果和更快的误差收敛速度。该方法可以有效地提高同步电机矢量控制的性能,具有很高的实用价值。

参考文献

尹忠刚, 靳海旭, 张彦平, 等.

基于扰动观测器的交流伺服系统低速爬行滤波反步控制方法

[J]. 电工技术学报, 2020, 35(S1):203-211.

[本文引用: 1]

YIN Zhonggang, JIN Haixu, ZHANG Yanping, et al.

Backstepping control method of low speed crawling filter for AC servo system based on disturbance observer

[J]. Acta Electrotechnics Sinica, 2020, 35(S1):203-211.

[本文引用: 1]

李柏玉, 陆永耕, 黄禹铭.

基于改进龙贝格观测器的控制系统的研究与仿真

[J]. 仪表技术, 2019(9):32-36.

[本文引用: 1]

LI Baiyu, LU Yonggeng, HUANG Yuming.

Research and simulation of control system based on improved Luenberger observer

[J]. Instrumentation Technology, 2019(9):32-36.

[本文引用: 1]

胡荣光.

开关磁阻电机位置传感器故障诊断与低速无位置传感器方法研究

[D]. 南京:南京航空航天大学, 2015.

[本文引用: 1]

HU Rongguang.

Fault diagnosis of switched reluctance motor position sensor and research on low speed sensorless method

[D]. Nanjing:Nanjing University of Aeronautics and Astronautics, 2015.

[本文引用: 1]

王逸之.

永磁同步牵引电机全速域无位置传感器控制研究

[D]. 北京:北京交通大学, 2019.

[本文引用: 1]

WANG Yizhi.

Research on full speed sensorless control of permanent magnet synchronous traction motor

[D]. Beijing:Beijing Jiaotong University, 2019.

[本文引用: 1]

孟柳.

基于半实物的高速永磁电机无速度传感器运行研究

[D]. 北京:北方工业大学, 2019.

[本文引用: 1]

MENG Liu.

Research on speed sensorless operation of high speed permanent magnet motor based on hardware in the loop

[D]. Beijing:North University of Technology, 2019.

[本文引用: 1]

杜思宸, 全力, 朱孝勇, 等.

基于高频注入的永磁同步电机零低速下位置传感器失效故障容错控制

[J]. 中国电机工程学报, 2019, 39(10):3038-3047.

[本文引用: 1]

DU Sichen, QUAN Li, ZHU Xiaoyong, et al.

Fault tolerance control of position sensor failure at zero low speed of permanent magnet synchronous motor based on high frequency injection

[J]. Proceedings of the CSEE, 2019, 39(10):3038-3047.

[本文引用: 1]

张凯泉.

基于龙伯格观测器法的永磁同步电机无感矢量控制算法改进研究

[D]. 长沙:湖南工业大学, 2018.

[本文引用: 1]

ZHANG Kaiquan.

Research on improvement of sensorless vector control algorithm of permanent magnet synchronous motor based on Luenberger observer method

[D]. Changsha:Hunan University of Technology, 2018.

[本文引用: 1]

刘立佳.

镗杆镗削过程振动控制

[J]. 科学技术创新, 2017(27):1-3.

[本文引用: 1]

LIU Lijia.

Vibration control in boring process of boring bar

[J]. Science and Technology Innovation, 2017(27):1-3.

[本文引用: 1]

高福隆.

面贴式永磁同步电机无位置传感器控制技术研究

[D]. 哈尔滨:哈尔滨工程大学, 2016.

[本文引用: 1]

GAO Fulong.

Research on sensorless control technology of surface mounted permanent magnet synchronous motor

[D]. Harbin:Harbin Engineering University, 2016.

[本文引用: 1]

徐东, 王田苗, 刘敬猛, 等.

基于参数辨识的永磁同步电机电流精确控制方法

[J]. 电力自动化设备, 2008(11):30-35.

[本文引用: 2]

XU Dong, WANG Tianmiao, LIU Jingmeng, et al.

Accurate current control method of permanent magnet synchronous motor based on parameter identification

[J]. Electric Power Automation Equipment, 2008(11):30-35.

[本文引用: 2]

何晓会.

基于惯量辨识的永磁同步电机自抗扰控制策略研究

[D]. 哈尔滨:哈尔滨工业大学, 2020.

[本文引用: 1]

HE Xiaohui.

Research on ADRC strategy of permanent magnet synchronous motor based on inertia identification

[D]. Harbin:Harbin Institute of Technology, 2020.

[本文引用: 1]

侯利民, 王红发, 刘建双, 等.

基于NDOB的PMSM调速系统最优滑模控制

[J]. 控制工程, 2017, 24(S1):64-68.

[本文引用: 2]

HOU Limin, WANG Hongfa, LIU Jianshuang, et al.

Optimal sliding mode control of PMSM speed regulation system based on NDOB

[J]. Control Engineering, 2017, 24(S1):64-68.

[本文引用: 2]

侯本帅.

基于滑模观测器与预测控制的永磁同步电机优化控制研究

[D]. 北京:北方工业大学, 2017.

[本文引用: 1]

HOU Benshuai.

Research on optimal control of permanent magnet synchronous motor based on sliding mode observer and predictive contro

[D]. Beijing:North China University of Technology, 2017.

[本文引用: 1]

刘庆飞.

旋转高频信号注入法在电梯门机无位置传感器驱动系统中的应用

[D]. 天津:天津大学, 2016.

[本文引用: 1]

LIU Qingfei.

Application of rotating high frequency signal injection method in sensorless driving system of elevator door motor

[D]. Tianjin:Tianjin University, 2016.

[本文引用: 1]

矫日华.

抓捕工具控制器及伺服控制策略研究

[D]. 哈尔滨:哈尔滨工业大学, 2019.

[本文引用: 1]

JIAO Rihua.

Research on capture tool controller and servo control strategy

[D]. Harbin:Harbin Institute of Technology, 2019.

[本文引用: 1]

/

〈 〉