近年来,多相永磁同步电机(Permanent magnet synchronous machine,PMSM)受到了工业和学术界的广泛关注。相对于三相电机,多相电机具有低压大功率输出、高可靠性以及适于容错运行等特性,在航空航天、舰艇舰船、风力发电等领域得到了越来越多的认可^[1,2,3]。对于多相电机而言,故障容错运行是一个显著优势。当电机发生缺相故障时,不需要改动任何硬件电路,仅需选择适当的容错控制策略便可降额继续运行,此时避免了停机或系统重组^[4,5,6]。针对非正弦反电动势五相PMSM缺相容错运行,国内外学者对降阶解耦模型的磁场定向控制(Field-oriented control,FOC)进行了大量的研究。文献[7]通过构建降阶Clark变换矩阵,建立了五相PMSM故障后的解耦模型,其解耦模型将使同步坐标系下的转矩及电压方程与正常状态一致,但磁场中存在的三次谐波会导致转矩脉动。文献[8]为抑制故障后产生的转矩脉动,构建同步坐标系下的解耦模型,在速度环采用了滑模控制,但它会使得系统产生抖动,并且控制器的设计较复杂。为此,文献[9]采用三次谐波电流注入法来抑制转矩脉动,根据瞬时功率理论和电机反电动势信息,可计算得到故障后的平均转矩和脉动转矩分量,令转矩脉动分量为零,得到基波和三次谐波电流参考值,该方法计算过程复杂,无法在线生成参考电流信号。文献[10]给出了单相开路故障后三次谐波电流的注入和在线计算方法,有效地抑制三次谐波磁链引起的转矩脉动,但选用传统PI控制器,其对交流参考电流值的跟踪没有达到最佳效果。

上述提到的方法只得到了电流的最优参考信号,然而,其对参考信号并没有实现很好的跟踪。对于参考电流信号的跟踪,通常采用的是滞环控 制^[11]和PI控制器^[12],滞环控制会带来开关频率不固定以及电流谐波较大的问题,而PI控制器可以完全消除直流信号的稳态误差,但对于交流电流信号却不能精确跟踪。比例谐振(Proportional resonance, PR)控制器^[10]可以有效地跟踪交流参考信号,但谐振控制器的带宽窄,只能对单一频率的信号进行补偿。

本文在五相PMSM 缺一相故障状态下,首先,通过基波空间和三次谐波空间的降阶变换矩阵,得到两个子空间同步坐标系下的转矩方程。然后,根据电机转矩方程,为了消除转矩脉动,分析了三次谐波电流注入率选取的方法,并根据最小铜耗及最大转矩原则对参考电流进行优化。针对传统PI控制器不能零稳态误差跟踪交流参考信号的问题,本文设计了QPR+PI控制器实现对交流参考电流进行精确跟踪。最后,由仿真和试验得到,故障后转矩脉动得到了有效抑制,设计的QPR+PI控制器也实现了对参考电流值的精确跟踪。

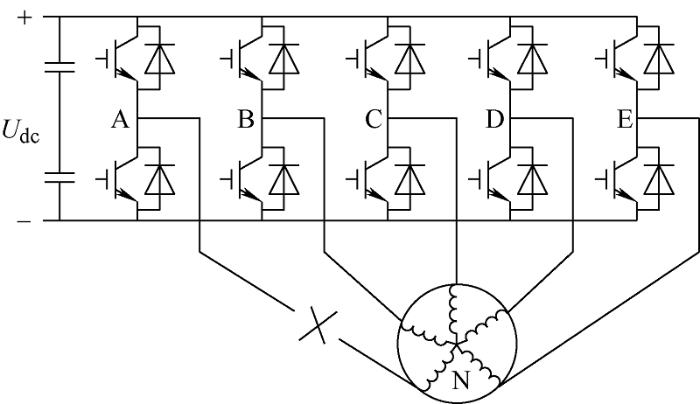
本文电机采用的是表贴式五相PMSM,为便于分析,假设电机A相发生缺相故障,五相PMSM缺A相故障后主电路结构图如图1所示,其中,定子绕组为星形连接,N为电机中性点,U_dc为直流母线电压。

在五相PMSM 缺A相故障前后,根据基波磁动势不变原则,重新构造的降阶Clark变换矩阵为

式中,γ=2π/5;修正系数n=-1。

从静止坐标系[α₁-β₁-z₁-o₁]到同步坐标系[d₁-q₁- z₁-o₁]的Park变换矩阵为

式中,θ为转子电角度。

定子电流在[B-C-D-E]、[α₁-β₁-z₁-o₁]和[d₁-q₁-z₁-o₁]各坐标系之间的变换关系为

由电机学原理得到,电磁转矩等于磁共能对机械角位移的偏导数

式中,W_co为磁共能;θ_m为转子机械角度;n_p为电机极对数;ψ_f为永磁体磁链;ψ_f1为永磁磁链的基波幅值;I_s为相电流矢量;L_s为相电感矩阵;i_d1、i_q1分别为d₁、q₁轴的电流分量;L_d1、L_q1分别为d₁、q₁轴的电感分量,对于表贴式PMSM,L_d1=L_q1。

在五相PMSM磁动势中,正弦波只是一种理想状态,实际中,一方面,由于永磁体的加工及安装误差等会造成磁动势中存在一定的三次谐波成分;另一方面,为增加电机功率密度和输出转矩,也需要有意识地注入三次谐波磁势。当电机发生缺一相故障时,三次谐波磁势会与基波电流作用产生转矩脉动。

考虑磁动势中的三次谐波分量时,此时永磁体磁链为

式中,${\psi _{{\rm{f}}3}}$为永磁磁链的三次谐波幅值。

由电机磁共能方法得到考虑三次谐波磁势的基波空间电磁转矩为

由式(6)可知,当电机缺一相故障后,三次谐波分量主要会引起二次和四次转矩脉动,因此,可通过三次谐波电流注入的方法来消除转矩 脉动。

在三次谐波空间中,按照基波降阶变换矩阵T₁(γ)的求取方式,得出三次谐波空间下的降阶Clark变换矩阵为

从静止坐标系[z₃-α₃-β₃-o₃]到同步坐标系[z₃-d₃-q₃-o₃]的Park变换矩阵为

三次谐波电流在[B-C-D-E]、[z₃-α₃-β₃-o₃]和[z₃-d₃-q₃-o₃]各坐标系之间的变换关系为

由磁共能方法可知,三次谐波电流得到的转矩方程表达式为

将式(7)和式(11)进行叠加,此时基波和三次谐波电流共同作用时所得到的电磁转矩为

对式(11)进行整理后,可得到转矩的平均值和各次转矩脉动分量为

本文采用i_d1=i_d3=0的矢量控制方式,还剩余i_q1、i_q3、i_z1、i_z3四个控制自由度,定义i_q3=-3ψ_f3i_q1/ψ_f1 =-k_e3i_q1,通过调整i_q1、i_q3控制转矩平均值和转矩脉动,调整i_z1、i_z3可对定子铜耗和电磁转矩进一步优化。观察式(12)中的二次和四次转矩脉动分量,当三次谐波电流注入率满足式(13)时,此时可以将二次转矩脉动t₂和四次转矩脉动t₄完全抵消。

式中,E₃、E₁为三次谐波磁势与基波磁势幅值。

根据文献[11],三次谐波电流得到的定子绕组铜耗可用r_s(i2 d3+i2 q3+i2 z3)表示,其中r_s为定子电阻,当满足式(14)时,其铜耗达到最小。

类似地,由基波电流和三次谐波电流共同作用得到的最小总铜耗r_s(i2 q1+i2 q3)可通过i_z1=i_z3=0实现,并且根据式(13)可知,此时一、三次转矩脉动分量t₁=t₃=0。

采用最小铜耗原则电机可以得到最小铜耗,但故障下剩余四相的相电流幅值分布不均匀,如果最大的相电流幅值达到功率器件所能承受的最大值时会限制电机的转矩输出能力。因此,根据文献[13],在电机故障下,为提高输出转矩能力,i_z1 和i_z3可通过变换矩阵作用到各相电流中,对各相电流进行调节,使得剩余四相电流幅值相等。

通过对式(3)进行变换可得到,当满足式(15)时,电机故障下的剩余相电流幅值相等。

类似地,在三次谐波电流的作用下,参考式(15)选取

此时由式(12)可知,一、三次转矩脉动(式(17))也可以完全抵消。

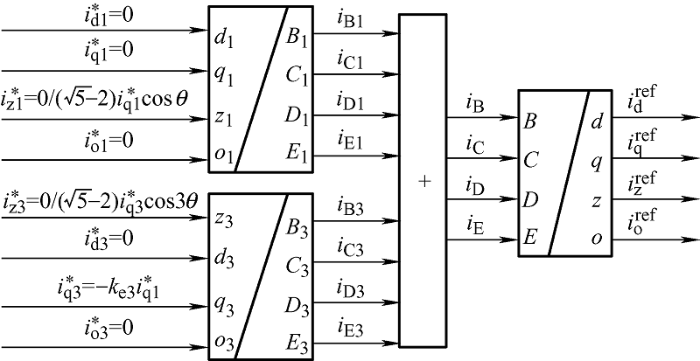
文献[10]研究了五相PMSM缺一相故障后同步旋转坐标系下交流参考电流信号的生成方法,其生成框图如图2所示。

图2中,基波空间和三次谐波空间下的广义零序电流分量i_z1、i_z3可根据最小铜耗原则和最大转矩原则来进行设定,将使得转矩脉动等于零的两个子空间在同步旋转坐标系下的电流给定值经过对应的降阶逆Park和逆Clark变换矩阵转换到自然坐标系下,进行叠加后再经过基波空间的降阶Clark和Park变换矩阵变换到基波同步坐标系得到交流参考电 流值。

电机缺一相故障后,为了抑制二次和四次转矩脉动,三次谐波电流经过降阶坐标变换生成同步坐标系下电流参考值后,d轴以及q轴参考电流信号中包含有二次、四次谐波分量,z轴参考电流信号中包含有三次谐波分量。对于传统PI控制器而言,它仅可以消除直流信号的稳态误差,但是对产生转矩脉动的谐波分量没有补偿作用,而基于内模原理的比例谐振(PR)控制器可实现对交流信号的无差补偿^[14],其PR控制器传递函数为

式中,K_p为比例系数;K_n是谐振项系数;ω_n是谐振角频率,ω_n = nω₀;n为谐波次数;ω₀为基波频率。

PR控制器在谐振频率处增益为无穷大,但由于它的带宽窄,所以仅可实现与谐振频率同频的谐波分量。实际中,电机转速通常会有一定程度的波动,电机转速的波动很有可能会使实际电流谐波分量的频率偏离谐振项的谐振频率,因此本文采用了准比例谐振(QPR)控制器,其传递函数表达式为

式中,ω_cn为截止频率,它可以适当地拓宽谐振频率的带宽,以至于确保稳态误差在一个理想的范围之内,并且它会根据电机实际转速的波动而进行相应的变化,因此,将避免谐振项失效的情况。

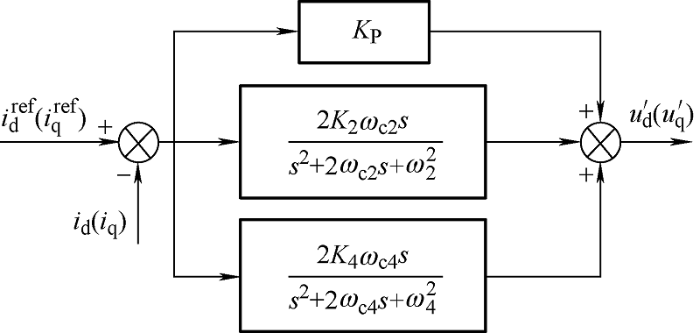
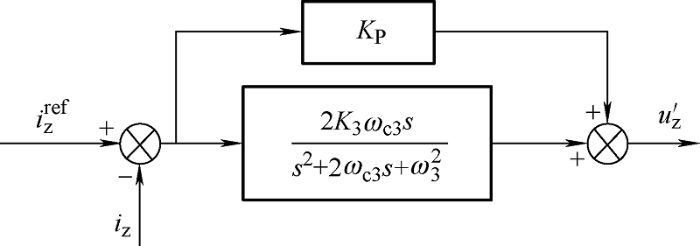
通过分析d轴和q轴电流参考值中包含二次及四次谐波分量,z轴参考电流值中包含三次谐波分量,因此,本文采用两个QPR控制器分别对d轴和q轴的二次及四次谐波分量进行跟踪,采用一个QPR控制器对z轴的三次谐波分量进行跟踪,控制框图如图3和图4所示,其中,K₂、K₃和K₄分别为二次、三次和四次谐振项增益系数,ω_c2、ω_c3和ω_c4分别为二次、三次和四次谐振项截止频率,ω₂、ω₃和ω₄分别为二次、三次和四次谐振频率,ω₂=2ω₀,ω₃=3ω₀,ω₄=4ω₀,${u_d}^\prime$、${u_q}^\prime$和${u_z}^\prime$分别为d轴、q轴和z轴QPR控制器输出电压。本文通过选取适当的参数实现了对交流参考电流值的精确跟踪。

在QPR控制器中有3个参数K_p、K_n和ω_cn,为了方便分析每个参数对控制器性能的影响,本文通过对3个参数进行定2变1的方法来对参数进行 分析。

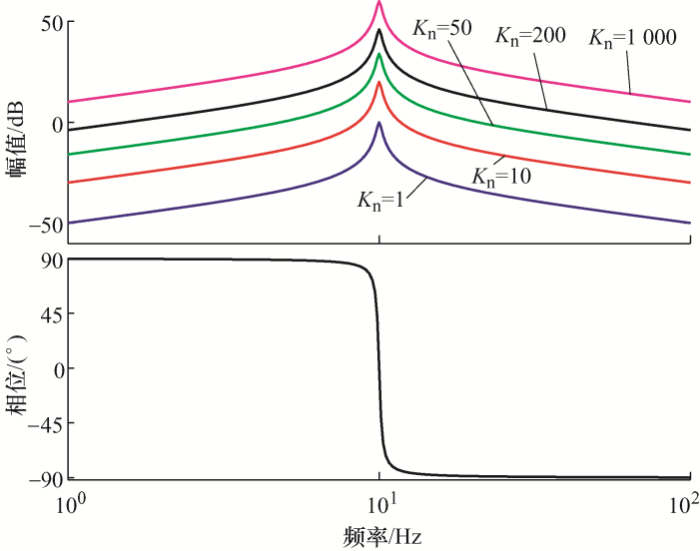
首先,固定K_p和ω_cn,考虑K_n变化对系统性能的影响。假设K_p=0,ω_cn=1,K_n分别取1、10、50、200、1 000时,得到QPR控制器的伯德图如图5所示。

由图5可得到,K_n进行变化只影响QPR控制器的增益,而控制器的带宽几乎没有影响。随着K_n的增大,控制器的增益就越大,使得控制器稳态误差越小,但K_n如果过大,会使远离基频附近的谐波分量放大,因此,必须合理选取K_n。

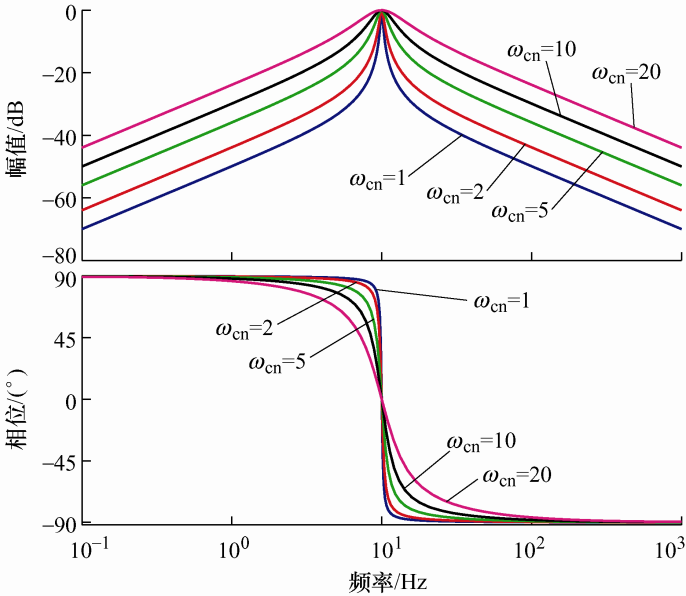
其次,固定K_p和K_n,考虑ω_cn变化对系统性能的影响。假设K_p=0,K_n=1,ω_cn分别取1、2、5、10、20时,得到QPR控制器的伯德图如图6所示。

由图6可知,随着ω_cn的增大,控制器的带宽明显增大,同时,在基频附近的增益没有变化,远离基频处的增益随ω_cn的增大而增大。但如果ω_cn过大,带宽增大太多,会造成谐振点的作用被减小。因此,需要折中考虑ω_cn。

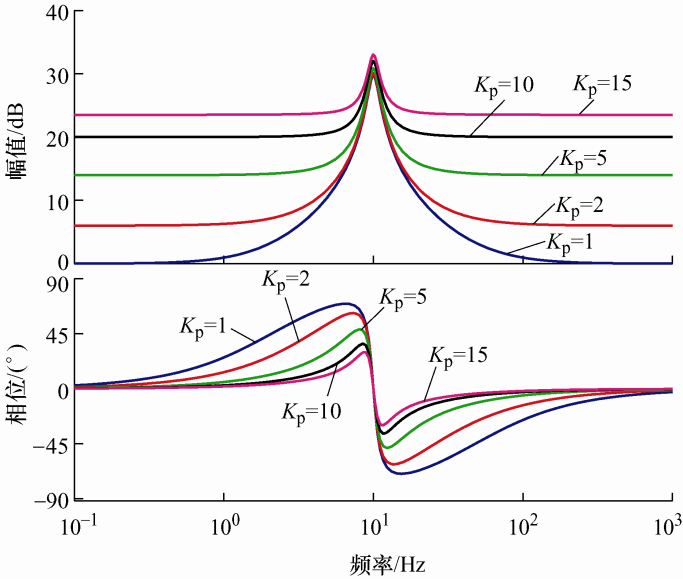
最后,固定K_n、ω_cn,考虑K_p变化对系统性能的影响。假设K_n=30,ω_cn=5,K_p分别取1、2、5、10、15时,得到QPR控制器的伯德图如图7所示。

由图7可知,随着K_p的增大,控制器的增益会增大,系统的动态响应速度越快,同时,可看出,带宽会相应变窄,在基频处峰值增益增加幅度变小,如果K_p选取过大,可能会削弱谐振作用,造成系统稳定性变差。因此,必须设置合适的K_p值。

通过以上分析,并进行反复的调试,其中,以d轴为例,d轴上的二次谐波分量最终选取的QPR控制器参数如下：K₂=30,ω_c2=5,K_p=3,四次谐波分量最终选取参数如下：K₄=20,ω_c4=5,K_p=3,并绘制QPR控制器伯德图进行分析,q轴和z轴的分析过程与d轴相同。

将d轴的参数代入式(19),得到d轴QPR控制器传递函数为

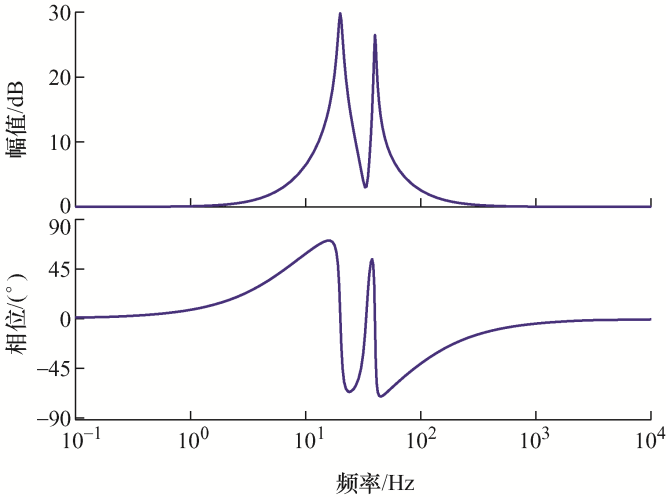
通过式(20),绘制d轴QPR控制器传递函数G_QPR(s)的伯德图如图8所示。

从图8可看出,d轴QPR控制器在二次和四次谐波频率处都有较大的增益和较宽的带宽,说明设计的 QPR控制器在二、四次谐波频率处有较好的跟踪性能。

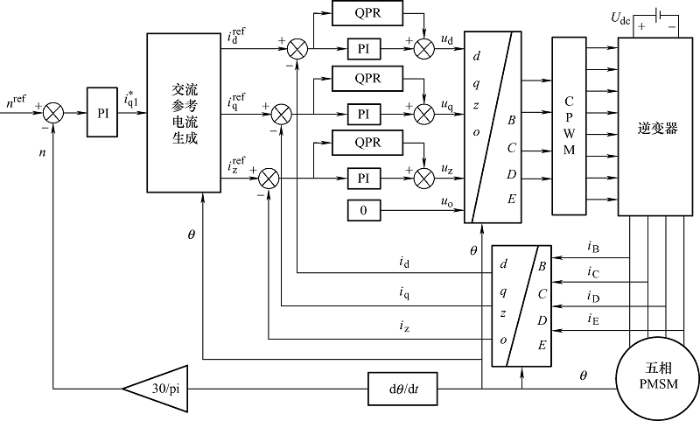
五相PMSM缺一相故障下的容错矢量控制框图如图9所示,转速环经过PI控制器得到电流给定值i* q1,然后根据图2中交流参考电流的生成方法分别得到d轴、q轴和z轴上含有谐波分量的交流参考电流值,再经过d轴、q轴和z轴上相对应的QPR+PI控制器对交流参考电流信号进行精确跟踪。

本文在Matlab/Simulink中完成了五相PMSM缺一相故障下的容错矢量控制仿真模型,并进行仿真结果分析。五相PMSM参数如表1所示。

在电机参数中ψ_f1 = 0.32 Wb,ψ_f3 = 0.020 8 Wb,因此,根据三次谐波电流注入率k_e3的选取式(13),可以得到k_e3为

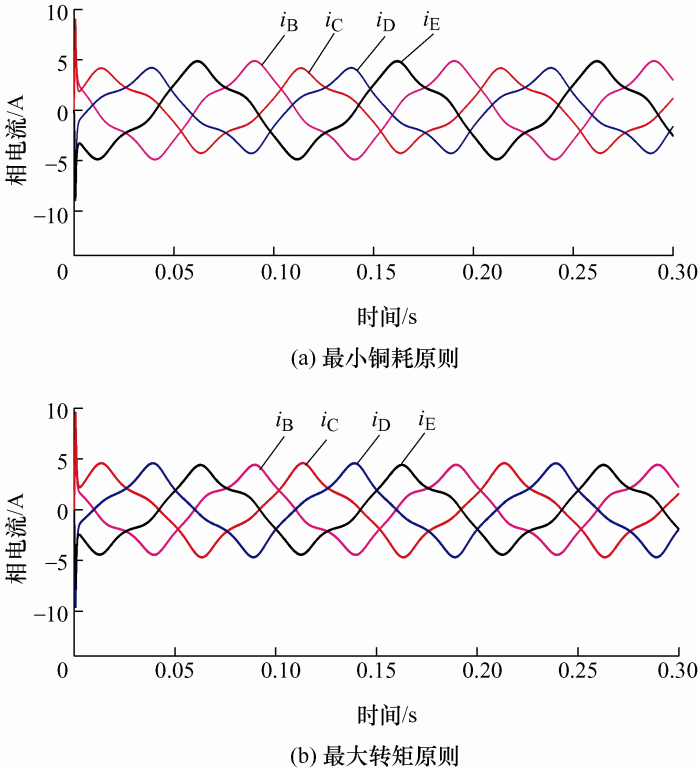
图10a和图10b为电机A相缺相故障下三次谐波电流注入后分别采用最小铜耗原则和最大转矩原则的相电流波形,因为在电流中注入了三次谐波电流,所以它们的相电流呈非正弦。在图10a中,B、E两相电流幅值高于C、D两相电流幅值,其相电流幅值分布不均匀。在图10b中,剩余各相电流幅值相等,因此提高了电机故障下的输出转矩。

在接下来的分析中,以最小铜耗原则为例进行分析,最大转矩原则分析与之相同。

为便于分析比较,定义转矩k、转速脉动h表达式分别为

式中,T_emax、T_emin和T_eavg分别为转矩的最大、最小和平均值;n_max、n_min和n_avg分别为转速的最大、最小和平均值。

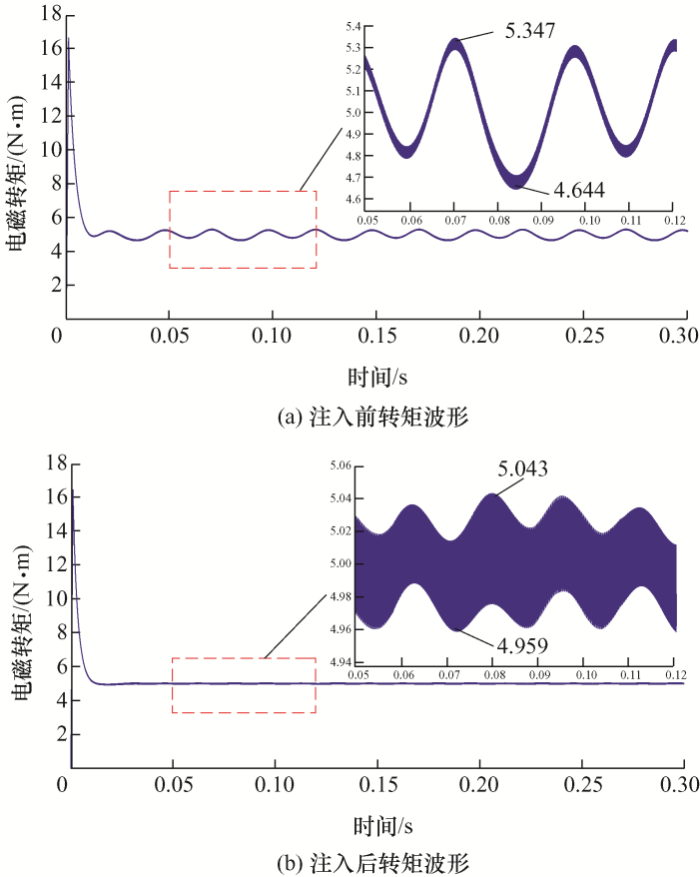
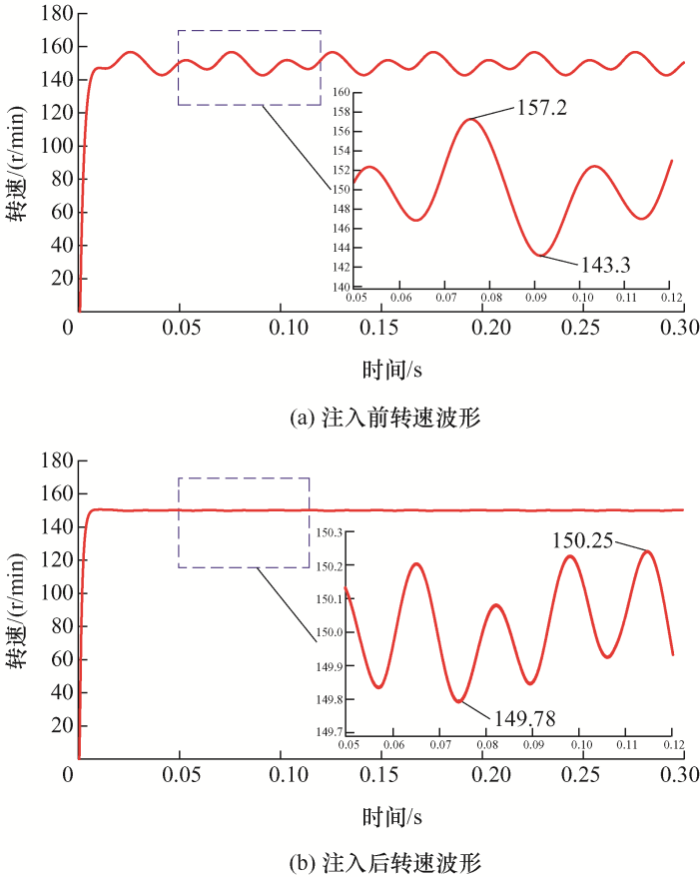
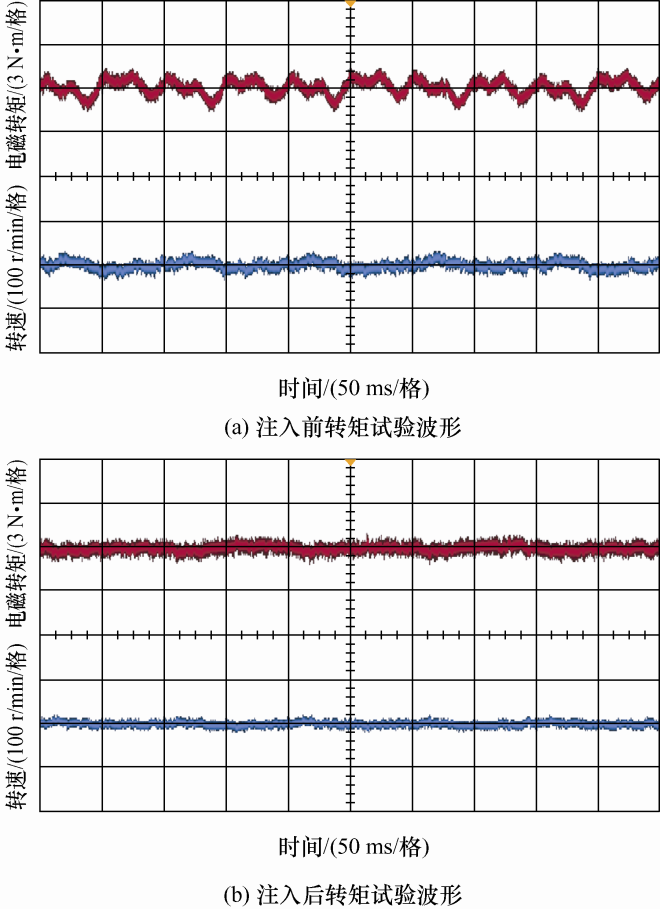
本文给定负载转矩5 N·m,给定转速150 r/min。图11a、11b和图12a、12b分别为三次谐波电流注入前和注入后的转矩以及转速波形,同时在图中也分别给出了各自对应的局部放大波形。根据式(22)和式(23)可得到,在三次谐波电流注入前和注入后的转矩以及转速脉动性能对比如表2所示。从表2得到,三次谐波电流注入前的转矩和转速中都存在较大的脉动,在三次谐波电流注入后有效地抑制了转矩和转速脉动。

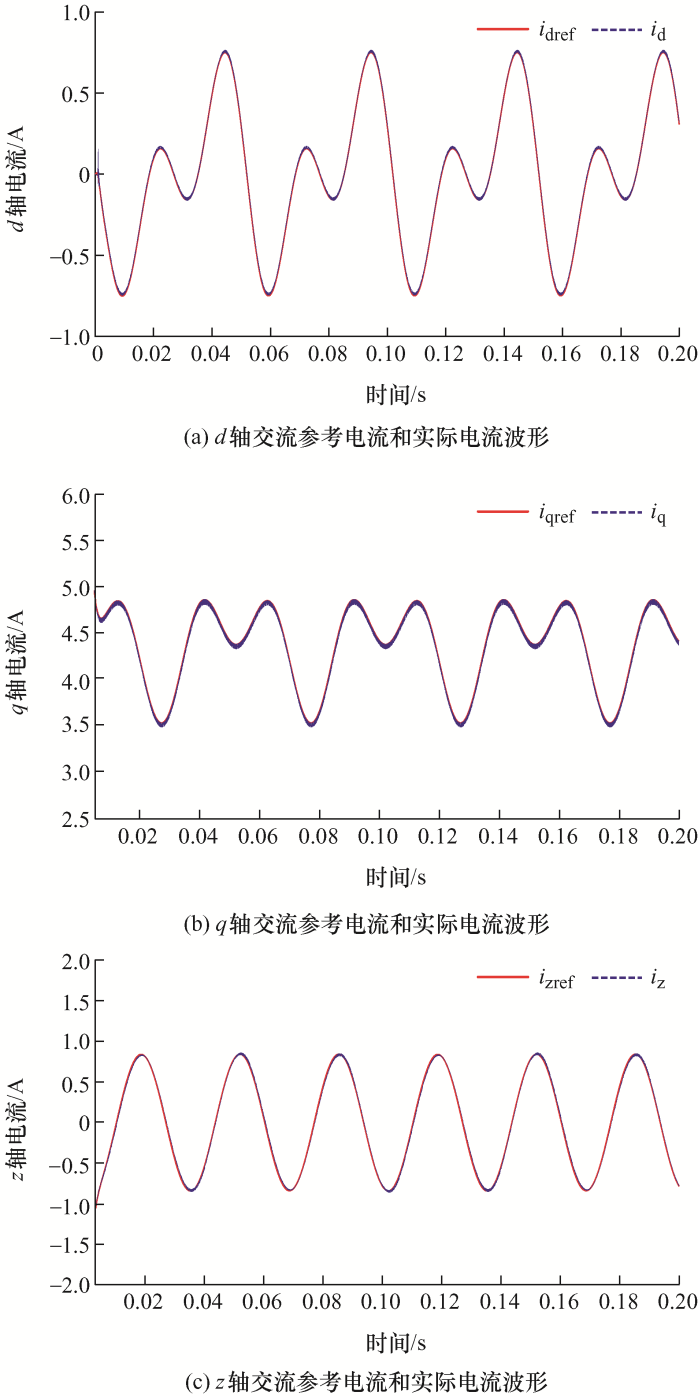
图13是在d-q-z同步坐标系下的交流参考电流和实际电流波形,由于在同步坐标系下参考电流信号生成时会包含有谐波分量,所以d-q-z坐标系参考电流不是恒量。由图13可看出,采用本文设计的QPR+PI控制器实现了对交流参考电流的精确跟踪,从而验证了本文设计的QPR+PI控制器的有效性。

为验证上述理论分析的可行性,搭建了如图14所示的五相 PMSM 试验平台。采用直流电机作为负载,主控制器采用英飞凌的XE164。五相PMSM的相关参数如下：定子电阻为0.5 Ω,直交轴电感为8.4 mH,电机极对数为4。试验中,开关频率为10 kHz,转速给定为150 r/min,负载转矩为5 N·m,直流母线电压200 V。

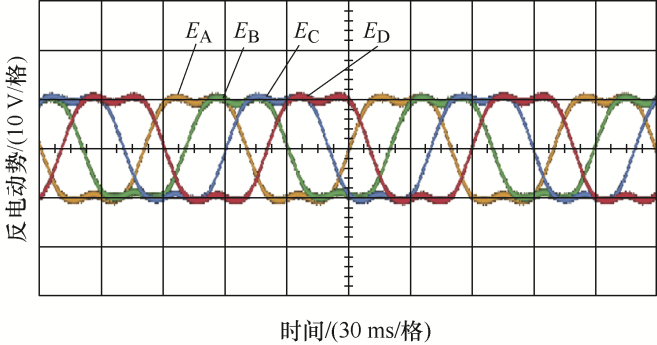
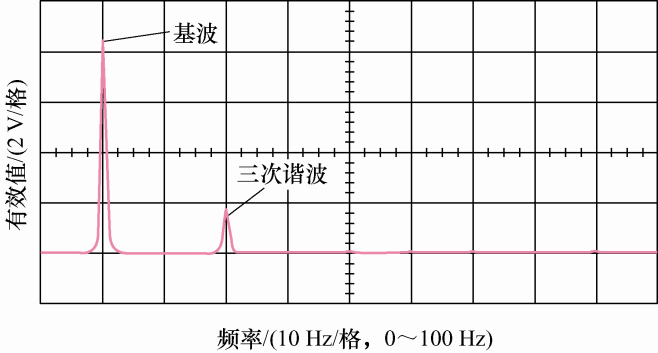
本文采用直流电机拖动五相永磁同步样机150 r/min旋转,得到电机的反电动势波形如图15所示,可看出反电动势中存在一定含量的三次谐波,其中对B相反电动势进行了频谱分析,如图16所示,经过分析可以得到反电动势中含有约19.5%的三次谐波分量。因此,在试验中三次谐波电流注入率取为19.5%。

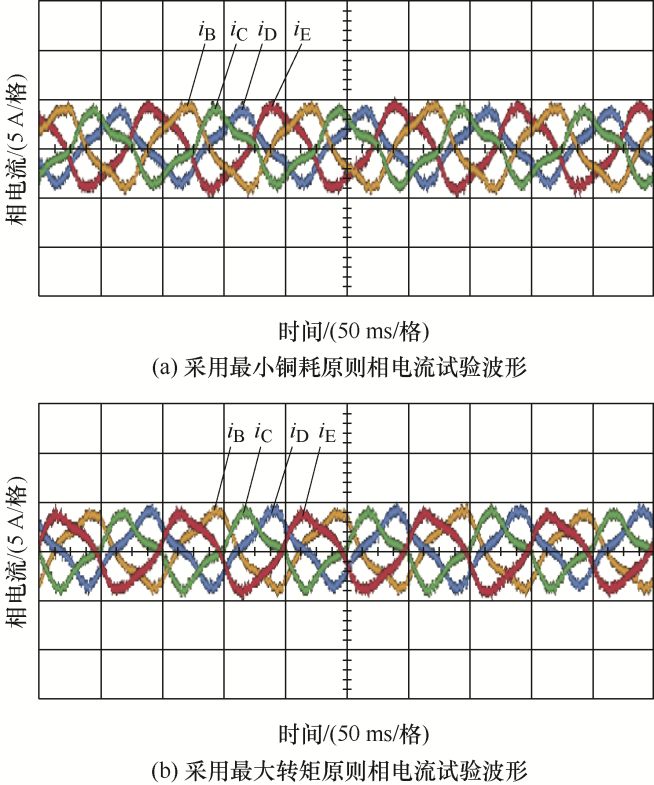
图17a和图17b为故障下三次谐波电流注入后分别采用最小铜耗原则和最大转矩原则的相电流试验波形,由于注入了三次谐波电流,所以剩余各相的相电流都呈非正弦。同时,图17a采用了最小铜耗原则,其相电流幅值不相等,在图17b采用最大转矩原则后各相电流幅值相等,可提高最大输出 转矩。

图18a和图18b分别为三次谐波电流注入前和注入后的转矩及转速试验波形,从两图可看出,在三次谐波电流注入前,转矩和转速波形中都会产生较大的脉动,当三次谐波电流注入后,转矩和转速脉动得到了有效的抑制。

表3为三次谐波电流注入前、后转矩和转速试验波形的脉动性能对比,其计算采用式(22)和式(23),从表3得到,三次谐波电流注入后转矩脉动可降低53.6%,转速脉动可降低54.1%,验证了理论分析的有效性。

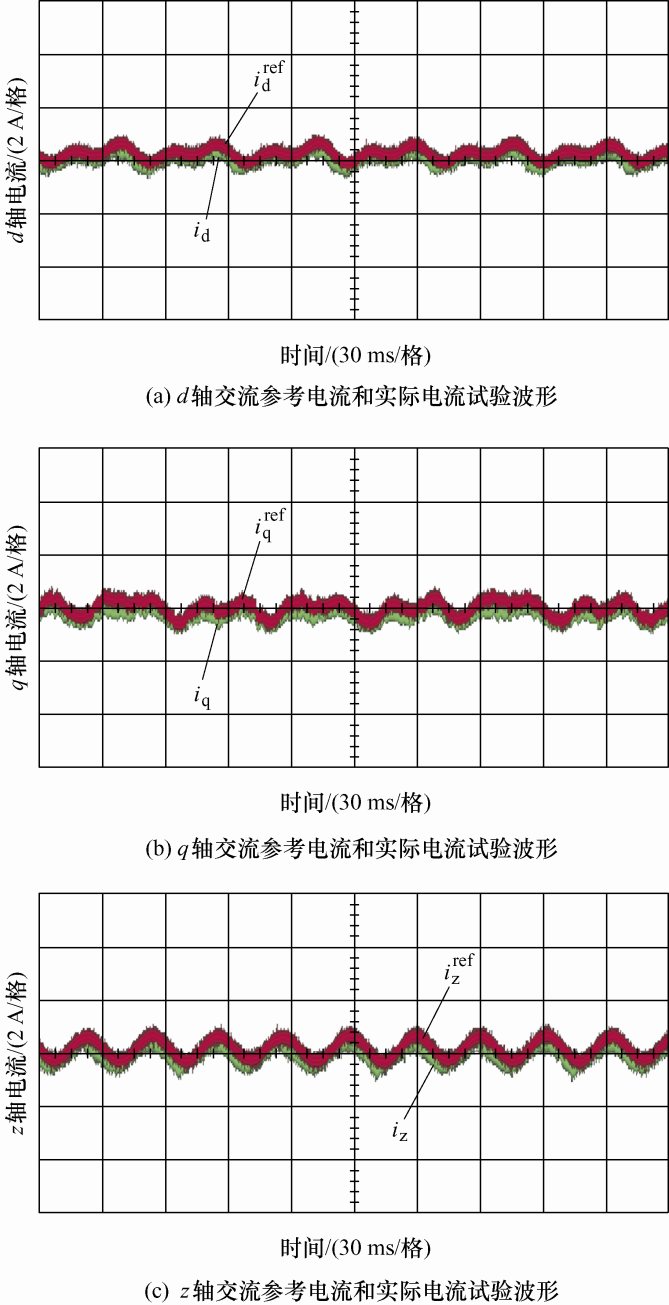
图19为d-q-z同步坐标系下的交流参考电流和实际电流试验波形,由图19可看出,d轴、q轴和z轴的实际电流都能够成功跟踪上各自的参考电流信号,说明本文设计的QPR+PI控制器对于交流参考电流有很好的跟踪效果。

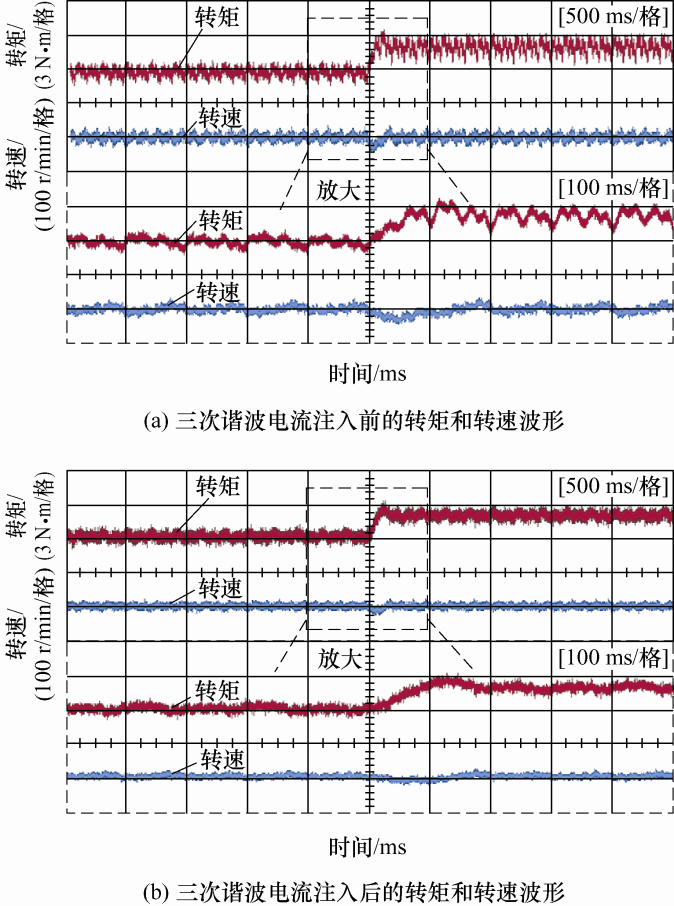
为了验证理论分析的动态性能,图20a和图20b给出了负载转矩从3 N·m突加到5 N·m时三次谐波电流注入前、后的转矩和转速波形,并给出了对应的局部放大波形。从两图可看出,三次谐波电流注入前,突加负载转矩时,转矩和转速依然存在较大脉动,三次谐波电流注入后,转矩和转速脉动得到明显减小,且突加负载转矩时,转矩和转速脉动同样可以有效抑制;同时可以看到,转速经过快速的调节后达到稳定值。

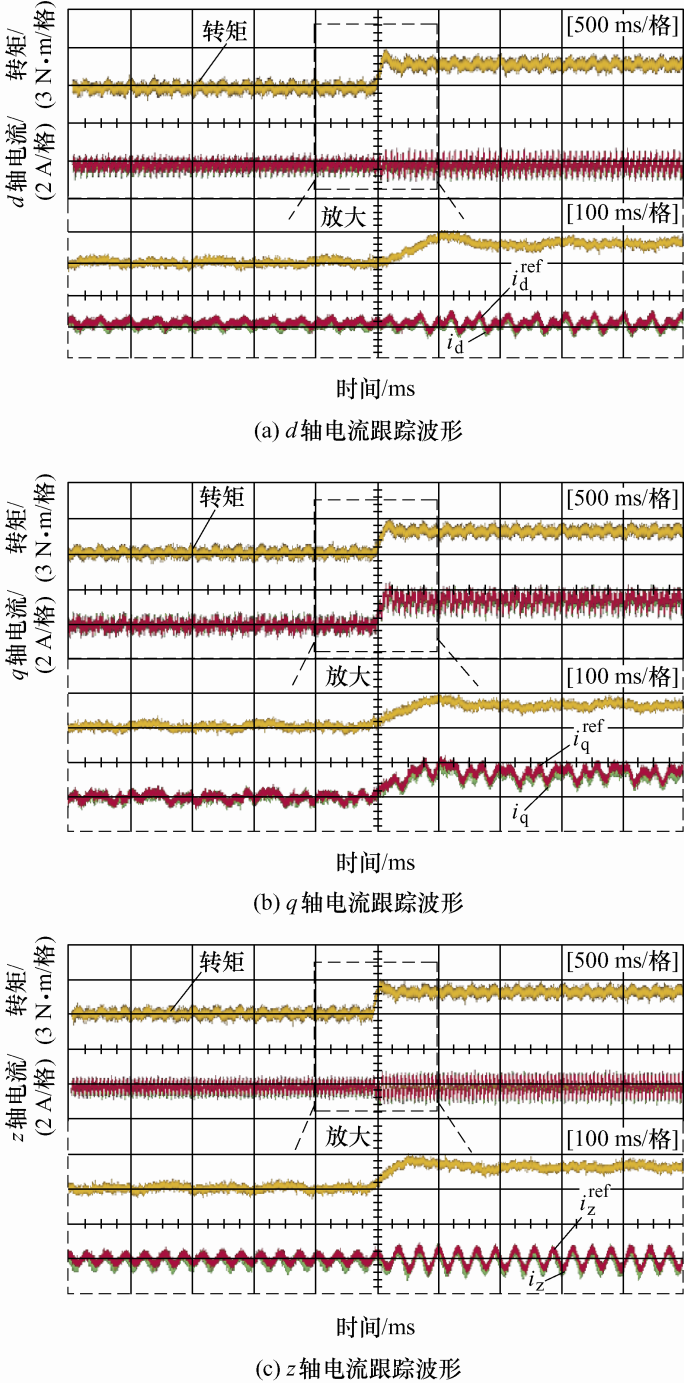
图21给出了负载转矩从3 N·m突加到5 N·m时d、q和z轴上交流参考电流和实际电流的跟踪波形,并给出了对应的局部放大波形。从图21中可看出,突加负载转矩后,d、q和z轴上的实际电流都能很好地跟踪上参考电流,说明QPR+PI控制器具有较好的动态性能。

本文针对非正弦反电动势五相永磁同步电机,在缺一相故障状态下,为了消除故障后产生的二次和四次转矩脉动分量,分析了三次谐波电流注入率的选取方法。针对传统PI控制器不能对交流信号进行精确跟踪问题,设计了QPR+PI控制器来对交流参考电流进行精确跟踪。通过仿真和试验验证对容错矢量控制策略进行了深入研究,具体结论如下所示。

(1) 从试验中可知,三次谐波电流注入前转矩脉动为58.2%,三次谐波电流注入后转矩脉动降低到27%,因此,电机故障后转矩脉动得到了有效的 抑制。

(2) 通过仿真和试验得到,本文设计的QPR+PI控制器对交流参考电流有着很好的跟踪性能,验证了QPR+PI控制器的有效性。

(3) 通过突加、减负载转矩对理论分析的动态性能进行了验证,结果表明该系统具有较好的动态性能。