基于新型权重因子校正和延时补偿的永磁同步电动机模型预测转矩控制 *

doi:10.11985/2021.01.004

基于新型权重因子校正和延时补偿的永磁同步电动机模型预测转矩控制 ^*

王海良^,¹^,², 刘世民^,³, 陈永清^,⁴, 尹玉才^,⁵

1.北京科技大学能源与环境工程学院北京 100083

2.新兴际华集团技术中心北京 100070

3.中国五矿集团(唐山曹妃店)矿山控股有限公司唐山 063200

4.泰豪军工集团研究院北京 100166

5.新兴重工集团有限公司北京 100070

PMSM Model Predictive Direct Torque Control Based on Novel Weighting Factor Tuning and Computation Delay Compensation

WANG Hailiang^,¹^,², LIU Shimin^,³, CHEN Yongqing^,⁴, YIN Yucai^,⁵

1. School of Energy and Environment Engineering, University of Science and Technology Beijing, Beijing 100083

2. XXCIG Technology Center, Beijing 100070

3. China Minmetals Group (Tangshan Caofedian) Mine Holding Co., Ltd., Tangshan 063200

4. Tellhow Jungong Group Research Institute, Beijing 100166

5. Xinxing Heavy Industry Group Co., Ltd., Beijing 100070

收稿日期: 2020-04-2 修回日期: 2020-05-22 网络出版日期: 2021-03-25

基金资助:

* 国家重点研发计划资助项目. 2018YFC0810002

Received: 2020-04-2 Revised: 2020-05-22 Online: 2021-03-25

作者简介 About authors

王海良,男,1964年生,硕士。主要研究方向为工业自动化及新能源、新材料。E-mail：wahal@163.com

刘世民,男,1965年生,教授级高级工程师。主要研究方向为工业自动化、电机控制系统调节。E-mail：liushimin_jd@126.com

陈永清,男,1969年生,教授级高级工程师。主要研究方向为永磁电机控制及电机优化设计。E-mail：chenyq00@vip.163.com

尹玉才,男,1964年生,高级工程师。主要研究方向为机械及自动控制。E-mail：13986363100@139.com

摘要

为解决永磁同步电动机(Permanent magnet synchronous motor,PMSM)模型预测直接转矩控制(Model predictive direct torque control,MPC-DTC)权重因子和计算延时问题,提出了新型权重因子校正和延时补偿策略,改善PMSM控制性能,完善模型预测转矩控制理论方法。为校核代价函数中的磁链和转矩权重因子,分析了权重因子的本质,利用标准化算法将磁链和转矩转换至无量纲、同幅值范围的变量,并根据转矩和磁链对控制电压波动的响应速度不同,理论地计算出MPC-DTC控制器中的权重因子。与传统的两步计算延时补偿策略不同,所提出的新型补偿方案基于“单周期双采样”算法,需要分三步执行：延时时间计算,补偿电流预测和补偿磁链及转矩预测。试验结果表明,提出的权重因子校核和延时补偿方法能够保证良好的系统性能。

关键词： 永磁同步电动机 ; 模型预测转矩控制 ; 权重因子校正 ; 计算延时补偿

Abstract

In order to tune the weighting factors and solve the computation delay problem for the PMSM model predictive direct torque control (MPC-DTC), a novel factor tuning method and a compensation method are proposed. The proposed techniques have improved the PMSM control performance and enriched the MPC-DTC theories. To tune the weighting factors for the flux and torque,their natures are analyzed firstly. Then, normalization method is applied to the system, removing the units of the two parameters and converting them into the same range. Finally, according to the different response speed of the flux and torque to the voltage variations, a theoretical analysis and tuning method is developed. By contrast to the two-step compensation strategy, the novel delay compensation method is based on dual sampling in one switching period. The implementation of the new method is divided into three steps: delay calculation, current compensation and flux/torque compensation. The experimental results verify that the proposed tuning and compensation methods can ensure that the PMSM has good performance.

Keywords： Permanent magnet synchronous motor (PMSM) ; model predictive direct torque control ; weighting factor tuning ; computation delay compensation

PDF (548KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

王海良, 刘世民, 陈永清, 尹玉才. 基于新型权重因子校正和延时补偿的永磁同步电动机模型预测转矩控制 ^*. 电气工程学报[J], 2021, 16(1): 26-33 doi:10.11985/2021.01.004

WANG Hailiang, LIU Shimin, CHEN Yongqing, YIN Yucai. PMSM Model Predictive Direct Torque Control Based on Novel Weighting Factor Tuning and Computation Delay Compensation. Journal of Electrical Engineering[J], 2021, 16(1): 26-33 doi:10.11985/2021.01.004

1 引言

永磁同步电动机(Permanent magnet synchronous motor,PMSM)具有功率因数大、效率高和功率密度大等优点,已经在电梯、风电系统和电动汽车等工业领域得到了广泛的应用^[1,2,3,4,5];同时,永磁同步电动机控制技术也在不断改进与完善^[6]。目前,广泛采用的高性能永磁同步电动机控制方法有矢量控制和直接转矩控制(Direct torque control,DTC)^[7]。与矢量控制相比,直接转矩控制通过选择合适的空间电压矢量,控制定子磁链运动,通过迅速改变负载角,实现对转矩的直接控制。由于该控制方法具有对电动机参数依赖少、鲁棒性强、结构简单和动态响应快的优点,已经成为了学者们的研究热点^[8]。然而,传统的DTC方法采用迟滞比较器和开关表,使得开关频率和转矩脉动很大^[9]。为解决以上问题,很多基于最优化控制理论的DTC方案已经出现,如模型预测直接转矩控制(Model predictive direct torque control,MPC-DTC)和无差拍转矩控制等^[10]。

由于MPC具有动态响应快和易于实现的优点,已经被广泛应用于电动机和功率变换器控制领域中。MPC-DTC以转矩和磁链为控制目标,通过代价函数选择使转矩和磁链跟踪误差最小的电压矢量,是一种最优化控制方法。目前,研究人员已经在MPC-DTC领域取得了一些成果,然而在应用过程中仍存在许多问题。首先,MPC-DTC代价函数中包含转矩和磁链两个物理量,由于它们的量纲和幅值范围等不同,需要设计权重因子来调整两参数在选择最优电压矢量时的重要性,目前权重因子校正主要依赖试凑和试验法,但是其过程比较繁琐。文献[11,12]提出了一种仅以转矩为控制目标的MPC-DTC,该方法将磁链预测过程与转矩计算相结合,省去了代价函数中的磁链项,可以避免权重因子的使用,但失去了跟踪磁链的功能。文献[13]研究了采用仿真和试验法校核权重因子的标准流程,通过仿真或试验参数化分析最佳参数,但由于参数化步长的限制,最佳权重因子依旧无法准确获得。除权重因子设计外,计算延时补偿是永磁同步电动机模型预测控制系统的另一挑战^[8]。文献[14]针对三相逆变器模型预测电流控制提出了一种两步预测补偿策略,被广泛应用到电动机控制领域^[15,16,17],但迄今为止还没有更多的补偿策略出现,方法的单一性限制了模型预测控制理论体系的进一步发展。

为了校正MPC-DTC代价函数中的权重因子,本文首先建立了永磁同步电动机离散预测模型,通过分析权重因子的本质,利用转矩和磁链对控制电压的响应速度不同,校核MPC控制器中的权重因子;此外,为降低转矩和电流波动并扩展模型预测控制理论,提出了一种新型的计算延时补偿策略,通过在一个控制周期内进行两次电流采样实现延时时间预估和延时补偿,提高系统的控制性能。

2 PMSM预测模型

在忽略铁心磁饱和且不计涡流和磁损耗的前提下,表贴式PMSM在αβ坐标系下的数学模型为

(1)$\frac{\mathrm{d} \psi_{\mathrm{s}}}{\mathrm{d} t}=\boldsymbol{u}_{\mathrm{s}}-i_{\mathrm{s}} R_{\mathrm{s}}$

(2)$\frac{\mathrm{d} i_{\mathrm{s}}}{\mathrm{d} t}=\frac{1}{L_{\mathrm{s}}}\left(\boldsymbol{u}_{\mathrm{s}}-i_{\mathrm{s}} R_{\mathrm{s}}-\mathrm{j} \frac{\sqrt{3}}{2} p \omega_{\mathrm{m}} \psi_{\mathrm{f}}\right)$

式中,u_s和i_s分别为定子电压和电流矢量;L_s和R_s分别为定子绕组电感和电阻;p为电动机极对数;ω_m为电动机转速;ψ_s和ψ_f分别为气隙磁链和永磁体磁链矢量,其中永磁体磁链满足

(3)$\psi_{\mathrm{f}}=\psi_{\mathrm{f}}(\cos \theta+j \sin \theta)$

式中,ψ_f为永磁体磁链幅值;θ为转子位置角度。

PMSM的电磁转矩方程为

(4)$T_{\mathrm{e}}=\frac{3}{2} p\left(\psi_{\mathrm{s}} \otimes i_{\mathrm{s}}\right)$

式中,T_e为输出电磁转矩;p为电动机极对数。

在k时刻,利用一阶欧拉法对式(1)和式(2)进行离散化,得到电动机磁链和电流的未来状态预测表达式

(5)$\boldsymbol{\psi}_{\mathrm{s}}(k+1)=\left(\boldsymbol{u}_{\mathrm{s}}(k)-\boldsymbol{i}_{\mathrm{s}}(k) R_{\mathrm{s}}\right) \cdot T+\boldsymbol{\psi}_{\mathrm{s}}(k)$

(6)$\begin{aligned}\boldsymbol{i}_{\mathrm{s}}(k+1)=& \frac{T}{L_{\mathrm{s}}} \boldsymbol{u}_{\mathrm{s}}(k)+\left(1-\frac{T R_{\mathrm{s}}}{L_{\mathrm{s}}}\right) \boldsymbol{i}_{\mathrm{s}}(k)- \mathrm{j} \frac{\sqrt{3}}{2 L_{\mathrm{s}}} T p \omega_{\mathrm{m}}(k) \psi_{\mathrm{f}}(k)\end{aligned}$

PMSM的电磁转矩方程为

(7)$T_{\mathrm{e}}(k+1)=\frac{3}{2} p\left(\psi_{\mathrm{s}}(k+1) \otimes i_{\mathrm{s}}(k+1)\right)$

式中,T为开关周期;u_s(k)为待选电压矢量(控制量);i_s(k)和ψ_s(k)为k时刻的状态量;i_s(k+1)和ψ_s(k+1)分别为k+1时刻的状态量。根据式(5)可知,当预测下一时刻磁链时,需要已知当前时刻磁链值ψ_s(k),但电动机中一般不会安装磁链传感器,因此,需要构建观测器实时检测电动机磁链值。将式(1)在k-1时刻利用欧拉法离散化,得到

(8)$\boldsymbol{\psi}_{\mathrm{s}}(k)=\left(\boldsymbol{u}_{\mathrm{s}}(k-1)-\boldsymbol{i}_{\mathrm{s}}(k-1) R_{\mathrm{s}}\right) \cdot T+\boldsymbol{\psi}_{\mathrm{s}}(k-1)$

与式(6)不同,u_s(k-1)为k-1时刻施加的最佳电压矢量,根据式(8)可知,ψ_s(k-1)又可根据前一时刻状态量计算得到。因此,当磁链初始值ψ_s(0)给定后,以后每一时刻的磁链都可观测。在t=0时,假设系统电流为0,气隙磁链只包含永磁体磁链,根据式(3)可知,电动机磁链初始值为

(9)$\psi_{\mathrm{s}}(0)=\psi_{\mathrm{f}}\left(\cos \theta_{0}+\mathrm{j} \sin \theta_{0}\right)$

式中,θ₀为转子初始位置。

3 PMSM模型预测转矩控制

3.1 MPC-DTC实现方法

3.1.1 系统原理

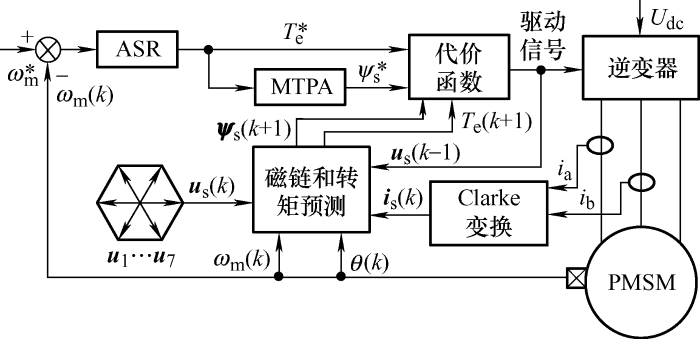
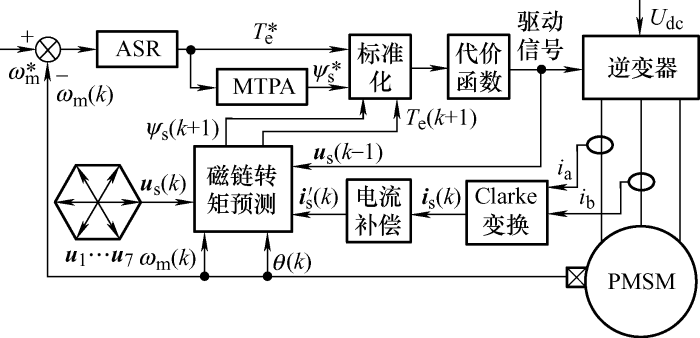
PMSM模型预测转矩控制原理框图如图1所示。电动机转速经过转速控制器(Automatic speed regulator,ASR)调节后产生参考转矩T_e^*,而参考磁链通过最大转矩电流比(Maximum torque per ampere,MTPA)算法计算而得,其中

(10)$\psi_{\mathrm{s}}^{*}=\sqrt{\psi_{\mathrm{f}}^{2}+\left(L_{\mathrm{q}} \cdot \frac{T_{\mathrm{e}}^{*}}{1.5 p \psi_{\mathrm{f}}}\right)^{2}}$

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 模型预测转矩控制原理框图

在一个采样周期内,根据当前电动机转速、位置、电流和上一周期状态信息,将7个待选电压矢量(u₁,u₂,…,u₇)分别代入预测模型得到预测磁链幅值ψ_s(k+1)和转矩T_e(k+1),并计算出对应的代价函数值,并通过比较选择使代价函数最小的电压矢量及开关状态发送该周期的控制信号,其中,以磁链和转矩为控制目标的代价函数为

(11)$J=\lambda\left|\psi_{\mathrm{s}}^{*}-\psi_{\mathrm{s}}(k+1)\right|+\left|T_{\mathrm{e}}^{*}-T_{\mathrm{e}}(k+1)\right|$

式中,λ为权重因子。

3.1.2 问题描述

首先,与传统的控制器(PI)不同,MPC-DTC控制器是基于最优控制理论的非线性控制器,目前,仍缺乏简单、高效的参数设计方法以保证系统的稳定性,而传统的试凑法具有过程复杂和可靠性低的缺点,因此,研究模型预测转矩控制器权重因子的本质和校核方法具有十分重要的工程价值。

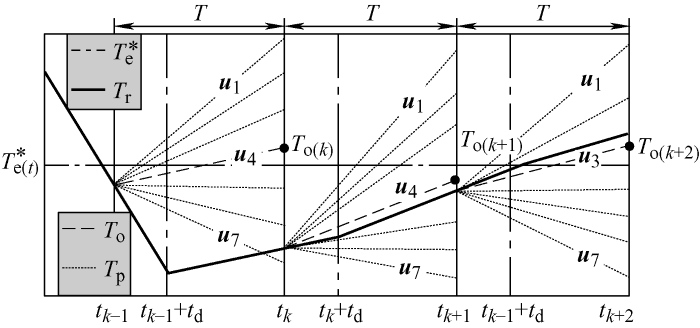
其次,以转矩跟踪为例,模型预测转矩控制过程如图2所示,T_r为电动机真实输出转矩,T_o为任一周期内优化选择的最佳电压矢量,T_p表示与7个电压矢量对应的下一时刻转矩估算值。在t_k_–1~t_k周期内,由图2可知,在不考虑计算延时情况下,即采样与最佳电压矢量施加都发生在t_k_–1时刻,u₄会使代价函数值最小,且当在该周期内发送对应的开关状态控制信号后,电动机转矩会具有最佳跟踪特性。然而,电压矢量与开关状态选择需要循环执行7次预测算法,加上排序,庞大的计算会导致信息采样与电压施加之间存在延时t_d。若在t_k_–1+t_d时刻施加u₄,一个采样周期后,转矩控制无法达到预期的效果。相比之下,若u₂或u₃作为该周期内的控制电压,转矩跟踪特性会更加优良。因此,计算延时会影响最佳控制电压选择过程,如果不采取有效的补偿措施,计算延时效应将持续存在于整个控制过程(例如t_k和t_k₊₁时刻),降低系统控制性能。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 模型预测转矩控制过程及延时问题

3.2 权重因子设计方法

3.2.1 权重因子本质

代价函数中必须采用权重因子调节磁链和转矩重要性的原因包括：① 两变量的量纲和幅值范围不同。首先,磁链的量纲为Wb而转矩的量纲为N·m,这导致两个参数属性具有本质不同;其次,电动机磁链幅值与其变化范围一般很小,特别是对于中小型电动机^{[9, 18-19]},其磁链范围在0.01~1.00 Wb,而电动机输出转矩的变化范围达到0~20 N·m。因此,在MPC-DTC算法中,需要首先消除磁链和转矩量纲和幅值范围之间的差异;② 磁链和转矩对控制变量的响应速度不同。该因素还可以表述为当同样的电压施加于电动机后,磁链和转矩在相同时间内的变化量不同,此时,变量的动态特性会影响其在代价函数中的重要性。此时,需要分析磁链和转矩响应速度之间的差异,并进行平衡,便可实现权重因子校正。

3.2.2 标准化

借助标幺化控制思想,为消除变量间的量纲与幅值差异,在把预测的未来磁链ψ_s(k+1)和转矩T_e(k+1)代入代价函数选择最优控制电压之前可通过除以最大值的方式进行标准化,即

(12)$\left\{\begin{array}{l}\psi_{\mathrm{sn}}^{*}=\frac{\psi_{\mathrm{s}}^{*}}{\psi_{\operatorname{smax}}} \\\psi_{\mathrm{sn}}(k+1)=\frac{\psi_{\mathrm{s}}(k+1)}{\psi_{\mathrm{smax}}}\end{array}\right.$

(13)$\left\{\begin{array}{l}T_{\mathrm{en}}^{*}=\frac{T_{\mathrm{e}}^{*}}{T_{\mathrm{emax}}} \\T_{\mathrm{en}}(k+1)=\frac{T_{\mathrm{en}}(k+1)}{T_{\mathrm{emax}}}\end{array}\right.$

式中,ψ_smax和T_emax分别是电动机最大磁链和最大转矩,其中,T_emax可设置为额定值,即T_emax=T_erated,而ψ_smax为电动机输出额定转矩时的磁链值,通过试验测得;ψ_sn^*和ψ_sn(k+1)为标准化的磁链,T_en^*和T_en(k+1)为标准化的转矩,它们的量纲统一为p.u.,且幅值范围为[0,1]。通过标准化操作,代价函数中的两变量具有了相同的量纲和幅值范围,只需要平衡它们对电压变化的响应速度即可完成参数校正。

3.2.3 响应速度平衡

为简化分析,将PMSM电动机模型转换到旋转轴坐标系下

(14)$\frac{\mathrm{d} \boldsymbol{\psi}_{\mathrm{sr}}}{\mathrm{d} t}=\boldsymbol{u}_{\mathrm{sr}}-\boldsymbol{i}_{\mathrm{sr}} R_{\mathrm{s}}$

(15)$\frac{di_{sr\_q}}{dt}=\frac{1}{L_{s}}(u_{sr\_q}-i_{sr\_q} R_{s}-p \omega_{m} \psi_{f})$

(16)$T_{\mathrm{e}}=\frac{3}{2} p \psi_{\mathrm{f}} i_{\mathrm{sr}_{-} \mathrm{q}}$

式中,u_sr和i_sr分别为定子电压和电流矢量;u_{sr_q}和i_{sr_q}分别为q轴电压和电流;ψ_sr为旋转坐标系下气隙磁链。离散化模型为

(17)$\boldsymbol{\psi}_{\mathrm{sr}}(k+1)=\left(\boldsymbol{u}_{\mathrm{sr}}(k)-\boldsymbol{i}_{\mathrm{sr}}(k) R_{\mathrm{s}}\right) \cdot T+\boldsymbol{\psi}_{\mathrm{sr}}(k)$

(18)$i_{sr\_q}(k+1)=\frac{T}{L_{s}} u_{sr\_q}(k)-\frac{T p \psi_{\mathrm{f}}}{L_{\mathrm{s}}} \omega_{m}(k)+(1-\frac{T R_{\mathrm{s}}}{L_{s}})i_{\mathrm{sr}_{-}q}(k)$

(19)$T_{\mathrm{e}}(k+1)=\frac{3}{2} p \psi_{\mathrm{f}} i_{\mathrm{sr}_{-9}}(k+1)$

在t_k~t_k₊₁周期内,假设施加电压发生扰动为Δu_sr(k)=( Δu_{sr_d}(k),Δu_{sr_q}(k)),根据式(17)和式(18),磁链和电流在相同时间(一个周期)内由该扰动造成的变化量为

(20)$\left|\Delta \boldsymbol{\psi}_{\mathrm{sr}}(k+1)\right|=\left|\Delta \boldsymbol{u}_{\mathrm{sr}}(k)\right| \cdot T$

(21)$|\Delta i_{sr\_q}(k+1)|=\frac{T}{L_{s}}| \Delta u_{sr\_q}(k)|$

式中,Δu_{sr_d}(k)和Δu_{sr_q}(k)数量级相当,假设两者相等,即

(22)$\left|\Delta \boldsymbol{\psi}_{\mathrm{sr}}(k+1)\right|=\sqrt{2}\left|\Delta u_{\mathrm{sr}_{-} \mathrm{q}}(k)\right| \cdot T$

根据式(19)可知,PMSM的电磁转矩在T内由Δu_sr(k)引起的变化量为

(23)$\begin{array}{c}\Delta T_{\mathrm{e}}(k+1)=\frac{3}{2} p \psi_{\mathrm{f}} \Delta i_{\mathrm{sr}_{-}q}(k+1)= \frac{3}{2} p \psi_{\mathrm{f}} \frac{T}{L_{\mathrm{s}}}\left|\Delta u_{\mathrm{sr}_{-} q}(k)\right|\end{array}$

根据式(22)和式(23)定义转矩磁链响应速度比δ为

(24)$\delta=\frac{\Delta T_{\mathrm{e}}(k+1)}{\left|\Delta \psi_{\mathrm{sr}}(k+1)\right|}=\frac{3 p \psi_{\mathrm{f}}}{2 \sqrt{2} L_{\mathrm{s}}}$

为平衡转矩磁链响应速度在代价函数中的影响,权重因子λ设置为

(25)$\lambda=\delta$

3.3 延时补偿策略

在t_k_–1~t_k周期内(图2),若在t_k_–1时刻获得 t_k_–1+t_d时刻的磁链和转矩值,并利用它们进行未来状态预测,MPC-DTC执行过程可等效为采样与最佳电压矢量施加都发生在t_k_–1+t_d时刻的无延时控制。由式(5)~(7)可知,为得到延时t_d后的磁链与转矩值,应预先估计该时刻的电流值。在此基础上,本文提出的延时补偿过程应包含三部分：① 延时时间计算;② 补偿电流预测;③ 补偿磁链和转矩预测。以α轴电流i_α为例,假设电流在一个采样周期内线性变化,补偿策略的具体实施过程如下。

3.3.1 延时时间计算

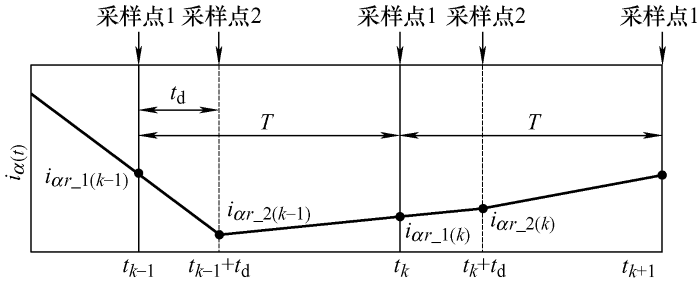
传统的MPC-DTC算法,在每个周期执行的初始阶段,进行一次电动机状态信息采样,且采集的信息直接用于预测算法中,导致工程师无法评估延时时间的长短以及其对电动机控制性能的影响,为此,图3设计了一种基于“单周期双采样”的延时时间估算方法。在无其他补偿算法执行时,在每一个采样周期内,电流采样操作会被执行两次：第一次仍然在每个周期的初始阶段,第二次则发生在发送开关状态信号之前。其中,在t_k_–1~t_k周期内,第一次采样电流为i_ar_{_1}(k–1),第二次采样电流为i_ar_{_2}(k–1);在t_k~t_k₊₁周期内,第一次和第二次采样电流分别为i_ar_{_1}(k)和i_ar_{_2}(k)。根据假设,计算延时时间可由式(26)计算得到

(26)$t_{\mathrm{d}}=\frac{\left|i_{a r_{-} 2}(k)-i_{a r_{-} 1}(k)\right|}{\left|i_{a r_{-} 2}(k)-i_{a r_{-} 2}(k-1)\right|} \cdot T$

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 延时时间计算

3.3.2 补偿电流预测

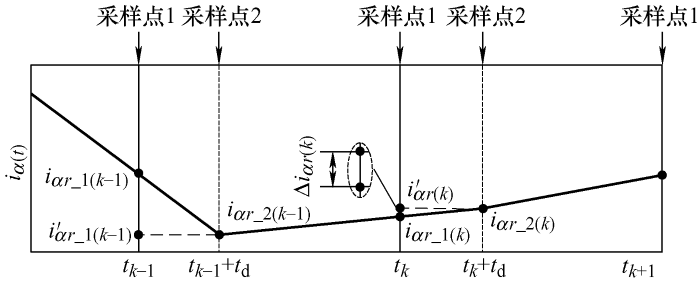
由图4可知,以t_k~t_k₊₁周期为例,获得计算延时时间后,在利用模型预测未来状态之前,可根据式(27)算得补偿电流

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 补偿电流预测策略

(27)$\Delta i_{\alpha r}(k)=\frac{i_{a r_{-} 1}(k)-i_{a r_{-} 2}(k-1)}{T-t_{\mathrm{d}}} \cdot t_{\mathrm{d}}$

则在t_k+t_d的电流为

(28)$i_{\alpha r}^{\prime}(k)=i_{a r_{-1}}(k)+\Delta i_{\alpha r}(k)$

同理,β轴补偿电流i^'_βr(k)也可得到。

利用i^'_αr(k) 和i^'_βr(k)进行未来电流、磁链和转矩预测时,模型预测直接转矩控制算法执行过程便可等效为采样与开关信号同时执行的无延时控制,且在t_k₊₁+t_d时刻,转矩和磁链控制达到预期跟踪效果,实现最优化控制过程。

3.3.3 补偿磁链和转矩预测

若利用补偿电流i^'_s(i^'_αr(k),i^'_βr(k))实现MPC-DTC算法,电动机磁链和电流的未来状态预测表达式需要修正为

(29)$\psi_{s}(k+1)=(u_{s}(k)-i_{s}^{\prime}(k) R_{s}) \cdot T+\psi_{s}(k)$

(30)$i_(k+1)=\frac{T}{L_{s}}u_{s}(k)+(1-\frac{TR_{s}}{L_{s}}) i_{s}^{\prime}(k) j \frac{\sqrt{3}}{2L_{s}} Tp \omega_{m}(k)\psi_{f}(k)$

进而,PMSM的补偿转矩可根据式(7)算得。

考虑权重因子校正和延时补偿的模型预测转矩控制原理框图如图5所示。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 考虑权重因子校正和延时补偿的MPC-DTC原理框图

4 试验验证

首先,试验是为了验证所设计的MPC-DTC控制器权重因子能够保证系统的动态以及稳态性能,其次,通过比较延时补偿前后的系统性能,验证本文提出的权重因子和延时补偿设计与分析方法是有效的。本文针对一台表贴式永磁同步电动机进行算法验证,其系统参数如表1所示。试验控制平台以DSP TMS320F2812为主控芯片,逆变器采用智能功率模块(IPM)PM75RLA12,开关电动机位置检测采用光电编码器,加载和记录转速由Magtrol公司的10 kW测功台完成,磁链和电磁转矩数据由数字处理器DSP记录,并通过RS-485发送至上位机。

表1 永磁同步电动机控制系统参数

数值	参数
额定转速/ (r·min^-1)	3 000
直流电压U_dc/V	300
额定转矩T_l / (N·m)	4.5
绕组电感L_s/H	0.001 7
极对数p	5
转动惯量J/(kg·m²)	0.000 6
摩擦因数B	0.000 3
转子磁链幅值Ψ_f/Wb	0.055
绕组电阻R_s/Ω	0.43
采样频率/kHz	10

新窗口打开| 下载CSV

根据式(24)和式(25)可得试验中磁链权重因子为λ=171.58。

4.1 稳态性能

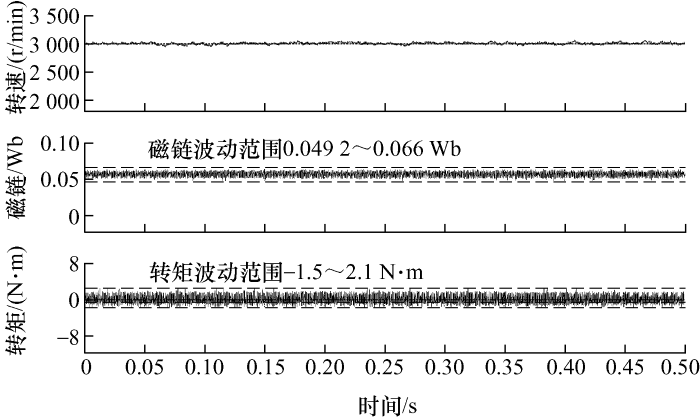
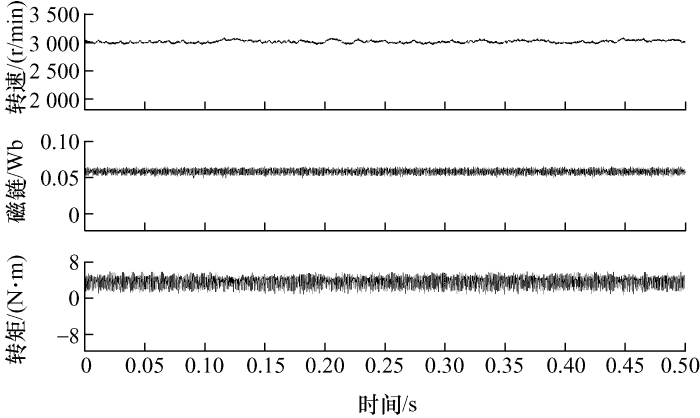
利用本文提出的MPC-DTC算法控制电动机旋转于3 000 r/min,图6和图7分别为电动机空载和负载(4.5 N·m)时的稳态特性。首先,电动机能按照给定参考转速旋转,稳态误差为0,说明所设计的磁链权重因子满足稳态性能要求;其次,空载状态下,平均气隙磁链约为0.057 6 Wb,负载时,磁链值略大于空载值(0.057 9 Wb);最后,虽然电动机转矩存在波动,但其平均输出值展现出了良好的跟踪性。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 带延时补偿空载稳态特性

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 带延时补偿负载稳态特性

4.2 动态性能

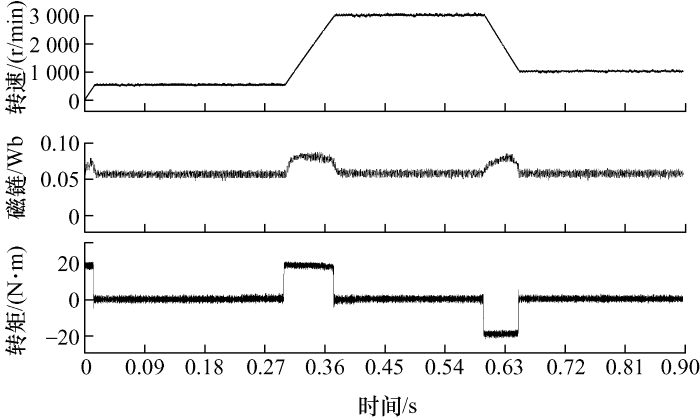
利用本文提出的方法控制电动机从0加速至500 r/min,在0.3 s时刻,设置参考转速为 3 000 r/min,并保持至0.6 s,然后,控制电动机降速至1 000 r/min。图8为电动机的加减速动态特性图。首先,在电动机加减速过程中,电动机磁链都会变大,当电动机转速再次达到稳定后,磁链恢复至0.056 Wb;其次,加减速过程中输出最大电磁转矩分别约为±20 N·m,这是由转速控制器限幅输出导致的,电动机稳定运行时,输出电磁转矩略大于0;当电动机从500 r/min加速至3 000 r/min,上升时间约为80 ms,超调非常小(小于10 r/min),且降速特性与加速特性非常相似,这表明所设计的权重因子及MPC-DTC算法具有良好的动态性能。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 带延时补偿加减速动态特性

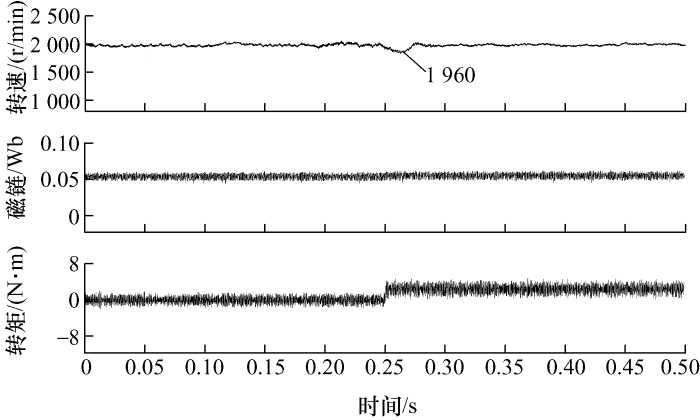
为验证电动机的抗负载干扰特性,控制电动机稳定运行至2 000 r/min,在0.25 s时刻,突加4.5 N·m负载转矩,图9为突加负载时的电动机动态特性。突加负载时,电动机转速大范围下降(94 r/min),但电动机转矩很快恢复至2 000 r/min,调节时间约为30 ms。试验表明,所设计的MPC-DTC参数具有良好的抗负载干扰特性。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 带延时补偿突加负载动态特性

4.3 延时补偿前后性能对比

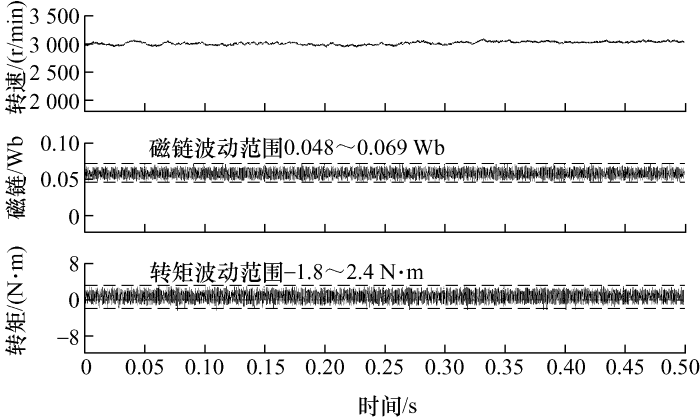
当采用无延时补偿的MPC-DTC算法控制电动机工作于3 000 r/min时,电动机的空载稳态特性如图10所示,可以看出,磁链和转矩脉动大小分别为0.021 Wb和4.2 N·m,与图6相比(磁链和转矩脉动分别为0.0178 Wb和3.6 N·m),脉动增长约为17%,所以,所提出的延时补偿策略能够降低控制磁链和转矩脉动,提高系统的性能。

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 无延时补偿空载稳态特性

5 结论

(1) 本文提出了新型预测转矩控制代价函数权重因子校核和计算延时补偿策略,解决了权重因子校正理论方法缺失的难题。

(2) 本文所提出的基于“单周期双采样”的计算延时补偿策略与传统补偿方法完全不同,完善了模型预测控制理论体系。

(3) 通过试验验证可得,所提出的权重因子校核方法能够保证良好的系统稳态和动态性能,且延时补偿策略能够进一步降低磁链和转矩脉动,改善PMSM系统的控制性能。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

黄志坡, 唐金城, 叶开明, 等.

六相串联三相双永磁同步电机直接转矩控制的研究

[J]. 微电机, 2018,51(12):32-41.