1 引言
随着越来越多的新能源接入,以及直流用电负荷的增多,为电网带来一系列电能质量问题。相较于交流配电网,直流配电网具有容量大、损耗小、电能质量好、无需无功补偿以及适用于各类电源与负载接入等优点,因此研究直流配电网具有较高的应用价值[1 ,2 ,3 ] 。
电能路由器是信息控制与能量控制结合的统一控制中心[4 ,5 ] ,是直流配电网关键设备,主要负责中压直流配网与低压直流微电网的能量与信息的统一管理。直流电能路由器由多组直流变换单元组合辅以高性能通信控制系统构成,对其进行宏观优化的综合控制是提升控制效果的有效途径[6 ] 。按照各个变换器分别进行独立控制时,这种控制易于实现,但是在端口能量变化的过程中会加重直流母线的能量承载压力,降低直流母线的响应性能。为了提升直流母线的瞬态响应性能,第一种是用容量、重量、体积更大的直流母线电容作为能量池,这种方法会增加变换器组的复杂度;第二种是使用宏观的整体控制技术搭建整个变换单元的端口功率等效电路,依靠变换器之间的相互关系进行整体式的综合控制。第二种方法将电能路由器看成能量变换的整体,控制能量在变换器之间传递的快速性和稳定性,能够增强直流母线的动态稳定性,进而减少母线电容[5 ] 。
无源控制方法是根据整体的能量作为控制目标,有稳定的性能[6 ] 。耗散性控制是利用系统的能量耗散建立关于系统能量的函数关系,设计关于能量函数的控制器,有良好的稳健程度[7 ,8 ,9 ] 。针对三端口交流电能路由器建立了针对高低压两级直流母线的能量平衡控制器,提高了控制的稳态性能,并调整了时间尺度控制方法,对于交流电能路由器有着较好的效果[6 ] 。文献[10 ] 针对配电网,设置了基于配 电网端口能量平衡的李雅普诺夫函数,根据运行情况确定控制目标,可以控制降低系统的运行成本。
上述及已有的文献研究中根据能量平衡关系进行控制时,仅对变换器母线能量聚合列出关系,并对多级关系进行解耦控制,针对端口的能量控制也仅仅是对于配电网进行控制,并未对单独电能路由器进行控制。本文针对直流配电网电能路由器单低压直流母线拓扑,利用路由器的各输入输出点的能量关系进行能量均衡控制。同时针对双有源桥输入均压和低压母线的能量稳定问题,采用两级控制模型,本文中的模型均采用理想模型。
2 直流电能路由器模型
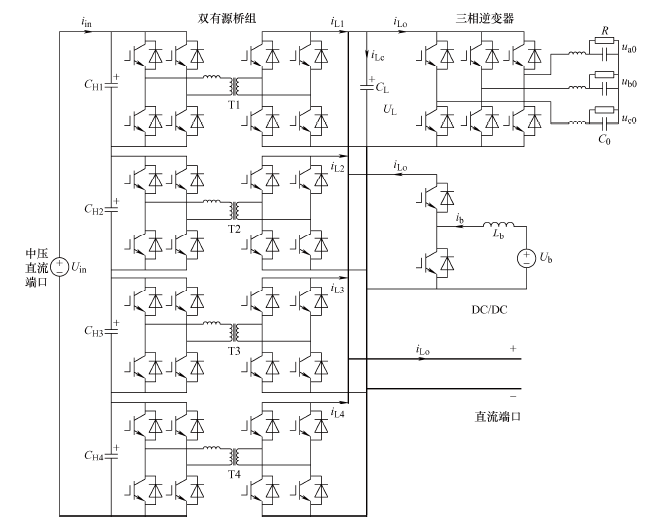
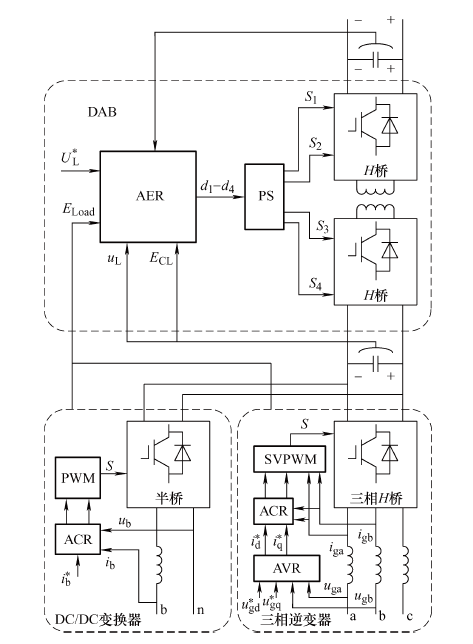
本文设计变换电路如图1 所示,为面向直流配电网的四端口直流电能路由器,其中大容量直流变换为提高系统容量采用4个模块化双有源直流变直流全桥(Dual active bridge,DAB)模块串入并出,将接入的中压直流变换为低压直流提供给低压直流端口,逆变器为三相两电平变换器,为配合现有家庭配网提供三相接口,直流母线并联一个DC/DC变换器供新能源或储能装置使用。
图1
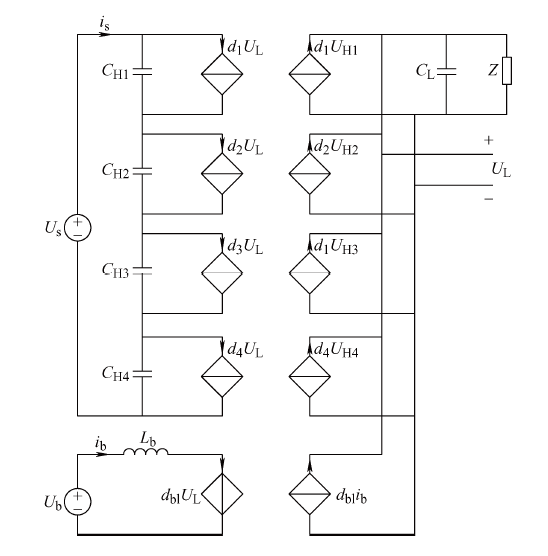
分别对变换电路各部分建立平均等效模型,对于逆变器及滤波的控制不作为本文主要研究点,为简化控制,将三相逆变输出滤波用一个等效阻抗代替[11 ] 。对于直流电能路由器的平均等效模型的端口流进流出的功率进行累计积分,可以得到各端口能量关系,得到直流电能路由器的平均等效电路图如图2 所示,其中$d_x$为第x个双有源桥单元的等效移相控制占空比,$U_H$以及$U_L$为变压器两侧电压值。
图2
(1) $\left\{ \begin{align} & {{E}_{\text{S}}}=\sum\limits_{i=1}^{4}{\Delta {{E}_{\text{CH}i}}}+\Delta {{E}_{\text{CL}}}+{{E}_{\text{Load}}} \\ & \Delta {{E}_{\text{CH1}}}=\frac{1}{2}{{C}_{\text{H1}}}(U_{\text{H}}^{*2}-U_{\text{H1}}^{2}) \\ & \Delta {{E}_{\text{CH2}}}=\frac{1}{2}{{C}_{\text{H2}}}(U_{\text{H}}^{*2}-U_{\text{H2}}^{2}) \\ & \Delta {{E}_{\text{CH3}}}=\frac{1}{2}{{C}_{\text{H3}}}(U_{\text{H}}^{*2}-U_{\text{H3}}^{2}) \\ & \Delta {{E}_{\text{CH4}}}=\frac{1}{2}{{C}_{\text{H4}}}(U_{\text{H}}^{*2}-U_{\text{H4}}^{2}) \\ & \Delta {{E}_{\text{CL}}}=\frac{1}{2}{{C}_{\text{L}}}(U_{\text{L}}^{*2}-U_{\text{L}}^{2}) \\ \end{align} \right.$
式中,变量的下标H、L分别表示直流电能路由器的高压直流输入侧与低压母线侧;$E_s$表示电能路由器注入的能量;$\Delta {{E}_{\text{CH}i}}$表示双有源变换单元前各个均压电容的能量;$\Delta {{E}_{\text{CL}}}$表示低压直流母线均压电容的能量;$E_{Load}$为负载输出的能量;上标*则表示该变量的相应给定值。端口能量模型中包含6个方程,反映了电能路由器运行时各个端口能量和内部无源器件存储的能量的变化关系。
由于串入并出的双有源变换桥模块高压端的均压电容并不能保证其品质的一致性,其均压问题会使得开关管应力过大,同时变换模块的前后级存在能量波动相互耦合的问题。本文首先针对低压母线的能量稳定设计了端口能量平衡的控制器,针对均压问题提出进一步优化控制目标的两级式综合控制方法。
3 端口能量平衡的控制方法
采用双有源桥模组串入并出控制低压直流母线电压时,以式(1)的能量模型作为控制的落脚点,考虑变换器件的开关能量损耗,将低压直流母线连接器件的所有开关损耗与无源损耗用$E_{Lossl}$表示,则直流母线上的能量在一个周期$T_s$内的能量平衡关系式
(2) ${{E}_{\text{4 }\!\!\_\!\!\text{ DAB}}}=\Delta {{E}_{\text{CL}}}+{{E}_{\text{Load}}}+{{E}_{\text{Loss1}}}$
式中,$E_{4DAB}$为并联四模块双有源桥传输到直流母线的能量和。
(3) ${{P}_{\text{4 }\!\!\_\!\!\text{ DAB}}}=\frac{1}{2}{{C}_{\text{L}}}\frac{U_{\text{L}}^{*2}-U_{\text{L}}^{2}}{{{T}_{\text{S}}}}+{{P}_{\text{Load}}}+{{P}_{\text{Loss1}}}$
式中,$P_{Load}$、$P_{Lossl}$分别为直流母线的消耗功率和损失功率。
(4) ${{P}_{\text{DAB}}}=\frac{n{{U}_{\text{H }\!\!\_\!\!\text{ s}}}{{U}_{\text{L }\!\!\_\!\!\text{ s}}}d(1-d)}{2{{f}_{\text{S}}}{{L}_{\text{k}}}}$
式中,$U_{Hs}$和$U_{Ls}$分别是双有源桥一、二次侧的电压值;n为隔离变压器变比;$f_s$为双有源桥的控制频率;$L_k$为隔离变压器的漏感。在均压的情况下,四组变换单元均功率传输,则式(3)可以改写成
(5) $4\times \frac{n{{U}_{\text{H }\!\!\_\!\!\text{ s}}}{{U}_{\text{L }\!\!\_\!\!\text{ s}}}d(1-d)}{2{{f}_{\text{S}}}{{L}_{\text{k}}}}=\frac{{{C}_{\text{L}}}(U_{\text{L}}^{*2}-U_{\text{L}}^{2})}{2{{T}_{\text{S}}}}+{{P}_{\text{Load}}}+{{P}_{\text{Loss1}}}$
(6) $d=\frac{2{{f}_{\text{S}}}{{L}_{\text{k}}}\left[ \frac{1}{2}{{C}_{\text{L}}}(U_{\text{L}}^{*2}-U_{\text{L}}^{2}){{f}_{\text{S}}}+{{P}_{\text{Load}}}+{{P}_{\text{Loss1}}} \right]}{4n{{U}_{\text{H }\!\!\_\!\!\text{ s}}}{{U}_{\text{L }\!\!\_\!\!\text{ s}}}}$
双有源桥控制器存在延迟,可以用一阶惯性环节代替,时间常数为$T_d$,双有源桥模型的传输系数为
(7) ${{k}_{\text{d1}}}=n{{U}_{\text{H1 }\!\!\_\!\!\text{ s}}}/(2{{f}_{\text{S}}}{{L}_{\text{k1}}})\ \ \ \ {{k}_{i}}=1/{{U}_{\text{L}}}$
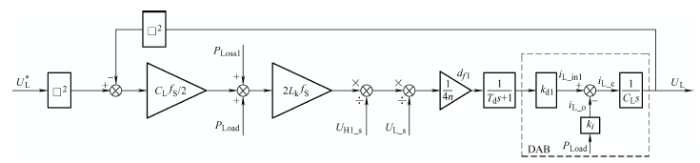
图3
对级联双有源桥采用能量平衡的控制方法进行均压控制。当电容能够均压时,四级联双有源桥传输功率相等,但是由于串联的均压电容不一致,在占空比相同的情况下,均压问题会导致双有源桥传输功率不相同,开关管应力不均。
理想情况下的双有源桥传输功率为式(3),当级联双有源桥均压不一致时,单级模块实际传输的功率与理想传输功率差额为
(8) $\Delta {{P}_{\text{DAB}\_i}}=\frac{n{{U}_{\text{L}}}d(1-d)({{U}_{\text{H }\!\!\_\!\!\text{ s}}}-{{U}_{\text{CH}i}})}{2{{f}_{\text{S}}}{{L}_{\text{k}}}}$
式中,$U_{CHi}$为存在电压偏差时各分压电容即双有源桥输入端的电压值。将功率偏差归算到各自的占空比即
(9) ${{d}_{i}}=d{{k}_{i}}=d\left[ 1+\frac{{{U}_{\text{H }\!\!\_\!\!\text{ s}}}-{{U}_{\text{CH}i}}}{{{U}_{\text{H }\!\!\_\!\!\text{ s}}}} \right]$
式中,$k_i$表示将功率偏差归算后,对原始占空比进行均压调整后的调整系数。可以看出,调整过程是一个根据能量均衡目标的一个比例调节环节。将这一均压环节代回到式(6)后得到均压后针对每一组双有源桥的占空比表达式
(10) ${{d}_{i}}=\frac{2{{f}_{\text{S}}}{{L}_{\text{k}}}({{U}_{\text{H }\!\!\_\!\!\text{ s}}}-{{U}_{\text{CH}i}})\left[ \frac{1}{2}{{C}_{\text{L}}}(U_{\text{L}}^{*2}-U_{\text{L}}^{2}){{f}_{\text{S}}}+{{P}_{\text{Load}}}+{{P}_{\text{Loss1}}} \right]}{4nU_{\text{H }\!\!\_\!\!\text{ s}}^{\text{2}}{{U}_{\text{L }\!\!\_\!\!\text{ s}}}}$
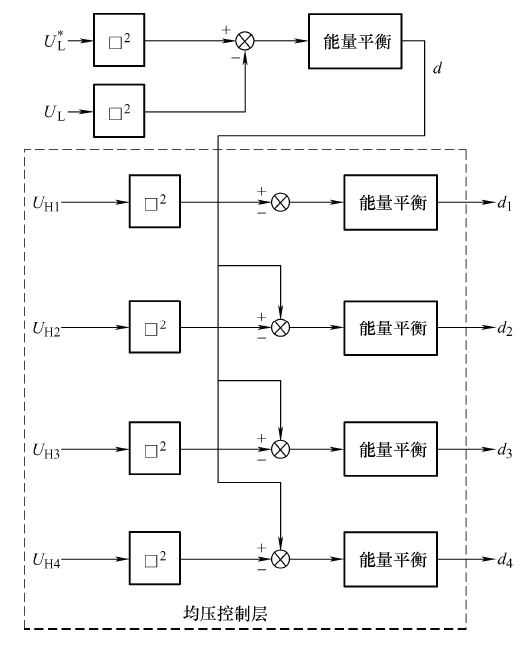
图4 为均压控制框图,系统通过平衡各个输入输出端口的能量,通过能量平衡控制器得出初步的双有源桥等效占空比d。继而通过对比各变换单元存在的功率偏差,与初步占空d比作比较。由于每组偏差各不相同,通过计算可以得出$d_1$~$d_4$,即各自单元的等效占空比。
图4
本文针对于电能路由器的综合型控制,对于双有源桥的控制采用基础的单移相控制方法,在单移相控制中,全桥电路的对角管的驱动脉冲相同,相同桥臂的驱动脉冲互补,分别在高频变压器的初级侧和次级侧产生占空比为50%的方波电压$v_{h1}$和$v_{h2}$。而在两个全桥之间的对应的开关管的驱动脉冲存在一个移相比D (或移相时间$DT_{hs}$),所以$v_{h1}$和$v_{h2}$之间也存在移相时间$DT_{hs}$,其中$T_{hs}$是半个开关周期。对于不同的功率传输方向,移相比D 的取值范围为(-0.5,0.5),功率总是从超前相位侧流向滞后相位侧。通过调节移相比D 就可以调节双有源桥的功率流动的大小和方向,进而也可以调节变换器输出电压的大小。
电能路由器并网时,高压直流端口连接中压直流配电网接入能量,综合控制器细节框图如图5 所示,能量控制器(Automatic energy regulator,AER)流入低压直流母线电压的能量与流出电能路由器的能量稳定;电流控制调节器(Automatic current regulator,ACR)用于协调中压配电网输入电流平衡;三相逆变器采用双闭环控制;DC/DC变换器采用Boost变换采用ACR控制输出电流。
图5
4 仿真分析
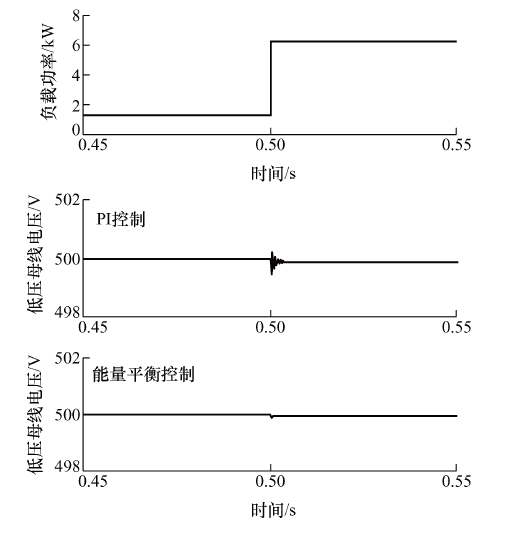
为验证端口能量综合控制的有效能,在Matlab/Simulink软件里面搭建了如图1 所示的系统模型进行仿真,与传统PI控制结果进行对比,证明端口能量平衡综合控制方法在负载功率变化的瞬态响应的有效性。仿真电路参数见表1 。
为了对比综合控制器和PI传统控制对稳态性能调节的效果,对低压直流母线的控制分别采用端口能量平衡综合控制器和PI控制器,低压直流母线电压波形图如图6 所示。仿真在0.50 s时,负载功率由1.2 kW突增至6.2 kW,由图5 可知,采用传统PI控制器时,由于各级变换器之间存在控制响应延迟,造成负荷波动时母线电压产生抖动,而端口能量平衡综合控制器由于从整体能量变化出发,所以系统的响应速度比较高,在仿真中只存在轻微抖动,综合控制器的效果比采用传统PI控制器的好。
图6
由于双有源桥的控制采用的是单移相控制,存在较大的功率回流,会导致输出电压存在较大的谐波。对于谐波,使用容量更大、性能更好的电容来改善输出是一种办法;第二是采用更加复杂的对于双有源桥的控制办法,比如双移相或者三移相控制方法。这些更加复杂的办法最后还是存在一个等效占空比$d_i$。作为综合控制,本文的重点在于电能路由器的中体控制上面。
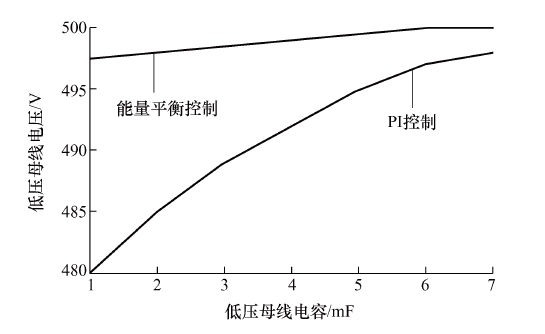
当低压直流母线电容值在较大范围变化时,对低压直流母线电压谐波峰值的影响如图7 所示。当直流母线电容增大时,直流母线电压响应的谐波峰值会减小。采用能量平衡控制的低压母线电压波动整体优于PI控制的低压直流母线电压。图7 表示在一定的母线电压瞬态峰值下,采用端口能量综合控制可以减少母线电容的设计容量,优化系统的体积与质量。
图7
5 结论
本文针对直流配电网电能路由器,分析了各端口能量流动情况,设计了基于端口能量平衡的综合控制器和能量平衡的均压控制方法。通过仿真对比分析了直流母线在负载突变的情况下不同控制方法中的响应情况,得到如下结论。
(1) 端口能量平衡控制在直流配电网电能路由器上的有效性能够综合控制能量在电能路由器上灵活稳定流动,提高母线运行的稳定性,降低电网波动。
(2) 本文提出的综合控制方法改善了变换器的响应性能,可以减小低压母线电容的设计容量,进而能够减少系统的体积。
参考文献
View Option
[1]
江道灼 , 郑欢 . 直流配电网研究现状与展望
[J]. 电力系统自动化 , 2012 ,36 (8 ):98 -104 .
[本文引用: 1]
Jiang Daozhuo Zheng Huan . Research status and developing prospect of DC distribution network
[J]. Automation of Electric Power Systems , 2012 ,36 (8 ):98 -104 .
[本文引用: 1]
[2]
宋强 , 赵彪 , 刘文华 , 等 . 智能直流配电网研究综述
[J]. 中国电机工程学报 , 2013 ,33 (25 ):9 -19,5 .
[本文引用: 1]
Song Qiang Zhao Biao Liu Wenhua , et al . An overview of research on smart DC distribution power network
[J]. Proceedings of the CSEE , 2013 ,33 (25 ):9 -19,5 .
[本文引用: 1]
[3]
Zhou Xuesong Wang Fuzhi Ma Youjie , et al . An overview on energy router based on various forms of energy
[C]// Proceedings of IEEE Chinese Control and Decision Conference,Yinchuan,China , 2016 :2901 -2906 .
[本文引用: 1]
[4]
Feng Gaohui Zhao Zhengming Yuan Liqiang , et al . Combined DC voltage control scheme for three-port energy router based on instantaneous energy balance
[J]. Proceedings of IEEE Energy Conversion Congress and Exposition(ECCE) , 2016 :1 -7 .
[本文引用: 1]
[5]
高帅 , 张兴 , 赵文广 , 等 . 双有源桥DC-DC变换器最小回流功率控制策略
[J]. 电气工程学报 , 2019 ,14 (2 ):24 -29 .
[本文引用: 2]
Gao Shuai Zhang Xing Zhao Wenguang , et al . Minimum reactive power control strategy for dual active bridge DC-DC converter
[J]. Journal of Electrical Engineering , 2019 ,14 (2 ):24 -29 .
[本文引用: 2]
[6]
冯高辉 , 赵争鸣 , 袁立强 . 基于能量平衡的电能路由器综合控制技术
[J]. 电工技术学报 , 2017 ,32 (14 ):34 -44 .
[本文引用: 3]
Feng Gaohui Zhao Zhengming Yuan Liqiang . Synthetical control technology of electric energy router based on energy balance relationship
[J]. Transactions of China Electrotechnical Society , 2017 ,32 (14 ):34 -44 .
[本文引用: 3]
[7]
Komurcugil H Kukrer O . A new control strategy for single-phase shunt active power filters using a Lyapunov function
[J]. IEEE Transactions on Industrial Electronics , 2006 ,53 (1 ):305 -312 .
[本文引用: 1]
[8]
Valderrama G E Stankovic A M Mattavelli P . Dissipativity based adaptive and robust control of UPS in unbalanced operation
[J]. IEEE Transactions on Power Electronics , 2003 ,18 (4 ):1056 -1062 .
[本文引用: 1]
[9]
雷涛 , 李龙春 , 邬岑颖 , 等 . 双有源桥DC-DC暂态直流偏置分析和抑制策略研究
[J]. 电气工程学报 , 2018 ,13 (7 ):8 -15 .
[本文引用: 1]
Lei Tao Li Longchun Wu Cenying , et al . Study of transient DC-DC bias analysis and suppression methods in dual active bridge converter
[J]. Journal of Electrical Engineering , 2018 ,13 (7 ):8 -15 .
[本文引用: 1]
[10]
盛万兴 , 李鹏华 , 段青 , 等 . 基于Lyapunov优化方法的含能量路由器的能源集线器能量管理策略研究
[J]. 中国电机工程学报 , 2019 ,39 (21 ):6212 -6225 .
[本文引用: 1]
Sheng Wanxing Li Penghua Duan Qing , et al . Research on energy management strategy of energy hub with energy router based on Lyapunov optimization method
[J]. Proceedings of the CSEE , 2019 ,39 (21 ):6212 -6225 .
[本文引用: 1]
[11]
Mao X Falcones S Ayyanar R . Energy-based control design for a solid state transformer
[C]// Proceedings of IEEE PES General Meeting,Minneapolis,MN,US , 2010 :1 -7 .
[本文引用: 1]
直流配电网研究现状与展望
1
2012
... 随着越来越多的新能源接入,以及直流用电负荷的增多,为电网带来一系列电能质量问题.相较于交流配电网,直流配电网具有容量大、损耗小、电能质量好、无需无功补偿以及适用于各类电源与负载接入等优点,因此研究直流配电网具有较高的应用价值[1 ,2 ,3 ] . ...
直流配电网研究现状与展望
1
2012
... 随着越来越多的新能源接入,以及直流用电负荷的增多,为电网带来一系列电能质量问题.相较于交流配电网,直流配电网具有容量大、损耗小、电能质量好、无需无功补偿以及适用于各类电源与负载接入等优点,因此研究直流配电网具有较高的应用价值[1 ,2 ,3 ] . ...
智能直流配电网研究综述
1
2013
... 随着越来越多的新能源接入,以及直流用电负荷的增多,为电网带来一系列电能质量问题.相较于交流配电网,直流配电网具有容量大、损耗小、电能质量好、无需无功补偿以及适用于各类电源与负载接入等优点,因此研究直流配电网具有较高的应用价值[1 ,2 ,3 ] . ...
智能直流配电网研究综述
1
2013
... 随着越来越多的新能源接入,以及直流用电负荷的增多,为电网带来一系列电能质量问题.相较于交流配电网,直流配电网具有容量大、损耗小、电能质量好、无需无功补偿以及适用于各类电源与负载接入等优点,因此研究直流配电网具有较高的应用价值[1 ,2 ,3 ] . ...
An overview on energy router based on various forms of energy
1
2016
... 随着越来越多的新能源接入,以及直流用电负荷的增多,为电网带来一系列电能质量问题.相较于交流配电网,直流配电网具有容量大、损耗小、电能质量好、无需无功补偿以及适用于各类电源与负载接入等优点,因此研究直流配电网具有较高的应用价值[1 ,2 ,3 ] . ...
Combined DC voltage control scheme for three-port energy router based on instantaneous energy balance
1
2016
... 电能路由器是信息控制与能量控制结合的统一控制中心[4 ,5 ] ,是直流配电网关键设备,主要负责中压直流配网与低压直流微电网的能量与信息的统一管理.直流电能路由器由多组直流变换单元组合辅以高性能通信控制系统构成,对其进行宏观优化的综合控制是提升控制效果的有效途径[6 ] .按照各个变换器分别进行独立控制时,这种控制易于实现,但是在端口能量变化的过程中会加重直流母线的能量承载压力,降低直流母线的响应性能.为了提升直流母线的瞬态响应性能,第一种是用容量、重量、体积更大的直流母线电容作为能量池,这种方法会增加变换器组的复杂度;第二种是使用宏观的整体控制技术搭建整个变换单元的端口功率等效电路,依靠变换器之间的相互关系进行整体式的综合控制.第二种方法将电能路由器看成能量变换的整体,控制能量在变换器之间传递的快速性和稳定性,能够增强直流母线的动态稳定性,进而减少母线电容[5 ] . ...
双有源桥DC-DC变换器最小回流功率控制策略
2
2019
... 电能路由器是信息控制与能量控制结合的统一控制中心[4 ,5 ] ,是直流配电网关键设备,主要负责中压直流配网与低压直流微电网的能量与信息的统一管理.直流电能路由器由多组直流变换单元组合辅以高性能通信控制系统构成,对其进行宏观优化的综合控制是提升控制效果的有效途径[6 ] .按照各个变换器分别进行独立控制时,这种控制易于实现,但是在端口能量变化的过程中会加重直流母线的能量承载压力,降低直流母线的响应性能.为了提升直流母线的瞬态响应性能,第一种是用容量、重量、体积更大的直流母线电容作为能量池,这种方法会增加变换器组的复杂度;第二种是使用宏观的整体控制技术搭建整个变换单元的端口功率等效电路,依靠变换器之间的相互关系进行整体式的综合控制.第二种方法将电能路由器看成能量变换的整体,控制能量在变换器之间传递的快速性和稳定性,能够增强直流母线的动态稳定性,进而减少母线电容[5 ] . ...
... [5 ]. ...
双有源桥DC-DC变换器最小回流功率控制策略
2
2019
... 电能路由器是信息控制与能量控制结合的统一控制中心[4 ,5 ] ,是直流配电网关键设备,主要负责中压直流配网与低压直流微电网的能量与信息的统一管理.直流电能路由器由多组直流变换单元组合辅以高性能通信控制系统构成,对其进行宏观优化的综合控制是提升控制效果的有效途径[6 ] .按照各个变换器分别进行独立控制时,这种控制易于实现,但是在端口能量变化的过程中会加重直流母线的能量承载压力,降低直流母线的响应性能.为了提升直流母线的瞬态响应性能,第一种是用容量、重量、体积更大的直流母线电容作为能量池,这种方法会增加变换器组的复杂度;第二种是使用宏观的整体控制技术搭建整个变换单元的端口功率等效电路,依靠变换器之间的相互关系进行整体式的综合控制.第二种方法将电能路由器看成能量变换的整体,控制能量在变换器之间传递的快速性和稳定性,能够增强直流母线的动态稳定性,进而减少母线电容[5 ] . ...
... [5 ]. ...
基于能量平衡的电能路由器综合控制技术
3
2017
... 电能路由器是信息控制与能量控制结合的统一控制中心[4 ,5 ] ,是直流配电网关键设备,主要负责中压直流配网与低压直流微电网的能量与信息的统一管理.直流电能路由器由多组直流变换单元组合辅以高性能通信控制系统构成,对其进行宏观优化的综合控制是提升控制效果的有效途径[6 ] .按照各个变换器分别进行独立控制时,这种控制易于实现,但是在端口能量变化的过程中会加重直流母线的能量承载压力,降低直流母线的响应性能.为了提升直流母线的瞬态响应性能,第一种是用容量、重量、体积更大的直流母线电容作为能量池,这种方法会增加变换器组的复杂度;第二种是使用宏观的整体控制技术搭建整个变换单元的端口功率等效电路,依靠变换器之间的相互关系进行整体式的综合控制.第二种方法将电能路由器看成能量变换的整体,控制能量在变换器之间传递的快速性和稳定性,能够增强直流母线的动态稳定性,进而减少母线电容[5 ] . ...
... 无源控制方法是根据整体的能量作为控制目标,有稳定的性能[6 ] .耗散性控制是利用系统的能量耗散建立关于系统能量的函数关系,设计关于能量函数的控制器,有良好的稳健程度[7 ,8 ,9 ] .针对三端口交流电能路由器建立了针对高低压两级直流母线的能量平衡控制器,提高了控制的稳态性能,并调整了时间尺度控制方法,对于交流电能路由器有着较好的效果[6 ] .文献[10 ] 针对配电网,设置了基于配 电网端口能量平衡的李雅普诺夫函数,根据运行情况确定控制目标,可以控制降低系统的运行成本. ...
... [6 ].文献[10 ] 针对配电网,设置了基于配 电网端口能量平衡的李雅普诺夫函数,根据运行情况确定控制目标,可以控制降低系统的运行成本. ...
基于能量平衡的电能路由器综合控制技术
3
2017
... 电能路由器是信息控制与能量控制结合的统一控制中心[4 ,5 ] ,是直流配电网关键设备,主要负责中压直流配网与低压直流微电网的能量与信息的统一管理.直流电能路由器由多组直流变换单元组合辅以高性能通信控制系统构成,对其进行宏观优化的综合控制是提升控制效果的有效途径[6 ] .按照各个变换器分别进行独立控制时,这种控制易于实现,但是在端口能量变化的过程中会加重直流母线的能量承载压力,降低直流母线的响应性能.为了提升直流母线的瞬态响应性能,第一种是用容量、重量、体积更大的直流母线电容作为能量池,这种方法会增加变换器组的复杂度;第二种是使用宏观的整体控制技术搭建整个变换单元的端口功率等效电路,依靠变换器之间的相互关系进行整体式的综合控制.第二种方法将电能路由器看成能量变换的整体,控制能量在变换器之间传递的快速性和稳定性,能够增强直流母线的动态稳定性,进而减少母线电容[5 ] . ...
... 无源控制方法是根据整体的能量作为控制目标,有稳定的性能[6 ] .耗散性控制是利用系统的能量耗散建立关于系统能量的函数关系,设计关于能量函数的控制器,有良好的稳健程度[7 ,8 ,9 ] .针对三端口交流电能路由器建立了针对高低压两级直流母线的能量平衡控制器,提高了控制的稳态性能,并调整了时间尺度控制方法,对于交流电能路由器有着较好的效果[6 ] .文献[10 ] 针对配电网,设置了基于配 电网端口能量平衡的李雅普诺夫函数,根据运行情况确定控制目标,可以控制降低系统的运行成本. ...
... [6 ].文献[10 ] 针对配电网,设置了基于配 电网端口能量平衡的李雅普诺夫函数,根据运行情况确定控制目标,可以控制降低系统的运行成本. ...
A new control strategy for single-phase shunt active power filters using a Lyapunov function
1
2006
... 无源控制方法是根据整体的能量作为控制目标,有稳定的性能[6 ] .耗散性控制是利用系统的能量耗散建立关于系统能量的函数关系,设计关于能量函数的控制器,有良好的稳健程度[7 ,8 ,9 ] .针对三端口交流电能路由器建立了针对高低压两级直流母线的能量平衡控制器,提高了控制的稳态性能,并调整了时间尺度控制方法,对于交流电能路由器有着较好的效果[6 ] .文献[10 ] 针对配电网,设置了基于配 电网端口能量平衡的李雅普诺夫函数,根据运行情况确定控制目标,可以控制降低系统的运行成本. ...
Dissipativity based adaptive and robust control of UPS in unbalanced operation
1
2003
... 无源控制方法是根据整体的能量作为控制目标,有稳定的性能[6 ] .耗散性控制是利用系统的能量耗散建立关于系统能量的函数关系,设计关于能量函数的控制器,有良好的稳健程度[7 ,8 ,9 ] .针对三端口交流电能路由器建立了针对高低压两级直流母线的能量平衡控制器,提高了控制的稳态性能,并调整了时间尺度控制方法,对于交流电能路由器有着较好的效果[6 ] .文献[10 ] 针对配电网,设置了基于配 电网端口能量平衡的李雅普诺夫函数,根据运行情况确定控制目标,可以控制降低系统的运行成本. ...
双有源桥DC-DC暂态直流偏置分析和抑制策略研究
1
2018
... 无源控制方法是根据整体的能量作为控制目标,有稳定的性能[6 ] .耗散性控制是利用系统的能量耗散建立关于系统能量的函数关系,设计关于能量函数的控制器,有良好的稳健程度[7 ,8 ,9 ] .针对三端口交流电能路由器建立了针对高低压两级直流母线的能量平衡控制器,提高了控制的稳态性能,并调整了时间尺度控制方法,对于交流电能路由器有着较好的效果[6 ] .文献[10 ] 针对配电网,设置了基于配 电网端口能量平衡的李雅普诺夫函数,根据运行情况确定控制目标,可以控制降低系统的运行成本. ...
双有源桥DC-DC暂态直流偏置分析和抑制策略研究
1
2018
... 无源控制方法是根据整体的能量作为控制目标,有稳定的性能[6 ] .耗散性控制是利用系统的能量耗散建立关于系统能量的函数关系,设计关于能量函数的控制器,有良好的稳健程度[7 ,8 ,9 ] .针对三端口交流电能路由器建立了针对高低压两级直流母线的能量平衡控制器,提高了控制的稳态性能,并调整了时间尺度控制方法,对于交流电能路由器有着较好的效果[6 ] .文献[10 ] 针对配电网,设置了基于配 电网端口能量平衡的李雅普诺夫函数,根据运行情况确定控制目标,可以控制降低系统的运行成本. ...
基于Lyapunov优化方法的含能量路由器的能源集线器能量管理策略研究
1
2019
... 无源控制方法是根据整体的能量作为控制目标,有稳定的性能[6 ] .耗散性控制是利用系统的能量耗散建立关于系统能量的函数关系,设计关于能量函数的控制器,有良好的稳健程度[7 ,8 ,9 ] .针对三端口交流电能路由器建立了针对高低压两级直流母线的能量平衡控制器,提高了控制的稳态性能,并调整了时间尺度控制方法,对于交流电能路由器有着较好的效果[6 ] .文献[10 ] 针对配电网,设置了基于配 电网端口能量平衡的李雅普诺夫函数,根据运行情况确定控制目标,可以控制降低系统的运行成本. ...
基于Lyapunov优化方法的含能量路由器的能源集线器能量管理策略研究
1
2019
... 无源控制方法是根据整体的能量作为控制目标,有稳定的性能[6 ] .耗散性控制是利用系统的能量耗散建立关于系统能量的函数关系,设计关于能量函数的控制器,有良好的稳健程度[7 ,8 ,9 ] .针对三端口交流电能路由器建立了针对高低压两级直流母线的能量平衡控制器,提高了控制的稳态性能,并调整了时间尺度控制方法,对于交流电能路由器有着较好的效果[6 ] .文献[10 ] 针对配电网,设置了基于配 电网端口能量平衡的李雅普诺夫函数,根据运行情况确定控制目标,可以控制降低系统的运行成本. ...
Energy-based control design for a solid state transformer
1
2010
... 分别对变换电路各部分建立平均等效模型,对于逆变器及滤波的控制不作为本文主要研究点,为简化控制,将三相逆变输出滤波用一个等效阻抗代替[11 ] .对于直流电能路由器的平均等效模型的端口流进流出的功率进行累计积分,可以得到各端口能量关系,得到直流电能路由器的平均等效电路图如图2 所示,其中$d_x$为第x个双有源桥单元的等效移相控制占空比,$U_H$以及$U_L$为变压器两侧电压值. ...