电气工程学报, 2020, 15(1): 23-28 doi: 10.11985/2020.01.003

特邀专栏: 微电网功率变换与稳定控制

基于旋转坐标变换的孤岛微网群广义下垂控制策略

张芮漩, 周念成, 孟潇潇

重庆大学输配电装备及系统安全与新技术国家重点实验室 重庆 400044

Generalized Sag Control Strategy for Isolated Island Microgrid Clusters Based on Rotation Coordinate Transformation

ZHANG Ruixuan, ZHOU Niancheng, MENG Xiaoxiao

State Key Laboratory of Power Transmission Equipment & System Security and New Technology, Chongqing University, Chongqing 400044 China

收稿日期: 2020-01-3   网络出版日期: 2020-03-25

Received: 2020-01-3   Online: 2020-03-25

作者简介 About authors

张芮漩,女,1997年生,硕士研究生。主要研究方向为电力系统运行与控制。E-mail：xx_zrx88@cqu.edu.cn

周念成,男,1969年生,博士研究生导师,教授。主要研究方向为电力系统保护和电能质量等方面。E-mail：cee_nczhou@cqu.edu.cn

孟潇潇,男,1992年生,博士研究生。主要研究方向为电力系统运行与控制、微电网控制技术。E-mail：mxxfreedom@cqu.edu.cn

摘要

微网群由多个电源和负荷集群构成,其控制设计较为复杂,分析孤岛微网群之间的联络线阻抗对两者交互功率控制的影响。考虑到微网群直接使用广义下垂控制策略不可行的问题,通过利用微网群结构简化及联络线阻抗约束,提出了一种微网群结构变换下的改进广义下垂控制策略。该策略基于坐标旋转理论,在任意的线路阻抗比之下,能够实现功率解耦控制、频率无差调节和有功功率均分,进而保证微网群运行的稳定性并提升系统动态响应。最后对提出的控制策略进行仿真分析,仿真结果证明所提控制策略具有可行性。

关键词： 微网群 ; 下垂控制 ; 广义下垂控制 ; 有功均分

Abstract

The microgrid clusters is composed of multiple power supply and load clusters, and its control design is complicated. The influence of tie line impedance between isolated island microgrid clusters on their interactive power control is analyzed. In view of the infeasibility of using generalized droop control strategy directly for microgrid clusters, an improved generalized droop control strategy based on microgrid clusters structure transformation is proposed in consideration of simplified microgrid clusters structure and tie line impedance constraint. Based on the coordinate rotation theory, this strategy can realize power decoupling control, frequency adjustment and active power equalization under arbitrary line impedance ratio, thus ensuring the stability of the operation of the microgrid clusters and improving the dynamic response of the system. Finally, the proposed control strategy is simulated and analyzed, and the simulation results prove the feasibility of the proposed control strategy.

Keywords： Microgrid clusters ; droop control ; generalized droop control ; active divide

PDF (8193KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

张芮漩, 周念成, 孟潇潇. 基于旋转坐标变换的孤岛微网群广义下垂控制策略. 电气工程学报[J], 2020, 15(1): 23-28 doi:10.11985/2020.01.003

ZHANG Ruixuan, ZHOU Niancheng, MENG Xiaoxiao. Generalized Sag Control Strategy for Isolated Island Microgrid Clusters Based on Rotation Coordinate Transformation. Journal of Electrical Engineering[J], 2020, 15(1): 23-28 doi:10.11985/2020.01.003

1 引言

如今,传统能源的紧缺问题越来越严重,相较于传统能源供电,微网供电方式大多采用的是清洁能源进行供电,这为可再生能源的利用开辟了一个新的方向[1]。在实际运用中,微网的控制是首先需要解决的问题,其控制方式可以分为主从控制和对等控制两类。前者利用全局信息实现控制,对通信的要求较高;后者利用本地信息实现控制,鲁棒性较好,利于实现即插即用[2,3]。微网群作为分布式发电网络的一个全新概念,不仅能有效集成各种分布式电源,还可以实现群内各子网之间的能量调度和互济,增强彼此间的可靠性[4]。微网群的研究处于起步阶段,目前微网群的基本概念和特征仍然缺乏清晰的定义、描述和相关的试验验证,未能建立微网群本身的研究框架体系,亟待开展大量深入的研究工作[5]。

单个微网,在对等控制中常将功率下垂特性引入微网,通过有差调节特性曲线实现负荷功率按容量分配[6]。相对于单个微网的控制,微网群的控制更加复杂,不仅要考虑各子微网内分布式电源的能量协调分配,还需要考虑各子微网之间的互联状态以及群级协作下各子微网之间的功率优化调配和协调控制[6]。文献[7]提出了一种微网群分级控制策略,通过增加群级的能量协调控制,并以微网群的经济性和最大能量利用率为目标进行功率的协调控制。文献[8]对多微网能量协调控制进行研究,提出用一种多微网的分层控制方法实现多微网能量协调,但未涉及微网群不同运行状态下功率分配的分析。上述所提控制策略均是基于通信的协调控制策略,较大程度地依赖通信系统。也有许多学者研究了微网群的下垂控制,文献[9,10,11]提出了一种基于下垂控制的能量协调管理方法,可实现对交直流混合微网两侧的功率交换进行有效控制,使得交直流混合微网实现功率自主协调控制成为可能,但上述所提控制方法会不可避免地造成能量的损耗。文献[12,13]对其做出了改进,规定只有混合微网在一定范围工作时,才进行功率交换控制,这样就可避免能量损耗,但是这种控制方法很有可能导致混合微网两侧工作电压偏离额定值较大。在混合微网两侧都重载运行或者轻载运行时,两侧依然存在能量交换,使得原本就重载运行或轻载运行的微网子网的工作电压偏离额定值更大。

本文针对微网群提出了一种基于旋转坐标变换的改进下垂控制方法。考虑到各个子微网之间存在的联络线线路阻抗,首先将各子微网之间的连接方式进行等效变换,再采用坐标旋转的虚拟功率方法,实现有功功率、无功功率解耦的微网群改进广义下垂控制。该控制策略可以在任意线路阻抗下实现对于频率的无差调节以及有功功率的均分,提高了微网群整体的稳定性,本文以三个微网形成的环网微网群为例进行对比与分析。

2 孤岛微网群的下垂控制模型

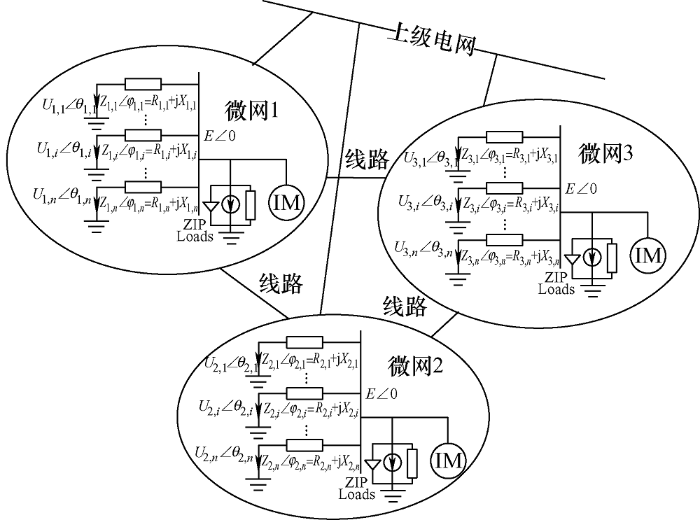
以图1所示微网群模型为例,根据单个微网的传统下垂控制原理,扩展至微网群的下垂控制[14,15,16,17,18]。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   孤岛微网群结构


由图1可知,单个微网的线路阻抗为ZiDφi=Ri+jXi,其中,Zi为单个微网线路的阻抗;φi为角度;Ri为电阻;Xi为电抗。第i台逆变器的输出功率为Si=Pi+jQi,其中,Si为第i台逆变器的输出功率;Pi为有功功率;Qi为无功功率。对于微网群中的第s个微网第i台逆变器(s=1,2,3,…;i=1,2,3,…),其输出的有功功率和无功功率表达式如式(1)所示

$\left\{ \begin{align} & {{P}_{s,i}}=\frac{(U_{s,i}^{2}-{{E}_{s,i}}{{U}_{s,i}}\cos {{\theta }_{s,i}}){{R}_{s,i}}+{{E}_{s,i}}{{U}_{s,i}}\sin {{\theta }_{s,i}}{{X}_{s,i}}}{Z_{s,i}^{2}} \\ & {{Q}_{s,i}}=\frac{(U_{s,i}^{2}-{{E}_{s,i}}{{U}_{s,i}}\cos {{\theta }_{s,i}}){{X}_{s,i}}-{{E}_{s,i}}{{U}_{s,i}}\sin {{\theta }_{s,i}}{{R}_{s,i}}}{Z_{s,i}^{2}} \\ \end{align} \right.$

式中,Ps,i为第s个微网i台逆变器的输出有功功率;Qs,i为第s个微网i台逆变器的输出无功功率;Us,i为i台逆变器的输出电压;Es,i为PCC点电压幅值;Zs,i、θs,i分别为逆变器与公共节点之间的线路阻抗幅值和相角。

当微网群中的线路阻抗为感性阻抗(R$\ll $X)时,式(1)可变换为式(2)

$\left\{ \begin{align} & {{P}_{s,i}}=\frac{{{E}_{s,i}}{{U}_{s,i}}\sin {{\theta }_{s,i}}}{{{X}_{s,i}}} \\ & {{Q}_{s,i}}=\frac{{{E}_{s,i}}{{U}_{s,i}}\cos {{\theta }_{s,i}}-U_{s,i}^{2}}{{{X}_{s,i}}} \\ \end{align} \right.$

通常情况下,如果θs,i足够小,有功功率主要是由θs,i决定的,无功功率主要是由逆变器输出电压Us,i决定的,在一定程度上,对有功功率和无功功率都能够进行独立的控制。传统的下垂特性控制为如式(3)所示

$\left\{ \begin{align} & {{\omega }_{s,i}}={{\omega }_{\text{0}(s,i)}}-{{k}_{p(s,i)}}({{P}_{s,i}}-{{P}_{ref(s,i)}}) \\ & {{U}_{s,i}}={{U}_{\text{0}(s,i)}}-{{k}_{q(s,i)}}({{Q}_{s,i}}-{{Q}_{ref(s,i)}}) \\ \end{align} \right.$

式中,ω0=2πf0,其中,f0为额定频率;U0为额定电压幅值;Pref、Qref分别为每台机组的额定有功功率和无功功率;kp、kq分别为有功功率、无功功率的下垂控制系数,通常为定值,按微网群中每台机组的最大容量选取。

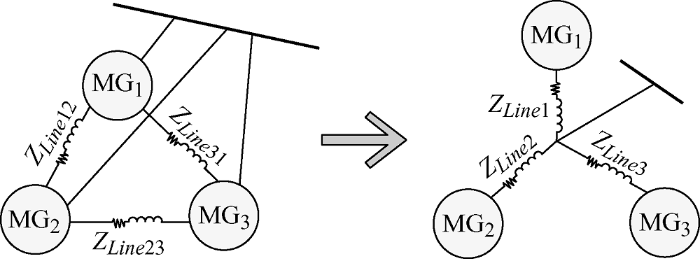
微网群在实现下垂控制时也会存在和单个微网一样的问题。在$X\gg \ R$时,可以进行P-f和Q-U的解耦控制,对频率和电压分别进行控制进而控制有功功率和无功功率,有功功率在此情况下能够按照设备容量实现均分。但是在阻抗呈现$X\approx R$或$X\ll \ R$特性时,下垂控制策略在微网中不再适用,且微网群在运用传统的广义下垂控制时,对于有功功率来说不能实现容量均分,而导致问题的原因,可能是相较于单个微网,各个微网之间添加了一些线路的连接,增加了广义下垂控制的复杂性。因此,在微网群的控制中,对微网群大的结构进行简化,再结合联络线上的阻抗对广义下垂控制的影响,对参数进行重新选择。微网群环网的简化结构如图2所示。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   微网群结构变换


在进行结构变换后,微网群的结构得到了简化,两两微网之间的阻抗变换公式如式(4)所示

$\left\{ \begin{align} & {{Z}_{Line1}}=\frac{{{Z}_{Line31}}{{Z}_{Line12}}}{{{Z}_{Line12}}+{{Z}_{Line23}}+{{Z}_{Line31}}} \\ & {{Z}_{Line2}}=\frac{{{Z}_{Line12}}{{Z}_{Line23}}}{{{Z}_{Line12}}+{{Z}_{Line23}}+{{Z}_{Line31}}} \\ & {{Z}_{Line3}}=\frac{{{Z}_{Line23}}{{Z}_{Line31}}}{{{Z}_{Line12}}+{{Z}_{Line23}}+{{Z}_{Line31}}} \\ \end{align} \right.$

在简化的微网群结构上对传统的广义下垂控制进行改进,实现有功功率的均分。

3 孤岛微网群的广义下垂改进控制

单个微网在广义下垂控制中引入了一种坐标旋转变换,实现了对有功和无功的解耦控制,并定义了一种新的有功功率和无功功率,即类有功、类无功。对于结构简化后的微网群,也可以引入类有功、类无功,相较于单个微网中的阻抗为每个逆变器线路上的阻抗,微网群广义下垂控制中的阻抗有一些变化,因为微网群中两两微网之间还需要考虑联络线上的线路阻抗,所以推导出微网群的广义下垂控制,其基本形式如式(5)所示

$\left\{ \begin{align} & {{{{P}'}}_{s,i}}=\frac{{{{{X}'}}_{s,i}}}{{{{{Z}'}}_{s,i}}}{{P}_{s,i}}-\frac{{{{{R}'}}_{s,i}}}{{{{{Z}'}}_{s,i}}}{{Q}_{s,i}} \\ & {{{{Q}'}}_{s,i}}=\frac{{{{{R}'}}_{s,i}}}{{{{{Z}'}}_{s,i}}}{{P}_{s,i}}+\frac{{{{{X}'}}_{s,i}}}{{{{{Z}'}}_{s,i}}}{{Q}_{s,i}} \\ \end{align} \right.$

式中,${{{Z}'}_{s,i}}=Z_{Line\ s}^{{}}+{{Z}_{s,I}}={{{R}'}_{s,i}}+\text{j}{{{X}'}_{s,i}}$,引入的线性坐标旋转正交变换矩阵如式(6)所示

${{T}_{PQs,i}}=\left[ \begin{align} & \sin {{{{\varphi }'}}_{s,i}}\text{ }-\cos {{{{\varphi }'}}_{s,i}} \\ & \cos {{{{\varphi }'}}_{s,i}}\text{ }\sin {{{{\varphi }'}}_{s,i}} \\ \end{align} \right]$

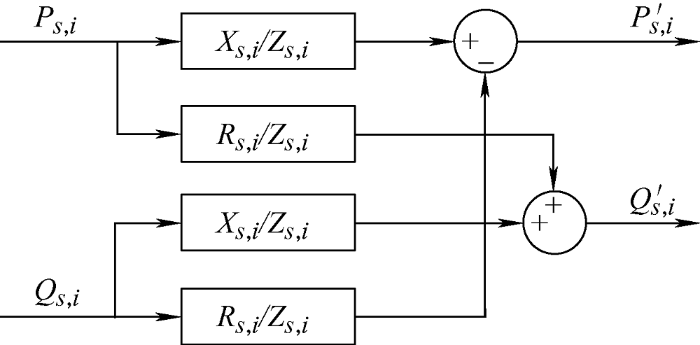
式中,${{{\varphi }'}_{s,i}}$=arctan(${{{X}'}_{s,i}}$/${{{R}'}_{s,i}}$)为等效线路的阻抗角,相角可以由频率的积分表示,对频率的控制就可以转换为间接控制相角和类有功功率。通过上述的坐标旋转变换,可以将实际的有功功率Ps,i和无功功率Qs,i转变为类有功功率${{{P}'}_{s,i}}$和类无功功率${{{Q}'}_{s,i}}$,从而类有功功率与频率,类无功功率与电压幅值呈现一一对应的关系,实现了对有功功率、无功功率的解耦控制。广义下垂控制对于线路呈阻性或感性时仍可以实现对于频率和电压的控制,其控制框图如图3所示。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   广义下垂控制结构框图


结合式(3)和(5)推导出微网群的下垂特性控制,如式(7)所示

$\begin{cases}\omega_{s,i}=\omega_{0(s,i)}-k_{p(s,i)} \left(\frac{X_{s,i}^{'}}{Z_{s,i}^{'}}P_{s,i}-\frac{R_{s,i}^{'}}{Z_{s,i}^{'}}Q_{s,i}\right) \\ U_{s,i}=U_{0(s,i)}-k_{q(s,i)} \left(\frac{R_{s,i}^{'}}{Z_{s,i}^{'}}P_{s,i}-\frac{X_{s,i}^{'}}{Z_{s,i}^{'}}Q_{s,i}\right)\end{cases}$

进行改进后的广义下垂控制,理论上不仅能实现微网群频率的近无差调节,还能对微网群的有功功率进行均分,如果想要完全实现无差调节,可以在后面加上一个高通滤波器,将有差的频率利用高通滤波器处理,实现无差调节。

4 仿真分析

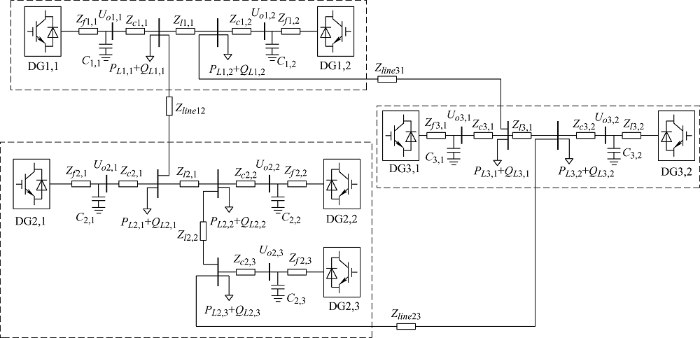
针对上述提出的微网群改进广义下垂控制,为了验证其理论分析的正确性,利用Matlab/Simulink搭建微网群的仿真模型,对微网群线路在不同线路阻抗特性下的情况,进行仿真分析,验证新控制策略的可行性。微网群的结构如图4所示。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   微网群仿真结构示意图


其微网群结构图所对应的模型参数如表1所示。系统搭建是由三组单个微网组成的微网群,其中两组微网里有两个逆变器,一组里有三个逆变器,仿真时首先设置分布式电源的线路阻抗呈现感性。

表1   仿真模型参数表

参数数值
LC滤波器电感Lf1,1-Lf3,3/H2×10-3
LC滤波器电阻Rf1,1-Rf3,3/Ω0.03
分布式电源线路电阻Rc1,1-Rc3,3/Ω0.03
分布式电源线路电感Lc1,1-Lc3,3/H2×10-3
DG1-1、DG1-2有功下垂系数kp1-1,kp1-2/(rad/W)11.5×10-5
DG1-1、DG1-2无功下垂系数kq1-1,kq1-2(rad/W)0.45×10-3
DG3-1、DG3-2有功下垂系数kp3-1,kp3-2/(rad/W)12.5×10-5
DG3-1、DG3-2无功下垂系数kq3-1,kq3-2/(rad/W)0.5×10-3
DG2-1、DG2-2、DG2-3有功下垂系数 kp2-1,kp2-2,kp2-3/(rad/W)12×10-5
DG2-1、DG2-2、DG2-3无功下垂系数kq2-1,kq2-2,kq2-3/(rad/W)0.5×10-3
微网联络线路阻抗Zline12R12/Ω
X12/H		0.053 67
1.124 12
微网联络线路阻抗Zline23R23/Ω
X23/H		0.053 67
1.124 12
微网联络线路阻抗Zline31R31/Ω
X31/H		0.035 68
0.747 32

新窗口打开| 下载CSV


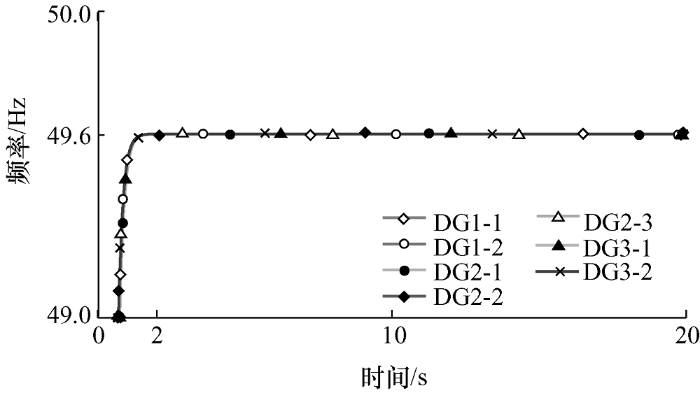
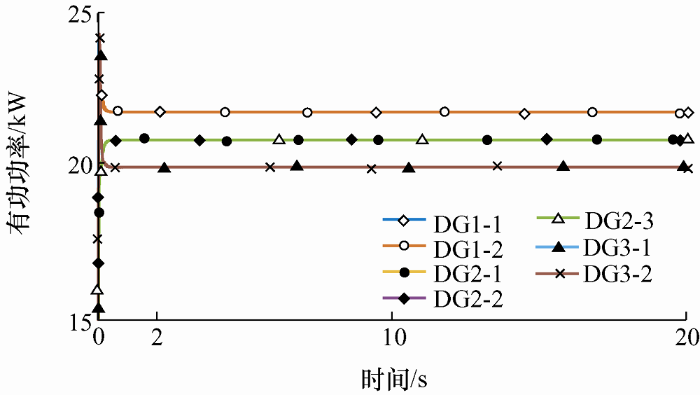
当$R\ll \ X$时,对微网群运用下垂控制策略的仿真波形如图5~9所示。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5   微网1、2、3下垂控制频率波形图


图6

新窗口打开| 下载原图ZIP| 生成PPT

图6   微网1、2、3下垂控制有功功率波形图


图7

新窗口打开| 下载原图ZIP| 生成PPT

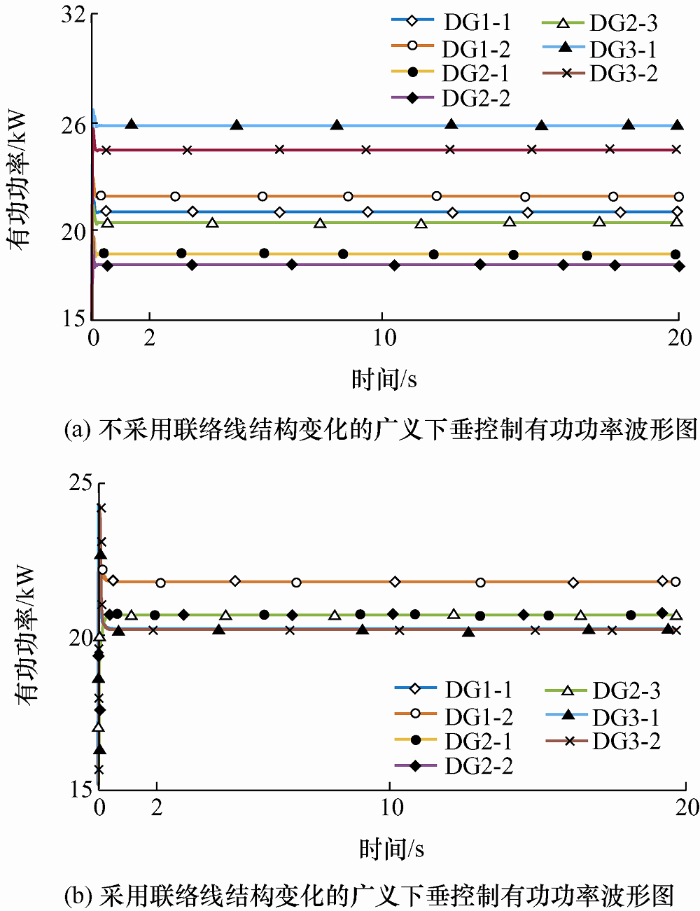
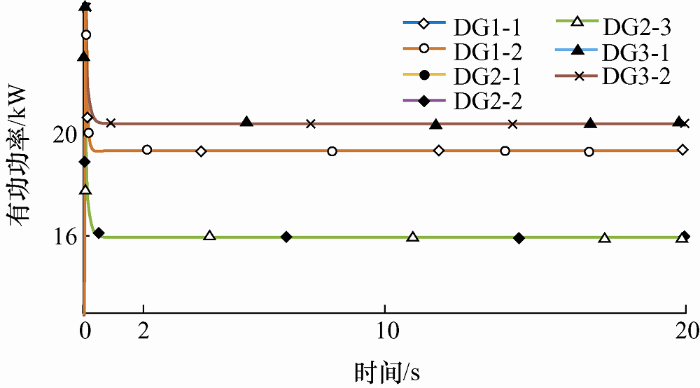
图7   传统广义下垂控制与改进广义下垂控制有功功率波形图


图8

新窗口打开| 下载原图ZIP| 生成PPT

图8   微网1、2、3广义下垂控制频率波形图


图9

新窗口打开| 下载原图ZIP| 生成PPT

图9   微网1、2、3广义下垂控制频率波形图


由图5可以看出,当控制策略为下垂控制时,频率不能实现无差调节,但是频率保持稳定状态;由图6可以看出,在下垂控制时有功功率是按照机组容量进行均分的,运用下垂控制策略时,系统整体稳定性较好,暂态过程的时间没有很长。在该阻抗性质的情况下,将控制策略直接改为广义下垂控制,不考虑各个微网之间阻抗的影响,按照传统的广义下垂控制进行仿真,如图7a所示,再将控制策略考虑各个微网之间的阻抗影响,改变阻抗参数后的广义下垂控制进行仿真,如图7b所示。

通过图7两个波形可以看出,不考虑微网之间的相互影响,直接对微网群进行广义下垂控制,会导致有功功率无法按照机组容量进行均分的;在对微网群进行结构简化和考虑微网联络线之间的阻抗之后,对于有功功率来说,实现了按容量均分。因此对于复杂的微网群结构,首先应该考虑将微网群进行简化,并且还要考虑微网之间联络线上的阻抗对于微网群控制的影响。

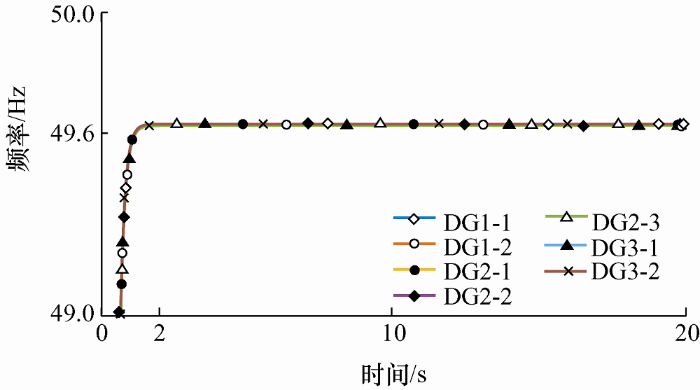
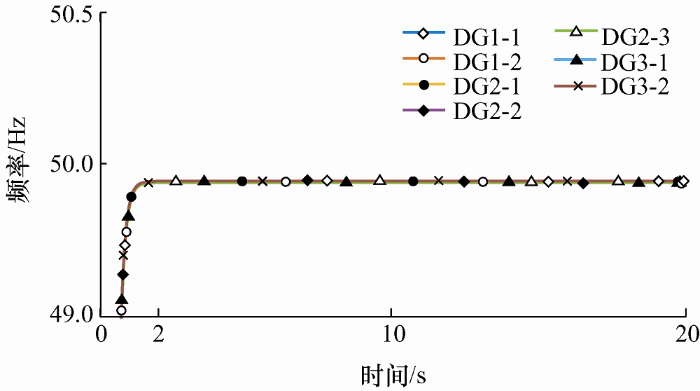
由图8的波形可以看出,在采用联络线结构变化后的频率波形与图5比较可以发现频率有一定的提高。

采用改进广义下垂控制策略时,频率相较于下垂控制策略来说更加接近额定频率,但不能实现完全的无差调节。改变阻抗性质,使分布式电源线路阻抗电感为2 mH,线路阻抗电阻为0.7 Ω时,两两微网之间的联络线以分布式电源线路X/R的值为参考改变,使得线路阻抗呈现阻感性,系统输出波形图如图9~10所示。

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10   微网1、2、3广义下垂控制有功功率波形图


上述几个波形图验证了当阻抗呈现$X\approx R$时,对于微网群,采用改进的广义策略仍能够使系统频率实现无差调节,且能保证有功功率按比例分配,微网群系统会更加稳定地运行。

5 结论

本文对微网群的复杂结构进行简化,针对微网群在直接运用传统广义下垂控制下不能实现有功功率按容量均分的问题进行改进。在传统广义下垂控制的基础上,提出了一种适用于微网群的广义下垂控制,并建立其完整详细的微网群模型,根据线路阻抗呈现出的不同性质,进行仿真分析。研究表明,在线路阻抗呈现电感性或阻感性时,微网群采用改进后的广义下垂控制策略,能够实现有功无功的解耦控制;输出频率稳定控制在额定频率左右,实现了对系统的无差调节;在实现无差调节的同时,系统有功功率的分布能按照容量比率进行分配,提升了系统的稳定性,证明了微网群运用改进后的广义下垂控制策略的可行性。

参考文献

Lasseter R H, Piagi P .

Microgrid:A conceptual solution

[C] // IEEE 35th Annual Power Electronics Specialists Conference,2004,Aachen,Germany. 2004: 4285-4290.

[本文引用: 1]

Tuladhar A, Jin H, Unger T , et al.

Control of parallel inverters in distributed AC power systems with consideration of line impedance effect

[J]. IEEE Trans on Industrial Application, 2000,36(1):131-138.

DOI:10.1109/28.821807      URL     [本文引用: 1]

吴鸣, 熊雄, 季宇 , 等.

微网群技术综述

[J]. 储能科学与技术, 2019,8(4):621-628.

[本文引用: 1]

Wu Ming, Xiong Xiong, Ji Yu , et al.

Overview on multi-microgrid technologies

[J]. Energy Storage Science and Technology, 2019,8(4):621-628.

[本文引用: 1]

肖湘宁 .

新一代电网中多源多变换复杂交直流系统的基础问题

[J]. 电工技术学报, 2015,30(15):1-14.

[本文引用: 1]

Xiao Xiangning .

Basic problems of the new complex AC-DC power grid with multiple energy resources and multiple conversions

[J]. Transactions of China Electrotechnical Society, 2015,30(15):1-14.

[本文引用: 1]

支娜, 肖曦, 田培根 , 等.

微网群控制技术研究现状与展望

[J]. 电力自动化设备, 2016,36(4):107-115.

[本文引用: 1]

Zhi Na, Xiao Xi, Tian Peigen , et al.

Research status and prospect of microgrid group control technology

[J]. Automation of Electric Power Systems, 2016,36(4):107-115.

[本文引用: 1]

周小平, 陈燕东, 周乐明 , 等.

一种微网群架构及其自主协调控制策略

[J]. 电工技术学报, 2017,32(10):123-134.

[本文引用: 2]

Zhou Xiaoping, Chen Yandong, Zhou Leming , et al.

A microgrid cluster structure and its autonomous coordination control strategy

[J]. Transactions of China Electrotechnical Society, 2017,32(10):123-134.

[本文引用: 2]

高春凤 .

微网群自助与协调控制关键技术研究

[D]. 北京:中国农业大学, 2014.

[本文引用: 1]

丁明, 马凯, 毕锐 .

基于多代理系统的多微网能量协调控制

[J]. 电力系统保护与控制, 2013,41(24):1-8.

DOI:10.7667/j.issn.1674-3415.2013.24.001      URL     [本文引用: 1]

Ding Ming, Ma Kai, Bi Rui .

Energy coordination control of multi-microgrid based on multi-agent systern

[J]. Power System Protection and Control, 2013,41(24):1-8.

DOI:10.7667/j.issn.1674-3415.2013.24.001      URL     [本文引用: 1]

Jin Chi, Loh P C, Wang Peng .

Autonomous operation of hybrid AC-DC microgrids

[J]. IEEE Transactions on Power Electronics, 2013,28(5):2214-2223.

DOI:10.1109/TPEL.2012.2214792      URL     [本文引用: 1]

This paper investigates on power-sharing issues of an autonomous hybrid microgrid. Unlike existing microgrids which are purely ac, the hybrid microgrid studied here comprises dc and ac subgrids interconnected by power electronic interfaces. The main challenge here is to manage power flows among all sources distributed throughout the two types of subgrids, which is certainly tougher than previous efforts developed for only ac or dc microgrid. This wider scope of control has not yet been investigated, and would certainly rely on the coordinated operation of dc sources, ac sources, and interlinking converters. Suitable control and normalization schemes are nowdeveloped for controlling them with the overall hybrid microgrid performance already verified in simulation and experiment.

Che Liang, Mohammad S, Ahmed A , et al.

Hierarchical coordination of a community microgrid with AC and DC microgrids

[J]. IEEE Transactions on Smart Grid, 2015,6(6):3042-3051.

DOI:10.1109/TSG.2015.2398853      URL     [本文引用: 1]

Balaguer I J, Lei Q, Yang S , et al.

Control for grid-connected and intentional islanding operations of distributed power generation

[J]. IEEE Transactions on Industrial Electronics, 2011,58(1):147-157.

DOI:10.1109/TIE.2010.2049709      URL     [本文引用: 1]

Navid E, Ebrahim F .

Power control and management in a hybrid AC/DC microgrid

[J]. IEEE Transactions on Smart Grid, 2014,5(3):1494-1505.

DOI:10.1109/TSG.2013.2294275      URL     [本文引用: 1]

Hybrid ac/dc microgrids have been planned for the better interconnection of different distributed generation systems (DG) to the power grid, and exploiting the prominent features of both ac and dc microgrids. Connecting these microgrids requires an interlinking ac/dc converter (IC) with a proper power management and control strategy. During the islanding operation of the hybrid ac/dc microgrid, the IC is intended to take the role of supplier to one microgrid and at the same time acts as a load to the other microgrid and the power management system should be able to share the power demand between the existing ac and dc sources in both microgrids. This paper considers the power flow control and management issues amongst multiple sources dispersed throughout both ac and dc microgrids. The paper proposes a decentralized power sharing method in order to eliminate the need for any communication between DGs or microgrids. This hybrid microgrid architecture allows different ac or dc loads and sources to be flexibly located in order to decrease the required power conversions stages and hence the system cost and efficiency. The performance of the proposed power control strategy is validated for different operating conditions, using simulation studies in the PSCAD/EMTDC software environment.

Wang Peng, Jin Chi, Zhu Dexuan , et al.

Distributed control for autonomous operation of a three-port AC/DC/DS hybrid microgrid

[J]. IEEE Transactions on Industrial Electronics, 2015,62(2):1279-1290.

DOI:10.1109/TIE.2014.2347913      URL     [本文引用: 1]

王成山, 肖朝霞, 王守相 .

微网综合控制与分析

[J]. 电力系统自动化, 2008,32(7), 98-103.

URL     [本文引用: 1]

考虑到微网内分布式电源和负荷所具有的分散性，根据分布式电源的类型以及与储能装置的不同组合方式，采用不同的控制策略分别进行了相应控制器的设计。基于下垂特性的电压/频率（ V/f）控制实现了负荷功率变化时不同分布式电源间变化功率的共享，且在微网孤岛运行时能为微网系统提供频率支撑;PQ控制可根据实际运行情况实现分布式电源有功和无功功率的指定控制。通过对微网孤岛运行模式和联网运行模式之间切换、孤岛模式下切/增负荷以及微网内某一电源功率变化3种情况下的运行特性进行分析，获得了微网中相应分布式电源的功率、电压、电流及系统频率的变化规律，证明了PQ -V/f综合控制策略的正确性和有效性。

Wang Chengshan, Xiao Zhaoxia, Wang Shouxiang .

Synthetical control and analysis of microgrid

[J]. Automation of Electric Power Systems, 2008,2(7):98-103.

URL     [本文引用: 1]

考虑到微网内分布式电源和负荷所具有的分散性，根据分布式电源的类型以及与储能装置的不同组合方式，采用不同的控制策略分别进行了相应控制器的设计。基于下垂特性的电压/频率（ V/f）控制实现了负荷功率变化时不同分布式电源间变化功率的共享，且在微网孤岛运行时能为微网系统提供频率支撑;PQ控制可根据实际运行情况实现分布式电源有功和无功功率的指定控制。通过对微网孤岛运行模式和联网运行模式之间切换、孤岛模式下切/增负荷以及微网内某一电源功率变化3种情况下的运行特性进行分析，获得了微网中相应分布式电源的功率、电压、电流及系统频率的变化规律，证明了PQ -V/f综合控制策略的正确性和有效性。

Lu Xiaoqing, Lai Jingang, Yu Xinghuo , et al.

Distributed coordination of islanded microgrid clusters using a two-layer intermittent communication network

[J]. IEEE Transactions on Industrial Informatics, 2018,14(9):3956-3969.

DOI:10.1109/TII.9424      URL     [本文引用: 1]

Lai Jingang, Lu Xiaoqing, Yu Xinghuo , et al.

Cluster-oriented distributed cooperative control for multiple AC microgrids

[J]. IEEE Transactions on Industrial Informatics, 2019,15(11):5906-5918.

DOI:10.1109/TII.9424      URL     [本文引用: 1]

Che Yanbo, Chen Jian, Zhao Bo .

Research and practice of integrated microgrid system control

[J]. Advanced Materials Research, 2011(225/226):504-507.

[本文引用: 1]

Lasseter R, Eto J, Schenkman B , et al.

Overview of the CERTS microgrid laboratory test bed

[J]. IEEE Transactions on Power Delivery, 2011,26:325-332.

DOI:10.1109/TPWRD.2010.2051819      URL     [本文引用: 1]

/

〈 〉