1 引言
网侧变流器作为分布式电源并网的通道,其控制性能决定着并网电能质量。在矢量控制系统中,参考相位角是重要的控制量,相位角的准确获取直接影响着坐标变换和dq轴电流电压的精确控制,通常使用锁相环(Phase-Locked Loop,PLL)来锁定基波正序电压的频率和相位角[1]。然而,由于微电网中非线性负荷的存在以及分布式电源离并网的切换,会使微电网存在大量的谐波分量,有时会发生三相电压不平衡的现象,大量的高低频谐波流入配电网,影响锁相环的检测精度。在电网谐波和电网电压不平衡的情况下,基于PLL的基波相位信息的检测很容易受到谐波的干扰,导致检测不精确,影响网侧变流器控制系统性能。因此,网侧变流器锁相环的设计显得尤为重要,需要能在各种扰动下准确获取电网电压正序分量的频率和相位信息。
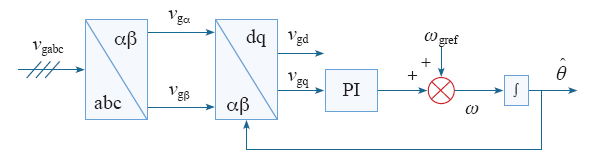
传统的电网电压同步化方法是基于同步旋转坐标系的锁相环(Synchronous Reference Frame-PLL,SRF-PLL),以基波q轴电压作为输入信号进行锁相,当电网电压处于较为理想的运行状态时,可以准确地获取相位信息,当在电网谐波下时,由于受到电压谐波的扰动,产生相位检测误差,检测到的频率也会发生周期性波动[2]。文献[3]提出的基于双dq坐标变换的锁相方法在一定程度上可以削弱因电压不平衡而引起的2倍频谐波分量产生的锁相误差,但是该方法并不能抑制多次谐波。文献[4]对基于双二阶广义积分器(Dual Second-Order Generalized Integrator,DSOGI)和复系数滤波器等锁相方法进行了介绍,这些方法都可以较为准确地获取到基波相位信息,但是在电网谐波或三相电压不平衡情况下,获取的基波频率和相位角都会存在偏差。其中,基于DSOGI的锁相方法谐振频率为基频,可以对高频谐波进行有效抑制,并实现对基波信号正负序分量的提取,从而获得较为准确的相位信息,但是对低频谐波分量没有很好的抗干扰能力,若电网中存在严重的低频谐波分量,提取出的正负序分量依然会存在较大的畸变,影响相位信息的精确锁定。
鉴于上述弊端,文献[5,6]提出多二阶广义积分器锁相环(Multiple Second-Order Generalized Integrator-PLL,MSOGI-PLL)的方法来消除各次谐波分量,可有效降低谐波对锁相的影响,但是该方法需要多个SOGI来分别提取出各次谐波,再进行消除后得到基波分量,这样无疑会增加算法的复杂程度,影响系统的动态响应。文献[7]在DSOGI-PLL的基础上,通过构建多个谐波消除模块,来降低谐波对锁相环的影响,该方法虽能够有效降低谐波的干扰,但同样在算法和实现上会变得复杂。文献[8]在基于复数滤波器锁相环的基础上,通过嵌入重复控制内模,不仅能够完全消除谐波,还简化了控制算法。依据上述文献,本文针对电网谐波背景下,提出了一种基于重复控制内模的DSOGI锁相环方法。首先建立电网电压的谐波数学模型,研究了相位误差产生的原理,对DSOGI和重复控制内模的特性进行分析,利用内模原理可将含有基波的各次谐波分量提取出来,通过50Hz陷波器滤除基波,得到各次谐波负反馈到输入端,从而消除全频段电压谐波,经DSOGI-PLL获得精确的基波相位信息,通过仿真,与几种传统的锁相法进行了对比分析。
2 锁相检测误差分析
在矢量控制系统中,基波电压正序分量相位角是坐标变换的重要基础,影响着dq轴电流分量的控制,在电网电压发生畸变的情况下,必然会导致锁相环的相频输出存在误差,常采用的SRF-PLL锁相方法以电网电压基波q轴分量作为输入信号,SRF-PLL锁相结构框图如图1所示。
图1
三相三线制系统中,不需要考虑零序分量,若把基波分量看成特殊的谐波,在其对应的旋转参考坐标系中则表现为直流分量,而其他次数的谐波分量则表现为交流分量,使得q轴电压分量含有交流扰动信号。在考虑到谐波的影响后,尤其是奇次谐波对锁相精度的影响,建立电网电压谐波数学模型,表达式如下所示[9]
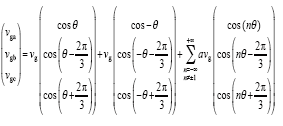
式中,第一项表示基波正序分量,第二项表示基波负序分量,第三项表示各次谐波分量;其中,n为奇数;vg为电网电压基波幅值;a为谐波幅值系数,设定各次谐波幅值相同;θ为电网电压基波正序分量相位角。
为了简化计算,对上述三项分别进行Park坐标变换,可以得到同步旋转坐标系下q轴电压表达式
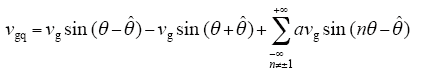
式中,
若假定θ =
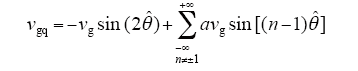
由锁相环的原理可知,只有当vgq = 0时,检测到的相位信息才会准确,由式(3)可以看出,基波负序分量对q轴电压会产生2倍频的电压波动,谐波分量会产生n - 1倍频的电压波动,若电网电压发生三相不平衡,同样可以推导出q轴电压表达式中存在2倍频的电压扰动,严重影响锁相环检测精度,使得相位角输出存在误差[10]。因此,有必要对基波电压进行正负序分离,提取正序电压分量,并消除各次谐波的干扰。
3 基于内模的DSOGI锁相方法
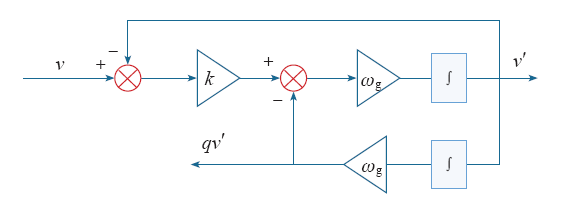
3.1 二阶广义积分器
相位的获取首要前提是得到αβ坐标系下的正序分量,根据对称分量法,可以得到两相静止坐标系下电压正负序分量表达式为
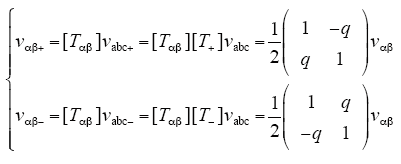
式中, 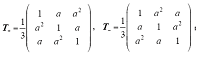
由上式可以得到αβ轴正序分量的表达式为
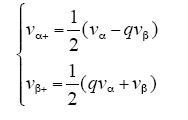
图2
传递函数可表示如下
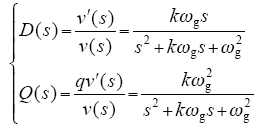
式中,ωg为谐振频率,即电网频率;k为阻尼系数,通常选取k = 1.414。
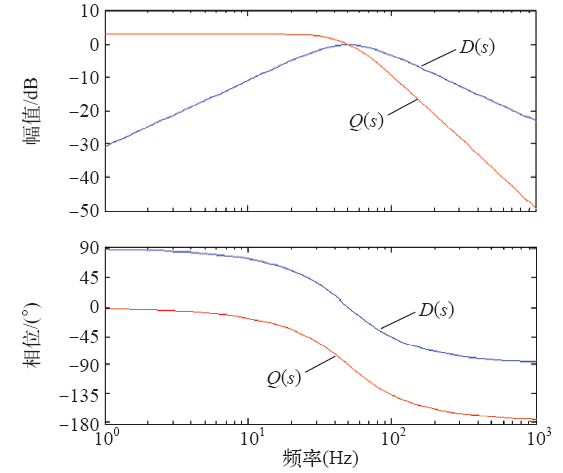
对上述传递函数进行频谱特性分析,伯德图如图3所示。
图3
从传递函数的幅频和相频曲线中可以看出,输出信号qv′比v′在相位上始终滞后90°,在谐振频率50Hz处,幅值增益为0,输出信号幅值不会发生变化,且可以无静差地跟踪输入信号的基频分量。从幅频曲线走势看,Q(s)相比于D(s)在高频谐波区域具有较好的滤波能力,但两者在低频谐波区域滤波能力都较弱。当电网电压中的低频谐波分量较多时,DSOGI不能完全滤除低频谐波,电压同步信号的提取会受到干扰,输出的基波频率存在小幅度振荡,获取相位角的精度也会存在小范围的偏差。
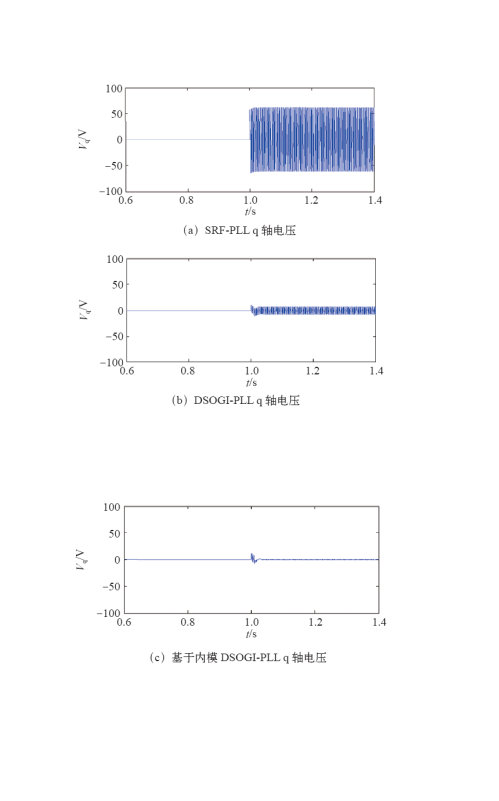
通过对DSOGI的特性进行分析,传统的DSOGI-PLL锁相方法结构如图4所示。由DSOGI对电压基波信号进行正负序分离后,得到正序基波电压作为SRF-PLL的输入信号,进而锁定相位角。当电网电压含有多次谐波分量时,虽然DSOGI能在一定程度上抑制谐波扰动,但是q轴电压分量仍然会存在波动。
图4
3.2 基于重复控制内模的谐波滤除环节
式中,T为外部信号的周期。
将连续域下的传递函数变换至离散域下,由z变换理论,z = e-Ts,则式(7)可表示为
式中,N = fs/f,f为基波信号的频率;fs为系统采样频率。
因G(z)固有的延迟环节,内模控制在第一个基频周期内不起作用,由于电网中含有奇次谐波较多,对锁相精度的影响较大,通常仅对奇次谐波信号进行抑制。在文献[14]中,提出一种改进型奇次谐波发生器的内模结构,该结构不仅减少了算法复杂程度,还降低了半个延迟周期,使得系统动态响应更好。表达式如下
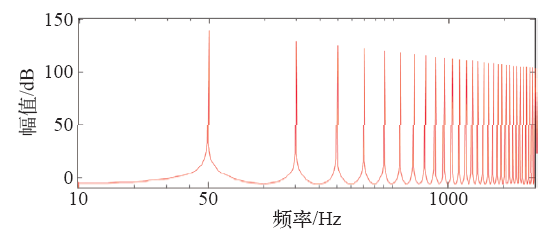
式(9)中,Q(z)通常为小于1的常数或加入的低通滤波器,能够削弱干扰,增加鲁棒性。图5为内模的幅值伯德图,由图中可以看出,在基波和各奇次谐波频率处都会产生幅值增益,能够有效跟踪各个奇次谐波。
图5
图6
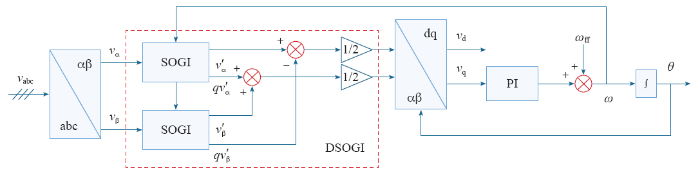
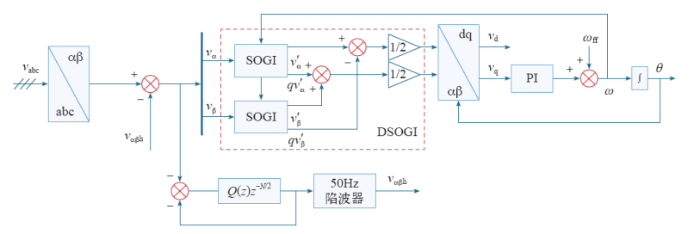
3.3 基于内模的DSOGI-PLL结构
所提出的基于内模的DSOGI-PLL锁相结构如图7所示,采集到的电网电压变换到两相静止坐标系下,通过基于重复控制内模的奇次谐波发生器,由于得到的信号中不仅包含谐波分量,也包含基频分量,因此,加入50Hz陷波器将基频分量滤除,从而得到全频段谐波信号,再将其负反馈到输入端,经过周期性的信号跟踪,便可完全消除谐波分量,得到的基频信号通过DSOGI进一步抑制谐波干扰,并进行正负序分离,得到正序电压分量输入到SRF-PLL,从而锁定相位角。
图7
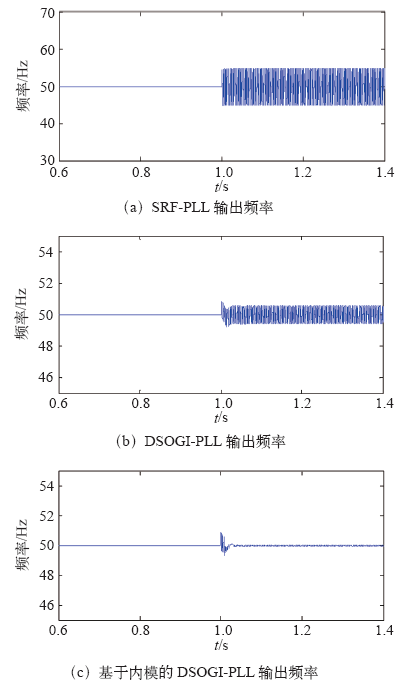
4 仿真验证
图8
图9
图10
图11
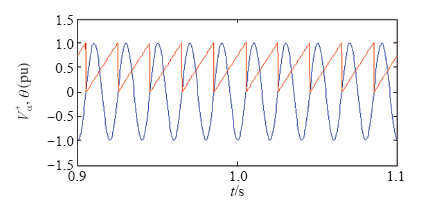
图11
基于内模的DSOGI-PLL 相位角与基波正序电压
Fig.11
Phase angle and fundamental positive sequence voltage under DSOGI-PLL based on internal model
5 结论
本文针对现有的锁相方法不能很好消除谐波的弊端,在DSOGI-PLL方法的基础上,提出了一种基于重复控制内模的DSOGI-PLL锁相方法,通过内模原理,消除谐波分量,由DSOGI进行基波正负序分离。该方法将q轴电压波动量降低至±0.8V左右,锁相频率稳定在50Hz,能在电网电压畸变的情况下,实现基波电压相位和频率的精确锁定。通过与几种传统的锁相方法进行仿真验证,表明了该方法可以在电网电压畸变的情况下,准确快速地锁定相位信息。
参考文献
并网功率变换器的电网电压同步算法
[J].
Grid voltage synchronization algorithms for grid-connected power converters
[J].
Influence of PLL in wind parks harmonic emissions
[C].
基于双dq坐标变换的三相电压锁相环的研究
[J].DOI:10.7667/j.issn.1674-3415.2014.10.018 URL [本文引用: 1]
Study of three-phase voltage phase locked loop based on double dq transformation
[J].DOI:10.7667/j.issn.1674-3415.2014.10.018 URL [本文引用: 1]
Design-oriented study of advanced synchronous reference frame phase-locked loops
[J].
DOI:10.1109/TPEL.2012.2204276
URL
[本文引用: 1]

In grid-connected applications, the synchronous reference frame phase-locked loop (SRF-PLL) is a commonly used synchronization technique due to the advantages it offers such as ease of implementation and robust performance. Under ideal grid conditions, the SRF-PLL enables a fast and accurate phase/frequency detection; however, unbalanced and distorted grid conditions highly degrade its performance. To overcome this drawback, several advanced PLLs have been proposed, such as the multiple reference frame-based PLL, the dual second-order generalized integrator-based PLL, and the multiple complex coefficient filter-based PLL. In this paper, a comprehensive design-oriented study of these advanced PLLs is presented. The starting point of this study is to derive the small-signal model of the aforementioned PLLs, which simplifies the parameter design and the stability analysis. Then, a systematic design procedure to fine tune the PLLs parameters is presented. The stability margin, the transient response, and the disturbance rejection capability are the key factors that are considered in the design procedure. Finally, the experimental results are presented to support the theoretical analysis.
Multi-resonant frequency-locked loop for grid synchronization of power converter under distorted grid conditions
[J].DOI:10.1109/TIE.2010.2042420 URL [本文引用: 1]
A stationary reference frame grid synchronization system for three-phase grid-connected power converters under adverse grid conditions
[J].DOI:10.1109/TPEL.2011.2159242 URL [本文引用: 1]
基于改进型DSOGI-PLL的电网电压同步信号检测
[J].
DOI:10.13334/j.0258-8013.pcsee.2016.09.005
URL
[本文引用: 1]

基于双二阶广义积分器的锁相环(dual second-order generalized integrator PLL,DSOGI-PLL)通过二阶广义积分器产生正交信号和滤除谐波,可实现在电网电压不对称和畸变情况下同步信号的提取。但当电网电压含有多次谐波时,基本二阶广义积分器的滤波效果不理想,锁相环提取的同步信号出现波动。文中通过构建谐波消除模块,在DSOGI-PLL的基础上,提出一种改进的锁相环结构。该锁相环在计算分离正负序电压之前先利用谐波消除模块消除电网电压中的各次谐波,从而消除谐波对锁相环的影响,准确地提取电网电压同步信号。MATLAB仿真和实验结果均表明,这种锁相环在电网电压不对称和含有多次谐波时能有效地提取基波的正负序分量、频率和相位。
Synchronizing signal detection for grid voltage based on modified DSOGI-PLL
[J].
DOI:10.13334/j.0258-8013.pcsee.2016.09.005
URL
[本文引用: 1]

基于双二阶广义积分器的锁相环(dual second-order generalized integrator PLL,DSOGI-PLL)通过二阶广义积分器产生正交信号和滤除谐波,可实现在电网电压不对称和畸变情况下同步信号的提取。但当电网电压含有多次谐波时,基本二阶广义积分器的滤波效果不理想,锁相环提取的同步信号出现波动。文中通过构建谐波消除模块,在DSOGI-PLL的基础上,提出一种改进的锁相环结构。该锁相环在计算分离正负序电压之前先利用谐波消除模块消除电网电压中的各次谐波,从而消除谐波对锁相环的影响,准确地提取电网电压同步信号。MATLAB仿真和实验结果均表明,这种锁相环在电网电压不对称和含有多次谐波时能有效地提取基波的正负序分量、频率和相位。
一种嵌入重复控制内模的三相锁相环的设计与实现
[J].
A novel three-phase phase-locked loop method based on internal model of repetitive control
[J].
谐波畸变电网下的频率自适应锁相方法
[J].为提高同步坐标系锁相环在谐波畸变电网环境下的控制性能,提出一种基于频率自适应滤波器的同步坐标系锁相方法。用数学解析方法证明了所用频率自适应滤波器的时域稳定性,讨论了滤波器的参数对其动稳态性能的影响。同步坐标系锁相方法的设计中,采用频率自适应滤波器在静止坐标系中分离出电网信号的基波正序分量,并在同步旋转坐标系中抑制锁相环输入信号中的2次谐波分量。该文基于频率自适应滤波器设计的同步坐标系锁相方法,实现了对谐波畸变电网中电网信号基波正序分量的精确锁相,且具有较快的动态响应速度。仿真和实验结果验证了所提锁相方法的有效性和可行性。
Frequency adaptive PLL under distorted grid conditions
[J].为提高同步坐标系锁相环在谐波畸变电网环境下的控制性能,提出一种基于频率自适应滤波器的同步坐标系锁相方法。用数学解析方法证明了所用频率自适应滤波器的时域稳定性,讨论了滤波器的参数对其动稳态性能的影响。同步坐标系锁相方法的设计中,采用频率自适应滤波器在静止坐标系中分离出电网信号的基波正序分量,并在同步旋转坐标系中抑制锁相环输入信号中的2次谐波分量。该文基于频率自适应滤波器设计的同步坐标系锁相方法,实现了对谐波畸变电网中电网信号基波正序分量的精确锁相,且具有较快的动态响应速度。仿真和实验结果验证了所提锁相方法的有效性和可行性。
基于双派克变换的新型三相锁相环技术
[J].
Novel three phase locked loop technique based on double Park transformation
[J].
基于二阶广义积分器的基波正负序分量检测方法
[J].
Detection of fundamental positive and negative sequence components based on second-order generalized integrator
[J].
考虑电网频率偏差的并网逆变器多内模重复控制
[J].
A multi-internal-model repetitive control for grid-connected inverter considering grid-frequency deviation
[J].
基于改进型重复控制算法的多功能并网逆变器设计
[J].
Corrective security-constrained optimal power flow with control of flexible AC transmission system devices
[J].
Research on fast transient and 6n±1 harmonics suppressing repetitive control scheme for three-phase grid-connected inverters
[J].
DOI:10.1049/iet-pel.2012.0348
URL
[本文引用: 1]

The repetitive control technique is widely adopted in ac systems, because of its excellent steady-state tracking performance and low total harmonic distortion. The repetitive control method with one-sixth of the system fundamental period T-0 as the delay time has been proposed to achieve fast transient response. In this study, an improved control scheme based on the T-0/6 repetitive control is proposed for three-phase grid-connected inverters. The proposed scheme adopts T-0/6 as the delay time in the positive-rotating and negative-rotating synchronous reference frames to suppress the 6n +/- 1 harmonics. Meanwhile, the proportional-integral regulator and the plug-in repetitive controller are combined to reinforce the system performance. A new auxiliary function based on the linear interpolation is proposed to maintain the ideal repetitive control performance when one-sixth of the ratio of the sampling frequency to the grid fundamental frequency is non-integer. The effectiveness of the proposed scheme on improving the T-0/6 repetitive control is confirmed by simulation and experimental results finally.
An improved repetitive control scheme for grid-connected inverter with frequency adaptive capability
[J].
DOI:10.1109/TIE.2012.2205364
URL
[本文引用: 1]

The power quality of grid-connected inverters has drawn a lot of attention with the increased application of distributed power generation systems. The repetitive control technique is widely adopted in these systems, due to its excellent tracking performance and low output total harmonic distortion (THD). However, in an actual system, the ratio of the sampling frequency to the grid frequency cannot always maintain an integer, and then, the resonant frequencies of the repetitive control technique will deviate from the real grid fundamental and harmonic frequencies. This will degrade the performance of the system, particularly when the grid frequency varies. Even if the ratio is a fixed integer, the auxiliary function for stabilization in the conventional repetitive control technique will also increase the steady-state tracking error and THD of the system. In this paper, an improved repetitive control scheme with a special designed finite impulse response (FIR) filter is proposed. The FIR filter cascaded with a traditional delay function can approximate the ideal repetitive control function of any ratio. The proposed scheme varies the FIR filter according to varied grid frequency and maintains its resonant frequencies matching the grid fundamental and harmonic ones. Finally, the simulation and experimental results show that the improved repetitive control scheme can effectively reduce the tracking error and compensate harmonics of the inverter systems.