1 引言
现有研究中对负荷恢复的优化进行了大量研究。文献[5]基于最短路径算法和遗传算法对配电网的负荷进行优化。文献[6]利用直角坐标的最优乘子牛顿潮流法与灵敏度技术对负荷恢复阶段的负荷恢复量进行优化。文献[7]用遗传模拟退火算法计算得到最大允许恢复负荷量。文献[8]采用基于电网分区的负荷恢复智能优化策略。文献[9]对网架重构过程中的负荷恢复进行优化,采用层次分析法和贪婪算法恢复尽可能多的负荷。文献[10]提出采用广域测量系统提供的实时精确数据使负荷恢复量最大化。文献[11]考虑了负荷恢复过程中的冷负荷恢复特性,用粒子群算法求解最大负荷恢复量。文献[12]考虑了负荷恢复过程中的暂态电压、频率变化,用自适应遗传算法求解负荷恢复量。
在网架重构阶段,现有研究主要通过智能算法得到满足约束条件的负荷分配方案,但由于智能算法求解速度较慢,且负荷分配主要是配合发电机出力,所以需要加快负荷分配方案的计算速度,从而加快网架重构的优化速度。
基于此,本文基于灵敏度法调整负荷分配方案,使各节点电压满足要求。首先对已恢复电网进行灵敏度分析,在潮流计算的基础上,计算过电压节点与所有负荷节点视在功率变化的灵敏度,对灵敏度最大的负荷节点,根据最大的灵敏度计算要投入的负荷量,将功率平均分配到各负荷节点,循环调用上述方法直至所有节点电压均满足要求。最后,以IEEE 39节点系统为例对本文方法进行验证。
2 灵敏度分析
2.1 灵敏度分析的数学模型
灵敏度分析基于潮流方程,潮流计算的基本方程是节点功率平衡方程
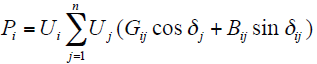
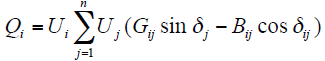
式中,Pi、Qi分别为节点的有功功率和无功功率;Ui、Uj分别为i、j节点的节点电压;Gij、Bij为节点导纳矩阵的元素的实部和虚部;δij为两节点之间电压相位的差值。
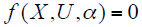
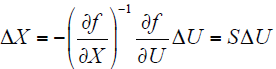
将潮流方程在运行点线性化可得式(4),即状态变量和控制变量之间的灵敏度矩阵表达式。
2.2 灵敏度指标
本文需要分析节点电压随负荷变化的灵敏度指标,根据这两个灵敏度指标可以求出将电压稳定到约束范围内需要的有功负荷和无功负荷调整量,上述两个指标的意义为:
(1)当PQ节点的有功功率增加时,该节点的电压下降;反之当PQ节点的有功功率减少时,该节点的电压上升。
(2)当PQ节点的无功功率增加时,该节点的电压下降;反之当PQ节点的无功功率减少时,该节点的电压上升。
3 基于灵敏度分析的电压越限调整策略
在负荷恢复过程中,发电机出力在缓慢增加,负荷的投入也受到功率增量的约束,本文采用灵敏度分析的方法调整负荷的投入,将电压限制到约束范围内。
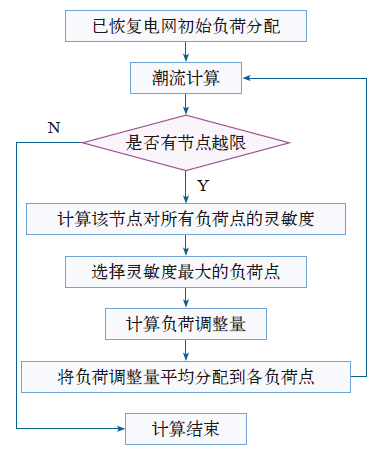
基本策略是找出电压越限最严重的节点,采用式(5)求出该点电压与系统所有负荷节点的视在功率变化灵敏度,找出其中灵敏度最大的负荷节点,根据式(6)求出需要投入的负荷量,如果调整的这个负荷量大于灵敏度最大负荷节点的总负荷量,将要调整的有功负荷量取该节点总负荷量。
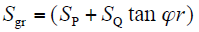
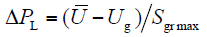
计算出电压调整需要的负荷量后,将这部分功率分配到各负荷节点,将电压调整的这部分功率平均分配给各负荷节点的负荷,无功负荷和有功负荷按相同的比例投入。采用平均分配的方式,各个越限点的电压就会有明显的下降,而且调整的次数也比较少,方法也是最简单。依据上述方法进行电压调整,如果调整后依旧有电压越限点,将重复此过程,直到电压满足要求。网架重构过程中负荷恢复程序流程图如下图所示。
图
4 算例分析
为了检验本文算法的有效性,以IEEE 39节点系统为例对本文方法的有效性进行仿真分析。假设节点31为黑启动电源和平衡机,装机容量为580MW。系统总恢复过程分为了9个时步,每个时步都起动一台发电机组,并恢复已建立网架中的部分重要负荷,具体恢复顺序见表1。
表1 每个时步的恢复路径
Tab.1
| 时 步 | 起动 机组 | 恢复路径 | 总恢复时间 /min |
|---|---|---|---|
| 1 | 32 | 31→6→11→10→32 | 20 |
| 2 | 33 | 6→5→4→14→15→16→19→33 | 55 |
| 3 | 36 | 16→24→23→36 | 70 |
| 4 | 35 | 16→21→22→35 | 85 |
| 5 | 30 | 4→3→2→30 | 100 |
| 6 | 37 | 2→25→37 | 110 |
| 7 | 34 | 19→20→34 | 120 |
| 8 | 38 | 3→18→17→27→26→29→38 | 150 |
| 9 | 39 | 5→8→9→39 | 165 |
以第二时步为例,说明负荷调整策略。在第一时步时,31节点上负荷全部投入,在第二时步时,发电机增加出力为41.6MW,将负荷分配到节点4、15、16,分配完成后系统潮流见表2。
表2 负荷分配后的潮流计算
Tab.2
| 节点 编号 | 电压 (pu) | 发电有功 /MW | 发电无功 /Mvar | 负荷有功 /MW | 负荷无功 /Mvar | 无功补偿 /Mvar |
|---|---|---|---|---|---|---|
| 4 | 1.0910 | 0 | 0 | 50 | 18.4 | 0 |
| 5 | 1.0810 | 0 | 0 | 0 | 0 | 0 |
| 6 | 1.0790 | 0 | 0 | 0 | 0 | 0 |
| 10 | 1.0710 | 0 | 0 | 0 | 0 | 0 |
| 11 | 1.0740 | 0 | 0 | 0 | 0 | 0 |
| 14 | 1.1020 | 0 | 0 | 0 | 0 | 0 |
| 15 | 1.1130 | 0 | 0 | 37.5 | 17.9 | 0 |
| 16 | 1.1170 | 0 | 0 | 0 | 0 | 0 |
| 19 | 1.1200 | 0 | 0 | 0 | 0 | 0 |
| 31 | 1.0000 | 22.2 | 0 | 9.2 | 4.6 | -29.1 |
| 32 | 0.9830 | 97.5 | -86.5 | 12.5 | 0 | 0 |
| 33 | 1.0470 | 0 | 0 | 10 | 0 | 0 |
表3 电压越限调整后的潮流计算结果
Tab.3
| 节点 编号 | 电压 (pu) | 发电有功 /MW | 发电无功 /Mvar | 负荷有功 /MW | 负荷无功 / Mvar | 无功补偿 / Mvar |
|---|---|---|---|---|---|---|
| 4 | 1.0500 | 0 | 0 | 147.9 | 54.4 | 0 |
| 5 | 1.0570 | 0 | 0 | 0 | 0 | 0 |
| 6 | 1.0580 | 0 | 0 | 0 | 0 | 0 |
| 10 | 1.0570 | 0 | 0 | 0 | 0 | 0 |
| 11 | 1.0580 | 0 | 0 | 0 | 0 | 0 |
| 14 | 1.0510 | 0 | 0 | 0 | 0 | 0 |
| 15 | 1.0470 | 0 | 0 | 126.6 | 60.60 | 0 |
| 16 | 1.0490 | 0 | 0 | 79.5 | 7.8 | 0 |
| 19 | 1.0520 | 0 | 0 | 0 | 0 | 0 |
| 31 | 1.0000 | 290.7 | 0 | 9.2 | 4.6 | 58.3 |
| 32 | 0.9830 | 97.5 | -24.9 | 12.5 | 0 | 0 |
| 33 | 0.9830 | 0 | 0 | 10 | 0 | 0 |
可以看出,各节点的电压都降到约束范围内,负荷有功无功都有所增加,整个系统功率保持在平衡状态,本文负荷调整策略有效。在每个时步中重复调用本文调整策略,可以快速实现恢复过程中负荷的调整,为网架重构的优化提供支持。
5 结论
针对停电系统恢复网架重构过程中负荷恢复引起的电压越限问题,本文提出了基于灵敏度法的负荷调整策略。对已恢复的电网进行潮流计算,选择电压越限节点,采用灵敏度法计算该节点对所有负荷点的灵敏度,取灵敏度最大的负荷点,基于灵敏度技术负荷调整量,将负荷调整量分配到其他负荷点,循环上述步骤直至所有节点电压均满足要求。IEEE 39节点系统仿真结果表明,本文方法能够有效地解决节点电压越限的问题,提高恢复过程中电网的安全性。
参考文献
海南电网“9·26”大面积停电事故的分析与总结
[J].
Review of blackout in hainan on september 26th--causes and recommendations
[J].
欧洲"11.4"大停电事故分析及对我国电网运行工作的启示
[J].The origin, spread and restoration of large-scale blackout occurred on Nov. 14, 2006 in UCTE Power Grid are described. According to the related investigation reports the direct causes led to the blackout are clarified; the situation of sectionalized UCTE Power Grid and the problems discovered by the blackout and the lessons from it are analyzed. According to the operational condition of interconnected interregional power grids in China, the lessons to be drawn by domestic power grid operation from the large-scale blackout in UCTE Power Grid are put forward.
Analysis of large-scale blackout in UCTE power grid and lessons to be drawn to power grid operation in China
[J].The origin, spread and restoration of large-scale blackout occurred on Nov. 14, 2006 in UCTE Power Grid are described. According to the related investigation reports the direct causes led to the blackout are clarified; the situation of sectionalized UCTE Power Grid and the problems discovered by the blackout and the lessons from it are analyzed. According to the operational condition of interconnected interregional power grids in China, the lessons to be drawn by domestic power grid operation from the large-scale blackout in UCTE Power Grid are put forward.
From generic restoration actions to specific restoration strategies
[J].DOI:10.1109/59.387912 URL [本文引用: 1]
A framework for power system restoration following a major power failure
[J].DOI:10.1109/59.466500 URL [本文引用: 1]
基于最短路算法和遗传算法的配电网络重构
[J].
Shortest path algorithm and genetic algorithm based distribution system reconfiguration
[J].
黑启动过程中的负荷恢复
[J].The load recovery and the connection of subsystems with power grid during the blackstart of subsystem are researched. Firstly, by means of integrating the rectangular coordinates based weighted optimal multiplier Newton-Raphson method with sensitivity analysis and adopting continuous linear programming method, both mathematical model and algorithm for restoration control to solve the infeasibility of N-1 power flows and out-of-limit states, which appear at load recovery stage, are established; secondly, the models and algorithms to simulate the frequency variation of subsystems at load recovery stage are established; finally, for the problem of connecting subsystems with power grid, a continuous linear programming based optimal generation re-dispatching method is also developed to control the voltage difference between different islands, thus the optimal voltage difference control at the position where the connection is taken place is effectively implemented. The effectiveness of the proposed model and algorithm is verified by simulation results of standard testing system and actual power grid.
Load recovery during power system blackstart
[J].The load recovery and the connection of subsystems with power grid during the blackstart of subsystem are researched. Firstly, by means of integrating the rectangular coordinates based weighted optimal multiplier Newton-Raphson method with sensitivity analysis and adopting continuous linear programming method, both mathematical model and algorithm for restoration control to solve the infeasibility of N-1 power flows and out-of-limit states, which appear at load recovery stage, are established; secondly, the models and algorithms to simulate the frequency variation of subsystems at load recovery stage are established; finally, for the problem of connecting subsystems with power grid, a continuous linear programming based optimal generation re-dispatching method is also developed to control the voltage difference between different islands, thus the optimal voltage difference control at the position where the connection is taken place is effectively implemented. The effectiveness of the proposed model and algorithm is verified by simulation results of standard testing system and actual power grid.
基于遗传模拟退火算法的负荷恢复计划制定
[J].The ultimate goal of system restoration after blackout is to restore load fully and rapidly. One of the most important things in load recovery is to control system frequency, and the effective method to keep the frequency stability is to control the balance between load recovery speed and the generator’s responses. A method using genetic simulated annealing algorithms is proposed for determination of load restoration plans on the basis of network reconfiguration, in which system frequency is calculated by extended power flow analysis and the various system constraints are treated by penalty functions. Through the calculation of the genetic group fitness, the optimal recovery path and the maximum load step can be determined. The efficiency and effectiveness of the proposed method are verified by the numerical results on the IEEE 30 and IEEE 118 systems.
Determination of the load restoration plans based on genetic simulated annealing algorithms
[J].The ultimate goal of system restoration after blackout is to restore load fully and rapidly. One of the most important things in load recovery is to control system frequency, and the effective method to keep the frequency stability is to control the balance between load recovery speed and the generator’s responses. A method using genetic simulated annealing algorithms is proposed for determination of load restoration plans on the basis of network reconfiguration, in which system frequency is calculated by extended power flow analysis and the various system constraints are treated by penalty functions. Through the calculation of the genetic group fitness, the optimal recovery path and the maximum load step can be determined. The efficiency and effectiveness of the proposed method are verified by the numerical results on the IEEE 30 and IEEE 118 systems.
基于电网分区的负荷恢复智能优化策略
[J].DOI:10.7667/j.issn.1674-3415.2011.02.001 URL [本文引用: 1]
Intelligent optimizaiton strategy for load restoration considering power grid partitioning
[J].DOI:10.7667/j.issn.1674-3415.2011.02.001 URL [本文引用: 1]
黑启动恢复中网架重构阶段的负荷恢复优化
[J].DOI:10.7667/j.issn.1674-3415.2011.17.006 URL [本文引用: 1]
Optimizaiton of load restoration during network reconfiguring process of black-start restoration
[J].DOI:10.7667/j.issn.1674-3415.2011.17.006 URL [本文引用: 1]
A wide area monitoring system based load restoration method
[J].
DOI:10.1109/TPWRS.2013.2249595
URL
[本文引用: 1]

Restoring a large-scale power system has always been a complicated and important issue. A lot of research work has been done on different aspects of the whole power system restoration procedure. However, more time will be required to complete the power system restoration process in an actual situation if accurate and real-time system data cannot be obtained. With the development of the wide area monitoring system (WAMS), power system operators are capable of accessing to more accurate data in the restoration stage after a major outage. The ultimate goal of the system restoration is to restore as much load as possible while in the shortest period of time after a blackout, and the restorable load can be estimated by employing WAMS. Moreover, discrete restorable loads are employed considering the limited number of circuit-breaker operations and the practical topology of distribution systems. In this work, a restorable load estimation method is proposed employing WAMS data after the network frame has been reenergized, and WAMS is also employed to monitor the system parameters in case the newly recovered system becomes unstable again. The proposed method has been validated with the New England 39-Bus system and an actual power system in Guangzhou, China.
基于粒子群优化的最优负荷恢复算法
[J].The optimal load restoration model concerning cold load pickup is formulated as an optimization problem subjected to the system operation constraints including frequency, voltage and generation output, so that the maximum load may be picked up when maintaining reasonable frequency and voltage profiles. With IPLAN programming language provided by PSS/E, particle swarm optimization algorithm is applied to solve the proposed optimization problem. In addition, penalty function is introduced to handle system operation constraints. The proposed method is able to determine the load positions and amounts that can be picked up without disturbing system security and stability. Simulation is performed on a test system and the results demonstrate the effectiveness of the proposed method.
Optimal load restoration algorithm based on PSO
[J].The optimal load restoration model concerning cold load pickup is formulated as an optimization problem subjected to the system operation constraints including frequency, voltage and generation output, so that the maximum load may be picked up when maintaining reasonable frequency and voltage profiles. With IPLAN programming language provided by PSS/E, particle swarm optimization algorithm is applied to solve the proposed optimization problem. In addition, penalty function is introduced to handle system operation constraints. The proposed method is able to determine the load positions and amounts that can be picked up without disturbing system security and stability. Simulation is performed on a test system and the results demonstrate the effectiveness of the proposed method.
黑启动中考虑动态过程的负荷最优恢复
[J].
Optimal load restoration consdering dynamic process during blackstart
[J].
灵敏度分析法在静态电压稳定中的应用
[J].
The application of sensitivity analysis in static voltage stability
[J].
准稳态灵敏度的分析方法
[J].
New sensitivity analysis method under quasi-steady-state for power systems
[J].
基于灵敏度分析与最优潮流的电网无功/电压考核方法
[J].
Power system reactive power/voltage assessment based on sensitivity analysis and optimal power flow
[J].