1 引言
随着电力电子技术、微电子技术和现代电机控制理论的迅速发展,交流电机获得快速的推广与应用[1]。在高性能交流电机控制方法中目前已经获得了广泛应用的控制方法有以下两类:矢量控制(FOC)[2,3,4]与直接转矩控制(DTC)[2,5-8]。直接转矩控制结构简单、动态响应快,由于其采用bang-bang控制器,通过控制器的误差输出信号以及定子磁链的位置信号从离线设计的开关表中选择合适的电压矢量作用于交流电机,导致对转矩与磁链的控制脉动较大且开关频率不固定,在一些高性能控制领域,应用受到一定的限制。矢量控制主要通过转子磁场定向,把定子电流分解成d、q轴电流,通过PI调节器来分别控制转子磁链与电磁转矩。这种解耦控制方法使矢量控制能够获得更好的稳态性能,满足高性能交流电机控制领域的要求。
随着现代工业的快速发展对调速系统的性能以及控制精度的进一步提高,传统的矢量控制技术并不能够满足现代工业控制精度的要求。传统矢量控制中线性PI调节器的电流内环分别采用d、q轴两个独立的控制环,受到环路间存在交叉耦合项、控制器离散化处理时产生的误差、数字控制系统延迟等因素的影响,同时该耦合项与同步角频率成正比,使得传统的线性PI调节器不能完全实现独立设计,从而导致交流电机的控制精度受到影响。在实际应用中大都采用数字控制系统,传统方法基于连续域设计的调节器,最终还需进行离散化处理,不可避免地引入误差。同时数字控制系统存在一拍延时,进一步降低了控制系统的性能。
为了解决d、q轴之间定子电流交叉耦合的问题,有学者提出了一些解决方法,但这些方法大都比较复杂[9]。文献[1]引入非线性补偿来抵消耦合项,计算表达式十分复杂而且参数整定过程繁琐。为避免复杂的解耦过程,一些方法基于复矢量设计调节器[10],另有一些方法直接在离散域设计电流调节器来避免离散化时带来的误差[11]。但是这些方法没有给出可调参数k的具体设计方法,在实际应用中仍需根据经验,反复试验调整才能确定。目前尚没有较好的方法能够同时满足:①消除d、q轴两个控制环的交叉耦合;②直接在离散域设计调节器,避免离散化误差;③考虑数字控制系统延迟的影响;④给出准确的控制器可调参数k的设计公式。因此,需要在现有的设计方法中,提出一种简单实用的方法,在获取更好的控制性能的同时提高方法的通用性和实用性。
本文提出将交流电机控制系统中的d、q轴电流环当作一个整体,直接在离散域中建立电流环的数学模型,同时考虑数字控制系统的一拍延迟,直接在离散域中设计电流调节器。以异步电机为例,将其作为控制对象,对异步电机的数学建模进行了详细的研究,然后按照工程应用中相位裕度至少45°[11],推导出电流调节器参数k的最大值解析表达式,但是此系数将为电流调节器带来一定的超调量。为了使电流调节器内环的超调量为零,本文根据自动控制原理,采用系统的阻尼比为1的最优设计方法,推导出电流调节器参数k的最优值,此时没有超调量并且具有较优的动态性能[12]。在阶跃信号的作用下,电流环没有超调量且系统响应迅速。为了验证所提出的离散域电流调节器设计方法的有效性,本文把这种新型交流电机在离散域中设计电流调节器的方法与异步电机矢量控制相结合,在两电平逆变器异步电机控制平台上进行了相应的仿真和实验验证,同时也给出了传统线性PI调节器与矢量控制的仿真与实验结果。仿真和实验结果表明,本文提出的新型离散域电流调节器在全速范围内都具有良好的动静态性能,有效扩大了矢量控制在工业当中的应用范围。
2 异步电机数学模型
异步电机在静止坐标系下矢量形式数学模型[13]可以表示为
电压方程
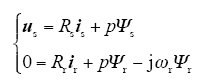
磁链方程
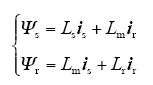
转矩方程
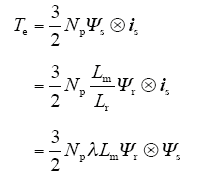
其中 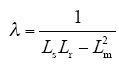
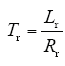
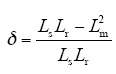
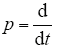
式中,Rs为电机定子电阻;Rr为转子电阻;Ls为定子电感;Lr为转子电感;Lm为定转子互感;Np为电机极对数;ωr为电机转速;us为定子电压;Ψs为定子磁链;Ψr为转子磁链矢量。
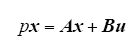
其中
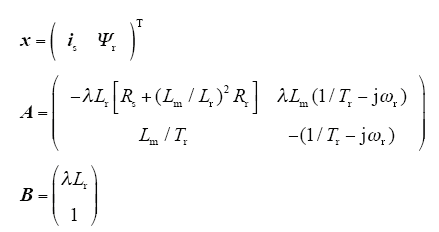
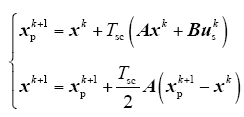
式中,xpk+1与Tsc分别为预测校正变量和控制周期,xk+1 = [isk+1 Ψrk+1]T为预测得到的下一时刻的状态变量。因此下一时刻的电磁转矩Tek+1能够被预测得到
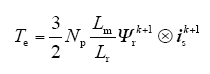
3 线性PI调节器
传统的线性PI调节器如下所示
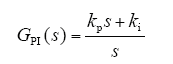
传统电流内环采用两个独立的PI 调节器分别对 d、q 轴电流环进行调节。如式(4)第一行所示,忽略d、q轴电流交叉耦合项以及反电动势项后,定子电流到电压的传递函数为
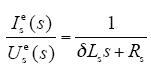
根据式(7)和式(8),电流内环的开环传递函数为
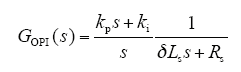
假设期望的电流环控制带宽为k,可得:kp = kδLs,ki = kRs。将kp、ki代入式(9)可得
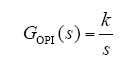
由此可见在理想情况下,采用线性 PI 调节器可将电流内环校正为一阶惯性环节,如下所示
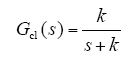
可见系统始终稳定且不存在超调,按照工程应用输出滞后参考值45°定义系统的控制带宽[11]ωc,易得
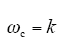
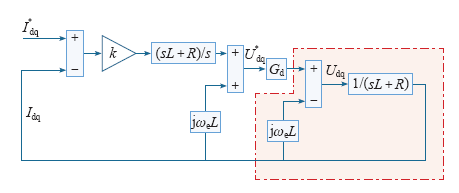
然而由于数字处理延迟环节Gd的存在且不为1,上述建模环节并不完全符合实际情况如图1所示,本文重点介绍离散域电流调节器在离散域中的设计方法,以及PI系数在理论上的设计,同时考虑数字系统一拍延时的影响。
图1
4 离散域电流调节器的设计
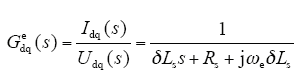
由于实际应用中大都采用数字控制系统,基于连续域设计的调节器最终还需进行离散化处理,为了避免离散化处理带来的误差,本文采用更为直接的设计方法在离散域设计电流调节器。在离散域建立电流内环数学模型[11]其表达式如下
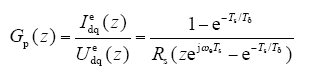
式中,Tδ = δLs/R;Ts为控制周期;z为Z变换算子;e为自然对数;ωe为同步电角速度;j为虚数单位。
然后再考虑在同步坐标系下补偿数字控制系统的一拍延迟,得到异步电机同步旋转坐标系下电流内环的离散域数学模型Gedq(z)
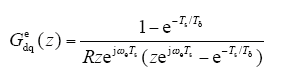
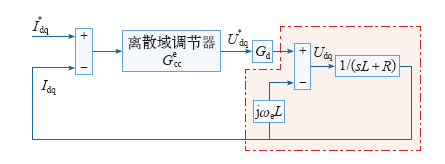
根据式(15)电流内环的数学模型,基于零极点对消的设计方法,直接设计含有可调参数的同步旋转坐标系下电流内环的离散域调节器Gedq(z)如式(16)所示,其整个的控制框图如图2所示。
图2
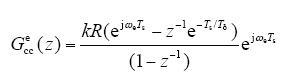
根据式(15)得到的离散域数学模型Gedq(z)和式(16)中得到的离散域调节器Gecc(z),可得到系统的开环传递函数
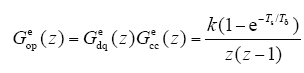
式中,k为可调参数;z为Z变换算子。
因此可以根据式(17)得到系统的闭环传递函数如下
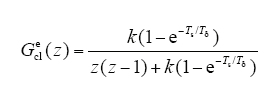
在实际应用中,由于受到噪声以及模型不精确等因素的影响,为保证系统的稳定性通常要求相位裕度至少为45°,根据剪切频率可以求得系数k的最大值。令式(17)中z = ejωTs,可得
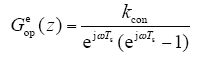
其中,kcon = k(1 - e-Ts/Tδ),由于Ts通常很小,为了保证控制精度,本文采用Pade近似[21]来化简式(19),可得
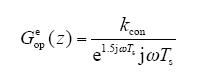
根据式(20)可得剪切频率为ωc = kcon/Ts,令此时的相位裕度为45°,因此可以求得最大的k值如下所示
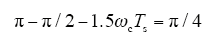
由式(21)可得k的最大值为
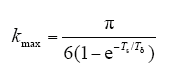
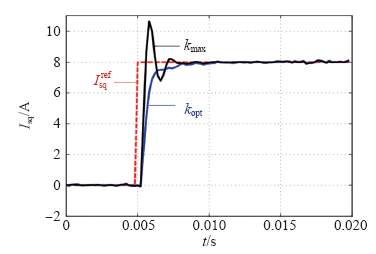
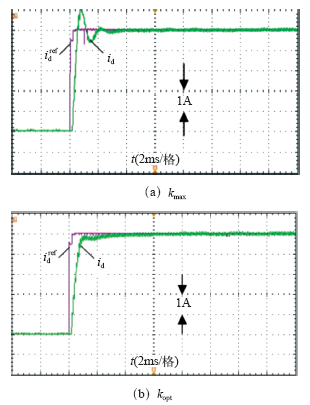
由于按照kmax对电流调节器进行参数整定时,虽然具有较快的上升速度但是超调量很大,如图3所示。因此有必要求得一个最优的系数kopt。
图3
图3
离散域调节器q轴电流阶跃响应
Fig.3
Simulation results of a step response of q-axis current in discrete-time regulator
根据式(17)的系统开环传递函数,可以得到系统的闭环特征方程
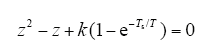
根据自动控制原理,当系统闭环特征方程的两个根均位于实轴时,系统无超调量,此时需满足
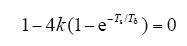
因此可以得到实现系统无超调的可调参数的最优值为
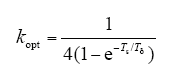
将式(25)中得到的最优值kopt,代入式(16)中的离散域调节器Gecc(z)中,即得到同步旋转坐标系下电流内环的离散域调节器
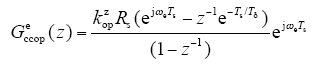
在仿真中采用式(25)中最优系数k之后,系统的闭环函数阶跃响应如图3所示,从图中可以看出,系统响应迅速并且没有超调,验证了本小节离散域调节器参数设计的有效性。现有文献[9,20]通过理论和实验研究表明,基于离散域设计的电流调节器具有良好的稳定特性和较好的参数鲁棒性。但是它们并未给出参数的优化设计原则,本节基于离散域设计与自动控制原理,从理论上推导出电流调节器参数k的解析表达式和最优值。下面将通过仿真和实验来验证本节电流调节器参数设计的有效性。
5 仿真与实验结果
5.1 仿真结果
为了验证本文中提出的算法有效性,在实验室一台2.2kW异步电机调速平台上进行了仿真和实验验证,电机参数见下表。PWM周期为200μs,传统线性PI按照最优设计调节器的系数为kop = 1 144。离散域调节器的增益系数根据式(25)设置为7.54。
表 仿真和实验参数
Tab
| 参数 | 数值 |
|---|---|
| Udc/V | 540 |
| Pn/kW | 2.2 |
| Un/V | 380 |
| fn/Hz | 50 |
| Np | 2 |
| Tn/N·m | 14 |
| Rs/Ω | 3.126 |
| Rr/Ω | 1.879 |
| Lm/Η | 0.221 |
| Ls/Η | 0.23 |
| Lr/Η | 0.23 |
| Ψs/Wb | 0.91 |
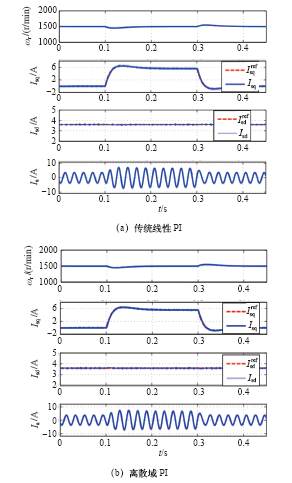
首先验证本文中离散域电流调节器参数设计的有效性,对q轴电流阶跃给定进行了仿真。电机初始转速为-1 500r/min,然后突加转矩开始加速,加速期间的q轴电流响应如图3所示。从图中可以看出,采用优化设计的增益系数后,q轴电流能迅速跟踪上给定值而且不存在超调。而按照最小相位裕度要求设计的参数kmax,q轴电流上升时间较短但存在较大超调,仿真结果与理论分析非常一致,从而间接验证了算法的正确性。对于离散域电流调节器,采用优化设计的增益参数后超调量大大减小同时又没有牺牲最终的整定时间。
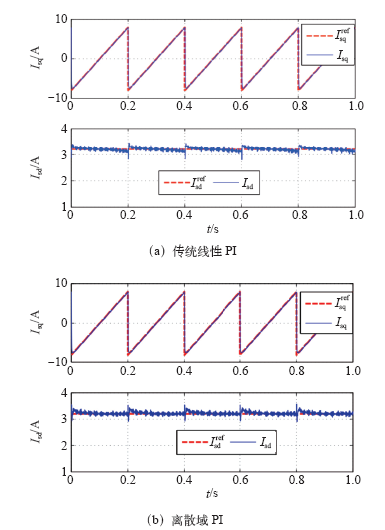
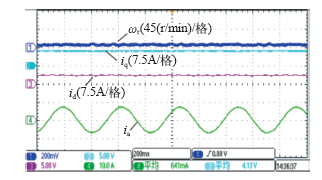
然后验证以上两种电流调节器在动态过程中的性能,稳态性能将通过实际实验进行比较。首先将励磁电流值固定为 3.2A,转矩电流给定为锯齿波,在这个过程中电机转速在750~1 500r/min变化,图4为相应的仿真波形,由于延迟环节的存在,d、q轴电流环之间存在一定的耦合,再加上仿真中同步电角速度经过滤波处理,因此d轴电流在大动态过程中略受影响。对于离散域电流调节器,d轴电流很快恢复至参考值,而基于传统PI线性调节器的d轴电流则一直受到变化的q轴电流影响,这是由于控制延迟的存在使得传统线性PI调节器难以通过前馈的方式来实现两个电流环的完全解耦。
图4
图4
给定q轴电流为锯齿波时的仿真波形
Fig.4
Simulation results of a given Saw tooth wave of q-axis current
图5
图5
1500r/min时突加、减负载的仿真波形
Fig.5
Simulation results of responses with sudden load change at 1500r/min
5.2 实验结果
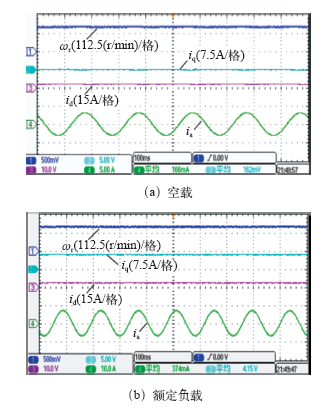
除了仿真验证,也在两电平交流调速实验平台上验证本文提出的离散域设计电流调节器的有效性。实验装置如图6所示,电机参数和系统采样频率与仿真一样,见上表。实验中采用DSP TMS320F28335来执行主算法,负载转矩通过磁粉制动器来加负载,电机的实际转速通过增量式编码器直接获得,电机的内部变量除了定子电流外都是通过控制板上的12位DA芯片输出到示波器上显示,其中定子电流是通过电流钳获得。1通道为实际测量转速,2通道为估计的q轴电流,3通道为估计的d轴电流。1~3通道在示波器上每格代表的数值已在图形中标注,4通道每格代表的电流大小示波器本身已标注在截图的左下角。
图6
图7
图7
不同调节器参数对应的d轴电流阶跃响应
Fig.7
A step response of d-axis current for different regulator parameter
图8
图9
图10
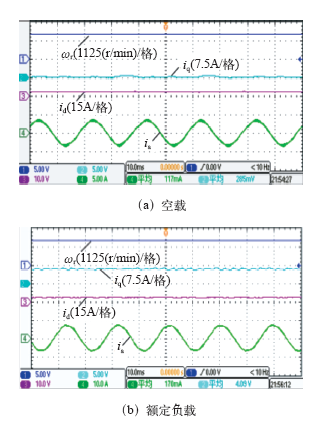
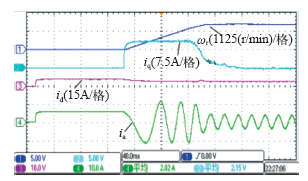
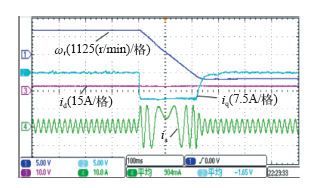
除了稳态性能的实验验证,本文还测试了此算法的动态实验如图11和图12所示,分别为系统的起动与高速正反转测试波形。为实现系统在起动时具有足够的带载能力,在起动前进行了直流预励磁处理,即令q轴电流为零并在d轴通入恒定的直流来对电机行励磁,当气隙磁通达到设定值时即可满载起动电机。从图11可以看出,d、q轴电流响应迅速,在动态过程中并未出现超调现象,验证了前面参数设计理论分析的正确性。图12为系统从1 500r/min到-1 500r/min的正反转测试波形。同样,q轴电流迅速增加至最大值,并且没有出现超调振荡现象,而且d轴电流在整个q轴电流波形变化的过程中始终稳定在参考值,从而验证了基于离散域电流调节器的设计能够在动态过程中实现d、q轴电流的解耦控制。另外,转速在过零区域切换过程平滑,表明整个系统具有良好的动态性能。
图11
图11
0~1500r/min空载起动波形
Fig.11
Starting response from 0 to 1500r/min without load
图12
6 结论
本文详细地研究了矢量控制中的电流环调节器的设计方法,主要介绍了传统线性PI电流调节器与基于离散域中设计的电流调节器,并且基于相位裕度和自动控制原理等理论分析方法,详细地推导出了离散域调节器的解析表达式,同时也在理论上推导出离散域调节器系数k的最优值,从而能保证系统无超调又能满足系统的动态响应,最终通过仿真与实验对两种调节器的设计进行了验证。由于离散域调节器的优势主要在高速弱磁部分与低载波比情况下[18,19],而本文并未考虑高速弱磁运行部分,所以两种调节器在仿真与实验中的性能区别不是很大。但是总体上而言,离散域调节器不像传统PI调节器那样将两个电流环分开考虑,所以离散域中直接设计电流调节器的结构要简单很多,同时也省去了传统线性PI调节器在实际应用中还需要离散化的步骤,从而减少了离散化过程中带来的误差。因此本文提出的离散域中直接设计电流调节器有效提高了矢量控制的工业应用。
参考文献
Development of PMSM drives for hybrid electric car applications
[J].
High performance VOC-FOC based wind generator system with induction machine
[C].
FOC and flux weakening for traction drive with permanent magnet synchronous motor
[C].
Model predictive direct torque control;part I: Concept, algorithm, and analysis
[J].
A novel duty cycle control strategy to reduce both torque and flux ripples for DTC of permanent magnet synchronous motor drives with switching frequency reduction
[J].
Sensorless direct torque and flux-controlled IPM synchronous motor drive at very low speed without signal injection
[J].
Predictive direct torque control for the PM synchronous machine
[J].
矢量控制系统的电流解耦及其调节器设计
[J].
Decoupling of current and design of controller for vector control system
[J].
Design of fast and robust current regulators for high-power drives based on complex state variables
[J].
Discrete-time current regulator design for AC machine drives
[J].
A simple tuning method aimed at optimal settling time and overshoot for synchronous PI current control in electric machines
[C].
Performance evaluation of an improved model predictive control with field oriented control as a benchmark
[J].
Model predictive torque control of induction motor drives with optimal duty cycle control
[J].
The representation of AC machine dynamics by complex signal flow graphs
[J].
Torque ripple reduction of model predictive torque control of induction motor drives
[C].
A compensation method for time delay of full-digital synchronous frame current regulator of PWM AC drives
[J].
Modified current control schemes for high-performance permanent magnet AC drives with low sampling to operating frequency ratio
[J].
Discrete-time domain modeling and design for AC machine current regulation