1 引言
随着数字信号处理器的迅速发展,更加先进的控制算法能够被应用在交流电机控制当中。模型预测控制(MPC)是最近才被提出来的一种新型控制方法,在20世纪90年代,德国学者Holtz最早把MPC[7]运用到交流电机控制领域中,MPC具有动态响应快、结构简单且易于处理非线性控制变量等优点,从而在学术界与工业界引起广泛的关注[8]。传统的模型预测转矩控制(MPTC)在目标函数中需要设计一个合适的权重系数来调节磁链幅值,但是权重系数的选择过程非常繁琐且复杂,由于缺乏相应的理论支持,通常需要大量的仿真以及实验来确定合适的权重系数。另外,为了获得较好的稳态性能,传统MPC需要提高系统的采样频率[9]。通过电机磁链与转矩的内在关系可以把转矩与定子磁链幅值转化成定子磁链矢量,从而避免MPTC中的权重系数设计[10,11,12],应用这种等效变换的控制方法称为模型预测磁链控制(MPFC)。当整个控制周期作用一个电压矢量时,MPFC的转矩与磁链的脉动较大,从而限制MPFC在高性能电机控制中的应用。
为了提高MPFC的稳态性能,占空比优化的概念被应用到MPFC中,即在整个控制周期作用多个电压矢量[13,14],然后采用磁链无差拍或者磁链脉动最小的方法来优化占空比。为了解决这个问题,一些学者提出了一种新型的多矢量选择方法,其控制周期中第一个电压矢量仍然选择上一时刻最后作用的电压矢量,然后再从所有的电压矢量中选择一个最优的电压矢量[15],这种方法有效减少系统的开关频率与程序计算时间,同时也能改善系统的稳态性能。为了进一步提高系统的稳态性能,降低系统的采样频率,可以在整个控制周期内作用3个电压矢量,这种方法在矢量选择以及占空比优化方面显著地提高了算法的复杂度,同时系统的开关频率也会显著增加。两电平中有7个不同的空间矢量,对于三矢量来说,矢量组合有73 = 343种,如果从这些组合中选择出最优的一组电压矢量,计算量非常大,难以在实际中应用。
为了解决上面三矢量方法中存在的一些问题,本文提出一种新型的三矢量MPFC,这种方法中,第一个矢量仍然选择上一个控制周期中最后作用的电压矢量,第二个矢量选择零矢量,第三个矢量从6个不同的电压矢量中选择最优的电压矢量,这种新型的方法显著地降低了算法的复杂度与开关频率,能极大地推广MPFC在工业当中的应用。为了降低逆变器的非线性对三矢量MPFC的影响,本文基于伏秒平衡的原理,又提出了一种改进型三矢量MPFC,为了突出新型三矢量MPFC的性能,基于空间矢量脉宽调制的MPFC(MPFC_SVM)被引入作为对比。首先通过仿真来验证本文提出的方法的有效性,然后在相同的开关频率下详细地比较了以上三种控制方法转矩与磁链脉动以及电流THD的大小。通过比较可得,在相同的开关频率下,新型的三矢量MPFC的转矩与磁链脉动以及电流THD要明显地低于改进型三矢量MPFC,而MPFC_SVM的转矩脉动最大,说明相比改进型三矢量MPFC与MPFC_SVM,本文提出的新型三矢量MPFC具有良好的稳态性能以及更低的开关频率,最终通过实验验证了本文提出的新型三矢量MPFC的有效性。
2 异步电机数学模型
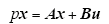
其中 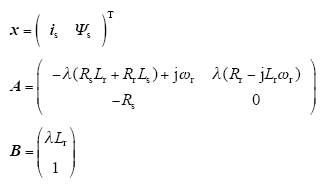
式中,λ = 1/(LsLr - Lm2 ); p = d/dt表示微分算子;Rs、Rr、Ls、Lr、Lm、ωr分别为电机定子电阻、转子电阻、定子电感、转子电感、定转子互感和电机转速;Ψs为定子磁链。
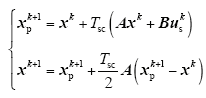
式中,xpk+1与Tsc分别为预测校正变量和控制周期;us为定子电压;xk+1 = [isk+1 Ψrk+1]T为预测得到的下一时刻的状态变量。因此下一时刻的电磁转矩Tek+1能够被预测得到
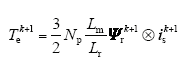
式中,Np为电机极对数;⊗为叉乘;Ψr为转子磁链矢量。
3 新型三矢量MPFC
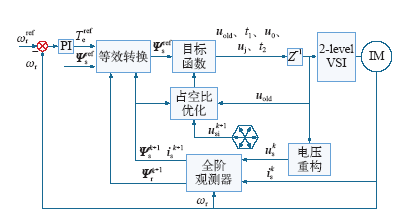
图1为感应电机新型三矢量MPFC的整体控制框图,包括以下几部分:转速外环、定子磁链等效转换、目标函数、全阶观测器、矢量选择及占空比优化。本文不考虑弱磁运行,因此定子磁链幅值的参考值设为额定值。下面对各部分进行详细的介绍。
图1
图1
异步电机新型三矢量MPFC框图
Fig.1
Control diagram of a novel three-vectors-based MPFC for IM drives
3.1 状态变量估计
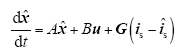
式中, 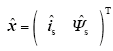
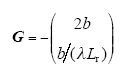
式中,b取-40,其已经被证明对于电机参数的变化具有很强的鲁棒性[20],限于篇幅本文不再赘述。
通过式(4)得到的状态变量可以估计出转子磁链矢量
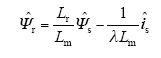
3.2 等效定子磁链矢量转化
传统的MPC以电磁转矩与定子磁链的幅值为控制目标,其相应的目标函数
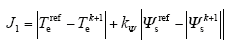
通过感应电机的内部关系式,可以把电磁转矩与定子磁链的幅值等效地转换成定子磁链矢量,从而省却了权重系数的设计,进一步提高了MPC的实用性。以该等效定子磁链矢量为控制目标,相应的目标函数为
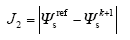
在不考虑弱磁以及效率优化的情况下,定子磁链的幅值设为额定值,即
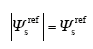
由于转子磁链矢量的估计值通过式(6)获得,把式(9)代入到式(3)可以得到转矩达到给定值时定子磁链矢量相角的参考值
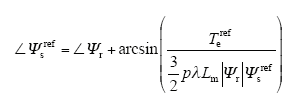
通过式(9)与式(10)可以得到定子磁链矢量的参考值
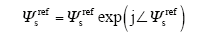
(1)通过式(4)得到 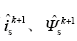
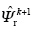
(2)基于异步电机的电流模型能够得到 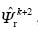
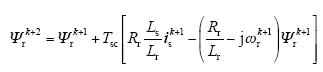
(3)通过Ψrk+2可以得到定子磁链矢量的相角在(k + 2)时刻的参考值如下
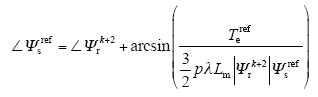
(4)与式(11)类似,可以得到定子磁链矢量在(k + 2)时刻的参考值,从而求得补偿一拍延时之后的目标函数如下
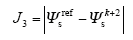
3.3 矢量选择
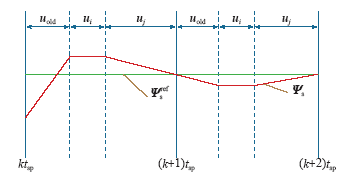
为了使MPFC获得更好的稳态性能,本文采用在一个控制周期内使用两个有效电压矢量以及一个零矢量类似于SVM的矢量选择,但与SVM不同的是,第一段电压矢量为上一个控制周期末段电压矢量的延续如图2所示,因此只需要在每个控制周期确定另外两个电压矢量。假设在每个控制内的作用电压矢量为uold、ui、uj,显然零矢量的位置决定了算法的计算量,因此需要研究3个矢量的作用顺序如下所述:
(1)如果uold为零矢量,那么ui、uj均为有效电压矢量,对于两电平逆变器驱动的调速系统来说,一共有6×6=36种组合,其计算量非常大。这说明零矢量不适合安排在3个电压矢量的末段位置,否则会导致下一控制周期的计算量显著地增加。
(2)如果ui为零矢量,这意味着uold,uj为有效电压矢量,由于uold已经确定为上一个控制周期末段的电压矢量,只需要确定uj,因此一共只有6次预测计算。而且由于uj为有效电压矢量,下一控制周期重复此步顺序,依然只需要6次预测计算。
(3)如果uj为零矢量,根据第(1)点所述,会导致下一控制周期有36种组合,其计算量增大。
综上所述,显然零矢量安排在中间位置时计算量最小,因此将3个电压矢量表述为:uold,u0,uj。其中,uold为上一时刻的最优电压矢量,uj为待选电压矢量,如图2所示。
图2
图3
图3
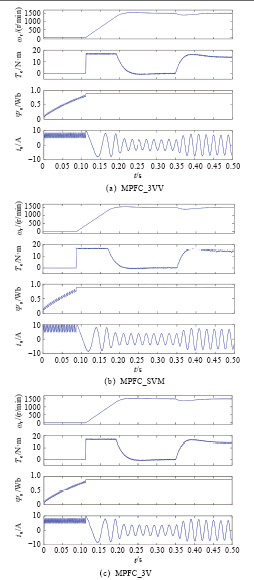
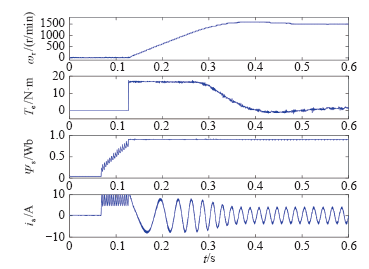
从静止起动到1500r/min的仿真波形
Fig.3
Simulated starting from standstill to 1500 r/min for MPFC_3VV、MPFC_SVM and MPFC_3V
3.4 矢量占空比优化
根据3.3节可得新型三矢量MPFC电压矢量顺序为uold∶u0∶uj,电压方程可以得到
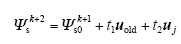
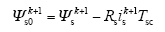
式中,t1、t2分别为uold、uj的作用时间,因此零矢量的作用时间为t0 = Tsc - t1 - t2。磁链矢量跟踪误差的平方为
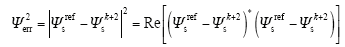
将式(15)代入式(17),然后分别对t1、t2求偏导,可以得到两个有效电压矢量的作用时间如下
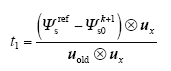
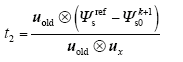
4 仿真与实验结果
4.1 仿真结果
基于本文提出的这种新型的三矢量MPFC,按照矢量顺序以及作用时间来控制逆变器的开通与关断,本文称之为MPFC_3VV。为了降低逆变器的非线性对三矢量MPFC的影响,按照伏秒平衡的原理,采用SVM的方式来控制逆变器的状态,本文简称之为 MPFC_3V。此外引入基于空间矢量脉宽调制与MPFC相结合的控制方法作为性能对比,本文称之为MPFC_SVM。为了验证以上提到的三种控制算法的有效性,在一台2.2kW感应电机调速平台上进行相应的仿真,感应电机参数见下表。最终在相同的开关频率下详细地比较了以上三种方法的控制性能。
表 仿真和实验参数
Tab
| 参数 | 数值 |
|---|---|
| Udc/V | 540 |
| Pn/kW | 2.2 |
| Un/V | 380 |
| fn/Hz | 50 |
| Np | 2 |
| Tn/N·m | 14 |
| Rs/Ω | 3.126 |
| Rr/Ω | 1.879 |
| Lm/H | 0.221 |
| Ls/H | 0.23 |
| Lr/H | 0.23 |
| Ψs/Wb | 0.91 |
图4
图4
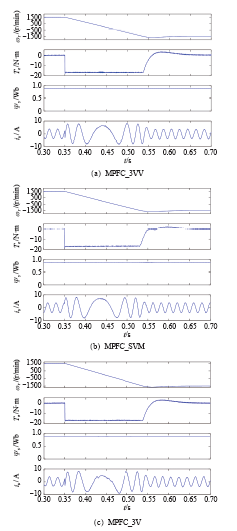
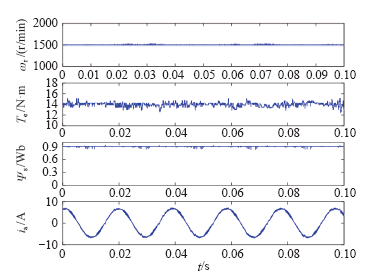
1500r/min正反转仿真波形
Fig.4
Simulated speed reversal at 1500r/min for MPFC_3VV、MPFC_SVM and MPFC_3V
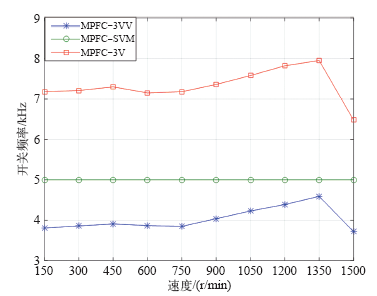
图5
从图5可知MPFC_3VV与MPFC_3V在全速范围内带额定载运行时平均开关频率分别为3.8kHz、7.2kHz左右,为了实现公平比较,需要将MPFC_3VV与MPFC_3V的采样频率分别设置为13kHz和7kHz,使得这两种方法的平均开关频率为5kHz,从而与7段式MPFC_SVM的开关频率基本上一致。
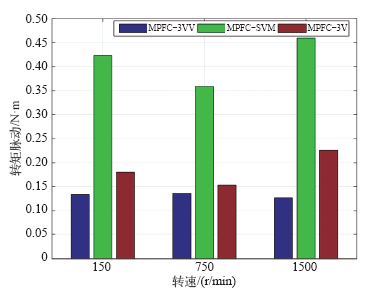
图6
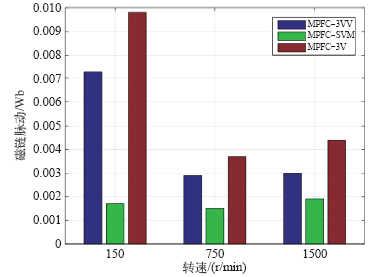
图7
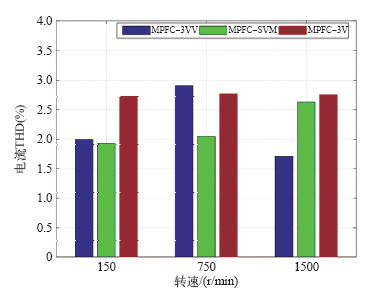
图8
4.2 实验结果
除了仿真验证,也在两电平交流调速实验平台验证本文提出的新型三矢量MPFC(MPFC_3VV)的有效性。实验装置如图9所示,电机参数和系统采样频率与仿真一样,见上表。实验中采用DSP TMS320F28335来执行主算法,通过磁粉制动器来加负载。1通道为实际测量转速,2通道为估计的电磁转矩,3通道为估计的定子磁链幅值,4通道为实测的a相电流。
图9
图10
图10
0~1500r/min空载起动波形
Fig.10
Starting response from standstill to 1500r/min without load
图11
5 结论
本文详细地研究了三矢量模型预测磁链控制,提出的新型三矢量MPFC(MPFC_3VV)具有计算量小、矢量选择简单且开关频率低等优点,同时也解决了传统MPTC中权重系数选择困难,以及传统三矢量MPFC中矢量选择繁琐且计算量大等问题。为了降低三矢量中逆变器非线性对控制性能的影响,提出了一种改进型的三矢量MPFC(MPFC_3V)。为了比较三矢量MPFC的性能,基于空间矢量脉宽调制的MPFC(MPFC_SVM)被引入作为对比。通过比较可得,在相同的开关频率下MPFC_3VV的转矩与磁链脉动以及电流THD要明显地低于MPFC_3V,而 MPFC_SVM 的转矩脉动最大,说明相比MPFC_3V与MPFC_SVM,本文提出的MPFC_3VV具有良好的稳态性能以及更低的开关频率。最终通过实验验证了本文提出的新型三矢量MPFC的有效性,从而扩大了MPFC在工业中的应用范围。无论是稳态性能还是动态性能,本文提出的新型三矢量MPFC都能够满足高性能交流电机控制领域当中的性能要求。
参考文献
FOC and DTC: two viable schemes for induction motors torque control
[J].
An improved direct torque control for three-level inverter-fed induction motor sensorless drive
[J].
Direct torque control of PWM inverter-fed AC motors - a survey
[J].
Predictive direct torque control for flux and torque ripple reduction
[J].
A novel duty cycle control strategy to reduce both torque and flux ripples for dtc of permanent magnet synchronous motor drives with switching frequency reduction
[J].
A predictive controller for the stator current vector of ac machines fed from a switched voltage source
[C].
Predictive control in power electronics and drives
[J].
Model predictive direct torque control; part I: concept, algorithm, and analysis
[J].
Predictive torque control of induction machines using immediate flux control
[J].
Model predictive control of induction motor drives: flux control versus torque control
[J].
Two-vector-based model predictive torque control without weighting factors for induction motor drives
[J].
Direct torque control of permanent magnet synchronous motor with reduced torque ripple and commutation frequency
[J].
Model predictive torque control of induction motor drives with optimal duty cycle control
[J].
Model predictive flux control of induction motor drives with switching instant optimization
[J].
The representation of AC machine dynamics by complex signal flow graphs
[J].
Torque ripple reduction of model predictive torque control of induction motor drives
[C].
An improved direct torque control for three-level inverter-fed induction motor sensorless drive
[J].
Speed sensorless control for three-level inverter-fed induction motors using an extended luenberger observer
Predictive torque and flux control without weighting factors
[J].
感应电机模型预测磁链控制
[J].
Model predictive flux control for induction motor drives
[J].
Guidelines for weighting factors design in model predictive control of power converters and drives
[C].
Predictive torque control of induction machines based on state-space models
[J].
Delay compensa-tion in model predictive current control of a three-phase inverter
[J].
Variable switching point predictive torque cont rol of induction machines
[J].
High- performance control strategies for electrical drives: an experimental assessment
[J].
An encoderless predicti ve torque control for an induction machine with a revised prediction model and efosmo
[J].