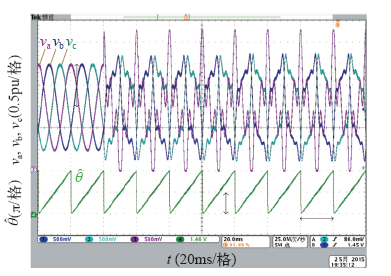
1 引言
电网电压相位实时检测是一项基本的技术,高精度、快速的锁相同步环节对并网型电力设备控制有重要的影响[1]。同步旋转坐标系下锁相环(Synchronous Reference Frame Phase-Locked Loop,SRF-PLL)是一种流行的实用化方法[2,3,4],其结构包括三个部分,鉴相器将三相电压信号利用Park变换检测相位偏差,环路滤波PI调节器滤除相位偏差中的高频成分,积分型振荡器利用偏差稳态量计算相位信息,通过不断地闭环调整,直到偏差为恒定值,输出信号实时跟踪输入信号。当三相电网电压平衡时,鉴相器输出为直流成分,SRF-PLL中的环路滤波器可设计为高带宽系统,获得足够稳态精度和较快的动态响应。实际电网系统由于负载不对称及其动态性,经常出现电压不平衡状态,此时,锁相同步环节应能追踪正序分量的相位[5]。当三相电网电压不平衡、含有谐波污染时,Park变换输出包含扰动分量,不能精确地反映基波正序分量相位偏差。为解决这一问题,一种方法是在获得电压信号后,在PLL环路外设置滤波器,精确得到基波正序分量,再进行锁相。但常用的各类低通滤波器无法区分同频率的正序、负序分量,使得相位检测存在误差。本文首先分析了不平衡三相电压αβ坐标系下的信号特征,指出了负序分量对SRF-PLL的影响。针对复系数滤波器的频率选择特性,将其应用于锁相环路前端滤波,以适应电网电压不平衡情况。其次,数字模拟仿真给出了不平衡、谐波输入条件和相位检测偏差范围。最后,构建了基于DSP的实验平台,给出了CCF滤波器的实现代码,测试波形验证了可行性。
2 不平衡电压信号特征
忽略零序分量,不平衡的三相电压可表示为[6]
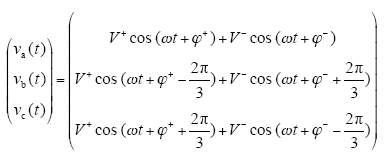
式中,V+为abc坐标系下的正序分量最大值;V-为负序分量最大值;φ+、φ-为初相位;ω为基波角频率,θ = ωt + φ+为待检测基波正序分量实时相位角。
应用Clark变换,可得
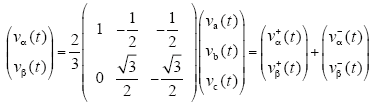
式中,vα+(t)、vβ+(t)为αβ坐标系下的正序分量,vα-(t)、vβ-(t)为负序分量,且
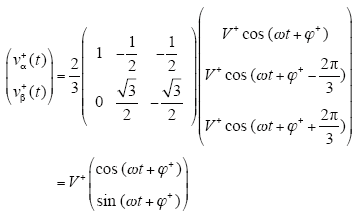
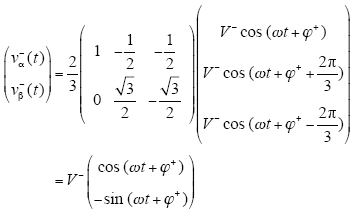
式(3)表明,αβ坐标系下正序分量是幅值为V+、以角速度ω逆时针旋转的电压空间矢量;式(4)表明,负序分量是幅值为V-、以角速度ω顺时针旋转的电压空间矢量。
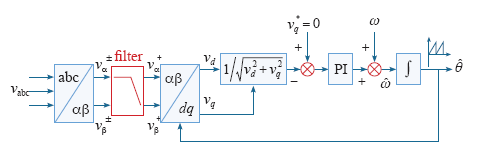
如图1所示,在SRF-PLL环路外配置带通滤波环节,只让αβ坐标系下的正序分量进入后续模块,消除负序分量的影响,可使系统适应电压不平衡状况。
图1
3 复系数滤波器
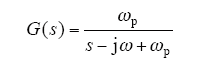
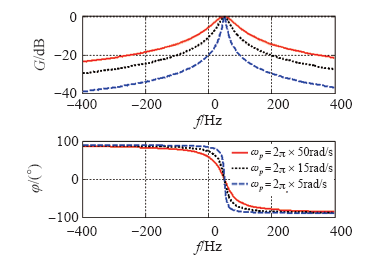
式中,ω = 2πf = 2π×50rad/s,ωp为剪切频率,其伯德图如图2所示;G(s)在ω处放大倍数为1,相位无滞后,而其余频带内均衰减,且在-ω处衰减。
图2
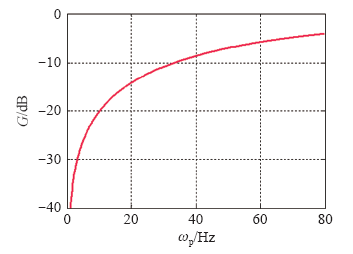
图3
图3
负序分量衰减与$\omega_{p}$的函数
Fig.3
Negative sequence attenuation as a function of $\omega_{p}$
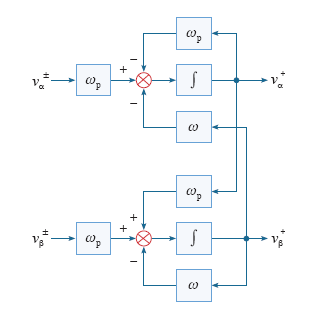
将CCF应用于图1中滤波位置构成CCF-SRF-PLL系统,将使得锁相系统适应不平衡状况,同时由于CCF对高次谐波呈现衰减特性,使得它也适应一定程度的谐波污染状况。
图4
4 数字仿真
为了验证CCF的有效性,利用Matlab/Simulink进行数字仿真。
图5
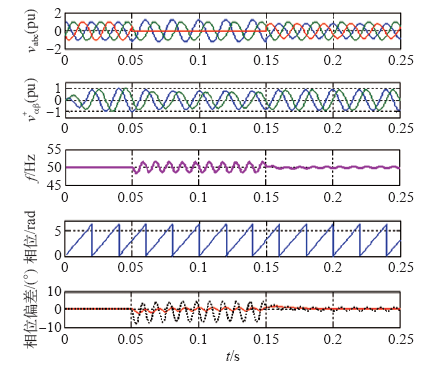
图5给出了不平衡情况下的仿真结果,从上往下的波形依次为三相电压vabc,v+αβ,频率检测值 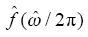
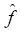
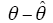
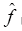
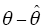
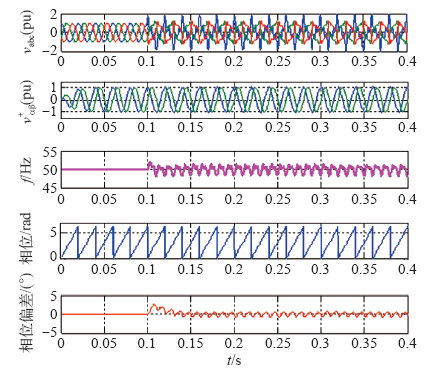
图6
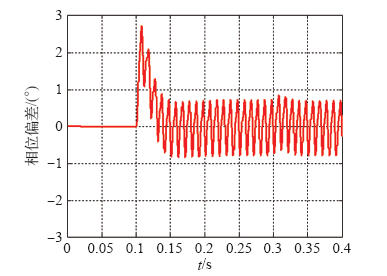
图7
5 实验结果
以浮点型TMS320F28335为核心,在CCS开发环境下,采用C语言编写软件实现CCF-SRF-PLL锁相算法。以DSP为核心的信号发生器模拟电网电压,经调理后送入片上12位A-D模块进行转换,片内定时器产生频率为10kHz的采样脉冲驱动中断程序运行,算法每0.000 1s执行一次。对于三角函数,调用优化后的浮点运算库直接计算。积分运算采用后向欧拉方法实现,PI调节器采用增量式结构以减小高速运算中的累计误差。
CCF的实现代码如下:
static float sum_alfa[2]={0};
static float sum_beta[2]={0};
sum_alfa[0]=sum_alfa[1];
sum_beta[0]=sum_beta[1];
ccf_out_filter.alpha[0]=ccf_out_filter.alpha[1];// refresh
ccf_out_filter.beta[0]=ccf_out_filter.beta[1];// refresh
sum_alfa[1]=(in_nofilter.alpha-ccf_out_filter.alpha[0])*wp-ccf_out_filter.beta[0]*2*pi*50;
ccf_out_filter.alpha[1]=out_filter.alpha[0]+(sum_alfa[0]+sum_alfa[1])*Ts*0.5;
sum_beta[1]=(in_nofilter.beta-ccf_out_filter.beta[0])*wp+ccf_out_filter.alphar[0]*2*pi*50;
ccf_out_filter.beta[1]=ccf_out_filter.beta[0]+(sum_beta[0]+sum_beta[1])*Ts*0.5.
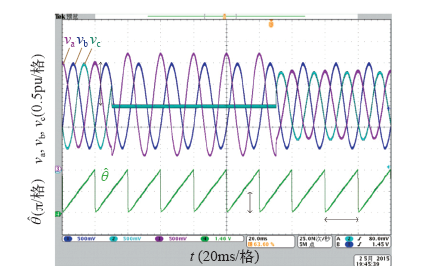
图8
图9
6 结束语
应用CCF滤波器在环路外前置滤波,从不平衡电压信号中分离出同频次的正、负序分量,仅使αβ坐标系下的正序分量作为SRF-PLL的输入,在电网电压不平衡、谐波污染状况下有效跟踪正序分量,稳态误差小。CCF参数调整便利,利用当前值交叉反馈得到滞后数据,数字化编程实现简单,运算量小。
参考文献
A phase tracking system for three phase utility interface inverters
[J].
三相数字锁相环的原理及性能
[J].
Principle and performance of the three-phase digital phase-locked loop
[J].
基于dq 变换的三相软件锁相环设计
[J].
Three-phase software phase-locked loop based on dq reference frame
[J].
Performance improvement of a prefiltered synchronous-reference-frame PLL by using a PID-type loop filter
[J].
dq -frame cascaded delayed signal cancellation-based PLL: analysis, design, and comparison with moving average filter-based PLL
[J].
Grid synchronization systems of three-phase grid-connected power converters: a complex-vector-filter perspective
[J].
Multiple-complex coefficient-filter-based phase-locked loop and synchronization technique for three-phase grid-interfaced converters in distributed utility networks
[J].