1 引言
1994年Johann W.Kolar教授提出了VIENNA型整流器,由于其具有低的开关频率数、高效率、低电压应力,功率密度高、输入电流正弦化、在电压不平衡及缺相条件下仍然可以工作,电感体积小等一系列优点[1],日益受到国内外学者的关注。由于VIENNA型整流器结构的特殊性,国内外学者主要集中在控制策略研究上[2,3,4];上述文献都是以单负载为研究对象,控制策略采用PI控制器、单周期控制方案及反馈线性化控制器,从不同角度提高了VIENNA型整流器控制性能,但没有全面提高整流器控制性能。在实际工程中,需VIENNA型为双负载供电(如多重化电路的输入侧等[5,6]),现在对双负载VIENNA型整流器控制的研究不多,本文基于无源控制理论研究VIENNA型整流器无源控制器。无源控制器设计可基于欧拉–拉格朗日(Euler-Lagrange,EL)[7]和PCHD两种模型,采用PCHD模型进行无源控制器设计不仅能进行阻尼注入,还能进行能量成形,设计更为灵活,所以本文基于PCHD数学模型设计无源控制器。此外,在文献[8]的基础上改进了中点电位平衡策略,引入了电容对中点电位的影响,可有效抑制中点电位波动。
2 VIENNA型整流器拓扑及数学模型
2.1 双负载VIENNA型整流器拓扑结构
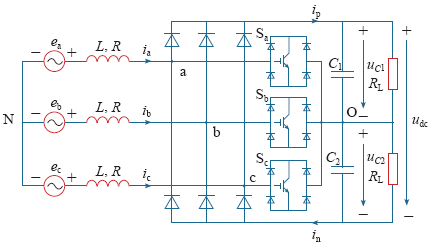
VIENNA型整流器根据开关管数目的不同可分为三开关和六开关两种,为简化控制,以三开关VIENNA型整流器作为研究对象,所研究的控制策略同样适用于六开关VIENNA型整流器。双负载VIENNA型整流器拓扑结构如图1所示,为建立其数学模型,假设:①三相正弦电源平衡且三相滤波阻抗参数相同;②滤波电感L是线性的,且不考虑饱和;③开关管无导通关断延时,无损耗。
图1
图1
双负载VIENNA型整流器主电路
Fig.1
The main circuit structure of double-load VIENNA-type rectifier
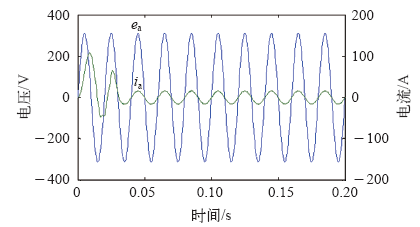
Si (i = a、b、c)为整流器开关函数,Si = 1时,功率开关管导通,Si = 0时,功率开关管关断。ea、eb、ec为电网三相交流电压;ia、ib、ic为电网三相交流电流;ip为整流器正向输出电流;in为整流器反向输出电流;R、L为滤波电抗器的电阻和电感;C为直流侧电容;uC1、uC2为直流侧电容输出电压。
2.2 VIENNA型整流器dq坐标系下数学模型
对于VIENNA型整流拓扑,当开关管关断时,开关侧所能实现的电位是由开关管所在相的电流方向决定的。当ii(i = a,b,c)流入a点时,sign(ii) = 1,当ii(i = a,b,c)流出a点时,sign(ii) = -1。针对双负载拓扑结构,为了数学模型有所简化,定义复合开关函数Si1、Si2(i = a、b、c)
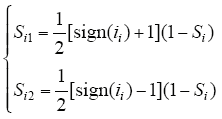
那么,在三相对称电源电压情况下,VIENNA型整流器在三相abc坐标系下的数学模型为
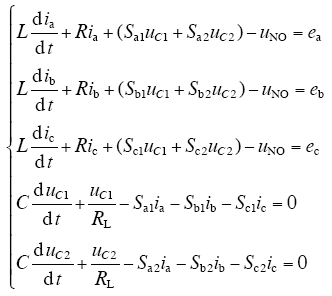
式中,uNO为电源中性点N与节点O之间的电压。
由于在三相abc坐标系的数学模型中存在时变的三相正弦交流电压,为了便于控制器的设计,通过等量变换到两相同步旋转坐标系统中,等量变换的矩阵为
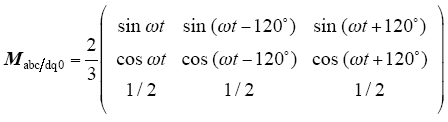
可得dq坐标系下的数学模型为
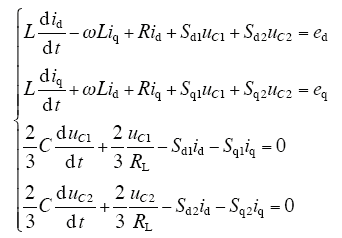
式中,id、iq为三相电网电流在dq轴分量;Sd1、Sd2、Sq1、Sq2为控制输入。
2.3 VIENNA型整流器PCHD数学模型
选取系统的状态变量
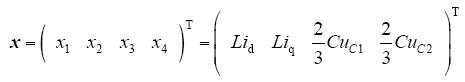
定义系统的哈密顿函数为
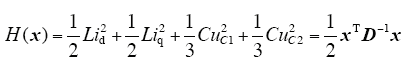
于是将式(4)整理成PCHD模型
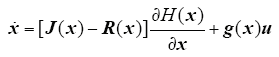
式中
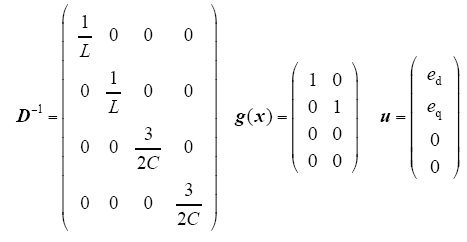
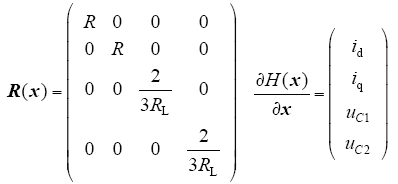
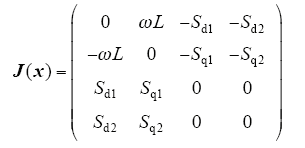
3 VIENNA型整流器控制器设计
基于PCHD模型设计无源电流控制器,直接控制交流电流,实现网侧单位功率因数、电流低谐波,采用PI控制器控制直流电压,有效抑制了稳态误差,这样就形成了以无源控制为主,PI控制为辅的混合控制策略。
3.1 期望稳定点
设期望平衡点为x* = [x1*x2*x3*x4*]T,VIENNA型整流器稳定运行时,期望功率因数为1,直流电压等于给定电压,给定电压按 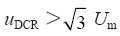
3.2 直流电压控制器设计
为消除系统稳态误差,电压外环控制器采用PI控制,传递函数为
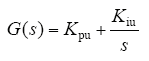
电压外环以直流侧的两个电容电压为控制对象,根据PI控制策略分别得出期望电流i*d1、i*d2,i*d1、i*d2分别为基于uC1、uC2的双电压外环控制器d轴电流稳态期望值,可按照典型Ⅱ型来选择比例积分参数。
3.3 无源电流控制器设计
为使系统在期望的平衡点x*处保持渐进稳定,构造一个期望的闭环哈密顿函数Hd(x),且Hd(x*) = 0。对于任意一个x ≠ x*,有Hd(x)>0。配置Ja(x)和Ra(x)[9],使
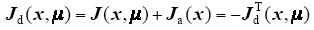
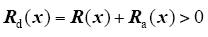
通过反馈控制律μ = α(x)使式(7)成为闭环耗散PCHD系统
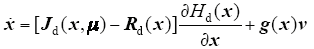
闭环哈密顿函数Hd(x)对于时间的导数为
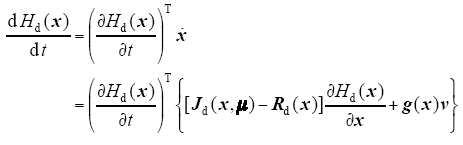
对于式(12),令 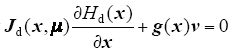
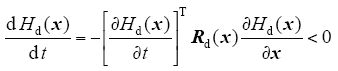
式(13)表明闭环哈密顿函数Hd(x)在平衡点是渐进稳定的。Hd(x)收敛到0的速度取决于Rd(x),由于Ra(x)>> R(x),所以Hd(x)→0收敛速度取决于阻尼注入矩阵Ra(x),R(x)影响很小。
因此反馈控制律μ = α(x)可根据式(7)、式(11)和式(12)联立得
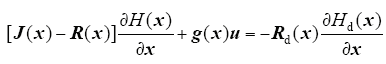
其中, 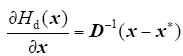
可得无源控制器为
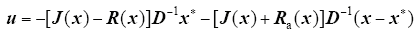
与文献[10]相比,消去了Ja(x),仅保留了系统的阻尼注入结构矩阵Ra(x),Ra(x) = diag{ra1,ra2,ra3,ra4}可在一定程度上减少参数调整的工作量。
根据式(15)得对应无源控制器的开关信号为
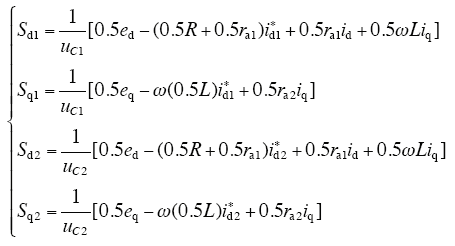
及恒等式为
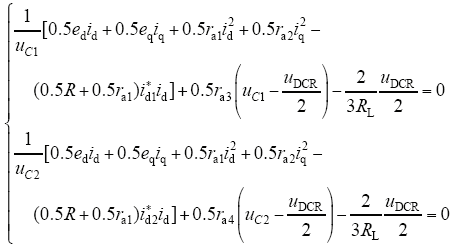
为了使式(17)恒成立,不妨设ra3 = ra4 = 0,ra1 = ra2 = ra,那么就可以得到阻尼注入矩阵为Ra(x) = diag{ra,ra,0,0}。
将上述分析的阻尼注入矩阵代入式(16)得最终开关函数
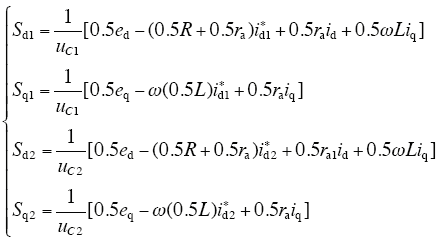
所得开关函数仅需要调整ra这一个参数,简化了控制算法。
将式(18)代入式(4)得
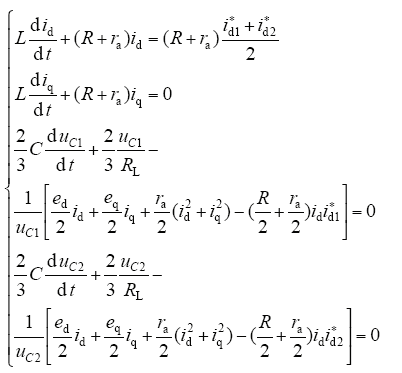
式(19)表明开关函数式(18)能够很好地实现系统的动态和静态解耦,控制性能很好。
本文采用空间矢量脉宽调制方法,需将开关信号转换为调制模块的控制信号vd、vq,由式(4)可得
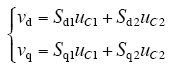
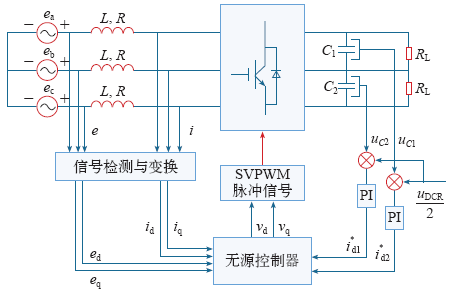
综合以上的控制策略,可得基于无源混合控制的VIENNA型整流器结构框图如图2所示。
图2
图2
双负载VIENNA型整流器控制框图
Fig.2
The overall control diagram of double-load VIENNA-type rectifier
4 中点电位平衡策略
图3
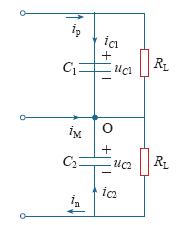
根据基尔霍夫电流定律得
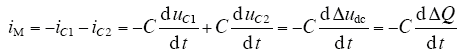
从电荷的角度出发,通过正负小矢量的作用,在一个开关周期内对电容上电荷的改变量再加上电容上个周期存在的电荷,保证在当前一个开关周期内两电容上电荷相等。具体分析如下,以Ⅰ大扇区[13]为例,对应的正小矢量为POO,负小矢量为ONN,对应平衡电流iM,电容C1电荷为Q1 = CuC1,电容C2电荷为Q2 = CuC2。
负小矢量作用在C2上一个开关周期,电荷改变量为
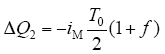
正小矢量作用在C1上一个开关周期,电荷改变量为
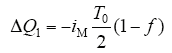
加入调节因子后需保证在下个周期前,电荷相等,那么中点电压就可以实现基本平衡。所以结合式(22)和式(23)可得
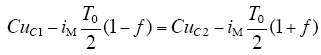
最终解得调节因子表达式为
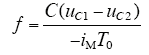
从上式可以看出调节因子相较于传统的中点电位平衡控制,考虑到电容值对中点电位的波动,所以根据电荷平衡原则调节中点电压平衡,更加精确。则正负小矢量时间分配
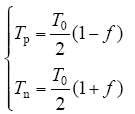
式中,Tp为正小矢量作用时间;Tn为负小矢量作用时间。
5 仿真研究
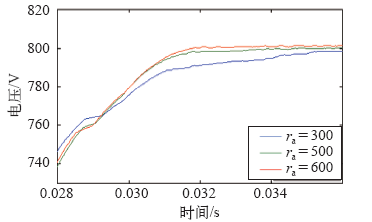
用 Matlab/Simulink 软件对系统进行仿真,参数设置如下:交流侧使用三相对称正弦电源,相电压220V、工频50Hz,电感参数为16mH、电阻0.3Ω,额定负载为两个等值电阻50Ω,调制频率5kHz,直流侧输出电压稳态期望值为800V,电容参数为2 200μF,由控制律可知,注入阻尼参数的大小ra与整流器的动态性能有很大的关系。当阻尼注入太小时系统反应较慢,直流侧输出电压稳定性能变差;当阻尼注入过大时,系统反应加快,但会导致输出电压有较大的超调量,图4为不同的阻尼注入时直流侧输出电压波形,经过仿真调试,选取500Ω较为合适。
图4
图5
图6
图7
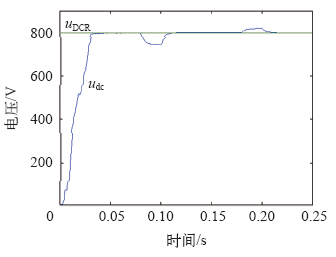
负载扰动的情况下,在0.08s时负载电阻从50Ω变为20Ω,持续0.02s,在0.1~0.18s之间依然为50Ω,在0.18s时负载电阻从50Ω变为100Ω,从仿真图8可以看出系统快速响应变化,电压虽受到负载波动影响,但是迅速又稳定到给定值,无源控制策略使系统在短时间内恢复正常,验证了系统良好的鲁棒性。
图8
6 结论
基于双负载VIENNA型整流器的PCHD模型及系统的无源性,通过互联和阻尼配置方法,设计了系统的控制器。在Matlab/Simulink环境下,搭建了仿真模型,仿真结果表明,通过配置阻尼参数,系统具有良好的动静态性能,整流器网侧实现了单位功率因数运行,系统的直流侧电压能够快速跟踪给定值,并且系统具有一定的抗负载扰动能力。因此基于PCHD模型的无源控制方法是可行的。
参考文献
A novel strategy for three-phase/switch/level(vienna) rectifier under severe unbalanced grids
[J].
DOI:10.1109/TIE.2012.2217721
URL
[本文引用: 1]

Unbalanced grids introduce performance deterioration for Vienna rectifier topology by producing twice fundamental frequency ripples in dc-link voltage and input active/reactive power. A common current reference generation for the purpose of eliminating the input power ripple, such as dual-frame hybrid vector control, can maintain constant input power and eliminate ripples in dc-link voltage under light voltage unbalanced grids. Under severe unbalanced grids, this type of a control method will fail to work. This paper first analyzes the theoretical operation area of a constant power control method under unbalanced grids, and then a novel control method is proposed. The proposed control method can work under severe unbalanced grids by injecting a small amount of input power ripple and balance the performance of working area and output dc voltage ripples. Finally, the experiment results using the constant power control method are given and validate the performance of the proposed control method.
Analysis of high-efficiency three-phase two- and three-level unidirectional hybrid rectifiers
[J].
DOI:10.1109/TIE.2012.2205358
URL
[本文引用: 1]

This paper presents highly efficient three-phase high-power-factor hybrid rectifiers assembled by the parallel connection of a three-phase diode-bridge rectifier and series dc-dc boost converter with a two- or three-level unidirectional pulse width modulation (PWM) rectifier. The idea is to obtain a rectifier that is robust, highly efficient, and simple as a diode-based rectifier and also able to benefit from the PWM rectifier capability to reduce the line current harmonic content. Exemplary three-phase unidirectional hybrid systems built with a two-level delta-switch rectifier and three-level T-type or VIENNA six-switch rectifiers are suggested. Additionally, control schemes, which are appropriate for safeguarding the high-power-factor operation while improving the power sharing rating of the hybrid paralleled rectifier units and able to handle a phase loss without changing the controller structure, are proposed. In order to evaluate the studied hybrid rectifiers, first, an efficiency comparison between two- and three-level hybrid systems with conventional PWM rectifiers is performed. After that, the loss calculations are extended to a variable chip area to allow a fair comparison between these rectifiers. Interestingly, it is shown that the presented hybrid systems not only can achieve a higher efficiency but also require less silicon area than the single PWM rectifiers they are based on. Finally, experimental results obtained with an assembled unidirectional hybrid delta-switch rectifier prototype are presented in order to demonstrate the performance and advantages of this solution.
单周期控制的三相三电平VIENNA整流器输出中点电位分析及控制方法研究
[J].三相三电平VIENNA整流器作为三电平Boost型中点箝位(neutral point clamped,NPC)结构变换器一种,具有电路结构简单、开关电压应力小、输入电流谐波含量低、可实现输入单位功率因数校正等优点,适合应用于高压中大功率场合。同时,三相功率因数校正(power factor correction,PFC)整流器的单周期控制方案因其控制简单,无需乘法器及采用输入电压受到广泛研究。输出中点电位波动是NPC结构变换器的一个固有问题,以基于单周期控制的三相三电平VIENNA整流器为研究对象,详细地分析整流器输出中点电位波动机理,根据单周期控制方案的特点,提出在三相输入电流采样中注入三次谐波电流分量,同时分析三次谐波电流注入后对整流器输出中点电位的影响,给出三次谐波电流最佳注入系数。在此基础之上,向传统单周期控制系统中继续引入均压环路,使得最终改进后的三相三电平VIENNA整流器单周期控制系统一方面可以提高整流器直流母线电压利用率,另一方面可以有效抑制中点电位的直流和交流波动。仿真与实验验证了所提出的改进单周期控制策略对于整流器输出中点电位平衡控制的有效性。
Study and analysis of neutral-point potential and control methods for one-cycle controlled three-phase three-level VIENNA rectifiers
[J].三相三电平VIENNA整流器作为三电平Boost型中点箝位(neutral point clamped,NPC)结构变换器一种,具有电路结构简单、开关电压应力小、输入电流谐波含量低、可实现输入单位功率因数校正等优点,适合应用于高压中大功率场合。同时,三相功率因数校正(power factor correction,PFC)整流器的单周期控制方案因其控制简单,无需乘法器及采用输入电压受到广泛研究。输出中点电位波动是NPC结构变换器的一个固有问题,以基于单周期控制的三相三电平VIENNA整流器为研究对象,详细地分析整流器输出中点电位波动机理,根据单周期控制方案的特点,提出在三相输入电流采样中注入三次谐波电流分量,同时分析三次谐波电流注入后对整流器输出中点电位的影响,给出三次谐波电流最佳注入系数。在此基础之上,向传统单周期控制系统中继续引入均压环路,使得最终改进后的三相三电平VIENNA整流器单周期控制系统一方面可以提高整流器直流母线电压利用率,另一方面可以有效抑制中点电位的直流和交流波动。仿真与实验验证了所提出的改进单周期控制策略对于整流器输出中点电位平衡控制的有效性。
Input-output linearization of a fourth-order input-affine system describing the evolution of a three-phase/switch/level (Vienna) rectifier
[J].
DOI:10.1049/iet-pel.2010.0158
URL
[本文引用: 1]

This study presents an analytical approach for proper selection of output functions to be regulated for the Vienna rectifier such that the resultant closed-loop systems are minimum phase. Specifically, two different adaptive control methodologies based on the input-output linearisation are developed and categorised. In the first category, three output functions are introduced and imposed to be zero by using three dynamic feedback laws. On the basis of states to be regulated, four different cases are studied and it is shown that only one of these cases results in a one-dimensional zero dynamics with an asymptotically stable equilibrium point. In the second category, two output functions are defined and output zeroing problem is solved with two control inputs. In addition, the remaining control is used to feedback linearise the resultant two-dimensional zero dynamics. Eighteen different cases are studied to demonstrate that only in one of these cases, the corresponding zero dynamics is feedback linearisable. Stability properties of the adaptive systems are investigated to show that the proposed adaptive controllers are capable of DC output voltage regulation and power factor correction in the presence of parametric and non-parametric uncertainties. Finally, simulation results are presented to confirm the validity of the developed approaches.
Modelling and control of three-phase/switch/level fixed-frequency PWM rectifier: state-space averaged model
[J].DOI:10.1049/ip-epa:20041042 URL [本文引用: 1]
基于无源性的光伏并网逆变器电流控制
[J].In view of the nonlinear mathematical model of the photovoltaic(PV) grid-connected inverter, the passivity-based control(PBC) is adapted for the inverter, and it can make the inverter possess excellent dynamic and static characteristics. In this paper the control law that can decouple dq axis currents at AC side of the grid based on the Euler-Lagrange(EL) model, and the passivity of inverter is proved. In order to improve the dynamic performance of the inverter, we can adopt the approach called injecting damping to optimize the controllerps adopted, and it can also make the current to fast track the desired one and track the PV array maximum power point. Simulation and 4kW prototype results show that the current control strategy of Photovoltaic grid-connected inverter based on passivity is practicable.
Current control strategy of photovoltaic grid-connected inverter based on passivity
[J].In view of the nonlinear mathematical model of the photovoltaic(PV) grid-connected inverter, the passivity-based control(PBC) is adapted for the inverter, and it can make the inverter possess excellent dynamic and static characteristics. In this paper the control law that can decouple dq axis currents at AC side of the grid based on the Euler-Lagrange(EL) model, and the passivity of inverter is proved. In order to improve the dynamic performance of the inverter, we can adopt the approach called injecting damping to optimize the controllerps adopted, and it can also make the current to fast track the desired one and track the PV array maximum power point. Simulation and 4kW prototype results show that the current control strategy of Photovoltaic grid-connected inverter based on passivity is practicable.
带中点电位平衡控制的VIENNA整流器简化SVPWM双闭环控制
[J].
Simplified SVPWM dual closed loop vector control method for VIENNA rectifier with midpoint potential balance control
[J].
具有阻感性负载PWM整流器的PCH建模与控制
[J].
DOI:10.1016/j.clnu.2019.11.039
URL
PMID:31882231
[本文引用: 1]

The effects of low-protein diet (LPD) on kidney function and nutrition in nephropathy are so far unclear.
PCH modeling and control of PWM rectifier with resistive inductive load
[J].
DOI:10.1016/j.clnu.2019.11.039
URL
PMID:31882231
[本文引用: 1]

The effects of low-protein diet (LPD) on kidney function and nutrition in nephropathy are so far unclear.
NPC型三电平逆变器中点电位平衡算法的研究
[J].
Research on neutral-point potential balance of three-level NPC-type inverter
[J].
基于SVPWM的Vienna整流器矢量控制策略的研究
[J].
Research of vector control strategy of the vienna rectifier based on SVPWM
[J].