1 引言
对于传统的逆变器控制策略而言,PI控制是并网逆变器控制中应用最成熟、最广泛的控制策略,它利用比例控制器P和积分控制器 I的控制规律,使控制器的输出同时成比例地反映输入信号及其积分。PI控制策略原理简单,容易实现,控制参数容易整定,能改善系统的动态性能和稳态性能,而且对系统参数不太敏感,可靠性高,鲁棒性强[1]。
比例谐振控制是在 PI 控制的基础上提出的,目的是解决 PI 控制中存在的稳态误差的问题。比例谐振控制在调节器中加进一个无损谐振环节,使控制器的增益在谐振频率处无穷大,以此来消除系统的稳态误差。对于逆变并网电流的控制,则是把电流频率(即电网频率)设定为谐振频率,把电流的误差减小为零。引入无损谐振环节后控制器有两个极点,这会减小系统回路增益的相角裕度,使系统不稳定,所以在控制器中再加入一个零点,解决了这一问题[2]。
比例谐振控制不但能在谐振频率处获得无穷大的增益,做到无静差跟踪,还可以针对特定次数的谐波配置相应的控制器,消除并网电流中特定次数的谐波。但是,比例谐振控制器的带宽窄,如果电网频率发生变化,偏离了设定的谐振频率,其增益下降非常明显,需要做进一步的改进[3]。
2 单相逆变器的拓扑结构与建模
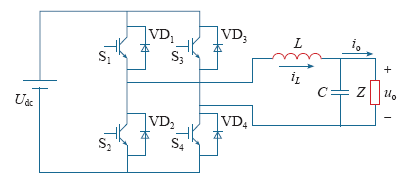
图1是单相逆变器系统的拓扑结构。该系统主要由直流电压源、逆变电路与LC滤波电路组成。
图1
其中,Udc为直流电压源;S1、S2、S3、S4为IGBT开关管;VD1、VD2、VD3、VD4为续流二极管;L、C分别为LC滤波电路的电感和电容;Z为负载。
图2
3 逆变器控制策略
3.1 传统比例积分PI控制原理
传统比例积分PI控制器的传递函数为
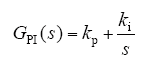
其在电网基波频率ω0处的增益为
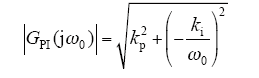
式中,ω0 = 2πf≈2×3.14f = 314rad/s,f取工频频率50Hz。
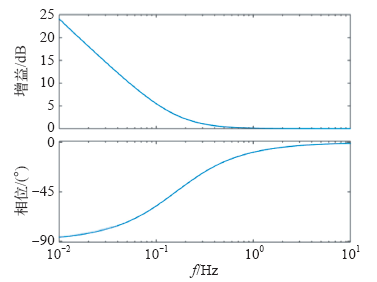
取kp = 1,ki = 1可以得到PI控制器的波特图,如图3所示。
图3
由式(1)和图3可以看出,PI控制器为一阶控制器,在电网的基波频率(50Hz)处的增益是有限值,在跟踪正弦信号时可能会出现稳态误差,即跟踪电流给定值时会出现相位误差及幅值误差,其在基波频率处的增益可通过增加比例放大系数来增大,即减小稳态静差,但不可能消除。因此,幅值误差表现并不明显,主要表现为相位误差[5]。
3.2 比例谐振(PR)控制原理
理想PR控制器的传递函数为
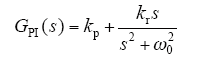
理想PR控制器在基波频率ω0处的增益为
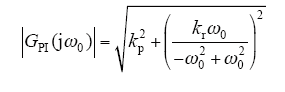
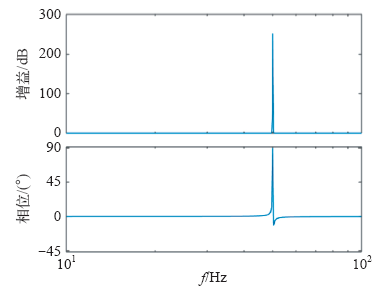
可以看到,由于控制器传递函数的jω轴上加入2个固定频率的开环极点,形成该频率下的谐振,使得PR控制器在基波频率处的增益趋近于无穷大。
取kp = 1,kr = 1可以得到理想PR控制器的波特图,如图4所示。
图4
在实际系统中,由于理想的PR控制器难以实现,且为避免增益无穷大带来的稳定性问题,可采用一种容易实现的准PR控制器,其传递函数为
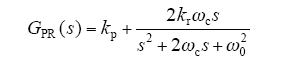
式中,ω0 = 2πf≈2×3.14f = 314rad/s,f取工频频率50Hz。
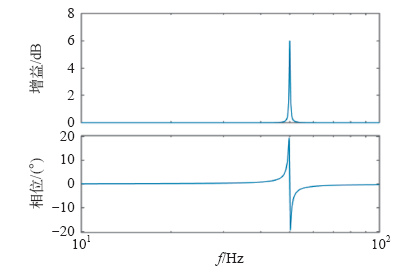
由式(5)可以知道,准PR控制器有 3个控制参数kp、kr和ωc,需要对其进行优化设计以提高系统的性能。
取kp = 1,kr = 1,ωc = 1可以得到准PR控制器的波特图,如图5所示。
图5
4 仿真计算研究
为了将PI控制器与准PR控制器的仿真效果进行对比研究,本文利用Simulink搭建逆变器仿真模型,本别对比两种控制器的电压跟踪效果与谐波含量。
4.1 滤波电路电感L与电容C值计算
滤波电感的最小值是由经过电感的电流纹波所决定的,电感电流的纹波过大不仅会影响到开关器件的开关损耗,而且还会影响到控制策略的实施,工程上一般要求电感电流纹波不超过10%的额定电流,则电感电流纹波最大值可计算如下[6]
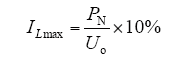
电感纹波的计算公式如下
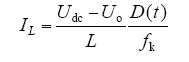
本文设计采用双极性PWM控制,可得输出电压与直流侧电压的关系为
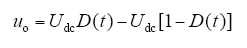
从而可根据SPWM调制原理,得到每个开关周期的占空比D(t)为
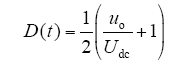
将式(9)代入式(7)可以得到
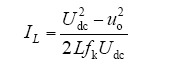
当uo = 0时,电感电流纹波IL有最大值
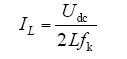
根据电感电流纹波不超过10%的额定电流要求,可以得到对电感电流纹波的限制如下
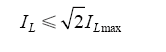
则根据式(12)可计算滤波电感最小值
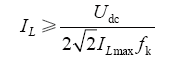
在电路运行工作中,如果负载发生变化,会导致输出电流io变化,流经电感的电流iL也会变化,为了保持uo不变,需改变控制开关管的占空比。由于电感为储能器件,不可能立刻跟随占空比的变化而变化,这样就会出现一个过渡过程。这个过渡时间应该尽可能小,这就要求选取的电感值不能够过大。
根据式(13)判断,电感选择是根据ILmax的值所决定的。考虑到负载的变化情况与实际中电感的价格,在仿真时电感取其最小值。
电容选择的同时也要考虑到之前电感的选择,电容值越大,其所产生的无功功率越大,且通过电感L与IGBT的电流也会越大,从而增大开关管的开关损耗,从而使电路的效率降低。但是考虑到电感与电容组成的LC滤波器的滤波效果,若要使其保持相同的滤波效果,电容越小,则需要电感的值就会越大,这样也会导致在电感上产生巨大的压降。
设计中,一般限制电容产生的无功不超过5%的系统额定功率,即
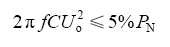
可以得到
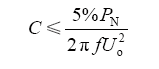
在实际电路中,由于器件本身的非理想特性、基准波也非标准的正弦波以及死区对输出的影响,所以在输出的波形中包含低次的谐波,C值必须取大一些,来抑制这些低次谐波,这里C取其最大值。
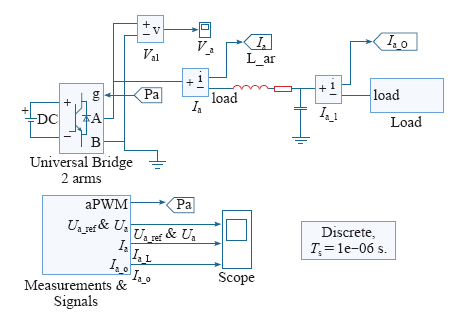
4.2 Simulink仿真
图6
图7
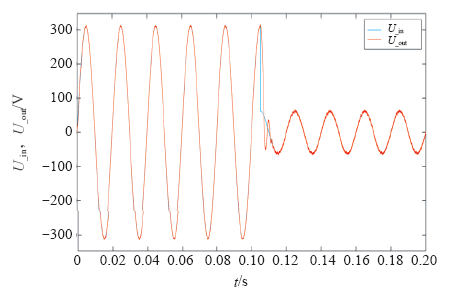
图7
PIP 控制的输出电压对给定电压的跟踪情况
Fig.7
The tracking of output voltage for given voltage based on PIP control system
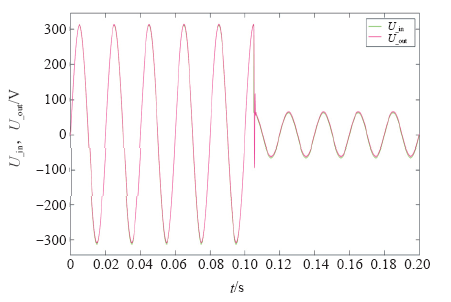
图8
图8
PRP 控制的输出电压对给定电压的跟踪情况
Fig.8
The tracking of output voltage for given voltage based on PRP control system
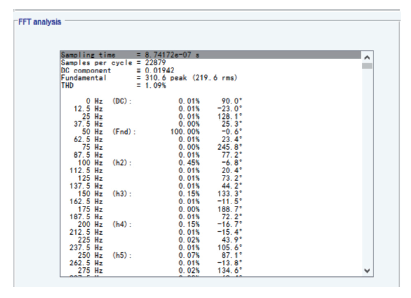
图9
图9
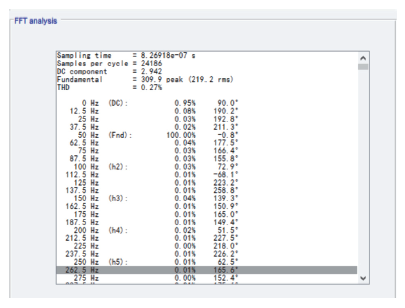
PIP 控制的输出电压的FFT 分析
Fig.9
The FFT analysis of output voltage based on PIP control system
图10
图10
PRP 控制的输出电压的FFT 分析
Fig.10
The FFT analysis of output voltage based on PRP control system
5 结论
根据实验仿真,可以得到PR控制逆变器能够达到PI控制几乎相同的效果,甚至在谐波控制方面效果更好,所以在逆变器控制的实际应用中,可以使用PR控制代替PI控制。
参考文献
基于PR与PI联合控制策略的光伏并网系统直流注入抑制技术
[J].
DC injection suppression technology of photovoltaic grid connected control strategy based on PR and PI
[J].
分布式发电系统中并网逆变器比例谐振控制
[J].
Proportional resonant control for grid connected inverters in distributed generation systems
[J].
基于PR控制的光伏并网电流优化控制
[J].
Optimization control of photovoltaic grid connected current based on PR control
[J].