0 引 言
在带钢冷、热轧制过程中,工作辊的磨损是不可避免的。轧辊磨损不仅增加了辊耗,而且改变了原始辊形,进而影响带钢板形、厚度及表面的控制[1]。在带钢冷轧生产中,当工作辊的磨损量达到亚微米数量级,就会对汽车面板、DI材镀锡板、超高强度冲压用钢板等高表面粗糙度要求(Ra=0.3~1.5 μm)的冷轧带钢的表面微观形貌的轧制转印生成产生影响,可能导致轧制后带钢表面微观形貌达不到要求,降低带钢的微观表面质量。在轧制印过程中,轧辊与带钢表面直接接触,其表面形貌的功能相当于“模具”,是决定带钢表面到要求,降低带钢的微观表面质量。在轧制转印过程中,轧辊与带钢表面直接接触,其质量的关键[2]。因此,面向钢板微观表面质量的控制需求,需要从细观尺度研究工作辊表面发生的亚微米数量级的、仅改变了微观形貌的表面磨损。但是,工作辊轧制磨损是十分复杂的力学行为。一般认为,磨粒磨损、粘着磨损和疲劳磨损是轧辊磨损的主要形式[3]。一直以来,针对冷轧工作辊磨损已经开展了较多的研究,尽管大多采取实验统计研究方法,但也取得许多重要成果。
根据文献检索,在实验研究方面,Bolt P H等人通过实际、模拟实验两方面研究了工作辊的磨损规律和材质的影响等,指出了镀锡板四辊、二辊生产中,工作辊磨损情况类似,主要是磨粒与疲劳磨损,此研究为冷轧工作辊磨损机理作出了解释[4];Shabani M O利用人工神经网络方法、有限元方法结合,研究化合物涂层的磨损性能,模型能较好地预测表面的耐磨性,但是模型中需要大量的实验数据,未能从理论上解释磨损过程[5];Wang Z J使用群体增长模型(PGM)来模拟磨合过程中的磨损,依旧通过统计学的规律得出了磨合过程的粗糙度变化,但是没有解释磨损的细观机理[6];姜增辉等针对不同牌号的硬质合金刀具进行实验,对比分析了不同硬质合金刀具的磨损形貌与磨损机理,研究了磨损机理对磨损速度的影响[7];朱亚琼等以缸套和活塞环为研究对象,设计贫油试验,获得了缸套从磨合磨损到正常磨损直至异常磨损的三维表面形貌,并利用二维离散小波进行分析[8];吴金平等实验分析了拉拔钢丝磨损失效后的硬质合金模具的磨损形貌,确定了以磨粒磨损、氧化磨损和粘着磨损为主的磨损机理[9]。
在理论研究方面,薛玉君等人评述了以线弹性断裂力学和弹塑性断裂力学理论为基础,借助于有限元法分析疲劳裂纹的萌生、裂纹的扩展方向和扩展速率,以及疲劳磨损机理应力分析方法,文章成功预测了裂纹的扩展,对研究细观疲劳磨损裂纹的扩展提出了一种方法[10];Shipway P H提出了一个磨粒磨损模型,假设的磨粒为棱柱形,通过解析计算得到磨损量,此模型揭示了磨粒磨损机理,但是研究对象为单个磨粒,与实际磨损量仍有较大差距[11];Liang F等人通过有限元模型计算应力,再通过蒙特卡洛方法预测随机磨损过程的磨损率,研究磨粒磨损中沟槽生成过程,模型很好的反映了磨粒磨损过程,但没有考虑到疲劳磨损[12];Hora C等人交替使用有限元及元胞自动机模拟涡轮叶片磨损,取得良好结果,揭示元胞自动机方法可以较好地应用磨损研究中[13];Tong J等人采用了离散元方法对仿生设计的脊状表面的磨粒磨损进行分析。研究模拟磨粒与实验表面间的磨粒磨损,离散元方法可以较好的应用于磨粒磨损,但此研究对象为贝壳,距离塑性材料相距较远[14];Hannes D通过粗糙点加载机制,与断裂力学应用,仿真了疲劳裂纹增长过程[15];Kris D M等建立了一种基于能量法的粗糙峰尺度的磨损模型,这个微观尺度理论模型,用于预测平面接触表面的磨损演化,可以得到粗糙峰退化修正的机理,但模型没有考虑磨损机理[16];Leonard B D等人采用了采用有限元-离散元结合方法来研究表面磨损,从机理上研究了表面的磨损,但与实际磨损情况符合较差[17]。
目前国内外关于磨损的研究主要集中在实验研究,对磨损机理的研究较少。而磨损机理的研究结果又通常与实际结果吻合性较差。针对这一问题,拟定引入元胞自动机方法建模和分析冷轧工作辊表面微观形貌在轧制区的接触磨损行为。 1 元胞自动机方法的选择 工作辊的磨损可以分为宏观尺度磨损与细观尺度磨损。宏观尺度磨损表现为轧辊尺寸、形状的改变,对板形、厚度控制质量产生影响;而细观尺度磨损不会明显改变工作辊形状和尺寸,而只是表现为轧辊表面粗糙度衰减和微观形貌的改变,见图 1、图 2和图 3,影响轧制转印,降低带钢的微观表面质量。
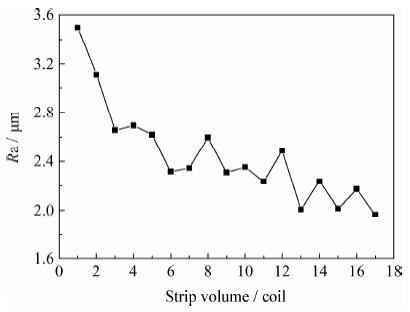 |
| 图 1 同一轧辊服役期内带钢表面粗糙度衰减规律Fig. 1 Change law of working roll the same roll service life surface roughness |
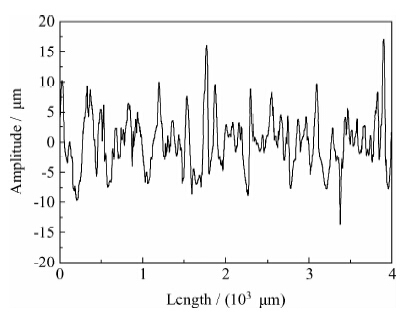 |
| 图 2 工作辊上机表面微观形貌Fig. 2 Surface microtopograph of the working roll before rolling |
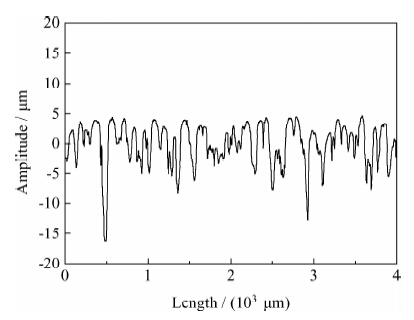 |
| 图 3 工作辊下机表面微观形貌Fig. 3 Surface microtopograph of the working roll after rolling |
尽管在宏观尺度上工作辊磨损总被假设为连续过程,但从细观尺度看,无论是接触咬合(粘着)磨损机理还是磨粒磨损机理,工作辊粗糙峰的磨损都应是不连续且随机的。因此提出假设,在细观尺度上,在工作辊与带钢之间的单位轧制压力与速度差的作用下,粗糙峰的磨损不连续且具有随机性,不同形状特征的单个粗糙峰发生不同速率磨损,各个粗糙峰的磨损叠加构成整个区域表面形貌的细观磨损过程。并且,选择应用元胞自动机方法,在细观尺度上离散表达工作辊表面微观形貌几何轮廓的复杂形态和细微结构,建模和仿真工作辊表面形貌亚微米数量级磨损。
元胞自动机(Cellular automata,CA)是基于数学的仿真模型,具有离散化的基本特征,能在离散的空间—时间上对复杂系统进行仿真模拟,适用于模拟转化规则相同的复杂系统,已成功模拟许多复杂问题,如繁殖、进化等过程。Hora C等人曾交替使用有限元及元胞自动机模拟涡轮叶片磨损问题,并取得良好结果[13];焦玉斌通过元胞自动机研究了电连接器的微动磨损过程等[18]。文中将元胞自动机方法引入板带轧制过程的工作辊表面细观磨损行为研究,采用元胞自动机方法对冷轧工作辊磨损过程进行建模和仿真,在大量工业生产中冷轧工作辊表面磨损行为实测研究与磨损失效机理分析的基础上,研究制定粗糙接触表面的接触咬合磨损、磨粒磨损等局部转换规则,建模仿真数学模型和求解算法,并在MATLAB仿真平台进行编程和仿真计算。 2 模型建立过程
根据在工业生产中测得的工作辊表面微观形貌数据,以及针对表面毛刺、尖峰的磨损规律的不同假设,对工作辊表面形貌变化进行仿真建模。为此,首先作如下假设和简化。
① 工作辊表面微观形貌的轮廓具有复杂形态和细微结构,需要在亚微米尺度几何描述,在元胞自动机模型中将工作辊表面形貌圆周向轮廓抽象简化为正弦曲线的叠加。
② 轧制区域内的接触弧长远大于粗糙峰尺寸,假设整个接触弧长上各段的磨损规律一致,在仿真中只选取接触弧上的一小段表面轮廓进行建模。
③ 在实际磨损过程中,即使相似结构也会因在轮廓上位置不同而具有不同的磨损速率,但在模型中假设表面轮廓上结构相似的部分具有完全一致的磨损过程和相同衰减速率。
④ 只研究工作辊表面发生在轧制区内的与带钢表面三体接触磨损,只取工作辊表面形貌作为分析对象,即假设工作辊具有粗糙表面而相对应的带钢表面为光滑表面。
⑤ 研究冷轧工作辊宏观磨损时一般假设其是疲劳磨损、磨粒磨损、腐蚀磨损、粘着磨损等共同作用结果,文中为了模拟轧辊表面微观形貌的细观尺度磨损而提出一种等效的磨损机制,假设轧辊表面粗糙峰的磨损由轧辊与带钢弹塑性接触咬合和界面间磨粒共同主导,表面每接触咬合一次就会“切削”式磨损一层,或者每接触咬合若干次会“剥落”式磨损一块,并且“剥落”式磨损的量值确定但位置(即磨粒出现的位置)随机。
⑥ 工作辊表面微观形貌有周期性也有一定随机性。但为了方便建模,根据在工厂实际测取的形貌数据,对工作辊表面抽象简化为规则形状并呈周期性均匀分布。 2.1 元胞空间及仿真工况的确定
仿真过程中,首先将工作辊表面轮廓曲线离散化,生成元胞空间。整个元胞空间由 1024×1024 个元胞的矩阵构成,采用的是四方网格的网络排列方式。元胞空间采用二维元胞自动机的 Moore 模型,除了位于边界处的元胞外,认为每一个中心元胞的周围有 8 个元胞与之构成关系。
工作辊的元胞突起部分的高度代表工作辊表面粗糙度值大小。给定所分析的工作辊表面粗糙为3.5 μm,则粗糙峰波峰距离波谷的最大高度为7 μm,粗糙峰底部最大宽度为70 μm。根据粗糙度定义式,在仿真数学模型中,生成形状比例相同的粗糙峰形状。
在当前板带冷轧生产中,由于带钢硬度增高造成轧制转印效率低和工作辊表面粗糙度参数衰减更加剧烈,导致了冲压用高强/超高强度带钢的微观表面质量问题最为严重也最难控制。因此选定高强度带钢冷轧工作辊表面形貌磨损为仿真研究对象。仿真研究所需有关高强度带钢冷轧的工艺及设备参数如表 1所示。
| Parameters | Values |
| Roughness of new roll/μm | 3.5 |
| Unit rolling force/MPa | 1 200 |
| Rolling speed/(m·s-1) | 8 |
| Rolling reduction/μm | 10 |
| Strip intensity/MPa | 800 |
此工况的主要特点是,工作辊上机粗糙度大,单位轧制压力大,带钢强度高,压下量小,工作辊表面磨损剧烈。 2.2 工作辊表面形貌的数学描述
通过实测分析可知,工作辊表面轮廓呈现出不规则波动,表面轮廓经分解可以得到高频部分(毛刺)和低频部分(基体),此时,任一工作辊表面都可由高频波与低频波叠加得到。为了方便建模和研究,采用低频的正弦曲线来模拟工作辊表面轮廓的基体,同时采用不同频率的高频率正弦曲线来模拟表面轮廓上的毛刺。
轧制过程中轧辊与带钢的接触区域如图 4所示,实测原始工作辊表面形貌轮廓曲线如图 5所示。从图 5中可以看出,工作辊上机前轮廓存在大量毛刺结构,毛刺与基体的组合叠加构成了典型机加工表面,毛刺对工作辊表面粗糙度磨损规律有着重要影响。图 5中低频部分周期为150 s,振幅为1.5 μm;高频第一部分周期为7 s,振幅为1.5 μm;高频第二部分周期为4 s,振幅为1.5 μm。将3条正弦曲线叠加,组成待分析的工作辊表面轮廓。
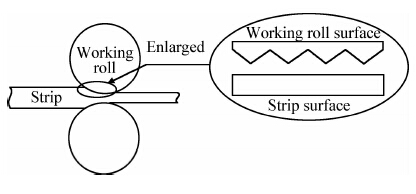 |
| 图 4 轧制区工作辊与带钢表面作用示意图Fig. 4 Schematic diagrams of the effects between the working roll and strip surface in the rolling zone |
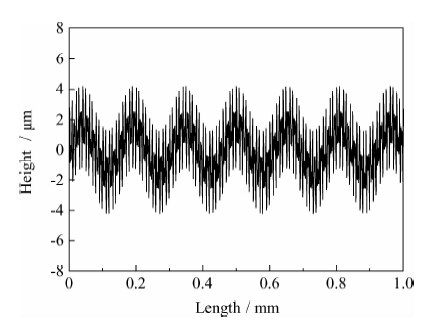 |
| 图 5 工作辊表面形貌的模拟轮廓曲线Fig. 5 Profile simulating curve of the working roll surface topograph |
研究假设表面发生接触即会产生接触咬合磨损,达到一定条件时发生磨粒磨损,不同形状轮廓由接触造成的元胞脱落时间不同,磨粒数量一定但磨粒产生位置和影响范围随机。
(1)接触咬合磨损转化规则
需对在MATLAB 中生成的不规则图形采用取整来进行表面的离散化,并采用逐点计数的方法求得磨损量,然后根据粗糙度计算公式求出各运行部工作辊表面的粗糙度。根据局部转换规则制定的接触咬合磨损的算法流程,如图 6所示。具体接触咬合磨损转换规则如下:假设小于45°的毛刺衰减准则为程序每运行1次,发生1次元胞状态的改变,即轧辊表面材料的磨损。通过大量的试验可知,45°~90°尖峰衰减的速率约为毛刺的1/8,因此其衰减准则为程序每运行8次,发生一次元胞状态的改变。同样,45°~135°钝峰的衰减准则为程序每运行20次,发生一次元胞状态的改变。
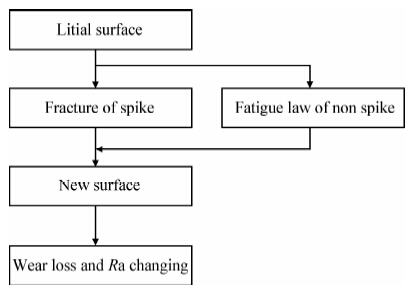 |
| 图 6 CA仿真接触咬合磨损仿真计算框图Fig. 6 Calculation flowchart of the adhesive wear simulation in cellular automata |
表面元胞按四方网格排列,每个元胞状态由其周围的8个元胞状态共同决定,可以通过每个元胞周围的同状态元胞个数对轮廓形状进行分类并确定不同转换规则。元胞状态转换时,对于不同的毛刺或基体结构,采用不同的转换步数,以区别反映工作辊表面不同细观结构磨损速率。
(2)磨粒磨损转换规则
在轧制区中,带钢表面同时发生二体磨损和三体磨损,硬度高的工作辊表面发生三体磨损的概率更高。假设磨粒发生位置和影响半径随机,参与磨损的磨粒数量恒定,不同形状轮廓磨粒的影响程度没有明显差异,根据局部转换规则制定出磨粒磨损的算法流程,如图 7所示。具体磨粒磨损转换规则如下:对于位置随机的磨粒磨损,模型中磨粒对于粗糙峰的影响半径为0.5~1.0 μm范围内的随机值与真实磨粒大小。一般认为,实际生产中磨粒磨损与接触咬合磨损对于轧辊表面整体磨损的贡献是相当的,为了与接触咬合磨损衰减速率相吻合,通过试验确定磨粒磨损的衰减准则为程序每运行8次才出现随机的磨粒磨损。
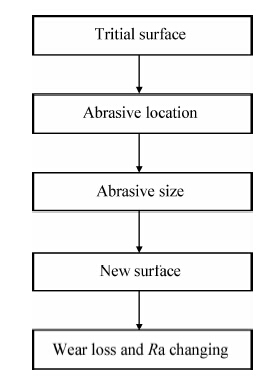 |
| 图 7 CA仿真磨粒磨损计算框图Fig. 7 Calculation flowchart of the abrasive wear simulation in cellular automata |
冷轧过程中由于工作辊表面磨粒刷的存在,磨粒数量是一定的,从而磨粒磨损与接触咬合磨损的相对数量基本保持恒定。通过数学叠加,将上述接触咬合磨损与磨粒磨损的磨损数学模型集成为一体,得到工作辊表面磨损的整体算法流程,如图 8所示。
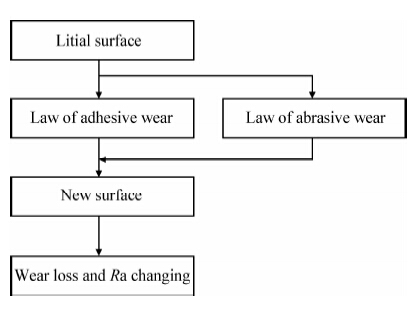 |
| 图 8 CA仿真整体计算流程图Fig. 8 Calculation flowchart of the whole simulation in cellular automata |
在完成工作辊表面形貌描述建模,根据元胞自动机方法基本原理建立了工作辊表面的接触咬合磨损与磨粒磨损共同作用下的磨损仿真模型及算法流程后,在MATLAB软件中实现编程和运行计算。针对前面所设定的仿真工况,带入程序进行仿真,提取仿真过程中随时间累计演变的磨损量与轧辊表面形貌,如图 9所示。同时根据磨损后的轧辊表面重新计算表面粗糙度值并给出磨损过程中的粗糙度衰减规律,如图 10所示。
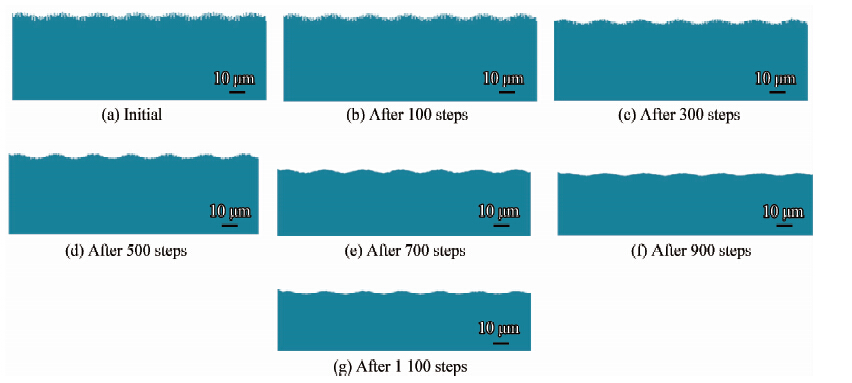 |
| 图 9 冷轧工作辊表面形貌磨损变化Fig. 9 Changing law of the working roll surface morphogies during cold rolling |
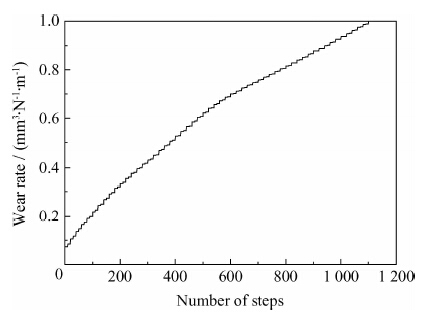 |
| 图 10 工作辊磨损过程磨损量变化规律Fig. 10 Changing law of the working roll wear loss during wearing |
图 9是元胞自动机模型给出的磨损发生的时间历程,不同阶段磨损后轧辊表面形貌。图中蓝色部分代表工作辊表面轮廓,前300步为磨损初始时期,工作辊原始表面轮廓存在大量毛刺,并且毛刺处在不同尺度上,尖细的毛刺数量较多;运行100步后,工作辊表面轮廓上的尖细毛刺衰减速度很快,轮廓的最大高度下降;运行300步后,工作辊表面轮廓上的尖细毛刺基本消失,尖细的毛刺所占比率明显减小,取而代之的是很多较为矮粗的尖峰,工作辊表面轮廓的集体形状初步可见;至第500步,矮粗尖峰磨损衰减,高度进一步降低,并且数量减小,粗糙峰基体的形状更加明显;至第700步,矮粗尖峰基本磨损殆尽,粗糙峰基体表面完全显露出来,轮廓形状参差不齐;第900步时,毛刺、尖峰与平台都几乎不复存在,可以清晰地观察到形状规则的粗糙度基体形状;至1 100步,粗糙峰基体形状进一步磨损,表面粗糙度值继续衰减。
可见,通过元胞自动机模拟冷轧平整过程中工作辊表面形貌的磨损演变过程,发现表面形貌磨损衰减规律,模型运行前300步工作辊表面形貌发生快速衰减、细小毛刺迅速消失,300~1 100步之间工作辊表面形貌的衰减速率趋于平稳,而后进入粗糙峰基体的磨损阶段。 3.2 粗糙度参数衰减的仿真结果
根据元胞自动机模型仿真得到的不同时刻的轧辊表面发生磨损后的形貌轮廓,获得磨损过程中工作辊表面粗糙度参数的磨损衰减历程,如图 10所示。在图 10中,横坐标为模型运行次数代表磨损时间,纵坐标为各步磨损量占总磨损量的比值,图中磨损曲线的斜率呈现先大后小的趋势,表明上机后工作辊辊身的磨损速率先快后慢。
为了验证图 10所示的仿真结果,在某钢厂超高强度带钢轧制实际生产过程中,完整跟踪实测了一对工作辊服役期内不同阶段的带钢及工作辊的表面粗糙度参数值,进而获得实际的工作辊粗糙度参数磨损衰减规律。
在此轧制过程中,工作辊上机粗糙度Ra为3.54 μm、下机粗糙度Ra为2.10 μm,带钢屈服强度在900 MPa以上,轧机的轧制压下量为6~19 μm,轧机的单位轧制压力在1 100~1 400 MPa内波动,轧制速度最高为9 m/s,与前述仿真工况相近。按一定规律抽查测得不同磨损阶段的带钢表面粗糙度Ra值,并利用已知的轧制转印率方程求得对应时刻的轧辊表面粗糙度值,再与实测得到的工作辊上机前和下机后的粗糙度值相组合,就可获得这对工作辊在整个轧制服役期内不同时刻的表面粗糙度Ra值,然后利用逐步回归法拟合得到工作辊表面粗糙度的磨损演变衰减规律。通过试验方法,对下机工作辊表面粗糙度特征进行观测,得到元胞自动机中与之近似的工作辊表面形貌所对应的运行步数,进而得到模型运行步数与实际生产中带钢卷数的对应关系。再次运行模型,并选取实测中一个轧制周期内由带钢表面粗糙度反推出的工作辊表面粗糙度,将实测所得工作辊表面Ra值衰减规律与元胞自动机模型仿真得到的Ra值衰减规律相对比做图,如图 8所示,定性地看,两条曲线基本吻合。
图 11为工作辊磨损过程中工作辊表面粗糙度变化规律。在图 11中,横坐标为运行次数,纵坐标为工作辊表面的粗糙度参数Ra值。从图中可以看出,前300步,粗糙度参数Ra值快速衰减,粗糙度衰减速率逐渐变缓;300步以后,粗糙度参数Ra值缓慢减小,Ra值衰减速率比较平稳。
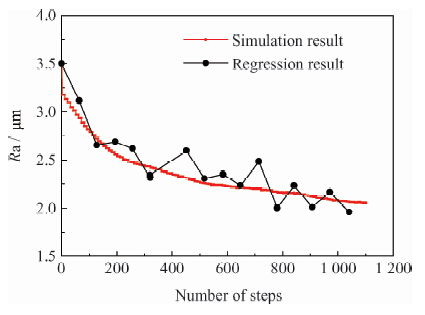 |
| 图 11 工作辊磨损过程表面粗糙度变化规律Fig. 11 Changing law of the working roll surface roughness during wearing |
由图 10和图 11可知,应用元胞自动机方法仿真所得工作辊表面磨损量的变化趋势与工业生产实测数据以及生产实际经验基本相符,其模拟得出的工作辊表面粗糙度参数变化趋势与现场实测得到的工作辊表面粗糙度衰减规律基本吻合。 4 结 论
(1) 通过不同频率正弦曲线组合叠加的方式,表征了工作辊表面微观形貌的圆周向轮廓,并采用四方格元胞体系、Moore 邻域结构生成元胞空间实现对工作辊表面二维形貌的模拟。通过邻居元胞数量,对不同的表面特征设置不同的转化规则,用以表达不同形貌工作辊表面的接触咬合磨损和磨粒磨损行为,引入位置随机的磨粒并设置随机化的转化规则来模拟随机磨粒磨损作用,建立了一个工作辊表面细观磨损的元胞自动机仿真模型。
(2) 将接触咬合磨损与磨粒磨损结合起来,模拟轧制过程中工作辊磨损的过程和规律,绘制其磨损量曲线以及粗糙度衰减曲线,获得不同尺度结构分层剥落的磨损机制下的工作辊表面细观磨损规律。模拟研究结果与在工业生产中实测统计得到的磨损规律基本吻合。
| [1] | 吴海淼, 吴炳胜, 赵立新. 板带轧机轧辊磨损数学模型研究 [J]. 轧钢, 2010, 27(5): 13-17.Wu H M, Wu B S, Zhao L X. Mathematical model of roll wear on plate and strip rolling mills [J]. Steel Rolling, 2010, 27(5): 13-17 (in Chinese). |
| 点击浏览原文 | |
| [2] | 王恩睿, 周素强, 王连轩. 高表面质量带钢轧辊磨削工艺研究 [C]. 南方金属, 2014(200): 1-4, 14.Wang E R, Zhou S Q, Wang L X. Study on the roll grinding process for cold rolled strip with high surface quality [J]. Southern Metals, 2014(200): 1-4, 14 (in Chinese). |
| 点击浏览原文 | |
| [3] | 吴海淼, 董建荣, 刘志民. 轧辊磨损数学模型研究 [J]. 润滑与密封, 2009, 34(8): 54-61.Wu H M, Dong J R, Liu Z M. Research on mathematical model of roll wear [J]. Lubrication Engineering, 2009, 34(8): 54-61 (in Chinese). |
| 点击浏览原文 | |
| [4] | Bolt P H, Batazzi D, Belfiore N P . Damage resistance and roughness retention of work rolls in cold rolling mills [J]. Revue de Métallurgie , 2010(107): 245-255. |
| 点击浏览原文 | |
| [5] | Shabani Mohsen Ostad, Ali Mazahery. Modeling of the wear behavior in A356-B4C composites [J]. Journal of Materials Science, 2011(46): 6700-8. |
| 点击浏览原文 | |
| [6] | Wang Z J, Zhou Q H. Applying a population growth model to simulate wear of rough surfaces during running-in [J]. Wear, 2012(294): 356-363. |
| 点击浏览原文 | |
| [7] | 姜增辉, 王琳琳, 石莉, 等. 硬质合金刀具切削Ti6Al4V的磨损机理及特征 [J]. 机械工程学报, 2014, 50(1): 178-184.Jiang Z R, Wang L L, Shi L, et al. Study on tool wear mechanism and characteristics of carbide tools in cutting Ti6Al4V [J]. Journal of Mechanical Engineering, 2014, 50(1): 178-184 (in Chinese). |
| 点击浏览原文 | |
| [8] | 朱亚琼, 沈岩, 金梅, 等. 缸套磨损表面波纹度和粗糙度形貌特征变化规律 [J]. 中国表面工程, 2014, 27(5): 59-64.Zhu Y Q, Shen Y, Jin M, et al. Metrological characteristics of cylinder liner wear surface waviness and roughness [J]. China Surface Engineering, 2014, 27(5): 59-64(in Chinese). |
| 点击浏览原文 | |
| [9] | 吴金平, 马明刚. 硬质合金拉丝模磨损形貌及机理研究 [J]. 煤矿机械, 2014, 35(6): 56-58.Wu J P, Ma M G. Research on wear morphology and mechanism of cemented carbide drawing die [J]. Coal Mine Machinery, 2014, 35(6): 56-58 (in Chinese). |
| 点击浏览原文 | |
| [10] | 薛玉君, 程先华, 黄文振. 断裂力学和有限元法在疲劳磨损研究中的应用 [J]. 机械强度, 2001, 23(3): 365-368.Xue Y J, Cheng X H, Huang W Z. Applications of fracture mechanics and finite element method in fatigue wear [J]. Journal of Mechanical Strength, 2001, 23(3): 365-368 (in Chinese). |
| 点击浏览原文 | |
| [11] | Shipway P H. A mechanical model for particle motion in the micro-scale abrasion wear test [J]. Wear, 2004(257): 984-991. |
| 点击浏览原文 | |
| [12] | Liang F, Liu W M, Du D S, et al. Predicting three-body abrasive wear using Monte Carlo methods [J]. Wear, 2004(256): 685-694. |
| 点击浏览原文 | |
| [13] | Hora C, Vesselenyi T, Dzitac S, et al. Wear simulation through cellular automata method [J]. Soft Computing Applications, 2009: 43-48. |
| 点击浏览原文 | |
| [14] | Tong J, Mohammad Almagzoub Mohammad, Zhang J B. DEM numerical simulation of abrasive wear characteristics of a bioinspired ridged surface [J]. Wear, 2010(7): 175-181. |
| 点击浏览原文 | |
| [15] | Hannes Dave, Alfredsson Bo. A fracture mechanical life prediction method for rolling contact fatigue based on the asperity point load mechanism [J]. Wear, 2012(83): 62-74. |
| 点击浏览原文 | |
| [16] | Kris De Moerlooze, Farid Al-Bender, Hendrik Van Brussel. A novel energy-based generic wear model at the asperity level [J]. Wear, 2011(270): 760-770. |
| 点击浏览原文 | |
| [17] | Benjamin D Leonard, Farshid Sadeghi, Sachin Shinde, et al. Rough surface and damage mechanics wear modeling using the combined finite-discrete element method [J]. Wear, 2013(305): 312-321. |
| 点击浏览原文 | |
| [18] | 焦玉斌. 基于元胞自动机法电连接器微动磨损仿真技术的研究 [D] . 黑龙江: 哈尔滨工业大学, 2011.Jiao Y B. Research on fretting wear simulation technique for electrical connector based cellular automation theory [D]. Heilongjiang: Harbin Institute of Technology, 2011 (in Chinese). |
| 点击浏览原文 |



