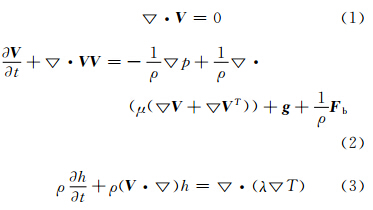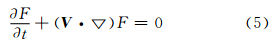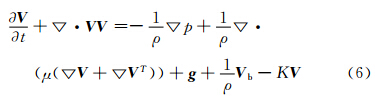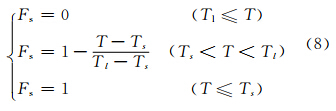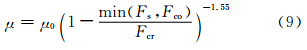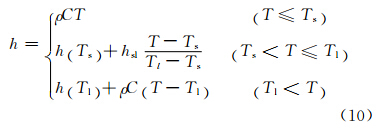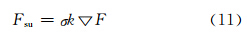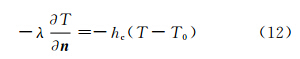3D打印技术是一系列在零件数字化模型驱动下通过材料的精确堆积方式制造零件原型或功能零件的工艺总称。特别是金属材料的3D打印技术,改变了传统的去除材料的加工方法,无需模具即可直接制造形状复杂、满足使用要求的零件,适合于单件或小批量零件生产,具有生产周期短、成本低等特点。该技术还可用于具有体积损失特征零件的再制造中。在众多金属零件的3D打印技术中,基于熔滴沉积的3D打印技术具有对基体的热输入小,沉积成形层完全致密等优点,如斯坦福大学与卡内基梅隆大学研究的形状沉积制造、麻省理工学院的均匀微滴喷射成形、加州大学的焊料微滴打印技术等[1]。对于熔滴沉积成形技术,熔滴碰撞基板时的动态变化及与基体间的热量传递过程在很大程度上影响到成形精度及成形质量。
采用数值模拟方法,建立熔滴在基板上的碰撞过程的数学模型,分析熔滴碰撞过程中的形态变化及温度变化情况,有助于分析熔滴温度、入射速度、尺寸等参数对成形精度及质量的影响规律,进而优化工艺参数,提高成形质量。国内外一些学者在这方面进行了相当多的研究[2,3,4,5,6,7,8,9,10]。国内的相关研究中,赖世强等人采用有限元数值分析方法研究了等离子喷涂中熔滴在基板上的扁平化过程,但没有耦合分析熔滴温度变化过程[5]。曾祥辉等人在基于有限体积法的FLUENT环境下,建立了锡合金在不锈钢基体上的变形过程二维数值分析模型,同时耦合分析了温度变化过程,用VOF法求解追踪了熔滴的自由界面[6]。国外Y. Wang[7]与M. H. Cho[4]等人分别建立了GMAW焊接中熔滴与熔池碰撞过程的数值分析模型,考虑了电弧作用于熔滴及熔池自由表面上的热流密度及电弧力的影响。
文中运用VOF自由界面追踪法,建立普通碳素钢材质熔滴在同材质基体上碰撞过程的三维数值分析模型,分析单个熔滴在基板上铺展及凝固的动态过程,并与Trapaga等人[11]的试验结果进行了对比验证。
1 数值分析方法 1.1 基本控制方程组
假设熔滴为不可压缩牛顿流,流动状态为层流,忽略温度变化对密度的影响。分别给出描述熔滴碰撞过程的基本方程组,即质量连续方程、动量与能量守恒方程:
式中,V为速度矢量,t为时间,ρ为密度,p为压力,μ为粘性系数,g为重力加速度,Fb为体积力,h 为焓,λ是热导率,T 为温度。
1.2 自由表面的追踪
熔滴与基板碰撞过程数值分析的关键是对动态自由表面的追踪。采用VOF法追踪确定熔滴表面,VOF法通过求解网格单元的体积分数F的值确定出熔滴界面位置。某网格单元的体积分数F被定义为流体在网格单元中所占的体积百分比,即
由上式可知,体积分数F为0~1之间的数值。当F=1时,网格单元内充满流体;当F=0时,网格单元内没有流体;当0<F<1时,网格单元内有部分流体,说明该单元内有熔滴表面。体积分数F满足下列关系式
同时求解上式与质量、动量守恒方程,可得体积分数F的分布,进而确定出熔滴的自由表面。这些含有部分流体的单元包含了熔滴的自由表面。 1.3 凝固与相变问题的处理
熔滴在下落及与基体碰撞过程中,与周围环境及基体间产生能量交换,温度会逐渐降低。当部分熔滴温度低于其熔点时,凝固现象就会发生。在熔滴未完全凝固前,存在液相、固相及液相与固相之间的半固相(也称为糊状区)。采用焓-多孔介质法处理凝固与相变问题。整个计算区域采用相同的控制方程,为了模拟凝固与相变问题,需要对控制方程进行适当修改。在动量守恒方程的最右侧加入项-KV,动量守恒方程变为
其中,K为阻力系数,其值与单元中物项(熔滴)的固相分数Fs有关,如下式所示:
式中,C0是阻力系数常数(对于钢材,其值为1),ε是一个非常小的数。固相分数Fs表示单元内固相体积所占物项总体积的百分比,若Fs=0,则表示单元内熔滴还未发生凝固;若Fs=1,则表示单元内熔滴已经全部凝固为固相;若0
为了更好的描述糊状区对凝固过程的影响,定义凝聚固相分数Fco与临界固相分数Fcr,其值分别为0.48和0.64[4]。Fco与Fcr将糊状区分为3个区域,各个区域的阻力系数及计算粘性系数都不同。
当Fs
式中,μ0为液相材料的粘性系数。此时的阻力系数K定义为零。
当Fco﹤Fs﹤Fcr时:阻力系数及粘性系数分别由式(7)与式(9)计算。
当Fs﹥ Fcr时:认为流体的刚性已经非常大,流动停止,此时阻力设系数为无限大。
为了模拟固液相变,焓与温度的关系定义为:
式中,C为比热,hsl为熔化潜热。
1.4 表面张力的处理
表面张力是熔滴动态模拟时必须考虑的因素。采用连续表面张力模型(Continuum surface force,CSF)计算表面张力作用。CSF模型将表面张力处理为体积力源项,添加到动量守恒方程中。根据CSF模型,表面张力可表示为
式中,Fsu为表面张力,σ为表面张力系数,k为自由表面曲率。
2 模型的建立
2.1 计算区域与网格单元
计算区域尺寸为4 mm×4 mm×5 mm,采用体立方六面体结构网格单元划分计算区域。网格单元大小影响到计算结果及计算时间。本模拟条件下网格单元尺寸大小为0.05 mm,计算网格如图 1所示。
需要定义材料的密度、表面张力系数等物理参数。熔滴与基板为同一材料,其物理性能参数如表 1所示,忽略了温度变化对这些参数的影响。
定义基板与熔滴的初始温度与速度条件。基板厚度为2 mm,温度为300 K。熔滴半径0.8 mm,距离基板2 mm,温度为2 000 K,z方向初始速度为-1 m/s,其余速度分量为零。基板与熔滴的初始位置及温度如图 2所示。
定义边界上的温度与速度条件。各边界上的速度分量均设为零。下表面及熔滴自由表面的温度边界为对流散热边界,即:
式中,hc为对流散热系数,T0为环境温度。侧表面处温度沿表面法线的偏导数为零。
3 结果及分析
根据有限体积单元法离散控制方程并求解,求解方法与步骤如文献[3]中所述。图 3是计算得到的熔滴与基板接触后不同时刻的三维形貌,图 4是不同时刻熔滴内各处速度矢量分布及温度变化情况的二维形貌。可以看出,熔滴以一定的初速度碰撞到基体时,在基体上迅速铺展,随后熔滴在基板上有一个振荡过程。在t=3.6 ms时熔滴与基板接触面的半径已达到1.3 mm,而此时熔滴与基板接触部位也已开始凝固。表面张力阻止了熔滴未凝固部分的进一步扩展,促使熔滴向上运动。在t=4.8~6 ms之间时,回荡的熔滴高度达到最大值,随后在重力的作用下逐步回落,但此时熔滴与基板接触面的半径基本不变。熔滴在基板上凝固前的振荡过程与熔滴的尺寸、碰撞速度及初始温度等特征量有关,并非熔滴的碰撞速度越大就越易产生振荡。相反的,当熔滴碰撞速度足够大时,惯性动量能够克服表面张力作用,使熔滴在未凝固前直接铺展在基体上。在时间t=18 ms后熔滴形态不再发生变化,只是熔滴仍未完全凝固。当t=70 ms时熔滴内不再有流动发生,已完全凝固为固态。
在熔滴与基板的碰撞过程中,熔滴与基板及周围空气发生热交换,其中通过热传导方式传递给基体的热量要远大于通过对流方式传递给周
围空气的热量。随着时间的增加,熔滴温度逐渐降低,基体温度逐渐增加。当熔滴温度小于其凝固温度1 768 K时,熔滴开始凝固。凝固现象首先发生在与基板接触的熔滴底部及外围部分,然后逐渐向熔滴上部扩展,在t=70 ms左右时熔滴完全凝固。这同时也说明熔滴热量主要是传递给基体。当t=100 ms时熔滴最高温度降至1 150 K左右。
Trapaga等人采用高速摄像技术观察了一个高温铜合金熔滴碰撞基板时其自由界面的动态变化过程[11],铜合金熔滴的初始温度为1 531 K,直径为4.67 mm,与基板接触时的速度为2.52 m/s。利用所建立的模型计算了相同条件下的铜合金熔滴碰撞基板时其自由界面的动态变化过程。图 5为模拟结果与Trapaga等人试验结果对比。可以看出:模拟结果与试验结果比较吻合,说明所建立的熔滴碰撞模型是可靠的。
(1) 基于VOF自由界面追踪法及处理凝固相变的焓-多孔介质法所建立的熔滴碰撞与凝固过程的三维数值分析模型,能够计算出熔滴自由界面的动态变化过程,以及伴随此过程中的温度变化情况。
(2) 对于一个初始速度1 m/s、温度为2 000 K的普通碳素钢材质的熔滴在同材质基体上的碰撞过程,模型计算结果表明,熔滴与基体接触后迅速铺展,随后有一个振荡过程,直到t=18 ms后熔滴形态不再发生变化,在t=70 ms时熔滴完全凝固。
(3) 从熔滴自由界面的动态变化过程这一特征量来讲,模拟结果与试验结果比较吻合。
(4) 利用所建立的数值分析模型,可进一步分析熔滴初始温度、速度、尺寸及基板温度等参数对熔滴沉积形态的影响规律。
图 1 网格单元示意图Fig. 1 Schematic diagram of the grid cells
Parameters Value
Density,ρ /(kg·m-3) 7 800
Specific heat,C /(J·kg-1.K-1) 686
Dynamic viscosity,μ0 /(kg·m-1.s-1) 6×103
Latent heat of fusion,hsl /(J·kg-1) 2.77×105
Thermal conductivity,λ /(W·m-1·K-1) 26
Solidus temperature,Ts/K 1 768
Liquid temperature,Tl/K 1 798
Surface tension,σ /(N·m-1) 1.8
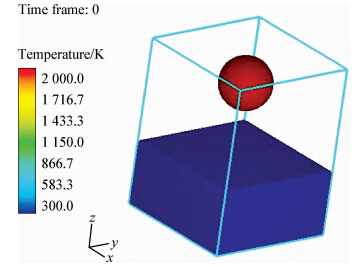
图 2 熔滴的初始条件Fig. 2 Initial condition of the droplet 
图 3 熔滴三维形貌与温度的分布Fig. 3 Three-dimensional distribution of the morphologies and temperature of droplets 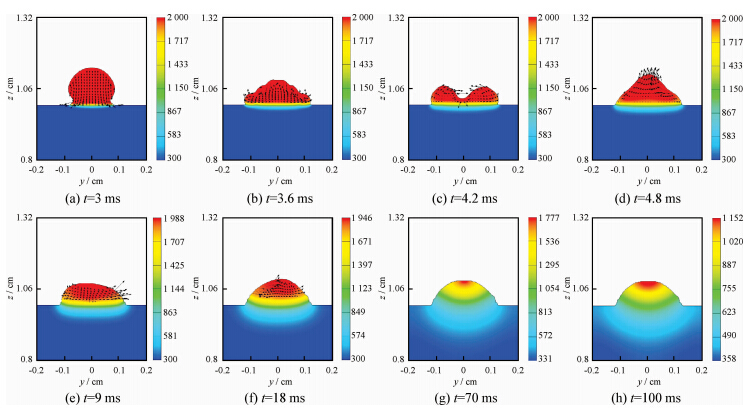
图 4 熔滴二维温度与速度的分布Fig. 4 Two-dimensional distribution of the temperature and velocity of droplets 
图 5 铜合金熔滴界面动态变化过程的试验结果与模拟结果对比Fig. 5 Comparison of the numerical and experimental results for dynamic evolution of Cu molten droplet surface
| [1] | 闫占功, 林峰, 齐海波, 等. 直接金属快速成形制造技术综述 [J]. 机械工程学报, 2005, 41(11): 1-7. |
| 点击浏览原文 | |
| [2] | Ghafouri-Azar R, Shakeri S, Chandra S, et al. Interactions between molten metal droplets impinging on a solid surface [J]. International Journal of Heat and Mass Transfer, 2003, 46(8): 1395-407. |
| 点击浏览原文 | |
| [3] | Pasandideh-Fard M, Chandra S, Mostaghimi J. A three-dimensional model of droplet impact and solidification [J]. International Journal of Heat and Mass Transfer, 2002, 45(11): 2229-42. |
| 点击浏览原文 | |
| [4] | Cho M H, Lim Y C, Farson D F. Simulation of weld pool dynamics in the stationary pulsed gas metal arc welding process and final weld shape [J]. Welding Journal, 2006, 85(12): 271-283. |
| 点击浏览原文 | |
| [5] | 赖世强, 冯志刚. 等离子喷涂过程中液态颗粒平化过程数值模拟 [J]. 焊接, 1998(6): 7-9, 13. |
| 点击浏览原文 | |
| [6] | 曾祥辉, 齐乐华, 蒋小珊, 等. 金属熔滴与基板碰撞变形的数值模拟 [J]. 哈尔滨工业大学学报, 2011, 43(3): 70-74. |
| 点击浏览原文 | |
| [7] | Wang Y, Tsai H L. Impingement of filler droplets and weld pool dynamics during gas metal arc welding process [J]. International Journal of Heat and Mass Transfer, 2001, 44(11): 2067-80. |
| [8] | Kumar A, Ghosh S, Dhindaw B K. Simulation of cooling of liquid Al-33 wt.% Cu droplet impinging on a metallic substrate and its experimental validation [J]. Acta Materialia, 2010, 58(1): 122-133. |
| 点击浏览原文 | |
| [9] | Delplanque J P, Rangel R H. A comparison of models, numerical simulation, and experimental results in droplet deposition processes [J]. Acta Materialia, 1998, 46(14): 4925-33. |
| 点击浏览原文 | |
| [10] | Amitesh Kumar. Solidification of impinging molten metal droplet on a cold substrate [J]. International Journal of Mechanical Engineering and Robotics Research, 2014, 3(2): 486-497. |
| 点击浏览原文 | |
| [11] | Trapaga G, Matthys E F, Valencia J J, et al. Fluid flow, heat transfer, and solidification of molten metal droplets impinging on substrates: comparison of numerical and experimental results [J]. Metallurgical Transactions B, 1992, 23(6): 701-718. |
| 点击浏览原文 |