2. 南车青岛四方机车车辆股份有限公司, 山东 青岛 266111
2. CSR Qingdao Sifang Co., Ltd., Qingdao 266111, Shandong
0 引 言
EA4T车轴是一种欧洲标准[1](EN13261:2003)规定的高速、重载铁道车辆用车轴,广泛应用于英、法、徳等国家的地铁及高速动车组机车中,具有优异的物理力学性能。近几年,我国已开展了EA4T车轴的国产化研究并投入应用[2,3]。
粱益龙[4,5,6]、郑业方[7]等研究了EA4T钢材料的微观组织结构、热处理工艺等内容,改善了材料的强度、韧性等力学性能,并分析了材料热处理缺陷产生的原因;孟扬等[8]研究了两种不同成分EA4T车轴钢的高周疲劳性能,发现合金元素含量的增加能提高钢淬透性,使晶粒细化,有效提高疲劳强度;徐刚等[9]对EA4T车轴钢高温热变形行为进行了研究,为该钢种制订合理的轧制控制工艺提供了理论依据;Ivo erny/等[10]评估了EA4T车轴热处理时裂纹扩展速率,研究了不同微观组织结构对疲劳裂纹扩展的影响;M. Luke等[11]采用有限元分析的方法预测了恒定载荷与变幅值载荷下EA4T车轴的疲劳裂纹扩展行为,并进行了1∶1与1∶3比例车轴的试验验证。可见,国内外学者主要对EA4T车轴的热处理工艺、热变形行为、裂纹扩展与疲劳寿命等方面进行了相关研究,而在通过改善加工工艺方法提高EA4T车轴使用寿命等方面少有介绍。
滚压表面强化技术(简称滚压)是一种简单有效的可以显著改善零件表面应力状态从而提高其抗疲劳性能的终加工工艺手段[12],自1929年首次在德国被用于机车轴的表面强化,目前已广泛应用于航空航天、汽车机车、精密机械、国防工业等领域[13],在诸多表面强化处理方法中具有显著优势[14]。为此,基于正交试验研究EA4T车轴滚压加工工艺,改善其表面粗糙度与残余应力分布等表面质量完整性指标,并建立表面质量完整性预测模型,提高EA4T车轴滚压加工质量。 1 方法与表征
根据L16(45)正交表设计四因素(滚压速度v、进给速度f、滚压深度h与滚压道次n)4水平正交试验,研究EA4T车轴滚压工艺对加工表面粗糙度与残余应力的影响。 1.1 滚压正交试验过程
采用肯纳可转位车刀在CKA6136数控车床上进行试件粗加工后,装夹JH-DG单滚R型滚压工具(滚轮直径36 mm)完成滚压加工,因素水平设置如表 1所示,滚压加工实况如图 1所示。
| Factors | Levels | |||
| 1 | 2 | 3 | 4 | |
| Burnishing speed,v/(m·min-1) | 80 | 100 | 120 | 140 |
| Feed speed,f/(mm·r-1) | 0.05 | 0.1 | 0.15 | 0.2 |
| Burnishing depth,h/mm | 0.02 | 0.04 | 0.06 | 0.08 |
| Burnishing passes,n | 1 | 2 | 3 | 4 |
 |
| 图 1 滚压加工试验 Fig. 1 Experiment of the burnishing process |
试验完成后采用TR200手持粗糙度仪测试表面粗糙度(滚压前表面粗糙度Ra=2.446 μm)。采用芬兰Xstress3000应力分析仪选用Cr靶、156.31°衍射角测试表面圆周方向与轴线方向残余应力(滚压前表面轴向残余应力σ=463.7 MPa,周向残余应力σ=481.3 MPa),每组工艺参数对应圆周表面均匀间隔取3个测量点求平均值。之后,制作相应试件抛光处理并采用MH-6型显微硬度计测量表面维氏硬度(载荷0.01 kg,滚压前表面显微硬度116.48 HV0.01)。测试结果见表 2和图 2。
| No. | Parameters | Test results | ||||||
| Burnishing speed,v/(m·min-1) | Feed speed, f/(mm·r-1) | Burnishing depth,h/mm | Burnishing passes,n | Surface roughness,Ra/μm | Microhardness/HV0.01 | Surface residual stress,σ/MPa | ||
| Axial direction | Circumferential direction | |||||||
| 1 | 80 | 0.05 | 0.02 | 1 | 0.38 | 117.85 | -602.7 | -332.9 |
| 2 | 80 | 0.10 | 0.04 | 2 | 0.57 | 124.34 | -681.9 | -359.7 |
| 3 | 80 | 0.15 | 0.06 | 3 | 0.96 | 124.68 | -648.0 | -323.2 |
| 4 | 80 | 0.20 | 0.08 | 4 | 1.18 | 126.44 | -636.8 | -309.9 |
| 5 | 100 | 0.05 | 0.04 | 3 | 0.31 | 145.72 | -710.7 | -381.8 |
| 6 | 100 | 0.10 | 0.02 | 4 | 0.60 | 162.71 | -594.0 | -352.2 |
| 7 | 100 | 0.15 | 0.08 | 1 | 1.18 | 152.01 | -655.0 | -281.0 |
| 8 | 100 | 0.20 | 0.06 | 2 | 1.29 | 166.74 | -576.0 | -305.0 |
| 9 | 120 | 0.05 | 0.06 | 4 | 0.30 | 120.00 | -732.0 | -371.3 |
| 10 | 120 | 0.10 | 0.08 | 3 | 0.61 | 123.23 | -748.0 | -367.6 |
| 11 | 120 | 0.15 | 0.02 | 2 | 1.08 | 156.80 | -596.9 | -314.2 |
| 12 | 120 | 0.20 | 0.04 | 1 | 1.59 | 167.85 | -508.5 | -225.5 |
| 13 | 140 | 0.05 | 0.08 | 2 | 0.24 | 162.60 | -799.4 | -390.9 |
| 14 | 140 | 0.10 | 0.06 | 1 | 0.61 | 146.67 | -678.0 | -319.4 |
| 15 | 140 | 0.15 | 0.04 | 4 | 1.07 | 166.32 | -660.7 | -360.4 |
| 16 | 140 | 0.20 | 0.02 | 3 | 1.81 | 145.50 | -583.1 | -338.2 |
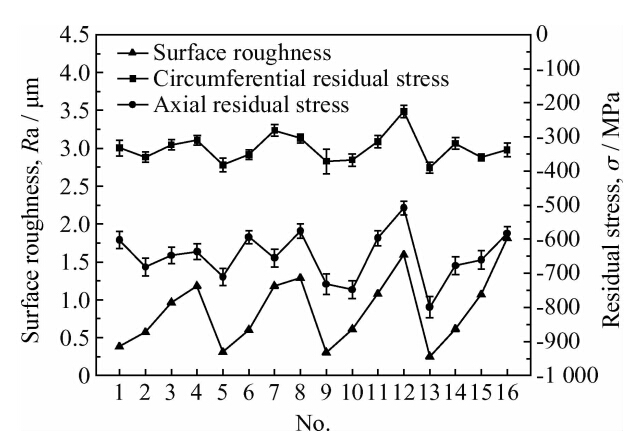 |
| 图 2 加工后表面粗糙度与残余应力 Fig. 2 Surface roughness and residual stress after burnishing |
从表 2和图 2看出,滚压加工不仅引起加工表面粗糙度、残余应力的波动变化,而且影响了表面硬度。加工表面残余压应力轴向大于周向,且两方向残余应力变化规律相似。表面粗糙度与残余应力变化规律具有一定相关性,在残余压应力较大的工艺参数下,表面粗糙度往往较小。
滚压后,表面粗糙度从2.446 μm降到0.244~1.812 μm,残余应力状态从拉应力变为压应力,且表面硬度也有不同程度提高。表明滚压加工能显著改善加工表面粗糙度、残余应力状态,引起表面层金属不同程度的硬化,最大硬化率达44.10%。 2 结果分析与工艺参数优化
采用方差分析(Analysis of variance,ANOVA)和信噪比(Signal-to-noise ratio)的方法对试验结果进行统计学分析,得到影响表面质量完整性显著性因素与最优参数水平。 2.1 方差分析
分别以表面粗糙度、残余应力与显微硬度为评价指标进行方差分析,置信水平为95%,结果如表 3所示。
| Evaluation index | Factors | Sum of squares | DOF | Mean squared errors | F | Contribution rate/% |
| Surface roughness | Burnishing speed,v | 0.059 | 3 | 0.020 | 0.932 | 1.73 |
| Feed speed,f | 3.142 | 3 | 1.048 | 49.332 | 91.70 | |
| Burnishing depth,h | 0.081 | 3 | 0.027 | 1.274 | 2.37 | |
| Burnishing passes,n | 0.080 | 3 | 0.027 | 1.256 | 2.34 | |
| Errors | 0.064 | 3 | 0.021 | 1.86 | ||
| Total | 3.427 | 15 | 100 | |||
| Circumferential residual stress | Burnishing speed,v | 2 236 | 3 | 745 | 2.852 | 8.45 |
| Feed speed,f | 12 957 | 3 | 4 319 | 16.527 | 48.95 | |
| Burnishing depth,h | 130 | 3 | 43 | 0.166 | 0.49 | |
| Burnishing passes,n | 10 362 | 3 | 3 454 | 13.217 | 39.15 | |
| Errors | 784 | 3 | 261 | 2.96 | ||
| Total | 26 469 | 15 | 100 | |||
| Axial residual stress | Burnishing speed,v | 4 985 | 3 | 1 662 | 3.414 | 6.03 |
| Feed speed,f | 39 802 | 3 | 13 267 | 27.262 | 48.18 | |
| Burnishing depth,h | 27 415 | 3 | 9 138 | 18.777 | 33.19 | |
| Burnishing passes,n | 8 948 | 3 | 2 983 | 6.129 | 10.83 | |
| Errors | 1 460 | 3 | 487 | 1.77 | ||
| Total | 82 610 | 15 | 100 | |||
| Microhardness | Burnishing speed,v | 2 887 | 3 | 962 | 3.964 | 54.70 |
| Feed speed,f | 686 | 3 | 229 | 0.942 | 13.00 | |
| Burnishing depth,h | 324 | 3 | 108 | 0.445 | 6.14 | |
| Burnishing passes,n | 653 | 3 | 218 | 0.896 | 12.37 | |
| Errors | 728 | 3 | 243 | 13.79 | ||
| Total | 5 278 | 15 | 100 |
方差分析F值的大小反应出某一因素是否显著,如果某一因素是显著的,则此因素任何小的变动都会对评价指标造成较大影响。贡献率为 各因素离差平方和所占比例,从表 3看出,在影响表面粗糙度的因素中,进给速度贡献率为91.70%,是显著性影响因素。进给速度与滚压道次是影响加工表面周向残余应力的显著性因素,贡献率分别为48.95%和39.15%,而影响轴向残余应力的显著性因素为进给速度与滚压深度,贡献率分别为48.18%和33.19%。相对其它工艺参数,滚压速度对表面显微硬度影响较大,贡献率为54.7%。 2.2 信噪比
在正交试验研究中,影响评价指标的因素分为两类,控制因素与噪声因素。控制因素为试验过程中可以控制的变量,如工艺参数,而噪声因素为试验过程中不可控制且对评价指标有影响的变量。控制因素占的比例越大或者噪声因素占的比例越小,则信噪比值越大,试验效果越好。常通过损失函数计算信噪比,对于表面粗糙度这类越小越好的评价指标与表面残余压应力这类越大越好的评价指标,分别采用式(1)和式(2)计算信噪比[15],16组试验结果对应的信噪比值如表 4所示。根据每个工艺因素对应水平的平均信噪比值的大小,进行水平优选,以达到最好的试验效果,工艺因素对应水平的平均信噪比值与水平优选结果如表 5所示,信噪比均值效应如图 3所示。
| (dB) | |||
| No. | Surface roughness | Surface residual stress | |
| Axial direction | Circumferential direction | ||
| 1 | 8.38 | 50.45 | 55.60 |
| 2 | 4.87 | 51.12 | 56.67 |
| 3 | 0.36 | 50.19 | 56.23 |
| 4 | -1.43 | 49.82 | 56.08 |
| 5 | 10.17 | 51.64 | 57.03 |
| 6 | 4.47 | 50.94 | 55.48 |
| 7 | -1.41 | 48.97 | 56.33 |
| 8 | -2.19 | 49.69 | 55.21 |
| 9 | 10.40 | 51.40 | 57.29 |
| 10 | 4.27 | 51.31 | 57.48 |
| 11 | -0.66 | 49.94 | 55.52 |
| 12 | -4.04 | 47.06 | 54.13 |
| 13 | 12.25 | 51.84 | 58.06 |
| 14 | 4.25 | 50.09 | 56.63 |
| 15 | -0.60 | 51.14 | 56.40 |
| 16 | -5.16 | 50.58 | 55.32 |
| Index | Signal-to-noise ratio/dB | Optimum level | ||||
| Level 1 | Level 2 | Level 3 | Level 4 | |||
| 1# | v | 3.04 | 2.76 | 2.49 | 2.69 | 1 |
| f | 10.30 | 4.46 | -0.58 | -3.21 | 1 | |
| h | 1.76 | 2.60 | 3.20 | 3.42 | 4 | |
| n | 1.80 | 3.57 | 2.41 | 3.21 | 2 | |
| 2# | v | 50.40 | 50.31 | 49.93 | 50.91 | 4 |
| f | 51.33 | 50.86 | 50.06 | 49.29 | 1 | |
| h | 50.48 | 50.24 | 50.34 | 50.49 | 4 | |
| n | 49.14 | 50.65 | 50.93 | 50.82 | 3 | |
| 3# | v | 56.15 | 56.01 | 56.10 | 56.60 | 4 |
| f | 57.00 | 56.56 | 56.12 | 55.18 | 1 | |
| h | 55.48 | 56.06 | 56.34 | 56.99 | 4 | |
| n | 55.67 | 56.36 | 56.52 | 56.31 | 3 | |
| Note:“1#”,“2#” and “3#” represent surface roughness,circumferential residual stress and axial residual stress,respectively. | ||||||
其中,ηij为信噪比,n为评价指标数,这里n=1,yij为每组试验参数下评价指标测试值。
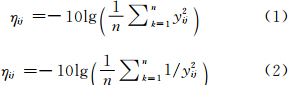
从图 3看出,对于表面粗糙度曲线,相对其它因素,信噪比随进给速度变化波动最大。这表明:进给速度为影响表面粗糙度的显著性因素,并且随着进给速度增加,信噪比减小,表面粗糙度增大。对于周向残余应力曲线,信噪比随进给速度与滚压道次的变化波动较大;而对于轴向残余应力曲线,信噪比随进给速度与滚压深度的变化波动较大,表明进给速度与滚压道次、进给速度与滚压深度分别是影响周向与轴向残余应力的显著性因素,并且随进给速度增加,信噪比减小,表面残余压应力减小,这与前述方差分析结果是一致的。
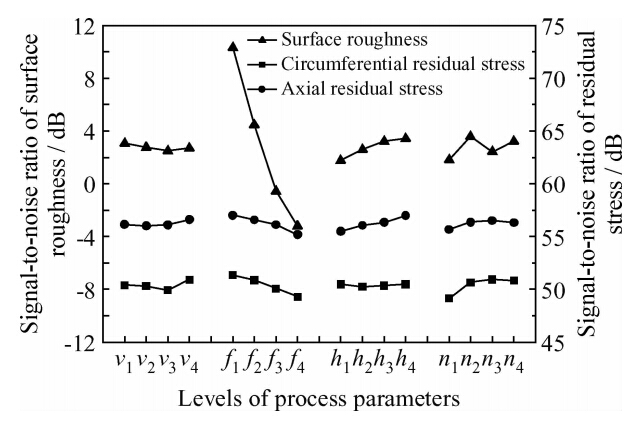 |
| 图 3 信噪比均值效应图 Fig. 3 Mean curves of the signal-to-noise ratio |
根据表 5得出了滚压正交试验理论最优参数水平,而在实际工艺参数选择时,可以根据表 3影响评价指标的显著性因素确定与其对应的最优参数水平。之后,其它非显著性因素的参数选择可以根据实际情况进行适当调整。 3 工艺参数与表面质量完整性关系模型
在机床特性、滚压工具结构与工件材料确定的条件下,建立滚压工艺参数与表面质量完整性之间的经验模型[16],如式(3)所示。线性化后采用多元线性回归分析的方法求得回归方程,求解过程如式(4)~式(6)所示,确定关系模型。之后,进行回归方程、回归系数的显著性检验与残差分析,判断多元线性回归模型的好坏。
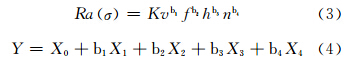
其中, Y=lgRa(lgσ),X0=lgK,X1=lgv,X2=lgf,X3=lgh,X4=lgn ,K为与机床特性、滚压工具与工件材料等相关的系数,b1、b2、b3、b4为常数。
考虑试验误差ε,由正交试验可以建立式(5)多元线性回归方程:

其中,
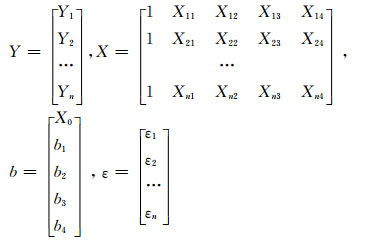
计算得
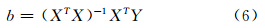
采用多元线性回归分析得到滚压工艺参数与表面粗糙度关系模型如式(7)所示,回归方程如式(8)所示。
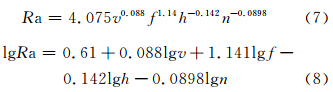
从上述预测模型看出,进给速度f对应指数的绝对值相对较大,其小的变动会对粗糙度Ra产生较大影响,且随进给速度f增加,粗糙度Ra增大。这是由于进给速度f直接影响到滚压过程未滚压金属残留面积,进给速度f增加,未滚压金属残留面积增大,粗糙度Ra增大。
根据式(7)得到粗糙度预测值,与测试值进行比较,如图 4所示,经计算,预测误差(|预测值-测试值|/测试值)的均值为8.65%。
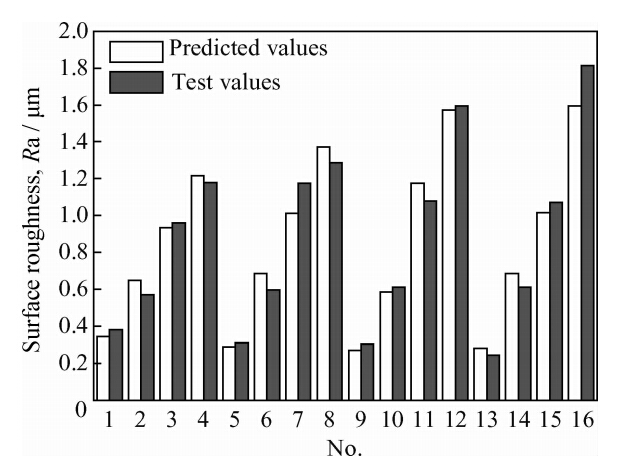 |
| 图 4 粗糙度预测值与测试值 Fig. 4 Predicted and test values of the surface roughness |
采用多元线性回归分析得到滚压工艺参数与表面残余应力关系模型如式(9)和式(10)所示,回归方程分别如式(11)和式(12)所示。
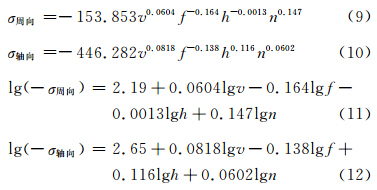
从上述预测模型看出,进给速度f对应指数的绝对值相对较大,其小的变动会对两方向残余应力产生较大影响,且随进给速度f增加,表面残余拉应力增大。这是由于滚压加工时,滚轮前方区域表层金属沿加工表面被压缩,垂直于加工表面被拉长,这种“塑性凸出”效应会使表层金属发生塑性变形,体积减小,滚压结束后表层金属受到内部金属弹性恢复作用,产生残余拉应力,且随进给速度f增加,“塑性凸出”效应增强,残余拉应力增大。
根据式(9)和式(10)得到表面残余应力预测值,与测试值进行比较,如图 5和图 6所示。经计算,预测误差(|预测值-测试值|/测试值)的均值周向5.82%、轴向3.93%。
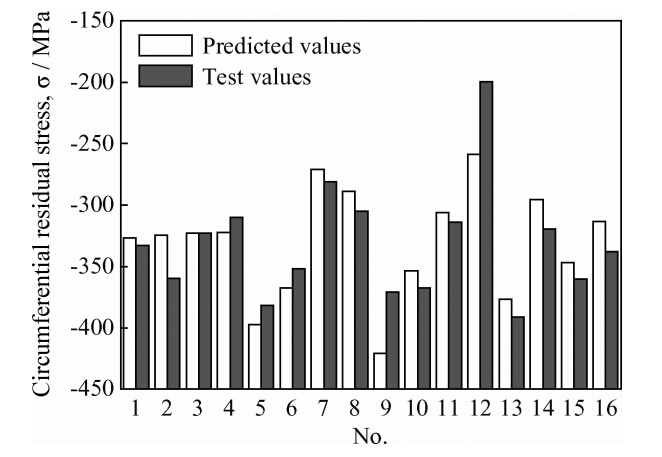 |
| 图 5 周向残余应力预测值与测试值 Fig. 5 Predicted and test values of the circumferential residual stress |
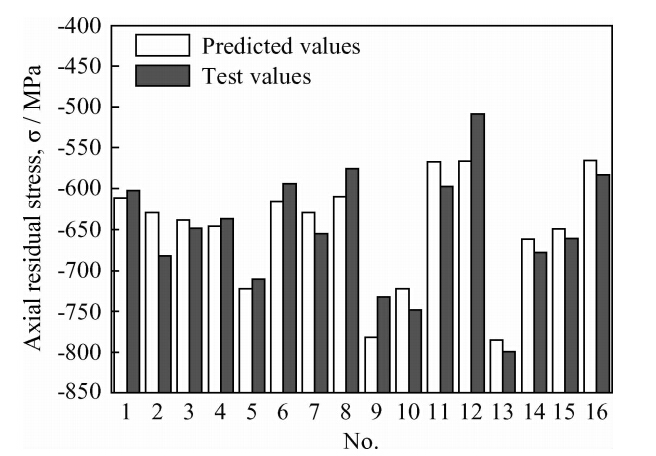 |
| 图 6 轴向残余应力预测值与测试值 Fig. 6 Predicted and test values of the axial residual stress |
为确定所建立的多元线性回归方程是否具有统计学上的合理性,进行回归方程、回归系数方差分析与残差分析,如表 6、表 7和图 7~9所示。
| Index | Source | DOF | Sum of squares | Mean squared error | F | P |
| 1# | Regression equation | 4 | 1.082 | 0.271 | 106.12 | 0 |
| Residual errors | 11 | 0.028 | 0.003 | |||
| Total | 15 | 1.110 | ||||
| 2# | Regression equation | 4 | 0.040 | 0.010 | 8.73 | 0.002 |
| Residual errors | 11 | 0.013 | 0.001 | |||
| Total | 15 | 0.053 | ||||
| 3# | Regression equation | 4 | 0.030 | 0.008 | 12.40 | 0 |
| Residual errors | 11 | 0.007 | 0.001 | |||
| Total | 15 | 0.037 |
方差分析中,P值为显著性检验时达到的显著性水平,代表了认为分析对象有显著性影响时犯错的概率,其值越小,可信度越高。在许多研究领域,0.05的P值被认为是可以接受错误的边界水平。
表 6中方差分析P值均小于0.05,表 7中方差分析(R-Sq)值均大于70%,说明回归方程与回归系数是极具统计学意义的。表 7中lgf对应P值为0,表明在预测模型中,进给速度是影响表面粗糙度的显著性因素。同样,表 7中各自变量P值的大小,表明了在预测模型中,进给速度与滚压道次是影响周向残余应力的显著性因素,而进给速度与滚压深度是影响轴向残余应力的显著性因素。这与方差分析一致,预测模型能较好的反映试验情况。
| Index | Variable | Coefficient | Standarderrors | T | P |
| 1# | lgK | 0.610 | 0.299 | 2.04 | 0.066 |
| lgv | 0.088 | 0.139 | 0.63 | 0.540 | |
| lgf | 1.137 | 0.056 | 20.37 | 0 | |
| lgh | -0.142 | 0.056 | -2.54 | 0.027 | |
| lgn | -0.090 | 0.056 | -1.61 | 0.136 | |
| S=0.050 5,R-Sq=97.5%,R-Sq(adjustment)=96.6% | |||||
| 2# | lgK | 2.187 | 0.200 | 10.9 | 0 |
| lgv | 0.060 | 0.094 | 0.65 | 0.532 | |
| lgf | -0.164 | 0.038 | -4.37 | 0.001 | |
| lgh | -0.001 | 0.038 | -0.03 | 0.973 | |
| lgn | -0.090 | 0.038 | 3.92 | 0.002 | |
| S=0.033 9,R-Sq=76.0%,R-Sq(adjustment)=67.3% | |||||
| 3# | lgK | 2.650 | 0.146 | 18.11 | 0 |
| lgv | 0.082 | 0.068 | 1.20 | 0.256 | |
| lgf | -0.138 | 0.027 | -5.03 | 0 | |
| lgh | 0.116 | 0.027 | 4.25 | 0.001 | |
| lgn | 0.060 | 0.027 | 2.20 | 0.050 | |
| S=0.024 8,R-Sq=81.8%,R-Sq(adjustment)=75.2% | |||||
| Note of Table 6 and Table 7:(a)“1#”,“2#” and “3#” represent surface roughness,circumferential residual stress and axial residual stress,respectively. (b) F is an index used to judge whether the object is significant in F-test,if F>F0.05(4,11)=3.36,the object has significant influence. (c) T is equal to the ratio of coefficient and standard errors represents an index used to judge whether the object is significant in T-test. | |||||
从图 7~9可以看出,残差成正态分布且残差是具有恒定方差的,说明回归方程具有统计学上的的合理性,即预测模型有效。
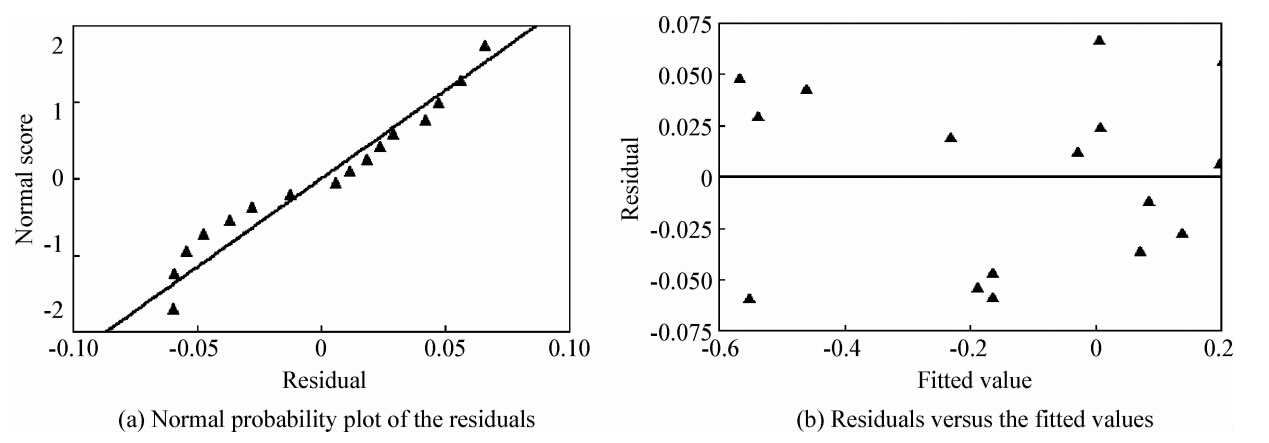 |
| 图 7 lgRa残差图 Fig. 7 Residual plots of the lgRa |
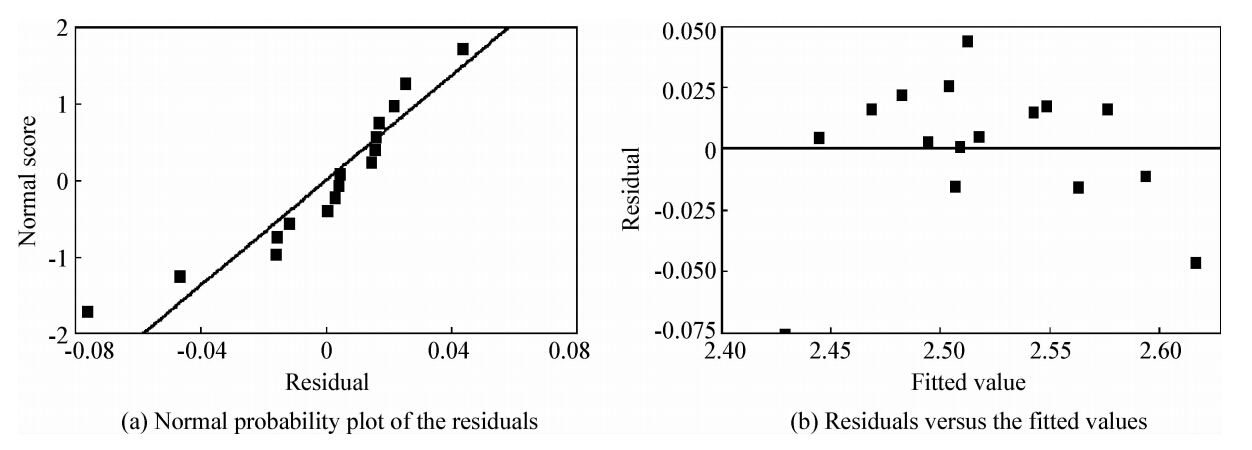 |
| 图 8 周向lgσ残差图 Fig. 8 Residual plots of the circumferential lgσ |
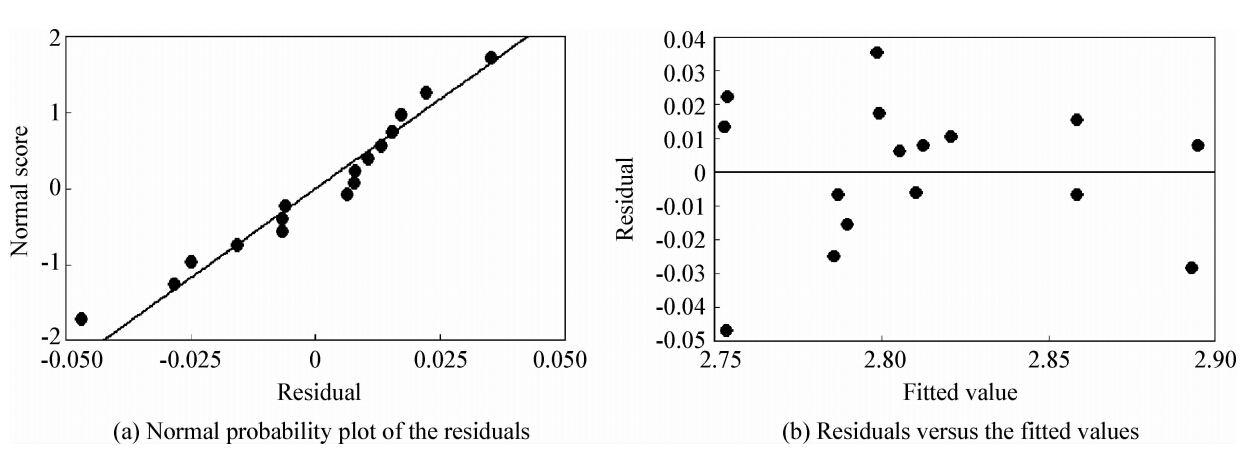 |
| 图 9 轴向lgσ残差图 Fig. 9 Residual plots of the axial lgσ |
(1) 滚压工艺参数对EA4T车轴表面质量完整性有重要影响。其中,进给速度对车轴表面粗糙度有显著性影响,贡献率为91.70%。进给速度与滚压道次、进给速度与滚压深度分别对车轴表面周向与轴向残余应力影响显著,贡献率分别达到48.95%、39.15%与48.18%、33.19%。随着滚压速度增大,车轴表面硬度有一定程度的提高,最大硬化率达到44.10%。
(2) 通过正交试验,以减小表面粗糙度、增大表面残余压应力为指标,采用方差分析与“信噪比”的方法得到了EA4T车轴滚压工艺最优参数水平。
(3) 建立了滚压工艺参数与EA4T车轴表面粗糙度、残余应力关系预测模型,并采用方差分析、残差分析方法验证模型在统计学上的有效性,且预测效果较好。
| [1] | BS EN13261-2003, 铁路应用-轮对和转向架-车轴-产品要求 [S]. |
| [2] | 刘军辉. EA4T车轴热处理工艺研究 [J]. 机械管理开发, 2012(4): 57-59. |
| 点击浏览原文 | |
| [3] | 覃作祥, 李芷慧, 周鹏. 25CrMo4钢先共析铁素体转变及其对力学性能的影响 [J]. 大连交通大学学报, 2011, 32(5): 62-66. |
| 点击浏览原文 | |
| [4] | 梁益龙, 王新, 孟阳, 等. 国产EA4T车轴钢的显微组织与强韧性研究 [J]. 热加工工艺, 2008, 37(16): 23-25. |
| 点击浏览原文 | |
| [5] | 王兴安, 梁益龙. EA4T车轴钢脉冲电流加热带状组织的消除 [J]. 热加工工艺, 2010, 39(18): 191-203. |
| 点击浏览原文 | |
| [6] | 王筑生, 梁益龙, 吴少斌, 等. 大截面EA4T车轴钢回火工艺对组织和性能的影响 [J]. 材料热处理学报, 2012, 33(5): 48-52. |
| 点击浏览原文 | |
| [7] | 郑业方, 杨军, 苏立武, 等. 热处理工艺对EA4T钢车轴组织与性能的影响 [J]. 金属热处理, 2011, 36(12): 38-40. |
| 点击浏览原文 | |
| [8] | 孟扬, 梁益龙. 不同成分EA4T车轴钢的高周疲劳性能 [J]. 机械工程材料, 2010, 34(4): 55-57. |
| 点击浏览原文 | |
| [9] | 徐刚, 李士琦, 王乐, 等. 高铁用EA4T车轴钢热变形行为及变形抗力模型的试验研究 [J]. 特殊钢, 2013, 34(3): 60-63. |
| 点击浏览原文 | |
| [10] | Ivo erny′, Václav Linhart. Effects of different microstructure on resistance of EA4T railway axle steel of equal strength to fatigue crack growth [J]. Key Engineering Materials, 2014, 592-593: 631-634. |
| [11] | Luke M, Varfolomeev′ I, Lütkepohl K, et al. Fatigue crack growth in railway axles: Assessment concept and validation tests [J]. Engineering Fracture Mechanics, 2011, 78(5): 714-730. |
| 点击浏览原文 | |
| [12] | 何嘉武, 马世宁, 巴德玛. 表面滚压强化技术研究与应用进展 [J]. 装甲兵工程学院学报, 2013, 27(3): 75-81. |
| 点击浏览原文 | |
| [13] | 赵婧, 夏伟, 李风雷, 等. 滚压表面强化机理的研究现状与进展 [J]. 工具技术, 2010, 44(11): 3-8. |
| 点击浏览原文 | |
| [14] | 刘福超, 雷丽萍, 曾攀. 滚压有限元模型数值模拟 [J]. 塑性工程学报, 2012, 19(2): 17-21. |
| 点击浏览原文 | |
| [15] | Adeel Ikram, Nadeem Ahmad Mufti, Muhammad Qaiser Saleem, et al. Parametric optimization for surface roughness, kerf and MRR in wire electrical discharge machining (WEDM) using Taguchi design of experiment [J]. Journal of Mechanical Science and Technology, 2013, 27(7): 2133-41. |
| 点击浏览原文 | |
| [16] | 王素玉, 艾兴, 赵军, 等. 高速铣削表面粗糙度建模与预报 [J]. 制造技术与机床, 2006(8): 65-68. |
| 点击浏览原文 |


