电气工程学报, 2024, 19(1): 57-66 doi: 10.11985/2024.01.006

特邀专栏:储能关键装备数字化智能安全管理技术

基于CEEMDAN功率分解的火电厂混合储能容量优化配置

戴申华,1, 王琨玥1, 曹蓓1, 张啸天2, 高萧2, 刘旭,2

1.中国大唐集团科学技术研究总院有限公司华东电力试验研究院 合肥 230031

2.省部共建电工装备可靠性与智能化国家重点实验室(河北工业大学) 天津 300130

Optimal Configuration of Hybrid Energy Storage Capacity in Thermal Power Plants Based on CEEMDAN Power Decomposition

DAI Shenhua,1, WANG Kunyue1, CAO Bei1, ZHANG Xiaotian2, GAO Xiao2, LIU Xu,2

1. East China Electric Power Test & Research Institute, China Datang Corporation Science and Technology General Research Institute Co., Ltd., Hefei 230031

2. State Key Laboratory of Reliability and Intelligence of Electrical Equipment (Hebei University of Technology), Tianjin 300130

收稿日期: 2023-10-11   修回日期: 2023-12-17  

Received: 2023-10-11   Revised: 2023-12-17  

作者简介 About authors

戴申华，男，1984年生，高级工程师。主要研究方向为电网与储能。E-mail：daishenhua1@126.com;

刘旭，男，1984年生，博士，教授，博士研究生导师。主要研究方向为新型永磁电机及开关磁阻电机驱动控制、电机驱动及集成技术。E-mail：liuxu@hebut.edu.cn

摘要

为了解决火电机组跟随自动发电量指令(Automatic generation control, AGC)响应延迟大、超调大等问题，提出一种基于完全噪声辅助聚合经验模态分解(Complete ensemble empirical mode decomposition with adaptive noise, CEEMDAN)的混合储能系统容量优化配置方法。首先，通过某时间段火电机组跟随AGC指令输出曲线，获得混合储能系统需要提供的功率。在此基础上，利用CEEMDAN将需求功率进行分解，获得不同频率下火电机组与AGC指令之间的误差。选择合适的储能元件，构建火电厂响应AGC指令的混合储能系统结构模型，在考虑能量型储能元件磷酸铁锂电池与功率型储能元件飞轮储能系统两类不同储能设备工作特性的情况下进行功率分配。在考虑储能系统荷电状态(State of charge, SOC)、容量与充放电功率等约束下，建立以综合成本最小为目标的容量优化配置模型，将功率分解结果与容量配置模型联合优化，获得最优功率分配情况和对应的储能配置方案。提供工程案例分析，结果表明所提方法可以有效弥补火电机组跟随AGC指令的延迟功率响应，提高火电机组供电可靠性和经济效益，同时相较于单一储能元件，本方案所设计混合储能系统拥有更优经济性。

关键词： AGC指令; 混合储能; CEEMDAN; 容量配置

Abstract

In order to solve the problem of considerable delay and error in response to automatic generation control(AGC) instructions in thermal power generating units, a method for optimizing the capacity configuration of a hybrid energy storage system based on complete ensemble empirical mode decomposition with adaptive noise(CEEMDAN) is developed. First, the power required by the hybrid energy storage system is obtainedby following the AGC instructionand its response curve of the thermal power generating units over a certain period of time. Based on this, the demand power is decomposed by using CEEMDAN to yield the error between the AGC instruction and its response curve of the thermal power generating units at different frequencies. By selecting the appropriate energy storage components, a hybrid energy storage system structure model that cooperates in the response of the AGC instructions in the thermal power plant is constructed, and the power distribution is carried outunder the condition of considering the working characteristics of two different types of energy storage equipment: energy-type lithium iron phosphate battery and power-type flywheel battery. Finally, a capacity optimization configuration model is established with the objective of minimizing overall costs while accounting for constraints such as the state of charge(SOC) of the energy storage system, capacity, and charge/discharge power. The results of the power decomposition are optimized synergistically with the capacity configuration model to determine the optimal power allocation and corresponding energy storage configuration scheme. An example is demonstrated to verify the effectiveness of the proposed method in compensating for the delayed power response resulting in thermal power generating units with high reliability and economic efficiency. And compared with a single energy storage element, the hybrid energy storage system designed in this scheme has better economy.

Keywords： AGC instruction; hybrid energy storage; complete ensemble empirical mode decomposition with adaptive noise; capacity confirguration

PDF (18882KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

戴申华, 王琨玥, 曹蓓, 张啸天, 高萧, 刘旭. 基于CEEMDAN功率分解的火电厂混合储能容量优化配置[J]. 电气工程学报, 2024, 19(1): 57-66 doi:10.11985/2024.01.006

DAI Shenhua, WANG Kunyue, CAO Bei, ZHANG Xiaotian, GAO Xiao, LIU Xu. Optimal Configuration of Hybrid Energy Storage Capacity in Thermal Power Plants Based on CEEMDAN Power Decomposition[J]. Chinese Journal of Electrical Engineering, 2024, 19(1): 57-66 doi:10.11985/2024.01.006

1 引言

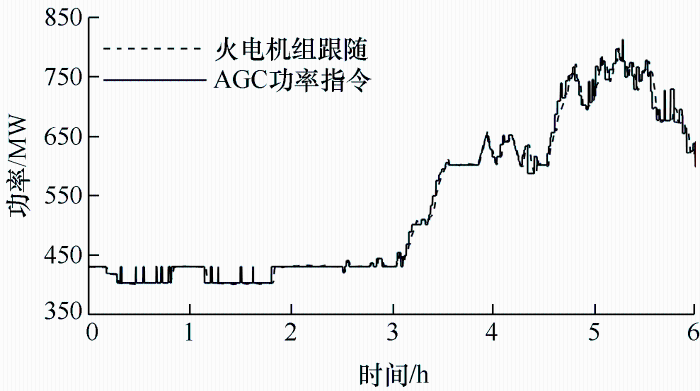
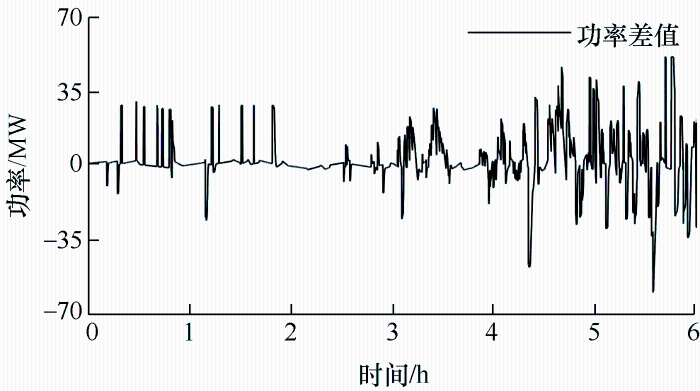
为了解决电力系统在运行中的频率调节和负荷分配问题，满足电能质量标准，自动发电控制(Automatic generation control, AGC)[1]作为主要解决手段成为并网发电厂有偿辅助服务之一，得到了广泛应用，有助于防止导致大范围停电或敏感设备损坏的频率偏差。电力调度交易机构依据用户端用电波动，向发电厂下发指令，通过考虑发电机组损耗、效率等因素，按特定优化调度指令发电以满足网侧频率与功率要求。但是由于火电机组本身惯性大、响应较慢，无法跟随快速变化的指令，进而影响发电厂收益，制约电网安全可靠运行。为此，寻找一种可靠的系统辅助火电机组跟随AGC指令成为了亟待解决的问题。

新型储能是建设新型电力系统、推动能源绿色低碳转型的重要设备基础和关键技术[2]，特别是功率型储能元件与能量型储能元件组成的混合储能系统，两者优势互补，有利于降低系统磨损、提高储能的经济效益[3]。闫群民等[4]提出一种混合储能功率均衡管理方法，以全寿命周期成本为目标，验证了所提方法的经济性。赵峰等[5]提出了一种利用变模态分解和自适应权重粒子群算法获得混合储能的容量配置，以系统年综合成本最小为目标，验证了所提方法的经济性。

功率型储能元件旨在短时间内提供高功率输出，包含飞轮、超级电容器和高功率密度电池等[6]；能量型储能系统旨在长时间存储大量能量，包含锂离子电池、液流电池和压缩空气储能等[7]。利用混合储能系统响应AGC指令信号的基本思想是将系统功率缺额按照频率进行分解，利用不同元件分别响应高、低频信号[8]。张梦田等[9]提出基于变模态分解的功率分配方法，将高频功率分配给超级电容器，由蓄电池补偿低频功率信号。宋杰等[10]提出一种基于EMD分解的混合储能辅助火电机组一次调频容量规划方法，将分解的高频信号分配给飞轮电池，将中低频分配给蓄电池。

除此之外，混合储能的成本是限制其大规模应用的主要因素，需要合理的容量配置以提高经济性。容量配置是一种多目标非线性的优化问题，智能优化算法在此类问题中得到了广泛应用[11]。王依妍 等[12]提出一种改进的麻雀搜索算法，对以经济性为目标建立的储能容量配置模型进行求解。李鑫等[13]提出一种变分模态分解的混合储能容量配置策略，以储能系统年均配置成本最小为目标进行混合储能系统容量优化配置。

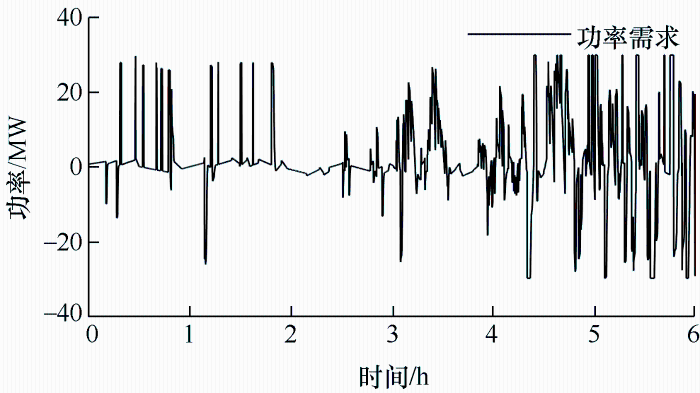
上述研究功率分配以一个频率界限或者直接将分解信号的一部分分配给一个储能元件，另一部分分配给其他储能元件，而将功率分配考虑进优化过程的研究较少。针对上述问题，本文提出以磷酸铁锂电池和飞轮储能组成的混合储能系统(Hybrid energy storage system, HESS)配合火电机组跟随AGC指令的功率分配与容量配置。CEEMDAN是一种具有较强抗模态混叠能力的信号处理方法，能够有效降低重构误差[14-15]。本文采用CEEMDAN将火电机组由于惯性而无法快速跟随AGC指令的差值分解成多个功率需求。根据磷酸铁锂电池[16]和飞轮储能系统[17-18]的响应特性，建立储能系统参与功率调节的成本函数，并以经济性最优为目标优化配置混合储能系统，从而获得功率分配及混合储能系统容量配置情况[19]。

2 混合储能辅助火电机组系统

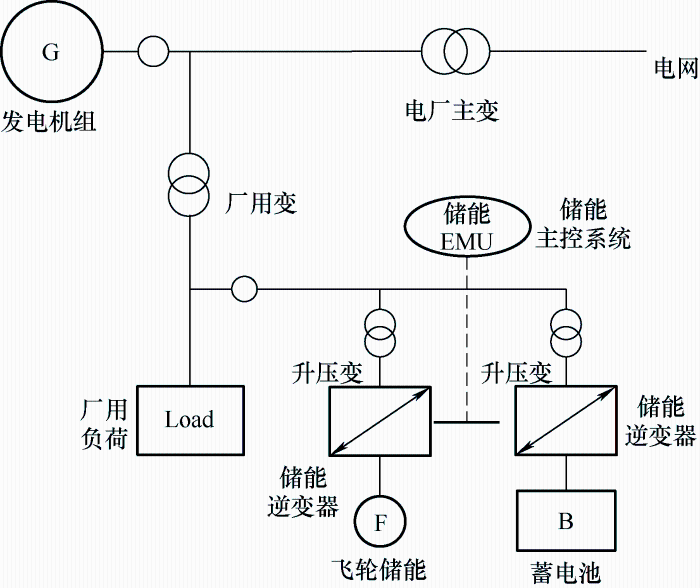
将蓄电池-飞轮储能系统混合储能系统加入辅助火电机组调节功率后，新型发电厂将包括发电机组和混合储能系统两部分。发电机组与混合储能系统的能量流通通过厂用变压器实现，信息交互通过混合储能系统的EMU实现，如图1所示。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   混合储能连接到电厂示意图


混合储能系统包含飞轮储能系统、蓄电池等。储能系统通过储能逆变器及变压器接入厂用电母线，在保证系统安全工作的情况下，进行功率补充。

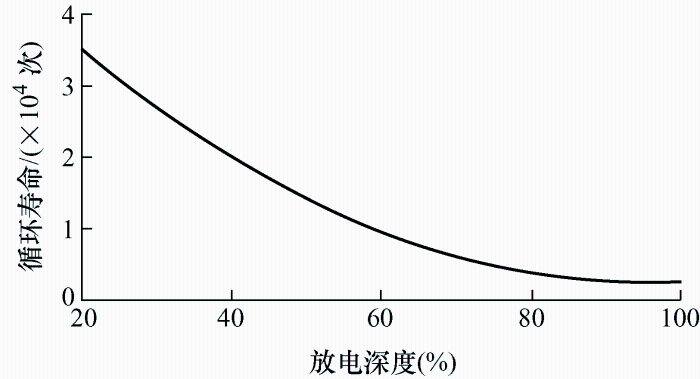
2.1 磷酸铁锂电池

磷酸铁锂电池作为一种储能装置，可以将化学能转化为电能，通过化学反应将化学物质转化为电荷，从而存储电能。其储能本质决定了在电池循环过程中会存在老化现象。锂电池的循环寿命受诸多因素影响，其中包括电池工作温度、放电倍率及放电深度等。储能系统中电池工作温度恒定、放电倍率限定为1C，因此影响储能电池循环寿命最主要因素考虑电池的放电深度。已知某型号磷酸铁锂电池在不同放电深度情况下的循环寿命，如表1所示[16]。

表1   某型号磷酸铁锂电池放电深度与循环寿命对应关系

放电深度(%)循环寿命/次
2034 957
4019 985
6010 019
803 221
1002 600

新窗口打开| 下载CSV


对表1中的数据进行曲线拟合，得到表征电池循环寿命与放电深度的对应关系，本文采用N阶函数法，具体表达式见式(1)，相应曲线如图2所示。将此函数嵌入成本函数，在优化迭代过程中进行电池更换次数的确定。

${{B}_{\mathrm{cyc}}}=56\ 910\cdot \mathrm{DO}{{\mathrm{D}}^{2}}-10\ 900\cdot \mathrm{DOD}+54\ 530$

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   循环寿命与放电深度的关系


2.2 飞轮储能系统

飞轮储能系统的基本原理是利用电能驱动电机高速旋转以完成电池充电，以动能的形式储存能量；在放电时，利用飞轮的惯性拖动电机发电，把存储的动能以电能的形式输出；在保持状态时，系统以最小损耗维持飞轮电机的运动状态，电池侧与电网侧没有能量流动。

飞轮储能系统依靠转子旋转储存能量，其储能量可以由式(2)表示

$E=1/2J{{\omega }^{2}}$

式中，E为飞轮储能系统储电量(J)；J为飞轮电机转子转动惯量(kg·m2)；ω为飞轮旋转角速度(rad/s)。

为研究飞轮储能系统的充放电控制策略以及功率分配策略，需要对飞轮储能系统的荷电状态进行检测。飞轮储能系统的荷电状态(State of charge, SOC)反映当前飞轮储能系统存储能量占放电容量的百分比，其计算方法如式(3)所示

$\mathrm{SOC}={{\omega }^{2}}/\omega _{\max }^{2}$

式中，ω为飞轮旋转角速度(rad/s)；ωmax为飞轮设定最高旋转角速度(rad/s)。

飞轮电池的运行功率由电磁转矩乘转速确定，无法在全荷电状态下保持满功率充放电，为保持充放电功率稳定，需要确定额定转矩时的最低转速限制。同时为了防止飞轮电池出现转速超限情况，充放电工作区最高转速应低于额定转速，因此飞轮电池的SOC工作区域如式(4)所示

$\mathrm{SOC} \in\left(\left(\omega_{\min }^{\prime} / \omega_{\max }\right)^{2},\left(\omega_{\max }^{\prime} / \omega_{\max }\right)^{2}\right)$

式中，$\omega_{\min }^{\prime}$为飞轮最低旋转角速度设定值(rad/s)；$\omega_{\max }^{\prime}$为飞轮最高旋转角速度设定值(rad/s)。

3 基于CEEMDAN的功率分解的混合储能容量配置

储能系统的成本一般包括初始购置成本和置换成本。初始购置成本包括储能选址、设备选购等，分为容量成本和功率成本。容量成本是指可存储能量设备(以千瓦时或兆瓦时为单位)的相关成本，代表实际储存介质(例如电池)及其相关基础设施的成本。功率成本是指与储能系统充放电速率(以千瓦或兆瓦为单位)相关的费用，代表了控制电力进出存储系统所需的电力电子设备、逆变器和其他设备成本。置换成本指当设备安全使用年限小于储能系统运行年限时而换新的成本。由于飞轮电池的寿命极长，在本文中认定为无限寿命，即在整个生命周期内无需更换。

3.1 磷酸铁锂电池与飞轮储能系统成本函数

在全寿命周期内磷酸铁锂电池投资成本的表达式为

${{C}_{\mathrm{BI}}}={{C}_{PB}}{{P}_{\mathrm{BO}}}+\sum\limits_{k=0}^{n}{{{C}_{\mathrm{CB}}}{{E}_{\mathrm{BO}}}{{(1+r)}^{-[\kappa {{T}_{\mathrm{LCC}}}/(n+1)]}}}$

式中，CPB为蓄电池的单位功率成本(元/kW)；PBO为优化后的蓄电池功率(kW)；CCB为蓄电池的单位容量成本(元/(kW·h))；EBO为优化后的蓄电池容量(kW·h)；r=6%，表示未来有限期预期收益折算成现值的比率；TLCC表示考虑到设备寿命历程所有环节而确定的时间，在本例中暂定20年；n为寿命无法达到20年设备的更换次数(共投入储能n+1次)，n=TLCC/Tlife，其中Tlife为储能等效循环寿命。电池放电深度选为60%，通过式(1)确定可用循环次数；基于雨滴流计法测量功率调节过程中电池循环次数，获得电池使用寿命。

蓄电池储能的运行成本包括运行修护成本、退役处理成本以及其他相关成本。其中，运行修护成本是为确保蓄电池储能高效可靠运行的费用，依据储能系统各设备运行年限增长而频率提高。由于磷酸铁锂电池内部金属元素可回收再次利用，其中的有害成分需要进行无害化处理，处理蓄电池储能设备所花费的资金为退役成本。储能系统运行周期内蓄电池运行修护成本的表达式如式(6)所示

$\begin{matrix} {{C}_{\mathrm{BOM}}}={{C}_{\mathrm{BPOM}}}{{P}_{\mathrm{BO}}}[{{(1+r)}^{({{T}_{\mathrm{LCC}}})}}-1]+ \\ \sum\limits_{t=1}^{{{T}_{\mathrm{LCC}}}}{{{C}_{\mathrm{EOM}}}W(t){{(1+r)}^{-t}}} \\ \end{matrix}$

式中，CBPOM为单位功率运维成本(元/kW)；CEOM为单位容量运维成本(元/kW)；W(t)为储能年充放电电量(元/(kW·h))。

全寿命周期蓄电池退役处理成本的表达式为

$\begin{matrix} {{C}_{\mathrm{BS}}}={{C}_{\mathrm{BPscr}}}{{P}_{\mathrm{BO}}}{{(1+r)}^{-{{T}_{\mathrm{LCC}}}}}+ \\ \sum\limits_{j=1}^{n+1}{{{C}_{\mathrm{BEscr}}}{{E}_{\mathrm{BO}}}{{(1+r)}^{-j{{T}_{\mathrm{LCC}}}(n+1)}}} \\ \end{matrix}$

式中，CBPscr为单位功率退役成本(元/kW)；CBEscr为单位容量退役成本(元/(kW·h))。

全寿命周期蓄电池退役处理成本的表达式为

${{C}_{\mathrm{Bat}}}={{C}_{\mathrm{BI}}}+{{C}_{\mathrm{BOM}}}+{{C}_{\mathrm{BS}}}$

在全寿命周期内飞轮储能系统投资成本的表达式为

${{C}_{\mathrm{FI}}}={{C}_{\mathrm{PF}}}{{P}_{\mathrm{FO}}}+{{C}_{\mathrm{CF}}}{{C}_{\mathrm{FO}}}$

式中，CPF为飞轮储能系统单位功率成本(元/kW)；PFO为优化后的飞轮储能系统功率(kW)；CCF为飞轮储能系统单位容量成本(元/(kW·h))；CFO为优化后的飞轮储能系统容量(kW·h)。

基于上文讨论，飞轮储能系统在全寿命周期内寿命无限长，无需更换，即无更换成本。由于飞轮储能系统的主要材料为金属，无需进行无害化处理，因此没有报废成本。

全寿命周期内飞轮储能系统运行维护成本的表达式为

${{C}_{\mathrm{FOM}}}={{C}_{\mathrm{FPOM}}}{{P}_{\mathrm{FO}}}[{{(1+r)}^{{{T}_{\mathrm{LCC}}}}}-1]$

式中，CFPOM为单位功率运维成本(元/kW)。

飞轮储能系统全寿命周期总成本表达式为

${{C}_{\mathrm{Flyw}}}={{C}_{\mathrm{FI}}}+{{C}_{\mathrm{FOM}}}$

3.2 约束条件

3.2.1 功率平衡约束

储能系统输出功率(磷酸铁锂电池与飞轮储能系统功率输出总和)等于发电机组无法满足指令功率的差值，如式(12)所示

$P_{t}^{B}+P_{t}^{\mathrm{F}}=P_{t}^{\mathrm{DP}}$

3.2.2 SOC约束

为保障储能系统运行在安全的范围之内，其蓄电池和飞轮储能系统SOC应控制在上下限，即

$\mathrm{SO}{{\mathrm{C}}_{t}}=\mathrm{SO}{{\mathrm{C}}_{t-1}}+\frac{1}{{{E}_{\mathrm{rat}}}}\int_{t-1}^{t}{({{P}_{t,\mathrm{cha}}}-{{P}_{t,\mathrm{dis}}})\mathrm{d}t}$
$\mathrm{SO}{{\mathrm{C}}_{t,\min }}\le \mathrm{SO}{{\mathrm{C}}_{t}}\le \mathrm{SO}{{\mathrm{C}}_{t,\max }}$

式中，Pt,cha表示t时刻的充电功率，Pt,dis表示t时刻的放电功率，在t时刻，至少有一值为0；SOCt,min和SOCt,max分别表示储能设备设定的SOC下限和SOC上限。

3.2.3 充放电功率和额定容量约束

为保障储能系统安全，发热量控制合理，蓄电池和飞轮储能系统充放电功率应控制在上下限，如式(15)、(16)所示，额定容量约束由式(17)表示。

$\left\{ \begin{matrix} P_{t,\max }^{\mathrm{cha}}=\min \left[ {{P}_{\mathrm{rat}}},\frac{(\mathrm{SO}{{\mathrm{C}}_{\max }}-\mathrm{SO}{{\mathrm{C}}_{t}}){{E}_{rat}}}{\Delta t} \right] \\ 0\le P_{t}^{\mathrm{cha}}\le P_{t,\max }^{\mathrm{cha}}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\\end{matrix} \right.$
$\left\{ \begin{matrix} P_{t,\max }^{\mathrm{dis}}=\max \left[ -{{P}_{\mathrm{rat}}},\frac{(\mathrm{SO}{{\mathrm{C}}_{\min }}-\mathrm{SO}{{\mathrm{C}}_{t}}){{E}_{rat}}}{\Delta t} \right] \\ P_{t,\max }^{\mathrm{dis}}\le P_{t}^{\mathrm{dis}}\le 0\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\\end{matrix} \right.$
${{E}_{\mathrm{rat}}}\ge \max \left[ \frac{\max \left( \sum\limits_{0}^{\kappa \Delta t}{P_{t}^{\mathrm{reg}}\Delta t} \right)}{\mathrm{SO}{{\mathrm{C}}_{\max }}-\mathrm{SO}{{\mathrm{C}}_{i}}},\frac{-\min \left( \sum\limits_{0}^{\kappa \Delta t}{P_{t}^{\mathrm{reg}}\Delta t} \right)}{\mathrm{SO}{{\mathrm{C}}_{i}}-\mathrm{SO}{{\mathrm{C}}_{\min }}} \right]$

3.3 基于CEEMDAN的配置优化

混合储能系统的容量配置问题由功率分配和配置优化两部分组成，为了建立以经济性最优为目标优化配置模型，本文采用基于CEEMDAN配置优化方案，相较于傅里叶变换、小波变换、EMD(经验模态分解)等，此方法在处理功率需求信号(非线性非平稳信号)更准确稳定。基于全寿命周期成本(Life cycle cost，LCC)理论，以飞轮电池和蓄电池的容量为优化对象，以全寿命周期经济性最优为优化目标，设置设备层与系统层约束条件对对象容量进行优化配置。储能系统的成本包括投资成本和运行成本。

在本文中，储能系统参与发电机组功率调节，在成本最低的目标下实现最优配置，可表示为

${{C}_{\mathrm{LCC}}}={{C}_{\mathrm{Bat}}}+{{C}_{\mathrm{Flyw}}}$

式中，CBat为蓄电池储能系统成本；CFlyw为飞轮储能系统储能系统成本。

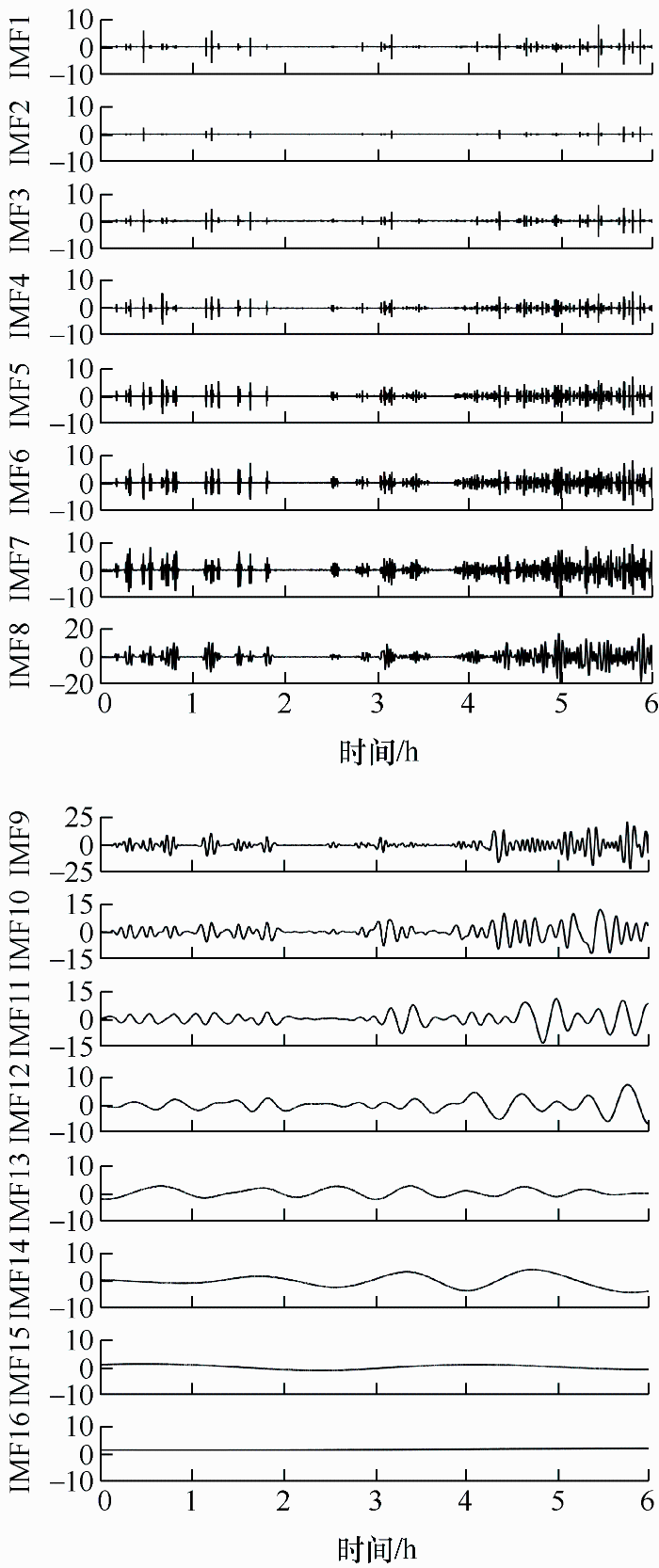
3.3.1 CEEMDAN功率分解

CEEMDAN(完全噪声辅助聚合经验模态分解)是在CEEMD(互补集合经验模态分解)的基础上进一步发展的一种基于自适应噪声控制的信号分解方法。与CEEMD不同，CEEMDAN在随机噪声的构建和添加中采用了自适应控制策略，以便更好地控制噪声的大小和分布，从而改善信号分解的准确性和稳定性。CEEMDAN算法的基本流程如下所示。

步骤1：将满足标准正态分布的高斯白噪声ωi[n]与其自适应系数εi-1所组成的噪声分量ε0ωi[n]加入原始信号x[n]，通过EMD实现x[n]+ ε0ωi[n]分解，以获得固有模态函数(Intrinsic mode functions, IMF) IMF1[n]。

$\mathrm{IM}{{\mathrm{F}}_{1}}[n]=\frac{1}{K}\sum\limits_{k=1}^{I}{\mathrm{IMF}_{1}^{k}[n]}$

式中，K为高斯白噪声序列；$IMF_{1}^{k}[n]$为第k次加入白噪声分解的第一个模态分量。

步骤2：计算CEEMDAN的第一个残差ri[n]。

${{r}_{i}}[n]=x[x]-\mathrm{IM}{{\mathrm{F}}_{1}}[n]$

步骤3：向第一个残差加入自适应白噪声ε1E1·(ωk[n])后，对ri[n]+ε1E1(ωk[n])再次进行EMD，计算第二个分量IMF2[n]。

$\mathrm{IM}{{\mathrm{F}}_{2}}[n]=\frac{1}{K}\sum\limits_{K=1}^{I}{{{E}_{1}}[{{r}_{1}}[n]}+{{\varepsilon }_{1}}{{E}_{1}}({{\omega }_{k}}[n])]$

式中，Ei(·)表示通过EMD将一个序列分解得到的IMFi分量。

步骤4：重复步骤2、3，直至残差无法再次进行EMD分解，求解得到残差和模态分量。

${{r}_{i}}[n]={{r}_{i-1}}[n]-\mathrm{IM}{{\mathrm{F}}_{i}}[n]$
$\mathrm{IM}{{\mathrm{F}}_{i+1}}[n]=\frac{1}{K}\sum\limits_{k=1}^{I}{{{E}_{1}}[{{r}_{i}}[n]}+{{\varepsilon }_{i}}{{E}_{i}}({{\omega }_{k}}[n])]$

步骤5：若无法进行Ei (·)时，则终止并得到残差R(n)。

$R(n)=x(n)-\sum\limits_{i=n}^{n}{\mathrm{IM}{{\mathrm{F}}_{i}}[n]}$

式中，n为IMF分量数量。

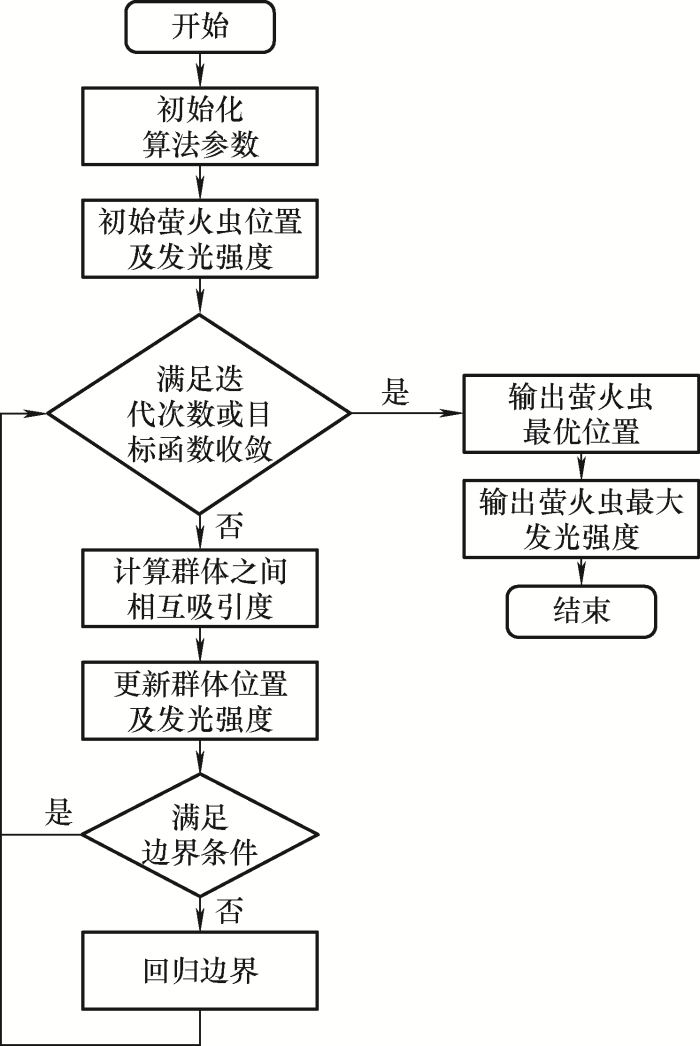
3.3.2 容量优化配置算法

本文采用改进的萤火虫算法求解目标函数，通过混沌序列初始化萤火虫位置，将搜索过程对应为混沌轨道的遍历过程，可以使搜索过程具有避免陷入局部最优解的能力，最终获得全局最优解或较为满意的解。在寻优的过程中，萤火虫的亮度和吸引度决定了萤火虫的移动方向和距离，其原理是将此过程转化为求解和优化目标函数的过程[20]。本案例属于强耦合性非线性优化问题，容易产生局部最优解，因此运用改进萤火虫算法求解储能系统容量配置问题，具体的步骤如图3所示。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   改进萤火虫算法流程图


3.3.3 基于不同模态分量分界点的容量配置过程

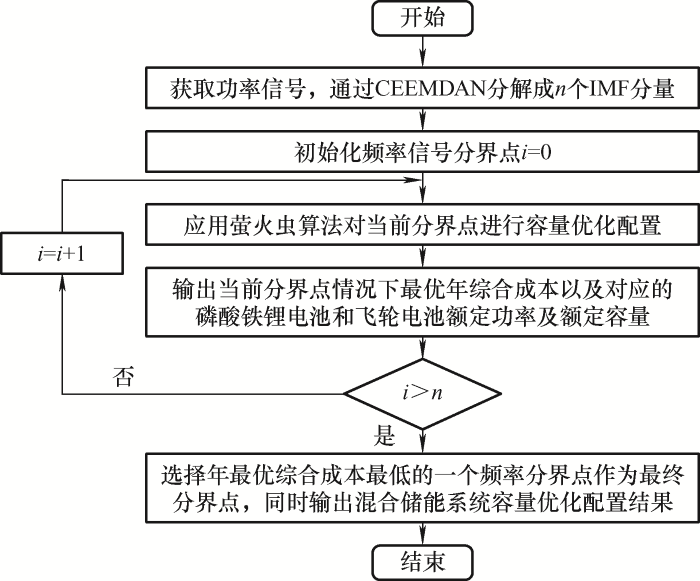
基于上述功率信号分解方案以及容量配置优化策略，为实现经济性最优目标，本文采用以各模态分量作为分界点，逐点进行容量配置优化的方法探寻系统整体经济性最优方案，该方案的流程图如图4所示。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   容量优化配置流程图


4 工程效果分析

以某地电网公司某时段AGC数据为基础，对储能系统进行容量优化配置以验证所提功率分配的先进性。采集获得的AGC数据共计6 h，应用数据处理软件对混合储能系统功率和容量进行优化配置。如图5所示为采样时间间隔为1 s的AGC指令及火力发电机跟随情况，需要储能系统弥补的功率如图6所示。通过分析数据，功率差值绝对值小于30 MW的指令占比超过95%，因此在本文中将AGC指令的范围控制在[-30 MW，30 MW]，其具体结果如图7所示。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5   火电机组跟踪AGC指令情况


图6

新窗口打开| 下载原图ZIP| 生成PPT

图6   储能系统需弥补功率情况


图7

新窗口打开| 下载原图ZIP| 生成PPT

图7   处理后储能系统需弥补功率情况


用CEEMDAN将AGC指令分解不同频率的IMF分量，如图8所示。从图8可以看出，调频AGC指令被分解成16阶固有模态函数，其频率依次降低，高频IMF分量的幅值也相对低频IMF分量更大。通过选择合适的分界点K将IMF分量划分给蓄电池和飞轮储能系统，可以充分调用两者调频特性的同时，保证储能系统的成本最低。以图6中进行处理的差值作为容量优化配置即模型求解的输入量，采用本文提出的基于CEEMDAN的配置优化方案，以各模态分量作为分界点进行容量优化配置。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8   CEEMDAN分解结果


求解混合储能系统优化配置模型，需要根据储能系统选取合适的参数，本文中蓄电池和飞轮储能系统相关参数如表2所示。其中蓄电池的功率成本与容量成本由储能配置中功率与容量之比确定，本文中蓄电池储能配置功率比容量为1；而飞轮储能系统功率成本与容量成本与配置功率、容量之比无关，功率与容量配置可根据最终优化结果定制。

表2   储能系统相关参数

对象性能指标数值
蓄电池单位功率成本/(元/kW)5 000
单位容量成本/[元/(kW·h)]2 000
运维成本/[元/(kW·h)]5×10-3
处置成本/(元/kW)1
处置成本/[元/(kW·h)]1
SOC上下限(0.2, 0.8)
飞轮储能系统单位功率成本/(元/kW)2 000
单位容量成本/[元/(kW·h)]10 000
运维成本/[元/(kW·h)]7.5×10-3
SOC上下限(0.50, 0.95)

新窗口打开| 下载CSV


图9、图10所示为将不同模态分量作为频率分界点时所对应的功率分配情况，可以看出蓄电池的配置功率与对应容量随分界点变化而减小，而飞轮储能系统配置的功率与容量随分界点变化而增大。当分界点过小时，飞轮储能系统承担功率较高致使其容量过大而导致容量成本过高；当分界点过大时，蓄电池承担高频分量功率较大，荷电状态变化幅度增大，电池充放电深度增加，严重影响其运行寿命，导致置换成本增加。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9   功率-分界点关系图


图10

新窗口打开| 下载原图ZIP| 生成PPT

图10   容量-模态分量关系图


不同分界点对应不同成本的关系如图11所示，当分界点小于12时，系统成本呈现减小趋势，当分界点大于12时，系统成本又呈现上升趋势。综合图11，当分界点为12时，储能系统的成本最低为2.19×108元。因此，通过将分界点与储能系统成本联合优化对功率分配及系统成本的经济性具有重要的现实意义。

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11   储能系统综合成本-模态分量关系图


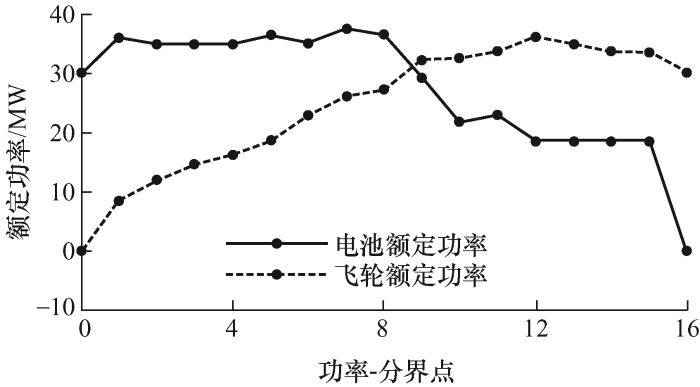
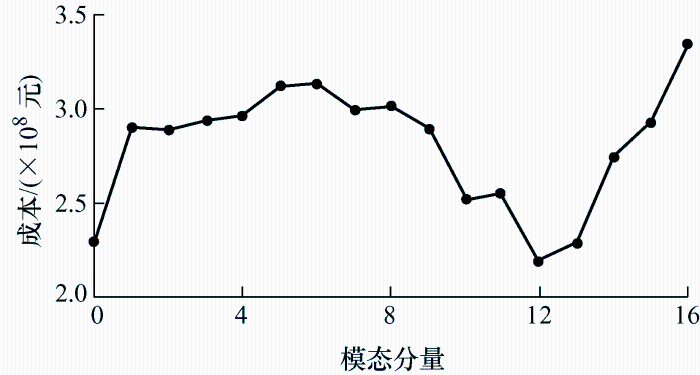
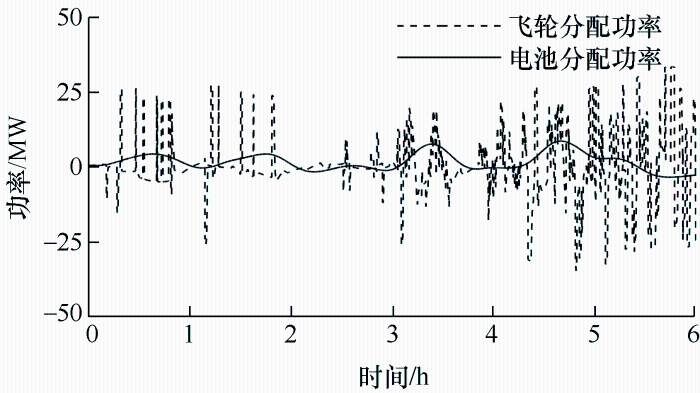
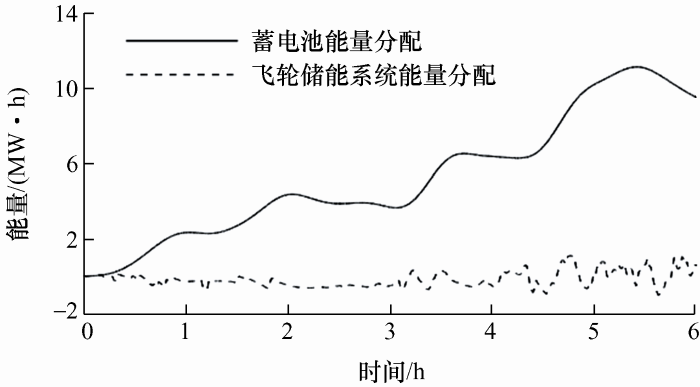
当分界点K为12时为最优频率分界点确定储能系统的参考功率，同时经过优化算法实现在该功率分配情况下储能系统经济成本配置最优方案。蓄电池作为能量型储能元件，其能量密度高、储能容量大，可承担低频功率；飞轮储能系统作为功率型储能元件，具有频繁和快速充放电的特性，可承担高频功率，因此将IMF1~IMF12高频功率分配给飞轮储能系统，将剩余的IMF分量分配给蓄电池。其功率分配结果如图12所示，对比两条曲线可以看出，飞轮储能系统通过快速跟踪响应使得高频功率迅速变化，而蓄电池的功率变换缓慢且充放电次数少。

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12   蓄电池和飞轮储能系统功率曲线


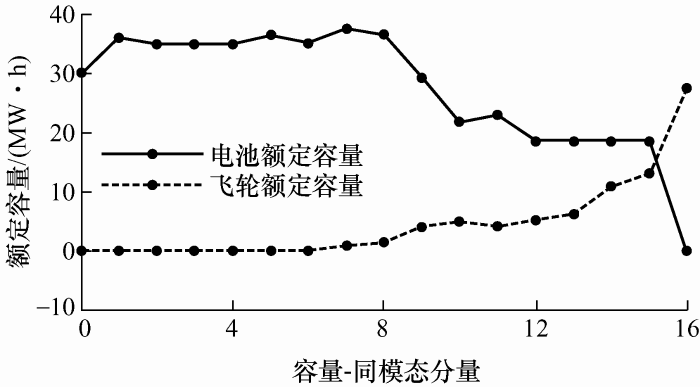
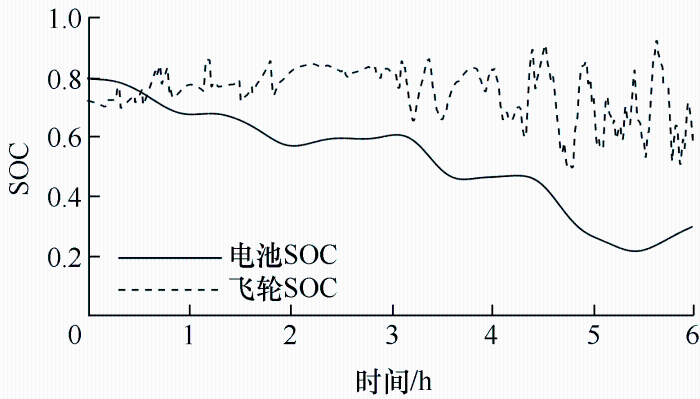
图13展示了分配功率后储能系统容量变化情况。通过CEEMDAN将功率信号分解，并通过优化配置方法确定分界点K，可有效延长储能系统的使用寿命，特别是蓄电池的使用年限。

图13

新窗口打开| 下载原图ZIP| 生成PPT

图13   蓄电池和飞轮储能系统能量曲线


最后，通过建立简化模型对容量配置结果进行验证，储能系统SOC状态变化如图14所示。由图14可知，储能系统在满足功率调节的同时，SOC工作在正常范围内，验证了容量配置的准确性。

图14

新窗口打开| 下载原图ZIP| 生成PPT

图14   储能系统SOC状态变化


为验证混合储能优于单独的储能系统，根据磷酸铁锂电池、飞轮储能系统储能特性，选取3种配置方案，分别为仅飞轮储能系统储能；蓄电池与飞轮储能系统混合储能；仅蓄电池储能，其不同配置方案下的储能容量优化配置结果如表3所示。在仅飞轮储能系统储能配置方案下，功率为30 MW，容量为27.40 MW·h，成本为0.334亿元；在蓄电池与飞轮储能系统混合储能配置方案下，蓄电池配置功率为18.57 MW、容量为18.57 MW·h，飞轮储能系统配置功率为36.03 MW、容量为4.94 MW·h，成本为0.219亿元；在仅蓄电池储能配置方案下，功率为30 MW，容量为30 MW·h，成本为0.229亿元。

表3   储能优化配置结果

参数蓄电池飞轮储能
系统		CEEMDAN
PbN/MW30—18.57
CbN/(MW·h)30—18.57
PfN/MW—3036.03
CfN/(MW·h)—27.404.94
成本/
(×108 元)		2.293.342.19

新窗口打开| 下载CSV


从经济性上看，通过CEEMDAN方法为混合储能系统进行功率分配可以降低系统的总成本。相对单一的蓄电池、飞轮储能系统总成本分别下降4.34%、34.43%。同时除经济条件外，混合储能系统相较纯蓄电池储能系统拥有较高的安全性及环保性，能减少蓄电池储能系统带来的运行环境管理、废料处理等问题的影响，综合考虑其配置结果与经济性，故选取混合储能方法作为弥补火电机组跟随AGC指令延迟功率的有效方案。

5 结论

由于火电机组惯性大、延迟大等特性，对AGC指令响应延迟，混合储能系统作为一种辅助手段，可以提高火电机组对AGC指令的响应。为了解决混合储能优化配置问题，本文提出一种基于CEEMDAN的火电厂混合储能系统容量配置方法。通过算例分析，得到以下结论。

(1) 为了解决混合储能系统的响应性能与最优经济成本问题，基于CEEMDAN分解需求功率，可以实现蓄电池与飞轮储能系统的优势互补。

(2) 基于改进萤火虫算法，在避免人为因素影响的同时结合寻优算法，可以实现功率分配与成本经济性的双层优化，在保证响应性能的基础上降低了混合储能系统的经济成本。

参考文献

陈沛, 张新松, 郭晓丽, 等.

考虑AGC指令随机特性的火-储混合电站二次调频研究

[J]. 电力系统保护与控制, 2023, 51(12):168-177.

[本文引用: 1]

CHEN Pei, ZHANG Xinsong, GUO Xiaoli, et al.

Research on secondary frequency modulation of thermal-storage hybrid power stations considering the random characteristics of AGC commands

[J]. Power System Protection and Control, 2023, 51(12):168-177.

[本文引用: 1]

王灿, 张羽, 田福银, 等.

基于双向主从博弈的储能电站与综合能源系统经济运行策略

[J]. 电工技术学报, 2023, 38(13):3436-3446,3472.

[本文引用: 1]

WANG Can, ZHANG Yu, TIAN Fuyin, et al.

Economic operation of energy storage power stations and integrated energy systems based on bidirectional master-slave game

[J]. Transactions of China Electrotechnical Society, 2023, 38(13):3436-3446,3472.

[本文引用: 1]

李斌, 叶季蕾, 张宇, 等.

含分布式新能源和机电混合储能接入的微网协调控制策略

[J]. 储能科学与技术, 2023, 12(5):1510-1515.

DOI:10.19799/j.cnki.2095-4239.2023.0075      [本文引用: 1]

含分布式光伏等新能源接入的微网作为大电网的补充目前应用日趋广泛，但是随着新能源在微网系统中的占比比例不断增加，其出力的波动直接影响到微电网系统整体的稳定性。飞轮储能属于功率型储能系统，能够适应短时高频次充放电，相比于超级电容系统其环境适应性更好且全寿命周期内无污染。飞轮与电池储能系统相结合能够平滑分布式新能源出力波动，提升微网系统稳定性，但是飞轮储能和电池储能运行特性差别较大，控制难度较高，目前在微网系统内应用较少。本文设计了一种含分布式光伏、电池/飞轮机电混合储能系统接入的交直流混合微网运行拓扑，并在此基础上提出了基于电池/飞轮机电混合储能系统的微网系统协调控制策略，根据飞轮和电池剩余容量的不同，将混合储能系统划分为不同状态，以此为依据同时考虑不同类型储能系统输出额定功率和分布式新能源功率波动大小，对飞轮和电池的充放电电流进行调节，从而减小由于新能源接入引起的微网内功率波动。本文基于MATLAB/Simulink环境搭建了基于交直流混合母线的微网系统，仿真结果验证了所提微网协调控制策略的有效性。

LI Bin, YE Jilei, ZHANG Yu, et al.

Coordinated control strategy for microgrid with access to distributed new energy and electromechanical hybrid energy storage

[J]. Energy Storage Science and Technology, 2023, 12(5):1510-1515.

DOI:10.19799/j.cnki.2095-4239.2023.0075      [本文引用: 1]

Microgrid systems with distributed photovoltaic and other new energy sources are becoming widely used to supplement large power grids. However, with the increasing proportion of new energy in microgrid systems, the fluctuation in their output directly affects the overall stability of the microgrid systems. Flywheel is a powerful energy storage system that can adapt to short-term high-frequency charging and discharging and has better environmental adaptability and lesser pollution throughout the life cycle than the supercapacitor system. The combination of the flywheel and battery energy storage systems can smooth the fluctuations in the distributed new energy output and improve the stability of the microgrid system. However, the operating characteristics of flywheel and battery energy storage are quite different, and the control is difficult; thus, it is currently less used in microgrid systems. Herein, an AC and DC hybrid microgrid operation topology with distributed photovoltaic and battery-flywheel electromechanical hybrid energy storage system access is designed. Based on this, a coordinated control strategy of a microgrid system based on battery-flywheel electromechanical hybrid energy storage system is proposed. The control strategy divides the hybrid energy storage system into different states according to the remaining capacity of the flywheel and battery. It takes the output-rated power of different energy storage systems and the fluctuations in distributed new energy power simultaneously and adjusts the charging and discharging currents of the flywheel and battery to reduce the power fluctuations in the microgrid caused by new energy access. Herein, a microgrid system is built based on MATLAB/Simulink, and the simulation results verify the effectiveness of the proposed microgrid-coordinated control strategy.

闫群民, 刘语忱, 董新洲, 等.

基于CEEMDAN-HT的平抑光伏出力混合储能容量优化配置

[J]. 电力系统保护与控制, 2022, 50(21):43-53.

[本文引用: 1]

YAN Qunmin, LIU Yuchen, DONG Xinzhou, et al.

Optimal allocation of hybrid energy storage capacity for stabilizing photovoltaic output based on CEEMDAN-HT

[J]. Power System Protection and Control, 2022, 50(21):43-53.

[本文引用: 1]

赵峰, 张帆, 陈小强, 等.

基于VMD-APSO的风电场混合储能系统容量优化配置

[J]. 高压电器, 2023, 59(6):120-127.

[本文引用: 1]

ZHAO Feng, ZHANG Fan, CHEN Xiaoqiang, et al.

Capacity optimization configuration of wind farm hybrid energy storage system based on VMD-APSO

[J]. High Voltage Apparatus, 2023, 59(6):120-127.

[本文引用: 1]

MOUSAVIG S M, FARAIIF, MAJAZI A, et al.

A comprehensive review of flywheel energy storage system technology

[J]. Renewable and Sustainable Energy Reviews, 2017,67:477-490.

[本文引用: 1]

SHARMA P, KUMAR V.

Current technology of supercapacitors:A review

[J]. Journal of Electronic Materials, 2020, 49(6):3520-3532.

DOI:10.1007/s11664-020-07992-4      [本文引用: 1]

张宇涵, 杜贵平, 雷雁雄, 等.

直流微网混合储能系统控制策略现状及展望

[J]. 电力系统保护与控制, 2021, 49(3):177-187.

[本文引用: 1]

ZHANG Yuhan, DU Guiping, LEl Yanxiong, et al.

Current status and prospects of control strategy for a DC micro grid hybrid energy storage system

[J]. Power System Protection and Control, 202l, 49(3):177-187.

[本文引用: 1]

张梦田, 田书, 曾志辉.

基于变分模态分解的混合储能容量优化配置

[J]. 储能科学与技术, 2020, 9(1):170-177.

DOI:10.19799/j.cnki.2095-4239.2019.0170      [本文引用: 1]

受光照强度、温度等影响，光伏发电具有随机性和间歇性，使光伏输出功率具有较大波动，影响电网的安全运行。针对光伏发电功率波动率较大这一情况，以蓄电池和超级电容器组成的混合储能系统为研究对象对光伏功率波动进行平抑，提出基于变分模态分解的功率分配方法，结合光伏功率波动率和储能响应特性，将光伏功率划分为符合国家标准的并网功率和高、低补偿功率，高、低补偿功率分别由超级电容器和蓄电池补偿，建立以混合储能系统年综合成本最小为目标函数的容量优化配置模型，考虑功率平衡、充放电功率限制及荷电状态等约束条件，采用对适应度值进行高斯加权的改进粒子群算法求解，得到满足系统补偿要求的储能设备的容量配置，实现混合储能系统的年综合成本最小化。通过算例，对比分析变分模态分解和经验模态分解两种分配方法的混合储能容量配置和成本，同时对比分析基于变分模态分解的混合储能和单一储能的容量配置结果和成本，结果表明所提方法平抑了光伏功率波动，降低了储能的容量和年综合成本，提高了系统的可靠性和经济性。

ZHANG Mengtian, TIAN Shu, ZENG Zhihui.

Optimal configuration of hybrid energy storage capacity based on variational mode decomposition

[J]. Energy Storage Science and Technology, 2020, 9(1):170-177.

DOI:10.19799/j.cnki.2095-4239.2019.0170      [本文引用: 1]

The variations in light intensity and temperature induce the photovoltaic power generation to become random and intermittent, causing the photovoltaic output power to fluctuate considerably and affecting the safe operation of the power grid. Thus, a hybrid energy storage system comprising a storage battery and supercapacitor is investigated to reduce photovoltaic power fluctuation. This study proposes a power allocation method for variational mode decomposition. Combined with the photovoltaic power volatility and energy storage response characteristics, the photovoltaic power is classified as grid-connected power, which satisfies the national standard, and high and low compensation power; supercapacitors and batteries are used to provide high and low compensation power. A capacity optimization configuration model is established by considering the minimum annual comprehensive cost of the hybrid energy storage system as the objective function. Considering constraints, including the power balance, charge and discharge power limitation, and state of charge, an improved particle swarm optimization algorithm based on the Gaussian weighting of fitness values is used. The capacity configuration of energy storage equipment that meets the system compensation requirements is obtained, and the annual comprehensive cost of the hybrid energy storage system is minimized. Using this example, the mixed storage capacity allocations and costs of variational and empirical mode decomposition are compared and analyzed, and the capacity allocation results of mixed and single energy storage based on variational mode decomposition are compared and analyzed. The proposed method can suppress photovoltaic power fluctuation, reduce the energy storage capacity and annual comprehensive cost, and improve the system reliability and economy.

宋杰, 耿林霄, 桑永福, 等.

基于EMD分解的混合储能辅助火电机组一次调频容量规划

[J]. 储能科学与技术, 2023, 12(2):2095-4239.

[本文引用: 1]

SONG Jie, GENG Linxiao, SANG Yongfu, et al.

Primary frequency regulation capacity planning of hybrid energy storage auxiliary thermal power units based on EMD decomposition

[J]. Energy Storage Science and Technology, 2023, 12(2):2095-4239.

[本文引用: 1]

CUI Y, GENG Z, ZHU Q, et al.

Multi-objective optimization methods and application in energy saving

[J]. Energy, 2017,125:681-704.

[本文引用: 1]

王依妍, 陈景文.

基于ISSA的光储微网混合储能容量优化配置

[J]. 智慧电力, 2023, 51(4):23-29,53.

[本文引用: 1]

WANG Yiyan, CHEN Jingwen.

Optimal configuration of hybrid energy storage capacity based on ISSA

[J]. Smart Power, 2023, 51(4):23-29,53.

[本文引用: 1]

李鑫, 王娟, 邱亚, 等.

基于VMD的混合储能容量优化配置

[J]. 太阳能学报, 2022, 43(2):88-96.

DOI:10.19912/j.0254-0096.tynxb.2020-0276      [本文引用: 1]

针对光伏发电输出功率的波动性以及混合储能容量优化,以光储联合的发电系统为研究对象,提出一种基于变分模态分解（VMD）的混合储能容量优化配置策略。该策略采用VMD对光伏输出功率进行处理,利用欧氏距离方法将相关模态和非相关模态进行区分,利用滑动平均法提取非相关模态中的持续分量信号,将其与相关模态进行重构作为满足国家标准的并网功率,并利用混合储能系统平抑非相关模态中的波动分量信号。建立以储能系统年均配置成本最小为目标函数的混合储能系统容量优化模型,采用改进的布谷鸟算法求解模型,得到满足系统要求的储能容量配置方案。在Matlab/Simulink上进行仿真和分析,验证所提策略的有效性与经济性。

LI Xin, WANG Juan, QIU Ya, et al.

Hybrid energy storage capacity optimization configuration based on VMD

[J]. Solar Energy Sinica, 2022, 43(2):88-96.

[本文引用: 1]

TORRES M E, COLOMINAS M A, SCHLOTTHAUER G, et al.

A complete ensemble empirical mode decomposition with adaptive noise

[C]// IEEE International Conference on Acoustics,Speech and Signal Processing (ICASSP), May 22-27,2011,Prague Congress Centre,Czechia Republic,IEEE,2011:4144-4147.

[本文引用: 1]

LI Ke, HUANG Wei, HU Gaoyuan, et al.

Ultra-short term power load forecasting based on CEEMDAN-SE and LSTM neural network

[J]. Energy and Buildings, 2023,279:112666.

[本文引用: 1]

OMAR N, MONEM M A, FIROUZ Y, et al.

Lithium iron phosphate-based battery:Assessment of the aging parameters and development of cycle life model

[J]. Applied Energy, 2014,113:1575-1585.

[本文引用: 2]

李忠瑞, 聂子玲, 艾胜, 等.

一种基于非线性扰动观测器的飞轮储能系统优化充电控制策略

[J]. 电工技术学报, 2023, 38(6):1506-1518.

[本文引用: 1]

LI Zhongrui, NIE Ziling, AI Sheng, et al.

An optimized charging control strategy for flywheel energy storage system based on nonlinear disturbance observe

[J]. Transactions of China Electrotechnical Society, 2023, 38(6):1506-1518.

[本文引用: 1]

涂伟超, 李文艳, 张强, 等.

飞轮储能在电力系统的工程应用

[J]. 储能科学与技术, 2020, 9(3):869-877.

DOI:10.19799/j.cnki.2095-4239.2019.0255      [本文引用: 1]

2018年底的统计数据表明，新能源发电装机首超水电，跃居我国第二大发电形式，但新能源本身固有的随机性和波动性对电网的稳定带来了挑战，并且新能源机组对电网调峰、调频的贡献可以忽略不计。建设一定规模以飞轮储能为代表的电网级灵活调节资源是应对这一挑战的途径之一，飞轮储能的工程价值则通过调频辅助服务市场等典型应用场景得以体现。本文通过对近年来飞轮储能工程项目进展情况的跟踪，介绍了飞轮储能技术的主要子系统及各大公司和研究机构的技术路线，归纳出飞轮储能在电力系统的工程应用主要包括电网调频、新能源消纳和微电网支撑等，应用于新能源消纳时飞轮储能有平滑出力和无功补偿等多种工作模式，可以弥补新能源发电的不确定性。但与功率型电池储能技术相比，制约飞轮储能技术大规模应用的瓶颈在于初始投资成本过高，电网级飞轮储能技术的发展方向应为更高的性价比，这样才能获得应有的市场份额。

TU Weichao, LI Wenyan, ZHANG Qiang, et al.

Engineering application of flywheel energy storage in power systems

[J]. Energy Storage Science and Technology, 2020, 9(3):869-877.

DOI:10.19799/j.cnki.2095-4239.2019.0255      [本文引用: 1]

The statistical data at the end of 2018 shows that the new energy power generation is the second largest power generation form in China, but the inherent randomness and volatility of the new energy itself have brought challenges to the stability of the power grid, and the contribution of the new energy units to the peak load regulation and frequency modulation of the power grid can be ignored. One of the ways to deal with this challenge is to build a certain scale of grid level flexible regulation resources represented by flywheel energy storage. The engineering value of flywheel energy storage is reflected by typical application scenarios such as frequency modulation auxiliary service market. By tracking the progress of flywheel energy storage project in recent years, this paper introduces the main subsystem of flywheel energy storage technology and the technical route of major companies and research institutions, and concludes that the engineering application of flywheel energy storage in power system mainly includes grid frequency modulation, renewable energy consumption and micro grid support. When applied to grid frequency modulation, flywheel changes its output according to the area control error of the grid. When applied to renewable energy consumption, flywheel facility has different control modes. In the power output smoothing control mode, the flywheel energy storage facility shall smooth the varying real power output from renewable energy on a continuous basis. By comparing the instantaneous real power output of renewable energy to the average real power output of renewable energy obtained over a field adjustable time period, the flywheel will adjust its power demands to ensure that the average real power output of renewable energy is equal to the sum of the instantaneous real power output of the flywheel and renewable energy. In the dynamic reactive power support control mode, the flywheel energy storage facility shall inject appropriate amount of reactive power at the grid so that the grid reactive power flow nullifies the grid voltage change as a result of average real power injection by renewable energy. The flywheel provide dynamic power support by operating the facility in variable power factor control mode. Reactive power absorption is a continuous function of two variables, one is grid voltage level and another is total real power output from renewable energy and the flywheel. The installation of flywheel energy storage device can make up for the uncertainty of renewable energy generation. However, compared with the power battery energy storage technology, the bottleneck restricting the large-scale application of flywheel energy storage technology lies in the high initial investment cost, and the development direction of grid level flywheel energy storage technology should be higher cost performance, so as to obtain the market share.

郭怿, 明波, 黄强, 等.

考虑输电功率平稳性的水-风-光-储多能互补日前鲁棒优化调度

[J]. 电工技术学报, 2023, 38(9):2350-2363.

[本文引用: 1]

GUO Yi, MING Bo, HUANG Qiang, et al.

Day-ahead robust optimal scheduling of hydro-wind-PV-storage complementary system considering the steadiness of power delivery

[J]. Transactions of China Electrotechnical Society, 2023, 38(9):2350-2363.

[本文引用: 1]

陈海东, 庄平, 夏建矿, 等.

基于改进萤火虫算法的分布式电源优化配置

[J]. 电力系统保护与控制, 2016, 44(1):149-154.

[本文引用: 1]

CHEN Haidong, ZHUANG Ping, XIA Jiankuang, et al.

Optimal configuration of distributed power based on improved firefly algorithm

[J]. Power System Protection and Control, 2016, 44(1):149-154.

[本文引用: 1]

/

〈 〉