1 引言
近年来,随着新能源技术快速发展,锂离子电池凭借其高能量密度、宽工作温度、无污染和长寿命等优势受到广泛关注[1 ] 。然而,锂离子电池内部存在不可逆的化学反应,在使用和储存过程中不可避免地会出现容量损失。循环寿命被定义为电池可用容量下降到初始值的一定百分比(通常以80%为阈值)时的充放电循环次数。当电池达到该失效阈值时,需要及时更换,以保证系统安全稳定运行。准确预测电池剩余使用寿命(Remaining useful life, RUL),对充分发挥电池性能,确保电池系统安全高效运行具有重要意义[2 ] 。
目前,电池RUL预测方法主要分为两大类:基于模型的方法和数据驱动的方法。基于模型的方法[3 -4 ] 主要通过搭建合适的电池模型模拟其电化学行为,捕获电池老化规律并预测RUL。文献[5 ]引入了一种基于电化学模型的粒子滤波(Particle filtering, PF)框架,把反映电池退化的模型参数看成状态变量,来预测电池RUL。文献[6 ]提出了一种改进粒子学习框架(Particle learning, PL)以预测RUL,通过新收集测量信息对状态粒子重采样,并传播到当前时刻生成状态后验粒子,有效防止了粒子退化。文献[7 ]建立了通用状态空间模型,并基于期望值最大化(Expectation maximization, EM)和扩展卡尔曼滤波(Extended Kalman filtering, EKF)算法对模型进行参数辨识与更新,从而可以准确描述电池的老化过程。然而,由于电池内部化学反应复杂,通常难以收集全面的内部参数,建立准确的老化模型。同时,电池状态易受到工作温度、放电深度、电流等外部因素的影响,使得该方法难以适应复杂的运行环境,可靠性低[8 ] 。近年来,数据驱动的方法被广泛应用于电池RUL预测。与基于模型的方法不同,数据驱动的方法不需要考虑电池内部复杂的工作原理,仅依赖于历史数据来描述电池老化过程。文献[9 ]利用支持向量机(Support vector machine, SVM)学习多个与电池容量衰减相关的特征数据,实现电池健康状态(State of health, SOH)和RUL的预测。文献[10 ]采用长短期记忆网络(Long short-term memory, LSTM)和递归神经网络(Recurrent neural network, RNN)学习电池老化信息,结合蒙特卡罗模拟实现RUL预测,预测精度与计算效率较高,可靠性强。但该方法需要大量训练数据和较高的硬件需求。近年来随着大数据与硬件设备的高速发展,数据驱动的方法成为当前电池寿命预测的热门研究方向。
事实上,锂离子电池是“电-热-力”多物理场耦合系统[11 ] ,容量衰减与性能退化是由于电池内部多种退化机理相互作用的结果。在充放电过程中,锂离子在正负极之间不断迁移,引起电池内部应力以及外部厚度发生变化[12 ] 。同时,电池老化过程中会出现不可逆的力学形变,致使电池性能下降,安全隐患增大。因此,在预测电池寿命时应充分考虑电池力学性能的变化。目前,已有学者针对电池应力及形变特性展开研究。文献[13 ]发现电池使用过程中的应力与SOH、SOC均具有一定相关性,并建立了应力-SOH/SOC模型。文献[14 ]研究了18650电池不同SOC在弯曲和压缩作用下的力学行为,指导单体电池和电池组的设计与监控。文献[15 ]通过测量电池循环过程中膨胀的变化,证明了膨胀是评估电池状态强有力的特征参数。
综上,现有RUL预测方法未充分考虑电池力学特征,未分析电池应力及形变特性与RUL之间的关系,导致RUL预测精度差、效率低。为此,本文提出一种考虑膨胀应力的锂离子电池RUL预测方法,以实现电池RUL精准高效预测。深入分析电池可逆膨胀和不可逆膨胀与容量之间的关系,并计算其相关性。将可逆膨胀和不可逆膨胀作为特征参数,构建并训练LSTM网络,获取RUL预测值。UMBL公开数据集上的验证结果表明,本文所提方法能够准确高效地预测电池寿命,鲁棒性强。
2 LSTM网络
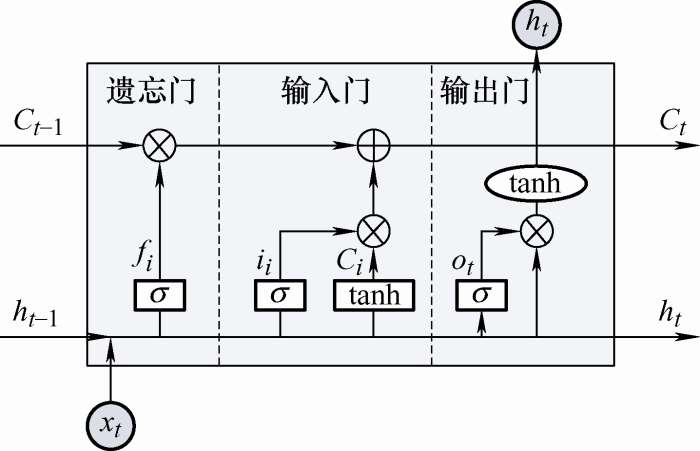
传统递归神经网络(RNN)[16 ] 广泛应用于处理时间、语音、文本等序列问题,然而,RNNs通常由于梯度消失与梯度爆炸的问题,使得其难以学习和保持长期依赖。为改进这些问题,LSTM神经网络[17 ] 被提出,其基本神经元如图1 所示。
图1
(1) ${{f}_{t}}=\sigma \left( {{W}_{f}}\left[ {{h}_{t-1}},{{x}_{t}} \right]+{{b}_{f}} \right)$
(2) ${{i}_{t}}=\sigma \left( {{W}_{i}}\left[ {{h}_{t-1}},{{x}_{t}} \right]+{{b}_{i}} \right)$
(3) ${{\tilde{C}}_{t}}=\tanh \left( {{W}_{c}}\left[ {{h}_{t-1}},{{x}_{t}} \right]+{{b}_{c}} \right)$
(4) ${{C}_{t}}={{f}_{t}}{{C}_{t-1}}+{{i}_{t}}{{\tilde{C}}_{t}}$
(5) ${{o}_{t}}=\sigma \left( {{W}_{o}}\left[ {{h}_{t-1}},{{x}_{t}} \right]+{{b}_{o}} \right)$
(6) ${{h}_{t}}={{o}_{t}}\tanh \left( {{C}_{t}} \right)$
式中,xt 为t 时刻的输入数据,ht -1 为t -1时刻的隐藏数据,Ct -1 为t -1时刻的网络状态;W f 、W i 、W c 、W o b f 、b i 、b c b o σ 为激活函数,本文激活函数选用sigmoid函数,其函数值范围为(0, 1),可以用于保留有用信息;tanh()为双曲正切函数。LSTM通过引入遗忘门、输入门与输出门,使得其在训练过程中可以更新单元状态和存储记忆信息,优化了传统的递归网络模型,提高了节点参数计算效率,在保持长期依赖上表现突出。
3 膨胀特征相关性分析
3.1 数据集介绍
本文电池数据选用UofM Pouch Cell Voltage and Expansion Cyclic Aging公开数据集[15 ] ,该数据集首次记录了电池机械特性的演变,涵盖了多种老化条件,记录了电池使用过程中电压、电流、温度、容量、电池膨胀等多组数据。电池由密歇根大学电池实验室(UMBL)制造,额定容量为5.0 A·h,工作电压区间为3.0~4.2 V。电池长、宽、厚度分别为132 mm、90 mm、40 mm。电池充放电策略如下:首先对电池长宽对应的表面均匀施加34.5 kPa的初始压力,并在给定温度环境内静置3 h直至达到热平衡后,恒流充电至4.2 V,之后恒压充电至电流小于C /50截止;然后,充电静置1 h,恒流放电至3.0 V。在本文试验中,选取其中的01、05、09、10号电池作为研究对象,电池参数如表1 所示。
3.2 膨胀应力分析
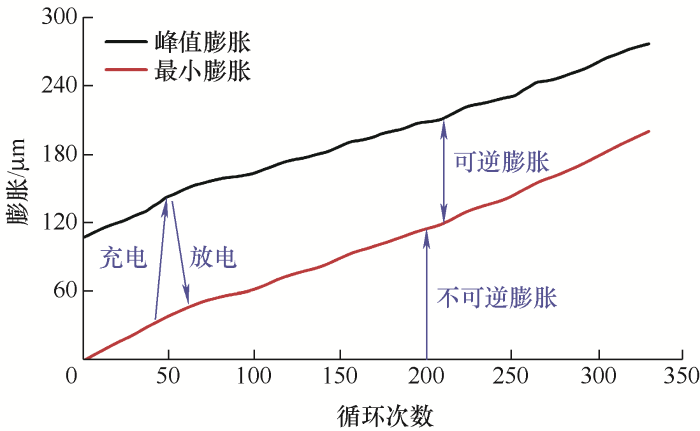
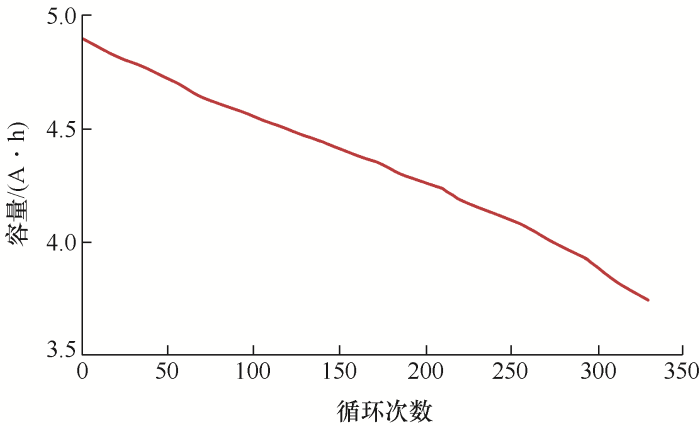
图2 展示了01号电池在循环充放电过程中峰值膨胀与最小膨胀变化曲线,其中峰值膨胀对应于电池充满电时电池厚度变化,最小膨胀对应于电池完全放电时电池厚度变化。可以看出,在电池充电过程中,电池厚度不断膨胀;放电过程中,电池厚度不断收缩。这种可逆的电池膨胀变化是由于该种电池厚度的变化是可逆的,即可逆膨胀。并且在电池完全放电后,电池膨胀相对于上次循环结束会存在不可逆的积累,即不可逆膨胀。结合图3 所示的容量变化曲线可以看出,随着电池的循环老化,可用容量不断衰减,可逆膨胀呈轻微衰减趋势,而不可逆膨胀明显增加,远大于可逆膨胀的减小。这主要是因为在电池使用过程中,由于锂离子的损失,电极中可供迁移的锂离子含量逐渐减小[18 ] ,可逆膨胀相应不断降低;同时,电池的老化伴随着内部聚合物变形,SEI膜增厚[19 ] ,使得电池内部应力明显增大,从而造成电池不可逆的膨胀不断累积。因此,可逆膨胀与不可逆膨胀都与容量的变化密切相关。
图2
图3
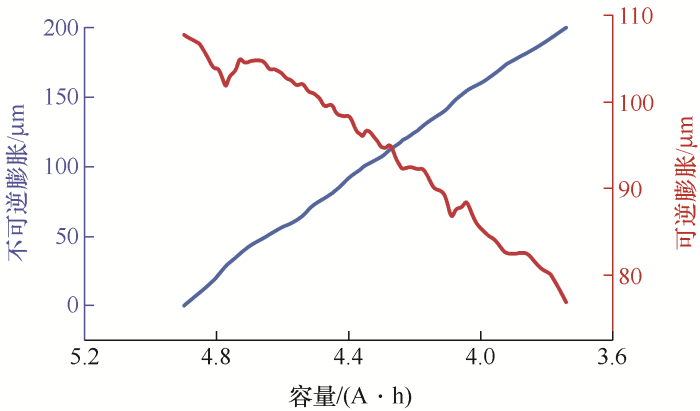
为了分析01号电池膨胀与容量之间的线性关系,绘制膨胀-容量曲线,如图4 所示,可以直观地看出电池容量与可逆膨胀、不可逆膨胀之间均具有良好的线性关系。在电池容量减少过程中,可逆膨胀同样减少,二者呈正相关;不可逆膨胀不断增加,与容量衰减呈负相关。
图4
为进一步证明电池膨胀特征与不同电池均具有强相关性,对表1 中的四组电池,采用皮尔逊相关性分析法进一步量化各电池膨胀与容量的相关性,并与容量和内阻、充放电时间的相关性进行对比。相关系数计算公式如下
(7) ${{\rho }_{\mathrm{X},\mathrm{Y}}}=\frac{\mathrm{Cov}(X,Y)}{{{\sigma }_{\mathrm{X}}}{{\sigma }_{\mathrm{Y}}}}$
式中,X 、Y 分别代表膨胀数据与容量数据;Cov(X ,Y )为二者之间的协方差矩阵;σ X 、σ Y 为其标准差。
相关性计算结果如表2 所示,可知对于多种测试条件,充放电时间、内阻、可逆膨胀、不可逆膨胀均与容量呈强相关性,其中“-”代表与容量负相关。相比于内阻与充电时间这两个传统RUL预测方法常用特征参数,可逆膨胀和不可逆膨胀与容量具有更强的线性关系。
根据以上分析,电池的膨胀变化反映了电池内部力学特征的变化,与电池容量变化密切相关且具有良好的线性关系,可以很好地表征电池老化状态,并且电池的厚度变化更易于测量。因此,可逆膨胀与不可逆膨胀可以作为RUL预测的特征参数。
3.3 基于LSTM的RUL预测模型
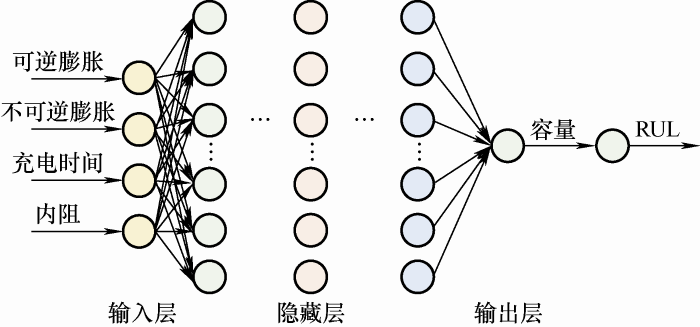
基于锂离子电池状态的长期依赖性,本文利用LSTM网络来预测电池剩余寿命;选择可逆膨胀、不可逆膨胀、充放电时间、内阻数据作为输入特征,用于训练网络;由输出层给出容量预测结果,并计算获得RUL预测值,基于LSTM的RUL预测模型基本结构如图5 所示。
图5
为了消除各指标之间不同尺度的影响,保证各数据指标之间的可比性,需要对输入数据归一化处理[20 ] ,把每个特征序列数值归一化至0~1。归一化公式为
(8) $x_{t}^{\prime}=\frac{x_{t}-\min (x)}{\max (x)-\min (x)}$
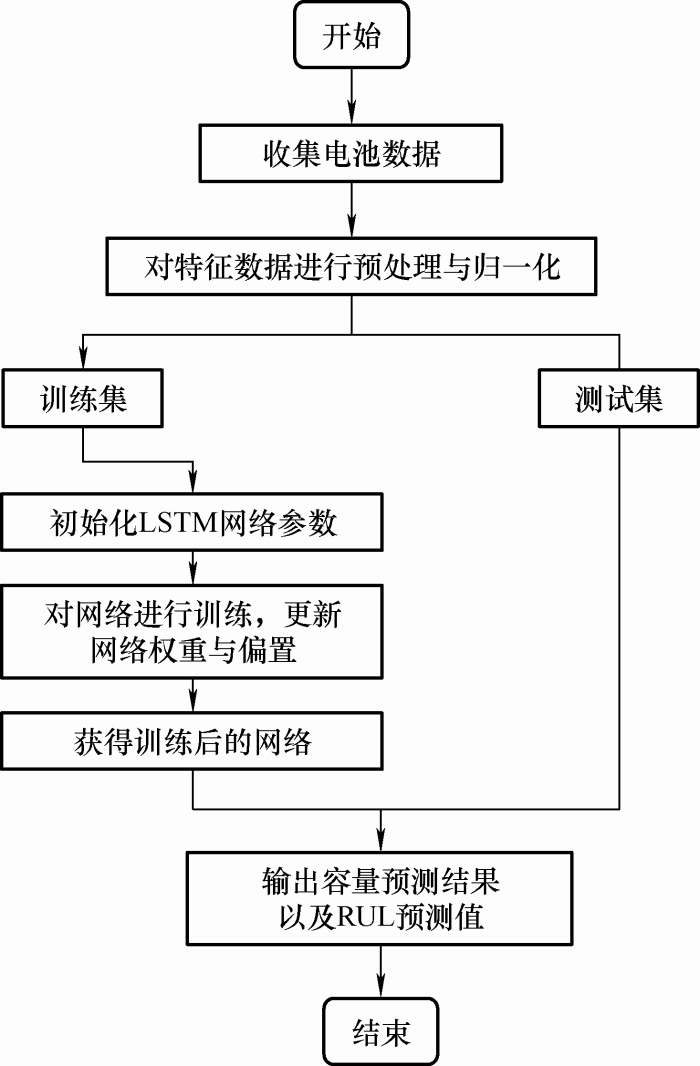
式中,xt 为电池在t 时刻工作参数;$x_{t}^{\prime}$ t 时刻归一化后的特征数据;min(x )和max(x )分别表示输入参数的最小值和最大值。RUL预测流程如图6 所示。
图6
步骤1:收集电池循环老化数据,获取容量膨胀、充放电时间、内阻等数据并进行预处理。
步骤2:对特征数据进行归一化,划分为训练集与测试集。
步骤3:设置网络的初始参数,包括隐藏层神经元个数、学习速率、最大迭代次数等。
步骤4:输入训练集对网络进行训练,并使用Adam优化器更新网络权重和偏置项。
步骤5:把测试集输入训练后的网络模型,输出容量与RUL预测值。
4 试验结果讨论
4.1 试验设置
为分析膨胀特征在电池RUL预测中的重要性,本节选用表1 中四组电池,在Matlab R2021a环境下进行试验验证。LSTM网络隐藏层神经元个数为200,全连接层神经元个数为1,采用Adam优化器,初始学习率设置为0.001,最大迭代次数为900次。RUL的预测结果通过均方根误差(Root mean square error, RMSE)、平均绝对误差(Maximum absolute error, MAE)、绝对误差(Absolute error, AE)三个指标进行评价。其中,RMSE、MAE用于评价容量变化趋势预测的准确性,AE用于评价RUL预测的准确性,公式如下
(9) $\mathrm{MAE}=\frac{1}{~N}\sum\limits_{i=1}^{N}{\left| {{y}_{i}}-{{\widehat{y}}_{i}} \right|}$
(10) $\mathrm{RMSE}=\sqrt{\frac{1}{~N}{{\sum\limits_{i=1}^{N}{\left( {{y}_{i}}-{{\widehat{y}}_{i}} \right)}}^{2}}}$
(11) $\mathrm{AE}=|{{T}_{\mathrm{RUL}}}-{{P}_{\mathrm{RUL}}}|$
式中,yi 与${{\hat{y}}_{i}}$ i 次循环的容量真实值与预测值;T RUL 为RUL真实值;P RUL 为RUL预测值。
4.2 RUL预测结果
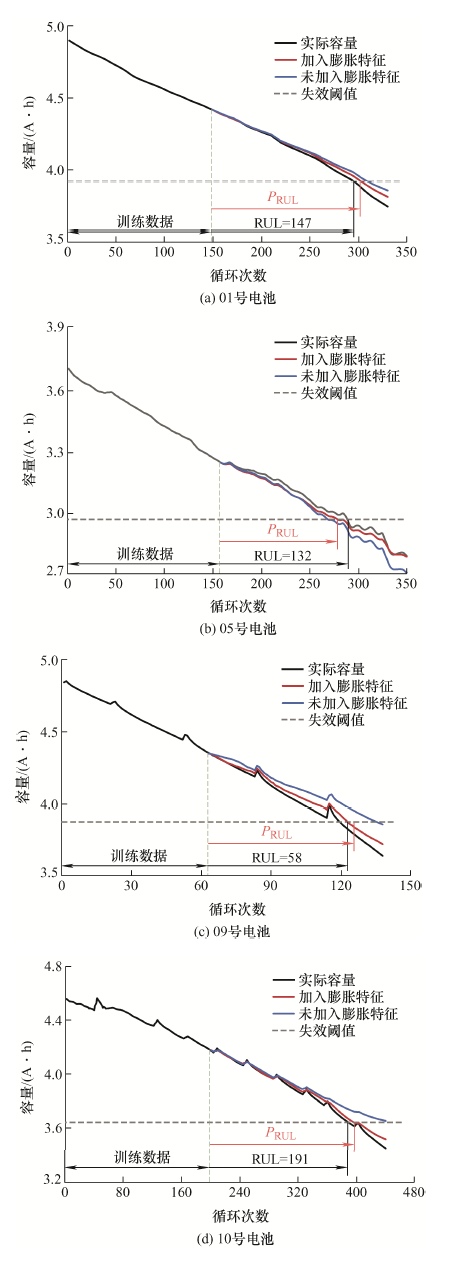
在实际情况中,电池已使用的循环次数不同,相应地,所能够采集的训练数据数量不同。为检验本文所提RUL估计方法的准确性与鲁棒性,更贴近实际应用情况,对每个电池设置45%与55%两个不同的训练集比例进行测试,并在不同训练集条件下,分别进行了考虑膨胀特征(记为方法A)与未考虑膨胀特征(记为方法B)的对比试验。其中,对于45%训练集的容量衰减趋势预测结果如图7 所示。
图7
通过图7 可以看出,在45%训练集比例条件下,本文提出的预测方法在4组电池上均实现了RUL的准确预测。相比于传统未考虑膨胀特征的预测方法,加入膨胀特征可以帮助网络更好地学习电池老化趋势,有效跟踪真实容量变化,更贴近实际应用情况,进一步提高了RUL预测精度。
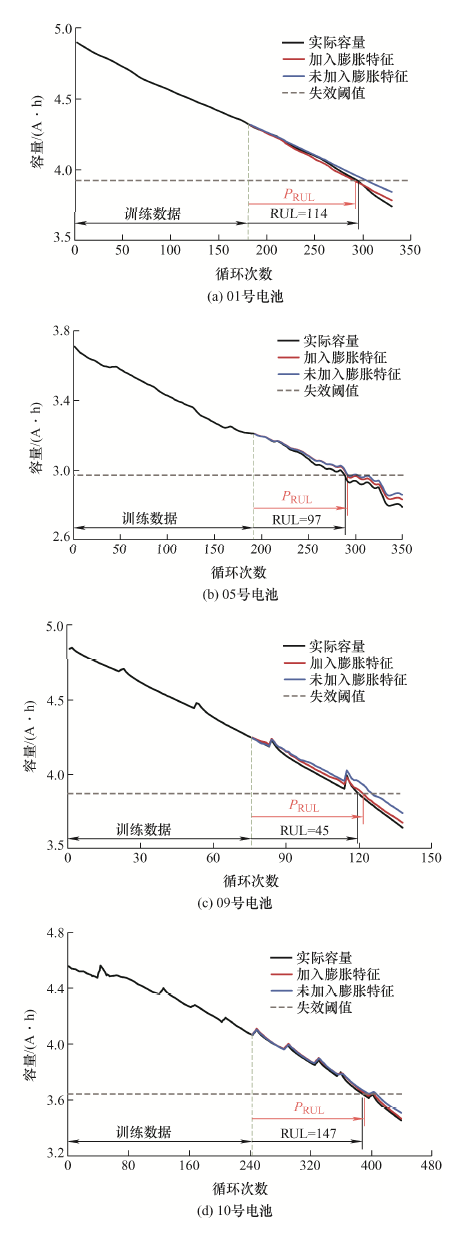
进一步增加10%训练集比例,容量变化曲线预测结果如图8 所示。对比图7 发现,55%训练集条件下,容量与RUL的预测获得了更准确的结果。这是由于不同的训练集会对预测结果产生一定的影响,对于LSTM网络,训练集占比的增加意味着网络模型可以学习更多的特征数据信息,增强网络的泛化性,优化预测效果。同时可以看出,对于不同比例的训练集,加入膨胀特征后,各电池预测精度都得到了提升。结合表3 中RUL预测结果与误差分析可知,在45%训练集条件下,加入膨胀特征后预测曲线RMSE、MAE分别在0.82%、0.70%以内,AE最大为10;在55%训练集条件下,加入膨胀特征后预测曲线RMSE、MAE分别在0.49%、0.46%以内,AE最大为3。结果表明,对于不同的训练集比例以及不同老化条件,本文提出的RUL预测方法均获得了准确的预测结果,鲁棒性强、适用范围广,总体性能令人满意。
图8
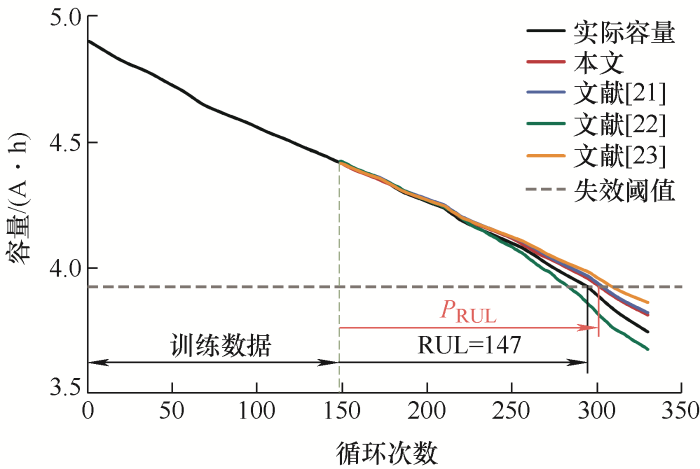
为进一步证明本文所提RUL预测方法的有效性与准确性,分别与文献[21 ]中提出的基于数据预处理和长短期记忆神经网络的预测方法、文献[22 ]中提出的基于Elman神经网络的预测方法、文献[23 ]中提出的基于Bi-GRU网络的预测方法进行比较。利用01号电池数据进行对比试验,训练集比例设置为45%。
各方法容量预测曲线如图9 所示,可以看出本文与文献[21 ]提出的预测方法相比更能充分学习电池老化特性,准确跟踪容量衰减趋势。进一步结合表4 展示的不同预测方法模型RUL预测结果及误差,对比发现,本文提出的RUL预测方法预测精度更高,RMSE与MAE值更低,RUL预测结果更准确。
图9
5 结论
本文提出了一种考虑电池膨胀的锂离子电池RUL预测方法,通过UMBL公开数据集进行了验证,可以得到如下结论。
(1) 可逆膨胀和不可逆膨胀均与电池容量变化密切相关,相关性与内阻等参数相比更强,能够更好地反映电池退化。
(2) 利用膨胀力预测电池剩余使用寿命能够获得更高的预测精度和更强的鲁棒性,最大RMSE与MAE分别小于0.82%、0.70%。
参考文献
View Option
[1]
梅简 , 张杰 , 刘双宇 , 等 . 电池储能技术发展现状
[J]. 浙江电力 , 2020 , 39 (3 ):75 -81 .
[本文引用: 1]
MEI Jian ZHANG Jie LIU Shuangyu et al. Development status of battery energy storage technology
[J]. Zhejiang Electric Power , 2020 , 39 (3 ):75 -81 .
[本文引用: 1]
[2]
陈琳 , 陈静 , 王惠民 , 等 . 基于小波包能量熵的电池剩余寿命预测
[J]. 电工技术学报 , 2020 , 35 (8 ):1827 -1835 .
[本文引用: 1]
CHEN Lin CHEN Jing WANG Huimin et al. Prediction of battery remaining useful life based on wavelet packet energy entropy
[J]. Transactions of China Electrotechnical Society , 2020 , 35 (8 ):1827 -1835 .
[本文引用: 1]
[3]
LI Junfu LYU Chao WANG Lixin et al. Remaining capacity estimation of Li-ion batteries based on temperature sample entropy and particle filter
[J]. Journal of Power Sources , 2014 , 268 (5 ):895 -903 .
DOI:10.1016/j.jpowsour.2014.06.133
URL
[本文引用: 1]
[4]
XING Yinjiao MA E W M TSUI K L et al. An ensemble model for predicting the remaining useful performance of lithium-ion batteries
[J]. Microelectronics Reliability , 2013 , 53 (6 ):811 -820 .
DOI:10.1016/j.microrel.2012.12.003
URL
[本文引用: 1]
[5]
LYU Chao LAI Qingzhi GE Tengfei et al. A lead-acid battery’s remaining useful life prediction by using electrochemical model in the particle filtering framework
[J]. Energy , 2017 , 120 (1 ):975 -984 .
DOI:10.1016/j.energy.2016.12.004
URL
[本文引用: 1]
[6]
LIU Zhenbao SUN Gaoyuan BU Shuhui et al. Particle learning framework for estimating the remaining useful life of lithium-ion batteries
[J]. IEEE Transactions on Instrumentation and Measurement , 2017 , 66 (2 ):280 -293 .
DOI:10.1109/TIM.2016.2622838
URL
[本文引用: 1]
[7]
XU Xin CHEN Nan A state-space-based prognostics model for lithium-ion battery degradation
[J]. Reliability Engineering & System Safety , 2017 ,159:47 -57 .
[本文引用: 1]
[8]
WAAG W FLEISCHER C SAUER D U Critical review of the methods for monitoring of lithium-ion batteries in electric and hybrid vehicles
[J]. Journal of Power Sources , 2014 , 258 (14 ):321 -339 .
DOI:10.1016/j.jpowsour.2014.02.064
URL
[本文引用: 1]
[9]
NUHIC A TERZIMEHIC T SOCZKA-GUTH T et al. Health diagnosis and remaining useful life prognostics of lithium-ion batteries using data-driven methods
[J]. Journal of Power Sources , 2013 , 239 (1 ):680 -688 .
DOI:10.1016/j.jpowsour.2012.11.146
URL
[本文引用: 1]
[10]
ZHANG Yongzhi XIONG Rui HE Hongwen et al. Long short-term memory recurrent neural network for remaining useful life prediction of lithium-ion batteries
[J]. IEEE Transactions on Vehicular Technology , 2018 , 67 (7 ):5695 -5705 .
DOI:10.1109/TVT.25
URL
[本文引用: 1]
[11]
尤贺泽 , 戴海峰 , 于臣臣 , 等 . 软包锂离子电池应力特性及其建模
[J]. 同济大学学报 , 2020 , 48 (2 ):231 -240 .
[本文引用: 1]
YOU Heze DAI Haifeng YU Chenchen et al. Stress properties and modeling of lithium-ion pouch batteries
[J]. Journal of Tongji University , 2020 , 48 (2 ):231 -240 .
[本文引用: 1]
[13]
CANNARELLA J ARNOLD C B State of health and charge measurements in lithium-ion batteries using mechanical stress
[J]. Journal of Power Sources , 2014 , 269 (10 ):7 -14 .
DOI:10.1016/j.jpowsour.2014.07.003
URL
[本文引用: 1]
[14]
XU Jun LIU Binghe HU Dayong State of charge dependent mechanical integrity behavior of 18650 lithium-ion batteries
[J]. Scientific Reports , 2016 , 6 (1 ):21829 .
DOI:10.1038/srep21829
[本文引用: 1]
Understanding the mechanism of mechanical deformation/stress-induced electrical failure of lithium–ion batteries (LIBs) is important in crash-safety design of power LIBs. The state of charge (SOC) of LIBs is a critical factor in their electrochemical performance; however, the influence of SOC with mechanical integrity of LIBs remains unclear. This study investigates the electrochemical failure behaviors of LIBs with various SOCs under both compression and bending loadings, underpinned by the short circuit phenomenon. Mechanical behaviors of the whole LIB body, which is regarded as an intact structure, were analyzed in terms of structure stiffness. Results showed that the mechanical behaviors of LIBs depend highly on SOC. Experimental verification on the cathode and anode sheet compression tests show that higher SOC with more lithium inserted in the anode leads to higher structure stiffness. In the bending tests, failure strain upon occurrence of short circuit has an inverse linear relationship with the SOC value. These results may shed light on the fundamental physical mechanism of mechanical integrity LIBs in relation to inherent electrochemical status.
[15]
MOHTAT P LEE S SIEGEL J et al. Reversible and irreversible expansion of lithium-ion batteries under a wide range of stress factors
[J]. Journal of the Electrochemical Society , 2021 ,168:100520.
[本文引用: 2]
[16]
WILLIAMS R J ZIPSER D A learning algorithm for continually running fully recurrent neural networks
[J]. Neural Computation , 1998 , 1 (2 ):270 -280 .
DOI:10.1162/neco.1989.1.2.270
URL
[本文引用: 1]
The exact form of a gradient-following learning algorithm for completely recurrent networks running in continually sampled time is derived and used as the basis for practical algorithms for temporal supervised learning tasks. These algorithms have (1) the advantage that they do not require a precisely defined training interval, operating while the network runs; and (2) the disadvantage that they require nonlocal communication in the network being trained and are computationally expensive. These algorithms allow networks having recurrent connections to learn complex tasks that require the retention of information over time periods having either fixed or indefinite length.
[17]
HOCHREITER S SCHMIDHUBER J Long short-term memory
[J]. Neural Computation , 1997 , 9 (8 ):1735 -1780 .
DOI:10.1162/neco.1997.9.8.1735
PMID:9377276
[本文引用: 1]
Learning to store information over extended time intervals by recurrent backpropagation takes a very long time, mostly because of insufficient, decaying error backflow. We briefly review Hochreiter's (1991) analysis of this problem, then address it by introducing a novel, efficient, gradient-based method called long short-term memory (LSTM). Truncating the gradient where this does not do harm, LSTM can learn to bridge minimal time lags in excess of 1000 discrete-time steps by enforcing constant error flow through constant error carousels within special units. Multiplicative gate units learn to open and close access to the constant error flow. LSTM is local in space and time; its computational complexity per time step and weight is O(1). Our experiments with artificial data involve local, distributed, real-valued, and noisy pattern representations. In comparisons with real-time recurrent learning, back propagation through time, recurrent cascade correlation, Elman nets, and neural sequence chunking, LSTM leads to many more successful runs, and learns much faster. LSTM also solves complex, artificial long-time-lag tasks that have never been solved by previous recurrent network algorithms.
[18]
WANG Xianming SONE Y SEGAMI G et al. Understanding volume change in lithium-ion cells during charging and discharging using in situ measurements
[J]. Journal of the Electrochemical Society , 2007 , 154 (1 ):A14.
[本文引用: 1]
[19]
牛少军 , 吴凯 , 朱国斌 , 等 . 锂离子电池硅基负极循环过程中的膨胀应力
[J]. 储能科学与技术 , 2022 , 11 (9 ):2989 -2994 .
DOI:10.19799/j.cnki.2095-4239.2022.0194
[本文引用: 1]
研究硅基负极在充放电及循环过程中的膨胀对开发下一代高比能锂离子动力电池具有重要意义。本工作采用商业化的SiO <sub>x</sub> /Graphite为负极匹配高比能镍钴锰酸锂[Li(Ni<sub>0.8</sub>Mn<sub>0.1</sub>Co<sub>0.1</sub>)O<sub>2</sub>,NCM811]正极,组装了60 Ah大软包电池,并对其进行循环膨胀应力、应力增长机理与膨胀应力的改善等方面的研究。结果表明SiO <sub>x</sub> 材料的构成为3~5 nm Si颗粒分散在无定形的SiO<sub>2</sub>内部,首次充放电比容量为1840.9/1380 mAh/g,库仑效率为75%。大软包电池单次充放电膨胀应力的变化为7320 N,约为石墨负极的4倍。工作温度越高容量衰减越快,衰减到70% SOH时,25、45和60 ℃对应的循环次数分别为980、850和500次,对应的最大膨胀应力分别为25107、25490、23667 N。此外,机理分析发现电池循环膨胀应力的增长和容量衰减之间为线性相关,CP(cross section polisher)-SEM分析发现膨胀应力的增加主要来自于SiO <sub>x</sub> 颗粒表面的破裂及副反应导致的SEI (solid electrolyte interphase)增厚。通过测定缓冲垫压缩曲线的方法筛选了合适的聚氨酯类缓冲垫,验证对循环无影响,但可以显著改善膨胀应力的增加,膨胀应力降低50%,这些结果将为更好地应用高比容量的硅基负极材料奠定基础。
NIU Shaojun WU Kai ZHU Guobin et al. Studies on the swelling force during cycling of Si-based anodes in lithium ion batteries
[J]. Energy Storage Science and Technology , 2022 , 11 (9 ):2989 -2994 .
DOI:10.19799/j.cnki.2095-4239.2022.0194
[本文引用: 1]
Studying the swelling force of Si-based anodes for the next generation of high energy lithium-ion batteries is crucial. In this study, we assembled 60-Ah large pouch batteries with commercialized SiO x /Graphite and NCM811 cathode, tested their cycle life and swelling force increase, and studied the relevant mechanisms and strategies for reducing the swelling force. The structure of SiO x was a 3~5 nm Si core distributed in amorphous SiO2, and the specific capacity of SiO x in the first cycle was 1380 mAh/g and the first columbic efficiency was ca. 75%. The swelling force increase during the first cycle was 7320 N, which was 4 times higher than that of graphite-based batteries. The cycling tests under different ambient temperatures showed high temperature-dependent tendency. At 25 ℃, 45 ℃, and 60 ℃, the cycle numbers were 980, 850, and 500, corresponding to 70% SOH, with the maximum swelling force being 25107, 25490, and 23667 N, respectively. The root cause for the swelling force increase was the solid electrolyte interface growth and thickening with repeated electrochemical cycles. The compression curve was applied to sorting appropriate cushion that can accommodate the swelling force. The results showed that polyurethane cushion had the best compression properties, reducing the swelling force by 50%. This study provides a foundation for using SiO x in large-scale lithium-ion batteries.
[20]
耿鑫月 , 胡昌华 , 郑建飞 , 等 . 双时间尺度下基于Transformer的锂电池剩余寿命预测
[J]. 空间控制技术与应用 , 2023 , 49 (4 ):119 -126 .
[本文引用: 1]
GENG Xinyue HU Changhua ZHENG Jianfei et al. Remaining life prediction of lithium batteries based on transformer at dual time scales
[J]. Aerospace Control and Application , 2023 , 49 (4 ):119 -126 .
[本文引用: 1]
[21]
黄凯 , 丁恒 , 郭永芳 , 等 . 基于数据预处理和长短期记忆神经网络的锂离子电池寿命预测
[J]. 电工技术学报 , 2022 , 37 (15 ):3753 -3766 .
[本文引用: 2]
HUANG Kai DING Heng GUO Yongfang et al. Prediction of remaining useful life of lithium-ion battery based on adaptive data preprocessing and long short-term memory network
[J]. Transactions of China Electrotechnical Society , 2022 , 37 (15 ):3753 -3766 .
[本文引用: 2]
[22]
李练兵 , 祝亚尊 , 田永嘉 , 等 . 基于Elman神经网络的锂离子电池RUL间接预测研究
[J]. 电源技术 , 2019 , 43 (6 ):1027 -1031 .
[本文引用: 1]
LI Lianbing ZHU Yazun TIAN Yongjia et al. RUL indirect prediction of lithium-ion battery based on Elman neural network
[J]. Chinese Journal of Power Sources , 2019 , 43 (6 ):1027 -1031 .
[本文引用: 1]
[23]
叶林峰 , 石元博 , 黄越洋 . 基于BiGRU网络的锂电池寿命预测
[J]. 电源技术 , 2021 , 45 (5 ):598 -601 .
[本文引用: 1]
YE Linfeng SHI Yuanbo HUANG Yueyang Lithium battery life prediction based on BiGRU network
[J]. Chinese Journal of Power Sources , 2021 , 45 (5 ):598 -601 .
[本文引用: 1]
电池储能技术发展现状
1
2020
... 近年来,随着新能源技术快速发展,锂离子电池凭借其高能量密度、宽工作温度、无污染和长寿命等优势受到广泛关注[1 ] .然而,锂离子电池内部存在不可逆的化学反应,在使用和储存过程中不可避免地会出现容量损失.循环寿命被定义为电池可用容量下降到初始值的一定百分比(通常以80%为阈值)时的充放电循环次数.当电池达到该失效阈值时,需要及时更换,以保证系统安全稳定运行.准确预测电池剩余使用寿命(Remaining useful life, RUL),对充分发挥电池性能,确保电池系统安全高效运行具有重要意义[2 ] . ...
Development status of battery energy storage technology
1
2020
... 近年来,随着新能源技术快速发展,锂离子电池凭借其高能量密度、宽工作温度、无污染和长寿命等优势受到广泛关注[1 ] .然而,锂离子电池内部存在不可逆的化学反应,在使用和储存过程中不可避免地会出现容量损失.循环寿命被定义为电池可用容量下降到初始值的一定百分比(通常以80%为阈值)时的充放电循环次数.当电池达到该失效阈值时,需要及时更换,以保证系统安全稳定运行.准确预测电池剩余使用寿命(Remaining useful life, RUL),对充分发挥电池性能,确保电池系统安全高效运行具有重要意义[2 ] . ...
基于小波包能量熵的电池剩余寿命预测
1
2020
... 近年来,随着新能源技术快速发展,锂离子电池凭借其高能量密度、宽工作温度、无污染和长寿命等优势受到广泛关注[1 ] .然而,锂离子电池内部存在不可逆的化学反应,在使用和储存过程中不可避免地会出现容量损失.循环寿命被定义为电池可用容量下降到初始值的一定百分比(通常以80%为阈值)时的充放电循环次数.当电池达到该失效阈值时,需要及时更换,以保证系统安全稳定运行.准确预测电池剩余使用寿命(Remaining useful life, RUL),对充分发挥电池性能,确保电池系统安全高效运行具有重要意义[2 ] . ...
Prediction of battery remaining useful life based on wavelet packet energy entropy
1
2020
... 近年来,随着新能源技术快速发展,锂离子电池凭借其高能量密度、宽工作温度、无污染和长寿命等优势受到广泛关注[1 ] .然而,锂离子电池内部存在不可逆的化学反应,在使用和储存过程中不可避免地会出现容量损失.循环寿命被定义为电池可用容量下降到初始值的一定百分比(通常以80%为阈值)时的充放电循环次数.当电池达到该失效阈值时,需要及时更换,以保证系统安全稳定运行.准确预测电池剩余使用寿命(Remaining useful life, RUL),对充分发挥电池性能,确保电池系统安全高效运行具有重要意义[2 ] . ...
Remaining capacity estimation of Li-ion batteries based on temperature sample entropy and particle filter
1
2014
... 目前,电池RUL预测方法主要分为两大类:基于模型的方法和数据驱动的方法.基于模型的方法[3 -4 ] 主要通过搭建合适的电池模型模拟其电化学行为,捕获电池老化规律并预测RUL.文献[5 ]引入了一种基于电化学模型的粒子滤波(Particle filtering, PF)框架,把反映电池退化的模型参数看成状态变量,来预测电池RUL.文献[6 ]提出了一种改进粒子学习框架(Particle learning, PL)以预测RUL,通过新收集测量信息对状态粒子重采样,并传播到当前时刻生成状态后验粒子,有效防止了粒子退化.文献[7 ]建立了通用状态空间模型,并基于期望值最大化(Expectation maximization, EM)和扩展卡尔曼滤波(Extended Kalman filtering, EKF)算法对模型进行参数辨识与更新,从而可以准确描述电池的老化过程.然而,由于电池内部化学反应复杂,通常难以收集全面的内部参数,建立准确的老化模型.同时,电池状态易受到工作温度、放电深度、电流等外部因素的影响,使得该方法难以适应复杂的运行环境,可靠性低[8 ] .近年来,数据驱动的方法被广泛应用于电池RUL预测.与基于模型的方法不同,数据驱动的方法不需要考虑电池内部复杂的工作原理,仅依赖于历史数据来描述电池老化过程.文献[9 ]利用支持向量机(Support vector machine, SVM)学习多个与电池容量衰减相关的特征数据,实现电池健康状态(State of health, SOH)和RUL的预测.文献[10 ]采用长短期记忆网络(Long short-term memory, LSTM)和递归神经网络(Recurrent neural network, RNN)学习电池老化信息,结合蒙特卡罗模拟实现RUL预测,预测精度与计算效率较高,可靠性强.但该方法需要大量训练数据和较高的硬件需求.近年来随着大数据与硬件设备的高速发展,数据驱动的方法成为当前电池寿命预测的热门研究方向. ...
An ensemble model for predicting the remaining useful performance of lithium-ion batteries
1
2013
... 目前,电池RUL预测方法主要分为两大类:基于模型的方法和数据驱动的方法.基于模型的方法[3 -4 ] 主要通过搭建合适的电池模型模拟其电化学行为,捕获电池老化规律并预测RUL.文献[5 ]引入了一种基于电化学模型的粒子滤波(Particle filtering, PF)框架,把反映电池退化的模型参数看成状态变量,来预测电池RUL.文献[6 ]提出了一种改进粒子学习框架(Particle learning, PL)以预测RUL,通过新收集测量信息对状态粒子重采样,并传播到当前时刻生成状态后验粒子,有效防止了粒子退化.文献[7 ]建立了通用状态空间模型,并基于期望值最大化(Expectation maximization, EM)和扩展卡尔曼滤波(Extended Kalman filtering, EKF)算法对模型进行参数辨识与更新,从而可以准确描述电池的老化过程.然而,由于电池内部化学反应复杂,通常难以收集全面的内部参数,建立准确的老化模型.同时,电池状态易受到工作温度、放电深度、电流等外部因素的影响,使得该方法难以适应复杂的运行环境,可靠性低[8 ] .近年来,数据驱动的方法被广泛应用于电池RUL预测.与基于模型的方法不同,数据驱动的方法不需要考虑电池内部复杂的工作原理,仅依赖于历史数据来描述电池老化过程.文献[9 ]利用支持向量机(Support vector machine, SVM)学习多个与电池容量衰减相关的特征数据,实现电池健康状态(State of health, SOH)和RUL的预测.文献[10 ]采用长短期记忆网络(Long short-term memory, LSTM)和递归神经网络(Recurrent neural network, RNN)学习电池老化信息,结合蒙特卡罗模拟实现RUL预测,预测精度与计算效率较高,可靠性强.但该方法需要大量训练数据和较高的硬件需求.近年来随着大数据与硬件设备的高速发展,数据驱动的方法成为当前电池寿命预测的热门研究方向. ...
A lead-acid battery’s remaining useful life prediction by using electrochemical model in the particle filtering framework
1
2017
... 目前,电池RUL预测方法主要分为两大类:基于模型的方法和数据驱动的方法.基于模型的方法[3 -4 ] 主要通过搭建合适的电池模型模拟其电化学行为,捕获电池老化规律并预测RUL.文献[5 ]引入了一种基于电化学模型的粒子滤波(Particle filtering, PF)框架,把反映电池退化的模型参数看成状态变量,来预测电池RUL.文献[6 ]提出了一种改进粒子学习框架(Particle learning, PL)以预测RUL,通过新收集测量信息对状态粒子重采样,并传播到当前时刻生成状态后验粒子,有效防止了粒子退化.文献[7 ]建立了通用状态空间模型,并基于期望值最大化(Expectation maximization, EM)和扩展卡尔曼滤波(Extended Kalman filtering, EKF)算法对模型进行参数辨识与更新,从而可以准确描述电池的老化过程.然而,由于电池内部化学反应复杂,通常难以收集全面的内部参数,建立准确的老化模型.同时,电池状态易受到工作温度、放电深度、电流等外部因素的影响,使得该方法难以适应复杂的运行环境,可靠性低[8 ] .近年来,数据驱动的方法被广泛应用于电池RUL预测.与基于模型的方法不同,数据驱动的方法不需要考虑电池内部复杂的工作原理,仅依赖于历史数据来描述电池老化过程.文献[9 ]利用支持向量机(Support vector machine, SVM)学习多个与电池容量衰减相关的特征数据,实现电池健康状态(State of health, SOH)和RUL的预测.文献[10 ]采用长短期记忆网络(Long short-term memory, LSTM)和递归神经网络(Recurrent neural network, RNN)学习电池老化信息,结合蒙特卡罗模拟实现RUL预测,预测精度与计算效率较高,可靠性强.但该方法需要大量训练数据和较高的硬件需求.近年来随着大数据与硬件设备的高速发展,数据驱动的方法成为当前电池寿命预测的热门研究方向. ...
Particle learning framework for estimating the remaining useful life of lithium-ion batteries
1
2017
... 目前,电池RUL预测方法主要分为两大类:基于模型的方法和数据驱动的方法.基于模型的方法[3 -4 ] 主要通过搭建合适的电池模型模拟其电化学行为,捕获电池老化规律并预测RUL.文献[5 ]引入了一种基于电化学模型的粒子滤波(Particle filtering, PF)框架,把反映电池退化的模型参数看成状态变量,来预测电池RUL.文献[6 ]提出了一种改进粒子学习框架(Particle learning, PL)以预测RUL,通过新收集测量信息对状态粒子重采样,并传播到当前时刻生成状态后验粒子,有效防止了粒子退化.文献[7 ]建立了通用状态空间模型,并基于期望值最大化(Expectation maximization, EM)和扩展卡尔曼滤波(Extended Kalman filtering, EKF)算法对模型进行参数辨识与更新,从而可以准确描述电池的老化过程.然而,由于电池内部化学反应复杂,通常难以收集全面的内部参数,建立准确的老化模型.同时,电池状态易受到工作温度、放电深度、电流等外部因素的影响,使得该方法难以适应复杂的运行环境,可靠性低[8 ] .近年来,数据驱动的方法被广泛应用于电池RUL预测.与基于模型的方法不同,数据驱动的方法不需要考虑电池内部复杂的工作原理,仅依赖于历史数据来描述电池老化过程.文献[9 ]利用支持向量机(Support vector machine, SVM)学习多个与电池容量衰减相关的特征数据,实现电池健康状态(State of health, SOH)和RUL的预测.文献[10 ]采用长短期记忆网络(Long short-term memory, LSTM)和递归神经网络(Recurrent neural network, RNN)学习电池老化信息,结合蒙特卡罗模拟实现RUL预测,预测精度与计算效率较高,可靠性强.但该方法需要大量训练数据和较高的硬件需求.近年来随着大数据与硬件设备的高速发展,数据驱动的方法成为当前电池寿命预测的热门研究方向. ...
A state-space-based prognostics model for lithium-ion battery degradation
1
2017
... 目前,电池RUL预测方法主要分为两大类:基于模型的方法和数据驱动的方法.基于模型的方法[3 -4 ] 主要通过搭建合适的电池模型模拟其电化学行为,捕获电池老化规律并预测RUL.文献[5 ]引入了一种基于电化学模型的粒子滤波(Particle filtering, PF)框架,把反映电池退化的模型参数看成状态变量,来预测电池RUL.文献[6 ]提出了一种改进粒子学习框架(Particle learning, PL)以预测RUL,通过新收集测量信息对状态粒子重采样,并传播到当前时刻生成状态后验粒子,有效防止了粒子退化.文献[7 ]建立了通用状态空间模型,并基于期望值最大化(Expectation maximization, EM)和扩展卡尔曼滤波(Extended Kalman filtering, EKF)算法对模型进行参数辨识与更新,从而可以准确描述电池的老化过程.然而,由于电池内部化学反应复杂,通常难以收集全面的内部参数,建立准确的老化模型.同时,电池状态易受到工作温度、放电深度、电流等外部因素的影响,使得该方法难以适应复杂的运行环境,可靠性低[8 ] .近年来,数据驱动的方法被广泛应用于电池RUL预测.与基于模型的方法不同,数据驱动的方法不需要考虑电池内部复杂的工作原理,仅依赖于历史数据来描述电池老化过程.文献[9 ]利用支持向量机(Support vector machine, SVM)学习多个与电池容量衰减相关的特征数据,实现电池健康状态(State of health, SOH)和RUL的预测.文献[10 ]采用长短期记忆网络(Long short-term memory, LSTM)和递归神经网络(Recurrent neural network, RNN)学习电池老化信息,结合蒙特卡罗模拟实现RUL预测,预测精度与计算效率较高,可靠性强.但该方法需要大量训练数据和较高的硬件需求.近年来随着大数据与硬件设备的高速发展,数据驱动的方法成为当前电池寿命预测的热门研究方向. ...
Critical review of the methods for monitoring of lithium-ion batteries in electric and hybrid vehicles
1
2014
... 目前,电池RUL预测方法主要分为两大类:基于模型的方法和数据驱动的方法.基于模型的方法[3 -4 ] 主要通过搭建合适的电池模型模拟其电化学行为,捕获电池老化规律并预测RUL.文献[5 ]引入了一种基于电化学模型的粒子滤波(Particle filtering, PF)框架,把反映电池退化的模型参数看成状态变量,来预测电池RUL.文献[6 ]提出了一种改进粒子学习框架(Particle learning, PL)以预测RUL,通过新收集测量信息对状态粒子重采样,并传播到当前时刻生成状态后验粒子,有效防止了粒子退化.文献[7 ]建立了通用状态空间模型,并基于期望值最大化(Expectation maximization, EM)和扩展卡尔曼滤波(Extended Kalman filtering, EKF)算法对模型进行参数辨识与更新,从而可以准确描述电池的老化过程.然而,由于电池内部化学反应复杂,通常难以收集全面的内部参数,建立准确的老化模型.同时,电池状态易受到工作温度、放电深度、电流等外部因素的影响,使得该方法难以适应复杂的运行环境,可靠性低[8 ] .近年来,数据驱动的方法被广泛应用于电池RUL预测.与基于模型的方法不同,数据驱动的方法不需要考虑电池内部复杂的工作原理,仅依赖于历史数据来描述电池老化过程.文献[9 ]利用支持向量机(Support vector machine, SVM)学习多个与电池容量衰减相关的特征数据,实现电池健康状态(State of health, SOH)和RUL的预测.文献[10 ]采用长短期记忆网络(Long short-term memory, LSTM)和递归神经网络(Recurrent neural network, RNN)学习电池老化信息,结合蒙特卡罗模拟实现RUL预测,预测精度与计算效率较高,可靠性强.但该方法需要大量训练数据和较高的硬件需求.近年来随着大数据与硬件设备的高速发展,数据驱动的方法成为当前电池寿命预测的热门研究方向. ...
Health diagnosis and remaining useful life prognostics of lithium-ion batteries using data-driven methods
1
2013
... 目前,电池RUL预测方法主要分为两大类:基于模型的方法和数据驱动的方法.基于模型的方法[3 -4 ] 主要通过搭建合适的电池模型模拟其电化学行为,捕获电池老化规律并预测RUL.文献[5 ]引入了一种基于电化学模型的粒子滤波(Particle filtering, PF)框架,把反映电池退化的模型参数看成状态变量,来预测电池RUL.文献[6 ]提出了一种改进粒子学习框架(Particle learning, PL)以预测RUL,通过新收集测量信息对状态粒子重采样,并传播到当前时刻生成状态后验粒子,有效防止了粒子退化.文献[7 ]建立了通用状态空间模型,并基于期望值最大化(Expectation maximization, EM)和扩展卡尔曼滤波(Extended Kalman filtering, EKF)算法对模型进行参数辨识与更新,从而可以准确描述电池的老化过程.然而,由于电池内部化学反应复杂,通常难以收集全面的内部参数,建立准确的老化模型.同时,电池状态易受到工作温度、放电深度、电流等外部因素的影响,使得该方法难以适应复杂的运行环境,可靠性低[8 ] .近年来,数据驱动的方法被广泛应用于电池RUL预测.与基于模型的方法不同,数据驱动的方法不需要考虑电池内部复杂的工作原理,仅依赖于历史数据来描述电池老化过程.文献[9 ]利用支持向量机(Support vector machine, SVM)学习多个与电池容量衰减相关的特征数据,实现电池健康状态(State of health, SOH)和RUL的预测.文献[10 ]采用长短期记忆网络(Long short-term memory, LSTM)和递归神经网络(Recurrent neural network, RNN)学习电池老化信息,结合蒙特卡罗模拟实现RUL预测,预测精度与计算效率较高,可靠性强.但该方法需要大量训练数据和较高的硬件需求.近年来随着大数据与硬件设备的高速发展,数据驱动的方法成为当前电池寿命预测的热门研究方向. ...
Long short-term memory recurrent neural network for remaining useful life prediction of lithium-ion batteries
1
2018
... 目前,电池RUL预测方法主要分为两大类:基于模型的方法和数据驱动的方法.基于模型的方法[3 -4 ] 主要通过搭建合适的电池模型模拟其电化学行为,捕获电池老化规律并预测RUL.文献[5 ]引入了一种基于电化学模型的粒子滤波(Particle filtering, PF)框架,把反映电池退化的模型参数看成状态变量,来预测电池RUL.文献[6 ]提出了一种改进粒子学习框架(Particle learning, PL)以预测RUL,通过新收集测量信息对状态粒子重采样,并传播到当前时刻生成状态后验粒子,有效防止了粒子退化.文献[7 ]建立了通用状态空间模型,并基于期望值最大化(Expectation maximization, EM)和扩展卡尔曼滤波(Extended Kalman filtering, EKF)算法对模型进行参数辨识与更新,从而可以准确描述电池的老化过程.然而,由于电池内部化学反应复杂,通常难以收集全面的内部参数,建立准确的老化模型.同时,电池状态易受到工作温度、放电深度、电流等外部因素的影响,使得该方法难以适应复杂的运行环境,可靠性低[8 ] .近年来,数据驱动的方法被广泛应用于电池RUL预测.与基于模型的方法不同,数据驱动的方法不需要考虑电池内部复杂的工作原理,仅依赖于历史数据来描述电池老化过程.文献[9 ]利用支持向量机(Support vector machine, SVM)学习多个与电池容量衰减相关的特征数据,实现电池健康状态(State of health, SOH)和RUL的预测.文献[10 ]采用长短期记忆网络(Long short-term memory, LSTM)和递归神经网络(Recurrent neural network, RNN)学习电池老化信息,结合蒙特卡罗模拟实现RUL预测,预测精度与计算效率较高,可靠性强.但该方法需要大量训练数据和较高的硬件需求.近年来随着大数据与硬件设备的高速发展,数据驱动的方法成为当前电池寿命预测的热门研究方向. ...
软包锂离子电池应力特性及其建模
1
2020
... 事实上,锂离子电池是“电-热-力”多物理场耦合系统[11 ] ,容量衰减与性能退化是由于电池内部多种退化机理相互作用的结果.在充放电过程中,锂离子在正负极之间不断迁移,引起电池内部应力以及外部厚度发生变化[12 ] .同时,电池老化过程中会出现不可逆的力学形变,致使电池性能下降,安全隐患增大.因此,在预测电池寿命时应充分考虑电池力学性能的变化.目前,已有学者针对电池应力及形变特性展开研究.文献[13 ]发现电池使用过程中的应力与SOH、SOC均具有一定相关性,并建立了应力-SOH/SOC模型.文献[14 ]研究了18650电池不同SOC在弯曲和压缩作用下的力学行为,指导单体电池和电池组的设计与监控.文献[15 ]通过测量电池循环过程中膨胀的变化,证明了膨胀是评估电池状态强有力的特征参数. ...
Stress properties and modeling of lithium-ion pouch batteries
1
2020
... 事实上,锂离子电池是“电-热-力”多物理场耦合系统[11 ] ,容量衰减与性能退化是由于电池内部多种退化机理相互作用的结果.在充放电过程中,锂离子在正负极之间不断迁移,引起电池内部应力以及外部厚度发生变化[12 ] .同时,电池老化过程中会出现不可逆的力学形变,致使电池性能下降,安全隐患增大.因此,在预测电池寿命时应充分考虑电池力学性能的变化.目前,已有学者针对电池应力及形变特性展开研究.文献[13 ]发现电池使用过程中的应力与SOH、SOC均具有一定相关性,并建立了应力-SOH/SOC模型.文献[14 ]研究了18650电池不同SOC在弯曲和压缩作用下的力学行为,指导单体电池和电池组的设计与监控.文献[15 ]通过测量电池循环过程中膨胀的变化,证明了膨胀是评估电池状态强有力的特征参数. ...
Stress evolution and capacity fade in constrained lithium-ion pouch cells
1
2014
... 事实上,锂离子电池是“电-热-力”多物理场耦合系统[11 ] ,容量衰减与性能退化是由于电池内部多种退化机理相互作用的结果.在充放电过程中,锂离子在正负极之间不断迁移,引起电池内部应力以及外部厚度发生变化[12 ] .同时,电池老化过程中会出现不可逆的力学形变,致使电池性能下降,安全隐患增大.因此,在预测电池寿命时应充分考虑电池力学性能的变化.目前,已有学者针对电池应力及形变特性展开研究.文献[13 ]发现电池使用过程中的应力与SOH、SOC均具有一定相关性,并建立了应力-SOH/SOC模型.文献[14 ]研究了18650电池不同SOC在弯曲和压缩作用下的力学行为,指导单体电池和电池组的设计与监控.文献[15 ]通过测量电池循环过程中膨胀的变化,证明了膨胀是评估电池状态强有力的特征参数. ...
State of health and charge measurements in lithium-ion batteries using mechanical stress
1
2014
... 事实上,锂离子电池是“电-热-力”多物理场耦合系统[11 ] ,容量衰减与性能退化是由于电池内部多种退化机理相互作用的结果.在充放电过程中,锂离子在正负极之间不断迁移,引起电池内部应力以及外部厚度发生变化[12 ] .同时,电池老化过程中会出现不可逆的力学形变,致使电池性能下降,安全隐患增大.因此,在预测电池寿命时应充分考虑电池力学性能的变化.目前,已有学者针对电池应力及形变特性展开研究.文献[13 ]发现电池使用过程中的应力与SOH、SOC均具有一定相关性,并建立了应力-SOH/SOC模型.文献[14 ]研究了18650电池不同SOC在弯曲和压缩作用下的力学行为,指导单体电池和电池组的设计与监控.文献[15 ]通过测量电池循环过程中膨胀的变化,证明了膨胀是评估电池状态强有力的特征参数. ...
State of charge dependent mechanical integrity behavior of 18650 lithium-ion batteries
1
2016
... 事实上,锂离子电池是“电-热-力”多物理场耦合系统[11 ] ,容量衰减与性能退化是由于电池内部多种退化机理相互作用的结果.在充放电过程中,锂离子在正负极之间不断迁移,引起电池内部应力以及外部厚度发生变化[12 ] .同时,电池老化过程中会出现不可逆的力学形变,致使电池性能下降,安全隐患增大.因此,在预测电池寿命时应充分考虑电池力学性能的变化.目前,已有学者针对电池应力及形变特性展开研究.文献[13 ]发现电池使用过程中的应力与SOH、SOC均具有一定相关性,并建立了应力-SOH/SOC模型.文献[14 ]研究了18650电池不同SOC在弯曲和压缩作用下的力学行为,指导单体电池和电池组的设计与监控.文献[15 ]通过测量电池循环过程中膨胀的变化,证明了膨胀是评估电池状态强有力的特征参数. ...
Reversible and irreversible expansion of lithium-ion batteries under a wide range of stress factors
2
2021
... 事实上,锂离子电池是“电-热-力”多物理场耦合系统[11 ] ,容量衰减与性能退化是由于电池内部多种退化机理相互作用的结果.在充放电过程中,锂离子在正负极之间不断迁移,引起电池内部应力以及外部厚度发生变化[12 ] .同时,电池老化过程中会出现不可逆的力学形变,致使电池性能下降,安全隐患增大.因此,在预测电池寿命时应充分考虑电池力学性能的变化.目前,已有学者针对电池应力及形变特性展开研究.文献[13 ]发现电池使用过程中的应力与SOH、SOC均具有一定相关性,并建立了应力-SOH/SOC模型.文献[14 ]研究了18650电池不同SOC在弯曲和压缩作用下的力学行为,指导单体电池和电池组的设计与监控.文献[15 ]通过测量电池循环过程中膨胀的变化,证明了膨胀是评估电池状态强有力的特征参数. ...
... 本文电池数据选用UofM Pouch Cell Voltage and Expansion Cyclic Aging公开数据集[15 ] ,该数据集首次记录了电池机械特性的演变,涵盖了多种老化条件,记录了电池使用过程中电压、电流、温度、容量、电池膨胀等多组数据.电池由密歇根大学电池实验室(UMBL)制造,额定容量为5.0 A·h,工作电压区间为3.0~4.2 V.电池长、宽、厚度分别为132 mm、90 mm、40 mm.电池充放电策略如下:首先对电池长宽对应的表面均匀施加34.5 kPa的初始压力,并在给定温度环境内静置3 h直至达到热平衡后,恒流充电至4.2 V,之后恒压充电至电流小于C /50截止;然后,充电静置1 h,恒流放电至3.0 V.在本文试验中,选取其中的01、05、09、10号电池作为研究对象,电池参数如表1 所示. ...
A learning algorithm for continually running fully recurrent neural networks
1
1998
... 传统递归神经网络(RNN)[16 ] 广泛应用于处理时间、语音、文本等序列问题,然而,RNNs通常由于梯度消失与梯度爆炸的问题,使得其难以学习和保持长期依赖.为改进这些问题,LSTM神经网络[17 ] 被提出,其基本神经元如图1 所示. ...
Long short-term memory
1
1997
... 传统递归神经网络(RNN)[16 ] 广泛应用于处理时间、语音、文本等序列问题,然而,RNNs通常由于梯度消失与梯度爆炸的问题,使得其难以学习和保持长期依赖.为改进这些问题,LSTM神经网络[17 ] 被提出,其基本神经元如图1 所示. ...
Understanding volume change in lithium-ion cells during charging and discharging using in situ measurements
1
2007
... 图2 展示了01号电池在循环充放电过程中峰值膨胀与最小膨胀变化曲线,其中峰值膨胀对应于电池充满电时电池厚度变化,最小膨胀对应于电池完全放电时电池厚度变化.可以看出,在电池充电过程中,电池厚度不断膨胀;放电过程中,电池厚度不断收缩.这种可逆的电池膨胀变化是由于该种电池厚度的变化是可逆的,即可逆膨胀.并且在电池完全放电后,电池膨胀相对于上次循环结束会存在不可逆的积累,即不可逆膨胀.结合图3 所示的容量变化曲线可以看出,随着电池的循环老化,可用容量不断衰减,可逆膨胀呈轻微衰减趋势,而不可逆膨胀明显增加,远大于可逆膨胀的减小.这主要是因为在电池使用过程中,由于锂离子的损失,电极中可供迁移的锂离子含量逐渐减小[18 ] ,可逆膨胀相应不断降低;同时,电池的老化伴随着内部聚合物变形,SEI膜增厚[19 ] ,使得电池内部应力明显增大,从而造成电池不可逆的膨胀不断累积.因此,可逆膨胀与不可逆膨胀都与容量的变化密切相关. ...
锂离子电池硅基负极循环过程中的膨胀应力
1
2022
... 图2 展示了01号电池在循环充放电过程中峰值膨胀与最小膨胀变化曲线,其中峰值膨胀对应于电池充满电时电池厚度变化,最小膨胀对应于电池完全放电时电池厚度变化.可以看出,在电池充电过程中,电池厚度不断膨胀;放电过程中,电池厚度不断收缩.这种可逆的电池膨胀变化是由于该种电池厚度的变化是可逆的,即可逆膨胀.并且在电池完全放电后,电池膨胀相对于上次循环结束会存在不可逆的积累,即不可逆膨胀.结合图3 所示的容量变化曲线可以看出,随着电池的循环老化,可用容量不断衰减,可逆膨胀呈轻微衰减趋势,而不可逆膨胀明显增加,远大于可逆膨胀的减小.这主要是因为在电池使用过程中,由于锂离子的损失,电极中可供迁移的锂离子含量逐渐减小[18 ] ,可逆膨胀相应不断降低;同时,电池的老化伴随着内部聚合物变形,SEI膜增厚[19 ] ,使得电池内部应力明显增大,从而造成电池不可逆的膨胀不断累积.因此,可逆膨胀与不可逆膨胀都与容量的变化密切相关. ...
Studies on the swelling force during cycling of Si-based anodes in lithium ion batteries
1
2022
... 图2 展示了01号电池在循环充放电过程中峰值膨胀与最小膨胀变化曲线,其中峰值膨胀对应于电池充满电时电池厚度变化,最小膨胀对应于电池完全放电时电池厚度变化.可以看出,在电池充电过程中,电池厚度不断膨胀;放电过程中,电池厚度不断收缩.这种可逆的电池膨胀变化是由于该种电池厚度的变化是可逆的,即可逆膨胀.并且在电池完全放电后,电池膨胀相对于上次循环结束会存在不可逆的积累,即不可逆膨胀.结合图3 所示的容量变化曲线可以看出,随着电池的循环老化,可用容量不断衰减,可逆膨胀呈轻微衰减趋势,而不可逆膨胀明显增加,远大于可逆膨胀的减小.这主要是因为在电池使用过程中,由于锂离子的损失,电极中可供迁移的锂离子含量逐渐减小[18 ] ,可逆膨胀相应不断降低;同时,电池的老化伴随着内部聚合物变形,SEI膜增厚[19 ] ,使得电池内部应力明显增大,从而造成电池不可逆的膨胀不断累积.因此,可逆膨胀与不可逆膨胀都与容量的变化密切相关. ...
双时间尺度下基于Transformer的锂电池剩余寿命预测
1
2023
... 为了消除各指标之间不同尺度的影响,保证各数据指标之间的可比性,需要对输入数据归一化处理[20 ] ,把每个特征序列数值归一化至0~1.归一化公式为 ...
Remaining life prediction of lithium batteries based on transformer at dual time scales
1
2023
... 为了消除各指标之间不同尺度的影响,保证各数据指标之间的可比性,需要对输入数据归一化处理[20 ] ,把每个特征序列数值归一化至0~1.归一化公式为 ...
基于数据预处理和长短期记忆神经网络的锂离子电池寿命预测
2
2022
... 为进一步证明本文所提RUL预测方法的有效性与准确性,分别与文献[21 ]中提出的基于数据预处理和长短期记忆神经网络的预测方法、文献[22 ]中提出的基于Elman神经网络的预测方法、文献[23 ]中提出的基于Bi-GRU网络的预测方法进行比较.利用01号电池数据进行对比试验,训练集比例设置为45%. ...
... 各方法容量预测曲线如图9 所示,可以看出本文与文献[21 ]提出的预测方法相比更能充分学习电池老化特性,准确跟踪容量衰减趋势.进一步结合表4 展示的不同预测方法模型RUL预测结果及误差,对比发现,本文提出的RUL预测方法预测精度更高,RMSE与MAE值更低,RUL预测结果更准确. ...
Prediction of remaining useful life of lithium-ion battery based on adaptive data preprocessing and long short-term memory network
2
2022
... 为进一步证明本文所提RUL预测方法的有效性与准确性,分别与文献[21 ]中提出的基于数据预处理和长短期记忆神经网络的预测方法、文献[22 ]中提出的基于Elman神经网络的预测方法、文献[23 ]中提出的基于Bi-GRU网络的预测方法进行比较.利用01号电池数据进行对比试验,训练集比例设置为45%. ...
... 各方法容量预测曲线如图9 所示,可以看出本文与文献[21 ]提出的预测方法相比更能充分学习电池老化特性,准确跟踪容量衰减趋势.进一步结合表4 展示的不同预测方法模型RUL预测结果及误差,对比发现,本文提出的RUL预测方法预测精度更高,RMSE与MAE值更低,RUL预测结果更准确. ...
基于Elman神经网络的锂离子电池RUL间接预测研究
1
2019
... 为进一步证明本文所提RUL预测方法的有效性与准确性,分别与文献[21 ]中提出的基于数据预处理和长短期记忆神经网络的预测方法、文献[22 ]中提出的基于Elman神经网络的预测方法、文献[23 ]中提出的基于Bi-GRU网络的预测方法进行比较.利用01号电池数据进行对比试验,训练集比例设置为45%. ...
RUL indirect prediction of lithium-ion battery based on Elman neural network
1
2019
... 为进一步证明本文所提RUL预测方法的有效性与准确性,分别与文献[21 ]中提出的基于数据预处理和长短期记忆神经网络的预测方法、文献[22 ]中提出的基于Elman神经网络的预测方法、文献[23 ]中提出的基于Bi-GRU网络的预测方法进行比较.利用01号电池数据进行对比试验,训练集比例设置为45%. ...
基于BiGRU网络的锂电池寿命预测
1
2021
... 为进一步证明本文所提RUL预测方法的有效性与准确性,分别与文献[21 ]中提出的基于数据预处理和长短期记忆神经网络的预测方法、文献[22 ]中提出的基于Elman神经网络的预测方法、文献[23 ]中提出的基于Bi-GRU网络的预测方法进行比较.利用01号电池数据进行对比试验,训练集比例设置为45%. ...
Lithium battery life prediction based on BiGRU network
1
2021
... 为进一步证明本文所提RUL预测方法的有效性与准确性,分别与文献[21 ]中提出的基于数据预处理和长短期记忆神经网络的预测方法、文献[22 ]中提出的基于Elman神经网络的预测方法、文献[23 ]中提出的基于Bi-GRU网络的预测方法进行比较.利用01号电池数据进行对比试验,训练集比例设置为45%. ...