1 引言
漏电断路器可以有效防止人体触电或漏电造成的火灾、爆炸等事故,其工作稳定性直接关系到整个系统的正常运行以及用电人员的生命财产安全。电子式漏电断路器凭借其工艺简单、成本低廉等特点在国内得到了广泛应用。在使用过程中,产品的材料老化、疲劳损伤均会随着使用时间的增加不断累积,从而降低产品的漏电保护性能,最终会导致产品失效。为了避免电子式漏电断路器超龄服役,保障用电人员的生命财产安全以及设备的正常运行,需要掌握其老化规律并能够有效地评估其使用寿命。
近年来,国内外研究人员在漏电断路器的可靠性[1⇓⇓⇓-5]和环境因素影响领域[6⇓⇓⇓-10]已有大量的研究成果,而对寿命预测领域的研究成果较少。加速老化试验和寿命预测作为可靠性理论中的一个重要分支,被广泛应用于低压电器的各个领域[11⇓⇓-14]。文献[15]给出了漏电断路器加速老化的试验方案,并提出了基于Winner过程的漏电断路器剩余寿命的概率密度函数和可靠度函数的预测方法;文献[16]基于恒定应力加速退化试验,使用Winner过程和Arrhenius模型对电子式漏电断路器进行了寿命评估;文献[17]基于Arrhenius模型给出了继电器在现场实际使用温度或给定温度下的使用寿命预测方法。随着相关学者对寿命预测方法的深入研究,文献[18⇓-20]将统计学理论和Arrhenius模型相结合,分别对试验数据的有效性、Arrhenius模型的适用性以及回归方程的显著性和相关性等方面进行了检验,提高了试验数据的有效性。
以上成果都是对寿命预测方法的应用研究,在已有的研究成果中,关于试验数据检验的相关研究成果虽然已被提出,但是对于拟合模型质量是否符合要求以及如何对模型进行修正的问题还尚未解决,检验体系尚不完善。基于已有研究成果,本文提出了一套完整的寿命预测方法,该方法使用Pearson检验确保了试验数据的线性相关性;使用White检验、Park检验以及Gleiser检验确保了拟合模型的同方差性,并通过加权最小二乘法对含有异方差的模型进行了修正;使用Shapiro-Wilk检验和Durbin-Watson检验确保了拟合模型的残差正态性与独立性,进一步提高了寿命预测的准确性。
2 漏电断路器的加速应力和特征参数选取
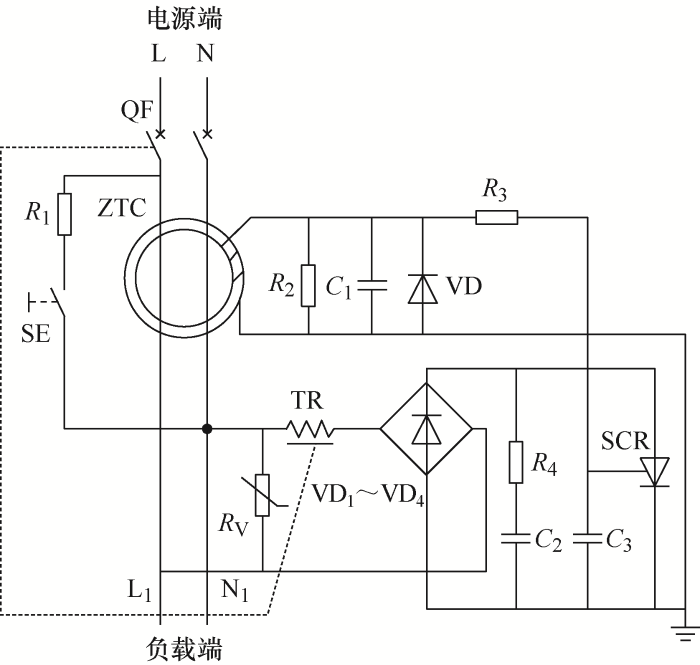
电子式漏电断路器电气原理图如图1所示,由原理图可知,当零序互感器(Zero current transformer, ZTC)一次侧检测到剩余电流的存在,ZTC二次侧就会产生感应电动势,R2和C1上会产生电压,此时R3、C3支路电压等于R2两端电压,其中C3两端电压为可控晶闸管(Silicon controlled rectifier, SCR)的开启电压,当C3两端电压达到开启电压时一定值时,会使晶闸管SCR导通,从而使漏电断路器动作。
图1
3 寿命预测模型
对于在正常使用环境下可靠性高且寿命长的产品,一般采用加速老化试验的方法评估其可靠性。由于电子式漏电断路器的剩余分断电流随着温度的增加而降低,因此可推断热应力会导致电子式漏电断路器的电子元件加速老化。阿伦尼斯(Arrhenius)模型描述了热应力和化学反应速度的关系,为加速老化试验提供了理论依据。通过Arrhenius方程不仅可以预测给定温度下的使用寿命,还可根据某一温度下的使用寿命推导出另一温度下的使用寿命,其具体表示如下
式中,K(t)表示反应速率,与在工作温度T下的老化失效时间t成反比关系;Aa表示比例常数;Ea为化学反应的活化能;R为波尔茨曼常数;T表示工作温度的绝对温度。对式(1)两边取对数并简单处理,可得到
令
在对试验数据进行处理分析后,将老化退出时间对数和工作温度的倒数采用最小二乘法进行线性拟合,从而求出活化能Ea与比例常数A,即可得到式(4)所示的漏电断路器寿命评估模型,根据该模型可计算不同温度TU下的使用寿命。
4 试验数据分析及拟合模型检验
4.1 试验数据分析
在进行模型拟合前,由于使用Arrhenius方程进行寿命评估时,需要每个温度下样本的老化退出时间数据满足对数正态分布、平均退出失效时间的对数和绝对温度的倒数存在线性关系以及各温度下的试验数据满足相同的老化机理。为了检验试验数据的有效性,提高拟合模型的质量,需要先对试验数据进行检验,只有通过检验的试验数据才可以用于模型拟合,试验数据检验包括正态性检验、方差齐性检验和相关性检验。
4.1.1 正态性检验
由于使用Arrhenius方程进行寿命评估时,需要每个温度下样本的老化退出时间满足对数正态分布,因此需要对各温度下样本的老化退出时间对数进行正态检验。常见的正态性检验方法有Anderson-Darling(AD)检验、Kolmogorov-Smirnov (K-S)检验和Shapiro-Wilk(W)检验等,而在《GB/T 4882—2001数据的统计处理和解释:正态性检验》中明确了W检验适用于3≤n≤50的小样本数据。考虑到试验样本较少,本文选取W检验对试验数据进行正态性检验。当显著性小于0.05时,则拒绝原假设,即认为数据样本不是来自正态总体,反之则认为来自正态总体。当各温度下样本的老化退出时间对数服从正态分布后,本文采用每一温度下样本数据的数学期望来表示该温度下的平均老化时间。
在得到平均退出时间后,由式(2)可知,平均退出时间的对数与试验温度的倒数存在线性相关性,由于因变量服从正态分布是线性回归的基本前提,因此需要对平均退出时间的对数进行正态性检验,检验方法同上。
4.1.2 方差齐性检验
虽然试验数据通过了正态性检验,但并不意味着所有数据都可以用来模型拟合。对于多应力水平下的加速老化试验,只有满足方差齐性的数据,才能表明在不同应力水平的加速老化试验服从相同的反应机理,此时的试验数据才可以用来模型拟合。否则,如果不同应力水平的加速老化试验涉及到的反应机理不同或不完全相同,此时通过试验数据拟合出的模型可能会因为方差不齐导致寿命预测时的精度降低,与实际产品寿命产生较大偏离。
常用的方差齐性检验有方差比、Hartley检验、Levene检验、Bartlett检验。其中方差比、Hartle检验和Bartlett检验需要待检验数据服从正态分布,而Levene检验不太依赖正态分布。在统计学中比较常用的是Levene检验,适用于多组方差的比较,且对正态性没有要求。综上所述,本文采用Levene检验对试验数据进行方差齐性检验,当检验结果的显著性水平大于给定的显著性水平时,认为数据满足方差齐性,否则,数据方差不齐。
4.1.3 相关性检验
使用Arrhenius方程进行寿命评估时,需要满足老化时间的对数与试验温度的倒数存在线性相关性,因此需要对平均老化时间的对数与试验温度的倒数进行相关性检验,将通过线性相关性检验的数据用来线性拟合,得到的拟合模型才有意义。
常用的相关性检验包括皮尔逊(Pearson)相关系数检验和斯皮尔曼(Spearman)相关系数检验,其中Pearson评估的是两个变量的线性关系,而Spearman评估的是两变量的单调关系。由于本文拟合的是线性方程,因此本文选取Pearson检验对试验数据进行检验。两个变量之间的皮尔逊相关系数
综上所述,在对模型进行回归前,为了保证试验数据满足Arrhenius模型的使用要求,需要对试验数据进行正态性检验、方差齐性检验以及相关性检验,如果检验不通过则试验数据无法使用Arrhenius模型进行寿命预测,需要找出并剔除异常数据同时再次对数据进行以上检验,直到检验通过。
4.2 拟合模型检验
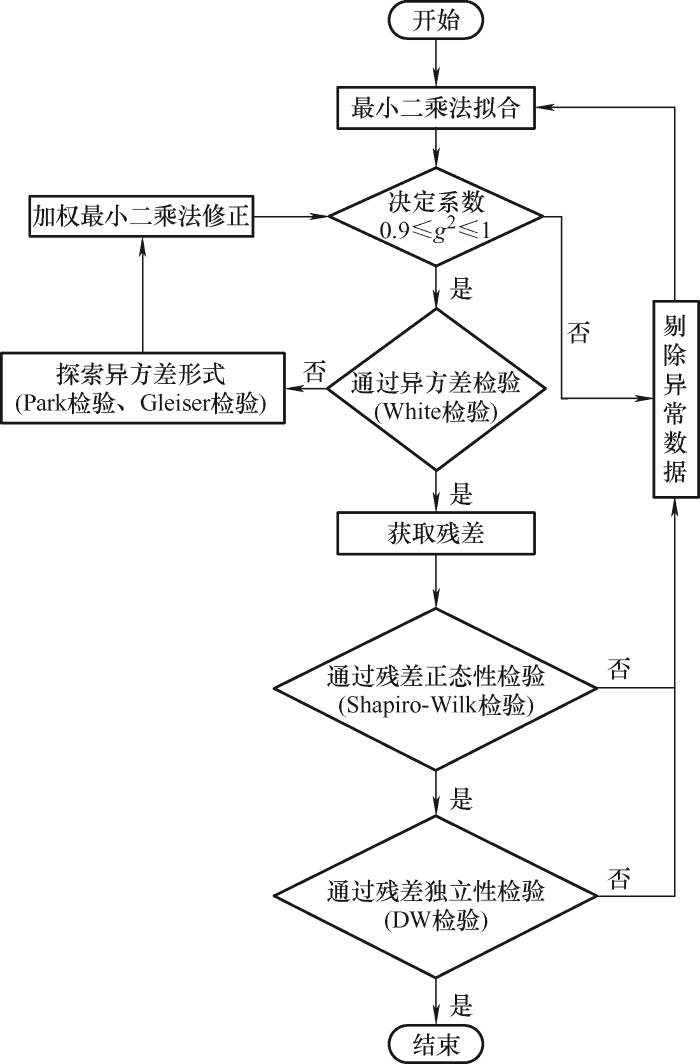
通过对Arrhenius模型的推导得知,平均老化失效时间的对数和绝对温度的倒数存在线性关系,最小二乘法(Ordinary least square, OLS)是线性回归中最常用的方法,在传统的寿命预测方法中,通过OLS方法拟合模型后,会直接参照模型的决定系数R2是否接近于1来评估拟合模型的质量,而在统计学中,拟合模型存在很多限制条件,上述步骤里只是构建了模型,至于模型质量如何,模型是否满足线性回归的前提条件,都需要进一步进行确认,检验过程如图2所示。如果直接拟合出来的模型进行寿命评估,一旦拟合模型不满足线性拟合的前提条件,将会导致寿命预测的结果偏离实际值,而这部分研究在已有的研究成果中多未提及。
图2
4.2.1 异方差检验
拟合模型的残差满足同方差性是线性回归的基本前提,即拟合值与真实值之间的差值-随机误差
当检验结果出现异方差时,需要对异方差进行处理,消除异方差常用的方法是加权最小二乘法(Weighted least squares, WLS),即对原模型进行加权处理,使其变成一个新的不存在异方差性的模型,其中关于权数变量的选择,本文采用Park检验得到的残差估计方程
4.2.2 残差正态性检验
拟合模型的残差具有正态性是线性回归的基本前提,如果拟合模型的残差不满足正态分布,说明模型中的残差不是随机的,或者说残差中的一部分与自变量有关系,就会导致整体模型构建较差,进而影响模型的预测效果。因此需要对拟合模型的残差进行正态性检验,检验方法同第4.1节。
4.2.3 残差独立性检验
拟合模型具有残差独立性是线性回归的基本前提之一,如果拟合模型存在残差独立性,说明可能存在与因变量相关的因素没有引入回归方程,导致整体模型构建较差,进而影响模型的预测效果。因此需要对拟合模型进行残差独立性检验。常用的残差独立性检验方法是德宾沃森(Durbin-Watson)检验,又称DW检验,其检验结果DW值一般介于0~4。得到检验结果后,根据解释变量数量k和样本容量n查DW分布表,得到临界值dl和du,当0<DW<dl时,表示存在正相关性;当dl<DW<du时,表示不能确定是否具有相关性;当du<DW<4-du时,表示不存在相关性;当4-du<DW<4-dl时,表示不能确定是否具有相关性;当4-dl<DW<4时,表示存在负相关性。
综上所述,在模型回归后,为了保证回归模型性的有效性,需要分别对模型进行残差独立性检验、残差正态性检验和异方差检验,三个检验必须全部通过,才能保证拟合模型的质量。其中,当检验结果出现异方差时,需要使用加权最小二乘法进行消除,并重复以上检验,直至回归的模型通过所有检验,模型才可以用来预测寿命。
5 算例分析
5.1 加速老化试验方案
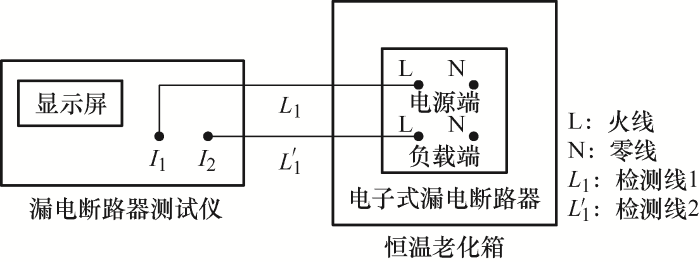
本次试验用到的试验设备包括恒温老化箱、漏电断路器测试仪以及同一型号的电子式漏电断路器,试验电路框图如图3所示,通过导线L、N为漏电断路器供电,保证漏电断路器能够正常运行。将电源端和负载端的火线端口通过导线L1和L'1连接至漏电断路器测试仪的检测端口I1、I2,并通过调节漏电断路器测试仪的可调电阻改变漏电断路器的漏电电流,直至漏电断路器动作,从而测定漏电断路器的剩余动作电流值。
图3
由于漏电断路器正常工作的温度范围在-25~+40 ℃,为保证加速老化试验效果,选择的最低加速应力水平应当接近漏电断路器正常工作的最高温度。试验样品的外部塑料材料为聚苯乙烯,当温度超过95 ℃时会发生软化,从而导致漏电断路器无法正常工作;其内部电路板选用的是环氧玻璃纤维板,在150 ℃的高温下仍有较高的力学强度;其内部含有多种电容,而在电容中最不耐高温的是电解电容,其可以承受的可靠工作温度为105 ℃;其内部所使用的电阻有碳膜电阻和金属电阻,碳膜电阻的耐热能力比金属电阻强,金属电阻因功率不同,耐温在125~235 ℃;其内部所用晶闸管的可靠工作温度在-45~125 ℃。综上所述,试验样品外部结构、内部电路板以及电阻、电容等电子元件的最高可靠工作温度都在95 ℃以上。为保证加速老化过程中老化机理不发生改变,选择的最高加速应力水平不应超过95 ℃,因此本文将最低加速应力设置为55 ℃,最高加速应力设置为90 ℃。
从同一批产品中随机选取48只电子式漏电断路器作为试验样品,将样品分为8组,分别在55 ℃、60 ℃、65 ℃、70 ℃、75 ℃、80 ℃、85 ℃、90 ℃温度下进行加速老化试验,以24 h作为一个加速老化周期,每个试验周期结束后,在常温(25 ℃)下冷却2 h,然后通过漏电断路器测试仪测定并记录各样本的剩余动作电流值,当样本的剩余动作电流减小至15 mA时,该样本退出试验。不同应力下各个样本的老化退出时间如表1所示。
表1 不同温度下的老化退出时间 h
| 样本序号 | 温度/℃ | |||
|---|---|---|---|---|
| 55 | 60 | 65 | 70 | |
| 1 | 8 643 | 6 990 | 5 636 | 4 435 |
| 2 | 9 108 | 7 465 | 6 077 | 4 773 |
| 3 | 8 875 | 7 273 | 5 717 | 4 627 |
| 4 | 8 675 | 7 237 | 5 691 | 4 502 |
| 5 | 8 483 | 6 934 | 5 537 | 4 371 |
| 6 | 9 047 | 7 403 | 5 916 | 4 710 |
| 样本序号 | 温度/℃ | |||
| 75 | 80 | 85 | 90 | |
| 1 | 3 690 | 3 014 | 2 363 | 1 265 |
| 2 | 3 920 | 3 093 | 2 465 | 1 319 |
| 3 | 3 761 | 3 034 | 2 421 | 1 270 |
| 4 | 3 703 | 3 073 | 2 402 | 1 277 |
| 5 | 3 607 | 2 972 | 2 341 | 1 256 |
| 6 | 3 840 | 3 082 | 2 442 | 1 295 |
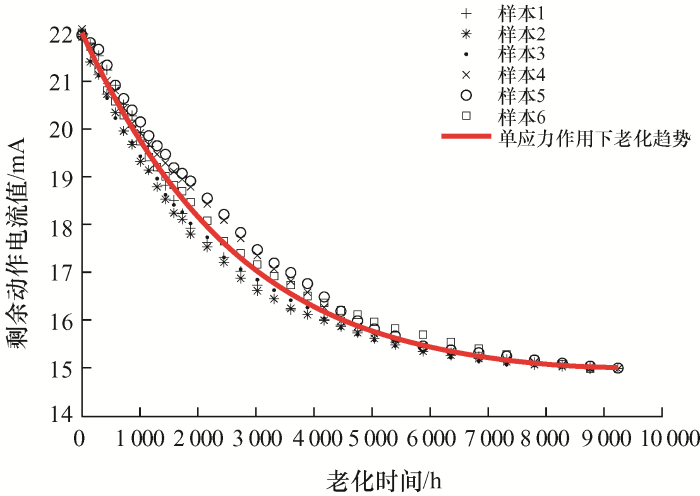
图4
5.2 试验数据检验
5.2.1 正态性检验
表2 老化退出时间对数正态性检验结果
| 检验参数 | 统计量 | 自由度 | 显著性 |
|---|---|---|---|
| 老化退出时对数(55 ℃) | 0.941 | 6 | 0.664 |
| 老化退出时对数(60 ℃) | 0.915 | 6 | 0.468 |
| 老化退出时对数(65 ℃) | 0.938 | 6 | 0.639 |
| 老化退出时对数(70 ℃) | 0.950 | 6 | 0.741 |
| 老化退出时对数(75 ℃) | 0.979 | 6 | 0.940 |
| 老化退出时对数(80 ℃) | 0.925 | 6 | 0.551 |
| 老化退出时对数(85 ℃) | 0.963 | 6 | 0.849 |
| 老化退出时对数(90 ℃) | 0.926 | 6 | 0.521 |
表3 平均退出时间
| 环境温度T/℃ | 1/T | 平均退出时间t/h | lnt |
|---|---|---|---|
| 328.15 | 0.003 047 | 8 805 | 9.083 |
| 333.15 | 0.003 002 | 7 217 | 8.884 |
| 338.15 | 0.002 957 | 5 763 | 8.659 |
| 343.15 | 0.002 914 | 4 570 | 8.427 |
| 348.15 | 0.002 872 | 3 753 | 8.230 |
| 353.15 | 0.002 832 | 3 045 | 8.021 |
| 358.15 | 0.002 792 | 2 406 | 7.786 |
| 363.15 | 0.002 754 | 1 280 | 7.155 |
5.2.2 方差齐性检验
根据第4.1.2节的介绍,在满足正态性检验后,为保证不同应力水平下的试验数据服从相同的老化机理,需要对试验数据进行方差齐性检验。使用Levene检验方法对表1中的老化退出时间对数进行方差齐性检验的显著性为0.194,大于给定的显著性水平0.05,即认为各组试验数据的方差没有显著性差异,满足方差齐性。
5.2.3 相关性检验
根据第4.1.3节的介绍,平均老化时间的对数与试验温度的倒数存在线性相关性,因此需要对平均老化时间的对数与试验温度的倒数进行相关性检验,使用DW检验方法计算得到的DW值为0.983,接近于1,表明两组数据间有着显著的线性关系。
5.3 拟合模型检验
在通过试验数据经过分析后,可以确定绝对环境温度55~90 ℃的老化试验数据满足寿命评估的基本要求,可针对这些数据进行模型拟合与寿命计算。使用传统的寿命预测方法对表3中的数据进行拟合,拟合模型为y=5 962.100x-8.987 229,拟合模型的决定系数R2=0.953>0.95,初步表明拟合情况较好,但是根据第4.2节的介绍,在模型拟合后,为了保证拟合模型性的质量,提高寿命预测的准确性,还需要进一步对拟合模型进行残差独立性检验、残差正态性检验和异方差检验。
5.3.1 异方差检验与消除
采用White检验对上述通过传统寿命预测方法得到的拟合模型进行异方差检验,通过计算得R2=0.825 8,nR2=6.60,当取显著水平α=0.05时,
表4 Gleiser检验结果
| 解释变量xh | 显著性p | 决定系数R2 |
|---|---|---|
| x0.5 | 0.038 5 | 0.535 3 |
| x-0.5 | 0.036 3 | 0.548 1 |
| x | 0.039 7 | 0.528 9 |
| x-1 | 0.034 1 | 0.554 9 |
| x2 | 0.042 2 | 0.515 9 |
| x-2 | 0.033 2 | 0.567 1 |
由Gleiser检测结果可知,取显著性水平α=0.05时,当解释变量的系数为±0.5、±1和±2时,辅助回归方程均能够通过显著性检验,说明存在这几种形式的异方差,Gleiser检验可以通过决定系数R2的大小来确定异方差的具体形式。本例中,当解释变量的系数为-2时的决定系数R2最大,可以据此来确定异方差的形式。
根据第4.2.1节的介绍,当拟合模型出现异方差时,需要通过加权最小二乘法对异方差进行消除,结合Park检验和Gleiser检验结果,本例中的权数变量选取1/x-2、1/e2和1/|e|,加权最小二乘法拟合结果如表5所示,通过决定系数R2可见拟合效果较好,但是并不能以此作为评判模型质量好与坏的标准。
表5 加权最小二乘法拟合结果
| 序号 | 权数变量 | 拟合模型 | 决定系数R2 |
|---|---|---|---|
| 1 | 1/x-2 | y=6 082.034x-9.334 013 | 0.95 |
| 2 | 1/|e| | y=5 259.743x-6.898 744 | 0.99 |
| 3 | 1/e2 | y=5 113.363x-6.462 814 | 0.99 |
由检测结果可知,经加权最小二乘法得到的三组拟合模型中,模型1的检验结果大于6.60,而另外两组模型都小于该指标,结果表明通过加权最小二乘法后,只有模型1成功消除了异方差。
5.3.2 残差正态性检验
根据第4.2.2节的介绍,为了确保模型的质量,需要进一步对通过加权最小二乘法拟合的模型进行残差正态性检验,检验结果如表7所示。
由表7可知模型1的显著性水平大于给定指标0.05,满足残差正态性要求,表明模型1的拟合质量较好。
5.3.3 残差独立性检验
根据第4.2.3节的介绍,为进一步验证拟合模型的质量,需要对拟合模型进行残差独立性检验,通过DW检验对模型1进行残差独立性检验,经检验得到的DW值为1.35,本例中解释变量为1,样本容量为8,查DW分布表可知,检验水平为0.05时,对应的DW检验上界值为1.332,下界值为0.763,由于1.380>1.332,表明该模型不存在自相关性,模型拟合质量较好。
5.4 寿命预测
通过异方差检验、残差正态性检验和残差独立性检验后,检验结果表明拟合模型1比其他两个拟合模型的质量好,为了说明不同拟合模型间的差异,根据式(1)~(4)分别使用上述四个模型对常温(25 ℃)下的漏电断路器进行寿命预测,预测结果如表8所示。
由预测结果可知,使用消除异方差且能通过残差正态性检验和残差独立性检验的拟合模型1的预测寿命为7.53年,使用传统预测方法得到的拟合模型以及没有通过检验的拟合模型得到的预测寿命均偏小。考虑到本文所使用方法不仅确保了试验数据的有效性、老化机理一致性、Arrhenius模型适用性,而且确保了试验数据的函数相关性以及拟合模型的质量,因此在理论上,该预测寿命更符合电子式漏电断路器的实际使用寿命。
6 结论
基于国内外学者的研究成果,本文以剩余动作电流作为加速老化试验的特征参量,以热应力作为加速应力,对电子式漏电断路器进行了加速老化试验。基于加速老化试验数据,通过统计学相关检验和Arrhenius方程对电子式漏电断路器进行了寿命评估,得到了以下结论。
(1) 通过对加速老化试验数据的分析,发现在不同的温度应力下,电子式漏电断路器的老化速度会随着温度应力的增加而增加,而在相同的温度应力下,随着老化时间的增加,其老化速率会不断减小。
(2) 使用本文所提方法对加速老化试验数据进行分析处理,预测出电子式漏电断路器在常温下的使用寿命为7.53年,电子式漏电断路器的推荐使用寿命一般在5~8年,预测结果表明使用所提方法对电子式漏电断路器进行寿命预测具有一定的参考价值。
(3) 为进一步说明拟合模型检验的必要性,本文使用传统寿命预测方法得到的模型以及未通过检验的模型对其进行寿命预测,对比发现,预测结果均偏小。
准确有效评估电子式漏电断路器的使用寿命,可以有效防止由于电子式漏电断路器超龄服役带来的损失,为电子式漏电断路器的维护运营提供参考,保障建筑供配电系统的稳定性与可靠性,不仅有经济效益,更具有社会效益。同时本文的研究成果也可以为其他产品的寿命预测提供参考。
参考文献
Quality of residual current-operated circuit breakers
[J].DOI:10.1002/etep.v6:3 URL [本文引用: 1]
Reliability on the unintended trips of residual current operated circuit breakers due to surge currents
[J].
漏电断路器的可靠性及其试验方法
[J].
Reliability of leakage circuit breaker and its test method
[J].
漏电断路器的拒动作与误动作的主要原因
[J].
The main reasons for the refusal and malfunction of the leakage circuit breaker
[J].
漏电保护器的故障原因探析
[J].
Analysis on the causes of the faults of the leakage protector
[J].
自适应漏电保护技术及其应用
[J].
Adaptive technology of leakage current operation protection and its application
[J].
剩余电流保护器的剩余动作电流温度特性研究
[J].
Research on temperature characteristics of residual operating current of residual current device
[J].
基于数据融合的温度对漏电断路器动作特性的影响研究
[J].
Research on effect of temperature on operating characteristics of residual current circuit breaker based on data fusion technology
[J].
新陈代谢灰色粒子滤波实现电池剩余寿命预测
[J].
Remaining useful life prediction of battery using metabolic grey particle filter
[J].
基于小波包能量熵的电池剩余寿命预测
[J].
Prediction of battery useful life based on wavelet packet energy entropy
[J].
基于粗糙集与证据理论的交流接触器预期电寿命预测
[J].
Expected electrical life prediction of AC contactor based on rough set and evidence theory
[J].
电机定子绝缘老化寿命预测研究进展
[J].
Research process on prediction of aging life of motor stator insulation
[J].
漏电断路器的步进加速退化试验方案研究
[J].
Research on step acceleration degradation test scheme of leakage circuit breaker
[J].
基于Wiener过程电子式漏电断路器的剩余寿命预测
[J].
Remaining life prediction of electronic residual current circuit breaker based on Wiener process
[J].
一种电磁继电器寿命评估的新方法
[J].
A new life evaluation method of electromagnetic relay
[J].
基于电-热加速老化的LED寿命评估检验方法研究
[J].
Research on the test method of LED life evaluation based on electro-thermal accelerated aging
[J].
基于统计检验的光电耦合器寿命预测模型研究
[J].
Research on life prediction model of optocoupler based on normal test
[J].
基于统计检验的发电机定子线棒绝缘热老化寿命评估
[J].
Thermal ageing life evaluation of stator bar insulation for generator based on statistical test
[J].
The effect of temperature on the reliability of electronic components
[C]//