基于EWT-FE分析联合改进SVM算法的GIS局部放电诊断方法*

doi:10.11985/2024.01.040

基于EWT-FE分析联合改进SVM算法的GIS局部放电诊断方法^*

王利猛^,, 王硕^,

现代电力系统仿真控制与绿色电能新技术教育部重点实验室(东北电力大学) 吉林 132012

Partial Discharge in GIS Diagnosis Method Based on EWT-FE Analysis and Improved SVM Algorithm

WANG Limeng^,, WANG Shuo^,

Key Laboratory of Modern Power System Simulation and Control & Renewable Energy Technology, Ministry of Education(Northeast Electric Power University), Jilin 132012

收稿日期: 2023-02-28 修回日期: 2023-06-21

基金资助:

国家重点研发计划(2018YFB09044703)
吉林省自然科学基金(YDZJ202101ZYTS149)

Received: 2023-02-28 Revised: 2023-06-21

作者简介 About authors

王利猛，男，1971年生，博士，副教授，硕士研究生导师。主要从事电力系统监测与控制方面的研究。E-mail：wlm_28@163.com;

王硕，男，1999年生，硕士研究生。主要从事电气设备故障诊断等方面的研究。E-mail：190196562@qq.com

摘要

为提高气体绝缘组合电器(Gas insulated switchgear，GIS)局部放电类型诊断的精度，提出了一种基于EWT-FE结合IHPO-SVM算法的GIS局部放电诊断方法。为深度挖掘局部放电信号内部特征，利用经验小波变换(Empirical wavelet transform，EWT)结合模糊熵(Fuzzy entropy，FE)算法对信号进行分解，并提取有效特征量；为提高支持向量机(Support vector machine，SVM)算法自适应能力与分类识别精度，提出利用经过余弦衰减计算方法以及指数下降函数改进的猎人猎物优化(Improved hunter-prey optimizer，IHPO)算法对SVM算法参数进行优化选取；搭建GIS局部放电试验模型，建立基于EWT-FE信号分析结合IHPO-SVM的局部放电识别模型，对所提算法有效性进行验证。试验结果表明，所提算法GIS局部放电类型诊断精度均大于95%，优于传统诊断算法。

关键词： 局部放电; 气体绝缘组合电器; 经验小波变换; 模糊熵; 改进猎人猎物优化算法; 支持向量机算法

Abstract

To improve the accuracy of partial discharge type diagnosis in of gas insulated switchgear(GIS), a method of partial discharge diagnosis in GIS based on EWT-FE and IHPO-SVM algorithm is proposed. To deeply explore the internal features of the partial discharge signal, the empirical wavelet transform(EWT) combined with the fuzzy entropy(FE) algorithm is used to decompose the signal and extract the effective feature quantity. To improve the adaptive capability and classification recognition accuracy of support vector machine(SVM) algorithm, the cosine decay calculation method and the exponential descent function are used to improve the hunter-prey algorithm, resulting in the improved hunter-prey optimizer(IHPO) algorithm, and the parameters of SVM are optimally selected by this method. Finally, an experimental model of GIS partial discharge is constructed, and a partial discharge identification model based on EWT-FE signal analysis combined with IHPO-SVM is established to verify the effectiveness of the proposed algorithm. The experimental results show that the diagnostic accuracy of the proposed algorithm for partial discharge type of GIS is more than 95%, which is better than the traditional diagnostic algorithm.

Keywords： Partial discharge; gas insulated switchgear; empirical wavelet transform; fuzzy entropy; improved hunter-prey optimizer; support vector machine

PDF (37868KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

王利猛, 王硕. 基于EWT-FE分析联合改进SVM算法的GIS局部放电诊断方法^*[J]. 电气工程学报, 2024, 19(1): 371-381 doi:10.11985/2024.01.040

WANG Limeng, WANG Shuo. Partial Discharge in GIS Diagnosis Method Based on EWT-FE Analysis and Improved SVM Algorithm[J]. Chinese Journal of Electrical Engineering, 2024, 19(1): 371-381 doi:10.11985/2024.01.040

1 引言

不同的局部放电类型可能会对气体绝缘组合电器(Gas insulated switchgear，GIS)的绝缘产生不同程度的危害^[1]。局部放电类型与其信号波形密切相关。例如，尖端放电具有放电脉冲密集、幅值分散的特点，而金属颗粒放电则表现出幅值变化范围较小、脉冲之间的间隔相对恒定的特点。然而，即便在某些放电信号特征不够显著的情况下，仍然难以区分^[2]。

应用信号分析方法对放电信号进行分解处理，能够更深入地挖掘其特征，提高后续诊断的准确性。其中，小波分析法在处理非线性不平稳信号时容易因预定义的固定窗口长度而产生过/欠包络与模态混叠现象^[3]。虽然经验模态分解法(Empirical mode decomposition，EMD)^[4-5]在信号分解过程中具有优秀的自适应能力，但缺乏严谨的理论基础，并存在严重的模态混叠与端点效应问题。尽管集合经验模态分解法(Ensemble empirical mode decomposition，EEMD)^[6]解决了部分模态混叠问题，但信号分解后仍存在显著的恢复误差。针对上述问题，本研究引入了具备严谨理论基础、强自适应能力、分解后恢复误差较小以及不存在端点效应的经验小波变换(Empirical wavelet transform，EWT)算法，作为处理局部放电信号的分解方法。然而，通过分解得到的各个分量仍然具有较大的数据量，不利于后续的分类处理。针对这一问题，描述信号复杂程度的熵理论得到了相关研究人员的关注。现阶段样本熵、近似熵计等广泛应用的熵计算方法已经取得了一定成果，但是均存在在熵值计算中对相似容限阈值大小敏感等问题^[7-8]，易产生较大的统计误差。相比之下，模糊熵使用模糊隶属函数取代硬阈值参数，可以更准确地度量非线性、非平稳的故障信号序列的复杂性。

针对局部放电类型诊断，在智能算法的不断研究与发展下，已经将一些模式识别算法应用于局部放电类型的识别与诊断，如神经网络^[9]、专家系统与支持向量机(Support vector machine，SVM)。尽管SVM算法在处理小样本和非线性问题方面具有出色的性能^[10-11]，但目前可用于GIS局部放电类型诊断的样本数据十分有限。然而，SVM算法仍然存在着一些不足：文献[12]未考虑SVM算法参数的选择问题，文献[13]使用粒子群算法优化SVM参数以提高分类准确性，但该算法容易陷入局部最优且收敛速度较慢。针对上述问题，引入了具有更好参数优化效果的改进猎人猎物优化(Improved hunter-prey optimizer，IHPO)算法，并结合余弦衰减计算方法和指数下降函数对其迭代过程进行改进，从而构建了基于IHPO-SVM的故障诊断模型。

因此，为提高GIS局部放电类型诊断的精度，本文提出了一种基于EWT-FE局部放电信号特征提取与IHPO-SVM算法相结合的局部放电类型诊断方法。为了有效挖掘不同类型的局部放电信号内部特征，首先使用EWT算法将局部放电信号分解为具有不同频率尺度特征的分量，然后运用模糊熵(Fuzzy entropy，FE)算法对分解得到的各分量进行熵值计算，进而得到原始信号特征向量。接着，将特征向量输入IHPO-SVM模型中进行故障类型诊断。最后，搭建了一个能够产生尖端放电、气隙放电、悬浮放电和金属颗粒放电等四种GIS典型局部放电信号的试验平台，通过试验验证了所提方法的有效性和实用性。

2 EWT-FE信号分析方法的建立

EWT算法首先对原始信号进行傅里叶变换，进而得到原始信号傅里叶谱，然后利用局部极大值原则对所求得的傅里叶谱进行分频分割，最后在分得的每个频段尺度上构造如式(1)、(2)所示的经验小波函数与经验尺度函数^[14]。

(1)$\psi_{n}(\omega)=\left\{\begin{array}{ll}1 & \omega_{n}+\tau_{n} \leqslant|\omega| \leqslant \omega_{n+1}-\tau_{n+1} \\\cos \left[\frac{\pi}{2} \beta\left(\frac{1}{2 \tau_{n+1}}\left(|\omega|-\omega_{n+1}+\tau_{n+1}\right)\right)\right] & \omega_{n+1}-\tau_{n+1} \leqslant|\omega| \leqslant \omega_{n+1}+\tau_{n+1} \\\sin \left[\frac{\pi}{2} \beta\left(\frac{1}{2 \tau_{n}}\left(|\omega|-\omega_{n}+\tau_{n}\right)\right)\right] & \omega_{n}-\tau_{n} \leqslant|\omega| \leqslant \omega_{n}+\tau_{n} \\0 & \text { 其他 }\end{array}\right.$

(2)$\phi_{n}(\omega)=\left\{\begin{array}{ll}1 & |\omega| \leqslant \omega_{n}-\tau_{n} \\\cos \left[\frac{\pi}{2} \beta\left(\frac{1}{2 \tau_{n}}\left(|\omega|-\omega_{n}+\tau_{n}\right)\right)\right] & \omega_{n}-\tau_{n} \leqslant|\omega| \leqslant \omega_{n}+\tau_{n} \\0 & \text { 其他 }\end{array}\right.$

式中，ω与ω_n分别为信号角频率与频谱分割边界。$\beta (x)$为如式(3)所示的函数

(3)$\beta (x)={{x}^{4}}\left( 35-84x+70{{x}^{2}}-20{{x}^{3}} \right)$

式中，${{\tau }_{n}}$与ω_n成正比例关系，r为两者间比例系数如式(4)所示

(4)${{\tau }_{n}}=r{{\omega }_{n}}$

式中，r满足式(5)所示关系

(5)$r<{{\min }_{n}}\left( \frac{{{\omega }_{n+1}}-{{\omega }_{n}}}{{{\omega }_{n+1}}+{{\omega }_{n}}} \right)$

由小波变换理论可知，细节系数与逼近系数分别如式(6)、(7)所示

(6)$W_{f}^{e}(n,t)=\left\langle f,{{\psi }_{n}} \right\rangle =\int{f\left( \tau \right)}\overline{{{\psi }_{n}}(\tau -t)}\mathrm{d}\tau ={{F}^{-1}}\left[ f(\omega )\overline{{{\psi }_{n}}(\omega )} \right]$

(7)$W_{f}^{e}(0,t)=\left\langle f,{{\phi }_{1}} \right\rangle =\int{f\left( \tau \right)}\overline{{{\phi }_{1}}(\tau -t)}\mathrm{d}\tau ={{F}^{-1}}\left[ f(\omega )\overline{{{\phi }_{1}}(\omega )} \right]$

联立式(6)、(7)，可得信号$f(t)$的重构形式如式(8)所示

(8)$f(t)=W_{f}^{e}(0,t)\times {{\phi }_{1}}(t)+\sum\limits_{n=1}^{N}{W_{f}^{e}(n,t)\times {{\psi }_{n}}(t)}$

由此，原始信号经EWT算法分解后得到的n+1个分量(Multi resolution analysis，MRA)如式(9)所示

(9)$\left\{ \begin{align} & {{f}_{0}}(t)=W_{f}^{e}(0,t)\times {{\phi }_{1}}(t) \\ & {{f}_{k}}(t)=W_{f}^{e}(k,t)\times {{\psi }_{k}}(t) \\ \end{align} \right.\ \ \ \ \ \ \ k=1,2,\cdots,n$

针对分解后信号复杂难以量化的问题，引入模糊熵(FE)算法来对EWT算法信号分解后得到的各个分量进行熵值计算，并将其作为反映局部放电的内部变化的量化指标，实现对原始信号的特征提取；FE算法具体计算流程参考文献[15]，本文不再赘述。

3 诊断识别模型的建立

3.1 IHPO算法的提出

猎食者优化(Hunter-prey optimizer，HPO)算法是启蒙于狩猎者捕猎行为而提出来的一种智能优化算法，寻优过程主要分为两个部分：狩猎者全局追踪捕食猎物的过程，在算法中体现的是全局搜索过程，与猎物逃脱向全局最优位置的过程，在算法中体现的是局部精确求解过程^[16]。两个过程按一定概率交错进行，以实现对最优值的求解。给出HPO算法具体建模过程如下所示。

对于种群个体个数为N、计算维度为D的HPO算法，其个体与适应度可表示为X={X₁,X₂,…,X_N}，X_i=[x_i₁,x_i₂,…,x_iD]与F(X_i)= f(x_i₁,x_i₂,…,x_iD)。给出HPO算法狩猎者全局追踪捕食猎物过程个体更新方式如式(10)所示

(10)$\begin{matrix} {{x}_{i,j}}(t+1)={{x}_{i,j}}(t)+0.5\left[ \left( 2CZ{{P}_{\mathrm{pos},j}}(t)-{{x}_{i,j}}(t) \right)+ \right. \\ \left. \left( 2(C-1)Z{{x}_{\mathrm{ave},j}}(t)-{{x}_{i,j}}(t) \right) \right] \\ \end{matrix}$

式中，t为当前迭代次数；x(t)为当前代狩猎者个体；C为控制狩猎者移动方向的趋向因子，算法方式如式(11)所示

(11)$C=1-t\times \frac{0.98}{{{T}_{\max }}}$

式中，T_max为最大迭代次数。式(10)中，Z为按式(12)、(13)计算所得的自适应值

(12)$\mathrm{ID}{{\mathrm{X}}_{i}}=\left\{ \begin{matrix} 0 & {{R}_{1i}}<C \\ 1 & \ \ \ \\\end{matrix} \right.\begin{matrix} {} & \ \ i=1,2,\cdots,D \\\end{matrix}$

(13)$Z={{R}_{2}}\centerdot IDX+{{R}_{3}}\otimes (\tilde{\ }IDX)$

式中，R₁与R₃均为服从[0,1]范围内均匀分布的D维随机向量，R₂为服从[0,1]范围内均匀分布的随机数。P_pos(t)为当前代猎物位置，是与平均位置欧式距离最大者。给出算法个体与平均距离的欧式距离计算方式如下所示。

首先，给出全体平均位置计算如式(14)所示

(14)${{x}_{\mathrm{ave}}}(t)=\frac{1}{N}\sum\limits_{i=1}^{N}{{{X}_{i}}}$

按式(15)、(16)更新计算种群各个体到全体平均位置的欧式距离

(15)$k=round(C\times N)$

(16)$D(i)=\sqrt{\sum\limits_{j=1}^{D}{{{\left( {{x}_{i,j}}-{{x}_{\mathrm{ave},j}} \right)}^{2}}}}\begin{matrix} {} & \ \ i=1,\cdots,k \\\end{matrix}$

上述为狩猎者全局搜索过程，而对于猎物逃脱局部开发过程如下所示。此时，猎物个体更新方式可如式(17)所示

(17)$\begin{matrix} {{x}_{i,j}}(t+1)={{g}_{\mathrm{best},j}}(t)+CZ\cos (2\mathrm{ }\!\!\pi\!\!\text{ }{{R}_{4}})\times \\ \left[ {{g}_{\mathrm{best},j}}(t)-{{x}_{i,j}}(t) \right] \\ \end{matrix}$

式中，g_best,_j(t)为当前代最优个体，R₄为[-1,1]范围内的随机数。

综上，给出HPO算法种群整体更新方式如式(18)所示

(18)$x_{i, j}(t)=\left\{\begin{array}{ll}\text { 式(16) } & r_{5}<\gamma \\\text { 式(23) } & \text { 其他 }\end{array}\right.$

式中，r₅为[0,1]范围的随机数，γ为算法开发与探索过程的控制参数。

由HPO算法计算过程可知，HPO是通过式(18)实现全局探索与局部开发两个过程的交替计算实现对最优值的求解的，由此可以看出，算法建模以及计算过程非常简单，但是，从其计算过程可以看出，原始算法中γ为一固定数值，而该参数对于平衡算法全局探索与局部开发的作用非常大，由此为实现算法计算前期广泛的全局探索以及计算后期精确的局部开发，提出利用式(19)对该参数进行改进计算

(19)$\gamma =0.9\cos \left( \frac{t}{{{T}_{\max }}}\times \frac{\mathrm{ }\!\!\pi\!\!\text{ }}{2} \right)+0.1$

由式(19)可以看出，在算法迭代计算前期，γ较大，狩猎者全局追踪的过程出现的概率较大，而在计算后期，γ迅速减小，使得猎物局部逃脱的过程出现的概率得以提高。由此，使得算法的全局与局部搜索过程更加平衡，有利于提高算法的迭代收敛速度。

另外，由式(11)~(17)可以看出，算法局部搜索范围是呈线性递减的，为了进一步提高算法收敛速度以及局部求解精度，参考麻雀搜索算法^[17]利用指数下降函数对参数C进行了改进计算。具体计算方式如式(20)所示

(20)$\mu =\mathrm{exp}\left( \frac{-i}{{{R}_{6}}{{T}_{\mathrm{max}}}} \right)$

由上，给出改进后算法种群个体位置更新方式如式(21)所示

(21)${{x}_{i,j}}(t+1)=\left\{ \begin{matrix} {{x}_{i,j}}(t)+0.5\left[ \left( 2CZ{{P}_{\mathrm{pos},j}}(t)-{{x}_{i,j}}(t) \right)+\left( 2\left( C-1 \right)Z{{x}_{\mathrm{ave},j}}(t)-{{x}_{i,j}}(t) \right) \right] & \ {{R}_{5}}<\gamma \\ {{g}_{\mathrm{best},j}}(t)+\mu Z\cos (2\mathrm{ }\!\!\pi\!\!\text{ }{{R}_{4}})\times \left( {{g}_{\mathrm{best},j}}(t)-{{x}_{i,j}}(t) \right)\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ & \\\end{matrix} \right.$

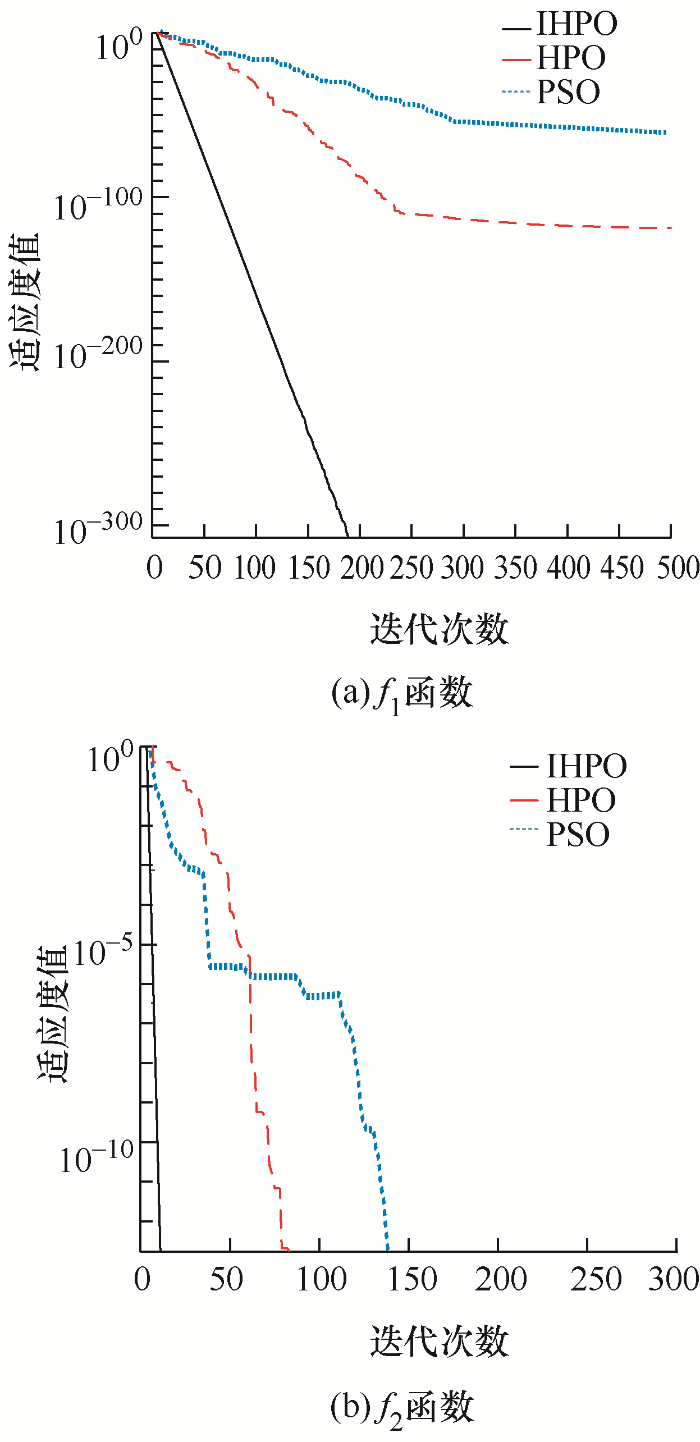
为验证所提IHPO算法的有效性以及优越性，分别利用HPO与IHPO两种算法对如式(22)所示的经典函数进行了50次求解。

(22)$\left\{ \begin{matrix} {{f}_{1}}=\text{Schwefel 1}\text{.2} \\ {{f}_{2}}=\text{Rastrigin}\ \ \ \ \ \\\end{matrix} \right.$

给出算法参数设置情况如下：设置三种算法种群个体总数均为30，最大迭代次数为500。给出计算结果如表1与图1所示。

表1 计算结果

函数	算法	均值	均方差
f₁	IHPO	0	0
	HPO	1.436×10^-97	5.866×10^-98
	PSO	3.657×10^-61	9.352×10^-62
f₂	IHPO	0	0
f₂	HPO	0	0
	PSO	0	0

新窗口打开| 下载CSV

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 算法迭代结果

由表1与图1所示三种算法对两例经典函数的计算结果可以看出，IHPO算法无论是在求解精度还是在迭代速度方面均有了很大的提升，由此可见IHPO算法具有较为优良的优化计算性能。

3.2 EWT-FE联合IHPO-SVM诊断模型的建立

针对具有小样本、非线性特征的局部放电类型诊断问题，建立以小结构风险为原则的多分类SVM诊断识别模型，模型具体计算流程见文献[18]。在SVM模型中，C为控制模型拟合程度的惩罚因子，g为径向基宽度参数^[19-20]；而SVM算法分类识别效果受C、g参数的影响很大，由此选择一组合适的参数对于提高SVM算法的分类识别精度具有重要的作用。针对此，提出一种基于IHPO算法的SVM参数优化选择方法。给出基于EWT-FE联合IHPO-SVM算法的局部放电类型诊断模型的具体建模过程如下所示。

步骤1：输入原始局部放电信号。

步骤2：利用EWT算法将原始局部放电信号分解为一系列具有一定频率尺度特征的分量信号。

步骤3：对分解得到分量分别进行模糊熵值计算，以获取原始局部放电信号特征向量。

步骤4：初始化SVM惩罚因子C与径向基宽度参数g的取值范围；初始化IHPO算法种群规模参数、最大迭代次数；在求解范围内随机初始化种群个体位置，并按式(23)求解种群个体适应度

(23)$\left\{ \begin{matrix} \text{min} & f(C,g)=\frac{\sum\limits_{i=1}^{N}{({{y}_{i}}-{{y}_{r}})}}{N} \\ \text{s}\text{.t}\text{.} & \begin{matrix} {{C}_{\min }}\le C\le {{C}_{\max }} & {{g}_{\min }}\le g\le {{g}_{\max }} \\\end{matrix} \\\end{matrix} \right.$

式中，y_r为分类识别结果。

步骤5：按式(19)~(21)更新IHPO算法个体位置；按式(23)求解更新后个体的适应度值。

步骤6：求取更新后个体最优位置，判断此时算法是否满足迭代计算结束条件，若满足则计算结束，并返回最优(C，g)参数。否则返回步骤5继续进行计算。

步骤7：利用经参数优化选择的SVM算法对局部放电信号类型进行诊断识别。给出整体诊断模型流程图如图2所示。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 诊断模型流程图

4 试验验证

4.1 试验平台

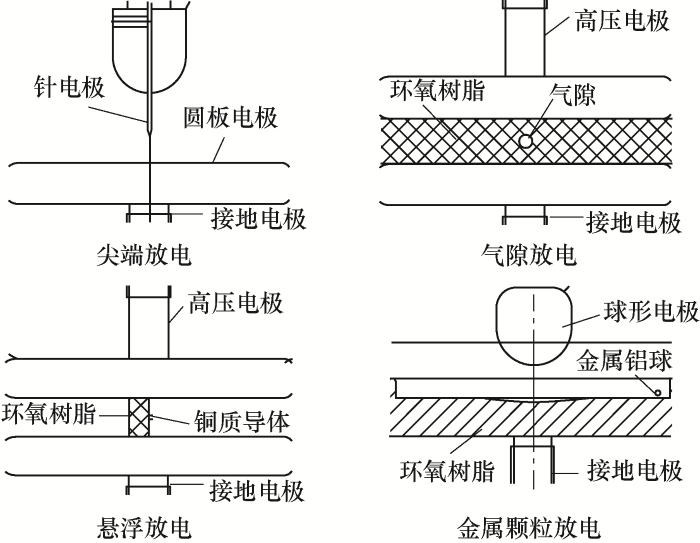
为模拟GIS内常见的四种典型局部放电的实际发生情况，在实验室中建立如图3所示的四种典型放电类型腔体。其中尖端放电采用的是放电针-平板放电形式，气隙放电采用的是环氧树脂内空穴放电形式，悬浮放电采用的是接地电极上放置环氧树脂材质板，其上放置铜质导体的形式，金属颗粒放电采用的是放置金属导电铝球的形式。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 放电腔体结构图

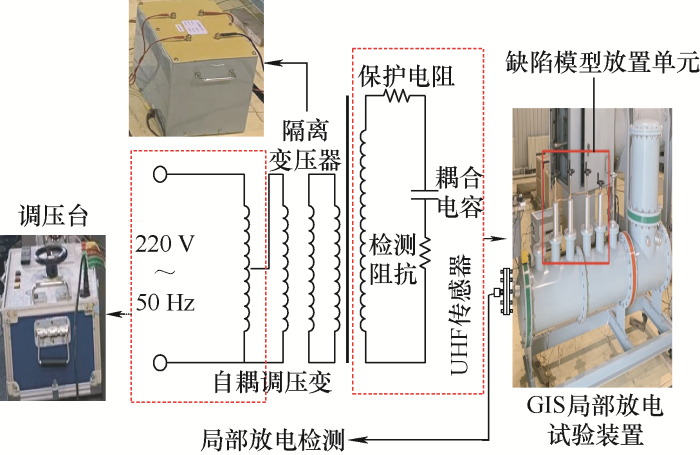
试验平台采用GZFZ-G110型局部放电模拟试验装置，具体的试验回路如图4所示。主要由调压台、额定电压为160 kV的工频隔离变压器、GIS罐体以及局部放电信号采集系统组成。其中GIS罐体内充有SF₆气体，内置耦合电容、保护电阻等。具体参数如表2所示。试验采用国家标准GB 1094.3—2003规定的加压时间及步骤：在进行试验时采用缓缓升压的方式，直至局部放电采集系统上出现稳定局部放电信号为止，此时维持当前电压，使用杭州国洲电力科技有限公司开发的上位机软件对特高频检波信号进行采集。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 试验平台布置图

表2 GZFZ-G110型装置参数表

参数	数值和类型
额定电压/kV	160
额定频率/Hz	50
耦合电容量/pF	50
特高频局放检测参数	带宽300~2 000 MHz；灵敏度：1 pC
检波信号接收频率带宽/MHz	0~25
装置自身放电量/pC	≤0.5
变压器变比	1 000：1
绝缘介质	SF₆气体
气体压力/MPa	≤0.35

新窗口打开| 下载CSV

4.2 局部放电信号采集及特征提取

利用搭建的局部放电信号采集试验平台进行多组试验，并从采集得到的大量局部放电信号中，随机选择四种局部放电信号各150个放电点信号作为局部放电类型诊断方法验证样本。对于局部放电信号特征向量的提取，首先利用基于局部最小值频谱分割法与分量分解数目为5的EWT算法对原始局部放电信号进行分解，给出四种典型局部放电原始信号及EWT分解结果如图5所示。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 局部放电信号及其分解波形

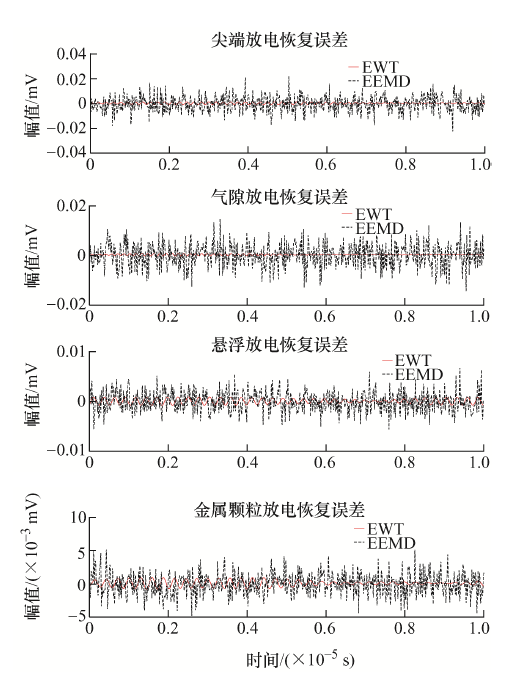
由给出的局部放电信号分解结果可以看出，原始放电信号经EWT算法分解之后得到的各分量均具有一定的频率与幅值特征，有效解决了EMD算法存在的模态混叠问题。另外，不同类型的局部放电信号分解得到的分量之间的细节特征也有着明显的差异，由此可以看出，原始信号经EWT算法分解后，其内部特征得到了有效挖掘，增强了原始信号的可分性。为体现EWT算法在信号重构方面的优势，给出如图6所示的EWT算法与噪声添加程度为0.2、添加次数为100次的EEMD算法重构误差对比图。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 恢复误差波形图

由重构恢复误差曲线联合前面结论可以看出，EWT算法对信号分解可以在有效缓解模态混叠问题的前提下最大程度地体现原始信号，而不至于因恢复误差较大而影响原始信号内部特征的展现。

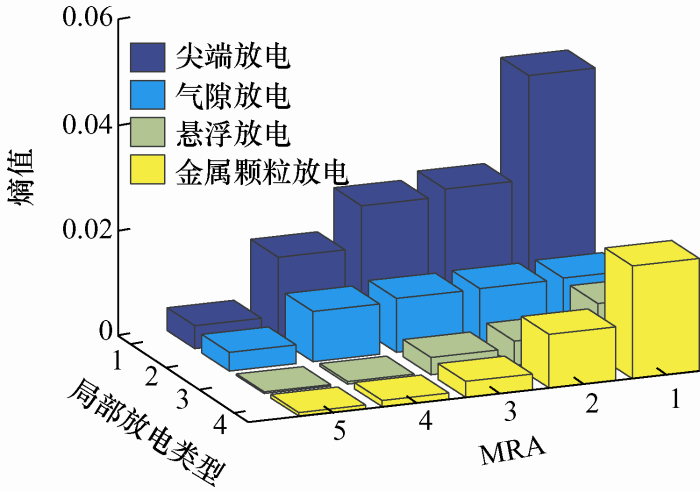
为了对EWT分解后的信号进行量化分析以便于后续局部放电类型诊断模型的搭建，利用模糊熵对EWT原始信号分解后的分量进行熵值计算。给出利用嵌入维度为2、模糊指数为2与相似容限阈值为0.15的模糊熵对四种局部放电信号分解后分量的熵值计算结果如图7所示。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 局部放电熵值计算结果

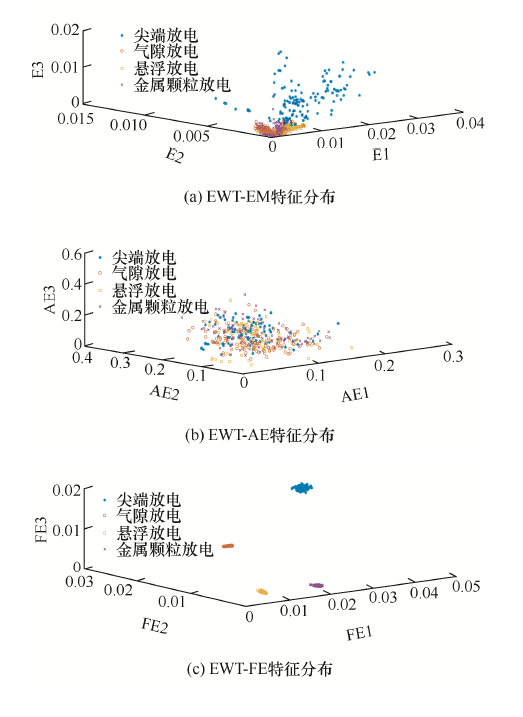
为验证模糊熵局部放电信号值计算的有效性与优越性，分别给出基于EWT能量矩(Energy moment, EM)、EWT近似熵与EWT模糊熵局部放电信号特征提取后特征值三维分布图如图8所示。其中模糊熵参数设置与前面相同，设置近似熵嵌入维度与相似容限阈值参数分别为2与0.15。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 三维特征值分布图

图8a为EWT能量矩局部放电信号特征提取方法，该方法尖端放电信号特征值分布半径较大，相对其他三种放电信号具有较好的可分性，但是，其他三种局部放电类型特征值分布较为集中且重叠严重，可分性较差。由图8b给出的EWT近似熵特征提取方法可以看出，四种放电类型特征值分布虽然较为分散，但是分布区域重叠严重，不利于后续的分类；图8c为EWT模糊熵局部放电特征提取方法四种放电类型特征值分布结果，可以看出，四种放电类型样本分布均较为集中且不存在区域重叠现象，具有良好的内聚性与可分性。由图5可以看出，局部放电信号经EWT算法分解后得到的各分量中，前三个分量所得复杂程度较高，且由图8c可以看出，前三个分量的熵值计算结果具有很好的内聚性与可分性，由此，选择前三个分量的模糊熵值计算结果作为局部放电信号的特征向量，给出部分经EWT-FE分析后四种局部放电信号的特征向量数据，如表3所示。

表3 部分局部放电样本特征向量

局放类型	FE1	FE2	FE3
尖端放电	0.044 7	0.024 9	0.015 5
	0.045 7	0.025 3	0.015 2
	0.044 3	0.025 3	0.015 2
气隙放电	0.010 0	0.010 6	0.010 3
	0.009 2	0.010 5	0.010 4
	0.009 4	0.010 5	0.010 4
悬浮放电	0.009 9	0.004 3	0.000 6
	0.009 9	0.004 3	0.000 5
	0.010 0	0.004 4	0.000 4
金属颗粒放电	0.021 1	0.003 1	0.000 9
	0.021 4	0.003 7	0.001 1
	0.020 7	0.003 3	0.001 0

新窗口打开| 下载CSV

4.3 识别效果分析

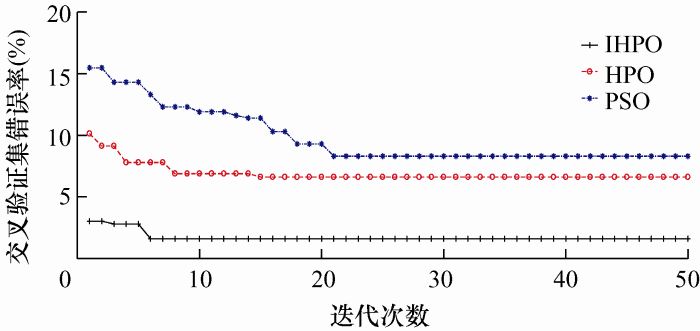
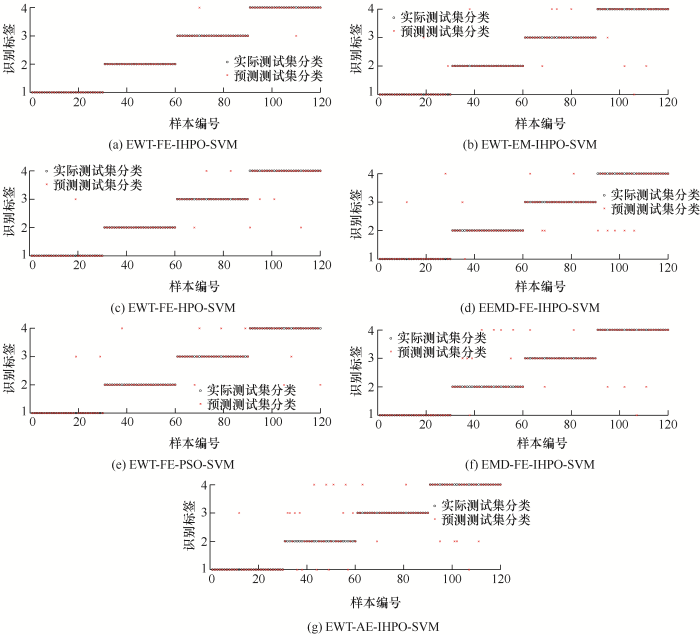
为验证所提局部放电类型诊断方法的有效性以及优越性，针对所采样的每种局部放电信号的150个样本，按训练集与测试集样本分布4∶1的比例对识别模型进行训练与识别验证。分别给出EWT-FE-PSO-SVM、EWT-FE-HPO-SVM、EWT-FE- IHPO-SVM、EMD-FE-IHPO-SVM、EEMD-FE-IHPO- SVM、EWT-EM-IHPO-SVM、EWT-AE-IHPO-SVM七种诊断模型的识别效果如表4与图9、10所示。给出上述算法的参数设置情况如下：设置SVM模型C与g取值范围均为[0.01,1 000]；设置三种优化算法种群数均为30、迭代次数均为50；对于EWT、EEMD、FE与AE参数设置与前文相同。

表4 局部放电类型诊断结果表

诊断方法	识别率(%)				总识别率(%)
诊断方法	尖端放电	气隙放电	悬浮放电	颗粒放电	总识别率(%)
EWT-FE-IHPO-SVM	100	100	96.67	96.67	98.33
EWT-FE-HPO-SVM	96.67	100	90	86.67	93.33
EWT-FE-PSO-SVM	93.33	93.33	86.67	90.00	91.67
EWT-EM-IHPO-SVM	93.33	96.67	86.67	86.67	90.83
EEMD-FE-IHPO-SVM	93.33	93.33	83.33	83.33	89.17
EMD-FE-IHPO-SVM	100	70	90	86.67	86.67
EWT-AE-IHPO-SVM	96.67	50	90	83.33	80

新窗口打开| 下载CSV

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 参数求解迭代过程

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 局部放电类型诊断效果

由表4与图9、10给出的试验结果可以得出以下结论。

(1) 对比EWT-FE-IHPO-SVM、EWT-FE-HPO- SVM与EWT-FE-PSO-SVM三种局部放电诊断方法联合图9所得SVM参数求解迭代曲线可以看出，IHPO算法无论在求解精度上还是迭代速度上均优于其他两种优化算法，由此验证了第4.1节所得结论。

(2) 由EWT-FE-IHPO-SVM、EEMD-FE-IHPO- SVM与EMD-FE-IHPO-SVM三种诊断模型的识别结果可以看出，利用EWT算法对原始局部放电信号进行分解相对EEMD与EMD两种信号模态分解算法来说，识别精度分别提高了10.27%与13.45%，由此可以看出，EWT信号分解方法能够更好地实现对原始信号内部特征的挖掘，所得分量能够更好地实现对原始信号的表征。

(3) EWT-FE-IHPO-SVM模型诊断精度为98.33%，对比EWT-EM-IHPO-SVM与EWT-AE- IHPO-SVM诊断模型，诊断精度分别提高了8.26%与22.91%，可以看出，FE熵值计算方法对于局部放电信号特征提取的结果更具可分性，由此验证了第4.2节所得结论。

4.4 对比试验验证分析

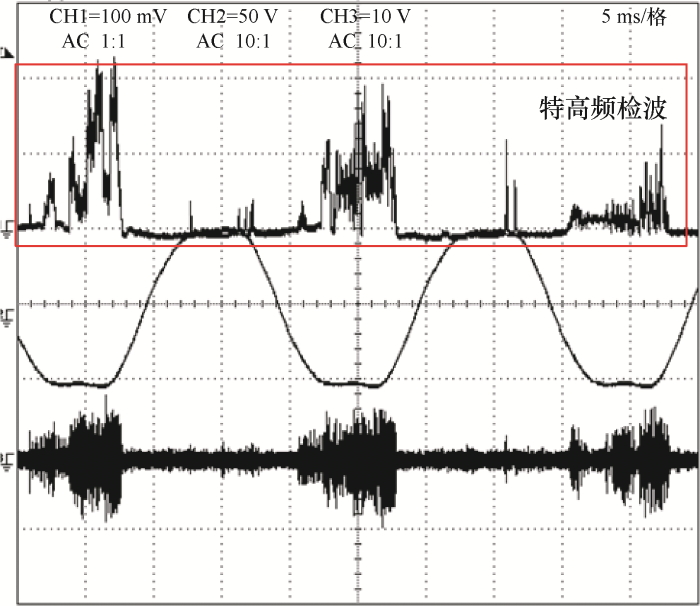
为了进一步验证本文所提模型对于其他场景的局部放电分类的有效性，利用装有GIS特高频在线检测装置得到的变电站故障录波数据作为测试集再次进行试验，给出采样GIS设备局部放电故障录波系统输出的局部放电信号图谱如图11所示，其中上曲线为特高频的检波输出信号，中曲线为参考电压，下曲线为常规局部放电信号。现场信号与试验测得GIS信号区别在于高压出线端部的悬浮性放电、移动手机、雷达站等装置所发射的UHF干扰信号频段与现场检测特高频信号重叠范围较多，导致信号波形特征显著性有所降低，使得放电类型诊断难度加大。

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 现场特高频检波输出信号

经手动筛选去除无效信号后，对四种典型局部放电信号分别收集103个放电信号，利用本文所提模型进行放电类型诊断，给出诊断结果如表5所示。

表5 现场局部放电信号诊断结果

放电类型	诊断准确率(%)
尖端放电	99.03
气隙放电	97.09
悬浮放电	98.06
金属颗粒放电	96.12

新窗口打开| 下载CSV

由诊断结果可以看出，利用本文所提诊断模型对所采集的现场局部信号进行诊断，虽然诊断精度有所下降，但不同类型诊断准确率均为95%以上，在实际现场噪声信号较为复杂的情况下仍有较高的准确度，由此可见，本文提出的局部放电类型诊断模型具有良好的应用前景。

5 结论

本文提出基于EWT-FE与IHPO-SVM算法的GIS局部放电类型诊断方法，主要结论如下所述。

(1) EWT结合模糊熵的方法在GIS局部放电信号分析过程当中，有效提取了不同局部放电类型的信号特征，提高了后续故障诊断模型的精度与效率。

(2) 通过经余弦衰减计算方法以及指数下降函数对传统HPO算法进行改进，其收敛迭代速度与精度均得到了提升，且参数寻优能力优于传统优化算法。

(3) 经试验分析得知，采用IHPO对SVM算法的参数进行优化选取，显著提升了SVM算法的分类识别性能，相对于HPO-SVM算法与PSO-SVM算法具有更高的局部放电诊断精度，具有很好的工程应用前景。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

臧旭, 马宏忠, 吴金利, 等.

基于振动原理的GIS母线导电杆松动故障分析与诊断

[J]. 电力系统保护与控制, 2021, 49(9):12-20.

[本文引用: 2]

ZANG

, MA

Hongzhong

, WU

Jinli

, et al.

Analysis and diagnosis of loose conductive bar of GIS bus based on vibration principle

[J]. Power System Protection and Control, 2021, 49(9):12-20.

[本文引用: 2]

[2]

, WANG

Zhixiang

, WANG

Xiaohua

, et al.

Chromatic processing for feature extraction of PD-induced UHF signals in GIS

[J]. Global Energy Interconnection, 2020, 3(5):494-503.

DOI:10.1016/j.gloei.2020.11.009 URL [本文引用: 1]

[3]

罗新, 牛海清, 胡日亮, 等.

基于小波包分解的XLPE配电电缆局部放电波形特征提取与识别

[J]. 高压电器, 2013, 49(11):110-116,122.