电气工程学报, 2024, 19(1): 351-357 doi: 10.11985/2024.01.038

新能源发电与电能存储

基于跃变探索式电导增量法的光伏阵列全局最大功率点跟踪控制研究

王艺博,1, 苏高民,2, 邱榕鑫,1

1.西交利物浦大学智能工程学院 苏州 215123

2.江苏集萃脑机融合智能技术研究所有限公司 苏州 215100

Research on Global Maximum Power Point Tracking Control of PV Arrays Based on Jump Explore Incremental Conductance Method

WANG Yibo,1, SU Gaomin,2, QIU Rongxin,1

1. School of Advanced Technology, Xi’an Jiaotong-Liverpool University, Suzhou 215123

2. Jiangsu JITRI Brain Machine Fusion Intelligence Institute, Suzhou 215100

收稿日期: 2023-02-1   修回日期: 2023-07-8  

Received: 2023-02-1   Revised: 2023-07-8  

作者简介 About authors

王艺博，男，1997年生，硕士研究生。主要研究方向为光伏并网发电技术、电池主动均衡。E-mail：chest_wang.hhht@foxmail.com;

苏高民，男，1989年生，硕士，中级工程师。主要研究方向为工业化产品算法性能优化。E-mail：sugaomin@jitri-bmf.com;

邱榕鑫，男，1997年生，硕士研究生。主要研究方向为DC-DC、HVDC和MPPT等。E-mail：Rongxin.Qiu21@student.xjtlu.edu.cn

摘要

实现光伏阵列最大功率点跟踪(Maximum power point tracking, MPPT)的传统算法已经较为成熟，但是在局部阴影出现后会发生寻优失效，难以实现全局最大功率跟踪(Global maximum power tracking, GMPPT)。为解决该问题，研究人员提出将粒子群(Particle swarm optimization, PSO)等群搜索算法应用在MPPT控制过程中，虽然能够控制工作点稳定在全局最大功率点处，但由于该算法收敛能力依赖于核心参数，在应用过程中有一定概率会导致系统振荡。针对以上问题，在电导增量法(Incremental conductance, INC)的基础上提出跃变探索式电导增量法(Jump explore incremental conductance, JEINC)，相较于传统电导增量法而言，具有较强的探索能力，能够在局部阴影下实现全局最大功率点跟踪控制，同时所提算法具有较好的收敛能力，在工作点位于最大功率点附近能够快速稳定。在三种光照环境下进行Matlab仿真，从稳定时间、暂态过程能量损耗率和振荡幅值三个方面验证了所提算法相较于电导增量法和粒子群算法的优越性。

关键词： 光伏阵列; 局部阴影; 全局最大功率点跟踪; 电导增量法; 粒子群算法

Abstract

The traditional algorithms for achieving the maximum power point tracking(MPPT) of photovoltaic(PV) arrays have been relatively mature, but it is difficult to achieve the global maximum power point tracking(GMPPT) after the appearance of local shadows. To solve this problem, researchers have proposed to apply swarm search algorithms such as particle swarm optimization(PSO) algorithm to the MPPT control process. Although the operating point can be controlled to be stable at the global maximum power point, the convergence ability of the algorithm depends on the core parameters, which will lead to system oscillation in the application process in a certain chance. In response to the above problems, the jump explore incremental conductance(JEINC) method which based on the incremental conductance(INC) method is proposed, which has a stronger exploratory capability than the traditional conductance increment method and can achieve the GMPPT control under partial shading condition, while the algorithm has a better convergence capability and can be quickly stabilized when the operating point is located near the maximum power point. Simulations in Matlab are performed in three lighting environments to verify the superiority of the proposed algorithm compared with the INC and PSO in terms of stabilization time, transient process energy, and tracking effect.

Keywords： Photovoltaic array; partial shading condition; global maximum power point tracking; conductivity increment method; particle swarm optimization

PDF (43262KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

王艺博, 苏高民, 邱榕鑫. 基于跃变探索式电导增量法的光伏阵列全局最大功率点跟踪控制研究[J]. 电气工程学报, 2024, 19(1): 351-357 doi:10.11985/2024.01.038

WANG Yibo, SU Gaomin, QIU Rongxin. Research on Global Maximum Power Point Tracking Control of PV Arrays Based on Jump Explore Incremental Conductance Method[J]. Chinese Journal of Electrical Engineering, 2024, 19(1): 351-357 doi:10.11985/2024.01.038

1 引言

高效利用太阳能发电是推动可持续发展的有效方法之一[1]。由于光伏阵列通常安置在室外，容易受到光照分布变化的影响，导致光伏阵列的输出功率-电压(Power-voltage, P-V)曲线出现多个峰值点[2-3]。目前主流的解决方法是在光伏阵列后接入DC-DC电路，如Boost[4]、Buck[5]等，同时，采集光伏阵列输出端口的电压和电流值，通过合适的最大功率点跟踪(Maximum power point tracking, MPPT)算法来调整负载与光伏阵列的等效电阻相匹配，从而使光伏阵列的工作点位于最大功率点(Maximum power point, MPP)处[6]。

目前，MPPT算法主要可以分为两种：传统算法和智能算法[7-8]。其中，传统算法以固定电压法、扰动观察法和电导增量法为主，这三种算法均能够在光伏阵列处于均匀光照工况下实现MPPT控制，但是，当光伏阵列被树木、云朵和建筑等局部遮挡后，传统算法将不能实现全局最大功率跟踪(Global maximum power point tracking, GMPPT)[9]。智能算法主要包括粒子群算法[10-11]、蚁群算法[12]及后续衍生的群智能搜索算法等，这类算法具有较强的探索能力，能够在局部阴影环境下控制光伏阵列的工作点位于最大功率点处，但是在收敛过程中，由于不同智能体切换时为硬切换过程，系统将会产生较大振荡，对于器件的防击穿性能要求较高[13]。同时，由于大部分群智能搜索算法参数较多，取值困难[14]，且收敛性难以确定，参数选取不当时会造成系统工作点振荡[15]。因此，将群智能搜索算法广泛应用在大规模光伏阵列的集中控制上仍有一定难度。本文基于电导增量法原理，结合电路振荡过程，提出一种能够让光伏阵列的工作点跳出局部最大功率点(Local maximum power point, LMPP)的方法。在Matlab/Simulink环境下设置不同的阴影环境进行离线仿真，验证了所提算法的可行性和优越性。

2 光伏MPPT系统架构

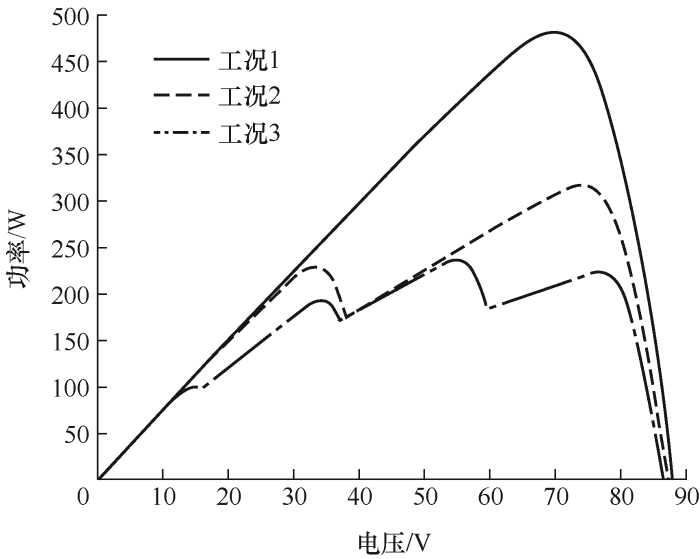
2.1 光伏阵列输出特性曲线

本次构造的光伏阵列由4个光伏电池串联而成，为了避免热斑效应，在每个光伏电池的输出端口处均并联一个二极管。单个光伏电池的电气参数如下：开路电压UOC=22.5 V，短路电流ISC=7.5 A，最大功率点对应电压UMPP=17.5 V，最大功率点对应电流IMPP=6.9 A。本次测试设定三种光照分布工况，每种工况下光伏阵列受到的光照强度如表1所示，三种工况下，环境温度均为25 ℃。图1中三条曲线分别对应三种工况下的光伏阵列P-U特性曲线，对应GMPP坐标分别为(70, 480)，(73, 316)，(55, 237)。

表1   三种工况下光照强度分布 lx

光伏模块工况一工况二工况三
PV11 0001 0001 000
PV21 0001 000800
PV31 000600600
PV41 000600400

新窗口打开| 下载CSV


图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   三种工况下光伏阵列输出特性曲线


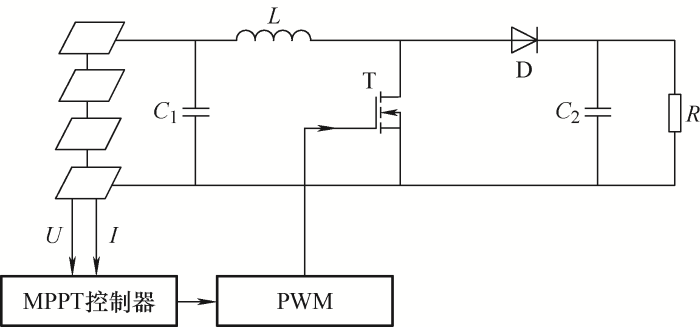
2.2 MPPT控制系统建模

通过Boost电路实现光伏阵列MPPT控制系统结构框图如图2所示，各元器件参数如表2所示。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   光伏阵列MPPT控制系统结构图


表2   控制系统结构参数选择

元器件参数参数值
滤波电容C1/μF60
升压电感L/mH100
母线电容C2/μF2
负载电阻R/Ω33
PWM开关频率f/Hz10 000

新窗口打开| 下载CSV


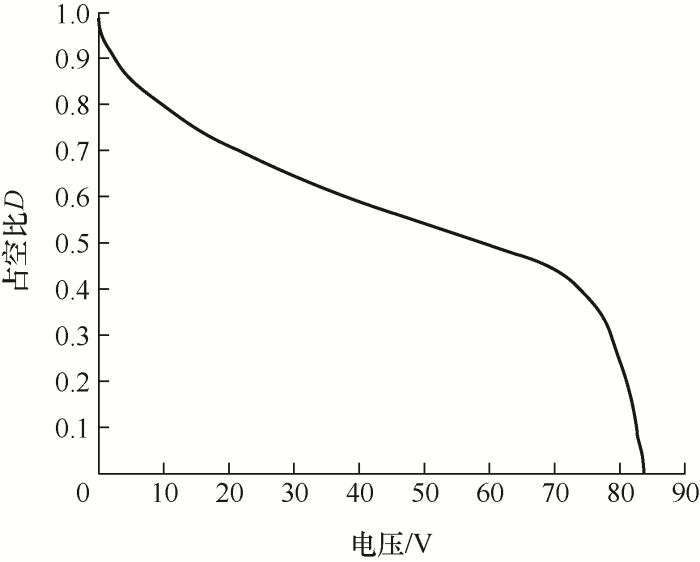
基于上述内容建立MPPT控制模型，在不同的占空比下，系统稳定后光伏阵列工作点对应电压值也不同。图3为占空比D与光伏阵列输出端口电压U间变化曲线，曲线非线性化程度主要与电路参数相关，D与U整体呈现负相关趋势。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   D-U关系曲线


3 MPPT控制算法

3.1 电导增量法

电导增量法(Incremental conductance, INC)的原理是通过前后两步功率变化量与电压变化量的比值大小来决定工作点的移动方向。由于INC算法能够在系统稳定后收敛于一点，已经被广泛应用到不同规模的光伏阵列MPPT控制过程中[16-17]。但是根据算法原理可以得出，当光伏阵列的输出特性曲线存在多个峰值点时，INC算法容易陷入LMPP，导致算法追踪失效。

3.2 粒子群算法

粒子群算法(Particle swarm optimization, PSO)是一种常用的群搜索算法，该算法主要通过不同智能体互相学习来实现全局优化。设算法中共有n个粒子均匀分布在解空间中，第i个粒子在第d维的坐标为xid，第k+1次迭代过程中的速度vid是基于第k次迭代数据来计算得到的，速度和位置的更新公式分别为式(1)和式(2)

$v_{id}^{k+1}=\omega v_{id}^{k}+{{c}_{1}}{{r}_{1}}(p_{id}^{k}-x_{id}^{k})+{{c}_{2}}{{r}_{2}}(p_{gd}^{k}-x_{gd}^{k})$
$x_{id}^{k+1}=x_{id}^{k}+v_{id}^{k+1}$

式中，ω为惯性权重系数；r1和r2为(0,1)之间的随机数；c1和c2分别为自我学习因子和社会学习因子； pid为粒子历史上的最优值；pgd为所有粒子的最优值。

目前，PSO已经被多次验证在MPPT控制过程中能够实现GMPPT控制，但是，由于该算法寻优效果依赖于三个参数，当参数选取不当时，可能会造成智能体不能稳定在同一点，进而导致系统工作点无法收敛[18]。同时，每个粒子切换过程为硬切换过程，这将导致系统在动态过程下产生剧烈振荡。因此，目前工业界难以应用该算法实现大规模光伏阵列GMPPT控制。

4 跃变探索式电导增量法

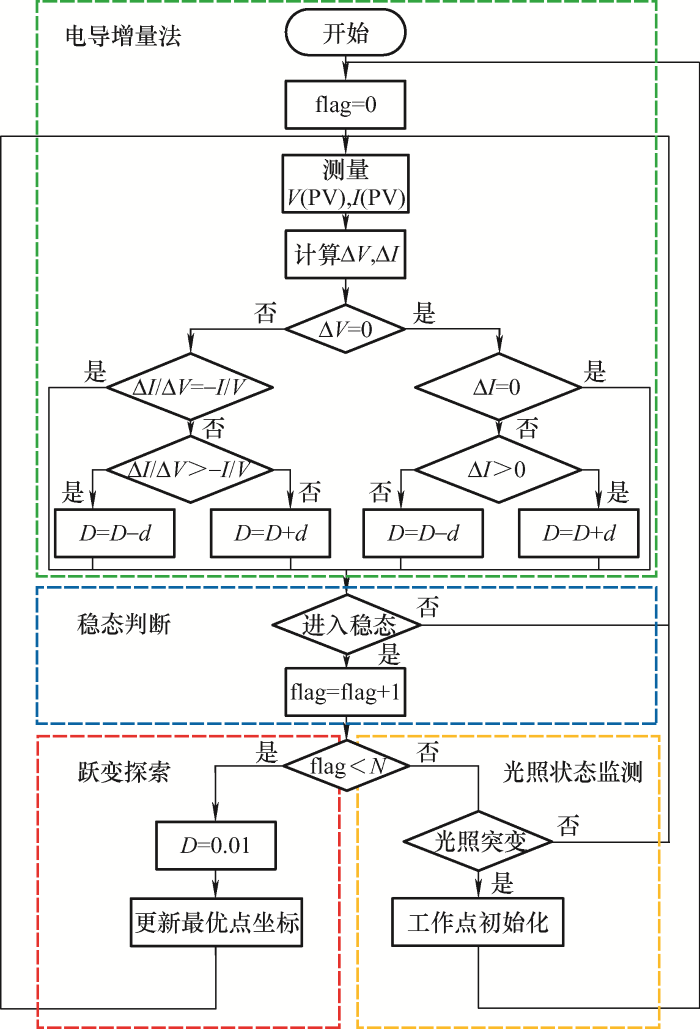
基于图3所示的D-U关系曲线和第3.1节所述INC算法原理构造跃变探索式电导增量法(Jump explore incremental conductance, JEINC)。图4为JEINC算法流程图，其中，flag为用于记录跃变次数的标志位，N为最大跃变次数，由于光伏阵列P-U曲线最大峰值点个数由串联支路中光伏组件个数决定[19]，为了保证光伏阵列工作点具有可靠的跳出局部最优点的能力，同时兼顾系统收敛速度，本文中N取值与串联支路中光伏组件的个数相同。进入稳态判断依据为式(3)，其中，Pn、P1、P2分别为本周期功率采样值、一周期前功率采样值和两周期前功率采样值。通过INC算法实现MPPT控制过程中，当光伏阵列的工作点经过一个峰值点时，由于功率变化方向相反，两个相邻量的差值符号必定相反。当到达LMPP后，JEINC算法将控制占空比置为0.01，即控制光伏阵列的输出端口电压值约为开路电压值，由于Boost电路中存在电感和电容，光伏阵列的工作点不能立即移动到开路电压值附近，而是会跳出该LMPP处，向前移动一定距离后继续寻优。在算法运行过程中，当功率值大于历史功率值，则会更新最优点坐标，每一次跃变结束后，根据图3所示关系，根据目前所在位置与最优点坐标关系控制占空比，返回到之前所经历过的最优点坐标位置处。当光伏阵列输出功率值满足式(4)时，说明外部光照强度发生突变，此时算法将会控制最大功率点先向电压值较低处移动，实现算法初始化，之后再重新进行GMPPT搜索。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   JEINC算法流程图


$({{P}_{n}}-{{P}_{1}})\times ({{P}_{1}}-{{P}_{2}})<0$
$\Delta P=\frac{\left| {{P}_{n}}-{{P}_{1}} \right|}{{{P}_{n}}}>0.1$

相较于传统INC算法和PSO算法而言，JEINC算法为INC算法提供了跳出局部最优点的机制，从而让光伏阵列的工作点能够在阴影环境下平稳过渡到GMPP位置处。

5 仿真验证

5.1 静态工况

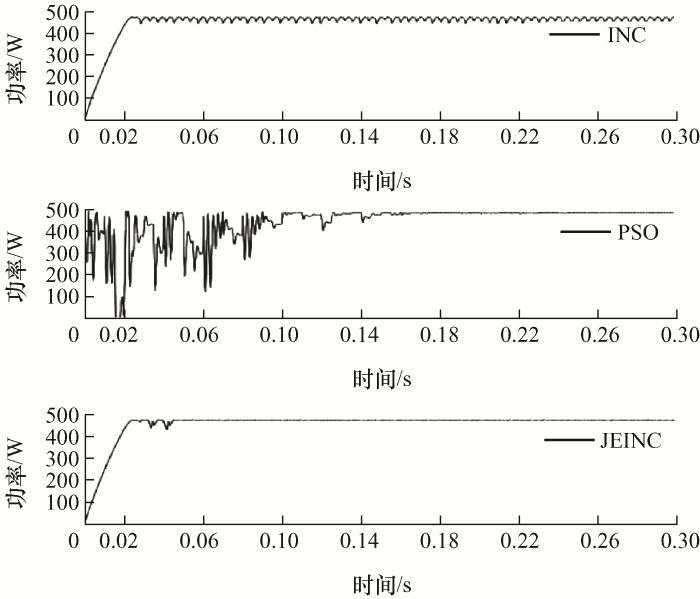
工况一为标准工况，光伏阵列输出特性曲线呈现单一峰值，分别通过INC、PSO和JEINC算法实现MPPT控制，输出功率波形如图5所示。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5   标准工况下输出功率波形图


在两种局部阴影工况下启动，通过INC、JEINC和PSO三种算法实现MPPT控制得到的输出功率波形图分别如图6a、6b所示。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6   工况二、三下输出功率波形图


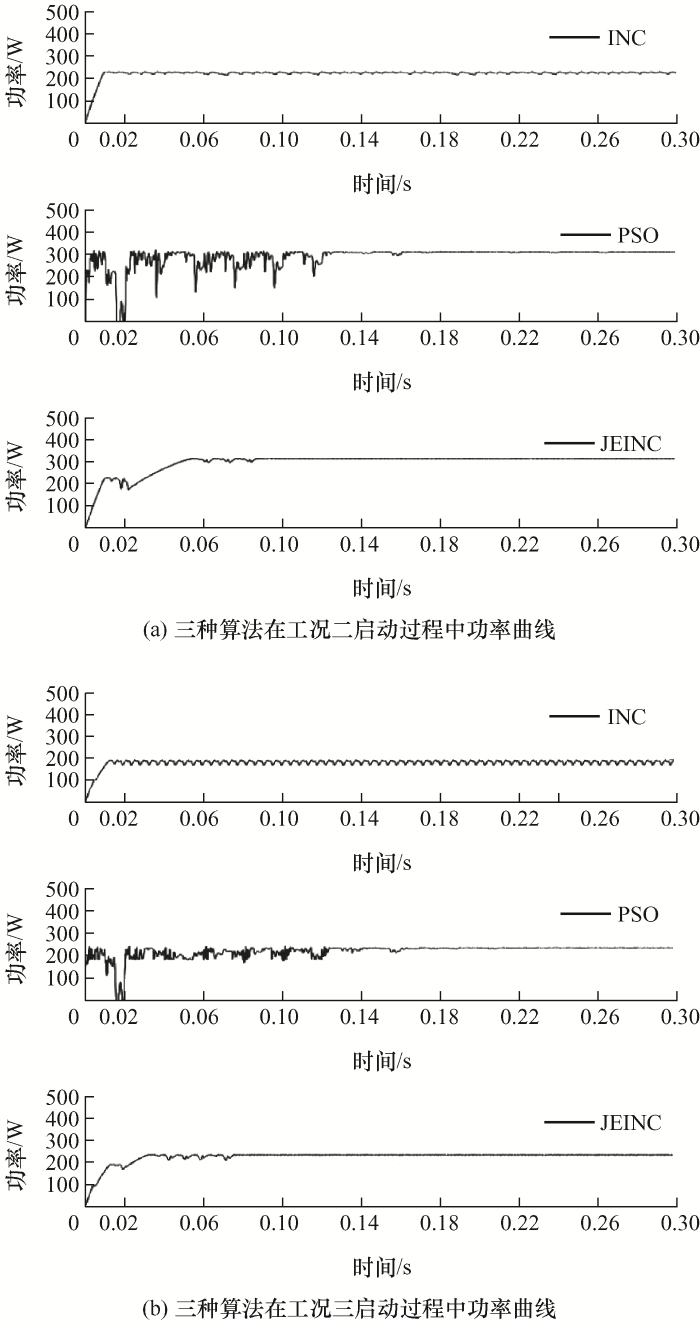
图5、图6的仿真结果总结于表3中，对比可得，在无阴影环境下，INC算法具有最快的MPPT控制速度，由于JEINC算法在工作点经过MPP点后将会继续探索，因此需要更长时间才能稳定，但探索过程中功率损耗较小，而PSO算法追踪速度较慢，且整个过程功率损耗较大，在进入稳态后，INC算法振荡严重，PSO和JEINC算法稳态时收敛性能较好。在两种存在局部阴影的工况下启动时，INC算法不能实现GMPPT，追踪失效，PSO算法在较长时间后能够实现GMPPT控制，而JEINC算法可以在落入LMPP后通过跃变探索功能跳出当前LMPP点，在工况二和工况三下均可实现GMPPT。系统稳定后，相较于PSO算法，JEINC算法可以控制光伏阵列工作点更为精确地落在MPP位置处，整个动态过程中功率损耗较低。

表3   INC、PSO和JEINC在三种工况下启动性能对比表

光照分布算法GMPPT稳定时间/s能量损耗率(%)振荡幅值/W
工况1INC实现0.034.10±15.00
PSO实现0.24710.00±7.25
JEINC实现0.0463.68±1.50
工况2INC未实现0.01245.14±7.50
PSO实现0.27210.70±0.60
JEINC实现0.0094.87±0.60
工况3INC未实现0.01421.84±12.10
PSO实现0.2357.65±3.00
JEINC实现0.0762.63±0.35

新窗口打开| 下载CSV


5.2 动态过程

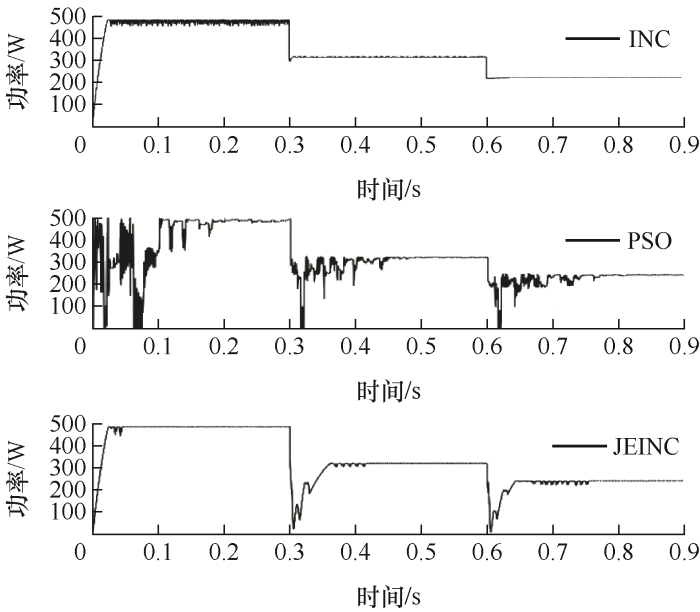
动态过程共分为三个阶段。在第一阶段中，光伏阵列在标准工况下启动，在0.3 s时，外界环境发生改变，光伏阵列接受到的光照强度突变为工况二状态，进入第二阶段，共持续0.3 s，之后光照分布突变为工况三，进入第三阶段。

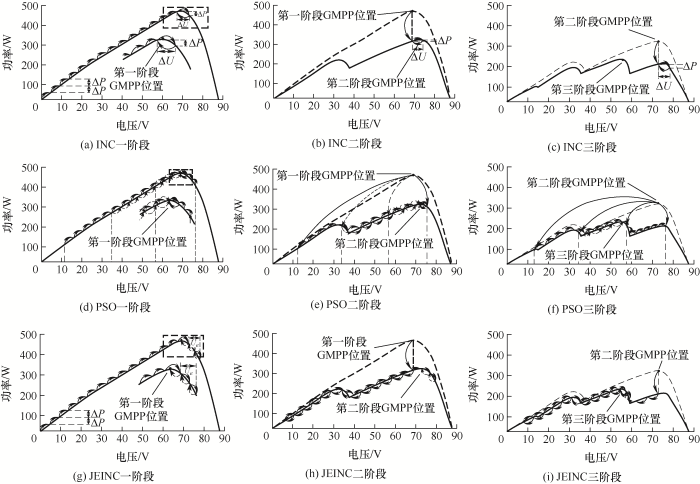
动态过程下通过三种算法实现MPPT控制得到的功率曲线如图7所示，每个阶段对应的工作点移动过程如图8所示，其中，图8a~8c、8d~8f、8g~8i分别为INC、PSO和JEINC在三个阶段下的动态过程原理图，每个图中实线为当前阶段的输出特性曲线，虚线为上一阶段输出特性曲线，最高点为MPP位置；INC对应三张图中，ΔU为电压变化量，ΔP为功率变化量；PSO对应三张图中，四种曲线分别代表四个粒子的移动过程；JEINC对应三张图中，继续向前探索，探索深度为Ue，探索N次后根据探索结果向MPP点靠拢，从而实现GMPPT控制，在图8g~8i中，粗实线表示INC寻优过程，双箭头为探索模式，虚线箭头表示结束探索，通过INC实现当前位置的MPPT，实线箭头为初始化过程，当外界环境突变时，光伏阵列工作点回到初始点附近，之后重新进行GMPPT控制。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7   三种算法在动态过程下功率曲线


图8

新窗口打开| 下载原图ZIP| 生成PPT

图8   动态过程中工作点移动过程原理图


6 结论

在现有光伏阵列MPPT研究基础上，本文提出了一种新的光伏阵列MPPT控制方法，通过判断光伏阵列的工作点所处位置修改步长，控制光伏阵列可以在不同光照分布下的稳定实现全局最大功率点跟踪。与传统控制方法相比，本文所提算法有以下几个特点。

(1) 在均匀光照环境下，该算法的功率损耗率显著小于采用PSO算法，与传统INC算法的功率损耗率差别较小；在阴影环境下，该算法可以跳出局部最优点，控制光伏阵列工作点平稳过渡到全局最优点处。

(2) 当外界环境发生变化时，该算法可以控制光伏阵列平稳过渡到新的全局最大功率点处，实现GMPPT控制，且动态过程中不会产生剧烈振荡。

(3) 算法收敛后，振荡幅值更小，具有较好的稳态精度。

参考文献

花赟昊, 朱武, 郭启明.

光伏发电系统MPPT算法研究综述

[J]. 电源技术, 2020, 44(12):1855-1858.

[本文引用: 1]

HUA Yunhao, ZHU Wu, GUO Qiming.

Review of MPPT algorithm of photovoltaic power generation system

[J]. Chinese Journal of Power Sources, 2020, 44(12):1855-1858.

[本文引用: 1]

DHIMISH M.

Assessing MPPT techniques on hot-spotted and partially shaded photovoltaic modules:Comprehensive review based on experimental data

[J]. IEEE Transactions on Electron Devices, 2019, 66(3):1132-1144.

DOI:10.1109/TED.2019.2894009      URL     [本文引用: 1]

马爱华, 李磊, 师贺.

光伏电池建模及变步长MPPT控制

[J]. 电气工程学报, 2017, 12(5):58-63.

[本文引用: 1]

MA Aihua, LI Lei, SHI He.

Modeling of photovoltaic cells and MPPT control algorithm with variable step

[J]. Journal of Electrical Engineering, 2017, 12(5):58-63.

[本文引用: 1]

SINGH S, MANNA S, MANSOORI M I H, et al.

Implementation of perturb & observe MPPT technique using Boost converter in PV system

[C]// 2020 International Conference on Computational Intelligence for Smart Power System and Sustainable Energy (CISPSSE),2020:1-4.

[本文引用: 1]

VENKATRAMANAN D, JOHN V.

Dynamic modeling and analysis of Buck converter based solar PV charge controller for improved MPPT performance

[J]. IEEE Transactions on Industry Applications, 2019, 55(6):6234-6246.

DOI:10.1109/TIA.28      URL     [本文引用: 1]

刘聘凭, 程若发, 许立斌, 等.

基于光伏MPPT采样电流的自适应变步长INC算法

[J]. 电源学报, 2023, 21(5):58-66.

DOI:10.13234/j.issn.2095-2805.2023.5.58      [本文引用: 1]

针对传统电导增量INC（incremental conductance）算法在跟踪最大功率点的过程中无法兼顾跟踪速度与稳态精度的问题,以及传统变步长算法在光照变化时容易发生误判的问题,提出了一种新型的自适应变步长INC算法。光照强度变化较大时,利用负载曲线与I-V特性曲线的工作原理,在暂稳态和非稳态下都可以根据最大功率点跟踪MPPT（maximum power point tracking）采样电流的变化,自适应调节跟踪速度;光照强度变化较小时,能够根据输出电压与功率的变化自适应减小步长,提高稳态精度。追踪速度是传统算法的9.3倍,是现有变步长算法的4.2倍,有效减少了光照强度变化带来的功率损失。

LIU Pinping, CHENG Ruofa, XU Libin, et al.

Adaptive variable-step INC algorithm for PV MPPT sampling current

[J]. Journal of Power Supply, 2023, 21(5):58-66.

DOI:10.13234/j.issn.2095-2805.2023.5.58      [本文引用: 1]

The traditional incremental conductance（INC） algorithm is unable to balance its tracking speed and steady-state accuracy in tracking the maximum power point, and the traditional variable-step algorithm is prone to misjudgment when solar irradiance changes. Aimed at these problems, a novel adaptive variable-step INC algorithm is proposed. When the solar irradiance varies greatly, it can adaptively adjust the tracking speed according to the changes in maximum power point tracking（MPPT） sampling current in transient and unsteady states by using the working principles for load curve and <em>I</em>-<em>V</em> characteristic curve. In the case of small changes in solar irradiance, it can adaptively reduce the step size according to the changes in output voltage and power, thus improving the accuracy in the steady state. The tracking speed of this algorithm is 9.3 times faster than that of the traditional algorithm and 4.2 times faster than that of the existing variable-step algorithm, which effectively reduces the power loss caused by changes in solar irradiance.

BOLLIPO R B, MIKKILI S, BONTHAGORLA P K, et al.

Hybrid,optimal,intelligent and classical PV MPPT techniques:A review

[J]. CSEE Journal of Power and Energy Systems, 2021, 7(1):9-33.

[本文引用: 1]

SINGH D, SINGH H.

Technical survey and review on MPPT techniques to attain maximum power of photovoltaic system

[C]// 2019 5th International Conference on Signal Processing,Computing and Control (ISPCC),2019: 265-268.

[本文引用: 1]

ROUTRAY D, ROUT P K, SAHU B K.

A brief review and comparative analysis of two classical MPPT techniques

[C]// 2021 International Conference in Advances in Power,Signal,and Information Technology (APSIT),2021:1-6.

[本文引用: 1]

HAYDER W, ABID A, HAMED M B, et al.

Comparison of MPPT methods FLC & PSO for PV system under variable irradiance and temperature

[C]// 2021 18th International Multi-Conference on Systems,Signals & Devices (SSD),2021: 1247-1251.

[本文引用: 1]

王凯丽, 张巧杰.

基于IPSO算法的光伏阵列多峰值MPPT研究

[J]. 电气工程学报, 2016, 11(10):53-58.

[本文引用: 1]

WANG Kaili, ZHANG Qiaojie.

Research on multi-peak MPPT of photovoltaic array based on IPSO algorithm

[J]. Journal of Electrical Engineering, 2016, 11(10):53-58.

DOI:10.12677/JEE.2023.112007      URL     [本文引用: 1]

王利峥, 刘光宇.

基于简化蚁群算法的光伏MPPT跟踪控制

[J]. 电源技术, 2020, 44(8):1152-1155.

[本文引用: 1]

WANG Lizheng, LIU Guangyu.

MPPT tracking control for photovoltaic system based on simplified ant colony algorithm

[J]. Chinese Journal of Power Sources, 2020, 44(8):1152-1155.

[本文引用: 1]

CHY D K, KHALILUZZAMAN M.

Experimental assessment of PV arrays connected to Buck-Boost converter using MPPT and non-MPPT technique by implementing in real time hardware

[C]// 2015 International Conference on Advances in Electrical Engineering (ICAEE),2015:306-309.

[本文引用: 1]

MIRJALILI S.

SCA:A sine cosine algorithm for solving optimization problems

[J]. Knowledge-Based Systems, 2016,96:120-133.

[本文引用: 1]

张慧斌, 王鸿斌, 胡志军.

PSO算法全局收敛性分析

[J]. 计算机工程与应用, 2011, 47(34):61-63.

[本文引用: 1]

ZHANG Huibin, WANG Hongbin, HU Zhijun.

Analysis of particle swarm optimization algorithm global convergence method

[J]. Computer Engineering and Applications, 2011, 47(34):61-63.

[本文引用: 1]

<FONT face=Verdana>In order to find out whether the PSO algorithm can search for global optimal solution，detailed explanation to global convergence criteria of random optimal algorithm is made.The theoretical analysis of global convergence of PSO algorithm is also done applying this global convergence criteria.The result of the PSO algorithm does not satisfy two conditions which the global convergence criteria of random optimization algorithm should have.This paper proves that the PSO algorithm does not guarantee global convergence.<BR></FONT>

HU T, WU Q, ZHOU D X.

Convergence of gradient descent for minimum error entropy principle in linear regression

[J]. IEEE Transactions on Signal Processing, 2016, 64(24):6571-6579.

DOI:10.1109/TSP.2016.2612169      URL     [本文引用: 1]

LIU F, DUAN S, LIU F, et al.

A variable step size INC MPPT method for PV systems

[J]. IEEE Transactions on Industrial Electronics, 2008, 55(7):2622-2628.

DOI:10.1109/TIE.2008.920550      URL     [本文引用: 1]

曾建潮, 崔志华.

一种保证全局收敛的PSO算法

[J]. 计算机研究与发展, 2004(8):1333-1338.

[本文引用: 1]

ZENG Jianchao, CUI Zhihua.

A guaranteed global convergence particle swarm optimizer

[J]. Journal of Computer Research and Development, 2004(8):1333-1338.

[本文引用: 1]

田盛. 光伏组件局部阴影下热斑效应优化配置研究[D]. 天津: 河北工业大学, 2016.

[本文引用: 1]

TIAN Sheng. The study of photovoltaic module structure optimizing caused by hot spot under partial shading[D]. Tianjin:Hebei University of Technology, 2016.

[本文引用: 1]

/

〈 〉