1 引言
随着传统能源储量的减少,新能源系统在传统电力系统中的渗透率不断提高。孤岛微电网是集成了分布式电源(Distributed generator,DG)、储能装置以及负荷的小型独立电力系统,也是解决能源问题和提高偏远地区电力需求的一种有效途径[1 ] 。由于风能、太阳能等新能源发电均采用电力电子变换装置,因此微电网系统是低电压、低惯性的小规模电力系统。而虚拟同步发电机(Virtual synchronous generator,VSG)控制方法是通过模拟同步发电机的机电暂态特性和阻尼特性,提高微电网对DG的接纳能力,进一步保证微电网系统的稳定运行[2 ] ,受到国内外学者的广泛关注。
微电网系统通常采用分层控制,可分为一次控制、二次控制和三次控制三个层次[3 ] 。VSG控制策略属于一次控制层,主要目的是为系统提供惯性并按设定的下垂特性参与系统功率调节,快速稳定每个DG的频率。但是一次控制属于有差控制,在缺乏电网支撑的条件下,孤岛微电网的动态特性容易受到影响,频率可能偏离参考值[4 ] 。为了提高控制精度,通常引入二次控制层进行校正,三次控制层主要考虑微电网的经济调度和优化运行。本文主要研究微电网的二次控制问题。目前在孤岛微电网的多机并联系统中,集中式二次控制应用较为广泛,然而集中控制过于依赖通信网络。近年来,分布式协同控制仅通过与邻居之间的简单信息交流便可达到一种稳定状态,从而影响其他支路保证整体系统的稳定运行,因此在孤岛微电网的分布式二次控制中逐渐成为学者们的研究重点[5 ] 。
分布式协同控制具有协调性优良,通信简单等优点,文献[6 ]将分布式一致性应用于微电网的控制策略中,基于平均一致性提出一种分布式比例积分控制器,保证了电压与频率的恢复。文献[7 ]在文献[6 ]的基础上引入一种分布式滑模控制器,可提高分布式比例积分器的收敛速度,不仅达到快速补偿的效果,还可提高系统的鲁棒性。文献[8 ]讨论了微电网一致性控制下的频率恢复和有功功率精确分配。然而分布式一致性算法主要应用于常规下垂交流微电网,但常规下垂控制存在惯性小、输出阻抗低的缺点,当微电网受到较大扰动时会影响系统的稳定性。近年来,一些学者利用VSG来解决上述问题,文献[9 ]通过模拟传统同步发电机转子的运动,为逆变器提供虚拟惯性和阻尼特性,达到一次调频的目的。文献[10 ]通过改进控制结构的方法进行二次调频,但是由于没有通信结构,面对较大的负荷波动仍需要对二次调频逆变器的数量进行调整。文献[11 ]提出将一致性用于VSG二次控制中,既保留了惯性和虚拟阻抗的特点,同时将频率恢复至额定值,但是频率的恢复时间长,影响微电网工作效率。文献[12 ]在文献[11 ]的基础上通过设计出预测VSG邻居和自身未来状态的控制器,进而提高并联VSG频率的恢复速度,但是恢复时间的不确定降低了其适用性。文献[13 -14 ]通过对一致性算法的改进提出有限时间一致性,可以在限定时间内完成收敛,但是在微电网初始状态未知的情况下难以确定收敛时间,随着初值的增大实际收敛时间也会增加,不利于微电网的应用。文献[15 -16 ]为解决初始状态问题,提出基于固定时间一致性的二次控制方案,该方案无需考虑系统的初始状态,并保证了电压和频率在有限时间内快速恢复,但是计算出来的稳态时间过于保守,与实际恢复时间有很大差别,并且协议参数的存在使得恢复时间也会随之改变。文献[17 ]使用基于固定时间一致性的二次频率控制,并验证了其即插即用特性,但是对于新投入的DG需要较长时间恢复稳定,影响了微电网的工作效率。
上述研究对分布式一致性在微电网中的应用进行了初步分析,目前的分布式一致性虽然能够解决VSG一次频率控制存在的偏差问题,但是并未考虑频率恢复速度的影响因素。为此,本文提出基于预定时一致性的VSG二次频率控制策略。该策略将每台VSG及其逆变器视为一个多智能体,通过调节与相邻VSG之间偏差进而达到全局优化,实现二次控制的无差调节。同时,该策略基于预定时系统对一致性进行改进,在预先确定频率恢复时间的条件下实现微电网频率的快速恢复。相较于现阶段一致性二次控制,本文采用的控制方案增加了自定义恢复时间环节,解决了频率恢复速度慢以及恢复速度受VSG初始状态与协议参数影响的问题。对于新投入的VSG,保证其快速稳定,提高系统的工作效率和灵活性。最后通过仿真验证所提控制策略的可行性和有效性。
2 VSG一次控制
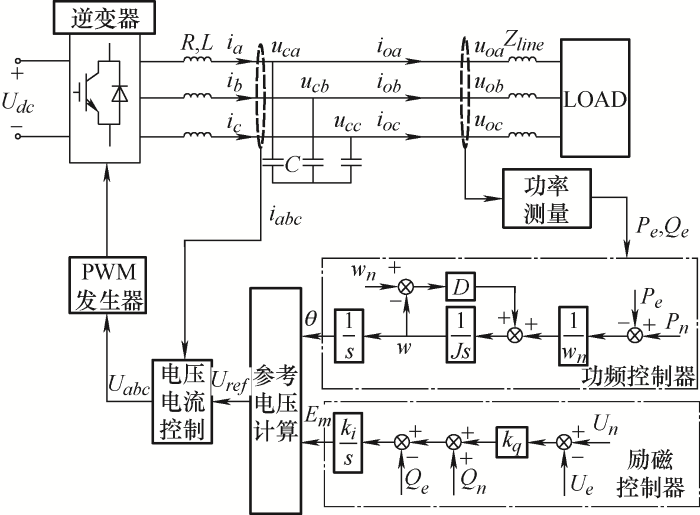
VSG模拟同步发电机的机电暂态特性和阻尼功率振荡的能力,使其能够动态的弥补功率差额,减少频率波动程度,进而改善系统稳定性提高微电网对分布式电源的接纳能力。图1 为VSG的典型控制结构,可控微源被视为理想的直流电源Udc 。逆变器采用三相桥式逆变电路,忽略逆变器开关过程的影响,其余部分主要包含LC滤波、线路阻抗Zline 、负载以及一些测量元件构成。R 、L 、C 分别为LC滤波器的电感内阻、滤波器电感和滤波器电容;ia 、ib 、ic 分别为三相电感电流;uc 代表滤波电容电压;io 、uo 分别代表逆变器输出电流和电压。通过励磁控制器得到的指令电压的幅值,以及功频控制器得到的相位信息合成得到电压电流控制环的输入信号Uref ,经过电压电流环得到的Uabc 作用于PWM发生器产生逆变器工作信号。
图1
VSG的功频控制器主要模拟了同步发电机的转子运动方程,模型的建立旨在体现同步发电机的基本特性,因此采用同步发电机的二阶模型
(1) $\left\{ \begin{align} & J\frac{\mathrm{d}w}{\mathrm{d}t}={{T}_{n}}-{{T}_{e}}-{{T}_{d}}=\frac{{{P}_{n}}}{{{w}_{N}}}-\frac{{{P}_{e}}}{{{w}_{N}}}-D(w-{{w}_{N}}) \\ & \frac{\mathrm{d}\theta }{\mathrm{d}t}=w \\ \end{align} \right.$
式中,Tn 为机械转矩;Te 为电磁转矩;Td 为阻尼转矩;Pe 为输出有功功率;Pn 为额定有功功率;D 为阻尼系数,模拟同步发电机阻尼振荡特性的能力;wn 和w 分别为额定角速度以及电气角速度;J 为转动惯量,是频率动态响应具备惯性的原因;θ 为转子角度。VSG的励磁控制器主要维持电压恒定与无功功率分配,提高电力系统稳定性。Un 、Ue 分别为额定电压与输出电压有效值;Qn 、Qe 分别为额定无功功率与输出无功;kq 为下垂系数;Em 为电压参考信号有效值。
VSG控制策略本质上仍属于有差控制,线路的变化会导致频率与额定值之间产生一定的偏差,因此针对该问题,本文引入二次控制来调节偏差。鉴于分布式协同一致性的优越性,以一致性为切入点,结合VSG本体控制达到无差控制的目的。
3 VSG二次控制
3.1 图论基础
多智能体网络可以定义为一个图G V E A N 个多智能体连接而成的连通图。其中V N }表示N 个节点的非空有限集合;E V V A aij ]表示邻接矩阵,其中(i , j )∈E i 可以收到节点j 传输的通信信息,有aij >0。如果aij =0,表示节点之间没有通信交流。N i j ∈V j , i )∈E i 的邻居节点集合。连通图的拉普拉斯矩阵与交互信息相关,可以定义为L D A N 维矩阵D di }称为度矩阵,拉普拉斯矩阵L L
基于图论的介绍,N 个多智能体存在的网络中第i 个智能体的动态模型可以描述为
(2) ${{\dot{x}}_{i}}={{u}_{i}},i\in \mathbf{V}:\left( 1,2,\cdots,N \right)$
(3) ${{u}_{i}}(t)=\underset{j\in {{N}_{i}}}{\mathop \sum }\,{{a}_{ij}}\left[ {{x}_{j}}(t)-{{x}_{i}}(t) \right]$
式中,xi (t )∈R 是第i 个智能体状态变量;ui (t )∈R 是第i 个智能体的控制输入。xi (0)表示系统的初始状态,在一致性的收敛作用下所有系统会趋近于初始状态的平均值,称系统达到平均一致性收敛。
这一协同控制的思想可以用于微电网中,将VSG控制的多DG视为多智能体节点,将频率和有功功率视为通信信息,通过相邻单元的状态信息估计全局参考信号。
3.2 结合预定时系统的一致性
在多DG的微电网系统中,微电网的电压和频率会存在一定的波动,为了限制这种偏差在允许范围以内,二次控制可考虑采用通信手段的介入。传统的通信控制方案多采用集中控制器来对各个DG进行控制,这种方案与稀疏通信的要求相矛盾。分布式协同控制可以保证只通过与邻居之间的信息交换来实现全局优化[18 ] 。平均一致性在微电网方面的引入降低了通信要求,但是需要较长时间才能够将偏差控制到允许范围以内。
为了提高收敛速度,有学者提出有限时间一致性与固定时间一致性,通过在时间方面进行限制进而提高收敛速度。但是,该方案在微电网中的应用需要考虑初始状态、协议参数等信息,这在多DG的微电网中往往难以获取。本文根据现阶段在时间方面可加速恢复的优点,对一致性进行改进,设计出适用于微电网系统的分布式协同一致性控制。该控制方案通过一致性算法结合预定时系统,达到定时控制的要求,保证微电网不会受到初始状态、协议参数等条件的限制仍然可以在设定时刻收敛,具体设计如下
(4) $\begin{matrix} {{u}_{i}}\left( t \right)=-\left( \frac{\dot{\xi }(t)}{2{{\lambda }_{2}}\left( \mathbf{L} \right)\left( 1-\xi \left( t \right)+\delta \right)}+1 \right)\times \\ \left( \sum\limits_{j\in {{N}_{i}}}{{{a}_{ij}}\left( {{x}_{i}}(t)-{{x}_{j}}(t) \right)} \right) \\ \end{matrix}$
(5) $\xi \left( t \right)=\left\{ \begin{align} & \frac{10}{t_{f}^{\text{6}}}{{t}^{6}}-\frac{24}{t_{f}^{\text{5}}}{{t}^{5}}+\frac{15}{t_{f}^{\text{4}}}{{t}^{4}}\ \ \ \ 0\le t\le {{t}_{f}} \\ & 1 \ \ \ t>{{t}_{f}} \\ \end{align} \right.$
式中,0<δ$\ll $ 1为极小常数;tf 是预定时间,用户可以根据需要自行设计;λ 2 (L $\dot{\xi }$ ( t )/2λ 2 (L ξ (t )+δ ))+1为预定时系统,保证一致性的定时收敛。此外,预定时系统不含未知参数,不会受到协议参数与初始状态的影响,保证了系统的可行性。
为了清楚阐明预定时系统的优势,对比固定时间一致性的典型结构[19 ] ,具体如式(6)所示
(6) $\begin{matrix} {{u}_{i}}=\alpha {{\left( \sum\limits_{j\in {{N}_{i}}}{{{a}_{ij}}\left( {{x}_{j}}(t)-{{x}_{i}}(t) \right)} \right)}^{\text{2}-\frac{u}{v}}}+ \\ \beta {{\left( \sum\limits_{j\in {{N}_{i}}}{{{a}_{ij}}\left( {{x}_{j}}(t)-{{x}_{i}}(t) \right)} \right)}^{\frac{u}{v}}} \\ \end{matrix}$
式中,α >0,β >0,v >u >0均表示为根据需要设计的协议参数,且u ,v 参数需要满足正奇数。固定时间上限估计值为
(7) ${{T}_{0}}\le {{T}_{\max }}=\frac{1}{{{\lambda }_{2}}\left( L \right)}\left( \frac{{{N}^{\frac{v-u}{2v}}}}{\alpha }\frac{v}{v-u}+\frac{1}{\beta }\frac{v}{v-u} \right)$
式中,λ 2 (L L T max 即可确定收敛时间上限,但是固定时间一致性对于最大时间的估计值过于保守,与实际收敛时间差距过大,并且收敛时间也会随参数而改变,不利于微电网的控制[20 ] 。
3.3 二次频率控制
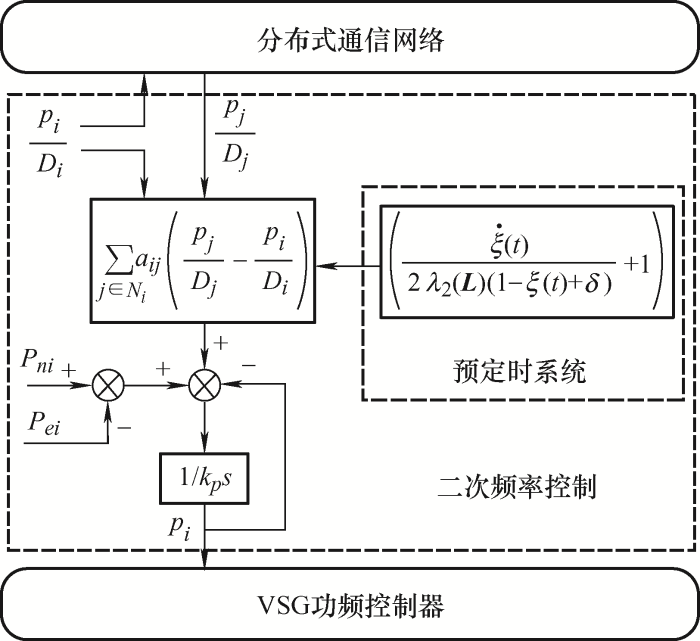
本文基于VSG的基本情况,设计适用于微电网孤岛模式下的分布式二次频率控制策略,通过将多智能体的分布式架构运用于VSG的有功控制环路设计一种简易通信的分布式控制器,并通过预定时系统加快频率恢复速度,提高微电网的工作效率,图2 是微电网第i 台VSG的二次频率控制框图,其表达式具体设计为
(8) $J{{w}_{N}}\frac{\mathrm{d}{{w}_{i}}}{\mathrm{d}t}={{P}_{ni}}-{{P}_{ei}}-{{p}_{i}}-{{D}_{i}}({{w}_{i}}-{{w}_{N}})$
(9) $\begin{matrix} {{k}_{p}}{{{\dot{p}}}_{i}}={{P}_{ni}}-{{P}_{ei}}-{{p}_{i}}+ \\ \left( \frac{\dot{\xi }(t)}{2{{\lambda }_{2}}\left( \mathbf{L} \right)\left( 1-\xi \left( t \right)+\delta \right)}+1 \right)\times \\ \underset{j\in {{N}_{i}}}{\mathop \sum }\,{{a}_{ij}}\left( \frac{{{p}_{j}}}{{{D}_{j}}}-\frac{{{p}_{i}}}{{{D}_{i}}} \right) \\ \end{matrix}$
式中,J 为VSG的转动惯量;wN 和wi 分别为额定角频率以及第i 台VSG测量角频率;Pni 和Pei 分别为第i 台VSG的额定功率和输出功率;Di 表示第i 台VSG的阻尼系数;kp 表示频率恢复系数;pi 表示第i 台VSG的有功功率补偿量。
图2
下面验证所提控制策略达到稳态时的频率恢复机制,令预定时系统($\dot{\xi }(t)$ λ 2 (L ξ (t )+δ ))+1=η ,对所提二次频率控制策略进行验证。
(10) $0={{P}_{ni}}-{{P}_{ei}}-{{p}_{i}}+\eta \times \underset{j\in {{N}_{i}}}{\mathop \sum }\,{{a}_{ij}}\left( \frac{{{p}_{j}}}{{{D}_{j}}}-\frac{{{p}_{i}}}{{{D}_{i}}} \right)$
根据图论的介绍,在一致性的收敛作用下所有系统会趋近于初始状态的平均值,此时当前节点的状态量与邻居的状态一致,因此有
(11) $\underset{j\in {{N}_{i}}}{\mathop \sum }\,{{a}_{ij}}\left( \frac{{{p}_{j}}}{{{D}_{j}}}-\frac{{{p}_{i}}}{{{D}_{i}}} \right)=0$
(12) ${{P}_{ni}}-{{P}_{ei}}-{{p}_{i}}=0$
将所得到的式(12)代入式(8)可知,在稳定状态下,等式左侧为零。此时wi =wN ,即经过二次调频控制策略的作用下,频率恢复至额定值。这从负荷的静态特性也可以得出,一致性算法改变了VSG的有功输出,使系统的有功功率在达到稳态时实现了供需平衡,进而保证了频率恢复。
下面对有功出力进行分析,根据式(9)和式(12)以及一致性收敛至初始状态平均值的特性,有
(13) $\frac{{{p}_{i}}}{{{D}_{i}}}=\frac{1}{n}\underset{j\in {{N}_{i}}}{\mathop \sum }\,\frac{{{p}_{j}}}{{{D}_{j}}}=\frac{1}{n}\underset{j\in {{N}_{i}}}{\mathop \sum }\,\frac{{{P}_{nj}}-{{P}_{ej}}}{{{D}_{j}}}$
式中,n 表示相邻VSG的数量,将式(13)代入式(8)可得
(14) $\frac{{{P}_{ei}}}{{{P}_{ni}}}=1-\frac{{{D}_{i}}}{n{{P}_{ni}}}\underset{j\in {{N}_{i}}}{\mathop \sum }\,\frac{{{P}_{nj}}-{{P}_{ej}}}{{{D}_{j}}}$
在稳定状态下pi /Di =pj /Dj ,因此在式(14)中未知量仅有Di /Pni ,为了使有功功率按照逆变器容量权重进行分配,需要保证Di /Pni 在各VSG中均相等。
该方案是在VSG调速器的基础上引入分布式控制器得到的,可解决传统二次控制存在的有功功率分配问题,并且无须考虑微电网的拓扑、馈线以及负荷信息,即可快速准确地分配有功出力,实现二次频率控制的目标,具有较强的可靠性和适用性。
3.4 二次频率控制定时恢复证明
预定时系统不含未知参数,并不会对二次控制效果产生影响。但是本文所提二次频率控制相比较于现阶段的二次控制,拥有定时的快速收敛特性。现证明式(8)和式(9)所提的VSG二次频率控制策略能够保证在预定时刻稳定收敛,基于无向连通图提出以下引理和定理。
定义1:如果对任意初值xi (0), i =1, 2,…, N ,若称一阶线性系统在预定时系统的作用下收敛,需要保证下列条件成立
(15) $\left\{ \begin{align} & \underset{t\to {{t}_{f}}}{\mathop{\lim }}\,|{{x}_{i}}(t)-{{x}_{0}}(t)|\le C \\ & |{{x}_{i}}(t)-{{x}_{0}}(t)|\le C\ \ \ \ \forall t>{{t}_{f}} \\ & \underset{t\to \infty }{\mathop{\lim }}\,|{{x}_{i}}(t)-{{x}_{0}}(t)|=0 \\ \end{align} \right.$
式中,C 是一个任意小的正常数;tf 表示自定义时间与初始状态无关,可以设计成任意小的值。
(16) $\left\{ \begin{align} & {{\mathbf{x}}^{\mathrm{T}}}\mathbf{Lx}\ge {{\lambda }_{2}}(\mathbf{L}){{\mathbf{x}}^{\mathrm{T}}}\mathbf{x} \\ & {{\mathbf{x}}^{\mathrm{T}}}({{\mathbf{L}}^{2}})\mathbf{x}\le {{\lambda }_{N}}({{\mathbf{L}}^{2}}){{\mathbf{x}}^{\mathrm{T}}}\mathbf{x} \\ \end{align} \right.$
式中,λ 2 (L λN (L 2 )分别为拉普拉斯矩阵的第二小特征值和拉普拉斯矩阵平方的最大特征值。
引理2:令式(4)中的$\dot{\xi }(t)$ λ 2 (L ξ (t )+δ )]=η ,此时式(4)可以表示为矩阵形式
(17) ${{\dot{x}}_{i}}\left( t \right)=-\left( \eta +1 \right)\mathbf{LX}$
(18) $x(t)={{x}_{0}}\left( 1-\frac{\xi (t)}{1+\delta } \right)$
由于在tf 处ξ (tf )=1,0<δ$\ll $ 1,因此x (t )的收敛效果接近于[δ/ (1+δ )]x 0 决定着最终的收敛效果,可以根据实际要求设计符合偏差范围的参数。
定理1:根据定义与引理1、2,结合预定时系统的一致性具有以下收敛条件
(19) $\left\{ \begin{align} & \underset{t\to {{t}_{f}}}{\mathop{\lim }}\,\left| {{x}_{i}}-{{x}_{j}} \right|\le (N-1)\sqrt{\frac{2\delta }{{{\lambda }_{2}}\left( 1+\delta \right)}V(0)} \\ & \left| {{x}_{i}}-{{x}_{j}} \right|\le (N-1)\sqrt{\frac{2\delta }{{{\lambda }_{2}}\left( 1+\delta \right)}V(0)}\ \ \ \ \forall t>{{t}_{f}} \\ & \\ & \underset{t\to \infty }{\mathop{\lim }}\,|{{x}_{i}}-{{x}_{j}}|=0 \\ \end{align} \right.$
当本文所设计的二次频率控制策略满足定理1时,表示满足在设定时刻完成功率精确分配以及频率恢复的任务。为简化方程令p /D =B V (t )=(B T LB L
(20) $\begin{matrix} \dot{V}(t)=\frac{1}{2}{{\mathbf{B}}^{\mathrm{T}}}\mathbf{L\dot{B}}\le -\frac{\eta }{2}{{\mathbf{B}}^{\mathrm{T}}}{{\mathbf{L}}^{2}}\mathbf{B}\le \\ -\frac{\eta }{2}\frac{{{\lambda }_{N}}({{\mathbf{L}}^{2}})}{{{\lambda }_{2}}(\mathbf{L})}{{\mathbf{B}}^{\mathrm{T}}}\mathbf{LB}\le -\frac{\eta }{2}{{\mathbf{B}}^{\mathrm{T}}}\mathbf{LB}=-\eta V(t)= \\ -\frac{\dot{\xi }(t)}{1-\xi (t)+\delta }V(t) \\ \end{matrix}$
结合引理2可知V (t )≤[δ /(1+δ )]V (0)。并根据引理1可以推导
(21) $V(t)=\frac{1}{2}{{\mathbf{B}}^{\mathrm{T}}}\mathbf{LB}\ge \frac{1}{2}{{\lambda }_{2}}(\mathbf{L}){{\mathbf{B}}^{\mathrm{T}}}\mathbf{B}$
(22) $\underset{t\to {{t}_{f}}}{\mathop{\lim }}\,|\mathbf{B}|\le \sqrt{\frac{2}{{{\lambda }_{2}}}V(t)}\le \sqrt{\frac{2}{{{\lambda }_{2}}}\frac{\delta }{1+\delta }V(0)}$
(23) $\underset{t\to {{t}_{f}}}{\mathop{\lim }}\,\left| {{\mathbf{B}}_{i}}-{{\mathbf{B}}_{j}} \right|\le (N-1)\sqrt{\frac{2\delta }{{{\lambda }_{2}}\left( 1+\delta \right)}V(0)}$
(24) $\dot{V}(t)=-\frac{\eta +1}{2}{{\mathbf{B}}^{T}}{{\mathbf{L}}^{2}}\mathbf{B}=-\frac{1}{2}{{\mathbf{B}}^{T}}{{\mathbf{L}}^{2}}\mathbf{B}\le 0$
导数小于等于零表示V (t )是一个单调不增函数,在t >tf 时会有
(25) $\left| {{\mathbf{B}}_{i}}-{{\mathbf{B}}_{j}} \right|\le (N-1)\sqrt{\frac{2\delta }{{{\lambda }_{2}}\left( 1+\delta \right)}V(0)}\ \ \ \ \forall t>{{t}_{f}}$
(26) $\underset{t\to \infty }{\mathop{\lim }}\,|{{\mathbf{B}}_{i}}-{{\mathbf{B}}_{j}}|=0$
根据以上证明可知,结合预定时系统设计的二次频率控制在设定时刻tf 处可以收敛到极小的值,并且在收敛时刻之后仍然保证收敛效果,验证了所提控制策略的定时恢复特性,进一步加快了频率恢复速度。
4 仿真验证
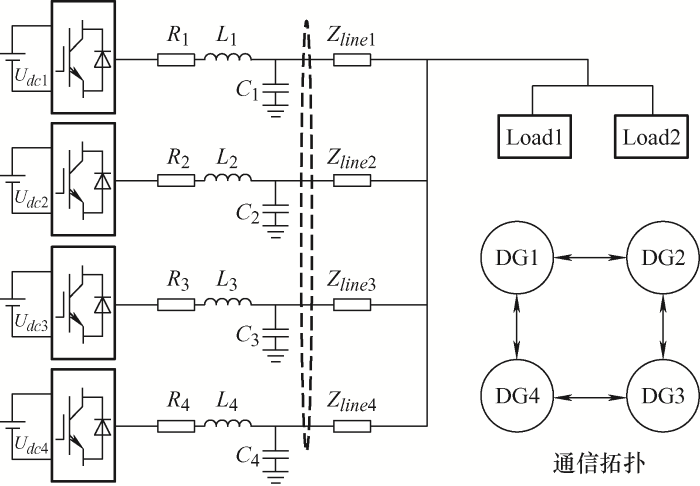
为了验证本文所提二次频率控制策略的定时恢复特性,基于Matlab/Simulink软件平台搭建如图3 所示的系统通信拓扑和四台并联DG的孤岛微电网系统的仿真模型。
图3
根据选择不同的参数来模拟实际情况,测试系统的主要仿真参数列于表1 中。
根据图3 所示的通信拓扑,可以得到邻接矩阵如式(27)所示,其中aij =1表示两分布式电源之间存在通信交流。
(27) $\mathbf{A}=\left[ \begin{matrix} 0 & 1 & 0 & 1 \\ 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 \\ 1 & 0 & 1 & 0 \\\end{matrix} \right]$
(28) $\mathbf{L=D}-\mathbf{A}=\left[ \begin{matrix} 2 & -1 & 0 & -1 \\ -1 & 2 & -1 & 0 \\ 0 & -1 & 2 & -1 \\ -1 & 0 & -1 & 2 \\\end{matrix} \right]$
进而计算出拉普拉斯矩阵的第二小特征值,即λ 2 (L
4.1 VSG分布式二次频率控制策略性能验证
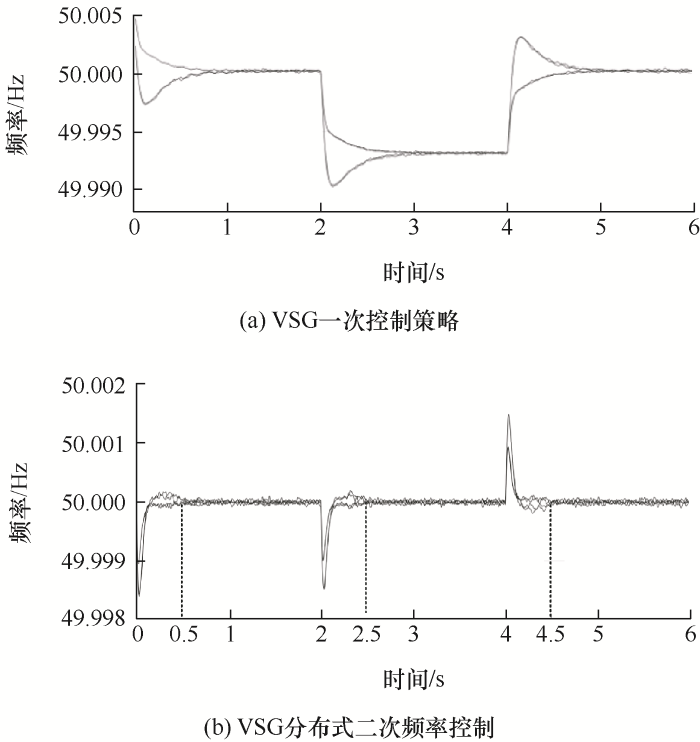
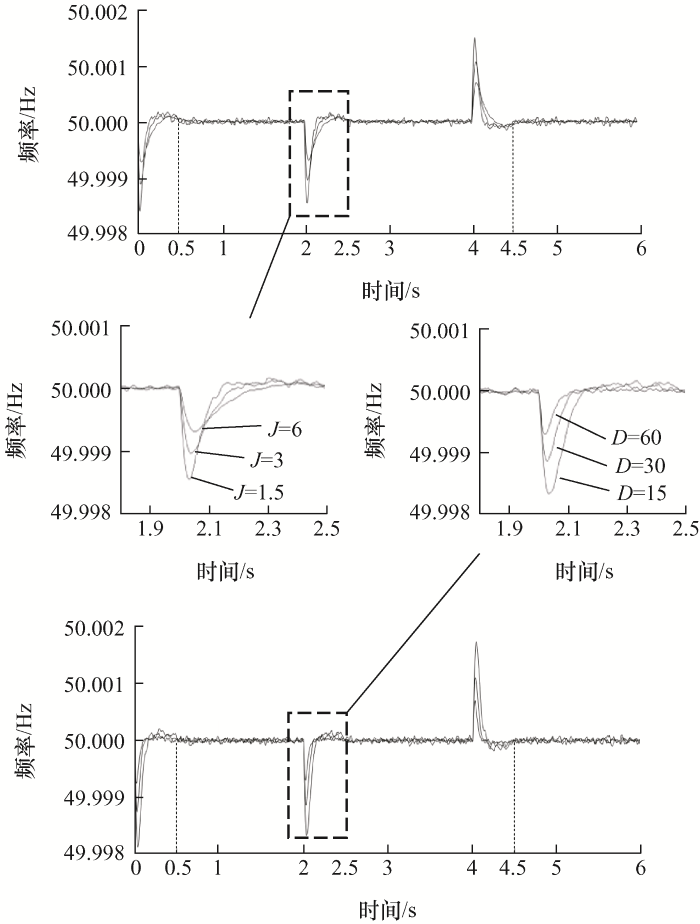
本文主要提出可定时恢复的VSG二次频率控制方案,快速恢复一次控制存在的偏差,提高工作效率,并且与传统下垂控制相比,VSG控制策略的优点在于能够为微电网提供惯性和阻尼。为了进一步验证所提控制策略的有效性,仿真工况设定为在初始时刻微电网仅接入Load1进行工作,在2 s时刻接入Load2并在4 s时刻Load2退出工作。图4 对比分析了一次控制与分布式二次控制下的频率响应,图5 以DG1为例通过改变惯性参数J 和阻尼参数D 验证系统能够提供虚拟惯性和阻尼特性,二次控制策略的频率恢复时间在此设定为0.5 s。
图4
图5
图5
所提控制策略在不同转动惯量J 和阻尼转矩D 下的频率响应
图4 显示所提分布式二次频率控制不仅能够解决一次控制存在的频率偏差问题,同样可以保证频率在设定时刻0.5 s内快速恢复。同时图5 可以看出,阻尼系数相同(D =15)时,随着转子惯性J 的增加,曲线向后移动并且峰值时间增加,另外转动惯量相同(J =1.5)时,阻尼系数D 越大,微电网系统的阻尼特性越明显,因此所提出的VSG分布式二次频率控制可以为电网系统提供所需的虚拟惯性和阻尼特性。此外当转动惯量参数增大,系统的频率变化更平缓,频率稳定时间变长,但是在预定时系统的控制下可以保证恢复时间在0.5 s内,因此在需要满足高惯性的情况下仍然可以保证系统频率的恢复速度,验证所提控制策略对微电网的可行性。
4.2 与现有分布式二次频率控制对比验证
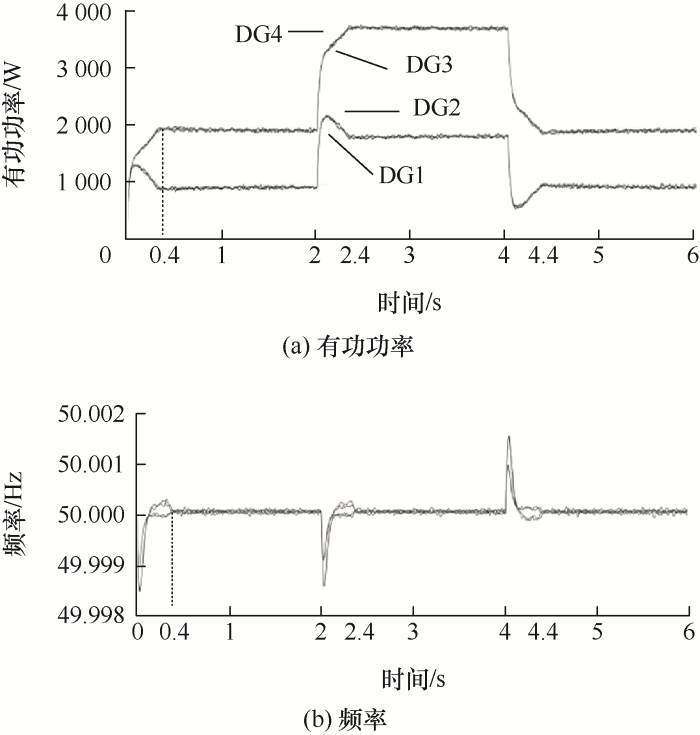
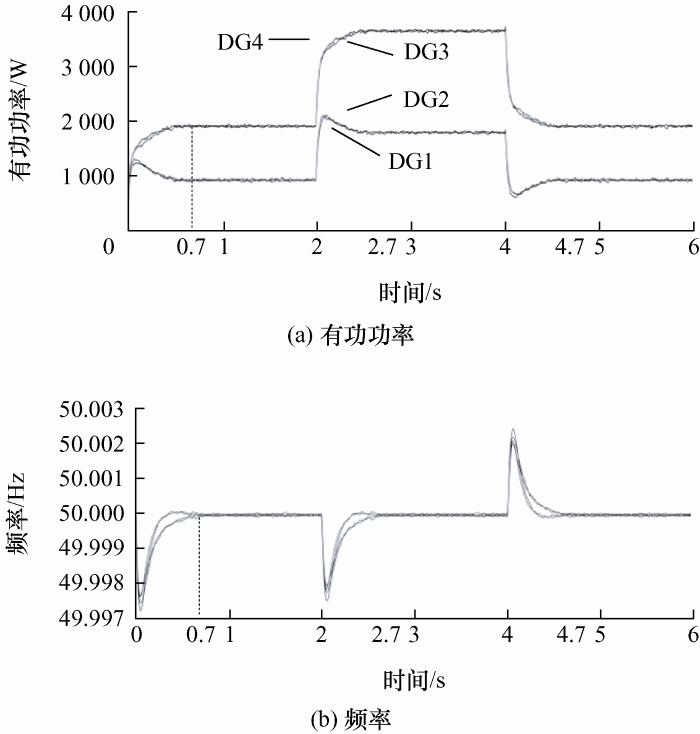
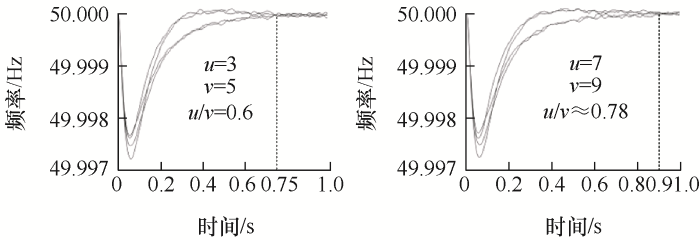
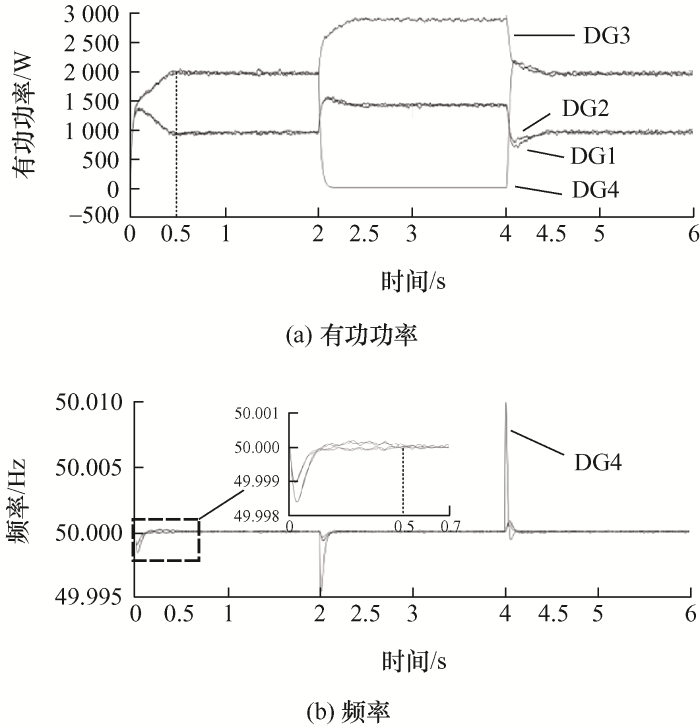
通过与现有固定时间一致性二次频率控制对比验证本文所提二次频率控制的快速恢复性能,并且通过调节现有分布式二次频率控制的参数指出现有控制方案存在的问题。仿真工况设定为在初始时刻微电网仅接入Load1进行工作,在2 s时刻接入Load2并在4 s时刻Load2退出工作。本文所提二次频率控制下的频率和有功功率输出仿真如图6 所示,现有二次频率控制对比仿真在同样工况下如图7 所示,图8 为调节现有二次控制参数对频率恢复时间的影响。本次仿真将时间设定为负载变化后的0.4 s,可以看出有功功率和频率的恢复均在0.4 s内完成。
图6
图7
图8
从图6 可以看出,DG1、2有功功率输出为1 kW,DG3、4有功功率输出为2 kW,增加Load2后DG1、2达到2 kW,DG3、4达到4 kW,可以按照额定容量进行比例分配,频率在0.4 s恢复稳定,相比较同工况下的图4b ,预定时系统的引入不仅加快了收敛速度,而且恢复时间的可调节更加提高了微电网的灵活性。目前分布式二次频率控制如图7 所示,功率虽然可以按照容量进行比例分配,但是功率和频率的恢复时间在0.7 s左右。从式(6)可知参数u 、v 对初始状态之间的差值进行放大进而影响收敛速度,图8 在不同参数下的频率恢复时间进一步验证目前分布式二次频率存在的问题,而本文所提二次频率控制并不存在未知参数,具体恢复时间用户可根据需求自行定义。
通过与现阶段一致性控制对比证明所提控制策略具有更加快速、准确的恢复性能,并且能够达到现阶段二次控制所不具备定时恢复的控制效果,进一步提高微电网的工作效率。
4.3 即插即用恢复性能验证
这部分测试了所提控制策略的即插即用能力,并验证新投入DG能够在规定时间达到稳定状态。首先,VSG二次控制策略下的DG1~4和Load1连接到微电网。在t =2 s时,DG4从网络断开,并在t =4 s时再次连接。在图9 中,断开DG4后,通过所提二次频率控制策略,将频率在设定时间0.5 s内快速恢复到参考值,保证了新投入DG能够更快地进入工作状态,提高微电网运行效率。同时功率平衡被打破,有功功率按照比例1∶1∶2进行重新分配。如图3 所示,当DG4断开时,剩余的通信链路仍然包含生成树,因此,DG1、DG2和DG3仍然可以达到二级控制的目的。如图9 所示,当DG4重新接入时,虽然系统出现了剧烈振荡,但仍能保持稳定,达到控制目标。
图9
5 试验验证
仿真验证了所提控制策略的快速收敛性能,本节将使用TMS320F28335控制器完成采样信号和控制信号的交互,通过示波器对信号进行观察,验证理论分析和仿真结果的正确性,试验场景如图10 所示。由于试验条件的限制,本文采用3台DG并保证两两之间通信交流。
图10
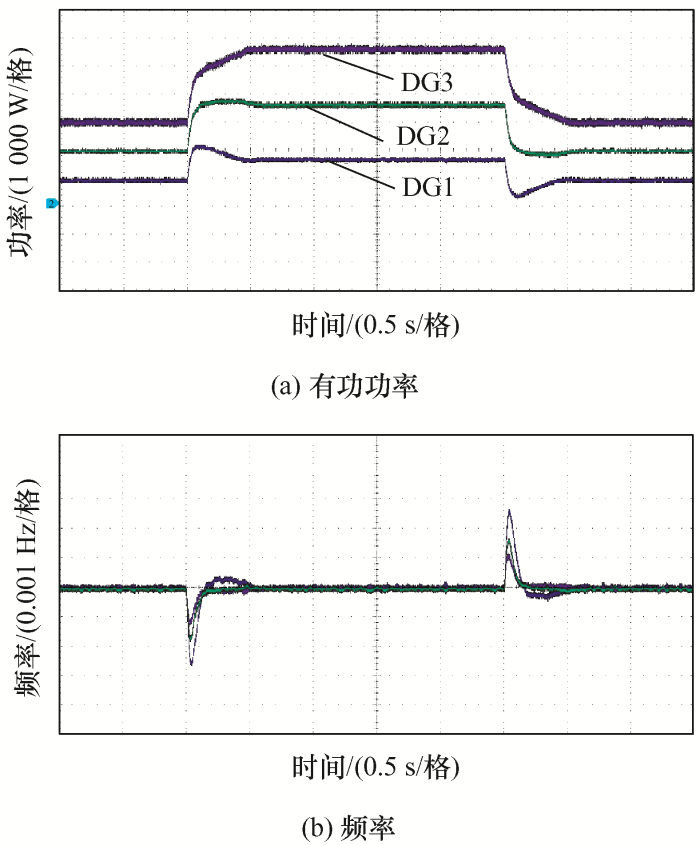
(1) 工况1:为保证功率按照容量进行精确均分,额定有功功率Pn 1 、Pn 2 和Pn 3 分别设为1 000 W、2 000 W和3 000 W,阻尼系数D 1 、D 2 和D 3 分别设为15、30和45,其余参数仍如表1 所示。试验工况设定初始时刻为携带无功为6 kW的Load1工作,一定时间后增加3 kW的Load2,预定时间设为负载变化后的0.5 s。
通过试验结果如图11 所示,有功功率在初始时刻按容量均分,分别为1 000 W、2 000 W、3 000 W,负载增加后3个DG的无功功率分别又增加1 000 W、2 000 W、3 000 W,在增加负载的0.5 s继续按照容量比例进行分配,同时频率维持在额定值,在负载变化时经过振荡,在0.5 s时刻恢复到额定值。
图11
从结果分析可知,在所提二次频率控制策略下有功功率与频率均具备良好的运行效果,一方面预定时系统的引入保证了收敛速度在0.5 s以内;另一方面,分布式一致性的控制性能将有功与频率稳定在需要的运行条件下。二次频率控制快速稳定性能验证了本文设计的初衷。
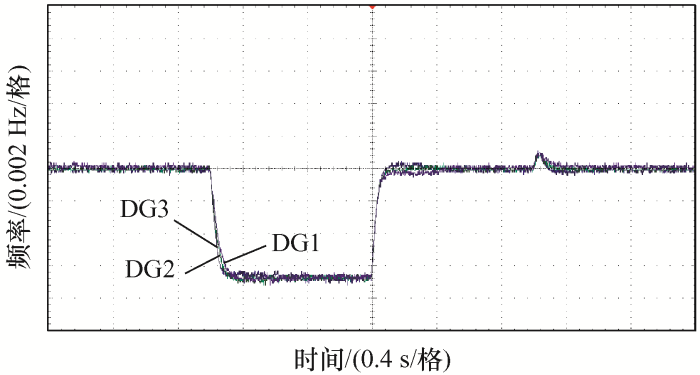
(2) 工况2:验证分布式协同二次调频控制效果。试验结果如图12 所示,设3台DG的容量相同,起始阶段为VSG一次控制运行在额定值时;第二阶段时增加Load2,可以发现仅在一次控制下负载增加造成了频率偏差;第三阶段引入分布式协同二次频率控制,在预定时系统的作用下,在引入后的0.5 s将频率恢复到额定值;第四阶段负载Load2退出运行,但是由于分布式协同二次控制仍在作用,频率在微小波动后稳定到额定值。从试验波形分析可知,分布式协同二次频率控制可以调节一次控制存在的偏差问题,并可以在预定时间内恢复到额定值。
图12
6 结论
针对传统虚拟同步发电机仅通过一次控制难以满足有功功率分配精度、频率恢复以及在多因素影响的情况下收敛速度慢的问题。本文将虚拟同步发电机与分布式控制相结合,提出结合预定时系统的分布式协同二次频率控制,并且通过仿真验证了所提控制策略在负荷变化、参数异构等情况下可以在特定时间内保证频率的恢复与有功功率分配,最后可以得出以下结论。
(1) VSG并联运行时由于参数异构频率会产生一定的偏差,所提控制方案可以同时实现频率无差控制以及有功分配。
(2) 所提控制策略可以通过定时恢复的特性,给予频率更快速的恢复性能。
(3) 相比较于现阶段的分布式二次控制,所提控制策略克服了微电网初始状态以及设计参数对恢复速度的影响。
参考文献
View Option
[1]
RAEISPOUR M ATRIANFAR H BAGHAEE H R et al. Resilient H∞ consensus-based control of autonomous AC microgrids with uncertain time-delayed communications
[J]. IEEE Transactions on Smart Grid , 2020 , 11 (5 ):3871 -3884 .
DOI:10.1109/TSG.5165411
URL
[本文引用: 1]
[2]
秦本双 , 徐永海 , 贾焦心 . 多VSG功频环路间交互影响的定量分析
[J]. 电网技术 , 2022 , 46 (2 ):757 -764 .
[本文引用: 1]
QIN Benshuang XU Yonghai JIA Jiaoxin Quantitative analysis on interactive influences among power-frequency loops of multi-VSG
[J]. Power System Technology , 2022 , 46 (2 ):757 -764 .
[本文引用: 1]
[3]
魏文军 , 唐彬峰 , 黄巨龙 , 等 . 基于有限时间一致性的微电网分层优化策略
[J]. 电力系统及其自动化学报 , 2020 , 32 (6 ):7 -13 .
[本文引用: 1]
WEI Wenjun TANG Binfeng HUANG Julong et al. Hierarchical optimization strategy for microgrid based on finite-time consensus
[J]. Proceedings of the CSU-EPSA , 2020 , 32 (6 ):7 -13 .
[本文引用: 1]
[4]
秦本双 , 徐永海 , 袁敞 , 等 . 多VSG并网系统的P/ω导纳建模及功频振荡分析
[J]. 中国电机工程学报 , 2020 , 40 (9 ):2932 -2942 .
[本文引用: 1]
QIN Benshuang XU Yonghai YUAN Chang et al. The P/ω admittance modeling and power-frequency oscillation analysis of multi-VSGs grid-connected systems
[J]. Proceedings of the CSEE , 2020 , 40 (9 ):2932 -2942 .
[本文引用: 1]
[5]
OLFATI-SABER R FAX J A MURRAY R M Consensus and cooperation in networked multi-agent systems
[J]. Proceedings of the IEEE , 2007 , 95 (1 ):215 -233 .
DOI:10.1109/JPROC.2006.887293
URL
[本文引用: 1]
[6]
SIMPSON-PORCO J W SHAFIEE Q DORFLER F et al. Secondary frequency and voltage control of islanded microgrids via distributed averaging
[J]. IEEE Transactions on Industrial Electronics , 2015 , 62 (11 ):7025 -7038 .
DOI:10.1109/TIE.2015.2436879
URL
[本文引用: 2]
[7]
LIU Jiayi LI Jiaqi SONG Huihui et al. Nonlinear secondary voltage control of islanded microgrid via distributed consistency
[J]. IEEE Transactions on Energy Conversion , 2020 , 35 (4 ):1964 -1972 .
DOI:10.1109/TEC.60
URL
[本文引用: 1]
[8]
HAN Hua HOU Xiaochao YANG Jian et al. Review of power sharing control strategies for islanding operation of AC microgrids
[J]. IEEE Transactions on Smart Grid , 2016 , 7 (1 ):200 -215 .
DOI:10.1109/TSG.2015.2434849
URL
[本文引用: 1]
[9]
ALIPOOR J MIURA Y ISE T Power system stabilization using virtual synchronous generator with alternating moment of inertia
[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics , 2015 , 3 (2 ):451 -458 .
DOI:10.1109/JESTPE.2014.2362530
URL
[本文引用: 1]
[10]
李斌 , 周林 , 余希瑞 , 等 . 基于改进虚拟同步发电机算法的微网逆变器二次调频方案
[J]. 电网技术 , 2017 , 41 (8 ):2680 -2687 .
[本文引用: 1]
LI Bin ZHOU Lin YU Xirui et al. Secondary frequency regulation for microgrid inverters based on improving virtual synchronous generator
[J]. Power System Technology , 2017 , 41 (8 ):2680 -2687 .
[本文引用: 1]
[11]
LU Linyu CHU C C Consensus-based secondary frequency and voltage droop control of virtual synchronous generators for isolated AC microgrids
[J]. IEEE Journal on Emerging and Selected Topics in Circuits and Systems , 2015 , 3 (5 ):443 -455 .
[本文引用: 2]
[12]
CHEN Laijun WANG Yuyang YANG Libin et al. Consensus control strategy with state predictor for virtual synchronous generators in isolated microgrid
[C]// 2016 IEEE International Conference on Power System Technology,Wollongong,NSW,Australia,2016:1 -5 .
[本文引用: 1]
[13]
GONG Ping HAN Qinglong LAN Weiyao et al. Finite-time consensus tracking for incommensurate fractional-order nonlinear multiagent systems with directed switching topologies
[J]. IEEE Transactions on Cybernetics , 2020 , 52 (1 ):65 -76 .
DOI:10.1109/TCYB.2020.2977169
URL
[本文引用: 1]
[14]
张昊 , 李昱 , 尹亚飞 , 等 . 基于动态一致性算法的直流微电网高品质协同控制
[J]. 电气工程学报 , 2022 , 17 (1 ):15 -21 .
[本文引用: 1]
ZHANG Hao LI Yu YIN Yafei et al. High quality cooperative control of DC microgrids using dynamic consensus algorithm
[J]. Journal of Electrical Engineering , 2022 , 17 (1 ):15 -21 .
[本文引用: 1]
[15]
SARRAFAN N ROSTAMI M A ZAREI J et al. Improved distributed prescribed finite-time secondary control of inverter-based microgrids:Design and real-time implementation
[J]. IEEE Transactions on Industrial Electronics , 2021 , 68 (11 ):11135 -11145 .
DOI:10.1109/TIE.2020.3031522
URL
[本文引用: 1]
[16]
NI Junkang CAO Hui LIU Xinghua et al. Fixed-time leader-follower consensus based secondary voltage control for microgrid under directed communication graph
[C]// 2021 IEEE International Conference on Real-time Computing and Robotics,Xining,China,IEEE,2021:566 -571 .
[本文引用: 1]
[17]
ZHAO Daduan ZHANG Chenghui SUN Yue et al. Distributed robust frequency restoration and active power sharing for autonomous microgrids with event-triggered strategy
[J]. IEEE Transactions on Smart Grid , 2021 , 12 (5 ):3819 -3834 .
DOI:10.1109/TSG.2021.3087960
URL
[本文引用: 1]
[18]
许振宇 , 陈殷 , 石梦璇 , 等 . 基于一致性算法的并联虚拟同步机系统小信号模型分析
[J]. 中国电机工程学报 , 2022 , 42 (7 ):2427 -2438 .
[本文引用: 1]
XU Zhenyu CHEN Yin SHI Mengxuan et al. Small-signal analysis of consensus-algorithm-based parallel virtual synchronization generators system
[J]. Proceedings of the CSEE , 2022 , 42 (7 ):2427 -2438 .
[本文引用: 1]
[19]
ZUO Zongyu TIE L Distributed robust finite-time nonlinear consensus protocols for multi-agent systems
[J]. International Journal of Systems Science , 2014 , 47 (6 ):1366 -1375 .
DOI:10.1080/00207721.2014.925608
URL
[本文引用: 1]
[20]
ALDANA-LOPEZ R GOMEZ-GUTIERREZ D JIMENEZ-RODRIGUEZ E et al. Generating new classes of fixed-time stable systems with predefined upper bound for the settling time
[J]. International Journal of Control , 2021 , 95 (10 ):2802 -2814 .
DOI:10.1080/00207179.2021.1936190
URL
[本文引用: 1]
Resilient H∞ consensus-based control of autonomous AC microgrids with uncertain time-delayed communications
1
2020
... 随着传统能源储量的减少,新能源系统在传统电力系统中的渗透率不断提高.孤岛微电网是集成了分布式电源(Distributed generator,DG)、储能装置以及负荷的小型独立电力系统,也是解决能源问题和提高偏远地区电力需求的一种有效途径[1 ] .由于风能、太阳能等新能源发电均采用电力电子变换装置,因此微电网系统是低电压、低惯性的小规模电力系统.而虚拟同步发电机(Virtual synchronous generator,VSG)控制方法是通过模拟同步发电机的机电暂态特性和阻尼特性,提高微电网对DG的接纳能力,进一步保证微电网系统的稳定运行[2 ] ,受到国内外学者的广泛关注. ...
多VSG功频环路间交互影响的定量分析
1
2022
... 随着传统能源储量的减少,新能源系统在传统电力系统中的渗透率不断提高.孤岛微电网是集成了分布式电源(Distributed generator,DG)、储能装置以及负荷的小型独立电力系统,也是解决能源问题和提高偏远地区电力需求的一种有效途径[1 ] .由于风能、太阳能等新能源发电均采用电力电子变换装置,因此微电网系统是低电压、低惯性的小规模电力系统.而虚拟同步发电机(Virtual synchronous generator,VSG)控制方法是通过模拟同步发电机的机电暂态特性和阻尼特性,提高微电网对DG的接纳能力,进一步保证微电网系统的稳定运行[2 ] ,受到国内外学者的广泛关注. ...
Quantitative analysis on interactive influences among power-frequency loops of multi-VSG
1
2022
... 随着传统能源储量的减少,新能源系统在传统电力系统中的渗透率不断提高.孤岛微电网是集成了分布式电源(Distributed generator,DG)、储能装置以及负荷的小型独立电力系统,也是解决能源问题和提高偏远地区电力需求的一种有效途径[1 ] .由于风能、太阳能等新能源发电均采用电力电子变换装置,因此微电网系统是低电压、低惯性的小规模电力系统.而虚拟同步发电机(Virtual synchronous generator,VSG)控制方法是通过模拟同步发电机的机电暂态特性和阻尼特性,提高微电网对DG的接纳能力,进一步保证微电网系统的稳定运行[2 ] ,受到国内外学者的广泛关注. ...
基于有限时间一致性的微电网分层优化策略
1
2020
... 微电网系统通常采用分层控制,可分为一次控制、二次控制和三次控制三个层次[3 ] .VSG控制策略属于一次控制层,主要目的是为系统提供惯性并按设定的下垂特性参与系统功率调节,快速稳定每个DG的频率.但是一次控制属于有差控制,在缺乏电网支撑的条件下,孤岛微电网的动态特性容易受到影响,频率可能偏离参考值[4 ] .为了提高控制精度,通常引入二次控制层进行校正,三次控制层主要考虑微电网的经济调度和优化运行.本文主要研究微电网的二次控制问题.目前在孤岛微电网的多机并联系统中,集中式二次控制应用较为广泛,然而集中控制过于依赖通信网络.近年来,分布式协同控制仅通过与邻居之间的简单信息交流便可达到一种稳定状态,从而影响其他支路保证整体系统的稳定运行,因此在孤岛微电网的分布式二次控制中逐渐成为学者们的研究重点[5 ] . ...
Hierarchical optimization strategy for microgrid based on finite-time consensus
1
2020
... 微电网系统通常采用分层控制,可分为一次控制、二次控制和三次控制三个层次[3 ] .VSG控制策略属于一次控制层,主要目的是为系统提供惯性并按设定的下垂特性参与系统功率调节,快速稳定每个DG的频率.但是一次控制属于有差控制,在缺乏电网支撑的条件下,孤岛微电网的动态特性容易受到影响,频率可能偏离参考值[4 ] .为了提高控制精度,通常引入二次控制层进行校正,三次控制层主要考虑微电网的经济调度和优化运行.本文主要研究微电网的二次控制问题.目前在孤岛微电网的多机并联系统中,集中式二次控制应用较为广泛,然而集中控制过于依赖通信网络.近年来,分布式协同控制仅通过与邻居之间的简单信息交流便可达到一种稳定状态,从而影响其他支路保证整体系统的稳定运行,因此在孤岛微电网的分布式二次控制中逐渐成为学者们的研究重点[5 ] . ...
多VSG并网系统的P/ω导纳建模及功频振荡分析
1
2020
... 微电网系统通常采用分层控制,可分为一次控制、二次控制和三次控制三个层次[3 ] .VSG控制策略属于一次控制层,主要目的是为系统提供惯性并按设定的下垂特性参与系统功率调节,快速稳定每个DG的频率.但是一次控制属于有差控制,在缺乏电网支撑的条件下,孤岛微电网的动态特性容易受到影响,频率可能偏离参考值[4 ] .为了提高控制精度,通常引入二次控制层进行校正,三次控制层主要考虑微电网的经济调度和优化运行.本文主要研究微电网的二次控制问题.目前在孤岛微电网的多机并联系统中,集中式二次控制应用较为广泛,然而集中控制过于依赖通信网络.近年来,分布式协同控制仅通过与邻居之间的简单信息交流便可达到一种稳定状态,从而影响其他支路保证整体系统的稳定运行,因此在孤岛微电网的分布式二次控制中逐渐成为学者们的研究重点[5 ] . ...
The P/ω admittance modeling and power-frequency oscillation analysis of multi-VSGs grid-connected systems
1
2020
... 微电网系统通常采用分层控制,可分为一次控制、二次控制和三次控制三个层次[3 ] .VSG控制策略属于一次控制层,主要目的是为系统提供惯性并按设定的下垂特性参与系统功率调节,快速稳定每个DG的频率.但是一次控制属于有差控制,在缺乏电网支撑的条件下,孤岛微电网的动态特性容易受到影响,频率可能偏离参考值[4 ] .为了提高控制精度,通常引入二次控制层进行校正,三次控制层主要考虑微电网的经济调度和优化运行.本文主要研究微电网的二次控制问题.目前在孤岛微电网的多机并联系统中,集中式二次控制应用较为广泛,然而集中控制过于依赖通信网络.近年来,分布式协同控制仅通过与邻居之间的简单信息交流便可达到一种稳定状态,从而影响其他支路保证整体系统的稳定运行,因此在孤岛微电网的分布式二次控制中逐渐成为学者们的研究重点[5 ] . ...
Consensus and cooperation in networked multi-agent systems
1
2007
... 微电网系统通常采用分层控制,可分为一次控制、二次控制和三次控制三个层次[3 ] .VSG控制策略属于一次控制层,主要目的是为系统提供惯性并按设定的下垂特性参与系统功率调节,快速稳定每个DG的频率.但是一次控制属于有差控制,在缺乏电网支撑的条件下,孤岛微电网的动态特性容易受到影响,频率可能偏离参考值[4 ] .为了提高控制精度,通常引入二次控制层进行校正,三次控制层主要考虑微电网的经济调度和优化运行.本文主要研究微电网的二次控制问题.目前在孤岛微电网的多机并联系统中,集中式二次控制应用较为广泛,然而集中控制过于依赖通信网络.近年来,分布式协同控制仅通过与邻居之间的简单信息交流便可达到一种稳定状态,从而影响其他支路保证整体系统的稳定运行,因此在孤岛微电网的分布式二次控制中逐渐成为学者们的研究重点[5 ] . ...
Secondary frequency and voltage control of islanded microgrids via distributed averaging
2
2015
... 分布式协同控制具有协调性优良,通信简单等优点,文献[6 ]将分布式一致性应用于微电网的控制策略中,基于平均一致性提出一种分布式比例积分控制器,保证了电压与频率的恢复.文献[7 ]在文献[6 ]的基础上引入一种分布式滑模控制器,可提高分布式比例积分器的收敛速度,不仅达到快速补偿的效果,还可提高系统的鲁棒性.文献[8 ]讨论了微电网一致性控制下的频率恢复和有功功率精确分配.然而分布式一致性算法主要应用于常规下垂交流微电网,但常规下垂控制存在惯性小、输出阻抗低的缺点,当微电网受到较大扰动时会影响系统的稳定性.近年来,一些学者利用VSG来解决上述问题,文献[9 ]通过模拟传统同步发电机转子的运动,为逆变器提供虚拟惯性和阻尼特性,达到一次调频的目的.文献[10 ]通过改进控制结构的方法进行二次调频,但是由于没有通信结构,面对较大的负荷波动仍需要对二次调频逆变器的数量进行调整.文献[11 ]提出将一致性用于VSG二次控制中,既保留了惯性和虚拟阻抗的特点,同时将频率恢复至额定值,但是频率的恢复时间长,影响微电网工作效率.文献[12 ]在文献[11 ]的基础上通过设计出预测VSG邻居和自身未来状态的控制器,进而提高并联VSG频率的恢复速度,但是恢复时间的不确定降低了其适用性.文献[13 -14 ]通过对一致性算法的改进提出有限时间一致性,可以在限定时间内完成收敛,但是在微电网初始状态未知的情况下难以确定收敛时间,随着初值的增大实际收敛时间也会增加,不利于微电网的应用.文献[15 -16 ]为解决初始状态问题,提出基于固定时间一致性的二次控制方案,该方案无需考虑系统的初始状态,并保证了电压和频率在有限时间内快速恢复,但是计算出来的稳态时间过于保守,与实际恢复时间有很大差别,并且协议参数的存在使得恢复时间也会随之改变.文献[17 ]使用基于固定时间一致性的二次频率控制,并验证了其即插即用特性,但是对于新投入的DG需要较长时间恢复稳定,影响了微电网的工作效率. ...
... ]在文献[6 ]的基础上引入一种分布式滑模控制器,可提高分布式比例积分器的收敛速度,不仅达到快速补偿的效果,还可提高系统的鲁棒性.文献[8 ]讨论了微电网一致性控制下的频率恢复和有功功率精确分配.然而分布式一致性算法主要应用于常规下垂交流微电网,但常规下垂控制存在惯性小、输出阻抗低的缺点,当微电网受到较大扰动时会影响系统的稳定性.近年来,一些学者利用VSG来解决上述问题,文献[9 ]通过模拟传统同步发电机转子的运动,为逆变器提供虚拟惯性和阻尼特性,达到一次调频的目的.文献[10 ]通过改进控制结构的方法进行二次调频,但是由于没有通信结构,面对较大的负荷波动仍需要对二次调频逆变器的数量进行调整.文献[11 ]提出将一致性用于VSG二次控制中,既保留了惯性和虚拟阻抗的特点,同时将频率恢复至额定值,但是频率的恢复时间长,影响微电网工作效率.文献[12 ]在文献[11 ]的基础上通过设计出预测VSG邻居和自身未来状态的控制器,进而提高并联VSG频率的恢复速度,但是恢复时间的不确定降低了其适用性.文献[13 -14 ]通过对一致性算法的改进提出有限时间一致性,可以在限定时间内完成收敛,但是在微电网初始状态未知的情况下难以确定收敛时间,随着初值的增大实际收敛时间也会增加,不利于微电网的应用.文献[15 -16 ]为解决初始状态问题,提出基于固定时间一致性的二次控制方案,该方案无需考虑系统的初始状态,并保证了电压和频率在有限时间内快速恢复,但是计算出来的稳态时间过于保守,与实际恢复时间有很大差别,并且协议参数的存在使得恢复时间也会随之改变.文献[17 ]使用基于固定时间一致性的二次频率控制,并验证了其即插即用特性,但是对于新投入的DG需要较长时间恢复稳定,影响了微电网的工作效率. ...
Nonlinear secondary voltage control of islanded microgrid via distributed consistency
1
2020
... 分布式协同控制具有协调性优良,通信简单等优点,文献[6 ]将分布式一致性应用于微电网的控制策略中,基于平均一致性提出一种分布式比例积分控制器,保证了电压与频率的恢复.文献[7 ]在文献[6 ]的基础上引入一种分布式滑模控制器,可提高分布式比例积分器的收敛速度,不仅达到快速补偿的效果,还可提高系统的鲁棒性.文献[8 ]讨论了微电网一致性控制下的频率恢复和有功功率精确分配.然而分布式一致性算法主要应用于常规下垂交流微电网,但常规下垂控制存在惯性小、输出阻抗低的缺点,当微电网受到较大扰动时会影响系统的稳定性.近年来,一些学者利用VSG来解决上述问题,文献[9 ]通过模拟传统同步发电机转子的运动,为逆变器提供虚拟惯性和阻尼特性,达到一次调频的目的.文献[10 ]通过改进控制结构的方法进行二次调频,但是由于没有通信结构,面对较大的负荷波动仍需要对二次调频逆变器的数量进行调整.文献[11 ]提出将一致性用于VSG二次控制中,既保留了惯性和虚拟阻抗的特点,同时将频率恢复至额定值,但是频率的恢复时间长,影响微电网工作效率.文献[12 ]在文献[11 ]的基础上通过设计出预测VSG邻居和自身未来状态的控制器,进而提高并联VSG频率的恢复速度,但是恢复时间的不确定降低了其适用性.文献[13 -14 ]通过对一致性算法的改进提出有限时间一致性,可以在限定时间内完成收敛,但是在微电网初始状态未知的情况下难以确定收敛时间,随着初值的增大实际收敛时间也会增加,不利于微电网的应用.文献[15 -16 ]为解决初始状态问题,提出基于固定时间一致性的二次控制方案,该方案无需考虑系统的初始状态,并保证了电压和频率在有限时间内快速恢复,但是计算出来的稳态时间过于保守,与实际恢复时间有很大差别,并且协议参数的存在使得恢复时间也会随之改变.文献[17 ]使用基于固定时间一致性的二次频率控制,并验证了其即插即用特性,但是对于新投入的DG需要较长时间恢复稳定,影响了微电网的工作效率. ...
Review of power sharing control strategies for islanding operation of AC microgrids
1
2016
... 分布式协同控制具有协调性优良,通信简单等优点,文献[6 ]将分布式一致性应用于微电网的控制策略中,基于平均一致性提出一种分布式比例积分控制器,保证了电压与频率的恢复.文献[7 ]在文献[6 ]的基础上引入一种分布式滑模控制器,可提高分布式比例积分器的收敛速度,不仅达到快速补偿的效果,还可提高系统的鲁棒性.文献[8 ]讨论了微电网一致性控制下的频率恢复和有功功率精确分配.然而分布式一致性算法主要应用于常规下垂交流微电网,但常规下垂控制存在惯性小、输出阻抗低的缺点,当微电网受到较大扰动时会影响系统的稳定性.近年来,一些学者利用VSG来解决上述问题,文献[9 ]通过模拟传统同步发电机转子的运动,为逆变器提供虚拟惯性和阻尼特性,达到一次调频的目的.文献[10 ]通过改进控制结构的方法进行二次调频,但是由于没有通信结构,面对较大的负荷波动仍需要对二次调频逆变器的数量进行调整.文献[11 ]提出将一致性用于VSG二次控制中,既保留了惯性和虚拟阻抗的特点,同时将频率恢复至额定值,但是频率的恢复时间长,影响微电网工作效率.文献[12 ]在文献[11 ]的基础上通过设计出预测VSG邻居和自身未来状态的控制器,进而提高并联VSG频率的恢复速度,但是恢复时间的不确定降低了其适用性.文献[13 -14 ]通过对一致性算法的改进提出有限时间一致性,可以在限定时间内完成收敛,但是在微电网初始状态未知的情况下难以确定收敛时间,随着初值的增大实际收敛时间也会增加,不利于微电网的应用.文献[15 -16 ]为解决初始状态问题,提出基于固定时间一致性的二次控制方案,该方案无需考虑系统的初始状态,并保证了电压和频率在有限时间内快速恢复,但是计算出来的稳态时间过于保守,与实际恢复时间有很大差别,并且协议参数的存在使得恢复时间也会随之改变.文献[17 ]使用基于固定时间一致性的二次频率控制,并验证了其即插即用特性,但是对于新投入的DG需要较长时间恢复稳定,影响了微电网的工作效率. ...
Power system stabilization using virtual synchronous generator with alternating moment of inertia
1
2015
... 分布式协同控制具有协调性优良,通信简单等优点,文献[6 ]将分布式一致性应用于微电网的控制策略中,基于平均一致性提出一种分布式比例积分控制器,保证了电压与频率的恢复.文献[7 ]在文献[6 ]的基础上引入一种分布式滑模控制器,可提高分布式比例积分器的收敛速度,不仅达到快速补偿的效果,还可提高系统的鲁棒性.文献[8 ]讨论了微电网一致性控制下的频率恢复和有功功率精确分配.然而分布式一致性算法主要应用于常规下垂交流微电网,但常规下垂控制存在惯性小、输出阻抗低的缺点,当微电网受到较大扰动时会影响系统的稳定性.近年来,一些学者利用VSG来解决上述问题,文献[9 ]通过模拟传统同步发电机转子的运动,为逆变器提供虚拟惯性和阻尼特性,达到一次调频的目的.文献[10 ]通过改进控制结构的方法进行二次调频,但是由于没有通信结构,面对较大的负荷波动仍需要对二次调频逆变器的数量进行调整.文献[11 ]提出将一致性用于VSG二次控制中,既保留了惯性和虚拟阻抗的特点,同时将频率恢复至额定值,但是频率的恢复时间长,影响微电网工作效率.文献[12 ]在文献[11 ]的基础上通过设计出预测VSG邻居和自身未来状态的控制器,进而提高并联VSG频率的恢复速度,但是恢复时间的不确定降低了其适用性.文献[13 -14 ]通过对一致性算法的改进提出有限时间一致性,可以在限定时间内完成收敛,但是在微电网初始状态未知的情况下难以确定收敛时间,随着初值的增大实际收敛时间也会增加,不利于微电网的应用.文献[15 -16 ]为解决初始状态问题,提出基于固定时间一致性的二次控制方案,该方案无需考虑系统的初始状态,并保证了电压和频率在有限时间内快速恢复,但是计算出来的稳态时间过于保守,与实际恢复时间有很大差别,并且协议参数的存在使得恢复时间也会随之改变.文献[17 ]使用基于固定时间一致性的二次频率控制,并验证了其即插即用特性,但是对于新投入的DG需要较长时间恢复稳定,影响了微电网的工作效率. ...
基于改进虚拟同步发电机算法的微网逆变器二次调频方案
1
2017
... 分布式协同控制具有协调性优良,通信简单等优点,文献[6 ]将分布式一致性应用于微电网的控制策略中,基于平均一致性提出一种分布式比例积分控制器,保证了电压与频率的恢复.文献[7 ]在文献[6 ]的基础上引入一种分布式滑模控制器,可提高分布式比例积分器的收敛速度,不仅达到快速补偿的效果,还可提高系统的鲁棒性.文献[8 ]讨论了微电网一致性控制下的频率恢复和有功功率精确分配.然而分布式一致性算法主要应用于常规下垂交流微电网,但常规下垂控制存在惯性小、输出阻抗低的缺点,当微电网受到较大扰动时会影响系统的稳定性.近年来,一些学者利用VSG来解决上述问题,文献[9 ]通过模拟传统同步发电机转子的运动,为逆变器提供虚拟惯性和阻尼特性,达到一次调频的目的.文献[10 ]通过改进控制结构的方法进行二次调频,但是由于没有通信结构,面对较大的负荷波动仍需要对二次调频逆变器的数量进行调整.文献[11 ]提出将一致性用于VSG二次控制中,既保留了惯性和虚拟阻抗的特点,同时将频率恢复至额定值,但是频率的恢复时间长,影响微电网工作效率.文献[12 ]在文献[11 ]的基础上通过设计出预测VSG邻居和自身未来状态的控制器,进而提高并联VSG频率的恢复速度,但是恢复时间的不确定降低了其适用性.文献[13 -14 ]通过对一致性算法的改进提出有限时间一致性,可以在限定时间内完成收敛,但是在微电网初始状态未知的情况下难以确定收敛时间,随着初值的增大实际收敛时间也会增加,不利于微电网的应用.文献[15 -16 ]为解决初始状态问题,提出基于固定时间一致性的二次控制方案,该方案无需考虑系统的初始状态,并保证了电压和频率在有限时间内快速恢复,但是计算出来的稳态时间过于保守,与实际恢复时间有很大差别,并且协议参数的存在使得恢复时间也会随之改变.文献[17 ]使用基于固定时间一致性的二次频率控制,并验证了其即插即用特性,但是对于新投入的DG需要较长时间恢复稳定,影响了微电网的工作效率. ...
Secondary frequency regulation for microgrid inverters based on improving virtual synchronous generator
1
2017
... 分布式协同控制具有协调性优良,通信简单等优点,文献[6 ]将分布式一致性应用于微电网的控制策略中,基于平均一致性提出一种分布式比例积分控制器,保证了电压与频率的恢复.文献[7 ]在文献[6 ]的基础上引入一种分布式滑模控制器,可提高分布式比例积分器的收敛速度,不仅达到快速补偿的效果,还可提高系统的鲁棒性.文献[8 ]讨论了微电网一致性控制下的频率恢复和有功功率精确分配.然而分布式一致性算法主要应用于常规下垂交流微电网,但常规下垂控制存在惯性小、输出阻抗低的缺点,当微电网受到较大扰动时会影响系统的稳定性.近年来,一些学者利用VSG来解决上述问题,文献[9 ]通过模拟传统同步发电机转子的运动,为逆变器提供虚拟惯性和阻尼特性,达到一次调频的目的.文献[10 ]通过改进控制结构的方法进行二次调频,但是由于没有通信结构,面对较大的负荷波动仍需要对二次调频逆变器的数量进行调整.文献[11 ]提出将一致性用于VSG二次控制中,既保留了惯性和虚拟阻抗的特点,同时将频率恢复至额定值,但是频率的恢复时间长,影响微电网工作效率.文献[12 ]在文献[11 ]的基础上通过设计出预测VSG邻居和自身未来状态的控制器,进而提高并联VSG频率的恢复速度,但是恢复时间的不确定降低了其适用性.文献[13 -14 ]通过对一致性算法的改进提出有限时间一致性,可以在限定时间内完成收敛,但是在微电网初始状态未知的情况下难以确定收敛时间,随着初值的增大实际收敛时间也会增加,不利于微电网的应用.文献[15 -16 ]为解决初始状态问题,提出基于固定时间一致性的二次控制方案,该方案无需考虑系统的初始状态,并保证了电压和频率在有限时间内快速恢复,但是计算出来的稳态时间过于保守,与实际恢复时间有很大差别,并且协议参数的存在使得恢复时间也会随之改变.文献[17 ]使用基于固定时间一致性的二次频率控制,并验证了其即插即用特性,但是对于新投入的DG需要较长时间恢复稳定,影响了微电网的工作效率. ...
Consensus-based secondary frequency and voltage droop control of virtual synchronous generators for isolated AC microgrids
2
2015
... 分布式协同控制具有协调性优良,通信简单等优点,文献[6 ]将分布式一致性应用于微电网的控制策略中,基于平均一致性提出一种分布式比例积分控制器,保证了电压与频率的恢复.文献[7 ]在文献[6 ]的基础上引入一种分布式滑模控制器,可提高分布式比例积分器的收敛速度,不仅达到快速补偿的效果,还可提高系统的鲁棒性.文献[8 ]讨论了微电网一致性控制下的频率恢复和有功功率精确分配.然而分布式一致性算法主要应用于常规下垂交流微电网,但常规下垂控制存在惯性小、输出阻抗低的缺点,当微电网受到较大扰动时会影响系统的稳定性.近年来,一些学者利用VSG来解决上述问题,文献[9 ]通过模拟传统同步发电机转子的运动,为逆变器提供虚拟惯性和阻尼特性,达到一次调频的目的.文献[10 ]通过改进控制结构的方法进行二次调频,但是由于没有通信结构,面对较大的负荷波动仍需要对二次调频逆变器的数量进行调整.文献[11 ]提出将一致性用于VSG二次控制中,既保留了惯性和虚拟阻抗的特点,同时将频率恢复至额定值,但是频率的恢复时间长,影响微电网工作效率.文献[12 ]在文献[11 ]的基础上通过设计出预测VSG邻居和自身未来状态的控制器,进而提高并联VSG频率的恢复速度,但是恢复时间的不确定降低了其适用性.文献[13 -14 ]通过对一致性算法的改进提出有限时间一致性,可以在限定时间内完成收敛,但是在微电网初始状态未知的情况下难以确定收敛时间,随着初值的增大实际收敛时间也会增加,不利于微电网的应用.文献[15 -16 ]为解决初始状态问题,提出基于固定时间一致性的二次控制方案,该方案无需考虑系统的初始状态,并保证了电压和频率在有限时间内快速恢复,但是计算出来的稳态时间过于保守,与实际恢复时间有很大差别,并且协议参数的存在使得恢复时间也会随之改变.文献[17 ]使用基于固定时间一致性的二次频率控制,并验证了其即插即用特性,但是对于新投入的DG需要较长时间恢复稳定,影响了微电网的工作效率. ...
... ]在文献[11 ]的基础上通过设计出预测VSG邻居和自身未来状态的控制器,进而提高并联VSG频率的恢复速度,但是恢复时间的不确定降低了其适用性.文献[13 -14 ]通过对一致性算法的改进提出有限时间一致性,可以在限定时间内完成收敛,但是在微电网初始状态未知的情况下难以确定收敛时间,随着初值的增大实际收敛时间也会增加,不利于微电网的应用.文献[15 -16 ]为解决初始状态问题,提出基于固定时间一致性的二次控制方案,该方案无需考虑系统的初始状态,并保证了电压和频率在有限时间内快速恢复,但是计算出来的稳态时间过于保守,与实际恢复时间有很大差别,并且协议参数的存在使得恢复时间也会随之改变.文献[17 ]使用基于固定时间一致性的二次频率控制,并验证了其即插即用特性,但是对于新投入的DG需要较长时间恢复稳定,影响了微电网的工作效率. ...
Consensus control strategy with state predictor for virtual synchronous generators in isolated microgrid
1
... 分布式协同控制具有协调性优良,通信简单等优点,文献[6 ]将分布式一致性应用于微电网的控制策略中,基于平均一致性提出一种分布式比例积分控制器,保证了电压与频率的恢复.文献[7 ]在文献[6 ]的基础上引入一种分布式滑模控制器,可提高分布式比例积分器的收敛速度,不仅达到快速补偿的效果,还可提高系统的鲁棒性.文献[8 ]讨论了微电网一致性控制下的频率恢复和有功功率精确分配.然而分布式一致性算法主要应用于常规下垂交流微电网,但常规下垂控制存在惯性小、输出阻抗低的缺点,当微电网受到较大扰动时会影响系统的稳定性.近年来,一些学者利用VSG来解决上述问题,文献[9 ]通过模拟传统同步发电机转子的运动,为逆变器提供虚拟惯性和阻尼特性,达到一次调频的目的.文献[10 ]通过改进控制结构的方法进行二次调频,但是由于没有通信结构,面对较大的负荷波动仍需要对二次调频逆变器的数量进行调整.文献[11 ]提出将一致性用于VSG二次控制中,既保留了惯性和虚拟阻抗的特点,同时将频率恢复至额定值,但是频率的恢复时间长,影响微电网工作效率.文献[12 ]在文献[11 ]的基础上通过设计出预测VSG邻居和自身未来状态的控制器,进而提高并联VSG频率的恢复速度,但是恢复时间的不确定降低了其适用性.文献[13 -14 ]通过对一致性算法的改进提出有限时间一致性,可以在限定时间内完成收敛,但是在微电网初始状态未知的情况下难以确定收敛时间,随着初值的增大实际收敛时间也会增加,不利于微电网的应用.文献[15 -16 ]为解决初始状态问题,提出基于固定时间一致性的二次控制方案,该方案无需考虑系统的初始状态,并保证了电压和频率在有限时间内快速恢复,但是计算出来的稳态时间过于保守,与实际恢复时间有很大差别,并且协议参数的存在使得恢复时间也会随之改变.文献[17 ]使用基于固定时间一致性的二次频率控制,并验证了其即插即用特性,但是对于新投入的DG需要较长时间恢复稳定,影响了微电网的工作效率. ...
Finite-time consensus tracking for incommensurate fractional-order nonlinear multiagent systems with directed switching topologies
1
2020
... 分布式协同控制具有协调性优良,通信简单等优点,文献[6 ]将分布式一致性应用于微电网的控制策略中,基于平均一致性提出一种分布式比例积分控制器,保证了电压与频率的恢复.文献[7 ]在文献[6 ]的基础上引入一种分布式滑模控制器,可提高分布式比例积分器的收敛速度,不仅达到快速补偿的效果,还可提高系统的鲁棒性.文献[8 ]讨论了微电网一致性控制下的频率恢复和有功功率精确分配.然而分布式一致性算法主要应用于常规下垂交流微电网,但常规下垂控制存在惯性小、输出阻抗低的缺点,当微电网受到较大扰动时会影响系统的稳定性.近年来,一些学者利用VSG来解决上述问题,文献[9 ]通过模拟传统同步发电机转子的运动,为逆变器提供虚拟惯性和阻尼特性,达到一次调频的目的.文献[10 ]通过改进控制结构的方法进行二次调频,但是由于没有通信结构,面对较大的负荷波动仍需要对二次调频逆变器的数量进行调整.文献[11 ]提出将一致性用于VSG二次控制中,既保留了惯性和虚拟阻抗的特点,同时将频率恢复至额定值,但是频率的恢复时间长,影响微电网工作效率.文献[12 ]在文献[11 ]的基础上通过设计出预测VSG邻居和自身未来状态的控制器,进而提高并联VSG频率的恢复速度,但是恢复时间的不确定降低了其适用性.文献[13 -14 ]通过对一致性算法的改进提出有限时间一致性,可以在限定时间内完成收敛,但是在微电网初始状态未知的情况下难以确定收敛时间,随着初值的增大实际收敛时间也会增加,不利于微电网的应用.文献[15 -16 ]为解决初始状态问题,提出基于固定时间一致性的二次控制方案,该方案无需考虑系统的初始状态,并保证了电压和频率在有限时间内快速恢复,但是计算出来的稳态时间过于保守,与实际恢复时间有很大差别,并且协议参数的存在使得恢复时间也会随之改变.文献[17 ]使用基于固定时间一致性的二次频率控制,并验证了其即插即用特性,但是对于新投入的DG需要较长时间恢复稳定,影响了微电网的工作效率. ...
基于动态一致性算法的直流微电网高品质协同控制
1
2022
... 分布式协同控制具有协调性优良,通信简单等优点,文献[6 ]将分布式一致性应用于微电网的控制策略中,基于平均一致性提出一种分布式比例积分控制器,保证了电压与频率的恢复.文献[7 ]在文献[6 ]的基础上引入一种分布式滑模控制器,可提高分布式比例积分器的收敛速度,不仅达到快速补偿的效果,还可提高系统的鲁棒性.文献[8 ]讨论了微电网一致性控制下的频率恢复和有功功率精确分配.然而分布式一致性算法主要应用于常规下垂交流微电网,但常规下垂控制存在惯性小、输出阻抗低的缺点,当微电网受到较大扰动时会影响系统的稳定性.近年来,一些学者利用VSG来解决上述问题,文献[9 ]通过模拟传统同步发电机转子的运动,为逆变器提供虚拟惯性和阻尼特性,达到一次调频的目的.文献[10 ]通过改进控制结构的方法进行二次调频,但是由于没有通信结构,面对较大的负荷波动仍需要对二次调频逆变器的数量进行调整.文献[11 ]提出将一致性用于VSG二次控制中,既保留了惯性和虚拟阻抗的特点,同时将频率恢复至额定值,但是频率的恢复时间长,影响微电网工作效率.文献[12 ]在文献[11 ]的基础上通过设计出预测VSG邻居和自身未来状态的控制器,进而提高并联VSG频率的恢复速度,但是恢复时间的不确定降低了其适用性.文献[13 -14 ]通过对一致性算法的改进提出有限时间一致性,可以在限定时间内完成收敛,但是在微电网初始状态未知的情况下难以确定收敛时间,随着初值的增大实际收敛时间也会增加,不利于微电网的应用.文献[15 -16 ]为解决初始状态问题,提出基于固定时间一致性的二次控制方案,该方案无需考虑系统的初始状态,并保证了电压和频率在有限时间内快速恢复,但是计算出来的稳态时间过于保守,与实际恢复时间有很大差别,并且协议参数的存在使得恢复时间也会随之改变.文献[17 ]使用基于固定时间一致性的二次频率控制,并验证了其即插即用特性,但是对于新投入的DG需要较长时间恢复稳定,影响了微电网的工作效率. ...
High quality cooperative control of DC microgrids using dynamic consensus algorithm
1
2022
... 分布式协同控制具有协调性优良,通信简单等优点,文献[6 ]将分布式一致性应用于微电网的控制策略中,基于平均一致性提出一种分布式比例积分控制器,保证了电压与频率的恢复.文献[7 ]在文献[6 ]的基础上引入一种分布式滑模控制器,可提高分布式比例积分器的收敛速度,不仅达到快速补偿的效果,还可提高系统的鲁棒性.文献[8 ]讨论了微电网一致性控制下的频率恢复和有功功率精确分配.然而分布式一致性算法主要应用于常规下垂交流微电网,但常规下垂控制存在惯性小、输出阻抗低的缺点,当微电网受到较大扰动时会影响系统的稳定性.近年来,一些学者利用VSG来解决上述问题,文献[9 ]通过模拟传统同步发电机转子的运动,为逆变器提供虚拟惯性和阻尼特性,达到一次调频的目的.文献[10 ]通过改进控制结构的方法进行二次调频,但是由于没有通信结构,面对较大的负荷波动仍需要对二次调频逆变器的数量进行调整.文献[11 ]提出将一致性用于VSG二次控制中,既保留了惯性和虚拟阻抗的特点,同时将频率恢复至额定值,但是频率的恢复时间长,影响微电网工作效率.文献[12 ]在文献[11 ]的基础上通过设计出预测VSG邻居和自身未来状态的控制器,进而提高并联VSG频率的恢复速度,但是恢复时间的不确定降低了其适用性.文献[13 -14 ]通过对一致性算法的改进提出有限时间一致性,可以在限定时间内完成收敛,但是在微电网初始状态未知的情况下难以确定收敛时间,随着初值的增大实际收敛时间也会增加,不利于微电网的应用.文献[15 -16 ]为解决初始状态问题,提出基于固定时间一致性的二次控制方案,该方案无需考虑系统的初始状态,并保证了电压和频率在有限时间内快速恢复,但是计算出来的稳态时间过于保守,与实际恢复时间有很大差别,并且协议参数的存在使得恢复时间也会随之改变.文献[17 ]使用基于固定时间一致性的二次频率控制,并验证了其即插即用特性,但是对于新投入的DG需要较长时间恢复稳定,影响了微电网的工作效率. ...
Improved distributed prescribed finite-time secondary control of inverter-based microgrids:Design and real-time implementation
1
2021
... 分布式协同控制具有协调性优良,通信简单等优点,文献[6 ]将分布式一致性应用于微电网的控制策略中,基于平均一致性提出一种分布式比例积分控制器,保证了电压与频率的恢复.文献[7 ]在文献[6 ]的基础上引入一种分布式滑模控制器,可提高分布式比例积分器的收敛速度,不仅达到快速补偿的效果,还可提高系统的鲁棒性.文献[8 ]讨论了微电网一致性控制下的频率恢复和有功功率精确分配.然而分布式一致性算法主要应用于常规下垂交流微电网,但常规下垂控制存在惯性小、输出阻抗低的缺点,当微电网受到较大扰动时会影响系统的稳定性.近年来,一些学者利用VSG来解决上述问题,文献[9 ]通过模拟传统同步发电机转子的运动,为逆变器提供虚拟惯性和阻尼特性,达到一次调频的目的.文献[10 ]通过改进控制结构的方法进行二次调频,但是由于没有通信结构,面对较大的负荷波动仍需要对二次调频逆变器的数量进行调整.文献[11 ]提出将一致性用于VSG二次控制中,既保留了惯性和虚拟阻抗的特点,同时将频率恢复至额定值,但是频率的恢复时间长,影响微电网工作效率.文献[12 ]在文献[11 ]的基础上通过设计出预测VSG邻居和自身未来状态的控制器,进而提高并联VSG频率的恢复速度,但是恢复时间的不确定降低了其适用性.文献[13 -14 ]通过对一致性算法的改进提出有限时间一致性,可以在限定时间内完成收敛,但是在微电网初始状态未知的情况下难以确定收敛时间,随着初值的增大实际收敛时间也会增加,不利于微电网的应用.文献[15 -16 ]为解决初始状态问题,提出基于固定时间一致性的二次控制方案,该方案无需考虑系统的初始状态,并保证了电压和频率在有限时间内快速恢复,但是计算出来的稳态时间过于保守,与实际恢复时间有很大差别,并且协议参数的存在使得恢复时间也会随之改变.文献[17 ]使用基于固定时间一致性的二次频率控制,并验证了其即插即用特性,但是对于新投入的DG需要较长时间恢复稳定,影响了微电网的工作效率. ...
Fixed-time leader-follower consensus based secondary voltage control for microgrid under directed communication graph
1
... 分布式协同控制具有协调性优良,通信简单等优点,文献[6 ]将分布式一致性应用于微电网的控制策略中,基于平均一致性提出一种分布式比例积分控制器,保证了电压与频率的恢复.文献[7 ]在文献[6 ]的基础上引入一种分布式滑模控制器,可提高分布式比例积分器的收敛速度,不仅达到快速补偿的效果,还可提高系统的鲁棒性.文献[8 ]讨论了微电网一致性控制下的频率恢复和有功功率精确分配.然而分布式一致性算法主要应用于常规下垂交流微电网,但常规下垂控制存在惯性小、输出阻抗低的缺点,当微电网受到较大扰动时会影响系统的稳定性.近年来,一些学者利用VSG来解决上述问题,文献[9 ]通过模拟传统同步发电机转子的运动,为逆变器提供虚拟惯性和阻尼特性,达到一次调频的目的.文献[10 ]通过改进控制结构的方法进行二次调频,但是由于没有通信结构,面对较大的负荷波动仍需要对二次调频逆变器的数量进行调整.文献[11 ]提出将一致性用于VSG二次控制中,既保留了惯性和虚拟阻抗的特点,同时将频率恢复至额定值,但是频率的恢复时间长,影响微电网工作效率.文献[12 ]在文献[11 ]的基础上通过设计出预测VSG邻居和自身未来状态的控制器,进而提高并联VSG频率的恢复速度,但是恢复时间的不确定降低了其适用性.文献[13 -14 ]通过对一致性算法的改进提出有限时间一致性,可以在限定时间内完成收敛,但是在微电网初始状态未知的情况下难以确定收敛时间,随着初值的增大实际收敛时间也会增加,不利于微电网的应用.文献[15 -16 ]为解决初始状态问题,提出基于固定时间一致性的二次控制方案,该方案无需考虑系统的初始状态,并保证了电压和频率在有限时间内快速恢复,但是计算出来的稳态时间过于保守,与实际恢复时间有很大差别,并且协议参数的存在使得恢复时间也会随之改变.文献[17 ]使用基于固定时间一致性的二次频率控制,并验证了其即插即用特性,但是对于新投入的DG需要较长时间恢复稳定,影响了微电网的工作效率. ...
Distributed robust frequency restoration and active power sharing for autonomous microgrids with event-triggered strategy
1
2021
... 分布式协同控制具有协调性优良,通信简单等优点,文献[6 ]将分布式一致性应用于微电网的控制策略中,基于平均一致性提出一种分布式比例积分控制器,保证了电压与频率的恢复.文献[7 ]在文献[6 ]的基础上引入一种分布式滑模控制器,可提高分布式比例积分器的收敛速度,不仅达到快速补偿的效果,还可提高系统的鲁棒性.文献[8 ]讨论了微电网一致性控制下的频率恢复和有功功率精确分配.然而分布式一致性算法主要应用于常规下垂交流微电网,但常规下垂控制存在惯性小、输出阻抗低的缺点,当微电网受到较大扰动时会影响系统的稳定性.近年来,一些学者利用VSG来解决上述问题,文献[9 ]通过模拟传统同步发电机转子的运动,为逆变器提供虚拟惯性和阻尼特性,达到一次调频的目的.文献[10 ]通过改进控制结构的方法进行二次调频,但是由于没有通信结构,面对较大的负荷波动仍需要对二次调频逆变器的数量进行调整.文献[11 ]提出将一致性用于VSG二次控制中,既保留了惯性和虚拟阻抗的特点,同时将频率恢复至额定值,但是频率的恢复时间长,影响微电网工作效率.文献[12 ]在文献[11 ]的基础上通过设计出预测VSG邻居和自身未来状态的控制器,进而提高并联VSG频率的恢复速度,但是恢复时间的不确定降低了其适用性.文献[13 -14 ]通过对一致性算法的改进提出有限时间一致性,可以在限定时间内完成收敛,但是在微电网初始状态未知的情况下难以确定收敛时间,随着初值的增大实际收敛时间也会增加,不利于微电网的应用.文献[15 -16 ]为解决初始状态问题,提出基于固定时间一致性的二次控制方案,该方案无需考虑系统的初始状态,并保证了电压和频率在有限时间内快速恢复,但是计算出来的稳态时间过于保守,与实际恢复时间有很大差别,并且协议参数的存在使得恢复时间也会随之改变.文献[17 ]使用基于固定时间一致性的二次频率控制,并验证了其即插即用特性,但是对于新投入的DG需要较长时间恢复稳定,影响了微电网的工作效率. ...
基于一致性算法的并联虚拟同步机系统小信号模型分析
1
2022
... 在多DG的微电网系统中,微电网的电压和频率会存在一定的波动,为了限制这种偏差在允许范围以内,二次控制可考虑采用通信手段的介入.传统的通信控制方案多采用集中控制器来对各个DG进行控制,这种方案与稀疏通信的要求相矛盾.分布式协同控制可以保证只通过与邻居之间的信息交换来实现全局优化[18 ] .平均一致性在微电网方面的引入降低了通信要求,但是需要较长时间才能够将偏差控制到允许范围以内. ...
Small-signal analysis of consensus-algorithm-based parallel virtual synchronization generators system
1
2022
... 在多DG的微电网系统中,微电网的电压和频率会存在一定的波动,为了限制这种偏差在允许范围以内,二次控制可考虑采用通信手段的介入.传统的通信控制方案多采用集中控制器来对各个DG进行控制,这种方案与稀疏通信的要求相矛盾.分布式协同控制可以保证只通过与邻居之间的信息交换来实现全局优化[18 ] .平均一致性在微电网方面的引入降低了通信要求,但是需要较长时间才能够将偏差控制到允许范围以内. ...
Distributed robust finite-time nonlinear consensus protocols for multi-agent systems
1
2014
... 为了清楚阐明预定时系统的优势,对比固定时间一致性的典型结构[19 ] ,具体如式(6)所示 ...
Generating new classes of fixed-time stable systems with predefined upper bound for the settling time
1
2021
... 式中,λ 2 (L L T max 即可确定收敛时间上限,但是固定时间一致性对于最大时间的估计值过于保守,与实际收敛时间差距过大,并且收敛时间也会随参数而改变,不利于微电网的控制[20 ] . ...