电气工程学报, 2024, 19(1): 33-48 doi: 10.11985/2024.01.004

特邀专栏:储能关键装备数字化智能安全管理技术

锂离子电池健康状态估算方法研究进展*

金建新,1, 虞儒新1, 刘刚1, 许林波1, 马延强2, 王浩彬2, 胡晨,3

1.浙江浙能嘉华发电有限公司 嘉兴 310007

2.河北创科电子科技有限公司 邯郸 056107

3.新能源与储能运行控制国家重点实验室(中国电力科学研究院有限公司) 北京 100192

Research Progress on State-of-health Estimating Method for Lithium-ion Batteries

JIN Jianxin,1, YU Ruxin1, LIU Gang1, XU Linbo1, MA Yanqiang2, WANG Haobin2, HU Chen,3

1. Zhejiang Zheneng Jiahua Electric Power Generation Co., Ltd., Jiaxing 310007

2. Hebei Chuangke Electronic Technology Co., Ltd., Handan 056107

3. Laboratory of Operation and Control of Renewable Energy & Storage Systems (China Electric Power Research Institute), Beijing 100192

收稿日期: 2023-10-8   修回日期: 2023-11-29  

基金资助: 浙江浙能嘉华发电有限公司科技资助项目(ZNKJ-2021-041)

Received: 2023-10-8   Revised: 2023-11-29  

作者简介 About authors

金建新，男，1971年生，高级工程师。主要研究方向为能源发电设备智能运维。E-mail：jinjianxin@zjenergy.com.cn;

胡晨，男，1971年生，博士研究生。主要研究方向为锂离子电池、铅炭电池等储能器件及电网大规模储能应用。E-mail：whhuchen@163.com

摘要

随着锂离子电池(Lithium-ion batteries，LIB)在电动汽车、储能电站和备用电源等领域的广泛应用，准确、及时地估计电池健康状态(State of health, SOH)是确保电池系统运行可靠性和安全性的关键因素。锂离子电池内部复杂的电化学反应和多变的外部使用条件，使得实现精准的健康状态估计具有挑战。随着人工智能、大数据分析等技术的快速发展，电池SOH评估的方法也逐渐多样化。首先介绍电池的老化机理和SOH概念，随后介绍了实验法、基于模型、数据驱动和融合方法，详细分析了每种方法的特点，并比较了在实际应用中相应的优势和局限性。最后，对SOH估算的未来趋势进行了展望。

关键词： 锂离子电池; 电池老化; 健康状态; 估算方法

Abstract

With the widespread application of lithium-ion batteries in electric vehicles, energy storage stations, it is the key to ensure the reliability and safety of the battery to accurately estimate the health state of the battery. The complex electrochemical reaction inside lithium-ion battery and the changeable external use conditions make it challenging to realize accurate health state estimation and life prediction. With the rapid development of technologies such as artificial intelligence and big data analysis, the methods of battery health assessment have been gradually diversified. First, the aging mechanism and SOH concept of batteries are introduced in this article. Next, different SOH estimation methods are categorized into four classes：experiment-based, model-based, data-driven, and hybrid methods. The characteristics of each method are analyzed in detail, and the corresponding advantages and limitations in practical applications are compared. Finally, the future trends of SOH estimation are prospected.

Keywords： Lithium-ion battery; battery aging; health status; evaluation method

PDF (30108KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

金建新, 虞儒新, 刘刚, 许林波, 马延强, 王浩彬, 胡晨. 锂离子电池健康状态估算方法研究进展*[J]. 电气工程学报, 2024, 19(1): 33-48 doi:10.11985/2024.01.004

JIN Jianxin, YU Ruxin, LIU Gang, XU Linbo, MA Yanqiang, WANG Haobin, HU Chen. Research Progress on State-of-health Estimating Method for Lithium-ion Batteries[J]. Chinese Journal of Electrical Engineering, 2024, 19(1): 33-48 doi:10.11985/2024.01.004

1 引言

锂离子电池具有能量密度高、自放电率低、使用寿命长等优点，被广泛应用于电动汽车、电网储能和备用电源等领域[1]。理想电池不会老化，其参数被认为是常数。但在实际运行中，电池的参数会随着老化程度不断变化，导致储存能量和提供电能的能力下降，甚至会出现局部短路、起火、爆炸等安全事故[2]。电池健康状态(State of health, SOH)随着使用寿命延长而不断下降，表现为容量损失和功率衰减。容量损失主要与电池内部副反应和电极结构破坏有关，功率衰减主要是由于电池电阻的增大。电池SOH是电池系统安全管理与运维的主要指标之一，但该指标无法由传感器直接测量，需要根据电池的电压、电流和温度等外在参数，采用合理的方法进行估算，因此精确地估算电池SOH是保证系统安全可靠运行的必要条件[3-4]。SOH研究有利于掌握电池老化影响因素和变化规律，为电池的实际使用和维护提供理论指导，保障电池系统安全可靠运行[5]。

本文综述了锂离子电池老化机理和国内外SOH的最新研究方法，详细介绍了各种方法的原理、优缺点及适用场景，并阐明未来的发展方向。

2 锂离子电池老化机理及SOH

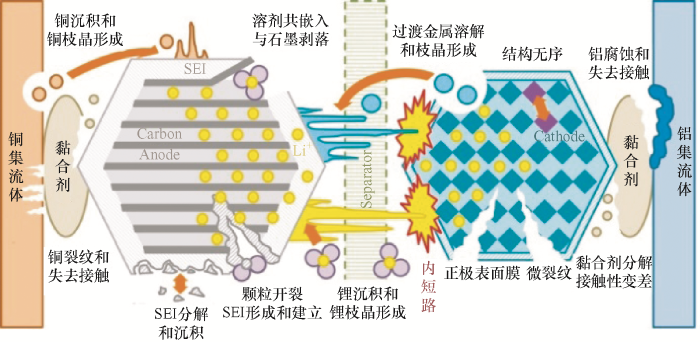
锂离子电池是一个复杂的电化学系统，老化失效机理复杂，其健康状况由多种内部因素和外部因素共同决定。内部因素是电池材料体系退化失效，包括正极、负极、电解液以及内部部件材料发生一系列的物理和化学变化，造成电池性能降低和剩余容量衰减。外部影响因素包括环境温度、充放电流大小、放电深度(Depth of discharge，DOD)、充放电电压、循环次数等[6]。了解电池的老化机制和影响因素有助于对电池状态和寿命的评估。

随着使用时间和循环次数的增加，电池内部电极材料体系发生复杂的物理和化学反应。通常，电池老化模式分为三类[7]：活性锂的损耗(Loss of lithium-ion inventory，LLI)、负极/正极活性物质损失(Loss of active material in the negative electrode，LAMNE；Loss of active material in the positive electrode，LAMPE)、电导率损失(Conductivity loss，CL)，电池的老化机理如图1所示[8]。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   锂离子电池老化机理[8]


锂离子电池的容量衰减与使用条件密切相关，如环境温度、充放电倍率、放电深度和充放截止电压等，这些外部因素通过影响内部因素加速电池老化。CUI等[9]对锂离子电池进行了大量的正交老化试验，结果显示对容量损失的影响因素，其重要程度顺序为温度>放电电流倍率>放电深度，即温度和充放电倍率是导致电池老化的最重要参数。

电池SOH表征当前电池相对于新电池存储电能的能力。随着电池使用寿命的延长，电池的容量、内阻、功率及循环次数等特征参数都会随着电池老化而发生变化，所以可以用容量、内阻、功率和剩余可充电次数等不同的特征参数来定义SOH[10]，如式(1)~(4)所示

$\mathrm{SOH}=\frac{{{C}_{\mathrm{curr}}}}{{{C}_{\mathrm{rated}}}}\times 100\%$
$\mathrm{SOH}=\frac{{{R}_{\mathrm{EOL}}}-{{R}_{\mathrm{curr}}}}{{{R}_{\mathrm{EOL}}}-{{R}_{\mathrm{new}}}}\times 100\%$
$\mathrm{SOH}=\frac{{{P}_{\mathrm{ocmp}}}-{{P}_{\min }}}{{{P}_{\mathrm{new}}}-{{P}_{\min }}}\times 100\%$
$\mathrm{SOH}=\frac{{{N}_{\mathrm{rem}}}}{{{N}_{\mathrm{tol}}}}\times 100\%$

式中，Ccurr为电池当前最大可用容量；Crated为电池标称容量；REOL为电池寿命终止时的内阻；Rcurr为电池当前内阻；Rnew为电池出厂时的内阻；Pocmp为电池当前启动功率；Pnew为新电池启动功率；Pmin为电池寿命终止时的启动功率；Nrem为电池剩余循环次数；Ntol为电池总循环次数。

目前，基于容量的SOH定义应用广泛。而基于内阻、功率、剩余可充电次数等参数的定义SOH应用相对较少，这是因为内阻、功率与温度、充电状态(State of charge，SOC)有关，不易准确测量；总循环次数和剩余循环次数无法准确预测。

3 电池SOH估计方法

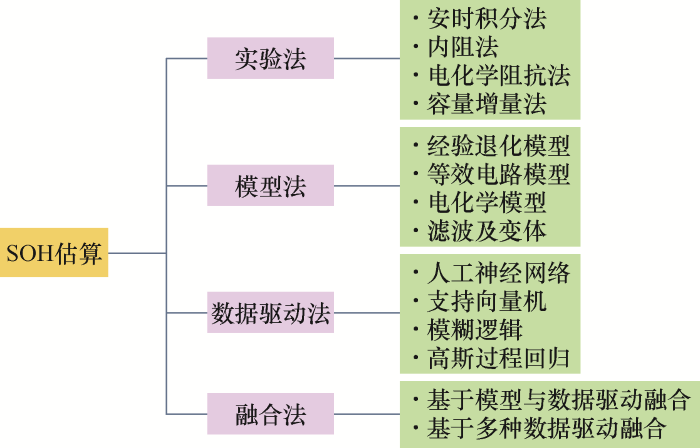
国内外对锂离子电池SOH预测进行了广泛研究，主要包括实验法、模型法、数据驱动法及融合法等，如图2所示。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   电池SOH估算方法的分类


3.1 实验法

实验法利用试验设备对蓄电池进行测试，通过相关的测试参数(通常是电池电压和电流)，获得标准老化特性参数(如容量、内阻、阻抗谱等)，来评价电池的劣化程度。主要分为直接测量法和间接分析法，具体包括安时积分法、欧姆电阻法、电化学阻抗谱法、容量增量法等。

3.1.1 安时积分法

安时积分法通过严格遵循SOH的定义来估算SOH。该方法在离线状态下对电池完全充放电，测量出当前的最大放电容量，如式(5)所示

${{C}_{\mathrm{curr}}}=\int_{{{t}_{1}}}^{{{t}_{2}}}{I\mathrm{d}t}$

式中，I是放电电流；t1和t2分别是放电过程的开始和结束时间。

安时积分法为一种离线方法，测试结果通常被视为SOH的真实值，用于验证其他SOH估计方法的准确性，还可以与其他方法结合使用。但安时积分法需要有特定试验条件，无法在实际工况条件下使用。

3.1.2 内阻法

锂离子电池的内阻被认为是SOH的一个重要指标，这一参数受到老化和退化的严重影响，当电池SOH减少时，内阻值增加。因此，内阻是与SOH强相关的指标，具有很好的预测性。

内阻法通常以脉冲电流对电池进行激励，即在电池上施加一个突变的电流ΔI，相应产生端电压的ΔU，依据欧姆定律和极化曲线拟合来估算内阻，R=ΔU/ΔI，最后根据内阻的变化估算SOH。

电池的内阻辨识算法常用插值法、卡尔曼滤波(Kalman filter，KF)、递推最小二乘(Recursive least square，RLS)等。梁培维等[11]采用三次样条插值法 (相比较而言，采用神经网络法运算更为复杂)，以欧姆内阻作为电池的健康因子，结合数据驱动法，建立健康因子与SOH的关系模型。试验表明，估算电池SOH误差小、精度高，验证了该方法的可行性。

欧姆电阻法的主要优点是简单，只需要测量电池的电压和电流，无需复杂的测量技术，成本低。欧姆内阻法SOH估算的难点在于SOH与内阻映射关系的提取，尤其当考虑温度、倍率和SOC等影响因素时，其映射关系的建立难度会明显增大。同时，由于只使用一个参数来估计SOH，因此，欧姆电阻法本身不够精确。

3.1.3 电化学阻抗谱法

电池的容量衰减与电池电极界面性质改变密切相关，在电池老化过程中固体电解质界面(Solid electrolyte interface, SEI)膜、活性材料和电解液等变化为容量衰减的主要因素，电化学阻抗谱法(Electrochemical impedance spectroscopy，EIS)具有反映电极过程动力学及界面结构信息的优点，这为基于电化学阻抗谱的SOH估计提供了理论支持。该方法基本思路如下：测量获取电池的不同老化阶段阻抗谱曲线，绘制Nyquist图，结合等效电路，采用数据拟合方法确定电路参数(如电阻、电容、电荷转移及Warburg系数等)，根据电路参数的变化预测电池SOH。

GALEOTTI等[12]拟合阻抗谱数据提取等效电路模型参数，引入了电池的欧姆电阻和可用容量之间的关系，通过证据理论(Theory of evidence, TOE)结合电池放电曲线和阻抗特征来估计SOH。试验结果显示，对于常规电池，SOH估算的最大误差为3.73%；对于异常电池，SOH估算的最大误差为8.66%。

EIS曲线含有丰富的电化学动力学和电极界面细节信息，结合电路模型，可以对蓄电池的SOH做出准确分析。但是EIS测量需要高精尖专业测试设备，对测试环境具有很高的要求，大多局限于实验室研究；而且目前EIS大多是在电池静态或离线测量，车载、备用电源和储能电站等场景的动态在线测量的研究存在挑战，因此，更简单、更通用的在线获取EIS参数的方法仍需要进一步研究。

3.1.4 容量增量法

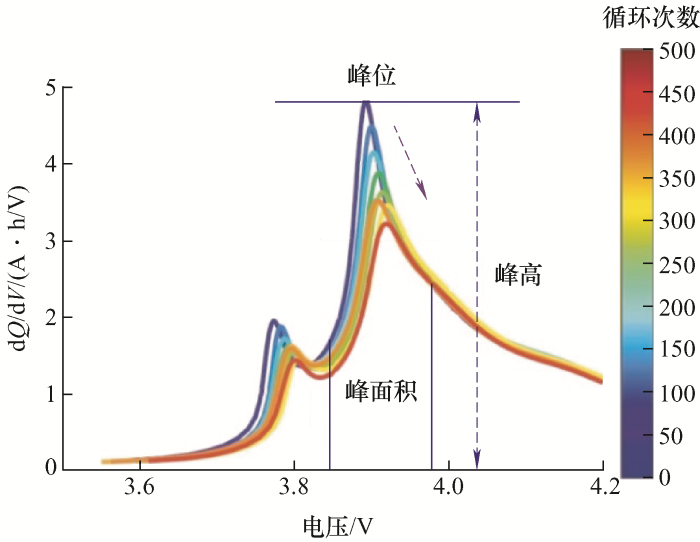
容量增量法(Incremental capacity analysis，ICA)原理是将充放电曲线(V-Q)中平缓的电压平台转换为能明确识别的增量容量IC曲线特征峰值，不同循环次数的IC曲线包含关于电压平台区域中的曲线特征差异明显，因此，可基于IC曲线包含的电池老化特征来估算当前电池实际可用容量[13]。通过提取诸如IC曲线的峰高、峰宽、峰面积、峰位置的特征量作为用于电池SOH评估的健康因子的变化(图3)，分析活性材料损失(LAM)、活性锂的损失(LLI)和电导率损失(CL)等老化机理。具体来说，IC曲线向更高电压移动可能与CL老化机理有关，相应表现为集流体腐蚀、黏合剂分解等现象。IC曲线中峰高降低则对应的活性材料损失(LAM)，即可能出现电极活性物质的颗粒破碎、结构衰变、过渡金属溶解等现象。峰面积降低表明电池在老化过程中活性锂含量逐渐减小，即活性锂的损失(LLI)，相应地出现固体电解质界面的生长和分解(SEI)、电解质分解等现象。增量容量IC曲线V~dQ/dV，通过对测量的V-Q曲线进行导数运算来获得，可用式(6)表示[14]

$IC=\frac{\mathrm{d}Q}{\mathrm{d}V}\approx \frac{\Delta Q}{\Delta V}=\frac{{{Q}_{t}}-{{Q}_{t-1}}}{{{V}_{t}}-{{V}_{t-1}}}$

式中，Qt与Vt分别为电池t时刻的容量与电压。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   不同循环次数下的增量容量曲线[13]


ICA法估算SOH的具体过程如下[15]：① 以微小电流(~1/20C)对100%SOC的电池完全放电，获取近似开路电势曲线；② 依据式(6)计算dQ/dV值；③ 提取IC曲线中的特征峰值，估算SOH。

通常，IC曲线受电流大小、采样频率和噪声的影响。当放电流倍率低于0.1C和高达1 Hz的采样频率将有助于获得精细的IC曲线，从而提高SOH评估的准确性。但是，电池通常以1/3C~1/2C倍率放电，因此，准确在线评估相对较高倍率充放电下电池的SOH在工程应用中更有意义。采样频率高可能导致数据存储空间不足和数据传输延迟，从而增加BMS的负担[16]。因此，在低采样频率下准确评估电池SOH也是研究人员关心的问题。此外，ICA方法需要通过各种滤波算法进行去噪，以获得平滑的IC曲线和清晰的特征量，但这可能导致数据失真。为了最大限度地减少降噪处理所造成的数据失真，ZHANG等[17]对基于ICA的估算SOH方法进行改进，即在ICA分析的基础上，引入了区域电压和区域三角形的概念，三角形两个边长被定义为区域边长，并被用作SOH评估的健康因子。采用区域三角形法对1/3C~1/2C放电倍率的三元电池和磷酸铁锂电池的SOH进行在线估算，采样频率低至每3~5 min/次，结果表明，SOH模型具有良好的估算精度和鲁棒性。LI等[14]提出了一种高斯滤波处理IC曲线的在线快速估算锂离子电池SOH的容量增量分析法。采用高斯滤波结合移动平均法对IC曲线进行平滑，这种改进的平滑方法在不改变IC曲线上的健康特征的情况下，可以完全滤除IC曲线上的噪声，并且完整保留IC曲线上的电池容量衰减相关健康特征信息。结果表明，最大估计误差小于2.5%，显示出该方法可以快速在线估算高倍率充电电池的SOH。

3.2 基于模型的估算方法

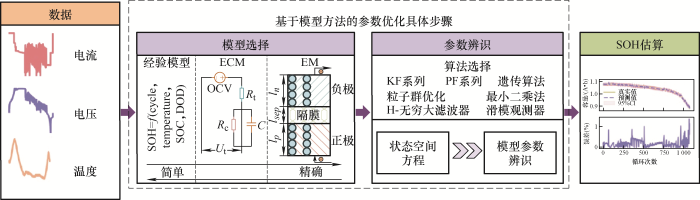
基于模型的方法使用间接方法来估计电池的SOH，首先建立电池模型(通常是表征电池容量衰减的数学函数或充放电特性的等效电路模型)，再根据直接测量的数据来识别模型参数。模型法主要包括经验退化模型(又称经验模型)、等效电路模型(Equivalent circuit model, ECM)以及电化学模型(Electrochemical model, EM)。从经验退化模型到ECM再到EM，精度逐渐提高，复杂性也有所增加。建立模型和参数辨识是此类方法的两个主要步骤，估计经验模型的参数通常是一些拟合系数，而ECM和EM的参数代表特定的物理参数。

基于模型方法的电池SOH估计方法的一般过程如图4所示[18]。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   基于模型方法的电池SOH预测技术流程[18]


3.2.1 经验退化模型方法

经验退化模型(Empirical degradation model，EDM)的基本原理是通过试验模拟电池老化(循环和日历老化过程)，测定温度、电流倍率、放电深度和循环次数等应力变量对电池的影响，并结合数学方程拟合，实现对电池SOH的估计，因此，经验退化模型也称为数学模型。阻抗经验退化模型和容量经验退化模型是二种常见的经验模型。阻抗经验退化模型是根据电池不同寿命时期的阻抗变化规律，进一步利用容量与阻抗关系估算电池SOH。容量经验退化模型通过试验数据分析在前后时间段的变化关系，获得电池容量的整体变化趋势，利用经验退化模型预测电池的健康状态和老化过程[19]。

经验退化模型是一种简单而成熟的方法，具有建模难度低、适用范围广的优点，但缺乏清晰的物理含义，其估算SOH的有效性和精确性依赖试验数据，不能保证良好的效果。

3.2.2 等效电路模型方法

等效电路模型(Equivalent-circuit model, ECM)属于半经验模型。ECM是利用电压源、电感、电阻、电容等电路元件通过不同组合方式来组成等效电路，并结合参数辨识算法，如最小二乘法(Least squares, LS)、卡尔曼滤波(KF)及其变体、粒子滤波(Particle filter, PF)及其变体等智能算法，仿真电池的充放电特性，并结合状态诊断方程实现电池SOH估算[20]。ECM通过电阻、电容等代替充放电过程中的极化反应和自放电反应，使极化效应和反应过程更接近电池的实际情况。因此，考虑得越多，电池型号就越复杂，但电池越符合实际使用。等效电路模型包括Rint、Thevenin、二阶RC、PNGV和GNL模型等[21](表1)。Rint模型由理想电压源和欧姆电阻串联而成，结构简单，易于参数辨识，但高倍率时仿真结果与测量值偏差较大，应用范围较小。Thevenin模型，也称一阶RC模型，是在Rint模型基础上增加了一个RC并联网络，RC并联网络主要用于描述电池在充放电过程中的电化学极化特性。二阶RC模型是在Rint模型基础上增加了二个RC并联网络，分别用于描述电池电化学极化和浓差极化。由于同时考虑了欧姆极化、电化学极化和浓差极化，在估计大倍率工况条件方面具有更高的精度。PNGV模型是Thevenin的派生模型，即在Thevenin模型的主线上串联了电容Coc，比Thevenin模型多了一个电容Coc来描述电流对OCV的影响，模型考虑温度影响，可描述开路电压、容量变化及电池内部反应过程。GNL模型同时考虑了欧姆极化、浓差极化、电化学极化及自放电因素对电池充放电行为的影响，模型的结构更接近于电池的内部特性，对电池倍率响应特性具有较好的仿真效果[22]。

表1   常用电池等效电路模型比较

模型名称模型结构描述方程参数优点缺点
Rint模型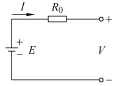V=E－IR0E为开路电压，R0为欧姆内阻，V为端电压，I为负载电流模型简单，易于参数辨识无法反映电池动态特性，精度低，应用范围较小
Thevenin模型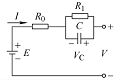V=E－IR0－VC
$I=\frac{{{V}_{C}}}{{{R}_{1}}}+C\frac{d{{v}_{c}}}{dt}$		R1和C为表述电池极化效应的电阻和电容RC回路用于模拟电池动态特性，考虑了欧姆极化和电化学极化，在实际工程应用中较多因模型参数为常数，模型精度较大程度上受温度变化和电池老化的影响
二阶RC模型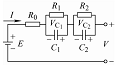$V=E-I{{R}_{0}}-{{V}_{C1}}-{{V}_{C2}}$$I=\frac{{{v}_{C1}}}{{{R}_{1}}}+{{c}_{1}}\frac{d{{V}_{C1}}}{dt}$R1和C1分别为电化学阻抗和电化学电容；R2和C2分别为浓差阻抗和浓差电容同时考虑了欧姆极化、电化学极化和浓差极化，在估计大倍率工况条件方面具有更高的精度结构复杂、参数较多，计算较为复杂
PNGV模型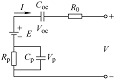$V=E-I{{R}_{0}}-{{V}_{P}}-{{V}_{\mathrm{OC}}}$
${{v}_{\mathrm{OC}}}=\frac{1}{{{C}_{\mathrm{OC}}}}$		COC为等效电容模型考虑温度影响，可描述开路电压、容量变化及电池内部反应过程，对电池各种工况适用性好，精确度较好串联电容的误差累积降低模型精确度，不能反映电池自放电问题
GNL模型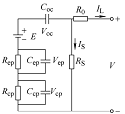$V=E-{{V}_{b}}-{{V}_{\text{ep}}}-{{I}_{L}}{{R}_{0}}$
$V\text{=}{{I}_{S}}{{R}_{S}}$		RS为自放电电阻相比于PNGV模型考虑了电池自放电问题和负载电流随时间累计引起的开路电压变化问题；估算精度更高，适用性更广相比于PNGV模型，计算更复杂，计算量更大

新窗口打开| 下载CSV


参数辨识也是估算电池SOH的重要环节，在建立电池等效模型后，需要辨识模型中的各参数。等效电路模型结构简单、参数少，故参数辨识较为容易。参数辨识有离线和在线两种方式。离线参数辨识主要有最小二乘法、最大似然函数法，离线参数辨识的模型参数是固定的，但随着电池老化和温度的改变，模型精度会逐渐降低。为提高模型估算精度，需要在线辨识模型的参数，实时修正。TOPAN等[23]利用递推最小二乘法(RLS)将LS转化为参数递推估计，减少了矩阵运算量。赵可沦等[24]利用含遗忘因子的递推最小二乘方法在线辨识模型参数，计算量小、精度高，而且避免算法出现数据饱和问题，提高了算法的实时跟踪与修正能力。为了进一步提高计算速度，KIM等[25]提出了一种基于快速UD递归最小二乘(FUDRLS)的参数估算方法，在保持数值稳定性的同时提高了速度。该参数辨识算法复杂度低、易于实现，适用于实时嵌入式BMS。孙金磊 等[26]通过建立Thevenin模型，利用基于双自适应双扩展卡尔曼滤波，可对电池状态参数和最大充入电量的联合估算，实现了在线估计电池健康状态。

等效电路模型具有结构简单、计算量小、计算仿真速度快，可数值化、便于嵌入电池管理系统，可实现电池SOH在线预测的功能，易于工程实现等优点，是在线状态估计应用最多的电池模型之一，也是电池模型的研究重点。

3.2.3 电化学模型方法

电化学模型(EM)是将电池简化为正极、负极、电解液和隔膜组成的系统，以多孔电极理论和离子扩散等电化学理论为基础，采用一系列复杂偏微分方程和代数方程，来模拟电池内部的电化学反应动力学、传质、传热等微观反应过程，建立模型，描述电池的充放电行为，分析电池老化机制及诊断其SOH状态。电化学模型主要有准二维模型(Pseudo two-dimensional, P2D)(图5)、单粒子模型(Single particle, SP)、增强型单粒子模型(Enhanced single particle, ESP)及多物理耦合模型(Multiphysical-coupling, MC)等四类[27]。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5   P2D模型的原理图[28]


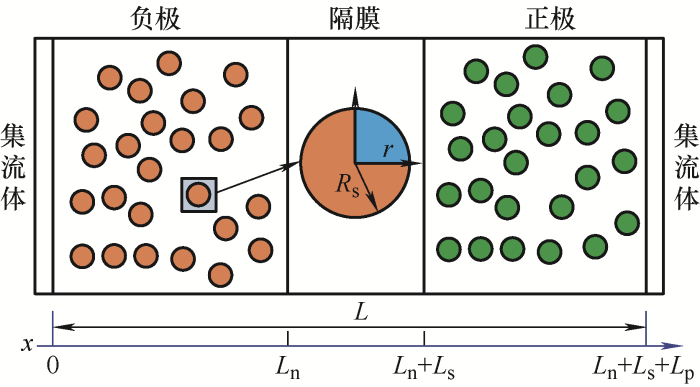
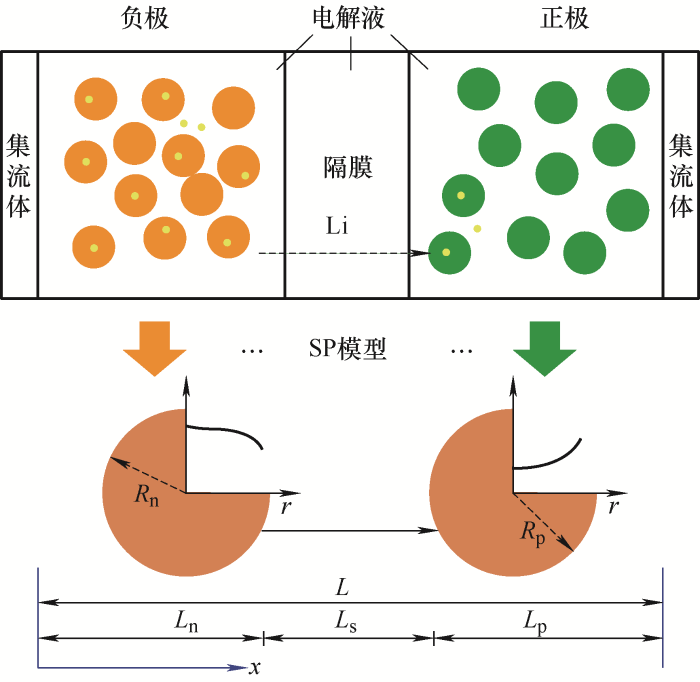
电化学模型使用偏微分方程来描述内部电化学反应，模型参数能准确反映内部物理化学反应的变化，预测准确性高。目前，用于估计SOH的常见电化学模型包括准二维(P2D)模型及其简化模型。但是，基于多孔电极理论和浓溶液理论的P2D模型是一种经典的电化学模型，需要求解一系列固液相偏微分方程组和代数方程，复杂程度高，计算量大，多用于电池多物理场分析和电池设计等方面，难以应用于在线估计，不适用于电池BMS。因此，通常P2D模型的简化方法主要分为两种：一是简化EM模型，最流行的是单粒子(SP)模型(图6)，它是一种具有最简化的参数和结构的电化学模型。该模型假设正负两个电极都分别理想化为一个单球形固体粒子，且认为电解液浓度不变和电极内各处的固相电势相等。单粒子(SP)模型优点是足够简单，计算速度快，在低倍率电流的情况下性能跟P2D相近，但是一旦电流倍率增大，单粒子模型的误差就会随之增大。为了改善SP模型在高倍率下精度较低的缺点，GRANDJEAN等[29]在考虑电解质浓度、电解质电势和电极电势的空间变化基础上，开发了一个带有电解质的SPe模型(Single-particle model with electrolyte dynamics, SPe)，SPe模型可通过多项式近似等方法将其转化为常微分方程求解，相比于SPM模型其精度有所提高，从而使其适用于高倍率放电应用。LI等[30]基于电池SEI生长引起的活性锂离子损失(LLI)，以及活性材料颗粒因体积膨胀产生的应力导致的裂纹引起的活性材料损失(LAM)，开发了基于SP的退化模型，这种低阶模型是循环次数和温度的函数，可在线快速预测容量衰减和电压曲线变化，预测精度高。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6   SP模型的结构示意图[28]


二是通过近似方法简化偏微分方程来求解P2D模型。简化方式主要有几何结构简化、简化固液相扩散过程和变换数学算法等。在保证模型精度的基础上，为了尽量降低复杂度，刘征宇等[31]提出了种包含液相简化的P2D(LSP2D)模型，将电池端电压化简成为耦合固相Li+浓度和液相Li+浓度的方程，再对表达演化规律的偏微分方程进行抛物线近似化简，最终简化为由多项式组成的模型。LSP2D简化模型结合了SP模型高速度和P2D模型高精度的优点，对于电池管理系统中参数的精准、快速估算具有重要意义。LV等[32]提出了一种简化的基于多孔电极理论和稀溶液理论的电化学模型，通过对开路电势、电极动力学过程近似处理，简化模型的控制方程，该模型具有检测时间短、求解速度快的特点。

3.2.4 滤波及其变体

滤波方法主要通过建立状态方程和性能参数来动态跟踪和预测电池的健康状态。常用的基于滤波的算法分为卡尔曼滤波(KF)、粒子滤波(PF)及其变体。滤波方法的计算包括预测和更新两个步骤，预测步骤根据状态方程，预测下一时刻的状态和协方差矩阵；更新步骤根据观测方程，校正预测的状态和协方差矩阵，得到最终的状态和协方差矩阵。估算电池的SOH过程如下：首先，通过构造状态方程来建立状态空间模型；然后，使用内阻、电容等参数，将SOH表征为状态变量，从而动态跟踪和预测电池SOH；最后，利用滤波算法来迭代求解[33]。

(1) KF。KF的核心原理是一种利用线性系统状态方程，通过系统输入输出观测数据，不断对锂电池的真实状态参数进行最小均方差的最优估计。卡尔曼滤波器最初用于线性系统，而电池状态是非线性的，经典卡尔曼滤波器无法实现有效的估计。因此，以电池模型为基础，发展出来一系列非线性系统的优化滤波方法，如扩展卡尔曼滤波(Extended Kalman filter，EKF)、双扩展卡尔曼滤波(Dual extended Kalman filter, DEKF)、无迹卡尔曼滤波(Unscented Kalman filter，UKF)等，在电池状态估计中得到广泛的应用[34]。

KF方法及其变体具有良好的误差纠正能力、能够对状态进行估计、基于观测值的实时更新等优点。在电池SOH估算的实际应用中，为了获得更高的预测精度，KF算法通常与其他算法结合使用。SONG等[35]提出了基于RVM和KF的融合框架来预测电池寿命。首先，KF用于优化估计器和更新训练数据集；然后将更新后的数据集应用于重新训练RVM模型；最后，借助KF算法估算出SOH。大多数离线KF算法不能准确描述电池的实际运行状况，而由两个扩展卡尔曼滤波器组成的DEKF可以同步估计电池参数和状态。邓涛等[36]使用Thevenin等效模型对电路进行建模，在EKF适用锂电池组这一非线性系统基础上，应用DEKF滤波法同时估计SOC和SOH，其中一个扩展卡尔曼滤波器估算SOC，称为参数估计，另一个扩展卡尔曼滤波器估算当前额定容量，计算得到当前时刻的SOH。FANG等[37]根据内阻与SOH的关系建立ECM，并采用遗忘因子递推最小二乘法在线辨识模型参数，最后利用DEKF算法在线联合估计SOC和SOH。

(2) PF。PF是一种基于贝叶斯滤波和蒙特卡洛采样的统计滤波算法，其主要思想是从重要性概率密度中取样产生一系列带权重的粒子集合，来近似系统随机变量的概率密度函数，以样本均值代替积分运算，从而获得系统真实状态的最小方差估计。在处理涉及非高斯的非线性系统问题时，PF及其变体是更好的选择，不需要大量的历史数据，适合在线应用。

BI等[38]提出了一种基于遗传重采样粒子滤波(GPF)的动态估计SOH方法，该方法可高效地解决非高斯问题，而且在等效电路模型精度不高的情况下也取得了良好的预测性能。针对复杂工况下粒子权值退化和样本贫化的问题，李鹏等[39]提出了基于改进蝴蝶优化算法和PF的联合算法，能有效改善传统PF算法粒子多样性丧失的问题，使SOH估计更适合实际应用。因电压迟滞效应，导致LiFePO4/C电池放电OCV小于真实的OCV值，充电OCV高于真实的OCV值，故其真实OCV模糊不清，这种模糊特性阻碍了SOH的准确估计。因此，像KF这样仅通过高斯概率密度函数的均值和方差来表示状态的方法往往会失败。PF通过使用蒙特卡罗采样方法克服了这个问题，该方法能够代表任何概率密度函数，模糊度可以被随机建模。因此，PF算法既能够在开始时找到正确值，并能正确地跟踪充电状态，这为SOH的估计奠定了良好基础。SCHWUNK等[40]使用PF来精确估计电池的SOH和SOC，从而避免建立复杂的模型带来的处理迟滞。

3.3 基于数据驱动的方法

随着大数据及人工智能技术的快速发展，数据驱动技术突破了复杂非线性系统难以建模的束缚，已成为当前电池健康分析的主要研究方向。数据驱动方法从性能数据(如电流、电压、阻抗和温度)中提取特征，使用机器学习和统计技术跟踪电池的老化并估计其SOH。数据驱动方法具体包括机器学习和统计方法，机器学习方法(Machine learning, ML)包括人工神经网络、支持向量机、模糊逻辑、高斯过程回归等方法。

机器学习方法的基本思想是通过采集大量的电池运行数据，建立外部健康特征与电池SOH的非线性映射关系来估算SOH，具体过程如下。首先，采集大量电池的电压、电流、电阻或阻抗等运行数据；然后，利用特征工程方法提取电池退化相关特征，借助数据驱动模型，分析、挖掘隐含的电池健康状态信息；最后，对电池进行离线或在线的退化分析，实现对电池的SOH估算。机器学习方法估计SOH的两个关键过程是健康因子(Health indicators，HI)提取和数据驱动算法构建。

3.3.1 人工神经网络

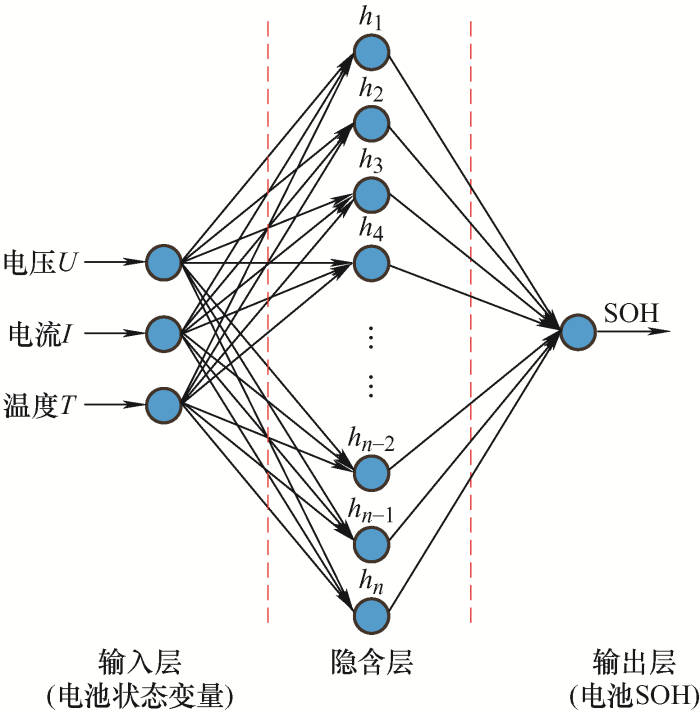
人工神经网络(Artificial neural network，ANN)通常被简称为神经网络，是一种模仿生物神经网络结构和功能、用于数据分类或数据预测的人工智能运算模型，其基本结构由输入层、隐含层、输出层组成，如图7所示[41]。在电池SOH预测领域，根据ANN的自主学习功能，将电压、充放电倍率和内阻等数据作为神经网络的输入，通过这些数据样本对神经元进行一系列的训练，调整其连接权值和阈值，建立数据模型可以快速输出符合条件的结果。常见的预测电池SOH神经网络有BP(Back propagation)神经网络、Elman神经网络、RBF(Radical basis function)神经网络等[42]。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7   用于SOH估算的典型BP神经网络结构[29]


徐元中等[43]提出一种基于模拟退火(Simulate anneal, SA)算法优化BP神经网络的锂离子电池SOH在线预测方法，以LiFePO4/C电池的微分电压、欧姆内阻和循环次数为健康状态因子输入量，建立了SA算法优化的BP神经网络来预测SOH。该方法充分利用SA算法寻找全局最优值的特点，避免了BP神经网络陷入局部最优。李文华等[44]提出了一种基于遗传算法(Genetic algorithm，GA)-Elman神经网络的锂电池SOH估计方法，该方法可以区分锂电池的不同老化模式且估计误差在5%以内，满足BMS预测的要求。该研究方法为振动条件下锂电池的老化机理诊断与SOH预测提供了依据，有助于BMS制定相关策略延长电池使用寿命。

3.3.2 支持向量机

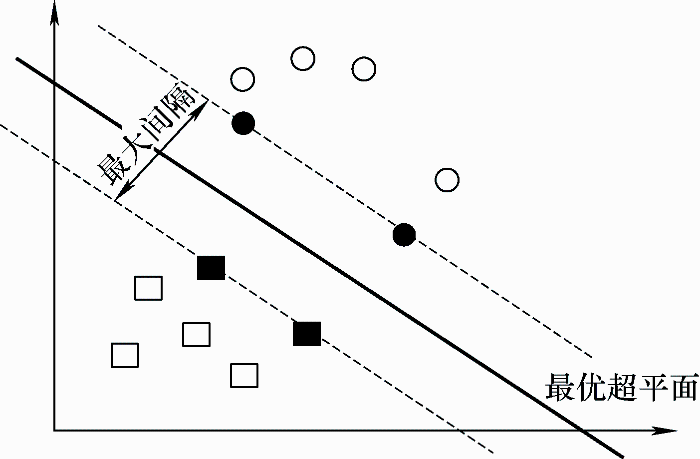
支持向量机(Support vector machine，SVM)是一种是在统计学习的基础上发展起来的新的机器学习方法。支持向量机可以理解成一个“最大间隔分类器”，基本思想就是在高维或无限维空间中构建一个超平面或一组超平面，使两类样本的间隔最大(图8)。SVM有三个非常重要的构件：最大间隔、高维映射和核函数。核函数是一种将低维空间中的数据映射到高维空间中的函数，可把低维空间的非线性问题转换为高维空间的线性问题来求解，这就将线性SVM扩展成了非线性SVM，从而使得SVM可以处理非线性问题。核函数将线性SVM扩展成了非线性SVM，使得SVM更具普适性。与ANN相比，SVM具有收敛快、计算量小、对小样本数据训练能力强、预测精度高等优点。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8   SVM工作原理图


最小二乘支持向量机(LS-SVM)是一种基于统计理论的改进型SVM算法，有较强的非线性映射能力，可将二次优化问题的解转化为线性方程组的求解，降低算法复杂度。针对电池估算SOH精度与速度难以兼顾的问题，徐彬翔等[45]通过对LS-SVM算法改进，包括设定合适的临界系数，舍弃某些支持向量，降低边界样本对算法的影响，提高了算法的鲁棒性与运行速度，从而实现快速准确估算锂电池的SOH。试验表明，所提出的电池SOH估计方法估计误差小于1%，运行速度最高可提升20%。陈璐等[46]以电池等压降放电时间作为间接健康因子，采用粒子群优化的最小二乘支持向量机算法，分别估算在4 ℃、24 ℃、43 ℃温度环境下2 A·h的18650型锂离子电池的健康状态和预测剩余寿命。其中，获取电池等压降放电时间要比直接计算电池放电容量更为方便和容易。试验结果表明，估算SOH结果的平均绝对百分比误差均小于1.05%，这说明最小二乘支持向量机算法具有良好适用性。

3.3.3 模糊逻辑

模糊逻辑系统(Fuzzy inference system，FIS)结构如图9所示，包含模糊产生器、模糊规则库、模糊推理机和模糊消除器。其中，模糊规则库由模糊IF-THEN规则集合组成，它是FIS的核心，用以描述系统的输入输出关系；模糊产生器将输入端确定的数据转化成模糊数据集合；模糊推理机在模糊规则的基础上进行推理；模糊消除器将推理结果去模糊化，转换成输出的精确量[47]。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9   模糊逻辑系统结构图


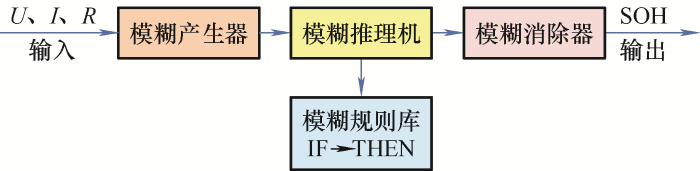
使用模糊逻辑的一般过程包括四个步骤。首先，建立一个规则库来描述输入和输出变量之间的关系；第二，将所有输入值模糊化成模糊隶属函数；第三，执行规则库中所有适用的规则来计算模糊输出函数；最后，模糊输出函数被去模糊以获得输出值[10]。采用模糊逻辑方法估算SOH时，模型的输入是与电池SOH相关的特征参量，输出的是电池SOH。为了实现该方法，首先基于训练数据集，建立描述特征参量的规则库。规则库可由专业经验或使用NN算法生成。训练数据集中的每组数据都是一个模糊集，然后所有输入值都被模糊化为模糊隶属函数。接下来，基于规则库计算模糊输出。最后，根据每个模糊集的SOH，利用基于模糊输出的SOH的加权平均值，计算出SOH的估计值。

基于专家经验的FIS具有很高的普适性，而基于神经网络的数据驱动法的预测精度和实用性好，它们都具有很强的非线性处理能力，无需建立精确的等效电路模型和高精度的硬件，对于锂离子电池这种复杂的非线性系统适用性更高。HE等[48]提出了一种基于模糊逻辑和神经网络的电池容量预测方法，选取NASA预测研究中心(Prognostics CoE, PCoE)公开的锂电池数据集进行测试，结果表明该方法对电池SOH的预测误差小于2%，具有良好的应用前景。樊欣欣等[49]提出了一种基于模糊逻辑预测电池的SOH在线检测法，利用开路电压(VOC)与SOC之间的线性关系，建立基于Q-VOC斜率与SOH规则库的FIS，对FIS的输入是Q-VOC图的斜率，输出SOH，该方法具有测试简单、在线测试时间短的优点。

3.3.4 高斯过程回归

高斯过程回归(Gaussian process regression，GPR)是基于贝叶斯理论和统计学习理论发展起来的一种概率机器学习方法，能够以概率的形式解释预测结果的不确定性，模型性质完全由均值函数和协方差函数确定。与人工神经网络、支持向量机等方法相比，GPR在处理小样本、高维、强非线性问题方面具有良好的适应能力，适用于强非线性的电池系统，因此被广泛应用于电池健康状态的预测。

GPR的核函数影响SOH估算精度，因此，展开GPR最优核函数的选择和核函数超参数优化的研究是当前热点。吕佳朋等[50]将高斯过程回归引入到锂电池容量退化预测中，提出了一种基于不同核函数的高斯过程回归的电池容量预测模型。试验采取均方根误差(Root mean square error，RMSE)和平方相关系数(R2)作为模型的评价指标，来评价模型的预测精度。陈琳等[51]融合自适应变异粒子群(AMPSO)和GPR，构建AMPSO-GPR算法来估算电池SOH，测试GPR的核函数分别为经过自适应变异粒子群优化后的Matern核、LIN核、RQ核和SE核时的SOH估算效果，得到最优核函数。AMPSO-GPR具有实时性，适用于电池SOH的在线检测。

3.4 融合法

采用单一的模型法或数据驱动法估算存在许多的局限性。基于模型的方法通常具有固定的参数，不能适应锂离子电池在动态环境下的退化[52]。基于数据驱动的方法严重依赖历史数据，而当电池在实际应用中历史数据数量少或质量差时，会造成电池SOH估计精度大幅度降低，导致评估结果不可靠[53]。融合模型可以充分发挥不同算法的优势，弥补单一模型的不足，其在精度、鲁棒性和效率等方面显著增强，成为研究热点。融合方法分为两类：基于模型方法和数据驱动方法的融合，以及不同数据驱动方法的融合。

3.4.1 模型与数据驱动的融合

基于电池内部反应机理构建模型，再通过电池历史数据辨识模型参数的方法虽然具有较好的可解释性，但因电池电化学反应是一个动态和非线性的过程，因此要获得一个精确的估算模型是十分困难的[54]。数据驱动方法的准确性依赖于大量高质量训练数据，但由部分数据训练所得的机器学习模型仅能适配部分场景和工况，而电池的老化因素和运行工况上存在多样性，难以保证学习到的特征组合在多个电池差异性维度上的泛化性，其应用受到一定限制[55]。因此，研究人员越来越青睐于将二者融合进行电池SOH估计，同时兼顾估计精度和模型的可解释性，成为未来的主流发展方向。HOU等[56]在电池老化基础上提出了一种双极化等效电路(DPEC)模型和多个数据驱动模型估算电池SOH。王萍等[57]提出一种基于等效电路模型-数据驱动法融合的多时间尺度状态联合估计锂电池SOH方法，试验结果表明所提方法具有较高精度和鲁棒性。崔显等[58]针对在可变工况下锂离子电池SOH估计方法失效的问题，提出了一种基于等效电路模型(ECM)和稀疏高斯过程回归(SGPR)的SOH在线估计方法。CHEN等[59]针对锂离子电池的非线性退化，提出了一种考虑电池在使用后期容量跳水的精确估算SOH的经验模型-数据驱动融合方法。该方法融合了基于多项式的经验模型和改进的GPR，前者用于从长期历史趋势中提取信息，后者用于从日常运行数据中提取部分电压曲线。经验模型可以提供基本的准确性，而GPR模型可以给出容量轨迹动态变化的精细描述。试验显示，即使在电池使用后期容量跳水的情况下，通过融合两个模型可以获得当前容量的准确估计。

3.4.2 多种数据驱动方法的融合

基于多种数据驱动方法融合可以提高SOH算法的鲁棒性，获得更高的估算精度。陈国麟等[60]提出了一种基于健康指标的卷积神经网络(Convolutional neural network, CNN)和Transformer融合的锂电池SOH估计方法。利用CNN强大的特征提取能力挖掘健康指标的局部特征，再利用Transformer算法的顺序处理能力挖掘健康指标的时序特征，融合健康指标中的局部特征和时序特征，得到SOH估计值。倪祥淦等[61]将局部加权线性回归(Locally weighted linear regression，LWLR)与双向长短期记忆(Bidirectional long short memory, BI-LSTM)神经网络模型相结合，提取特征与容量之间的非线性关系，SOH估计结果的最大相对误差仅为1.601%。YU[62]开发了一种基于GPR和多尺度逻辑回归法融合的方法，结合不同尺度的时间序列预测，对电池健康变化的全局和局部趋势进行建模，使预测模型能够捕捉电池真实的SOH退化趋势。LIN等[63]提出了一种基于多特征的多模型融合方法估计电池SOH。首先，分别通过使用多元线性回归、支持向量回归和高斯过程回归模型产生初步SOH预测。随后，使用随机森林模型来融合初步的SOH预测。试验结果表明，与单一特征或单一模型估计方法相比，该方法具有更高的精度和更强的鲁棒性。

融合法能够显著提高电池SOH估算的精度和泛化能力，但是其复杂度也会急剧增加。融合法的算法参数较多、参数辨识难度增大，这也是亟待解决的问题[64]。

4 不同方法的评估和比较

目前，锂离子电池SOH的估计方法主要分为实验法、模型法、数据驱动法和融合法。

实验法一般通过离线方法，直接测量电池电压、电流、容量及阻抗等与电池SOH密切相关的特征参数，评估电池老化程度。其中，安时积分法是估算SOH最简单和最精确的方法，但该方法需要特定试验环境和条件，离线测量时间长，频繁使用此种方法会加速电池老化。欧姆内阻法的优点是简单、成本低，但因仅使用一个参数来估算SOH，精确度低，不建议单独使用这种方法。电化学阻抗谱法可得到电池内部各组分阻抗，比起其他方法获得的电池信息更为全面，但仪器价格昂贵，试验过程中外界条件须保持稳定。容量增量法能有效识别容量损失机制，精确获取电池内丰富的电化学反应信息，但是，其估算SOH受电流大小、采样频率和噪声的影响。总之，实验法对测量环境和设备的要求高，几乎不可能在电池实际运行条件下应用，通常用于校准和结果精度检查[65]。

基于模型的SOH估计方法的核心思想是通过经验公式、等效电路或电化学机理来简化模拟电池受外部因素(温度、充放电倍率、充放电截止电压等)和内部因素(正负极、电解液中或界面上发生的多种电化学反应)引起的老化现象。基于经验退化模型方法计算简单，但精度低，需要针对特定电池进行建模，适用性较差。等效电路模型的准确性与电路电子元件的数量和识别参数的准确性有关，模型结构简单、模型参数较少、计算量小，可实现在线预测，但是工况复杂时存在无法准确识别模型参数的问题。电化学模型参数具有明确的物理意义，能准确反映内部物理化学反应的变化，具有清晰、精度高、通用性好等显著的优势，但电化学模型控制方程复杂、参数多、运算量大，难以应用于在线估计[66]。

数据驱动法的核心思想是基于电池的历史运行数据，使用智能机器学习算法或统计算法，将电池外部特征映射至容量衰减来预测电池SOH。与模型法相比，数据驱动法并没有建立有意义的模型，不需要具体的电池材料特性、结构或失效机制的知识，避免了物理建模和参数辨识问题，从而简化建模任务。数据驱动法只依赖于数据本身，具有较强的灵活性，适合应用在不同的场合[67]。因此，数据驱动法更灵活，预测精度高，但也存在计算量大的缺点。鉴于大数据和人工智能技术的快速发展，这为锂离子电池在线精确估算SOH提供了有力的工具[68]。

融合法是将不同的方法相结合，克服了单一模型法或数据驱动法预测精度低、可靠性差或误判的缺点，是未来锂离子电池SOH估算的发展方向。

通过对电池SOH估算方法总结，可大致了解各自优缺点，如表2所示。

表2   电池不同SOH估计方法优缺点比较

电池SOH估计方法优点缺点
实验法安时积分法估算非常准确测试时间长，会导致容量衰减，仅适用于特定实验室条件
欧姆内阻法简单易行、快速不太准确
电化学阻抗谱法估算准确，反映信息全实施过程复杂、需要专业仪器、成本较高
容量增量法对电池类型不敏感，并能有效识别容量损失机制，精确获取电池内丰富的电化学反应信息受电流大小、采样频率和噪声的影响
模型法经验模型法建模难度低，应用范围广缺乏清晰的物理含义，精度低，不能考虑运行工况、受环境影响
等效电路模型法利用电路元件建模简单，可实现在线预测工况复杂时不适用；精度低
电化学模型法预测精度高，可以给出电池退化的详细解释模型参数多，建模困难、计算量大，鲁棒性差
卡尔曼滤波及变体
粒子滤波		适用于实时处理，预测精度高
概率预测，表达不确定性能力强		方法复杂，计算量大，初始化过程复杂；退化模型的建立应准确
数据驱动法人工神经网络具有非线性特征和自学能力需要大量数据训练，精度受训练数据和训练方法影响大，不适合小样本
支持向量机计算量小，预测精度高长期预测效果不佳、适用于小样本
模糊逻辑可对复杂的非线性系统进行建模自学习能力和适应能力较弱
高斯过程回归适用于小样本、高维的回归问题；适应性强计算复杂度高、抗干扰性差
融合法模型法与数据驱动法融合精度更高、增加了模型可解释性计算复杂度高
多种数据驱动法融合精度更高、泛化能力更强输入数据量大，计算复杂度高

新窗口打开| 下载CSV


5 结论与展望

本文主要从锂离子电池的老化机理入手，分析了导致电池老化机理的内因和外在因素，并将SOH的估算方法分为实验法、模型法、数据驱动法和融合法。实验法通过直接测量和间接分析的结果为后续的模型实现提供了强有力的基础；再详细总结了基于模型法、数据驱动和混合法的SOH最新进展；最后，对各种方法的优缺点进行了讨论。其中，融合法结合基于模型和数据驱动法的优点，提供更精确的预测估计精度，可有效避免系统误差和偶然误差对SOH估计的不利影响，将会成为未来发展趋势。

电池SOH估算技术挑战和未来发展聚焦在如下几个方面。

(1) 为了提高SOH估算的准确性，需要进一步研究电池失效机理和开发高效、准确的参数识别方法。无论基于模型法还是数据驱动法，均要对电池老化机理完整理解基础上建模，或者对全程衰退过程中健康特征的辨识。

(2) 推动基于模型-数据融合驱动的发展，实现变老化工况下电池SOH的在线快速、精确估算。随着云平台和机器学习技术的发展，迁移学习、强化学习、无监督学习等技术在SOH估计方面将有望取得重要突破。

(3) 开发面向工程应用的SOH估算方法和技术。目前的方法多是针对单体电池进行的，而在许多实际应用中，锂离子电池以串并联连接起来以构建满足特定能量和功率要求的电池组，电池组的运行工况比单体电池更加复杂多变，因此需要进一步构建电池组相关的退化模型和预测算法。

(4) 发展新型电池传感技术，通过在电池内外置入化学离子浓度、泄漏气体浓度、压力等新型传感器，获取更多电池监测和检测参数，该技术的发展有利于快速、直接获取和应用SOH的相关参数。

参考文献

ZHONG R, DU C Q.

A review of machine learning state-of-charge and state-of-health estimation algorithms for lithium-ion batteries

[J]. Energy Reports, 2023,9:2993-3021.

[本文引用: 1]

XIAO Y Q, WEN J S, YAO L.

A comprehensive review of the lithium-ion battery state of health prognosis methods combining aging mechanism analysis

[J]. Journal of Energy Storage, 2023,65:107347.

[本文引用: 1]

梁新成, 张勉, 黄国钧, 等.

基于BMS的锂离子电池建模方法综述

[J]. 储能科学与技术, 2020, 9(6):1933-1939.

DOI:10.19799/j.cnki.2095-4239.2020.0166      [本文引用: 1]

电池管理系统(battery management system, BMS)是电动车辆的技术核心，而精确的电池模型是实现BMS的关键。电池模型的精度与材料、环境温度、工作模式、老化程度等密切相关，而在建模时完整地包含上述因素是非常困难的。本文在简单介绍BMS功能和结构的基础上，通过对近几年锂离子电池建模文献的整理，着重介绍了电学特性模型、热模型及电-热耦合模型的建模方法。由于电-热模型综合了其他两种方法的优点，模型相对简单且在实际中使用较多。在此基础上阐述了三种模型在电池内部状态如电池荷电状态(state of charge, SOC)、电池健康状态(state of health, SOH)、温度等参数估计中的应用。特别是SOH的状态估计，除受电流、温度、SOC等因素影响外，还与机械振动及过电势等密切相关。考虑到状态估计变量之间的相互耦合如电池的SOC、内部温度等，故需进一步提高耦合参数的估计精度以确保BMS工作的可靠性。在未来，还需要继续对模型进行降阶，以实现BMS工作的实时性。

LIANG Xincheng, ZHANG Mian, HUANG Guojun, et al.

Review on lithium-ion battery modeling methods based on BMS

[J]. Energy Storage Science and Technology, 2020, 9(6):1933-1939.

DOI:10.19799/j.cnki.2095-4239.2020.0166      [本文引用: 1]

Beset by energy shortage and environmental pollution with the sharp rise in car ownership, electric vehicles (EVs) are currently receiving high praise from people. However, the energy used in EVs must be supplied by hundreds of cells when they are driven for a limited energy density of the lithium ion; as a result, the battery management system (BMS) can be viewed as the core technology for EVs. Unluckily, some parameters cannot be measured directly and are obtained only through model estimation. The appropriate model of a lithium-ion battery is the key to the efficiency, precision, and stability of the BMS. Several factors, including material, ambient temperature, work mode, and aging degree, are well known to be closely related to the lithium-ion battery model; nevertheless, having such elements during modeling is difficult. This study introduces the function and structure of the BMS, enabling the listing of concerned references regarding the battery model in the recent years. Three sorts of model (i.e., electrical characteristic, thermal, and electric-thermal coupling models) are then discussed separately. Although the first and second models can clearly reveal the work mechanism of the lithium-ion battery, the large amount of calculation makes it hard to be accepted in engineering considering the current situation. Adversely, the third model combines the advantages of the two models and is widely used for its relative simplicity. Herein, the applications of such models on internal states, such as state of charge (SOC), state of health (SOH), and inner temperature of battery, are described based on a correlative discussion. The SOC variable of EV is as significant as the oil gauge of the internal combustion engine vehicle; thus, it is relatively mature. The SOH is influenced by the current, temperature, and SOC and is very relevant to mechanical vibration and overpotential. Meanwhile, the internal temperature is vital to the capacity, discharging efficiency, span life, and safety of the lithium-ion battery; therefor, how to maintain the proper temperature is very crucial. Considering the coupling of estimation variables (e.g., SOC and inner temperature variable), the estimation accuracy should be greatly enhanced to ensure the BMS reliability. In the future, the lithium-ion battery model is expected to be simplified continually, thereby enabling the invariable satisfaction of a real-time BMS.

董海斌, 羡学磊, 马建琴, 等.

锰酸锂电池热失控特性研究

[J]. 消防科学与技术, 2022, 41(1):21-25.

[本文引用: 1]

DONG Haibin, XIAN Xuelei, MA Jianqin, et al.

Research on thermal runaway characteristics of lithium manganate battery

[J]. Fire Science and Technology, 2022, 41(1):21-25.

DOI:10.3210/fst.41.21      URL     [本文引用: 1]

薄利明, 郑惠萍, 张世锋, 等.

锂电池健康状态均衡技术综述

[J]. 电测与仪表, 2022,4:11-18.

[本文引用: 1]

BO Liming, ZHENG Huiping, ZHANG Shifeng, et al.

Review on health state equalization technology for lithium batteries

[J]. Electrical Measurement & Instrumentation, 2022,4:11-18.

[本文引用: 1]

TIAN H X, QIN P L, LI K, et al.

A review of the state of health for lithium-ion batteries:Research status and suggestions

[J]. Journal of Cleaner Production, 2020, 261(10):120813.

DOI:10.1016/j.jclepro.2020.120813      URL     [本文引用: 1]

PASTOR-FERNANDEZ C, UDDIN K, CHOUCHELAMANE G H, et al.

A comparison between electrochemical impedance spectroscopy and incremental capacity-differential voltage as Li-ion diagnostic techniques to identify and quantify the effects of degradation modes within battery management systems

[J]. Journal of Power Sources, 2017,360:301-318.

[本文引用: 1]

CHRISTOPH R B, MATTHEW R R, EUAN M, et al.

Degradation diagnostics for lithium ion cells

[J]. Journal of Power Sources, 2017,341:373-386.

[本文引用: 2]

CUI Y Z, DU C Y, YIN G P, et al.

Multi-stress factor model for cycle lifetime prediction of lithium ion batteries with shallow-depth discharge

[J]. Journal of Power Sources, 2015,279:123-132.

[本文引用: 1]

JIANG S D, SONG Z X.

A review on the state of health estimation methods of lead-acid batteries

[J]. Journal of Power Sources, 2022,517:1-18.

[本文引用: 2]

梁培维, 张彦会.

基于欧姆内阻对锂电池健康状态的估算

[J]. 电源技术, 2019, 43(10):1623-1704.

[本文引用: 1]

LIANG Peiwei, ZHANG Yanhui.

Estimation of lithium battery health based on ohmic internal resistance

[J]. Chinese Journal of Power Sources, 2019, 43(10):1623-1704.

[本文引用: 1]

GALEOTTI M, CINÀ L, GIAMMANCO C, et al.

Performance analysis and SOH (state of health) evaluation of lithium polymer batteries through electrochemical impedance spectroscopy

[J]. Energy, 2015,89:678-686.

[本文引用: 1]

XIA F, WANG K G, CHEN J J.

State of health and remaining useful life prediction of lithium-ion batteries based on a disturbance-free incremental capacity and differential voltage

[J]. Journal of Energy Storage, 2023,64:107161.

[本文引用: 2]

LI Y, ABDEL-MONEM M, GOPALAKRISHNAN R, et al.

A quick on-line state of health estimation method for Li-ion battery with incremental capacity curves processed by Gaussian filter

[J]. Journal of Power Sources, 2018,373:40-53.

[本文引用: 2]

ZHENG Y J, OUYANG M G, LI X J, et al.

Recording frequency optimization for massive battery data storage in battery management systems

[J]. Applied Energy, 2016,183:380-389.

[本文引用: 1]

HUANG S, LIU C, SUN H, et al.

State of health estimation of lithium-ion batteries based on the regional frequency

[J]. Journal of Power Sources, 2022,518:230773.

[本文引用: 1]

ZHANG Y, CAI Y X, LIU W, et al.

State of health estimation of lithium-ion batteries based on the regional triangle

[J]. Journal of Energy Storage, 2023,69:107918.

[本文引用: 1]

CHE Y H, HU X S, LIN X K, et al.

Health prognostics for lithium-ion batteries:Mechanisms,methods,and prospects

[J]. Energy & Environmental Science, 2023,16:338-371.

[本文引用: 2]

吴盛军, 袁晓冬, 徐青山, 等.

锂电池健康状态评估综述

[J]. 电源技术, 2017, 41(12):1788-1792.

[本文引用: 1]

WU Shengjun, YUAN Xiaodong, XU Qingshan, et al.

Review on lithium-ion battery health state assessment

[J]. Chinese Journal of Power Sources, 2017, 41(12):1788-1792.

[本文引用: 1]

高仁璟, 吕治强, 赵帅, 等.

基于电化学模型的锂离子电池健康状态估算

[J]. 北京理工大学学报, 2022, 42(9):791-797.

[本文引用: 1]

GAO Renjing, LÜ Zhiqiang, ZHAO Shuai, et al.

Health state estimation of Li-ion batteries based on electrochemical model

[J]. Transactions of Beijing Institute of Technology, 2022, 42(9):791-797.

[本文引用: 1]

武龙星, 庞辉, 晋佳敏, 等.

基于电化学模型的锂离子电池荷电状态估计方法综述

[J]. 电工技术学报, 2022, 37(7):1703-1725.

[本文引用: 1]

WU Longxing, PANG Hui, JIN Jiamin, et al.

A review of SOC estimation methods for lithium-ion batteries based on electrochemical model

[J]. Transactions of China Electrotechnical Society, 2022, 37(7):1703-1725.

[本文引用: 1]

REN L C, ZHU G R, KANG J Q, et al.

An algorithm for state of charge estimation based on a single particle model

[J]. Journal of Energy Storage, 2021, 39(7):102644-102651.

DOI:10.1016/j.est.2021.102644      URL     [本文引用: 1]

TOPAN P A, RAMADAN M N, FATHONI G, et al.

State of charge (SOC) and state of health (SOH) estimation on lithium polymer battery via Kalman filter

[C]// 2016 2nd International Conference on Science and Technology-Computer (ICST), October 27-28,2016,Yogyakarta,Indonesia. IEEE,2016:93-96.

[本文引用: 1]

赵可沦, 江境宏, 邓进, 等.

基于遗忘因子递推最小二乘法的锂电池等效电路模型参数辨识方法

[J]. 电子测量技术, 2022, 45(23):53-58.

[本文引用: 1]

ZHAO Kelun, JIANG Jinghong, DENG Jin, et al.

Parameter identification method of lithium battery equivalent circuit model based on forgetting factor recursive least square

[J]. Electronic Measurement Technology, 2022, 45(23):53-58.

[本文引用: 1]

KIM T, WANG Y, SAHINOGLU Z, et al.

Fast UD factorization based RLS online parameter identification for model-based condition monitoring of lithium-ion batteries

[C]// 2014 American Control Conference,June 04-06,2014,Portland,OR,USA. IEEE,2014:4410-4415.

[本文引用: 1]

孙金磊, 唐传雨, 李磊, 等.

基于状态与模型参数联合估计的老化电池可充入电量估计方法

[J]. 电工技术学报, 2022, 37(22):5886-5898.

[本文引用: 1]

SUN Jinlei, TANG Chuanyu, LI Lei, et al.

An estimation method of rechargeable electric quantity for aging battery based on joint estimation of state and model parameters

[J]. Transactions of China Electrotechnical Society, 2022, 37(22):5886-5898.

[本文引用: 1]

HU X S, CHE Y H, LIN X K, et al.

Battery health prediction using fusion-based feature selection and machine learning

[J]. IEEE Transactions on Transportation Electrification, 2021, 7(2):382-398.

DOI:10.1109/TTE.2020.3017090      URL     [本文引用: 1]

车云弘, 邓忠伟, 李佳承, 等.

基于数据驱动的电池系统泛化SOH估计方法

[J]. 机械工程学报, 2022, 58(20):253-263.

[本文引用: 2]

CHE Yunhong, DENG Zhongwei, LI Jiacheng, et al.

Generalized data-driven SOH estimation method for battery systems

[J]. Journal of Mechanical Engineering, 2022, 58(20):253-263.

[本文引用: 2]

GRANDJEAN L L, ODIO M X, WIDANAGE W D.

Global sensitivity analysis of the single particle lithium-ion battery model with electrolyte

[C]//2019 IEEE Vehicle Power and Propulsion Conference (VPPC),2019:1-7.

[本文引用: 2]

LI J, ADEWUYI K, LOTFI N.

A single particle model with chemical/mechanical degradation physics for lithium ion battery state of health (SOH) estimation

[J]. Applied Energy, 2018,212:178-190.

[本文引用: 1]

刘征宇, 杨昆, 魏自红.

包含液相扩散方程简化的锂离子电池电化学模型

[J]. 物理学报, 2019, 68(9):251-258.

[本文引用: 1]

LIU Zhengyu, YANG Kun, WEI Zihong.

Electrochemical model of lithium ion battery with simplified liquid phase diffusion equation

[J]. Acta Physica Sinica, 2019, 68(9):251-258.

[本文引用: 1]

LV C, LAI Q Z, GE T F.

A lead-acid battery’s remaining useful life prediction by using electrochemical model in the particle filtering framework

[J]. Energy, 2017,124:975-984.

[本文引用: 1]

郭桐, 刘涛, 方德宇, 等.

锂离子电池健康评估研究进展

[J]. 电池工业, 2023, 27(1):48-54.

[本文引用: 1]

GUO Tong, LIU Tao, FANG Deyu, et al.

Research progress in health assessment of lithium-ion batteries

[J]. Chinese Battery Industry, 2023,2023, 27(1):48-54.

[本文引用: 1]

SHRIVASTAVA P, NAIDU P A, SHARMA S, et al.

Review on technological advancement of lithium-ion battery states estimation methods for electric vehicle applications

[J]. Journal of Energy Storage, 2023,64:107159.

[本文引用: 1]

SONG Y C, LIU D T, HOU Y D, et al.

Satellite lithium-ion battery remaining useful life estimation with an iterative updated RVM fused with the KF algorithm

[J]. Chinese Journal of Aeronautics, 2018, 31(1):31-40.

DOI:10.1016/j.cja.2017.11.010      URL     [本文引用: 1]

邓涛, 罗卫兴, 李志飞, 等.

双卡尔曼滤波法估计电动汽车电池健康状态

[J]. 电池, 2018, 48(2):95-99.

[本文引用: 1]

DENG Tao, LUO Weixing, LI Zhifei, et al.

Estimation state of health of electric vehicle battery by dual Kalman filter

[J]. Battery Bimonthly, 2018, 48(2):95-99.

[本文引用: 1]

FANG L L, LI J Q, PENG B, et al.

Online estimation and error analysis of both SOC and SOH of lithium-ion battery based on DEKF method

[J]. Energy Procedia,2019:158:3008-3013.

[本文引用: 1]

BI J, ZHANG T, YU H Y, et al.

State-of-health estimation of lithium-ion battery packs in electric vehicles based on genetic resampling particle filter

[J]. Applied Energy, 2016,182:558-568.

[本文引用: 1]

李鹏, 李立伟, 杨玉新.

基于IBOA-PF的锂电池健康状态预测

[J]. 储能科学与技术, 2021, 10(2):705-713.

DOI:10.19799/j.cnki.2095-4239.2020.0391      [本文引用: 1]

应用传统的粒子滤波(PF)算法估计锂电池健康状态(SOH)时，会出现粒子权值退化和样本贫化而导致预测精度较低的问题。为了解决该问题，本工作提出了基于改进蝴蝶优化算法和粒子滤波(IBOA-PF)的联合算法，在基本蝴蝶优化算法(BOA)的基础上，用混沌数替代固定的切换概率，并引入共生生物搜索的互生阶段，弥补了蝴蝶算法易陷入局部最优和开发能力差的局限性，提高了BOA的收敛速度，再用蝴蝶表示粒子，用蝴蝶向食物移动的过程表示粒子变化为更符合真实后验分布的新采样值。然后基于双指数经验模型和时间指标(TI)构建了非线性系统的状态空间模型，用单纯形法改进高斯牛顿法进行参数拟合，提出了一种基于IBOA-PF的锂电池SOH估计方法。仿真实验结果表明，该方法优于传统PF方法，具有较高的精确度和较好的适应性。

LI Peng, LI Liwei, YANG Yuxin.

Estimation of lithium-ion battery state of health based on IBOA-PF

[J]. Energy Storage Science and Technology, 2021, 10(2):705-713.

DOI:10.19799/j.cnki.2095-4239.2020.0391      [本文引用: 1]

When the traditional particle filter (PF) algorithm is used to estimate the state of health (SOH) of lithium-ion batteries, several problems arise, such as particle weight degeneration and species decrease, leading to lower prediction accuracy. In this paper, a novel hybrid algorithm, the improved butterfly optimization algorithm based on PF (IBOA-PF), is proposed to solve these problems. This algorithm based on the basic butterfly optimization algorithm (BOA) replaces the stable switching probability with the chaotic maps. It uses the mutualism phase of symbiosis organism search to make up for the limitations of the butterfly algorithm (i.e., it easily falls into the local optimum and has poor development ability) and improve the convergence speed of BOA. Butterflies are used to represent particles, and the process of butterflies moving to the food is similar to the change of particles having better values that are more possibly equal to the true values. This paper proposed an SOH estimation method using IBOA-PF for lithium batteries based on the double exponential model and time index (TI), constructed the state-space model of the nonlinear system, used the simplex method to improve the Gauss-Newton method for parameter fitting, and estimated SOH. The simulation results show that this method is superior to the traditional PF method, with higher accuracy and better adaptability.

SCHWUNK S, ARMBRUSTER N, STRAUB S, et al.

Particle filter for state of charge and state of health estimation for lithium-ion phosphate batteries

[J]. Journal of Power Sources, 2013,239:705-710.

[本文引用: 1]

LIU Yuefeng, HE Yingjie, BIAN Haodong, et al.

A review of lithium-ion battery state of charge estimation based on deep learning:Directions for improvement and future trends

[J]. Journal of Energy Storage, 2022,52:104664.

[本文引用: 1]

李建林, 肖珩.

锂离子电池建模现状综述

[J]. 储能科学与技术, 2022, 11(2):697-703.

DOI:10.19799/j.cnki.2095-4239.2021.0450      [本文引用: 1]

简述了我国用于大规模储能的锂离子电池建模技术的最新研究进展。由于储能技术可以起到平抑波动、提高电能质量的作用，所以近年来电网对于储能的需求也逐年增大。大规模储能系统由锂电池组、双向逆变器和电池能量管理系统组成，在双向逆变器和电池能量管理系统有现成可用模型的前提下，建立精确、可靠的锂离子电池模型便成了实现大规模储能工程应用的重点。本文阐述了目前流行的电池建模方法：通过对电池电化学反应过程的模拟形成了电化学模型，虽然精度较高，但是模型复杂，使用时应当对其做适当简化，一般用于电池原理分析；通过对电池外特性不同程度的模拟形成了不同的等效电路模型，虽然不注重对原理的仿真，但是比较适合在工程实践中应用；通过对电池输入输出关系的研究形成了神经网络模型，但是其精度对于数据的数量和质量要求较高；最后总结指出为了更好地实现在电力系统中的应用，应当更加深入地研究锂离子电池反应原理并对其进行方程量化描述，提升模型在不同场景下的应用能力。

LI Jianlin, XIAO Heng.

Review on modeling of lithium-ion battery

[J]. Energy Storage Science and Technology, 2022, 11(2):697-703.

DOI:10.19799/j.cnki.2095-4239.2021.0450      [本文引用: 1]

The latest research on lithium-ion battery modeling technology for large-scale energy storage in China is described briefly. Because energy storage technology can stabilize fluctuations and improve power quality, the energy storage demand in power grids has increased yearly. The large-scale energy storage system comprises a lithium battery pack, bidirectional inverter, and battery energy management system. Assuming the bidirectional inverter and battery energy management system have ready-made models, developing an accurate and reliable lithium-ion battery model has become the focus of applying large-scale energy storage engineering. This study describes current popular battery modeling methods. The electrochemical model is constructed by simulating the battery electrochemical reaction process. Although the accuracy is high, the model is complex; therefore, it should be properly simplified for use. It is typically used for battery principle analysis. Different equivalent circuit models are designed using different simulation degrees of the battery's external characteristics. Although we do not pay attention to simulating the principle, it is more suitable for application in engineering practice. The neural network model is constructed by studying the relationship between battery input and output, but its accuracy requires high quantity and quality data. Finally, to better realize the application in power systems, the reaction principle of lithium-ion batteries should be studied more deeply and described quantitatively to improve the application ability of the model in various scenarios.

徐元中, 曹翰林, 吴铁洲.

基于SA-BP神经网络算法的电池SOH预测

[J]. 电源技术, 2020, 44(3):341-345.

[本文引用: 1]

XU Yuanzhong, CAO Hanlin, WU Tiezhou.

Estimation of SOH for battery based on SA-BP neural network

[J]. Chinese Journal of Power Sources, 2020, 44(3):341-345.

[本文引用: 1]

李文华, 邵方旭, 暴二平, 等.

六自由度振动老化条件下锂离子电池的衰退机理诊断与SOH预测

[J]. 仪器仪表学报, 2021, 41(8):62-69.

[本文引用: 1]

LI Wenhua, SHAO Fangxu, BAO Erping, et al.

Diagnosis of degradation mechanism and SOH prediction of lithium-ion batteries under 6-DOF vibration and aging conditions

[J]. Chinese Journal of Scientific Instrument, 2021, 41(8):62-69.

[本文引用: 1]

徐彬翔, 郑林锋, 黄乙恒, 等.

基于改进最小二乘支持向量机的锂离子电池健康状态快速估计方法

[J]. 电气工程学报, 2022, 17(4):11-19.

[本文引用: 1]

XU Binxiang, ZHENG Linfeng, HUANG Yiheng, et al.

Fast estimating the state of health of lithium-ion batteries based on improved least squares support vector machine

[J]. Journal of Electrical Engineering, 2022, 17(4):11-19.

[本文引用: 1]

陈璐, 于仲安, 熊莹燕.

不同温度下基于PSO-LSSVM的锂电池SOH估计与RUL预测

[J]. 传感器与微系统, 2023, 42(6):141-145.

[本文引用: 1]

CHEN Lu, YU Zhongan, XIONG Yingyan.

SOH estimation and RUL prediction of Li battery based on PSO-LSSVM at different temperatures

[J]. Transducer and Microsystem Technologies, 2023, 42(6):141-145.

[本文引用: 1]

SALKIND A J, FENNIE C, SINGH P, et al.

Determination of state-of-charge and state-of-health of batteries by fuzzy logic methodology

[J]. Journal of Power Sources, 1999,80:293-300.

[本文引用: 1]

HE T T, XU Z P, XIE Q, et al.

A method of battery capacity prediction based on fuzzy logic and neural networks

[J]. Earth and Environmental Science, 2020,558:052015.

[本文引用: 1]

樊欣欣, 陈秀国, 王建宾, 等.

基于模糊逻辑的变电站蓄电池在线健康状态评估

[J]. 电子器件, 2021, 44(1):136-140.

[本文引用: 1]

FAN Xinxin, CHEN Xiuguo, WANG Jianbin, et al.

On-line health assessment of substation battery based on fuzzy logic

[J]. Chinese Journal of Electron Devices, 2021, 44(1):136-140.

[本文引用: 1]

吕佳朋, 史贤俊, 王康.

基于高斯过程回归的电池容量预测模型

[J]. 电子测量技术, 2020, 43(3):43-48.

[本文引用: 1]

LÜ Jiapeng, SHI Xianjun, WANG Kang.

Battery capacity prediction model based on Gaussian process regression

[J]. Electronic Measurement Technology, 2020, 43(3):43-48.

[本文引用: 1]

陈琳, 刘博豪, 丁云辉, 等.

采用粒子群优化和高斯回归实现电池SOH估计

[J]. 汽车工程, 2021, 43(10):1472-1478.

DOI:10.19562/j.chinasae.qcgc.2021.10.008      [本文引用: 1]

为准确估算锂离子电池非线性退化过程中的健康状态(SOH),提出融合自适应变异粒子群优化器和高斯过程回归的AMPSO-GPR算法。首先提取欧姆内阻增量和电压样本熵作为电池退化表征量,然后引入自适应变异粒子群(AMPSO)优化高斯过程回归(GPR)核函数的超参数,构建基于AMPSO-GPR的SOH估算框架,用提取的退化表征量实现SOH估算;最后,通过对比AMPSO-GPR采用不同核函数时SOH估算结果,得到最优核函数。实验结果表明,AMPSO-GPR算法可以有效地估算电池SOH,且最大估算误差不超过2.08%。

CHEN Lin, LIU Bohao, DING Yunhui, et al.

Estimation of battery state-of-health using particle swarm optimization with Gauss process regression

[J]. Automotive Engineering, 2021, 43(10):1472-1478.

[本文引用: 1]

张兴红, 徐翊, 巩泽浩, 等.

融合电化学阻抗与容量增量曲线特征的锂电池健康状态算法研究

[J]. 重庆理工大学学报, 2023, 37(5):265-272.

[本文引用: 1]

ZHANG Xinghong, XU Yi, GONG Zehao, et al.

Algorithm research on health state of a lithium battery by integrating the features of electrochemical impedance and incremental capacity curves

[J]. Journal of Chongqing University of Technology, 2023, 37(5):265-272.

[本文引用: 1]

CHEN Liping, XIE Siqiang, ANTÓNIO M L, et al.

A new SOH estimation method for Lithium-ion batteries based on model-data-fusion

[J]. Energy, 2024,286:129597.

[本文引用: 1]

HE Jiabei, TIAN Yi, WU Lifeng.

A hybrid data-driven method for rapid prediction of lithium-ion battery capacity

[J]. Reliability Engineering and System Safety, 2022,226:108674.

[本文引用: 1]

MA Zeyu, YANG Ruixin, WANG Zhenpo.

A novel data-model fusion state-of-health estimation approach for lithiumion batteries

[J]. Applied Energy, 2019,237:836-847.

[本文引用: 1]

HOU Y K, ZANG Z S, LIU P, et al.

Research on a novel data-driven aging estimation method for battery systems in real-world electric vehicles

[J]. Advances in Mechanical Engineering, 2021, 13(7):1-14.

[本文引用: 1]

王萍, 彭香园, 程泽, 等.

基于数据驱动模型融合的锂离子电池多时间尺度状态联合估计方法

[J]. 汽车工程, 2022, 44(3):362-378.

[本文引用: 1]

WANG Ping, PENG Xiangyuan, CHENG Ze, et al.

A multi-time scale joint state estimation method for lithium-ion batteries based on data-driven model fusion

[J]. Automotive Engineering, 2022, 44(3):362-378.

[本文引用: 1]

崔显, 陈自强.

基于ECM和SGPR的高鲁棒性锂离子电池健康状态估计方法

[J/OL]. 上海交通大学学报:1-23[2023-03-10]. https://doi.org/10.16183/j.cnki.jsjtu.2022.221..

URL     [本文引用: 1]

CUI Xian, CHEN Ziqiang. et al.

A highly robust state of health estimation method of lithium-ion battery based on ECM and SGPR

[J/OL]. Journal of Shanghai Jiaotong University:1-23[2023-03-10]. https://doi.org/10.16183/j.cnki.jsjtu.2022.221..

URL     [本文引用: 1]

CHEN Dan, MENG Jinhao, HUANG Huanyang, et al.

An empirical-data hybrid driven approach for remaining useful life prediction of lithium-ion batteries considering capacity diving

[J]. Energy, 2022,245:123222.

[本文引用: 1]

陈国麟, 姚行艳.

基于CNN-Transformer的锂离子电池健康状态估计

[J]. 重庆工商大学学报, 2024, 41(2):66-73.

[本文引用: 1]

CHEN Guolin, YAO Xingyan.

State of health estimation of lithium-ion battery based on CNN-Transformer

[J]. Journal of Chongqing Technology and Business University, 2024, 41(2):66-73.

[本文引用: 1]

倪祥淦, 何志刚, 胡帅, 等.

基于BI-LSTM神经网络的宽采样频率电池SOH估算

[J]. 车用发动机, 2022(5):44-50.

[本文引用: 1]

NI Xianggan, HE Zhigang, HU Shuai, et al.

Battery SOH estimation with wide sampling frequency based on BI-LSTM neural network

[J]. Vehicle Engine, 2022(5):44-50.

[本文引用: 1]

YU J.

State of health prediction of lithium-ion batteries:Multiscale logic regression and Gaussian process regression ensemble

[J]. Reliability Engineering & System Safety, 2018,174:82-95.

[本文引用: 1]

LIN M Q, WU D G, MENG J H, et al.

A multi-feature-based multi-model fusion method for state of health estimation of lithium-ion batteries

[J]. Journal of Power Sources, 2022,518:230774.

[本文引用: 1]

蔡艳平, 陈万, 苏延召, 等.

锂离子电池剩余寿命预测方法综述

[J]. 电源技术, 2021, 45(5):678-682.

[本文引用: 1]

CAI Yanping, CHEN Wan, SU Yanzhao, et al.

Review of remaining useful life prediction for lithium ion batteries

[J]. Chinese Journal of Power Sources, 2021, 45(5):678-682.

[本文引用: 1]

WEI Zhongbao, LENG Feng, HE Zhongjie, et al.

Online state of charge and state of health estimation for lithium-ion battery based on a data-model fusion method

[J]. Energies, 2018, 11(7):1810-1823.

DOI:10.3390/en11071810      URL     [本文引用: 1]

晏莉琴, 马尚德, 罗英, 等.

锂离子电池快速寿命评价技术与方法

[J]. 上海航天, 2023, 40(1):123-135.

[本文引用: 1]

YAN Liqin, MA Shangde, LUO Ying, et al.

Overview of rapid lifetime evaluation technologies and methods for lithium-ion batteries

[J]. Aerospace Shanghai, 2023, 40(1):123-135.

[本文引用: 1]

HONG Shiding, QIN Chaokui, LAI Xin, et al.

State-of- health estimation and remaining useful life prediction for lithium-ion batteries based on an improved particle filter algorithm

[J]. Journal of Energy Storage, 2023,64:107179.

[本文引用: 1]

王震坡, 王秋诗, 刘鹏, 等.

大数据驱动的动力电池健康状态估计方法综述

[J]. 机械工程学报, 2023, 59(2):151-168.

DOI:10.3901/JME.2023.02.151      [本文引用: 1]

动力电池健康状态估计是电池管理系统关键算法之一，对提高动力电池能量利用效率、降低电池热失控风险，以及动力电池的维保和残值评估具有重要意义。对比分析试验法、模型法、数据驱动法的优势和不足，并以数据驱动方法为核心，分别从动力电池健康状态数据集构建、健康状态特征参数提取、健康状态估计模型三个方面对现阶段健康状态估计方法的理论基础和技术方案进行综述。总结常用的大数据采集方法以及数据预处理方法，明确大数据在健康状态评估中的意义。比较现有健康状态特征提取方法，对其优劣以及适用场景做了分析。阐述不同健康状态估计模型的基本原理，提出模型融合是未来技术发展方向。最后，面向未来大数据实车应用场景，对动力电池健康状态估计方面存在的问题和发展前景进行了总结和展望。

WANG Zhenpo, WANG Qiushi, LIU Peng, et al.

Review on techniques for power battery state of health estimation driven by big data methods

[J]. Journal of Mechanical Engineering, 2023, 59(2):151-168.

DOI:10.3901/JME.2023.02.151      [本文引用: 1]

State of health estimation of power batteries is one of the key algorithms of the battery management systems, which is of great significance for improving power battery energy utilization efficiency, reducing thermal runaway risk, as well as power battery maintenance and residual value evaluation. Comparative analysis has been done on experimental-based, model-based and data-driven methods, and data-driven methods are elaborated from three aspects:dataset construction, health indicators extraction, model establishment. The big data collection methods and data preprocessing methods are summarized. The health indicators extraction methods are compared by their pros and cons and applicable scenarios. The basic principles of different health state estimation models are discussed. The conclusion that model fusion is the direction of future technology development is proposed. Finally, facing the future application scenarios of big data in electric vehicles, the current issue and prospective are depicted.

/

〈 〉