1 引言
随着我国特高压骨干网架的加快建设,综合考虑为地区经济发展提供更多有效的建设用地,以新能源输出为主的西北地区,超特高压输电线路会与配电线路接近段共用走廊运行[1 ⇓ ⇓ ⇓ ⇓ -6 ] 。共用走廊输电线路与配电线路并不是全线并行,而是在某些特殊的山区、线路密集区等土地资源匮乏和电力负荷比较重的区域会存在一定的接近段并行。这时在全线某段区域内750 kV超高压输电线路会非常接近共用走廊的配电线路,两者并行高度与长度不一样的环境之下,必然会存在不容忽视的电能质量影响,对配电线路的安全可靠运行造成巨大隐患,这在国内外尚无先例,也少有文献对此问题进行专门探讨研究。此外,超特高压输电线路在接近段并行区间可能不是完全换位的。不完全换位或者不换位超高压线路可能加剧与配电线路之间的电能质量问题[2 ⇓ ⇓ -5 ] 。
同输电线路电磁环境研究相比,共用走廊的超特高压输电线路对配电线路电能质量的影响相关方面研究较少,工程中的实际问题无相应的解决治理措施[7 ⇓ ⇓ -10 ] 。目前,朱军等[10 ] 通过研究一种共走廊非全线并行架设的高压输电线路中电气量的不平衡度,分析出线路不平衡电流产生的原因及影响因素。中国电力科学研究院吴桂芳等[7 ] 分析了800 kV直流线路、1 000 kV交流线路,提出这类线路并行架设时保证安全可靠的最小接近距离。山东农业大学王冉冉等[8 ] 对特高压交流输电线路下钢架建筑的感应电压和感应电流进行分析和仿真计算。中国电力科学研究院赵永生等[9 ] 通过研究同走廊高压交直流线路,对混合电场进行了分析。
目前国内外针对特高压并行架设的输电线路中一些电磁环境、感应电压、感应电流、混合电场计算方面积累了丰富的经验,如架空输电线路架设距离越小,电压等级越高,混合电场直流分量和离子流密度越小。在超特高压输电线路对共走廊并行运行的配电线路电能质量研究可以借鉴以上经验[11 -12 ] 。
本文采用电磁耦合计算方法,结合电磁场经典理论,分析了共用走廊超高压输电线路对配电线路电能质量的影响,分析了接近段并行超高压输电线路高度、35 kV配电线路长度对配电线路电能质量的容性耦合、感性耦合、阻性耦合等最大综合影响的情况,提出在配电线路上,通过加装屏蔽地线、并联电容器、并联电抗器等综合式治理方案,降低共用走廊超高压输电线路电能质量的影响,提高配电线路抗电磁能力,确保配电线路的可靠高效运行。综合治理方案可为新能源输送密集地区超特高压输电工程建设、变电站选址等提供指导。
2 超高压输电线路与配电线路接近并行段的电磁干扰问题
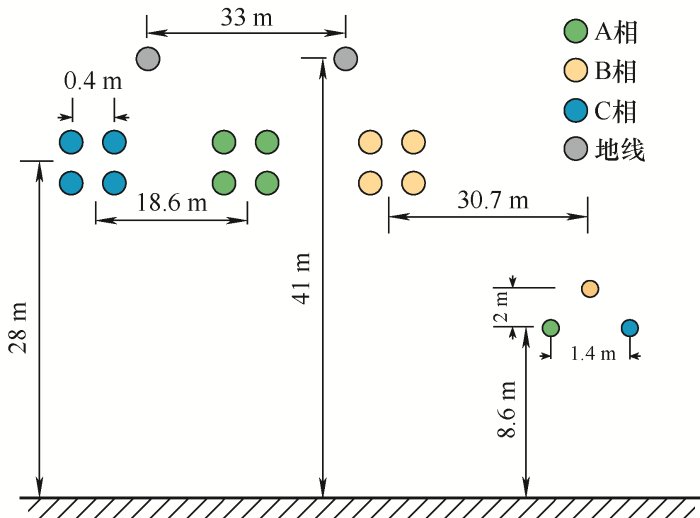
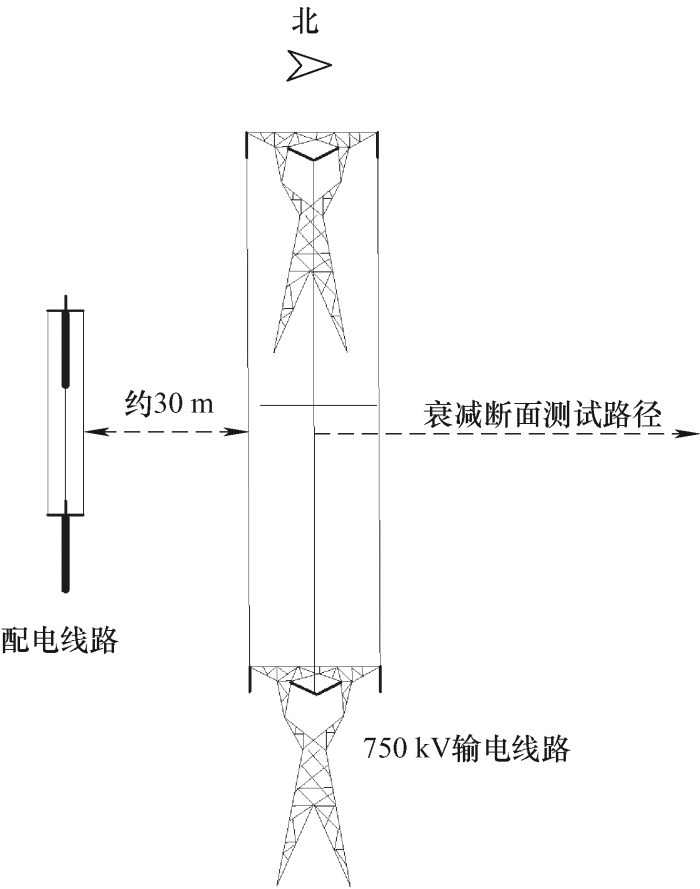
35 kV配电线路与共用走廊的750 kV输电线路密集接近,穿越750 kV同塔四回的输电线路,其线路相对位置示意图如图1 所示。
图1
在同走廊的750 kV超高压输电线路与配电线路之间电磁环境非常复杂,超高压输电线路在复杂环境中长期运行时,因各种因素难免会发生各种短路故障,在接近并行段短路故障的发生概率会增大。在多发短路故障情况中,单相接地短路故障的发生概率较大,因此,单相接地短路故障在线路防护设计中是设计者最主要考虑的问题。目前现有网架系统中安装的保护装置可实现对短路故障快速切除,在短路瞬间产生的零序电流流经输电线路,可对接近段距离并行的配电线路产生电磁感应的影响(感性耦合),同时流经铁塔接地装置可以对其周围产生地电位影响(阻性耦合),当感性耦合和阻性耦合同时叠加产生时,会成为综合性的影响因素。由于线路之间互阻很小,阻性耦合不用考虑。线路并行接近时电磁感应耦合远小于电容耦合[8 ⇓ -10 ] 。
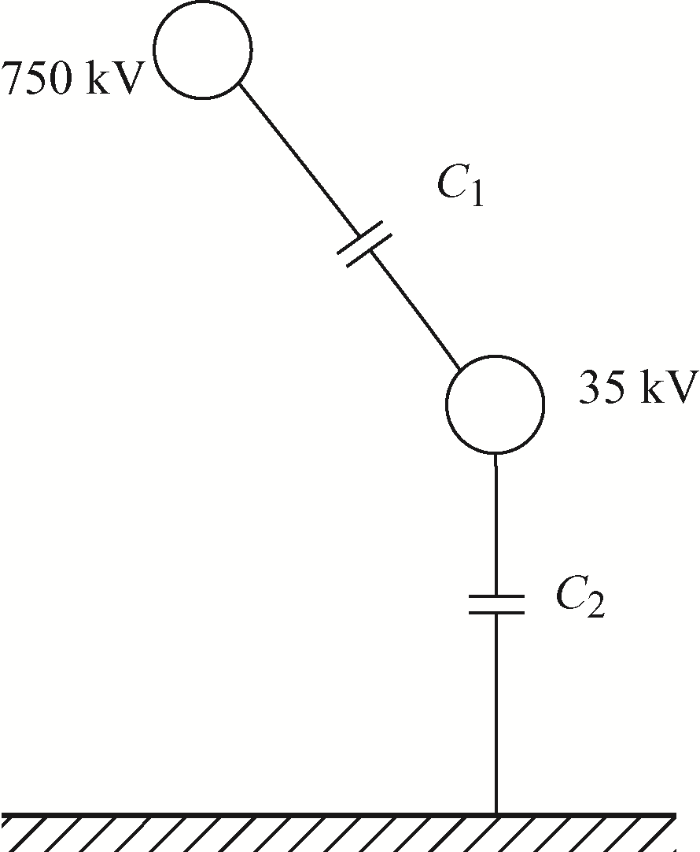
根据电磁场理论计算,容性耦合影响与作用电流及耦合系数相关,耦合的相互作用如图2 所示。750 kV线路通过互容C 1 将电压传递至35 kV线路,35 kV线路对地存在电容C 2 ,因此,35 kV线路上的电压高低取决于电容C 1 与C 2 之间的比值。
图2
3 电磁耦合的计算原理
3.1 输电线路电磁感应计算
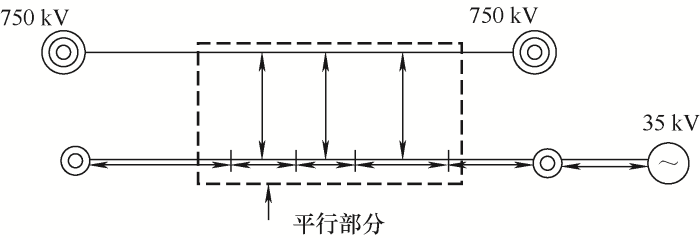
超特高压输电线路的理论模型如图3 所示,该线路模型参数是共用走廊并行运行的750 kV输电线路和配电线路,对于不同的电压等级以及不同的杆塔上架设的输配电线路,通过假设,得到750 kV线路A、B、C三相和配电线路a、b、c三相的自电容和互电容C L [12 ⇓ -14 ]
(1) $\boldsymbol{C}=\left[\begin{array}{c}C_{\mathrm{aa}} C_{\mathrm{ab}} C_{\mathrm{ac}} C_{\mathrm{aA}} C_{\mathrm{aB}} C_{\mathrm{ac}} \\C_{\mathrm{ba}} C_{\mathrm{bb}} C_{\mathrm{bc}} C_{\mathrm{bA}} C_{\mathrm{bB}} C_{\mathrm{bC}} \\C_{\mathrm{ca}} C_{\mathrm{cb}} C_{\mathrm{cc}} C_{\mathrm{cA}} C_{\mathrm{cB}} C_{\mathrm{cC}} \\C_{\mathrm{Aa}} C_{\mathrm{Ab}} C_{\mathrm{Ac}} C_{\mathrm{AA}} C_{\mathrm{AB}} C_{\mathrm{AC}} \\C_{\mathrm{Ba}} C_{\mathrm{Bb}} C_{\mathrm{Bc}} C_{\mathrm{BA}} C_{\mathrm{BB}} C_{\mathrm{BC}} \\C_{\mathrm{Ca}} C_{\mathrm{Cb}} C_{\mathrm{Cc}} C_{\mathrm{CA}} C_{\mathrm{CB}} C_{\mathrm{CC}}\end{array}\right]=\left[\begin{array}{l}C_{1} C_{\mathrm{m}} \\C_{\mathrm{m}} C_{2}\end{array}\right]$
(2) $\boldsymbol{L}=\left[\begin{array}{c}L_{\mathrm{aa}} L_{\mathrm{ab}} L_{\mathrm{ac}} L_{\mathrm{aA}} L_{\mathrm{aB}} L_{\mathrm{aC}} \\L_{\mathrm{ba}} L_{\mathrm{bb}} L_{\mathrm{bc}} L_{\mathrm{bA}} L_{\mathrm{bB}} L_{\mathrm{bC}} \\L_{\mathrm{ca}} L_{\mathrm{cb}} L_{\mathrm{cc}} L_{\mathrm{cA}} L_{\mathrm{cB}} L_{\mathrm{cC}} \\L_{\mathrm{Aa}} L_{\mathrm{Ab}} L_{\mathrm{Ac}} L_{\mathrm{AA}} L_{\mathrm{AB}} L_{\mathrm{AC}} \\L_{\mathrm{Ba}} L_{\mathrm{Bb}} L_{\mathrm{Bc}} L_{\mathrm{BA}} L_{\mathrm{BB}} L_{\mathrm{BC}} \\L_{\mathrm{Ca}} L_{\mathrm{Cb}} L_{\mathrm{Cc}} L_{\mathrm{CA}} L_{\mathrm{CB}} L_{\mathrm{CC}}\end{array}\right]=\left[\begin{array}{l}L_{1} L_{\mathrm{m}} \\L_{\mathrm{m}} L_{2}\end{array}\right]$
式中,A、B、C、a、b、c分别表示750 kV输电线路Ⅰ和配电线路Ⅱ的各个相别。
图3
设${{\dot{U}}_{\text{abc}}}={{\left[ {{{\dot{U}}}_{\text{a}}}{{{\dot{U}}}_{\text{b}}}{{{\dot{U}}}_{c}} \right]}^{\mathrm{T}}}$ ${{\dot{I}}_{\text{abc}}}={{\left[ {{{\dot{I}}}_{\text{a}}}{{{\dot{I}}}_{\text{b}}}{{{\dot{I}}}_{\text{c}}} \right]}^{\mathrm{T}}}$ ${{\dot{U}}_{\text{ABC}}}={{\left[ {{{\dot{U}}}_{\text{A}}}{{{\dot{U}}}_{\text{B}}}{{{\dot{U}}}_{\text{C}}} \right]}^{\mathrm{T}}}$ ${{\dot{I}}_{\text{ABC}}}={{\left[ {{{\dot{I}}}_{\text{A}}}{{{\dot{I}}}_{\text{B}}}{{{\dot{I}}}_{\text{C}}} \right]}^{\mathrm{T}}}$
下面是针对两条输电线路中的一条停电运行的不同状态下的理论分析。
(1) 假设被感应的一条输电输电线路的两端是悬空状态,被感应的线路的感应电压是在电容耦合时发生的,则有
(3) $\left[\begin{array}{c}C_{1} C_{\mathrm{m}} \\C_{\mathrm{m}} C_{2}\end{array}\right]\left[\begin{array}{l}\dot{U}_{\mathrm{abc}} \\\dot{U}_{\mathrm{ABC}}\end{array}\right]=\left[\begin{array}{c}\boldsymbol{Q}_{\mathrm{abc}} \\0\end{array}\right]$
(4) $\left\{ \begin{align} & {{C}_{1}}{{{\dot{U}}}_{\text{abc}}}+{{C}_{\text{m}}}{{{\dot{U}}}_{\text{ABC}}}={{Q}_{\text{abc}}} \\ & {{C}_{\text{m}}}{{{\dot{U}}}_{\text{abc}}}+{{C}_{2}}{{{\dot{U}}}_{\text{ABC}}}=0 \\ \end{align} \right.$
(5) ${{\dot{U}}_{\text{ABC}}}=-C_{2}^{-1}{{C}_{\text{m}}}{{\dot{U}}_{\text{abc}}}$
假设输电线路的一头悬空,$\Delta {{\dot{U}}_{\text{ABC}}}$
(6) $\mathrm{j} \omega\left[\begin{array}{l}L_{1} L_{\mathrm{m}} \\L_{\mathrm{m}} L_{2}\end{array}\right]\left[\begin{array}{c}I_{\mathrm{abc}} \\0\end{array}\right]=\left[\begin{array}{c}\Delta \dot{U}_{\mathrm{abc}} \\\Delta \dot{U}_{\mathrm{ABC}}\end{array}\right]$
(7) $\left\{ \begin{align} & j\omega {{L}_{1}}{{I}_{\text{abc}}}=\Delta {{{\dot{U}}}_{\text{abc}}} \\ & j\omega {{L}_{\text{m}}}{{I}_{\text{abc}}}=\Delta {{{\dot{U}}}_{\text{ABC}}} \\ \end{align} \right.$
(8) ${{\dot{U}}_{\text{ABC}}}=j\omega {{L}_{\text{m}}}{{I}_{\text{abc}}}$
(2) 当被感应输电线路的两端接地,此时在感应输电线路上有感应电流流过,可以得出
(9) $\mathrm{j} \omega\left[\begin{array}{l}L_{1} L_{\mathrm{m}} \\L_{\mathrm{m}} L_{2}\end{array}\right]\left[\begin{array}{l}I_{\mathrm{abc}} \\I_{\mathrm{ABC}}\end{array}\right]=\left[\begin{array}{l}\Delta \dot{U}_{\mathrm{abc}} \\\Delta \dot{U}_{\mathrm{ABC}}\end{array}\right]$
(10) ${{I}_{\text{ABC}}}=-L_{2}^{-1}{{L}_{\text{m}}}{{I}_{\text{abc}}}$
根据初步计算,输送功率为900 MW时,式(1)~(5)的计算结果如表1 所示,引起电压升高的关键原因是电容耦合,超高压输电线路通过互容将电压传递至配电线路,由于配电线路中性点不接地,必然造成零序电压升高。同时,由于配电线路没有换位,三相对地电容不平衡,加剧了零序电压升高的情况。
3.2 架空地线的磁屏蔽
750 kV超高压输电线路通常在安装时安装架空地线,架空地线可屏蔽部分电磁感应。假设不考虑750 kV输电塔上的分流因素(因铁塔的接地电阻一般都比较大),可简化屏蔽系数的计算过程。当有2根架空地线时,整个线路的平均屏蔽系数为
(11) ${{k}_{j}}=1-\frac{j\omega {{M}_{\text{m}}}}{\frac{2{{R}_{\text{g}}}}{{{l}_{\text{px}}}}+\frac{{{R}_{\text{s}}}}{2}+\frac{j\omega \left( {{L}_{\text{s}}}+{{M}_{\text{ss}}} \right)}{2}}$
式中,M m 为输电线路与架空地线间单位长度互感系数;k j 为屏蔽系数;l px 为架空地线架设长度;R g 为架空地线两端接地电阻;L s 为架空地线单位长度自感系数;R s 为架空地线有效电阻;M ss 为2根架空地线间单位长度互感系数。
因修建改造完成后的输电线路结构一般不变,但可以通过检修时,将架空地线由钢绞线换成良导体导线就能降低架空地线有效电阻,进而降低屏蔽系数。
当架空地线的有效电阻阻值比较小时,架空地线对发生短路的短路点处的入地电流系数和短路点附近的架空地线返流屏蔽效应具有较好的作用,因此可选用相分量模型中广义双侧消去法进行计算。
4 35 kV线路长度和750 kV线路高度变化对感应电压的影响分析
根据相互之间的影响分析,造成超高压输电线路与配电线路之间电能质量影响的因素是配电线路长度与超高压输电线路的高度,本文从两方面进行仿真验证分析。
4.1 35 kV线路长度对感应电压的影响
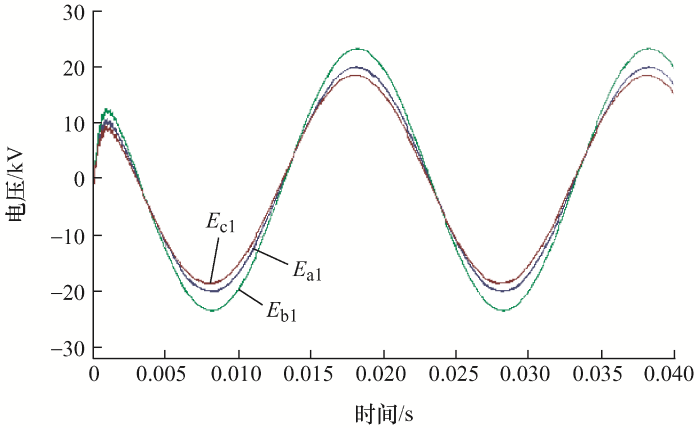
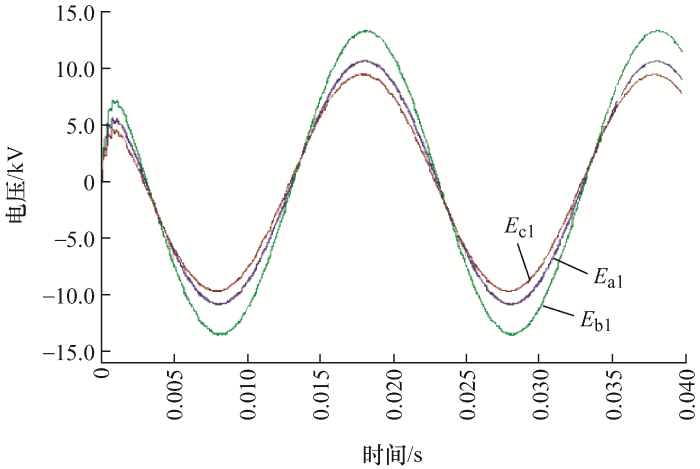
在PSCAD中搭建耦合模型[15 ⇓ -17 ] ,500 kV三相电压源经过900 MV·A升压变为750 kV线路电压,并在此三相末端接入377 Ω匹配电阻消除折反射。设置超高压输电线路与配电线路之间的耦合段长18 km,当配电线路长度为20 km时,线路上三相感应电压波形如图4 所示。
图4
保持耦合段长度为18 km不变,改变配电线路的长度,使得配电线路的长度从20 km变化至50 km(包括配电线路母线上连接的全部线路),线路上感应电压的大小如表2 所示。
由表2 可以看出,随着配电线路长度的增加,线路的电容增加,感应电压随之减小。
4.2 750 kV线路高度变化对35 kV线路感应电压的影响
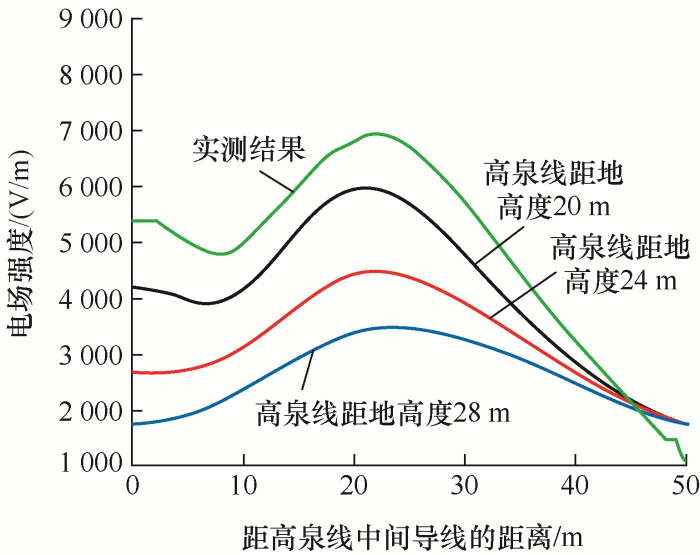
根据计算分析,超高压输电线路高度会影响配电线路上的感应电压大小,由于线路弧垂影响,超高压输电线路最低点离地面高度约为20 m,考虑弧垂后线路平均距地高度为28 m,因此计算了超高压输电线路高度分别为20 m、24 m和28 m时,配电线路静电感应电压大小(本文计算电压都指有效值),如表3 所示。
750 kV输电线路档距与35 kV配电线路档距之间的间距为30 m,此处750 kV超高压输电线路弧垂处线高约20.3 m,35 kV配电线路弧垂处线高约8.8 m。利用工频电磁场测试仪在此区段对750 kV超高压输电线路及两线路之间30 m内的工频电磁场进行测试,测点平面布置图如图5 所示。现场实测数据如表4 所示。
图5
图5
超高压输电线路与配电线路间距30 m区段测点
将表3 的计算数据与表4 的实测数据进行对比,比对结果如图6 所示。
图6
由图6 可以看出,随着超高压输电线路距离地面高度的减小,计算结果与实测结果之间的差别越来越小。
5 在超高压输电线路与配电线路上采取的组合式防护方案
根据图2 可知,当C 1 减小或者C 2 增大时,配电线路上的感应电压将会减小。综合考虑经济性,解决配电线路电能质量问题主要从增大C 2 来开展。
5.1 35 kV导线上方加装屏蔽线
线路三相的静电感应电压的大小与对地高度近似呈正比关系,因此降低三相线路的静电感应电压的最简单方法即为降低配电线路的高度[18 ] ,将三相线路的对地高度都降低至5 m,三相导线呈水平排列,同时增加屏蔽地线。
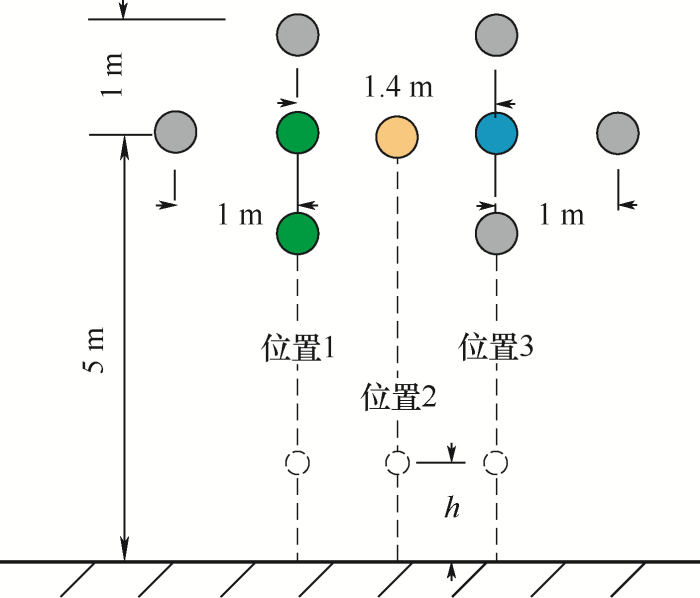
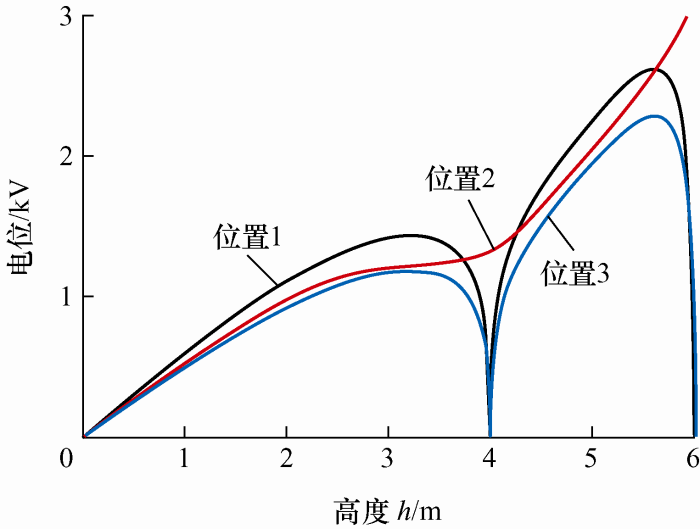
取六根避雷线,在导线周围排布,在导线的上方、两侧和下方分别布置两根避雷线,分别距导线1 m,如图7 所示。三相导线下方的位置1、位置2、位置3的电位随着高度的变化如图8 所示。
图7
图8
当配电线路高度分别为5~9 m时,三相静电感应电压的大小如表5 所示。考虑到超高压输电线路与配电线路并非始终平行,按照表5 中数据实施后,真正的零序电压能降低至1 kV以下。
在配电线路上下左右加入六根避雷线后,A、B、C三相电压分别是2.26 kV、2.07 kV和1.95 kV。图8 位置1和位置3的曲线在高度h =4 m时电位降低至0,这是由于此处是下避雷线的位置。
5.2 35 kV线路的末端并联电容器
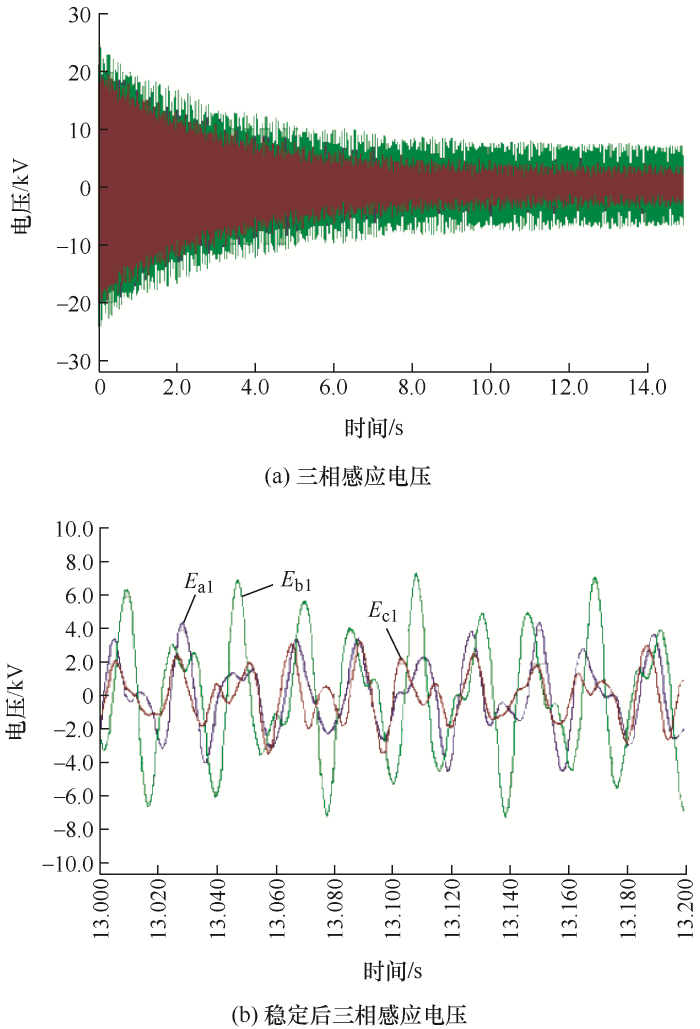
假设配电线路的长度为20 km,与超高压输电线路的耦合长度为18 km。在配电线路末端三相分别并联不同大小的电容,当电容为0.1 μF时,配电线路的感应电压三相半峰值分别为10.736 kV、13.418 kV和9.548 kV,如图9 所示。
图9
同样计算了电容为0.5 μF、1 μF、5 μF时,三相感应电压的半峰值如表6 所示。表6 中的数据反映了变化的趋势,当电容比较大后,电容值与零序电压成反比。
5.3 35 kV线路的末端加装并联电抗器
从电路的角度,为了降低感应电压,只需要减小线路对地电容对应的容抗即可,因此,可以直接在配电线路上并联电抗[19 ] 。
假设配电线路长度为20 km,与超高压输电线路的耦合长度为18 km。在配电线路末端三相分别并联不同大小的电感,通过仿真计算得出,当并联电感为10 H时,配电线路的感应电压三相半峰值分别为5.142 kV、7.697 kV和3.988 kV,三相电压波形如图10 所示。
图10
同理计算了并联1 H、5 H电感时,三相感应电压的半峰值如表7 所示。
由表7 可以看出,配电线路三相电压振荡是由于没有增加匹配电阻,波在线路末端折反射造成。由于电感与线路对地电容之间存在过补偿、欠补偿等问题,因此并联电容在不同运行方式下所需要的大小不一样[20 ] 。针对此论文中的配电线路,应并联5 H的电感。
6 结论
本文针对750 kV超高压输电线路对共用走廊并行配电线路三相电压不平衡的影响进行了分析,并提出了相应的治理措施,主要结论如下所述。
(1) 提出了超高压输电线路与配电线路共用走廊运行时三相电压不平衡计算方法。计算表明引起电压升高的关键原因是电容耦合,超高压输电线路通过互容将电压传递至配电线路,由于配电线路中性点不接地,必然造成零序电压升高。同时,由于配电线路没有换位,三相对地电容不平衡,加剧了零序电压升高的情况。
(2) 针对超高压输电线路与配电线路共走廊运行时的三相不平衡问题,提出了在配电线路加装屏蔽线、末端并联小电容,在配电线路负荷侧并联电容器,在配电线路负荷侧并联电抗器三种解决方案。通过对比分析,可用于解决实际工程中的问题。
(3) 计算表明,在配电线路负荷侧并联电容器,可降低静电感应电压,并联电容值越大,降低零序电压的效果越好。在配电线路上加装屏蔽线、并联电抗器都可以降低线路感应电压,确保线路的正常运行。
参考文献
View Option
[1]
牛浩然 , 谭杰 , 周杰 , 等 . 同塔六回输电线路感应电压与感应电流的计算分析
[J]. 电力学报 , 2019 , 34 (2 ):123 -129 .
[本文引用: 1]
NIU Haoran TAN Jie ZHOU Jie et al. Calculation and analysis of induced voltage and induced current of six circuit transmission lines on the same tower
[J]. Journal of Electric Power , 2019 , 34 (2 ):123 -129 .
[本文引用: 1]
[2]
苏超 , 刘振声 , 李黎 , 等 . 220 kV 架空输电线路下工频电场的电磁感应仿真分析
[J]. 广东电力 , 2018 , 31 (1 ):106 -112 .
[本文引用: 2]
SU Chao LIU Zhensheng LI Li et al. Simulation analysis on electromagnetic induction of power frequency electric field under 220 kV overhead transmission lines
[J]. Guangdong Electric Power , 2018 , 31 (1 ):106 -112 .
[本文引用: 2]
[3]
黄国平 , 黄华斌 . 500 kV/220 kV混压同塔四回输电线路接地开关的改造方案
[J]. 广东电力 , 2021 , 34 (11 ):67 -74 .
[本文引用: 2]
HUANG Guoping HUANG Huabin Transformation plan of grounding switches of 500 kV/220 kV four-loop mixed voltage transmission lines on the same tower
[J]. Guangdong Electric Power , 2021 , 34 (11 ):67 -74 .
[本文引用: 2]
[4]
孙劼 , 金益迥 , 刘光 , 等 . 基于解析法的架空地线感应电流分布特性分析
[J]. 广东电力 , 2021 , 34 (4 ):123 -131 .
[本文引用: 2]
SUN Jie JIN Yijiong LIU Guang et al. Analysis of induction current distribution on overhead ground wires based on analytic method
[J]. Guangdong Electric Power , 2021 , 34 (4 ):123 -131 .
[本文引用: 2]
[5]
熊鑫欣 , 李春亮 , 江子豪 , 等 . 同塔多回线路的感应电压的电路模型与有限元模型的计算及分析
[J]. 广东电力 , 2017 , 30 (4 ):115 -119 .
[本文引用: 2]
XIONG Xinxin LI Chunliang JIANG Zihao et al. Calculation and analysis on circuit model and finite element model of induced voltage of multi-circuit transmission lines on same tower
[J]. Guangdong Electric Power , 2017 , 30 (4 ):115 -119 .
[本文引用: 2]
[6]
聂程 , 郭少锋 , 牛海清 , 等 . 隧道集群敷设高压电缆多物理场电路耦合仿真及其典型运行状态分析
[J]. 广东电力 , 2021 , 34 (2 ):68 -76 .
[本文引用: 1]
NIE Cheng GUO Shaofeng NIU Haiqing et al. Simulation of multi-physical field coupling circuit of high voltage cable cluster laying in tunnel and analysis of typical operating states
[J]. Guangdong Electric Power , 2021 , 34 (2 ):68 -76 .
[本文引用: 1]
[7]
吴桂芳 , 余军 , 郭贤珊 , 等 . ±800 kV直流和1 000 kV交流线路同走廊时的最小接近距离研究
[J]. 中国电力 , 2007 , 40 (12 ):22 -26 .
[本文引用: 2]
WU Guifang YU Jun GUO Xianshan et al. Study on least approaching distances between ±800 kV DC transmission line and 1 000 kV AC transmission line in a hybrid corridor
[J]. Electric Power , 2007 , 40 (12 ):22 -26 .
[本文引用: 2]
[8]
王冉冉 , 徐静 , 李子扬 , 等 . 特高压交流输电线路下钢架建筑的感应电压、电流仿真分析
[J]. 高电压技术 , 2021 , 47 (2 ):724 -731 .
[本文引用: 3]
WANG Ranran XU Jing LI Ziyang et al. Simulation analysis for induced voltage and induced current in the steel frame construction under UHV AC transmission lines
[J]. High Voltage Engineering , 2021 , 47 (2 ):724 -731 .
[本文引用: 3]
[9]
赵永生 , 张文亮 . 同走廊高压交、直流输电线路混合电场分析
[J]. 高电压技术 , 2014 , 40 (3 ):923 -929 .
[本文引用: 3]
ZHAO Yongsheng ZHANG Wenliang Hybrid electric field analysis of HVAC and HVDC transmission lines in one corridor
[J]. High Voltage Engineering , 2014 , 40 (3 ):923 -929 .
[本文引用: 3]
[10]
朱军 , 熊万亮 , 曹晓斌 , 等 . 共用走廊高压输电线路间耦合影响分析
[J]. 华东电力 , 2011 , 39 (12 ):2021 -2025 .
[本文引用: 3]
ZHU Jun XIONG Wanliang CAO Xiaobin et al. Coupling effects among high voltage transmission lines in joint-use corridor
[J]. East China Electric Power , 2011 , 39 (12 ):2021 -2025 .
[本文引用: 3]
[11]
唐伟华 . 500 kV同塔双回输电线路感应电压电流对运维的影响与防控策略 [D]. 广州 : 华南理工大学 , 2020 .
[本文引用: 1]
TANG Weihua Influence of induced voltage and current on operation and maintenance of 500 kV double-circuit transmission lines on the same tower and its prevention and control strategy [D]. Guangzhou : South China University of Technology , 2020 .
[本文引用: 1]
[12]
周文灿 . 架空输电线路感应电压的计算方法研究 [D]. 北京 : 华北电力大学 , 2017 .
[本文引用: 2]
ZHOU Wencan Study on calculation method of induced voltage of overhead transmission line [D]. Beijing : North China Electric Power University , 2017 .
[本文引用: 2]
[13]
DING Hui ZHANG Yi GOLE A M et al. Analysis of coupling effects on overhead VSC-HVDC transmission lines from AC lines with shared right of way
[J]. IEEE Transactions on Power Delivery , 2017 , 25 (4 ):2976 -2986 .
DOI:10.1109/TPWRD.2010.2043373
URL
[本文引用: 1]
[14]
吴勋 , 尹创荣 , 陈冠豪 , 等 . 架空地线与预绞丝端口接触压力的仿真分析
[J]. 广东电力 , 2019 , 32 (11 ):151 -156 .
[本文引用: 1]
WU Xun YIN Chuangrong CHEN Guanhao et al. Simulation analysis of contact pressure between overhead ground wire and preformed armor rod port
[J]. Guangdong Electric Power , 2019 , 32 (11 ):151 -156 .
[本文引用: 1]
[15]
TANG Jian ZENG Rong MA Hongbin et al. Analysis of electromagnetic interference on DC line from parallel AC line in close proximity
[J]. IEEE Transactions on Power Delivery , 2018 , 22 (4 ):2401 -2408 .
DOI:10.1109/TPWRD.2007.905334
URL
[本文引用: 1]
[16]
范松海 , 谢彦斌 , 刘益岑 , 等 . 逐塔接地条件下OPGW地线取能方法研究
[J]. 高压电器 , 2017 , 53 (11 ):141 -145 .
[本文引用: 1]
FAN Songhai XIE Yanbin LIU Yicen et al. Study on power tapping method from optical power ground wire grounded to each tower of transmission line
[J]. High Voltage Apparatus , 2017 , 53 (11 ):141 -145 .
[本文引用: 1]
[17]
邓元实 , 范松海 , 龚奕宇 , 等 . 500 kV架空地线与OPGW绝缘化改造后感应电压研究
[J]. 电磁避雷器 , 2020 , 298 (6 ):21 -27 .
[本文引用: 1]
DENG Yuanshi FAN Songhai GONG Yiyu et al. Study on induced voltage after insulation reconstruction of 500 kV transmission line overhead ground wire and OPGW
[J]. Insulators and Surge Arresters , 2020 , 298 (6 ):21 -27 .
[本文引用: 1]
[18]
史志强 , 邹德华 , 俞乾 , 等 . 750 kV同塔双回输电线路感应电压和电流的研究
[J]. 高压电器 , 2018 , 54 (8 ):120 -126 .
[本文引用: 1]
SHI Zhiqiang ZOU Dehua YU Qian et al. Study on the induced voltage and current on the 750 kV double circuit transmission line on the same tower
[J]. High Voltage Apparatus , 2018 , 54 (8 ):120 -136 .
[本文引用: 1]
[19]
STEVEN C C RAYMOND P C 工程数值方法 [M]. 北京 : 清华大学出版社 , 2010 .
[本文引用: 1]
STEVEN C C RAYMOND P C Numerical methods for engineers [M]. Beijing : Tsinghua University Press , 2010 .
[本文引用: 1]
[20]
王长清 . 现代计算电磁学基础 [M]. 北京 : 北京大学出版社 , 2005 .
[本文引用: 1]
WANG Changqing Fundamentals of modern computational electromagnetics [M]. Beijing : Peking University Press , 2005 .
[本文引用: 1]
同塔六回输电线路感应电压与感应电流的计算分析
1
2019
... 随着我国特高压骨干网架的加快建设,综合考虑为地区经济发展提供更多有效的建设用地,以新能源输出为主的西北地区,超特高压输电线路会与配电线路接近段共用走廊运行[1 ⇓ ⇓ ⇓ ⇓ -6 ] .共用走廊输电线路与配电线路并不是全线并行,而是在某些特殊的山区、线路密集区等土地资源匮乏和电力负荷比较重的区域会存在一定的接近段并行.这时在全线某段区域内750 kV超高压输电线路会非常接近共用走廊的配电线路,两者并行高度与长度不一样的环境之下,必然会存在不容忽视的电能质量影响,对配电线路的安全可靠运行造成巨大隐患,这在国内外尚无先例,也少有文献对此问题进行专门探讨研究.此外,超特高压输电线路在接近段并行区间可能不是完全换位的.不完全换位或者不换位超高压线路可能加剧与配电线路之间的电能质量问题[2 ⇓ ⇓ -5 ] . ...
Calculation and analysis of induced voltage and induced current of six circuit transmission lines on the same tower
1
2019
... 随着我国特高压骨干网架的加快建设,综合考虑为地区经济发展提供更多有效的建设用地,以新能源输出为主的西北地区,超特高压输电线路会与配电线路接近段共用走廊运行[1 ⇓ ⇓ ⇓ ⇓ -6 ] .共用走廊输电线路与配电线路并不是全线并行,而是在某些特殊的山区、线路密集区等土地资源匮乏和电力负荷比较重的区域会存在一定的接近段并行.这时在全线某段区域内750 kV超高压输电线路会非常接近共用走廊的配电线路,两者并行高度与长度不一样的环境之下,必然会存在不容忽视的电能质量影响,对配电线路的安全可靠运行造成巨大隐患,这在国内外尚无先例,也少有文献对此问题进行专门探讨研究.此外,超特高压输电线路在接近段并行区间可能不是完全换位的.不完全换位或者不换位超高压线路可能加剧与配电线路之间的电能质量问题[2 ⇓ ⇓ -5 ] . ...
220 kV 架空输电线路下工频电场的电磁感应仿真分析
2
2018
... 随着我国特高压骨干网架的加快建设,综合考虑为地区经济发展提供更多有效的建设用地,以新能源输出为主的西北地区,超特高压输电线路会与配电线路接近段共用走廊运行[1 ⇓ ⇓ ⇓ ⇓ -6 ] .共用走廊输电线路与配电线路并不是全线并行,而是在某些特殊的山区、线路密集区等土地资源匮乏和电力负荷比较重的区域会存在一定的接近段并行.这时在全线某段区域内750 kV超高压输电线路会非常接近共用走廊的配电线路,两者并行高度与长度不一样的环境之下,必然会存在不容忽视的电能质量影响,对配电线路的安全可靠运行造成巨大隐患,这在国内外尚无先例,也少有文献对此问题进行专门探讨研究.此外,超特高压输电线路在接近段并行区间可能不是完全换位的.不完全换位或者不换位超高压线路可能加剧与配电线路之间的电能质量问题[2 ⇓ ⇓ -5 ] . ...
... [2 ⇓ ⇓ -5 ]. ...
Simulation analysis on electromagnetic induction of power frequency electric field under 220 kV overhead transmission lines
2
2018
... 随着我国特高压骨干网架的加快建设,综合考虑为地区经济发展提供更多有效的建设用地,以新能源输出为主的西北地区,超特高压输电线路会与配电线路接近段共用走廊运行[1 ⇓ ⇓ ⇓ ⇓ -6 ] .共用走廊输电线路与配电线路并不是全线并行,而是在某些特殊的山区、线路密集区等土地资源匮乏和电力负荷比较重的区域会存在一定的接近段并行.这时在全线某段区域内750 kV超高压输电线路会非常接近共用走廊的配电线路,两者并行高度与长度不一样的环境之下,必然会存在不容忽视的电能质量影响,对配电线路的安全可靠运行造成巨大隐患,这在国内外尚无先例,也少有文献对此问题进行专门探讨研究.此外,超特高压输电线路在接近段并行区间可能不是完全换位的.不完全换位或者不换位超高压线路可能加剧与配电线路之间的电能质量问题[2 ⇓ ⇓ -5 ] . ...
... [2 ⇓ ⇓ -5 ]. ...
500 kV/220 kV混压同塔四回输电线路接地开关的改造方案
2
2021
... 随着我国特高压骨干网架的加快建设,综合考虑为地区经济发展提供更多有效的建设用地,以新能源输出为主的西北地区,超特高压输电线路会与配电线路接近段共用走廊运行[1 ⇓ ⇓ ⇓ ⇓ -6 ] .共用走廊输电线路与配电线路并不是全线并行,而是在某些特殊的山区、线路密集区等土地资源匮乏和电力负荷比较重的区域会存在一定的接近段并行.这时在全线某段区域内750 kV超高压输电线路会非常接近共用走廊的配电线路,两者并行高度与长度不一样的环境之下,必然会存在不容忽视的电能质量影响,对配电线路的安全可靠运行造成巨大隐患,这在国内外尚无先例,也少有文献对此问题进行专门探讨研究.此外,超特高压输电线路在接近段并行区间可能不是完全换位的.不完全换位或者不换位超高压线路可能加剧与配电线路之间的电能质量问题[2 ⇓ ⇓ -5 ] . ...
... ⇓ ⇓ -5 ]. ...
Transformation plan of grounding switches of 500 kV/220 kV four-loop mixed voltage transmission lines on the same tower
2
2021
... 随着我国特高压骨干网架的加快建设,综合考虑为地区经济发展提供更多有效的建设用地,以新能源输出为主的西北地区,超特高压输电线路会与配电线路接近段共用走廊运行[1 ⇓ ⇓ ⇓ ⇓ -6 ] .共用走廊输电线路与配电线路并不是全线并行,而是在某些特殊的山区、线路密集区等土地资源匮乏和电力负荷比较重的区域会存在一定的接近段并行.这时在全线某段区域内750 kV超高压输电线路会非常接近共用走廊的配电线路,两者并行高度与长度不一样的环境之下,必然会存在不容忽视的电能质量影响,对配电线路的安全可靠运行造成巨大隐患,这在国内外尚无先例,也少有文献对此问题进行专门探讨研究.此外,超特高压输电线路在接近段并行区间可能不是完全换位的.不完全换位或者不换位超高压线路可能加剧与配电线路之间的电能质量问题[2 ⇓ ⇓ -5 ] . ...
... ⇓ ⇓ -5 ]. ...
基于解析法的架空地线感应电流分布特性分析
2
2021
... 随着我国特高压骨干网架的加快建设,综合考虑为地区经济发展提供更多有效的建设用地,以新能源输出为主的西北地区,超特高压输电线路会与配电线路接近段共用走廊运行[1 ⇓ ⇓ ⇓ ⇓ -6 ] .共用走廊输电线路与配电线路并不是全线并行,而是在某些特殊的山区、线路密集区等土地资源匮乏和电力负荷比较重的区域会存在一定的接近段并行.这时在全线某段区域内750 kV超高压输电线路会非常接近共用走廊的配电线路,两者并行高度与长度不一样的环境之下,必然会存在不容忽视的电能质量影响,对配电线路的安全可靠运行造成巨大隐患,这在国内外尚无先例,也少有文献对此问题进行专门探讨研究.此外,超特高压输电线路在接近段并行区间可能不是完全换位的.不完全换位或者不换位超高压线路可能加剧与配电线路之间的电能质量问题[2 ⇓ ⇓ -5 ] . ...
... ⇓ -5 ]. ...
Analysis of induction current distribution on overhead ground wires based on analytic method
2
2021
... 随着我国特高压骨干网架的加快建设,综合考虑为地区经济发展提供更多有效的建设用地,以新能源输出为主的西北地区,超特高压输电线路会与配电线路接近段共用走廊运行[1 ⇓ ⇓ ⇓ ⇓ -6 ] .共用走廊输电线路与配电线路并不是全线并行,而是在某些特殊的山区、线路密集区等土地资源匮乏和电力负荷比较重的区域会存在一定的接近段并行.这时在全线某段区域内750 kV超高压输电线路会非常接近共用走廊的配电线路,两者并行高度与长度不一样的环境之下,必然会存在不容忽视的电能质量影响,对配电线路的安全可靠运行造成巨大隐患,这在国内外尚无先例,也少有文献对此问题进行专门探讨研究.此外,超特高压输电线路在接近段并行区间可能不是完全换位的.不完全换位或者不换位超高压线路可能加剧与配电线路之间的电能质量问题[2 ⇓ ⇓ -5 ] . ...
... ⇓ -5 ]. ...
同塔多回线路的感应电压的电路模型与有限元模型的计算及分析
2
2017
... 随着我国特高压骨干网架的加快建设,综合考虑为地区经济发展提供更多有效的建设用地,以新能源输出为主的西北地区,超特高压输电线路会与配电线路接近段共用走廊运行[1 ⇓ ⇓ ⇓ ⇓ -6 ] .共用走廊输电线路与配电线路并不是全线并行,而是在某些特殊的山区、线路密集区等土地资源匮乏和电力负荷比较重的区域会存在一定的接近段并行.这时在全线某段区域内750 kV超高压输电线路会非常接近共用走廊的配电线路,两者并行高度与长度不一样的环境之下,必然会存在不容忽视的电能质量影响,对配电线路的安全可靠运行造成巨大隐患,这在国内外尚无先例,也少有文献对此问题进行专门探讨研究.此外,超特高压输电线路在接近段并行区间可能不是完全换位的.不完全换位或者不换位超高压线路可能加剧与配电线路之间的电能质量问题[2 ⇓ ⇓ -5 ] . ...
... -5 ]. ...
Calculation and analysis on circuit model and finite element model of induced voltage of multi-circuit transmission lines on same tower
2
2017
... 随着我国特高压骨干网架的加快建设,综合考虑为地区经济发展提供更多有效的建设用地,以新能源输出为主的西北地区,超特高压输电线路会与配电线路接近段共用走廊运行[1 ⇓ ⇓ ⇓ ⇓ -6 ] .共用走廊输电线路与配电线路并不是全线并行,而是在某些特殊的山区、线路密集区等土地资源匮乏和电力负荷比较重的区域会存在一定的接近段并行.这时在全线某段区域内750 kV超高压输电线路会非常接近共用走廊的配电线路,两者并行高度与长度不一样的环境之下,必然会存在不容忽视的电能质量影响,对配电线路的安全可靠运行造成巨大隐患,这在国内外尚无先例,也少有文献对此问题进行专门探讨研究.此外,超特高压输电线路在接近段并行区间可能不是完全换位的.不完全换位或者不换位超高压线路可能加剧与配电线路之间的电能质量问题[2 ⇓ ⇓ -5 ] . ...
... -5 ]. ...
隧道集群敷设高压电缆多物理场电路耦合仿真及其典型运行状态分析
1
2021
... 随着我国特高压骨干网架的加快建设,综合考虑为地区经济发展提供更多有效的建设用地,以新能源输出为主的西北地区,超特高压输电线路会与配电线路接近段共用走廊运行[1 ⇓ ⇓ ⇓ ⇓ -6 ] .共用走廊输电线路与配电线路并不是全线并行,而是在某些特殊的山区、线路密集区等土地资源匮乏和电力负荷比较重的区域会存在一定的接近段并行.这时在全线某段区域内750 kV超高压输电线路会非常接近共用走廊的配电线路,两者并行高度与长度不一样的环境之下,必然会存在不容忽视的电能质量影响,对配电线路的安全可靠运行造成巨大隐患,这在国内外尚无先例,也少有文献对此问题进行专门探讨研究.此外,超特高压输电线路在接近段并行区间可能不是完全换位的.不完全换位或者不换位超高压线路可能加剧与配电线路之间的电能质量问题[2 ⇓ ⇓ -5 ] . ...
Simulation of multi-physical field coupling circuit of high voltage cable cluster laying in tunnel and analysis of typical operating states
1
2021
... 随着我国特高压骨干网架的加快建设,综合考虑为地区经济发展提供更多有效的建设用地,以新能源输出为主的西北地区,超特高压输电线路会与配电线路接近段共用走廊运行[1 ⇓ ⇓ ⇓ ⇓ -6 ] .共用走廊输电线路与配电线路并不是全线并行,而是在某些特殊的山区、线路密集区等土地资源匮乏和电力负荷比较重的区域会存在一定的接近段并行.这时在全线某段区域内750 kV超高压输电线路会非常接近共用走廊的配电线路,两者并行高度与长度不一样的环境之下,必然会存在不容忽视的电能质量影响,对配电线路的安全可靠运行造成巨大隐患,这在国内外尚无先例,也少有文献对此问题进行专门探讨研究.此外,超特高压输电线路在接近段并行区间可能不是完全换位的.不完全换位或者不换位超高压线路可能加剧与配电线路之间的电能质量问题[2 ⇓ ⇓ -5 ] . ...
±800 kV直流和1 000 kV交流线路同走廊时的最小接近距离研究
2
2007
... 同输电线路电磁环境研究相比,共用走廊的超特高压输电线路对配电线路电能质量的影响相关方面研究较少,工程中的实际问题无相应的解决治理措施[7 ⇓ ⇓ -10 ] .目前,朱军等[10 ] 通过研究一种共走廊非全线并行架设的高压输电线路中电气量的不平衡度,分析出线路不平衡电流产生的原因及影响因素.中国电力科学研究院吴桂芳等[7 ] 分析了800 kV直流线路、1 000 kV交流线路,提出这类线路并行架设时保证安全可靠的最小接近距离.山东农业大学王冉冉等[8 ] 对特高压交流输电线路下钢架建筑的感应电压和感应电流进行分析和仿真计算.中国电力科学研究院赵永生等[9 ] 通过研究同走廊高压交直流线路,对混合电场进行了分析. ...
... [7 ]分析了800 kV直流线路、1 000 kV交流线路,提出这类线路并行架设时保证安全可靠的最小接近距离.山东农业大学王冉冉等[8 ] 对特高压交流输电线路下钢架建筑的感应电压和感应电流进行分析和仿真计算.中国电力科学研究院赵永生等[9 ] 通过研究同走廊高压交直流线路,对混合电场进行了分析. ...
Study on least approaching distances between ±800 kV DC transmission line and 1 000 kV AC transmission line in a hybrid corridor
2
2007
... 同输电线路电磁环境研究相比,共用走廊的超特高压输电线路对配电线路电能质量的影响相关方面研究较少,工程中的实际问题无相应的解决治理措施[7 ⇓ ⇓ -10 ] .目前,朱军等[10 ] 通过研究一种共走廊非全线并行架设的高压输电线路中电气量的不平衡度,分析出线路不平衡电流产生的原因及影响因素.中国电力科学研究院吴桂芳等[7 ] 分析了800 kV直流线路、1 000 kV交流线路,提出这类线路并行架设时保证安全可靠的最小接近距离.山东农业大学王冉冉等[8 ] 对特高压交流输电线路下钢架建筑的感应电压和感应电流进行分析和仿真计算.中国电力科学研究院赵永生等[9 ] 通过研究同走廊高压交直流线路,对混合电场进行了分析. ...
... [7 ]分析了800 kV直流线路、1 000 kV交流线路,提出这类线路并行架设时保证安全可靠的最小接近距离.山东农业大学王冉冉等[8 ] 对特高压交流输电线路下钢架建筑的感应电压和感应电流进行分析和仿真计算.中国电力科学研究院赵永生等[9 ] 通过研究同走廊高压交直流线路,对混合电场进行了分析. ...
特高压交流输电线路下钢架建筑的感应电压、电流仿真分析
3
2021
... 同输电线路电磁环境研究相比,共用走廊的超特高压输电线路对配电线路电能质量的影响相关方面研究较少,工程中的实际问题无相应的解决治理措施[7 ⇓ ⇓ -10 ] .目前,朱军等[10 ] 通过研究一种共走廊非全线并行架设的高压输电线路中电气量的不平衡度,分析出线路不平衡电流产生的原因及影响因素.中国电力科学研究院吴桂芳等[7 ] 分析了800 kV直流线路、1 000 kV交流线路,提出这类线路并行架设时保证安全可靠的最小接近距离.山东农业大学王冉冉等[8 ] 对特高压交流输电线路下钢架建筑的感应电压和感应电流进行分析和仿真计算.中国电力科学研究院赵永生等[9 ] 通过研究同走廊高压交直流线路,对混合电场进行了分析. ...
... [8 ]对特高压交流输电线路下钢架建筑的感应电压和感应电流进行分析和仿真计算.中国电力科学研究院赵永生等[9 ] 通过研究同走廊高压交直流线路,对混合电场进行了分析. ...
... 在同走廊的750 kV超高压输电线路与配电线路之间电磁环境非常复杂,超高压输电线路在复杂环境中长期运行时,因各种因素难免会发生各种短路故障,在接近并行段短路故障的发生概率会增大.在多发短路故障情况中,单相接地短路故障的发生概率较大,因此,单相接地短路故障在线路防护设计中是设计者最主要考虑的问题.目前现有网架系统中安装的保护装置可实现对短路故障快速切除,在短路瞬间产生的零序电流流经输电线路,可对接近段距离并行的配电线路产生电磁感应的影响(感性耦合),同时流经铁塔接地装置可以对其周围产生地电位影响(阻性耦合),当感性耦合和阻性耦合同时叠加产生时,会成为综合性的影响因素.由于线路之间互阻很小,阻性耦合不用考虑.线路并行接近时电磁感应耦合远小于电容耦合[8 ⇓ -10 ] . ...
Simulation analysis for induced voltage and induced current in the steel frame construction under UHV AC transmission lines
3
2021
... 同输电线路电磁环境研究相比,共用走廊的超特高压输电线路对配电线路电能质量的影响相关方面研究较少,工程中的实际问题无相应的解决治理措施[7 ⇓ ⇓ -10 ] .目前,朱军等[10 ] 通过研究一种共走廊非全线并行架设的高压输电线路中电气量的不平衡度,分析出线路不平衡电流产生的原因及影响因素.中国电力科学研究院吴桂芳等[7 ] 分析了800 kV直流线路、1 000 kV交流线路,提出这类线路并行架设时保证安全可靠的最小接近距离.山东农业大学王冉冉等[8 ] 对特高压交流输电线路下钢架建筑的感应电压和感应电流进行分析和仿真计算.中国电力科学研究院赵永生等[9 ] 通过研究同走廊高压交直流线路,对混合电场进行了分析. ...
... [8 ]对特高压交流输电线路下钢架建筑的感应电压和感应电流进行分析和仿真计算.中国电力科学研究院赵永生等[9 ] 通过研究同走廊高压交直流线路,对混合电场进行了分析. ...
... 在同走廊的750 kV超高压输电线路与配电线路之间电磁环境非常复杂,超高压输电线路在复杂环境中长期运行时,因各种因素难免会发生各种短路故障,在接近并行段短路故障的发生概率会增大.在多发短路故障情况中,单相接地短路故障的发生概率较大,因此,单相接地短路故障在线路防护设计中是设计者最主要考虑的问题.目前现有网架系统中安装的保护装置可实现对短路故障快速切除,在短路瞬间产生的零序电流流经输电线路,可对接近段距离并行的配电线路产生电磁感应的影响(感性耦合),同时流经铁塔接地装置可以对其周围产生地电位影响(阻性耦合),当感性耦合和阻性耦合同时叠加产生时,会成为综合性的影响因素.由于线路之间互阻很小,阻性耦合不用考虑.线路并行接近时电磁感应耦合远小于电容耦合[8 ⇓ -10 ] . ...
同走廊高压交、直流输电线路混合电场分析
3
2014
... 同输电线路电磁环境研究相比,共用走廊的超特高压输电线路对配电线路电能质量的影响相关方面研究较少,工程中的实际问题无相应的解决治理措施[7 ⇓ ⇓ -10 ] .目前,朱军等[10 ] 通过研究一种共走廊非全线并行架设的高压输电线路中电气量的不平衡度,分析出线路不平衡电流产生的原因及影响因素.中国电力科学研究院吴桂芳等[7 ] 分析了800 kV直流线路、1 000 kV交流线路,提出这类线路并行架设时保证安全可靠的最小接近距离.山东农业大学王冉冉等[8 ] 对特高压交流输电线路下钢架建筑的感应电压和感应电流进行分析和仿真计算.中国电力科学研究院赵永生等[9 ] 通过研究同走廊高压交直流线路,对混合电场进行了分析. ...
... [9 ]通过研究同走廊高压交直流线路,对混合电场进行了分析. ...
... 在同走廊的750 kV超高压输电线路与配电线路之间电磁环境非常复杂,超高压输电线路在复杂环境中长期运行时,因各种因素难免会发生各种短路故障,在接近并行段短路故障的发生概率会增大.在多发短路故障情况中,单相接地短路故障的发生概率较大,因此,单相接地短路故障在线路防护设计中是设计者最主要考虑的问题.目前现有网架系统中安装的保护装置可实现对短路故障快速切除,在短路瞬间产生的零序电流流经输电线路,可对接近段距离并行的配电线路产生电磁感应的影响(感性耦合),同时流经铁塔接地装置可以对其周围产生地电位影响(阻性耦合),当感性耦合和阻性耦合同时叠加产生时,会成为综合性的影响因素.由于线路之间互阻很小,阻性耦合不用考虑.线路并行接近时电磁感应耦合远小于电容耦合[8 ⇓ -10 ] . ...
Hybrid electric field analysis of HVAC and HVDC transmission lines in one corridor
3
2014
... 同输电线路电磁环境研究相比,共用走廊的超特高压输电线路对配电线路电能质量的影响相关方面研究较少,工程中的实际问题无相应的解决治理措施[7 ⇓ ⇓ -10 ] .目前,朱军等[10 ] 通过研究一种共走廊非全线并行架设的高压输电线路中电气量的不平衡度,分析出线路不平衡电流产生的原因及影响因素.中国电力科学研究院吴桂芳等[7 ] 分析了800 kV直流线路、1 000 kV交流线路,提出这类线路并行架设时保证安全可靠的最小接近距离.山东农业大学王冉冉等[8 ] 对特高压交流输电线路下钢架建筑的感应电压和感应电流进行分析和仿真计算.中国电力科学研究院赵永生等[9 ] 通过研究同走廊高压交直流线路,对混合电场进行了分析. ...
... [9 ]通过研究同走廊高压交直流线路,对混合电场进行了分析. ...
... 在同走廊的750 kV超高压输电线路与配电线路之间电磁环境非常复杂,超高压输电线路在复杂环境中长期运行时,因各种因素难免会发生各种短路故障,在接近并行段短路故障的发生概率会增大.在多发短路故障情况中,单相接地短路故障的发生概率较大,因此,单相接地短路故障在线路防护设计中是设计者最主要考虑的问题.目前现有网架系统中安装的保护装置可实现对短路故障快速切除,在短路瞬间产生的零序电流流经输电线路,可对接近段距离并行的配电线路产生电磁感应的影响(感性耦合),同时流经铁塔接地装置可以对其周围产生地电位影响(阻性耦合),当感性耦合和阻性耦合同时叠加产生时,会成为综合性的影响因素.由于线路之间互阻很小,阻性耦合不用考虑.线路并行接近时电磁感应耦合远小于电容耦合[8 ⇓ -10 ] . ...
共用走廊高压输电线路间耦合影响分析
3
2011
... 同输电线路电磁环境研究相比,共用走廊的超特高压输电线路对配电线路电能质量的影响相关方面研究较少,工程中的实际问题无相应的解决治理措施[7 ⇓ ⇓ -10 ] .目前,朱军等[10 ] 通过研究一种共走廊非全线并行架设的高压输电线路中电气量的不平衡度,分析出线路不平衡电流产生的原因及影响因素.中国电力科学研究院吴桂芳等[7 ] 分析了800 kV直流线路、1 000 kV交流线路,提出这类线路并行架设时保证安全可靠的最小接近距离.山东农业大学王冉冉等[8 ] 对特高压交流输电线路下钢架建筑的感应电压和感应电流进行分析和仿真计算.中国电力科学研究院赵永生等[9 ] 通过研究同走廊高压交直流线路,对混合电场进行了分析. ...
... [10 ]通过研究一种共走廊非全线并行架设的高压输电线路中电气量的不平衡度,分析出线路不平衡电流产生的原因及影响因素.中国电力科学研究院吴桂芳等[7 ] 分析了800 kV直流线路、1 000 kV交流线路,提出这类线路并行架设时保证安全可靠的最小接近距离.山东农业大学王冉冉等[8 ] 对特高压交流输电线路下钢架建筑的感应电压和感应电流进行分析和仿真计算.中国电力科学研究院赵永生等[9 ] 通过研究同走廊高压交直流线路,对混合电场进行了分析. ...
... 在同走廊的750 kV超高压输电线路与配电线路之间电磁环境非常复杂,超高压输电线路在复杂环境中长期运行时,因各种因素难免会发生各种短路故障,在接近并行段短路故障的发生概率会增大.在多发短路故障情况中,单相接地短路故障的发生概率较大,因此,单相接地短路故障在线路防护设计中是设计者最主要考虑的问题.目前现有网架系统中安装的保护装置可实现对短路故障快速切除,在短路瞬间产生的零序电流流经输电线路,可对接近段距离并行的配电线路产生电磁感应的影响(感性耦合),同时流经铁塔接地装置可以对其周围产生地电位影响(阻性耦合),当感性耦合和阻性耦合同时叠加产生时,会成为综合性的影响因素.由于线路之间互阻很小,阻性耦合不用考虑.线路并行接近时电磁感应耦合远小于电容耦合[8 ⇓ -10 ] . ...
Coupling effects among high voltage transmission lines in joint-use corridor
3
2011
... 同输电线路电磁环境研究相比,共用走廊的超特高压输电线路对配电线路电能质量的影响相关方面研究较少,工程中的实际问题无相应的解决治理措施[7 ⇓ ⇓ -10 ] .目前,朱军等[10 ] 通过研究一种共走廊非全线并行架设的高压输电线路中电气量的不平衡度,分析出线路不平衡电流产生的原因及影响因素.中国电力科学研究院吴桂芳等[7 ] 分析了800 kV直流线路、1 000 kV交流线路,提出这类线路并行架设时保证安全可靠的最小接近距离.山东农业大学王冉冉等[8 ] 对特高压交流输电线路下钢架建筑的感应电压和感应电流进行分析和仿真计算.中国电力科学研究院赵永生等[9 ] 通过研究同走廊高压交直流线路,对混合电场进行了分析. ...
... [10 ]通过研究一种共走廊非全线并行架设的高压输电线路中电气量的不平衡度,分析出线路不平衡电流产生的原因及影响因素.中国电力科学研究院吴桂芳等[7 ] 分析了800 kV直流线路、1 000 kV交流线路,提出这类线路并行架设时保证安全可靠的最小接近距离.山东农业大学王冉冉等[8 ] 对特高压交流输电线路下钢架建筑的感应电压和感应电流进行分析和仿真计算.中国电力科学研究院赵永生等[9 ] 通过研究同走廊高压交直流线路,对混合电场进行了分析. ...
... 在同走廊的750 kV超高压输电线路与配电线路之间电磁环境非常复杂,超高压输电线路在复杂环境中长期运行时,因各种因素难免会发生各种短路故障,在接近并行段短路故障的发生概率会增大.在多发短路故障情况中,单相接地短路故障的发生概率较大,因此,单相接地短路故障在线路防护设计中是设计者最主要考虑的问题.目前现有网架系统中安装的保护装置可实现对短路故障快速切除,在短路瞬间产生的零序电流流经输电线路,可对接近段距离并行的配电线路产生电磁感应的影响(感性耦合),同时流经铁塔接地装置可以对其周围产生地电位影响(阻性耦合),当感性耦合和阻性耦合同时叠加产生时,会成为综合性的影响因素.由于线路之间互阻很小,阻性耦合不用考虑.线路并行接近时电磁感应耦合远小于电容耦合[8 ⇓ -10 ] . ...
1
2020
... 目前国内外针对特高压并行架设的输电线路中一些电磁环境、感应电压、感应电流、混合电场计算方面积累了丰富的经验,如架空输电线路架设距离越小,电压等级越高,混合电场直流分量和离子流密度越小.在超特高压输电线路对共走廊并行运行的配电线路电能质量研究可以借鉴以上经验[11 -12 ] . ...
1
2020
... 目前国内外针对特高压并行架设的输电线路中一些电磁环境、感应电压、感应电流、混合电场计算方面积累了丰富的经验,如架空输电线路架设距离越小,电压等级越高,混合电场直流分量和离子流密度越小.在超特高压输电线路对共走廊并行运行的配电线路电能质量研究可以借鉴以上经验[11 -12 ] . ...
2
2017
... 目前国内外针对特高压并行架设的输电线路中一些电磁环境、感应电压、感应电流、混合电场计算方面积累了丰富的经验,如架空输电线路架设距离越小,电压等级越高,混合电场直流分量和离子流密度越小.在超特高压输电线路对共走廊并行运行的配电线路电能质量研究可以借鉴以上经验[11 -12 ] . ...
... 超特高压输电线路的理论模型如图3 所示,该线路模型参数是共用走廊并行运行的750 kV输电线路和配电线路,对于不同的电压等级以及不同的杆塔上架设的输配电线路,通过假设,得到750 kV线路A、B、C三相和配电线路a、b、c三相的自电容和互电容C L [12 ⇓ -14 ] ...
2
2017
... 目前国内外针对特高压并行架设的输电线路中一些电磁环境、感应电压、感应电流、混合电场计算方面积累了丰富的经验,如架空输电线路架设距离越小,电压等级越高,混合电场直流分量和离子流密度越小.在超特高压输电线路对共走廊并行运行的配电线路电能质量研究可以借鉴以上经验[11 -12 ] . ...
... 超特高压输电线路的理论模型如图3 所示,该线路模型参数是共用走廊并行运行的750 kV输电线路和配电线路,对于不同的电压等级以及不同的杆塔上架设的输配电线路,通过假设,得到750 kV线路A、B、C三相和配电线路a、b、c三相的自电容和互电容C L [12 ⇓ -14 ] ...
Analysis of coupling effects on overhead VSC-HVDC transmission lines from AC lines with shared right of way
1
2017
... 超特高压输电线路的理论模型如图3 所示,该线路模型参数是共用走廊并行运行的750 kV输电线路和配电线路,对于不同的电压等级以及不同的杆塔上架设的输配电线路,通过假设,得到750 kV线路A、B、C三相和配电线路a、b、c三相的自电容和互电容C L [12 ⇓ -14 ] ...
架空地线与预绞丝端口接触压力的仿真分析
1
2019
... 超特高压输电线路的理论模型如图3 所示,该线路模型参数是共用走廊并行运行的750 kV输电线路和配电线路,对于不同的电压等级以及不同的杆塔上架设的输配电线路,通过假设,得到750 kV线路A、B、C三相和配电线路a、b、c三相的自电容和互电容C L [12 ⇓ -14 ] ...
Simulation analysis of contact pressure between overhead ground wire and preformed armor rod port
1
2019
... 超特高压输电线路的理论模型如图3 所示,该线路模型参数是共用走廊并行运行的750 kV输电线路和配电线路,对于不同的电压等级以及不同的杆塔上架设的输配电线路,通过假设,得到750 kV线路A、B、C三相和配电线路a、b、c三相的自电容和互电容C L [12 ⇓ -14 ] ...
Analysis of electromagnetic interference on DC line from parallel AC line in close proximity
1
2018
... 在PSCAD中搭建耦合模型[15 ⇓ -17 ] ,500 kV三相电压源经过900 MV·A升压变为750 kV线路电压,并在此三相末端接入377 Ω匹配电阻消除折反射.设置超高压输电线路与配电线路之间的耦合段长18 km,当配电线路长度为20 km时,线路上三相感应电压波形如图4 所示. ...
逐塔接地条件下OPGW地线取能方法研究
1
2017
... 在PSCAD中搭建耦合模型[15 ⇓ -17 ] ,500 kV三相电压源经过900 MV·A升压变为750 kV线路电压,并在此三相末端接入377 Ω匹配电阻消除折反射.设置超高压输电线路与配电线路之间的耦合段长18 km,当配电线路长度为20 km时,线路上三相感应电压波形如图4 所示. ...
Study on power tapping method from optical power ground wire grounded to each tower of transmission line
1
2017
... 在PSCAD中搭建耦合模型[15 ⇓ -17 ] ,500 kV三相电压源经过900 MV·A升压变为750 kV线路电压,并在此三相末端接入377 Ω匹配电阻消除折反射.设置超高压输电线路与配电线路之间的耦合段长18 km,当配电线路长度为20 km时,线路上三相感应电压波形如图4 所示. ...
500 kV架空地线与OPGW绝缘化改造后感应电压研究
1
2020
... 在PSCAD中搭建耦合模型[15 ⇓ -17 ] ,500 kV三相电压源经过900 MV·A升压变为750 kV线路电压,并在此三相末端接入377 Ω匹配电阻消除折反射.设置超高压输电线路与配电线路之间的耦合段长18 km,当配电线路长度为20 km时,线路上三相感应电压波形如图4 所示. ...
Study on induced voltage after insulation reconstruction of 500 kV transmission line overhead ground wire and OPGW
1
2020
... 在PSCAD中搭建耦合模型[15 ⇓ -17 ] ,500 kV三相电压源经过900 MV·A升压变为750 kV线路电压,并在此三相末端接入377 Ω匹配电阻消除折反射.设置超高压输电线路与配电线路之间的耦合段长18 km,当配电线路长度为20 km时,线路上三相感应电压波形如图4 所示. ...
750 kV同塔双回输电线路感应电压和电流的研究
1
2018
... 线路三相的静电感应电压的大小与对地高度近似呈正比关系,因此降低三相线路的静电感应电压的最简单方法即为降低配电线路的高度[18 ] ,将三相线路的对地高度都降低至5 m,三相导线呈水平排列,同时增加屏蔽地线. ...
Study on the induced voltage and current on the 750 kV double circuit transmission line on the same tower
1
2018
... 线路三相的静电感应电压的大小与对地高度近似呈正比关系,因此降低三相线路的静电感应电压的最简单方法即为降低配电线路的高度[18 ] ,将三相线路的对地高度都降低至5 m,三相导线呈水平排列,同时增加屏蔽地线. ...
1
2010
... 从电路的角度,为了降低感应电压,只需要减小线路对地电容对应的容抗即可,因此,可以直接在配电线路上并联电抗[19 ] . ...
1
2010
... 从电路的角度,为了降低感应电压,只需要减小线路对地电容对应的容抗即可,因此,可以直接在配电线路上并联电抗[19 ] . ...
1
2005
... 由表7 可以看出,配电线路三相电压振荡是由于没有增加匹配电阻,波在线路末端折反射造成.由于电感与线路对地电容之间存在过补偿、欠补偿等问题,因此并联电容在不同运行方式下所需要的大小不一样[20 ] .针对此论文中的配电线路,应并联5 H的电感. ...
1
2005
... 由表7 可以看出,配电线路三相电压振荡是由于没有增加匹配电阻,波在线路末端折反射造成.由于电感与线路对地电容之间存在过补偿、欠补偿等问题,因此并联电容在不同运行方式下所需要的大小不一样[20 ] .针对此论文中的配电线路,应并联5 H的电感. ...