1 引言
作为建设智能电网(Smart grid,SG)的关键一环,位于输电系统和用电设备之间的智能配电网(Smart distribution network,SDN)结合各种先进的通信技术与智能化管理系统,向用户提供优质可靠的电能供应[1 ] ,其通信网络性能的好坏将影响整个配电系统的稳定运行。因此,在一些有线与无线公网等通信方式均无法到达的配电区域,拥有自组网、建设成本少以及数据传输安全等优点的无线传感器网络(Wireless sensor networks,WSNs)可作为配电通信系统中辅助通信的最佳选择,可以很好地解决配电网中“最后一公里”通信连接的难题。但由于配电通信系统对通信数据的可靠性、实时传输要求较高,而无线传感器节点自身拥有的计算能力较小且可使用能量有限,节点在部署后其二次能源的补充会非常困难,如何在满足配电网通信数据可靠、实时传输要求的基础上,进一步减小传感器节点能耗,延长网络使用寿命,成为当前在智能配电网WSNs领域的研究重点[2 ⇓ ⇓ -5 ] 。
路由算法作为提升WSNs网络性能最有效的手段,近年来受到了众多研究人员的广泛关注。文献[6 ]提出一种多队列理论来建立网络传输时延模型,通过对多跳网络节点MAC层与网络层有效连接,降低智能电网中多跳路由的时延,但其跳数设置固定,灵活性较差。文献[7 ]为满足链路传输的可靠性指标,提出了长跳步可靠性保证机会路由算法,通过减少大量不必要的数据传输提升了端到端数据传输接收率,但对于数据传输的实时性没有进行充分考虑。文献[8 ]提出了一种保障配电网QoS的多径路由算法MRFD,该算法仅充分考虑了可靠性与实时性指标,未对网络寿命做出优化。文献[9 ]通过计算路径损耗和能量损耗权重的综合值,实现最佳可靠传输路径的选择,降低了节点端到端数据传输时的丢包率,但是该算法如果不增加网络开销,容易造成数据丢失。WSNs的路由问题是一种很典型的NP-Hard问题,相比于文献[10 ]提出的多播路由算法以及其他元启发式优化算法,和声搜索算法(Harmony search algorithm,HS)有着实现简单、灵活性高的特点,更适合于情况复杂多变的配电网通信。文献[11 ]提出了一种多跳和声搜索路由算法,通过对多跳传输的能量模型进行设计以及在和声库中引入了音调调整率来减少WSNs中的能量消耗,但性能提升不是很明显。文献[12 ]提出一种能量有效的和声多跳自适应路由算法,仅通过对参数进行自适应调整来达到延长网络寿命的目的,没有对转发节点的选择加以约束,可能导致数据回传增加算法运行时间。文献[13 ]提出基于和声搜索的能量有效路由算法,该算法对经典和声搜索算法进行改进,主要是运用提升边缘节点利用率的思想,通过角度偏移方法和节点移除策略来延长网络寿命,但没有考虑服务质量。
针对上述问题,本文着重考虑在配电网通信需求下,延长传感器节点使用寿命的问题,在经典HS算法基础上进行改进,采用自适应和声库取值概率(Harmony memory considering rate,HMCR)、音调微调概率(Pitch adjusting rate,PAR)来避免算法陷入局部最优;通过优化下一跳节点的选择来规定数据的传输方向,避免数据回传,减少算法的无效运行;允许和声记忆库(Harmony memory,HM)可以拥有不同的维数并使用结合能耗、时延和丢包率的节点选择概率函数选取最优传输路径。通过仿真试验表明,该算法能更好地均衡能耗提升网络使用寿命,降低数据延迟和丢包,从而有效满足了智能配电终端通信业务需求。
2 配电网环境下通信网络需求
2.1 配电网结构特点
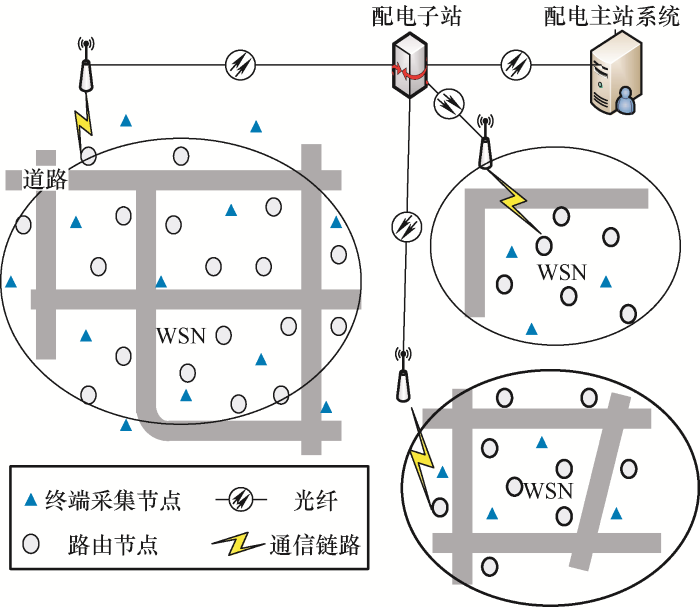
配电网自动化体系大致可分为三层[8 ] ,第一层为配电网中服务器、工作站、网络设备以及相应的配套软件共同组成的主站层,也是整个体系中的核心部分,负责将配电终端所采集的信息收集起来或转发;第二层为布置在变电站或开闭所中,实现管辖范围内配电SCADA以及故障诊断功能的子站层,这部分可以实现对配电线路的监控,并留有空间拓展,以完成对本地配电信息的实时监控;第三层则为配电网中重要组成部分的终端层,这一层包括FTU、DTU、TTU等终端,主要作用是完成对设备的监测并将信息及时采集并上传。如图1 所示是配电网通信结构,各层的通信方式都可以根据其自身的特点来选取。对于配电通信系统,无线传感器网络可以收集和传输各种故障、保护信息、居民用电信息等。
图1
2.2 配电通信网业务需求
根据中国电力行业通信规范,配电通信网络以数据业务为主,语音和视频业务所占比例较小。数据服务主要传输周期性数据,也会有一些随机突发数据。配电网服务根据不同的需求进行分类,大致可分为两类:一类是数据随机、丢包率高的感知监测服务,如对居民用电和峰值用电的监测;另一类则是对延迟和可靠性要求较低的服务:如负载控制和管理通信服务。配电网应根据用户的要求进行,如负荷管理、电能质量监测等。一般来说,这种服务的延迟要求是分钟级的,即对实时性的要求非常低。因此,在这种情况下,应该努力平衡网络能耗,延长网络生命周期。本文算法将主要针对第二种业务,在满足时延和可靠性的基础上,尽量提升网络寿命。
3 相关模型
3.1 网络模型
该算法将主要针对在不可补充能量并大范围分布的无线传感器节点环境下的传感器节点使用情况,因此做出如下约定:① 在L ×L 的矩形区域内随机布撒n 个节点;② 节点位置一旦确定,将不能移动,各个节点初始能量相同并且不可进行二次能源补充;③ sink节点具有一定的计算能力与存储空间,拥有回收所有监测信息的能力;④ 各个节点间传递信息的过程均遵循能量传输模型;⑤ 所有节点拥有唯一ID。
3.2 能耗模型和干扰模型
本文使用文献[14 ]中提供的能耗模型来计算传递信息过程中节点的能量消耗。节点能耗大多是由于数据包长度、节点与节点间的距离等因素导致,其中信息的传输过程会产生大量的能量消耗,占据了总消耗能量中的绝大部分,因此,在能耗模型中,只考虑在通信过程中产生的能量损失。
(1) ${{E}_{Tx}}(l,d)=\left\{ \begin{matrix} l{{E}_{ls}}+l{{\varepsilon }_{fs}}{{d}^{2}}\ \ \ \ \ d<{{d}_{0}} \\ l{{E}_{ls}}+l{{\varepsilon }_{mp}}{{d}^{4}}\ \ \ \ \ d\ge {{d}_{0}} \\\end{matrix} \right.$
(2) ${{E}_{Rx}}(l)=l{{E}_{ls}}$
(3) ${{d}_{0}}=\sqrt{\frac{{{\varepsilon }_{fs}}}{{{\varepsilon }_{mp}}}}$
式中,${{E}_{Tx}}$ ${{E}_{Rx}}$ ${{E}_{ls}}$ ${{\varepsilon }_{fs}}$ ${{\varepsilon }_{mp}}$ l 为发送的数据包大小;d 为节点间通信距离;${{d}_{0}}$
通常,在配网区域中会出现电磁干扰。因此,为体现该算法适用于配电区域,将设置干扰源,其中的干扰公式如下[15 ]
(4) $C(i)={{C}_{initial}}+\sum\limits_{i=1}^{3}{\frac{0.2({{R}_{i}}-{{d}_{i}})}{{{R}_{i}}}}$
式中,${{C}_{initial}}$ ${{d}_{i}}$
3.3 路径评价函数
整个算法的最终评价目标实际上是算法中的评价函数,尤其是在目标函数的筛选过程,其很大程度上将决定路径选择是否成功。因此,在该文设计多目标函数时,将衡量能量消耗、时延以及丢包率这三大因素,从而保证整个过程向最优解的方向逐渐靠近。
(5) ${{f}_{1}}=\min \sum\limits_{i=1}^{n}{{{E}_{i}}/{{E}_{avg}}\cdot {{E}_{\min }}}$
式中,n 为路径中的节点总数;${{E}_{i}}$ ${{E}_{avg}}$ ${{E}_{\min }}$
(2) 从链路传输可靠性出发,以端到端传输丢包率最低为目标
(6) ${{f}_{2}}=\min \sum\limits_{i=1}^{n}{({{S}_{i}}-}{{N}_{R}})/{{N}_{R}}$
式中,${{S}_{i}}$ ${{N}_{R}}$
(7) ${{f}_{3}}=\min (\sum\limits_{i=1}^{n}{{{D}_{i}}+{{D}_{other}})/{{D}_{avg}}\cdot n}$
式中,${{D}_{i}}$ ${{D}_{other}}$ ${{D}_{avg}}$
综上,由于上述目标函数量纲均有所差异,因此对各目标函数值进行归一化处理,以能耗、时延、丢包率为指标,建立加权的目标函数$f$
(8) $F=\frac{1}{{{F}_{1}}^{\alpha }\cdot {{F}_{2}}^{\beta }\cdot {{F}_{3}}^{\lambda }}$
式中,${{F}_{1}}$ ${{F}_{2}}$ ${{F}_{3}}$ $\alpha $ $\beta $ $\lambda $
4 算法描述
4.1 和声算法
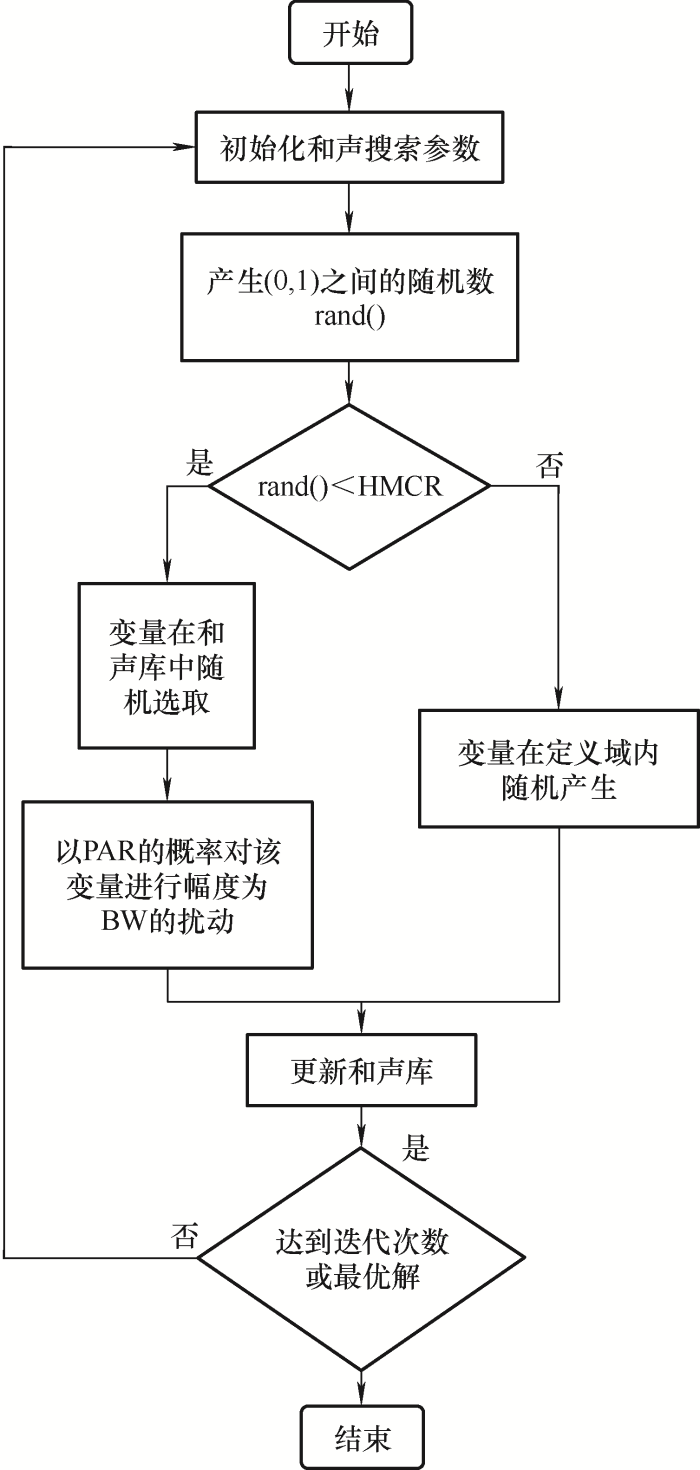
和声搜索算法是一种启发式算法[16 ] ,是模仿音乐家即兴创作而产生的,由GEEM等[17 ] 在2001年提出。该算法共有五个步骤。
(9) $\min f(x),x=\left\{ {{x}_{1}},{{x}_{2}},\cdots,{{x}_{n}} \right\}\in {{R}^{n}}$
式中,${{x}_{1}},{{x}_{2}},\cdots,{{x}_{n}}$
定义参数数值。主要参数有和声库大小HMS,和声记忆库保留概率HMCR,扰动概率PAR,音调微调幅度BW以及最大迭代次数${{T}_{\max }}$ [18 ] 。
步骤2:初始化和声记忆库。从解空间里随机生成HMS个和声放入和声记忆库HM,并记录对应的$f(x)$
(10) $HM=\left[ \begin{matrix} {{X}^{1}} \\ {{X}^{2}} \\ \vdots \\ {{X}^{HMS}} \\ \end{matrix} \right]=\left[ \begin{matrix} x_{1}^{1} & x_{2}^{1} & \cdots & x_{n}^{1} & f\left( {{X}^{1}} \right) \\ x_{1}^{2} & x_{2}^{2} & \cdots & x_{n}^{2} & f\left( {{X}^{2}} \right) \\ \vdots & \vdots & {} & \vdots & \vdots \\ x_{1}^{HMS} & x_{2}^{HMS} & \cdots & x_{n}^{HMS} & f\left( {{X}^{HMS}} \right) \\ \end{matrix} \right]$
步骤3:即兴创作。取一个在[0,1 ]内的随机数r 1 ,若${{r}_{1}}<\mathrm{HMCR}$ 1 ]内取一个随机数r 2 ,若${{r}_{2}}<\mathrm{PAR}$ X new 。
步骤4:更新和声记忆库。对X new 进行评估得f (X new )。若新得到f (X new )的函数值优于HM中的最差一个,即f (X new )< f (X worst ),则将X new 代替HM中函数值最差的和声X worst ;否则,不做修改。
步骤5:检查算法是否终止。重复步骤3~5,直到迭代次数达到${{T}_{\max }}$
图2
4.2 改进的和声算法
传统HS算法逻辑比较简单,易于实现,仅通过对HMCR和PAR的调整就能达到对整个流程的控制[19 ] 。但在路由寻址的问题上,由于HS算法大多用于处理连续值的优化,而每个节点的ID编码唯一且随机布撒,路径选择往往是离散的,因此,针对WSN路由问题的特点以及为满足配电通信需求,需要对经典HS算法进行改进。
4.2.1 参数自适应
通常情况下,HS算法中HMCR与PAR的值是固定设置,但HS算法中参数对于算法结果的影响是非常大的,固定设置参数容易导致算法陷入局部最优[20 ] ,因此,本文采用自适应调整的方法对HMCR和PAR的取值改进。在算法运行的初期,和声库中初始解向量质量较差容易存在较大的误差,因此取较大HMCR;在寻优中后期,质量较好的解向量在和声库中逐渐增多,各解向量之间误差也变小,故HMCR取较小值,而PAR则需要取较大值,从而加快该算法收敛,提升全局最优搜索能力。
(11) $\mathrm{HMCR}=\mathrm{HMC}{{\mathrm{R}}_{\max }}-(\mathrm{HMC}{{\mathrm{R}}_{\max }}-\mathrm{HMC}{{\mathrm{R}}_{\min }})\times {{T}_{i}}/{{T}_{\max }}$
(12) $\mathrm{PAR}=\mathrm{PA}{{\mathrm{R}}_{\min }}+(\mathrm{PA}{{\mathrm{R}}_{\max }}-\mathrm{PA}{{\mathrm{R}}_{\min }})\times {{T}_{i}}/{{T}_{\max }}$
式中,$\mathrm{HMC}{{\mathrm{R}}_{\max }}$ $\mathrm{HMC}{{\mathrm{R}}_{\min }}$ $\mathrm{PA}{{\mathrm{R}}_{\max }}$ $\mathrm{PA}{{\mathrm{R}}_{\min }}$ ${{T}_{i}}$ ${{T}_{\max }}$
4.2.2 优化转发节点集
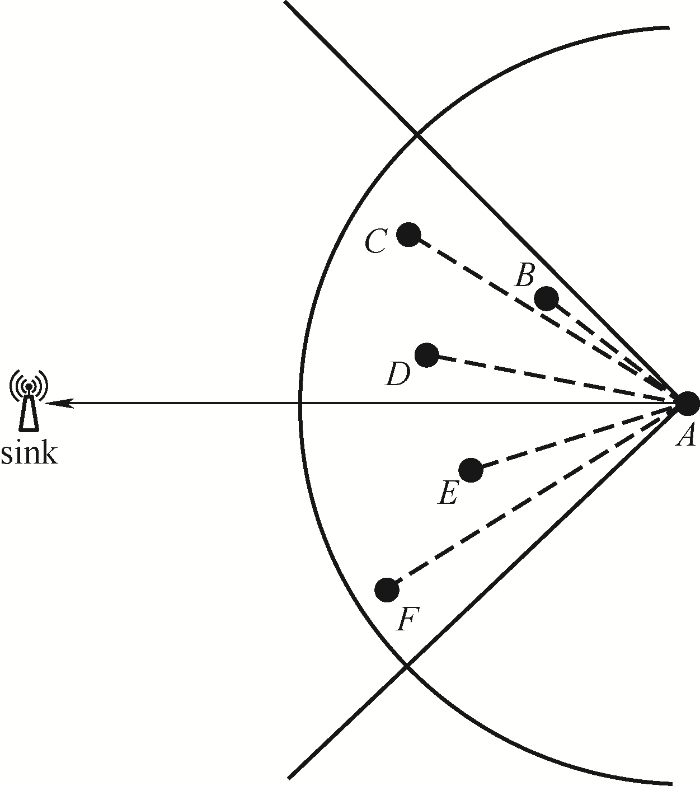
路径搜索中下一跳节点转发机制往往对整个传输路径的建立起着至关重要的作用,而转发节点集是转发机制中的关键一点。因此,本文将对转发节点集进行改进,在路径搜索的过程中设置前传区域,使得下一节点从前传区域内选择,防止数据回传,保证数据朝着目标节点正向传输,以降低端到端传输时延并进一步提高整个网络传输可靠性。如图3 所示,A 为传感器节点,sink为最终目的节点。A 节点的前传区域定义是:以A 节点为圆心,A 节点的通信距离R 为半径的圆与以sink节点连接A 节点的直线为对称轴的等腰直角三角形相交的部分。而处于前传区域内的节点,例如图3 中B 、C 、D 、E 、F 节点的集合即为A 节点的优化转发节点集${{S}_{A}}$
图3
(13) ${{S}_{A}}\in \mathrm{FTN}(A)$
(14) $\mathrm{FTN}(A)=\odot A\bigcap Rt\vartriangle A$
式中,$\odot A$ A 为圆心的圆;$Rt\vartriangle A$ A 节点的直线为对称轴的等腰直角三角形。
4.2.3 和声库生成规则
和声搜索算法中新和声的产生比较依赖于初始和声库,其中对于搜索结果影响最大的就是初始解的好坏程度。因此,本文将对经典轮盘法中的节点选择概率公式进行改进,通过引入链路传输可靠性,再结合转发节点集中节点的剩余能量,在均衡能耗的同时选择可靠性更高的传输路径。
数据传输的可靠性问题通常可以用端到端的传输成功率来表示,因此,链路可靠性依据可以用目标节点在接收数据时的丢包率来表示,并且该值越小代表其路径可靠性越好,计算公式如下
(15) $D=\frac{{{N}_{S}}-{{N}_{R}}}{{{N}_{S}}}$
式中,${{N}_{S}}$ ${{N}_{R}}$ D 为丢包率。
根据本文的轮盘法选择机制,在一条路径初始化时,节点i 在优化转发节点集中选择下一跳节点的概率为$P(i,j)$ i 的选择概率$P(i,j)$
(16) $P(i,j)=\left\{ \begin{matrix} \frac{\sum\limits_{k\in N}{\left( \frac{1}{{{E}_{k}}}+\frac{1}{{{D}_{ik}}} \right)-\left( \frac{1}{{{E}_{j}}}+\frac{1}{{{D}_{ij}}} \right)}}{\left[ C(\mathrm{Q}{{\mathrm{N}}_{i}})-1 \right]\times \sum\limits_{k\in N}{\left( \frac{{{D}_{j}}}{{{D}_{ik}}}+\frac{1}{{{E}_{j}}} \right)}}\begin{matrix} {} & {} \\ \end{matrix}j\in \mathrm{Q}{{\mathrm{N}}_{i}} \\ 0\begin{matrix} \begin{matrix} \begin{matrix} {} & {} & {} & {} \\ \end{matrix} & {} & {} & {} \\ \end{matrix} & {} & {} & {} \\ \end{matrix}\ \ \ \ \ \ \ \\ \end{matrix} \right.$
式中,${{E}_{j}}$ j 的剩余能量;${{E}_{k}}$ k 的剩余能量;${{D}_{ij}}$ i 与节点j 传输数据的丢包率;${{D}_{ik}}$ i 与节点k 传输数据的丢包率;$\mathrm{Q}{{\mathrm{N}}_{i}}$ i 下一跳节点集合;$C(\mathrm{Q}{{\mathrm{N}}_{i}})$ $\mathrm{Q}{{\mathrm{N}}_{i}}$
(1) for t =1,2,3,…,${{T}_{\max }}$
(3) if $rand<\mathrm{HMCR}$
(5) if $rand<\mathrm{PAR}$
(9) if新路径$\mathrm{Path}$
(13) $P\leftarrow \mathrm{Path}$
5 仿真试验结果分析
为验证所提方法性能,将在Matlab 2021b环境下进行仿真试验。根据有效的通信半径,在环境范围为180 m×180 m的区域当中,随机布撒试验节点200个,其他仿真参数如表1 所示。将在试验时着重在网络使用寿命(即网络中节点死亡时间)、端到端传输时延(即节点平均传输数据时间)以及可靠性(端到端数据丢包率)三个方面与文献[8 ]和文献[12 ]中的算法进行对比分析。
5.1 网络使用寿命
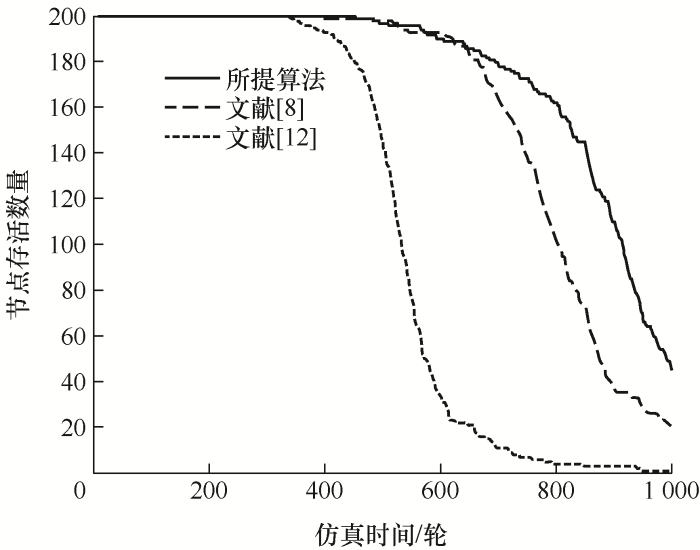
由于网络节点能量难以获取,且部分节点由于能量耗尽而死亡对整个网络将会有巨大的影响。因此,无线传感器网络使用寿命是评价整个网络性能好坏的重要指标之一。节点存活数量图是指网络系统中的节点数目随着网络运行时间变化的情况,各算法网络初始设置均相同,系统中存活的节点数量越多则代表网络越完整即系统运行越稳定。
为更加全面地验证所提算法在网络使用寿命方面的性能,将在两种不同试验环境下与文献[8 ]和文献[12 ]算法进行对比,即模拟两种不同的节点发送形式。
试验场景1(固定节点发送形式):所有节点剩余能量相同,需要发送的数据包均从同一固定设置好的节点发出,然后传给sink节点。
试验场景2(全节点循环发送形式):所有节点剩余能量相同,需要发送的数据包从随机选出的节点发出,然后传送给sink节点。
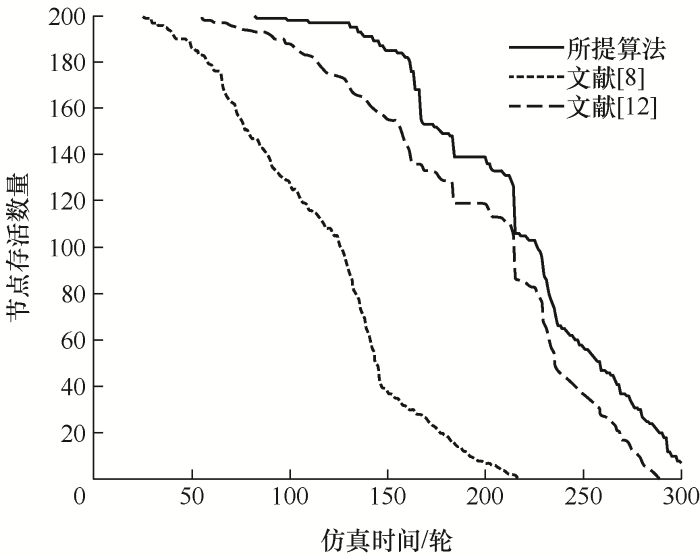
如图4 所示,在试验场景1的环境下,固定节点进行数据传输,可以看出,文献[8 ]方法与文献[12 ]的方法首次出现节点死亡是在342轮和399轮,而所提算法在460轮才出现第一个死亡节点,如图5 所示,在试验场景2的环境下,所有节点随机循环发送数据,三种算法首次出现节点死亡是在37轮、58轮和69轮。因此,在试验场景1下所提算法相比文献[8 ]与文献[12 ]中的方法分别有34.5%和15.2%的性能提升,在试验场景2下,所提算法相比文献[8 ] 与文献[12 ]的算法也分别有28.5%和8.6%的性能提升。总的来说,得益于对节点转发的优化设计和对参数自适应改进,使得算法减少了无效运行,无论是固定节点发送数据还是节点循环发送数据均有着优异的性能表现。
图4
图5
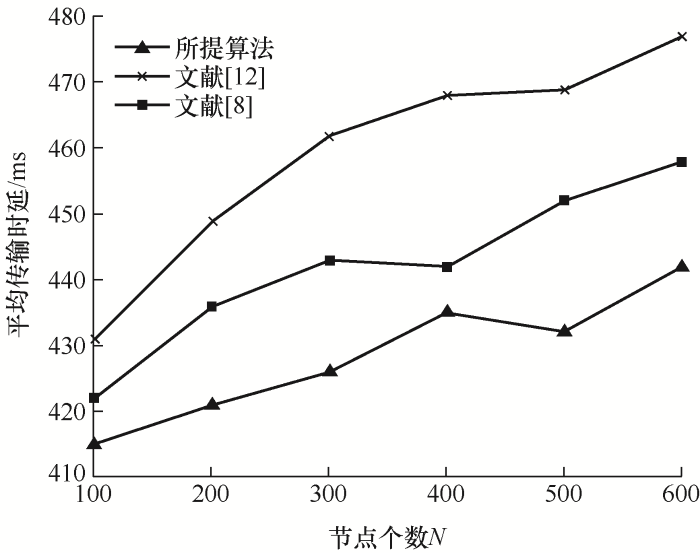
5.2 端到端传输时延
为降低时延,所提算法通过对下一跳节点集优化,约束其传输方向,保证数据的正向传输,避免数据回传,使得算法在较短时间能够求出最短路径。为验证其时延性能,在不同节点密度下,分别进行多次试验得到的最短路径平均时延,如图6 所示,可以看出相较于文献[8 ]的算法,所提算法求得的最短路径平均时延降低延迟效果明显,有着3%~6%的性能提升。
图6
表2 为本算法与MRFD算法延迟优化对比,在节点密度100~600的范围内,算法的平均时延在428.5 ms,对于日常居民用电情况监测信息时延应满足1 s内要求和负荷控制与管理等通信业务信息时延满足分钟级要求,所提算法均可以满足。
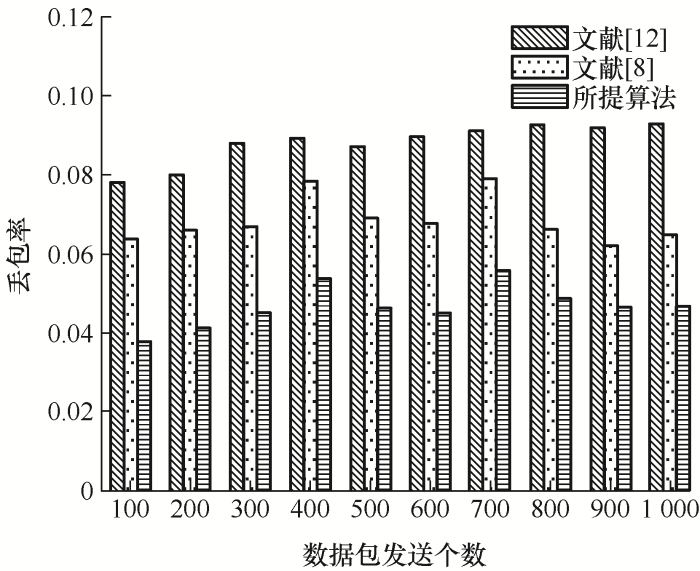
5.3 可靠性
从图7 可以看出在发送不同大小数据包的场景下,三种方法均有着丢包率的波动,但所提方法相较于文献[8 ]与文献[12 ]方法丢包率更低,介于3.5%~6%。这是由于所提方法在节点选择概率公式中综合考虑了丢包率和时延等因素,使得从和声库生成阶段到新解产生阶段都能够在保证可靠性的前提下搜索路径,使得所提算法即便是在更注重能耗的情况下也能使得数据传输更可靠。
图7
6 结论
本文提出了一种基于改进和声搜索的无线传感器网络多路径QoS路由算法,所提算法以HS算法为基础,以适应配电网的QoS需求做出针对性的改进,可以得出以下结论。
(1) 针对HS算法固定参数容易导致算法收敛速度慢等问题,利用自适应HMCR和PAR参数来避免算法陷入局部最优,同时也能降低节点间数据传输时延。
(2) 为避免网络中数据回传,通过构建前传区域来约束节点传输数据的方向,以达到降低时延,提升可靠性的目的。
(3) 改进了下一节点选择的概率公式,通过在公式中增加丢包率来影响下一节点的选择,从而使得路径的可靠性得到提升。
但该算法在网络能耗与网络吞吐量方面依旧有提升空间,并且目前还处在理论研究阶段,与配电网实际运行情况还有一定差距,后续还需要进一步完善。
参考文献
View Option
[1]
何奉禄 , 陈佳琦 , 李钦豪 , 等 . 智能电网中的物联网技术应用与发展
[J]. 电力系统保护与控制 , 2020 , 48 (3 ):58 -69 .
[本文引用: 3]
HE Fenglu CHEN Jiaqi LI Qinhao et al. Application and development of internet of things in smart grid
[J]. Power System Protection and Control , 2020 , 48 (3 ):58 -69 .
[本文引用: 3]
[2]
赵彦平 , 唐国琦 , 李良 , 等 . 智能电网中基于平衡树的无线Mesh接入网络路由算法
[J]. 重庆邮电大学学报 , 2018 , 30 (2 ):178 -183 .
[本文引用: 1]
ZHAO Yanping TANG Guoqi LI Liang et al. Wireless Mesh access network routing algorithm based on balanced tree in smart grid
[J]. Journal of Chongqing University of Posts and Telecommunications , 2018 , 30 (2 ):178 -183 .
[本文引用: 1]
[3]
王哲 , 赵宏大 , 朱铭霞 , 等 . 电力无线专网在泛在电力物联网中的应用
[J]. 中国电力 , 2019 , 52 (12 ):27 -38 .
[本文引用: 1]
WANG Zhe ZHAO Hongda ZHU Mingxia et al. Application of power wireless private network in ubiquitous power internet of things
[J]. Electric Power , 2019 , 52 (12 ):27 -38 .
[本文引用: 1]
[4]
赵萌萌 , 唐平舟 , 孙堃 , 等 . 泛在电力物联网发展与展望
[J]. 华北电力大学学报 , 2020 , 47 (5 ):63 -74 .
[本文引用: 1]
ZHAO Mengmeng TANG Pingzhou SUN Kun et al. Development and prospect of ubiquitous electric internet of things
[J]. Journal of North China Electric Power University , 2020 , 47 (5 ):63 -74 .
[本文引用: 1]
[5]
张强 , 孙雨耕 , 杨挺 , 等 . 无线传感器网络在智能电网中的应用
[J]. 中国电力 , 2010 , 43 (6 ):31 -36 .
[本文引用: 1]
ZHANG Qiang SUN Yugeng YANG Ting et al. Application of wireless sensor network in smart power grid
[J]. Electric Power , 2010 , 43 (6 ):31 -36 .
[本文引用: 1]
[6]
孙伟 , 丁震 , 王建平 . 基于多跳无线传感器网络的智能电网延时优化研究
[J]. 电子测量与仪器学报 , 2019 , 33 (8 ):140 -146 .
[本文引用: 1]
SUN Wei DING Zhen WANG Jianping Research on time-delay optimization of smart grid based on multi-hop wireless sensor network
[J]. Journal of Electronic Measurement and Instrument , 2019 , 33 (8 ):140 -146 .
[本文引用: 1]
[7]
刘小涛 , 陈珍萍 , 黄友锐 . 智能配电网WSNs可靠性保障机会路由算法研究
[J]. 传感技术学报 , 2019 , 32 (9 ):1388 -1394 .
[本文引用: 1]
LIU Xiaotao CHEN Zhenping HUANG Yourui Probabilistic routing algorithm for WSNs reliability assurance in smart distribution networks
[J]. Chinese Journal of Sensors and Transducers , 2019 , 32 (9 ):1388 -1394 .
[本文引用: 1]
[8]
孙毅 , 刘浩程 , 曾璐琨 , 等 . 面向配电通信网的WMSNs多路径QoS路由算法
[J]. 计算机应用研究 , 2016 , 33 (11 ):3387 -3390 ,3395.
[本文引用: 9]
SUN Yi LIU Haocheng ZENG Lukun et al. QoS assured multipath routing algorithm for distribution communication network
[J]. Application Research of Computers , 2016 , 33 (11 ):3387 -3390 ,3395.
[本文引用: 9]
[9]
肖振锋 , 辛培哲 , 伍晓平 , 等 . 满足可靠及泛在需求的无线传感器网络部署研究
[J]. 武汉大学学报 , 2019 , 52 (5 ):446 -450 .
[本文引用: 1]
XIAO Zhenfeng XIN Peizhe WU Xiaoping et al. Research on wireless sensor network deployment to meet reliable and ubiquitous requirements
[J]. Engineering Journal of Wuhan University , 2019 , 52 (5 ):446 -450 .
[本文引用: 1]
[10]
陈岩 , 李晓卉 , 丁月民 , 等 . 面向输电线故障信息传输的多播路由
[J]. 计算机工程与设计 , 2020 , 41 (1 ):21 -26 .
[本文引用: 1]
CHEN Yan LI Xiaohui DING Yuemin et al. Multicast routing for transmission of fault information on power transmission line
[J]. Computer Engineering and Design , 2020 , 41 (1 ):21 -26 .
[本文引用: 1]
[11]
ZARDOSHT M J PARHIZGAR N Energy optimization in multi-hop wireless sensor networks based on proposed harmony search routing algorithm
[J]. Wireless Personal Communications , 2021 ,118:2717 -2731 .
[本文引用: 1]
[12]
WANG Xuan WANG Weidong LI Xiuhua et al. Adaptive multi-hop routing algorithm based on harmony search in WSNs
[C]// 2017 9th International Conference on Advanced Infocomm Technology, November 22-24,2017 ,Chengdu,China. IEEE,2017:189 -194 .
[本文引用: 7]
[13]
王宝亮 , 彭程 , 李科 . 基于和声搜索的能量有效路由算法
[J]. 计算机工程与设计 , 2021 , 42 (9 ):2401 -2407 .
[本文引用: 1]
WANG Baoliang PENG Cheng LI Ke Energy efficient routing algorithm based on harmony search
[J]. Computer Engineering and Design , 2021 , 42 (9 ):2401 -2407 .
[本文引用: 1]
[14]
ZHANG Degan LI Guang ZHENG Ke et al. An energy-balanced routing method based on forward-aware factor for wireless sensor networks
[J]. IEEE Transactions on Industrial Informatics , 2014 , 10 (1 ):766 -773 .
DOI:10.1109/TII.2013.2250910
URL
[本文引用: 1]
[15]
冯森 . 面向智能配用电的无线传感器网络路由优化协议研究 [D]. 北京 : 华北电力大学 , 2015 .
[本文引用: 1]
FENG Sen Research on routing optimization protocol for intelligent power distribution in wireless sensor networks [D]. Beijing : North China Electric Power University , 2015 .
[本文引用: 1]
[16]
ZHU Qidan TANG Xiangmeng LI Yong et al. An improved differential-based harmony search algorithm with linear dynamic domain
[J]. Knowledge-based Systems , 2020 ,187:104809.
[本文引用: 1]
[17]
GEEM Z W KIM J H LOGANATHAN G V A new heuristic optimization algorithm:Harmony search
[J]. Simulation , 2001 , 76 (2 ):60 -68 .
DOI:10.1177/003754970107600201
URL
[本文引用: 1]
Many optimization problems in various fields have been solved using diverse optimization al gorithms. Traditional optimization techniques such as linear programming (LP), non-linear programming (NLP), and dynamic program ming (DP) have had major roles in solving these problems. However, their drawbacks generate demand for other types of algorithms, such as heuristic optimization approaches (simulated annealing, tabu search, and evolutionary algo rithms). However, there are still some possibili ties of devising new heuristic algorithms based on analogies with natural or artificial phenom ena. A new heuristic algorithm, mimicking the improvisation of music players, has been devel oped and named Harmony Search (HS). The performance of the algorithm is illustrated with a traveling salesman problem (TSP), a specific academic optimization problem, and a least-cost pipe network design problem.
[18]
周雅兰 , 黄韬 . 和声搜索算法改进与应用
[J]. 计算机科学 , 2014 , 6 (41 ):52 -75 .
[本文引用: 1]
ZHOU Yalan HUANG Tao Improvement and application of harmony search algorithm
[J]. Computer Science , 2014 , 6 (41 ):52 -75 .
[本文引用: 1]
[19]
HESAR A S KAMEL S R HOUSHMAND M A quantum multi-objective optimization algorithm based on harmony search method
[J]. Soft Computing , 2021 , 25 (14 ):9427 -9439 .
DOI:10.1007/s00500-021-05799-x
[本文引用: 1]
[20]
KANG Diwen MO Liping WANG Fangling et al. Adaptive harmony search algorithm utilizing differential evolution and opposition-based learning
[J]. Mathematical Biosciences and Engineering , 2021 , 18 (4 ):4226 -4246 .
DOI:10.3934/mbe.2021212
PMID:34198434
[本文引用: 1]
An adaptive harmony search algorithm utilizing differential evolution and opposition-based learning (AHS-DE-OBL) is proposed to overcome the drawbacks of the harmony search (HS) algorithm, such as its low fine-tuning ability, slow convergence speed, and easily falling into a local optimum. In AHS-DE-OBL, three main innovative strategies are adopted. First, inspired by the differential evolution algorithm, the differential harmonies in the population are used to randomly perturb individuals to improve the fine-tuning ability. Then, the search domain is adaptively adjusted to accelerate the algorithm convergence. Finally, an opposition-based learning strategy is introduced to prevent the algorithm from falling into a local optimum. The experimental results show that the proposed algorithm has a better global search ability and faster convergence speed than other selected improved harmony search algorithms and selected metaheuristic approaches.
智能电网中的物联网技术应用与发展
3
2020
... 作为建设智能电网(Smart grid,SG)的关键一环,位于输电系统和用电设备之间的智能配电网(Smart distribution network,SDN)结合各种先进的通信技术与智能化管理系统,向用户提供优质可靠的电能供应[1 ] ,其通信网络性能的好坏将影响整个配电系统的稳定运行.因此,在一些有线与无线公网等通信方式均无法到达的配电区域,拥有自组网、建设成本少以及数据传输安全等优点的无线传感器网络(Wireless sensor networks,WSNs)可作为配电通信系统中辅助通信的最佳选择,可以很好地解决配电网中“最后一公里”通信连接的难题.但由于配电通信系统对通信数据的可靠性、实时传输要求较高,而无线传感器节点自身拥有的计算能力较小且可使用能量有限,节点在部署后其二次能源的补充会非常困难,如何在满足配电网通信数据可靠、实时传输要求的基础上,进一步减小传感器节点能耗,延长网络使用寿命,成为当前在智能配电网WSNs领域的研究重点[2 ⇓ ⇓ -5 ] . ...
... 步骤3:即兴创作.取一个在[0,1 ]内的随机数r 1 ,若${{r}_{1}}<\mathrm{HMCR}$ 1 ]内取一个随机数r 2 ,若${{r}_{2}}<\mathrm{PAR}$ X new . ...
... ,则和声变量将从HM中随机选取一个产生;否则,在解空间范围内产生.如果该和声变量是从HM中得到的,下一步将进行微调,即在[0,1 ]内取一个随机数r 2 ,若${{r}_{2}}<\mathrm{PAR}$ X new . ...
Application and development of internet of things in smart grid
3
2020
... 作为建设智能电网(Smart grid,SG)的关键一环,位于输电系统和用电设备之间的智能配电网(Smart distribution network,SDN)结合各种先进的通信技术与智能化管理系统,向用户提供优质可靠的电能供应[1 ] ,其通信网络性能的好坏将影响整个配电系统的稳定运行.因此,在一些有线与无线公网等通信方式均无法到达的配电区域,拥有自组网、建设成本少以及数据传输安全等优点的无线传感器网络(Wireless sensor networks,WSNs)可作为配电通信系统中辅助通信的最佳选择,可以很好地解决配电网中“最后一公里”通信连接的难题.但由于配电通信系统对通信数据的可靠性、实时传输要求较高,而无线传感器节点自身拥有的计算能力较小且可使用能量有限,节点在部署后其二次能源的补充会非常困难,如何在满足配电网通信数据可靠、实时传输要求的基础上,进一步减小传感器节点能耗,延长网络使用寿命,成为当前在智能配电网WSNs领域的研究重点[2 ⇓ ⇓ -5 ] . ...
... 步骤3:即兴创作.取一个在[0,1 ]内的随机数r 1 ,若${{r}_{1}}<\mathrm{HMCR}$ 1 ]内取一个随机数r 2 ,若${{r}_{2}}<\mathrm{PAR}$ X new . ...
... ,则和声变量将从HM中随机选取一个产生;否则,在解空间范围内产生.如果该和声变量是从HM中得到的,下一步将进行微调,即在[0,1 ]内取一个随机数r 2 ,若${{r}_{2}}<\mathrm{PAR}$ X new . ...
智能电网中基于平衡树的无线Mesh接入网络路由算法
1
2018
... 作为建设智能电网(Smart grid,SG)的关键一环,位于输电系统和用电设备之间的智能配电网(Smart distribution network,SDN)结合各种先进的通信技术与智能化管理系统,向用户提供优质可靠的电能供应[1 ] ,其通信网络性能的好坏将影响整个配电系统的稳定运行.因此,在一些有线与无线公网等通信方式均无法到达的配电区域,拥有自组网、建设成本少以及数据传输安全等优点的无线传感器网络(Wireless sensor networks,WSNs)可作为配电通信系统中辅助通信的最佳选择,可以很好地解决配电网中“最后一公里”通信连接的难题.但由于配电通信系统对通信数据的可靠性、实时传输要求较高,而无线传感器节点自身拥有的计算能力较小且可使用能量有限,节点在部署后其二次能源的补充会非常困难,如何在满足配电网通信数据可靠、实时传输要求的基础上,进一步减小传感器节点能耗,延长网络使用寿命,成为当前在智能配电网WSNs领域的研究重点[2 ⇓ ⇓ -5 ] . ...
Wireless Mesh access network routing algorithm based on balanced tree in smart grid
1
2018
... 作为建设智能电网(Smart grid,SG)的关键一环,位于输电系统和用电设备之间的智能配电网(Smart distribution network,SDN)结合各种先进的通信技术与智能化管理系统,向用户提供优质可靠的电能供应[1 ] ,其通信网络性能的好坏将影响整个配电系统的稳定运行.因此,在一些有线与无线公网等通信方式均无法到达的配电区域,拥有自组网、建设成本少以及数据传输安全等优点的无线传感器网络(Wireless sensor networks,WSNs)可作为配电通信系统中辅助通信的最佳选择,可以很好地解决配电网中“最后一公里”通信连接的难题.但由于配电通信系统对通信数据的可靠性、实时传输要求较高,而无线传感器节点自身拥有的计算能力较小且可使用能量有限,节点在部署后其二次能源的补充会非常困难,如何在满足配电网通信数据可靠、实时传输要求的基础上,进一步减小传感器节点能耗,延长网络使用寿命,成为当前在智能配电网WSNs领域的研究重点[2 ⇓ ⇓ -5 ] . ...
电力无线专网在泛在电力物联网中的应用
1
2019
... 作为建设智能电网(Smart grid,SG)的关键一环,位于输电系统和用电设备之间的智能配电网(Smart distribution network,SDN)结合各种先进的通信技术与智能化管理系统,向用户提供优质可靠的电能供应[1 ] ,其通信网络性能的好坏将影响整个配电系统的稳定运行.因此,在一些有线与无线公网等通信方式均无法到达的配电区域,拥有自组网、建设成本少以及数据传输安全等优点的无线传感器网络(Wireless sensor networks,WSNs)可作为配电通信系统中辅助通信的最佳选择,可以很好地解决配电网中“最后一公里”通信连接的难题.但由于配电通信系统对通信数据的可靠性、实时传输要求较高,而无线传感器节点自身拥有的计算能力较小且可使用能量有限,节点在部署后其二次能源的补充会非常困难,如何在满足配电网通信数据可靠、实时传输要求的基础上,进一步减小传感器节点能耗,延长网络使用寿命,成为当前在智能配电网WSNs领域的研究重点[2 ⇓ ⇓ -5 ] . ...
Application of power wireless private network in ubiquitous power internet of things
1
2019
... 作为建设智能电网(Smart grid,SG)的关键一环,位于输电系统和用电设备之间的智能配电网(Smart distribution network,SDN)结合各种先进的通信技术与智能化管理系统,向用户提供优质可靠的电能供应[1 ] ,其通信网络性能的好坏将影响整个配电系统的稳定运行.因此,在一些有线与无线公网等通信方式均无法到达的配电区域,拥有自组网、建设成本少以及数据传输安全等优点的无线传感器网络(Wireless sensor networks,WSNs)可作为配电通信系统中辅助通信的最佳选择,可以很好地解决配电网中“最后一公里”通信连接的难题.但由于配电通信系统对通信数据的可靠性、实时传输要求较高,而无线传感器节点自身拥有的计算能力较小且可使用能量有限,节点在部署后其二次能源的补充会非常困难,如何在满足配电网通信数据可靠、实时传输要求的基础上,进一步减小传感器节点能耗,延长网络使用寿命,成为当前在智能配电网WSNs领域的研究重点[2 ⇓ ⇓ -5 ] . ...
泛在电力物联网发展与展望
1
2020
... 作为建设智能电网(Smart grid,SG)的关键一环,位于输电系统和用电设备之间的智能配电网(Smart distribution network,SDN)结合各种先进的通信技术与智能化管理系统,向用户提供优质可靠的电能供应[1 ] ,其通信网络性能的好坏将影响整个配电系统的稳定运行.因此,在一些有线与无线公网等通信方式均无法到达的配电区域,拥有自组网、建设成本少以及数据传输安全等优点的无线传感器网络(Wireless sensor networks,WSNs)可作为配电通信系统中辅助通信的最佳选择,可以很好地解决配电网中“最后一公里”通信连接的难题.但由于配电通信系统对通信数据的可靠性、实时传输要求较高,而无线传感器节点自身拥有的计算能力较小且可使用能量有限,节点在部署后其二次能源的补充会非常困难,如何在满足配电网通信数据可靠、实时传输要求的基础上,进一步减小传感器节点能耗,延长网络使用寿命,成为当前在智能配电网WSNs领域的研究重点[2 ⇓ ⇓ -5 ] . ...
Development and prospect of ubiquitous electric internet of things
1
2020
... 作为建设智能电网(Smart grid,SG)的关键一环,位于输电系统和用电设备之间的智能配电网(Smart distribution network,SDN)结合各种先进的通信技术与智能化管理系统,向用户提供优质可靠的电能供应[1 ] ,其通信网络性能的好坏将影响整个配电系统的稳定运行.因此,在一些有线与无线公网等通信方式均无法到达的配电区域,拥有自组网、建设成本少以及数据传输安全等优点的无线传感器网络(Wireless sensor networks,WSNs)可作为配电通信系统中辅助通信的最佳选择,可以很好地解决配电网中“最后一公里”通信连接的难题.但由于配电通信系统对通信数据的可靠性、实时传输要求较高,而无线传感器节点自身拥有的计算能力较小且可使用能量有限,节点在部署后其二次能源的补充会非常困难,如何在满足配电网通信数据可靠、实时传输要求的基础上,进一步减小传感器节点能耗,延长网络使用寿命,成为当前在智能配电网WSNs领域的研究重点[2 ⇓ ⇓ -5 ] . ...
无线传感器网络在智能电网中的应用
1
2010
... 作为建设智能电网(Smart grid,SG)的关键一环,位于输电系统和用电设备之间的智能配电网(Smart distribution network,SDN)结合各种先进的通信技术与智能化管理系统,向用户提供优质可靠的电能供应[1 ] ,其通信网络性能的好坏将影响整个配电系统的稳定运行.因此,在一些有线与无线公网等通信方式均无法到达的配电区域,拥有自组网、建设成本少以及数据传输安全等优点的无线传感器网络(Wireless sensor networks,WSNs)可作为配电通信系统中辅助通信的最佳选择,可以很好地解决配电网中“最后一公里”通信连接的难题.但由于配电通信系统对通信数据的可靠性、实时传输要求较高,而无线传感器节点自身拥有的计算能力较小且可使用能量有限,节点在部署后其二次能源的补充会非常困难,如何在满足配电网通信数据可靠、实时传输要求的基础上,进一步减小传感器节点能耗,延长网络使用寿命,成为当前在智能配电网WSNs领域的研究重点[2 ⇓ ⇓ -5 ] . ...
Application of wireless sensor network in smart power grid
1
2010
... 作为建设智能电网(Smart grid,SG)的关键一环,位于输电系统和用电设备之间的智能配电网(Smart distribution network,SDN)结合各种先进的通信技术与智能化管理系统,向用户提供优质可靠的电能供应[1 ] ,其通信网络性能的好坏将影响整个配电系统的稳定运行.因此,在一些有线与无线公网等通信方式均无法到达的配电区域,拥有自组网、建设成本少以及数据传输安全等优点的无线传感器网络(Wireless sensor networks,WSNs)可作为配电通信系统中辅助通信的最佳选择,可以很好地解决配电网中“最后一公里”通信连接的难题.但由于配电通信系统对通信数据的可靠性、实时传输要求较高,而无线传感器节点自身拥有的计算能力较小且可使用能量有限,节点在部署后其二次能源的补充会非常困难,如何在满足配电网通信数据可靠、实时传输要求的基础上,进一步减小传感器节点能耗,延长网络使用寿命,成为当前在智能配电网WSNs领域的研究重点[2 ⇓ ⇓ -5 ] . ...
基于多跳无线传感器网络的智能电网延时优化研究
1
2019
... 路由算法作为提升WSNs网络性能最有效的手段,近年来受到了众多研究人员的广泛关注.文献[6 ]提出一种多队列理论来建立网络传输时延模型,通过对多跳网络节点MAC层与网络层有效连接,降低智能电网中多跳路由的时延,但其跳数设置固定,灵活性较差.文献[7 ]为满足链路传输的可靠性指标,提出了长跳步可靠性保证机会路由算法,通过减少大量不必要的数据传输提升了端到端数据传输接收率,但对于数据传输的实时性没有进行充分考虑.文献[8 ]提出了一种保障配电网QoS的多径路由算法MRFD,该算法仅充分考虑了可靠性与实时性指标,未对网络寿命做出优化.文献[9 ]通过计算路径损耗和能量损耗权重的综合值,实现最佳可靠传输路径的选择,降低了节点端到端数据传输时的丢包率,但是该算法如果不增加网络开销,容易造成数据丢失.WSNs的路由问题是一种很典型的NP-Hard问题,相比于文献[10 ]提出的多播路由算法以及其他元启发式优化算法,和声搜索算法(Harmony search algorithm,HS)有着实现简单、灵活性高的特点,更适合于情况复杂多变的配电网通信.文献[11 ]提出了一种多跳和声搜索路由算法,通过对多跳传输的能量模型进行设计以及在和声库中引入了音调调整率来减少WSNs中的能量消耗,但性能提升不是很明显.文献[12 ]提出一种能量有效的和声多跳自适应路由算法,仅通过对参数进行自适应调整来达到延长网络寿命的目的,没有对转发节点的选择加以约束,可能导致数据回传增加算法运行时间.文献[13 ]提出基于和声搜索的能量有效路由算法,该算法对经典和声搜索算法进行改进,主要是运用提升边缘节点利用率的思想,通过角度偏移方法和节点移除策略来延长网络寿命,但没有考虑服务质量. ...
Research on time-delay optimization of smart grid based on multi-hop wireless sensor network
1
2019
... 路由算法作为提升WSNs网络性能最有效的手段,近年来受到了众多研究人员的广泛关注.文献[6 ]提出一种多队列理论来建立网络传输时延模型,通过对多跳网络节点MAC层与网络层有效连接,降低智能电网中多跳路由的时延,但其跳数设置固定,灵活性较差.文献[7 ]为满足链路传输的可靠性指标,提出了长跳步可靠性保证机会路由算法,通过减少大量不必要的数据传输提升了端到端数据传输接收率,但对于数据传输的实时性没有进行充分考虑.文献[8 ]提出了一种保障配电网QoS的多径路由算法MRFD,该算法仅充分考虑了可靠性与实时性指标,未对网络寿命做出优化.文献[9 ]通过计算路径损耗和能量损耗权重的综合值,实现最佳可靠传输路径的选择,降低了节点端到端数据传输时的丢包率,但是该算法如果不增加网络开销,容易造成数据丢失.WSNs的路由问题是一种很典型的NP-Hard问题,相比于文献[10 ]提出的多播路由算法以及其他元启发式优化算法,和声搜索算法(Harmony search algorithm,HS)有着实现简单、灵活性高的特点,更适合于情况复杂多变的配电网通信.文献[11 ]提出了一种多跳和声搜索路由算法,通过对多跳传输的能量模型进行设计以及在和声库中引入了音调调整率来减少WSNs中的能量消耗,但性能提升不是很明显.文献[12 ]提出一种能量有效的和声多跳自适应路由算法,仅通过对参数进行自适应调整来达到延长网络寿命的目的,没有对转发节点的选择加以约束,可能导致数据回传增加算法运行时间.文献[13 ]提出基于和声搜索的能量有效路由算法,该算法对经典和声搜索算法进行改进,主要是运用提升边缘节点利用率的思想,通过角度偏移方法和节点移除策略来延长网络寿命,但没有考虑服务质量. ...
智能配电网WSNs可靠性保障机会路由算法研究
1
2019
... 路由算法作为提升WSNs网络性能最有效的手段,近年来受到了众多研究人员的广泛关注.文献[6 ]提出一种多队列理论来建立网络传输时延模型,通过对多跳网络节点MAC层与网络层有效连接,降低智能电网中多跳路由的时延,但其跳数设置固定,灵活性较差.文献[7 ]为满足链路传输的可靠性指标,提出了长跳步可靠性保证机会路由算法,通过减少大量不必要的数据传输提升了端到端数据传输接收率,但对于数据传输的实时性没有进行充分考虑.文献[8 ]提出了一种保障配电网QoS的多径路由算法MRFD,该算法仅充分考虑了可靠性与实时性指标,未对网络寿命做出优化.文献[9 ]通过计算路径损耗和能量损耗权重的综合值,实现最佳可靠传输路径的选择,降低了节点端到端数据传输时的丢包率,但是该算法如果不增加网络开销,容易造成数据丢失.WSNs的路由问题是一种很典型的NP-Hard问题,相比于文献[10 ]提出的多播路由算法以及其他元启发式优化算法,和声搜索算法(Harmony search algorithm,HS)有着实现简单、灵活性高的特点,更适合于情况复杂多变的配电网通信.文献[11 ]提出了一种多跳和声搜索路由算法,通过对多跳传输的能量模型进行设计以及在和声库中引入了音调调整率来减少WSNs中的能量消耗,但性能提升不是很明显.文献[12 ]提出一种能量有效的和声多跳自适应路由算法,仅通过对参数进行自适应调整来达到延长网络寿命的目的,没有对转发节点的选择加以约束,可能导致数据回传增加算法运行时间.文献[13 ]提出基于和声搜索的能量有效路由算法,该算法对经典和声搜索算法进行改进,主要是运用提升边缘节点利用率的思想,通过角度偏移方法和节点移除策略来延长网络寿命,但没有考虑服务质量. ...
Probabilistic routing algorithm for WSNs reliability assurance in smart distribution networks
1
2019
... 路由算法作为提升WSNs网络性能最有效的手段,近年来受到了众多研究人员的广泛关注.文献[6 ]提出一种多队列理论来建立网络传输时延模型,通过对多跳网络节点MAC层与网络层有效连接,降低智能电网中多跳路由的时延,但其跳数设置固定,灵活性较差.文献[7 ]为满足链路传输的可靠性指标,提出了长跳步可靠性保证机会路由算法,通过减少大量不必要的数据传输提升了端到端数据传输接收率,但对于数据传输的实时性没有进行充分考虑.文献[8 ]提出了一种保障配电网QoS的多径路由算法MRFD,该算法仅充分考虑了可靠性与实时性指标,未对网络寿命做出优化.文献[9 ]通过计算路径损耗和能量损耗权重的综合值,实现最佳可靠传输路径的选择,降低了节点端到端数据传输时的丢包率,但是该算法如果不增加网络开销,容易造成数据丢失.WSNs的路由问题是一种很典型的NP-Hard问题,相比于文献[10 ]提出的多播路由算法以及其他元启发式优化算法,和声搜索算法(Harmony search algorithm,HS)有着实现简单、灵活性高的特点,更适合于情况复杂多变的配电网通信.文献[11 ]提出了一种多跳和声搜索路由算法,通过对多跳传输的能量模型进行设计以及在和声库中引入了音调调整率来减少WSNs中的能量消耗,但性能提升不是很明显.文献[12 ]提出一种能量有效的和声多跳自适应路由算法,仅通过对参数进行自适应调整来达到延长网络寿命的目的,没有对转发节点的选择加以约束,可能导致数据回传增加算法运行时间.文献[13 ]提出基于和声搜索的能量有效路由算法,该算法对经典和声搜索算法进行改进,主要是运用提升边缘节点利用率的思想,通过角度偏移方法和节点移除策略来延长网络寿命,但没有考虑服务质量. ...
面向配电通信网的WMSNs多路径QoS路由算法
9
2016
... 路由算法作为提升WSNs网络性能最有效的手段,近年来受到了众多研究人员的广泛关注.文献[6 ]提出一种多队列理论来建立网络传输时延模型,通过对多跳网络节点MAC层与网络层有效连接,降低智能电网中多跳路由的时延,但其跳数设置固定,灵活性较差.文献[7 ]为满足链路传输的可靠性指标,提出了长跳步可靠性保证机会路由算法,通过减少大量不必要的数据传输提升了端到端数据传输接收率,但对于数据传输的实时性没有进行充分考虑.文献[8 ]提出了一种保障配电网QoS的多径路由算法MRFD,该算法仅充分考虑了可靠性与实时性指标,未对网络寿命做出优化.文献[9 ]通过计算路径损耗和能量损耗权重的综合值,实现最佳可靠传输路径的选择,降低了节点端到端数据传输时的丢包率,但是该算法如果不增加网络开销,容易造成数据丢失.WSNs的路由问题是一种很典型的NP-Hard问题,相比于文献[10 ]提出的多播路由算法以及其他元启发式优化算法,和声搜索算法(Harmony search algorithm,HS)有着实现简单、灵活性高的特点,更适合于情况复杂多变的配电网通信.文献[11 ]提出了一种多跳和声搜索路由算法,通过对多跳传输的能量模型进行设计以及在和声库中引入了音调调整率来减少WSNs中的能量消耗,但性能提升不是很明显.文献[12 ]提出一种能量有效的和声多跳自适应路由算法,仅通过对参数进行自适应调整来达到延长网络寿命的目的,没有对转发节点的选择加以约束,可能导致数据回传增加算法运行时间.文献[13 ]提出基于和声搜索的能量有效路由算法,该算法对经典和声搜索算法进行改进,主要是运用提升边缘节点利用率的思想,通过角度偏移方法和节点移除策略来延长网络寿命,但没有考虑服务质量. ...
... 配电网自动化体系大致可分为三层[8 ] ,第一层为配电网中服务器、工作站、网络设备以及相应的配套软件共同组成的主站层,也是整个体系中的核心部分,负责将配电终端所采集的信息收集起来或转发;第二层为布置在变电站或开闭所中,实现管辖范围内配电SCADA以及故障诊断功能的子站层,这部分可以实现对配电线路的监控,并留有空间拓展,以完成对本地配电信息的实时监控;第三层则为配电网中重要组成部分的终端层,这一层包括FTU、DTU、TTU等终端,主要作用是完成对设备的监测并将信息及时采集并上传.如图1 所示是配电网通信结构,各层的通信方式都可以根据其自身的特点来选取.对于配电通信系统,无线传感器网络可以收集和传输各种故障、保护信息、居民用电信息等. ...
... 为验证所提方法性能,将在Matlab 2021b环境下进行仿真试验.根据有效的通信半径,在环境范围为180 m×180 m的区域当中,随机布撒试验节点200个,其他仿真参数如表1 所示.将在试验时着重在网络使用寿命(即网络中节点死亡时间)、端到端传输时延(即节点平均传输数据时间)以及可靠性(端到端数据丢包率)三个方面与文献[8 ]和文献[12 ]中的算法进行对比分析. ...
... 为更加全面地验证所提算法在网络使用寿命方面的性能,将在两种不同试验环境下与文献[8 ]和文献[12 ]算法进行对比,即模拟两种不同的节点发送形式. ...
... 如图4 所示,在试验场景1的环境下,固定节点进行数据传输,可以看出,文献[8 ]方法与文献[12 ]的方法首次出现节点死亡是在342轮和399轮,而所提算法在460轮才出现第一个死亡节点,如图5 所示,在试验场景2的环境下,所有节点随机循环发送数据,三种算法首次出现节点死亡是在37轮、58轮和69轮.因此,在试验场景1下所提算法相比文献[8 ]与文献[12 ]中的方法分别有34.5%和15.2%的性能提升,在试验场景2下,所提算法相比文献[8 ] 与文献[12 ]的算法也分别有28.5%和8.6%的性能提升.总的来说,得益于对节点转发的优化设计和对参数自适应改进,使得算法减少了无效运行,无论是固定节点发送数据还是节点循环发送数据均有着优异的性能表现. ...
... 所示,在试验场景2的环境下,所有节点随机循环发送数据,三种算法首次出现节点死亡是在37轮、58轮和69轮.因此,在试验场景1下所提算法相比文献[8 ]与文献[12 ]中的方法分别有34.5%和15.2%的性能提升,在试验场景2下,所提算法相比文献[8 ] 与文献[12 ]的算法也分别有28.5%和8.6%的性能提升.总的来说,得益于对节点转发的优化设计和对参数自适应改进,使得算法减少了无效运行,无论是固定节点发送数据还是节点循环发送数据均有着优异的性能表现. ...
... ]中的方法分别有34.5%和15.2%的性能提升,在试验场景2下,所提算法相比文献[8 ] 与文献[12 ]的算法也分别有28.5%和8.6%的性能提升.总的来说,得益于对节点转发的优化设计和对参数自适应改进,使得算法减少了无效运行,无论是固定节点发送数据还是节点循环发送数据均有着优异的性能表现. ...
... 为降低时延,所提算法通过对下一跳节点集优化,约束其传输方向,保证数据的正向传输,避免数据回传,使得算法在较短时间能够求出最短路径.为验证其时延性能,在不同节点密度下,分别进行多次试验得到的最短路径平均时延,如图6 所示,可以看出相较于文献[8 ]的算法,所提算法求得的最短路径平均时延降低延迟效果明显,有着3%~6%的性能提升. ...
... 从图7 可以看出在发送不同大小数据包的场景下,三种方法均有着丢包率的波动,但所提方法相较于文献[8 ]与文献[12 ]方法丢包率更低,介于3.5%~6%.这是由于所提方法在节点选择概率公式中综合考虑了丢包率和时延等因素,使得从和声库生成阶段到新解产生阶段都能够在保证可靠性的前提下搜索路径,使得所提算法即便是在更注重能耗的情况下也能使得数据传输更可靠. ...
QoS assured multipath routing algorithm for distribution communication network
9
2016
... 路由算法作为提升WSNs网络性能最有效的手段,近年来受到了众多研究人员的广泛关注.文献[6 ]提出一种多队列理论来建立网络传输时延模型,通过对多跳网络节点MAC层与网络层有效连接,降低智能电网中多跳路由的时延,但其跳数设置固定,灵活性较差.文献[7 ]为满足链路传输的可靠性指标,提出了长跳步可靠性保证机会路由算法,通过减少大量不必要的数据传输提升了端到端数据传输接收率,但对于数据传输的实时性没有进行充分考虑.文献[8 ]提出了一种保障配电网QoS的多径路由算法MRFD,该算法仅充分考虑了可靠性与实时性指标,未对网络寿命做出优化.文献[9 ]通过计算路径损耗和能量损耗权重的综合值,实现最佳可靠传输路径的选择,降低了节点端到端数据传输时的丢包率,但是该算法如果不增加网络开销,容易造成数据丢失.WSNs的路由问题是一种很典型的NP-Hard问题,相比于文献[10 ]提出的多播路由算法以及其他元启发式优化算法,和声搜索算法(Harmony search algorithm,HS)有着实现简单、灵活性高的特点,更适合于情况复杂多变的配电网通信.文献[11 ]提出了一种多跳和声搜索路由算法,通过对多跳传输的能量模型进行设计以及在和声库中引入了音调调整率来减少WSNs中的能量消耗,但性能提升不是很明显.文献[12 ]提出一种能量有效的和声多跳自适应路由算法,仅通过对参数进行自适应调整来达到延长网络寿命的目的,没有对转发节点的选择加以约束,可能导致数据回传增加算法运行时间.文献[13 ]提出基于和声搜索的能量有效路由算法,该算法对经典和声搜索算法进行改进,主要是运用提升边缘节点利用率的思想,通过角度偏移方法和节点移除策略来延长网络寿命,但没有考虑服务质量. ...
... 配电网自动化体系大致可分为三层[8 ] ,第一层为配电网中服务器、工作站、网络设备以及相应的配套软件共同组成的主站层,也是整个体系中的核心部分,负责将配电终端所采集的信息收集起来或转发;第二层为布置在变电站或开闭所中,实现管辖范围内配电SCADA以及故障诊断功能的子站层,这部分可以实现对配电线路的监控,并留有空间拓展,以完成对本地配电信息的实时监控;第三层则为配电网中重要组成部分的终端层,这一层包括FTU、DTU、TTU等终端,主要作用是完成对设备的监测并将信息及时采集并上传.如图1 所示是配电网通信结构,各层的通信方式都可以根据其自身的特点来选取.对于配电通信系统,无线传感器网络可以收集和传输各种故障、保护信息、居民用电信息等. ...
... 为验证所提方法性能,将在Matlab 2021b环境下进行仿真试验.根据有效的通信半径,在环境范围为180 m×180 m的区域当中,随机布撒试验节点200个,其他仿真参数如表1 所示.将在试验时着重在网络使用寿命(即网络中节点死亡时间)、端到端传输时延(即节点平均传输数据时间)以及可靠性(端到端数据丢包率)三个方面与文献[8 ]和文献[12 ]中的算法进行对比分析. ...
... 为更加全面地验证所提算法在网络使用寿命方面的性能,将在两种不同试验环境下与文献[8 ]和文献[12 ]算法进行对比,即模拟两种不同的节点发送形式. ...
... 如图4 所示,在试验场景1的环境下,固定节点进行数据传输,可以看出,文献[8 ]方法与文献[12 ]的方法首次出现节点死亡是在342轮和399轮,而所提算法在460轮才出现第一个死亡节点,如图5 所示,在试验场景2的环境下,所有节点随机循环发送数据,三种算法首次出现节点死亡是在37轮、58轮和69轮.因此,在试验场景1下所提算法相比文献[8 ]与文献[12 ]中的方法分别有34.5%和15.2%的性能提升,在试验场景2下,所提算法相比文献[8 ] 与文献[12 ]的算法也分别有28.5%和8.6%的性能提升.总的来说,得益于对节点转发的优化设计和对参数自适应改进,使得算法减少了无效运行,无论是固定节点发送数据还是节点循环发送数据均有着优异的性能表现. ...
... 所示,在试验场景2的环境下,所有节点随机循环发送数据,三种算法首次出现节点死亡是在37轮、58轮和69轮.因此,在试验场景1下所提算法相比文献[8 ]与文献[12 ]中的方法分别有34.5%和15.2%的性能提升,在试验场景2下,所提算法相比文献[8 ] 与文献[12 ]的算法也分别有28.5%和8.6%的性能提升.总的来说,得益于对节点转发的优化设计和对参数自适应改进,使得算法减少了无效运行,无论是固定节点发送数据还是节点循环发送数据均有着优异的性能表现. ...
... ]中的方法分别有34.5%和15.2%的性能提升,在试验场景2下,所提算法相比文献[8 ] 与文献[12 ]的算法也分别有28.5%和8.6%的性能提升.总的来说,得益于对节点转发的优化设计和对参数自适应改进,使得算法减少了无效运行,无论是固定节点发送数据还是节点循环发送数据均有着优异的性能表现. ...
... 为降低时延,所提算法通过对下一跳节点集优化,约束其传输方向,保证数据的正向传输,避免数据回传,使得算法在较短时间能够求出最短路径.为验证其时延性能,在不同节点密度下,分别进行多次试验得到的最短路径平均时延,如图6 所示,可以看出相较于文献[8 ]的算法,所提算法求得的最短路径平均时延降低延迟效果明显,有着3%~6%的性能提升. ...
... 从图7 可以看出在发送不同大小数据包的场景下,三种方法均有着丢包率的波动,但所提方法相较于文献[8 ]与文献[12 ]方法丢包率更低,介于3.5%~6%.这是由于所提方法在节点选择概率公式中综合考虑了丢包率和时延等因素,使得从和声库生成阶段到新解产生阶段都能够在保证可靠性的前提下搜索路径,使得所提算法即便是在更注重能耗的情况下也能使得数据传输更可靠. ...
满足可靠及泛在需求的无线传感器网络部署研究
1
2019
... 路由算法作为提升WSNs网络性能最有效的手段,近年来受到了众多研究人员的广泛关注.文献[6 ]提出一种多队列理论来建立网络传输时延模型,通过对多跳网络节点MAC层与网络层有效连接,降低智能电网中多跳路由的时延,但其跳数设置固定,灵活性较差.文献[7 ]为满足链路传输的可靠性指标,提出了长跳步可靠性保证机会路由算法,通过减少大量不必要的数据传输提升了端到端数据传输接收率,但对于数据传输的实时性没有进行充分考虑.文献[8 ]提出了一种保障配电网QoS的多径路由算法MRFD,该算法仅充分考虑了可靠性与实时性指标,未对网络寿命做出优化.文献[9 ]通过计算路径损耗和能量损耗权重的综合值,实现最佳可靠传输路径的选择,降低了节点端到端数据传输时的丢包率,但是该算法如果不增加网络开销,容易造成数据丢失.WSNs的路由问题是一种很典型的NP-Hard问题,相比于文献[10 ]提出的多播路由算法以及其他元启发式优化算法,和声搜索算法(Harmony search algorithm,HS)有着实现简单、灵活性高的特点,更适合于情况复杂多变的配电网通信.文献[11 ]提出了一种多跳和声搜索路由算法,通过对多跳传输的能量模型进行设计以及在和声库中引入了音调调整率来减少WSNs中的能量消耗,但性能提升不是很明显.文献[12 ]提出一种能量有效的和声多跳自适应路由算法,仅通过对参数进行自适应调整来达到延长网络寿命的目的,没有对转发节点的选择加以约束,可能导致数据回传增加算法运行时间.文献[13 ]提出基于和声搜索的能量有效路由算法,该算法对经典和声搜索算法进行改进,主要是运用提升边缘节点利用率的思想,通过角度偏移方法和节点移除策略来延长网络寿命,但没有考虑服务质量. ...
Research on wireless sensor network deployment to meet reliable and ubiquitous requirements
1
2019
... 路由算法作为提升WSNs网络性能最有效的手段,近年来受到了众多研究人员的广泛关注.文献[6 ]提出一种多队列理论来建立网络传输时延模型,通过对多跳网络节点MAC层与网络层有效连接,降低智能电网中多跳路由的时延,但其跳数设置固定,灵活性较差.文献[7 ]为满足链路传输的可靠性指标,提出了长跳步可靠性保证机会路由算法,通过减少大量不必要的数据传输提升了端到端数据传输接收率,但对于数据传输的实时性没有进行充分考虑.文献[8 ]提出了一种保障配电网QoS的多径路由算法MRFD,该算法仅充分考虑了可靠性与实时性指标,未对网络寿命做出优化.文献[9 ]通过计算路径损耗和能量损耗权重的综合值,实现最佳可靠传输路径的选择,降低了节点端到端数据传输时的丢包率,但是该算法如果不增加网络开销,容易造成数据丢失.WSNs的路由问题是一种很典型的NP-Hard问题,相比于文献[10 ]提出的多播路由算法以及其他元启发式优化算法,和声搜索算法(Harmony search algorithm,HS)有着实现简单、灵活性高的特点,更适合于情况复杂多变的配电网通信.文献[11 ]提出了一种多跳和声搜索路由算法,通过对多跳传输的能量模型进行设计以及在和声库中引入了音调调整率来减少WSNs中的能量消耗,但性能提升不是很明显.文献[12 ]提出一种能量有效的和声多跳自适应路由算法,仅通过对参数进行自适应调整来达到延长网络寿命的目的,没有对转发节点的选择加以约束,可能导致数据回传增加算法运行时间.文献[13 ]提出基于和声搜索的能量有效路由算法,该算法对经典和声搜索算法进行改进,主要是运用提升边缘节点利用率的思想,通过角度偏移方法和节点移除策略来延长网络寿命,但没有考虑服务质量. ...
面向输电线故障信息传输的多播路由
1
2020
... 路由算法作为提升WSNs网络性能最有效的手段,近年来受到了众多研究人员的广泛关注.文献[6 ]提出一种多队列理论来建立网络传输时延模型,通过对多跳网络节点MAC层与网络层有效连接,降低智能电网中多跳路由的时延,但其跳数设置固定,灵活性较差.文献[7 ]为满足链路传输的可靠性指标,提出了长跳步可靠性保证机会路由算法,通过减少大量不必要的数据传输提升了端到端数据传输接收率,但对于数据传输的实时性没有进行充分考虑.文献[8 ]提出了一种保障配电网QoS的多径路由算法MRFD,该算法仅充分考虑了可靠性与实时性指标,未对网络寿命做出优化.文献[9 ]通过计算路径损耗和能量损耗权重的综合值,实现最佳可靠传输路径的选择,降低了节点端到端数据传输时的丢包率,但是该算法如果不增加网络开销,容易造成数据丢失.WSNs的路由问题是一种很典型的NP-Hard问题,相比于文献[10 ]提出的多播路由算法以及其他元启发式优化算法,和声搜索算法(Harmony search algorithm,HS)有着实现简单、灵活性高的特点,更适合于情况复杂多变的配电网通信.文献[11 ]提出了一种多跳和声搜索路由算法,通过对多跳传输的能量模型进行设计以及在和声库中引入了音调调整率来减少WSNs中的能量消耗,但性能提升不是很明显.文献[12 ]提出一种能量有效的和声多跳自适应路由算法,仅通过对参数进行自适应调整来达到延长网络寿命的目的,没有对转发节点的选择加以约束,可能导致数据回传增加算法运行时间.文献[13 ]提出基于和声搜索的能量有效路由算法,该算法对经典和声搜索算法进行改进,主要是运用提升边缘节点利用率的思想,通过角度偏移方法和节点移除策略来延长网络寿命,但没有考虑服务质量. ...
Multicast routing for transmission of fault information on power transmission line
1
2020
... 路由算法作为提升WSNs网络性能最有效的手段,近年来受到了众多研究人员的广泛关注.文献[6 ]提出一种多队列理论来建立网络传输时延模型,通过对多跳网络节点MAC层与网络层有效连接,降低智能电网中多跳路由的时延,但其跳数设置固定,灵活性较差.文献[7 ]为满足链路传输的可靠性指标,提出了长跳步可靠性保证机会路由算法,通过减少大量不必要的数据传输提升了端到端数据传输接收率,但对于数据传输的实时性没有进行充分考虑.文献[8 ]提出了一种保障配电网QoS的多径路由算法MRFD,该算法仅充分考虑了可靠性与实时性指标,未对网络寿命做出优化.文献[9 ]通过计算路径损耗和能量损耗权重的综合值,实现最佳可靠传输路径的选择,降低了节点端到端数据传输时的丢包率,但是该算法如果不增加网络开销,容易造成数据丢失.WSNs的路由问题是一种很典型的NP-Hard问题,相比于文献[10 ]提出的多播路由算法以及其他元启发式优化算法,和声搜索算法(Harmony search algorithm,HS)有着实现简单、灵活性高的特点,更适合于情况复杂多变的配电网通信.文献[11 ]提出了一种多跳和声搜索路由算法,通过对多跳传输的能量模型进行设计以及在和声库中引入了音调调整率来减少WSNs中的能量消耗,但性能提升不是很明显.文献[12 ]提出一种能量有效的和声多跳自适应路由算法,仅通过对参数进行自适应调整来达到延长网络寿命的目的,没有对转发节点的选择加以约束,可能导致数据回传增加算法运行时间.文献[13 ]提出基于和声搜索的能量有效路由算法,该算法对经典和声搜索算法进行改进,主要是运用提升边缘节点利用率的思想,通过角度偏移方法和节点移除策略来延长网络寿命,但没有考虑服务质量. ...
Energy optimization in multi-hop wireless sensor networks based on proposed harmony search routing algorithm
1
2021
... 路由算法作为提升WSNs网络性能最有效的手段,近年来受到了众多研究人员的广泛关注.文献[6 ]提出一种多队列理论来建立网络传输时延模型,通过对多跳网络节点MAC层与网络层有效连接,降低智能电网中多跳路由的时延,但其跳数设置固定,灵活性较差.文献[7 ]为满足链路传输的可靠性指标,提出了长跳步可靠性保证机会路由算法,通过减少大量不必要的数据传输提升了端到端数据传输接收率,但对于数据传输的实时性没有进行充分考虑.文献[8 ]提出了一种保障配电网QoS的多径路由算法MRFD,该算法仅充分考虑了可靠性与实时性指标,未对网络寿命做出优化.文献[9 ]通过计算路径损耗和能量损耗权重的综合值,实现最佳可靠传输路径的选择,降低了节点端到端数据传输时的丢包率,但是该算法如果不增加网络开销,容易造成数据丢失.WSNs的路由问题是一种很典型的NP-Hard问题,相比于文献[10 ]提出的多播路由算法以及其他元启发式优化算法,和声搜索算法(Harmony search algorithm,HS)有着实现简单、灵活性高的特点,更适合于情况复杂多变的配电网通信.文献[11 ]提出了一种多跳和声搜索路由算法,通过对多跳传输的能量模型进行设计以及在和声库中引入了音调调整率来减少WSNs中的能量消耗,但性能提升不是很明显.文献[12 ]提出一种能量有效的和声多跳自适应路由算法,仅通过对参数进行自适应调整来达到延长网络寿命的目的,没有对转发节点的选择加以约束,可能导致数据回传增加算法运行时间.文献[13 ]提出基于和声搜索的能量有效路由算法,该算法对经典和声搜索算法进行改进,主要是运用提升边缘节点利用率的思想,通过角度偏移方法和节点移除策略来延长网络寿命,但没有考虑服务质量. ...
Adaptive multi-hop routing algorithm based on harmony search in WSNs
7
2017
... 路由算法作为提升WSNs网络性能最有效的手段,近年来受到了众多研究人员的广泛关注.文献[6 ]提出一种多队列理论来建立网络传输时延模型,通过对多跳网络节点MAC层与网络层有效连接,降低智能电网中多跳路由的时延,但其跳数设置固定,灵活性较差.文献[7 ]为满足链路传输的可靠性指标,提出了长跳步可靠性保证机会路由算法,通过减少大量不必要的数据传输提升了端到端数据传输接收率,但对于数据传输的实时性没有进行充分考虑.文献[8 ]提出了一种保障配电网QoS的多径路由算法MRFD,该算法仅充分考虑了可靠性与实时性指标,未对网络寿命做出优化.文献[9 ]通过计算路径损耗和能量损耗权重的综合值,实现最佳可靠传输路径的选择,降低了节点端到端数据传输时的丢包率,但是该算法如果不增加网络开销,容易造成数据丢失.WSNs的路由问题是一种很典型的NP-Hard问题,相比于文献[10 ]提出的多播路由算法以及其他元启发式优化算法,和声搜索算法(Harmony search algorithm,HS)有着实现简单、灵活性高的特点,更适合于情况复杂多变的配电网通信.文献[11 ]提出了一种多跳和声搜索路由算法,通过对多跳传输的能量模型进行设计以及在和声库中引入了音调调整率来减少WSNs中的能量消耗,但性能提升不是很明显.文献[12 ]提出一种能量有效的和声多跳自适应路由算法,仅通过对参数进行自适应调整来达到延长网络寿命的目的,没有对转发节点的选择加以约束,可能导致数据回传增加算法运行时间.文献[13 ]提出基于和声搜索的能量有效路由算法,该算法对经典和声搜索算法进行改进,主要是运用提升边缘节点利用率的思想,通过角度偏移方法和节点移除策略来延长网络寿命,但没有考虑服务质量. ...
... 为验证所提方法性能,将在Matlab 2021b环境下进行仿真试验.根据有效的通信半径,在环境范围为180 m×180 m的区域当中,随机布撒试验节点200个,其他仿真参数如表1 所示.将在试验时着重在网络使用寿命(即网络中节点死亡时间)、端到端传输时延(即节点平均传输数据时间)以及可靠性(端到端数据丢包率)三个方面与文献[8 ]和文献[12 ]中的算法进行对比分析. ...
... 为更加全面地验证所提算法在网络使用寿命方面的性能,将在两种不同试验环境下与文献[8 ]和文献[12 ]算法进行对比,即模拟两种不同的节点发送形式. ...
... 如图4 所示,在试验场景1的环境下,固定节点进行数据传输,可以看出,文献[8 ]方法与文献[12 ]的方法首次出现节点死亡是在342轮和399轮,而所提算法在460轮才出现第一个死亡节点,如图5 所示,在试验场景2的环境下,所有节点随机循环发送数据,三种算法首次出现节点死亡是在37轮、58轮和69轮.因此,在试验场景1下所提算法相比文献[8 ]与文献[12 ]中的方法分别有34.5%和15.2%的性能提升,在试验场景2下,所提算法相比文献[8 ] 与文献[12 ]的算法也分别有28.5%和8.6%的性能提升.总的来说,得益于对节点转发的优化设计和对参数自适应改进,使得算法减少了无效运行,无论是固定节点发送数据还是节点循环发送数据均有着优异的性能表现. ...
... ]与文献[12 ]中的方法分别有34.5%和15.2%的性能提升,在试验场景2下,所提算法相比文献[8 ] 与文献[12 ]的算法也分别有28.5%和8.6%的性能提升.总的来说,得益于对节点转发的优化设计和对参数自适应改进,使得算法减少了无效运行,无论是固定节点发送数据还是节点循环发送数据均有着优异的性能表现. ...
... ] 与文献[12 ]的算法也分别有28.5%和8.6%的性能提升.总的来说,得益于对节点转发的优化设计和对参数自适应改进,使得算法减少了无效运行,无论是固定节点发送数据还是节点循环发送数据均有着优异的性能表现. ...
... 从图7 可以看出在发送不同大小数据包的场景下,三种方法均有着丢包率的波动,但所提方法相较于文献[8 ]与文献[12 ]方法丢包率更低,介于3.5%~6%.这是由于所提方法在节点选择概率公式中综合考虑了丢包率和时延等因素,使得从和声库生成阶段到新解产生阶段都能够在保证可靠性的前提下搜索路径,使得所提算法即便是在更注重能耗的情况下也能使得数据传输更可靠. ...
基于和声搜索的能量有效路由算法
1
2021
... 路由算法作为提升WSNs网络性能最有效的手段,近年来受到了众多研究人员的广泛关注.文献[6 ]提出一种多队列理论来建立网络传输时延模型,通过对多跳网络节点MAC层与网络层有效连接,降低智能电网中多跳路由的时延,但其跳数设置固定,灵活性较差.文献[7 ]为满足链路传输的可靠性指标,提出了长跳步可靠性保证机会路由算法,通过减少大量不必要的数据传输提升了端到端数据传输接收率,但对于数据传输的实时性没有进行充分考虑.文献[8 ]提出了一种保障配电网QoS的多径路由算法MRFD,该算法仅充分考虑了可靠性与实时性指标,未对网络寿命做出优化.文献[9 ]通过计算路径损耗和能量损耗权重的综合值,实现最佳可靠传输路径的选择,降低了节点端到端数据传输时的丢包率,但是该算法如果不增加网络开销,容易造成数据丢失.WSNs的路由问题是一种很典型的NP-Hard问题,相比于文献[10 ]提出的多播路由算法以及其他元启发式优化算法,和声搜索算法(Harmony search algorithm,HS)有着实现简单、灵活性高的特点,更适合于情况复杂多变的配电网通信.文献[11 ]提出了一种多跳和声搜索路由算法,通过对多跳传输的能量模型进行设计以及在和声库中引入了音调调整率来减少WSNs中的能量消耗,但性能提升不是很明显.文献[12 ]提出一种能量有效的和声多跳自适应路由算法,仅通过对参数进行自适应调整来达到延长网络寿命的目的,没有对转发节点的选择加以约束,可能导致数据回传增加算法运行时间.文献[13 ]提出基于和声搜索的能量有效路由算法,该算法对经典和声搜索算法进行改进,主要是运用提升边缘节点利用率的思想,通过角度偏移方法和节点移除策略来延长网络寿命,但没有考虑服务质量. ...
Energy efficient routing algorithm based on harmony search
1
2021
... 路由算法作为提升WSNs网络性能最有效的手段,近年来受到了众多研究人员的广泛关注.文献[6 ]提出一种多队列理论来建立网络传输时延模型,通过对多跳网络节点MAC层与网络层有效连接,降低智能电网中多跳路由的时延,但其跳数设置固定,灵活性较差.文献[7 ]为满足链路传输的可靠性指标,提出了长跳步可靠性保证机会路由算法,通过减少大量不必要的数据传输提升了端到端数据传输接收率,但对于数据传输的实时性没有进行充分考虑.文献[8 ]提出了一种保障配电网QoS的多径路由算法MRFD,该算法仅充分考虑了可靠性与实时性指标,未对网络寿命做出优化.文献[9 ]通过计算路径损耗和能量损耗权重的综合值,实现最佳可靠传输路径的选择,降低了节点端到端数据传输时的丢包率,但是该算法如果不增加网络开销,容易造成数据丢失.WSNs的路由问题是一种很典型的NP-Hard问题,相比于文献[10 ]提出的多播路由算法以及其他元启发式优化算法,和声搜索算法(Harmony search algorithm,HS)有着实现简单、灵活性高的特点,更适合于情况复杂多变的配电网通信.文献[11 ]提出了一种多跳和声搜索路由算法,通过对多跳传输的能量模型进行设计以及在和声库中引入了音调调整率来减少WSNs中的能量消耗,但性能提升不是很明显.文献[12 ]提出一种能量有效的和声多跳自适应路由算法,仅通过对参数进行自适应调整来达到延长网络寿命的目的,没有对转发节点的选择加以约束,可能导致数据回传增加算法运行时间.文献[13 ]提出基于和声搜索的能量有效路由算法,该算法对经典和声搜索算法进行改进,主要是运用提升边缘节点利用率的思想,通过角度偏移方法和节点移除策略来延长网络寿命,但没有考虑服务质量. ...
An energy-balanced routing method based on forward-aware factor for wireless sensor networks
1
2014
... 本文使用文献[14 ]中提供的能耗模型来计算传递信息过程中节点的能量消耗.节点能耗大多是由于数据包长度、节点与节点间的距离等因素导致,其中信息的传输过程会产生大量的能量消耗,占据了总消耗能量中的绝大部分,因此,在能耗模型中,只考虑在通信过程中产生的能量损失. ...
1
2015
... 通常,在配网区域中会出现电磁干扰.因此,为体现该算法适用于配电区域,将设置干扰源,其中的干扰公式如下[15 ] ...
1
2015
... 通常,在配网区域中会出现电磁干扰.因此,为体现该算法适用于配电区域,将设置干扰源,其中的干扰公式如下[15 ] ...
An improved differential-based harmony search algorithm with linear dynamic domain
1
2020
... 和声搜索算法是一种启发式算法[16 ] ,是模仿音乐家即兴创作而产生的,由GEEM等[17 ] 在2001年提出.该算法共有五个步骤. ...
A new heuristic optimization algorithm:Harmony search
1
2001
... 和声搜索算法是一种启发式算法[16 ] ,是模仿音乐家即兴创作而产生的,由GEEM等[17 ] 在2001年提出.该算法共有五个步骤. ...
和声搜索算法改进与应用
1
2014
... 定义参数数值.主要参数有和声库大小HMS,和声记忆库保留概率HMCR,扰动概率PAR,音调微调幅度BW以及最大迭代次数${{T}_{\max }}$ [18 ] . ...
Improvement and application of harmony search algorithm
1
2014
... 定义参数数值.主要参数有和声库大小HMS,和声记忆库保留概率HMCR,扰动概率PAR,音调微调幅度BW以及最大迭代次数${{T}_{\max }}$ [18 ] . ...
A quantum multi-objective optimization algorithm based on harmony search method
1
2021
... 传统HS算法逻辑比较简单,易于实现,仅通过对HMCR和PAR的调整就能达到对整个流程的控制[19 ] .但在路由寻址的问题上,由于HS算法大多用于处理连续值的优化,而每个节点的ID编码唯一且随机布撒,路径选择往往是离散的,因此,针对WSN路由问题的特点以及为满足配电通信需求,需要对经典HS算法进行改进. ...
Adaptive harmony search algorithm utilizing differential evolution and opposition-based learning
1
2021
... 通常情况下,HS算法中HMCR与PAR的值是固定设置,但HS算法中参数对于算法结果的影响是非常大的,固定设置参数容易导致算法陷入局部最优[20 ] ,因此,本文采用自适应调整的方法对HMCR和PAR的取值改进.在算法运行的初期,和声库中初始解向量质量较差容易存在较大的误差,因此取较大HMCR;在寻优中后期,质量较好的解向量在和声库中逐渐增多,各解向量之间误差也变小,故HMCR取较小值,而PAR则需要取较大值,从而加快该算法收敛,提升全局最优搜索能力. ...