计及新能源虚拟惯量的电力系统最低惯量评估*

doi:10.11985/2024.01.027

计及新能源虚拟惯量的电力系统最低惯量评估^*

王毅^,¹^,², 陈中^,³, 周涛^,⁴, 刘勃³, 刘子诚⁴

1.智能电网保护和运行控制国家重点实验室南京 211106

2.南瑞集团(国网电力科学研究院)有限公司南京 211106

3.东南大学电气工程学院南京 210096

4.南京理工大学自动化学院南京 210094

Evaluation of Minimum Inertia of Power System Considering Virtual Inertia of Renewable Energy

WANG Yi^,¹^,², CHEN Zhong^,³, ZHOU Tao^,⁴, LIU Bo³, LIU Zicheng⁴

1. State Key Laboratory of Smart Grid Protection and Control, Nanjing 211106

2. NARI Group Corporation, Nanjing 211106

3. School of Electrical Engineering, Southeast University, Nanjing 210096

4. School of Automation, Nanjing University of Science and Technology, Nanjing 210094

收稿日期: 2023-02-19 修回日期: 2023-06-26

基金资助:

智能电网保护和运行控制国家重点实验室开放课题资助项目(SGNR 0000KJJS2200305)

Received: 2023-02-19 Revised: 2023-06-26

作者简介 About authors

王毅，男，1980年生，高级工程师。主要研究方向为电力系统运行与控制。E-mail：wongyee@outlook.com;

陈中，男，1975年生，研究员，博士研究生导师。主要研究方向为电力系统稳定与控制、电动汽车与电网互动。E-mail：zhongchen@seu.edu.cn;

周涛，男，1991年生，博士，讲师。主要研究方向为电力系统运行与控制、新型电力系统频率稳定。E-mail：zhoutaonjust@njust.edu.cn

摘要

电网频率安全和稳定性是电力系统的重要性能指标，而电力系统的惯量水平是影响频率响应能力的关键因素。由于我国实施双碳战略，新能源发电比例持续提高，导致电力系统的惯量水平不断下降，使得电网在遭受有功扰动时的频率波动加剧，系统运行边界收缩。为了提高电力系统在高新能源渗透场景下的惯量态势感知能力，增强电力系统对有功扰动的频率适应性、量化系统运行边界，基于电力系统频率响应模型，分析了电网在受到有功扰动后不同时间尺度下的频率响应过程，构建了系统频率响应数学关系。基于频率响应全过程，构建计及新能源虚拟惯量的电力系统最低惯量评估模型及其求解算法。最后，基于IEEE-39节点模型，通过仿真试验验证了所提方法的有效性和准确性。

关键词： 低惯量电力系统; 虚拟惯量; 最低惯量评估; 频率稳定性

Abstract

Grid frequency security and stability are important performance indicators of the power system, and the inertia level of the power system is a key factor affecting the frequency response capability. Due to the implementation of the dual-carbon strategy in China, the proportion of new energy generation continues to increase, resulting in a continuous decline in the inertia level of the power system, which intensifies the frequency fluctuation of the power grid when it suffers from active perturbations and shrinks the system operation boundary. In order to improve the inertia situational awareness of the power system in the high-tech energy penetration scenario, enhance the frequency adaptability of the power system to active perturbations, and quantify the system operation boundary, based on the frequency response model of the power system, the frequency response process of the power grid in different time scales after being subjected to active perturbations is analyzed, and the mathematical relationship of the system frequency response is constructed. Based on the frequency response process, the minimum inertia assessment model and its solution algorithm are constructed to take into account the virtual inertia of new energy sources. Finally, based on the IEEE-39 node model, the effectiveness and accuracy of the proposed method are verified through simulation experiments.

Keywords： Low inertia power system; virtual inertia; minimum inertia evaluation; frequency stability

PDF (17731KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

王毅, 陈中, 周涛, 刘勃, 刘子诚. 计及新能源虚拟惯量的电力系统最低惯量评估^*[J]. 电气工程学报, 2024, 19(1): 254-260 doi:10.11985/2024.01.027

WANG Yi, CHEN Zhong, ZHOU Tao, LIU Bo, LIU Zicheng. Evaluation of Minimum Inertia of Power System Considering Virtual Inertia of Renewable Energy[J]. Chinese Journal of Electrical Engineering, 2024, 19(1): 254-260 doi:10.11985/2024.01.027

1 引言

近年来，国内外电力系统正逐步从常规电源主导的传统同步机发电系统，向风电、光伏等新能源主导的新型电力系统转变^[1⇓-3]。2021年，我国可再生能源新增装机1.34亿千瓦，占据全国新增发电装机的76.1%。新能源发电机组自身不具备同步机旋转惯量，使电网因为缺乏惯量支撑导致系统频率不稳定。高比例新能源接入下的电力系统由于低惯量引起的频率稳定性问题日益突出，研究电力系统最低惯量需求的评估方法对系统的安全稳定运行具有重要意义^[4⇓⇓-7]。

目前针对系统最低惯量需求评估的研究，一般采用系统频率变化率(Rate of change of frequency，RoCoF)和系统最大频率偏差指标估算电力系统惯量临界值。文献[8]综合考虑了RoCoF和频率偏差双重指标约束，建立了在孤岛和并网模式下保持频率稳定性的最低惯量需求评估模型。文献[9]在考虑频率稳定约束的基础上，构建了面向实际电网调度运行需求的惯量安全域快速评估模型和方法。然而上述方法均没有考虑在发电侧的新能源发电机组虚拟惯量的作用。同时评估模型所设置的约束条件也并未考虑发电机组的处理约束，因此构建完整且准确的电力系统最低惯量评估模型是十分必要的。

为增强在高比例新能源接入场景下电力系统惯量态势感知能力，提升电力系统在有功扰动下的频率适应性，本文首先基于电力系统频率响应模型，分析受扰动后电网各个时间尺度下的频率响应过程，构建系统频率响应数学关系；基于频率响应全过程，构建计及新能源虚拟惯量的电力系统最低惯量评估模型及其求解算法；最后基于IEEE-39节点模型验证本文所提方法的准确性。

2 电力系统频率响应模型

2.1 系统频率响应过程

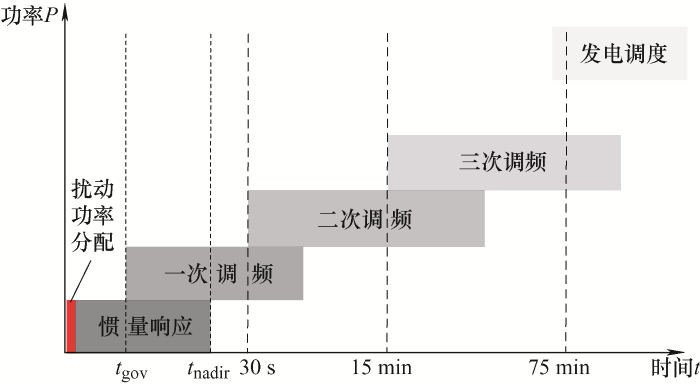
当系统受到故障冲击出现失电、失负荷或负荷有功功率急剧波动时，系统有功-频率的平衡遭到破坏。系统频率响应过程按时间尺度的顺序可分为惯量响应、一次调频、二次调频和三次调频^[10⇓-12]，如图1所示。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 电力系统频率响应过程

当系统发生有功功率扰动，首先是系统的惯量响应阶段。存储在具有转动惯量的同步发电机的动能，根据各个同步发电机的惯量大小释放或吸收，从而减小不平衡功率进而阻止系统频率发生变化。在t_gov时刻，系统进行一次调频系统响应。当频率偏差超过死区下限，调速器发出调节信号增加原动机阀门，增强发电机发出的机械功率。在一次调频系统容量充足的条件下，机组持续增加有功出力，系统频率逐渐恢复，系统达到稳定状态^[13]。系统的转子运动方程如下

(1)$2{{H}_{\text{g}}}\frac{\text{d}\Delta f(t)}{\text{d}t}+D\Delta f(t)=\Delta {{P}_{\text{g}}}+\Delta {{P}_{\text{m}}}-\Delta {{P}_{\text{d}}}$

式中，ΔP_d为系统负荷的有功功率扰动；H_g为同步发电机组的惯性时间常数；Δf(t)为系统的频率扰动；ΔP_m为新能源虚拟惯量所参与的一次调频调节量；ΔP_g为同步机电源一次调频系统受频率扰动以后的调节量；D为系统阻尼系数。

2.2 系统频率响应模型

为提升新能源发电机组的频率响应能力，通过对换流器控制策略的改进，使其具备惯量响应能力，与同步机相同的外特性。新能源虚拟惯量能量来源具有多种形式，例如静止储能、风机旋转动能，能够有效瞬时提供功率支撑，抑制扰动下频率的快速变化^[14⇓-16]。

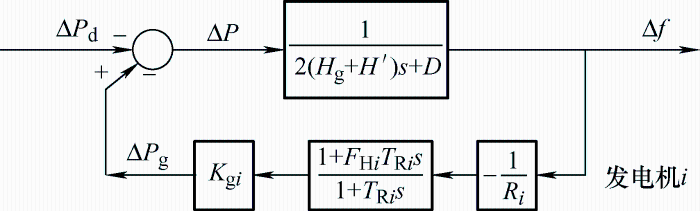
图2给出了电力系统多机频率响应模型，其中包括一次调频系统、新能源虚拟惯量一次调频系统。由于同步机一次调频系统中调速器时间常数和蒸汽箱时间常数的数值远远小于再热时间常数，因此一次调频系统可采用低阶模型。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 电力系统频率响应模型

图2中，${{F}_{\text{H}i}}$为第$i$台发电机组的高压涡轮部分系数，T_R_i为第$i$台发电机组的再热时间常数，${{R}_{i}}$为第$i$台发电机组的调速器调速系数。${H}'$为新能源发电机组的虚拟惯性常数，K_g_i表示第$i$台发电机组所占系统比例系数，表达式为

(2)${{K}_{\text{g}i}}=\frac{{{S}_{i}}}{\sum\limits_{i=1}^{M}{{{S}_{i}}}}$

式中，${{S}_{i}}$为常规机组$i$的额定容量；M电力系统中同步发电机组的数量。

由图2模型可知，系统接入一次调频系统的频率响应表达式为

(3)$\Delta f(t)=\frac{R\Delta P}{DR+1}\centerdot [1+\alpha \exp (-\varsigma {{\omega }_{\text{n}}}t)\sin ({{\omega }_{\mathrm{r}}}t+\varphi )]$

(4)$\varsigma =\left[ \frac{2HR+(DR+{{K}_{\text{g}}}{{F}_{\text{H}}}){{T}_{\text{R}}}}{2(DR+{{K}_{\text{g}}})} \right]{{\omega }_{\text{n}}}$

(5)${{\omega }_{\text{n}}}=\sqrt{\frac{DR+{{K}_{\text{g}}}}{2HR{{T}_{\text{R}}}}}$

(6)$\alpha \text{=}\sqrt{\frac{1-2{{T}_{\text{R}}}\varsigma {{\omega }_{\text{n}}}\text{+}{{T}_{\text{R}}}^{2}{{\omega }_{\text{n}}}^{2}}{1-{{\varsigma }^{2}}}}$

(7)${{\omega }_{\text{r}}}={{\omega }_{\text{n}}}\sqrt{1-{{\varsigma }^{2}}}$

(8)$\varphi ={{\tan }^{-1}}\left( \frac{{{\omega }_{\text{r}}}{{T}_{\text{R}}}}{1-\varsigma {{\omega }_{\text{n}}}{{T}_{\text{R}}}} \right)-{{\tan }^{-1}}\left( \frac{\sqrt{1-{{\varsigma }^{2}}}}{-\varsigma } \right)$

(9)$H={{H}_{\text{g}}}+{H}'$

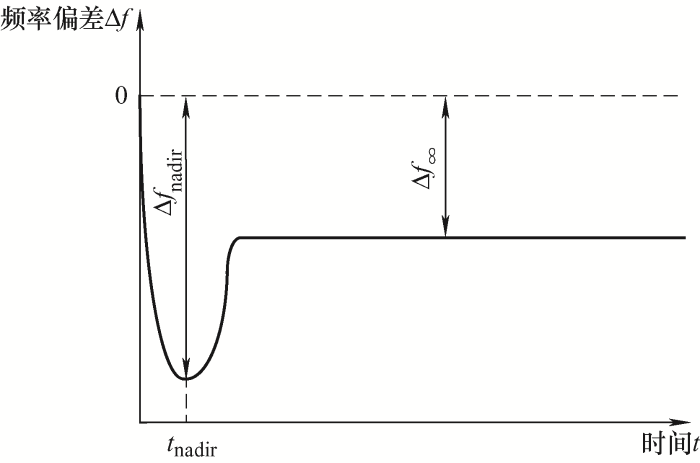
式中，${{\omega }_{\text{n}}}$表示自然振荡频率；$\varsigma $表示阻尼比；${{\omega }_{\mathrm{r}}}$表示阻尼频率；$\alpha $和$\varphi $为方便求解所设的代数式；$H$为系统总惯量。

nadir点是系统扰动发生后的频率最大偏差点，在${{t}_{\text{nadir}}}$时刻，系统频率变化率RoCoF = 0，其原理图如图3所示。根据式(3)可求解出系统的RoCoF以及nadir点的数学关系式如下

(10)$\mathrm{RoCoF}=-\frac{R\Delta P}{DR+1}\centerdot \alpha {{\omega }_{\text{n}}}\exp \left( -\varsigma {{\omega }_{\text{n}}}t \right)\sin ({{\omega }_{\mathrm{r}}}t+\varphi )$

(11)${{t}_{\text{nadir}}}=\frac{1}{{{\omega }_{\text{r}}}}{{\tan }^{-1}}\left( \frac{{{\omega }_{\text{r}}}{{T}_{\text{R}}}}{\varsigma {{\omega }_{\text{n}}}{{T}_{\text{R}}}-1} \right)$

(12)$\Delta {{f}_{\text{nadir}}}=\frac{R\Delta P}{DR+1}\centerdot \left( 1+\sqrt{1-{{\varsigma }^{2}}}\alpha \exp \left( -\varsigma {{\omega }_{\text{n}}}{{t}_{\text{nadir}}} \right) \right)$

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 系统频率曲线

3 计及新能源虚拟惯量的最低惯量评估

3.1 基本模型

模型以满足系统频率稳定性为目标，以电力系统最低惯量作为目标函数。模型目标函数如下所示

(13)$\min {{E}_{\text{sys}}}=\min (\sum\limits_{i=1}^{M}{{{H}_{\text{g}i}}{{S}_{i}}{{x}_{i}}+\sum\limits_{j=1}^{W}{{{{{H}'}}_{j}}{{S}_{j}}{{y}_{j}})}}$

式中，${{E}_{\text{sys}}}$为系统中最低惯量总需求，其中包括同步机的转动惯量和新能源发电机组的虚拟惯量。

模型设置有三个约束条件，分别为RoCoF约束、频率最大偏差约束和容量约束。频率变化率和频率偏差是表征系统频率稳定性的重要指标，根据式(10)~(12)，在系统发生预想有功扰动以后，系统RoCoF在扰动初始时刻(t = 0 s)为最大值，可得到该指标数值如式(14)所示。由此可得到RoCoF指标和最大频率偏差指标的约束条件分别为

(14)$\mathrm{RoCo}{{\mathrm{F}}_{0}}=-\frac{R\Delta P}{DR+1}\centerdot \alpha {{\omega }_{\text{n}}}\sin \varphi $

(15)$-\mathrm{RoCo}{{\mathrm{F}}_{\max }}\le \mathrm{RoCo}{{\mathrm{F}}_{0}}\le \mathrm{RoCo}{{\mathrm{F}}_{\max }}$

(16)$-\Delta {{f}_{\max }}\le \Delta {{f}_{\text{nadir}}}\le \Delta {{f}_{\max }}$

式中，$\mathrm{RoCo}{{\mathrm{F}}_{\max }}$和$\Delta {{f}_{\max }}$为保持电力系统频率稳定情况下，所允许的频率变化率最大值和频率变化量的最大值。最大频率偏差值$\Delta {{f}_{\max }}$和最大频率变化率$\mathrm{RoCo}{{\mathrm{F}}_{\max }}$通常用作电力系统中保护元件和控制装置的触发信号，我国要求$\Delta {{f}_{\max }}$不超过0.2 Hz^[17]。

单台发电机调频系统的调节量会受到其自身容量的限制。因此应设置电源备用容量约束，表达式如下所示

(17)$\Delta {{P}_{\text{g}i,t}}=-\left[ \frac{{{F}_{\text{H}i}}}{{{R}_{i}}}\delta (t)+\frac{1-{{F}_{\text{H}i}}}{{{R}_{i}}{{T}_{\text{R}i}}}\centerdot \text{exp}\left( -\frac{1}{{{T}_{\text{R}i}}}t \right) \right]\centerdot \Delta {{f}_{t}}$

(18)$\Delta {{P}_{\text{g}i,\min }}\le \Delta {{P}_{\text{g}i,t}}\le \Delta {{P}_{\text{g}i,\max }}$

式中，$\Delta {{P}_{\text{g}i,\min }}$和$\Delta {{P}_{\text{g}i,\max }}$为单台发电机一次调频设备调节量功率的最小值和最大值。

3.2 求解算法

蚁群算法(Ant colony algorithm，ACO)可用来求解分布式约束优化问题，其主要采用分工合作机制、分集更新和随机扰动等策略。该算法能够有效提高算法收敛速度和求解质量，防止算法陷入局部优化^[18-19]。

该算法在初始化阶段，需要初始化蚁群信息，令蚁群的数量为M，分散各节点，寻优明确蚁群n的起始信息要素，其具体表达为

(19)$\Delta \theta (n)=\exp [-{{g}^{*}}({{X}_{n}})]$

式中，${{X}_{n}}$表示蚂蚁的起始位置，若函数$g(X)$为无穷大，则信息素值为0。适应函数更新后表达式为

(20)${{g}^{*}}({{X}_{\mathrm{n}}})=\frac{g({{X}_{\mathrm{n}}})}{{{g}_{\mathrm{avg}}}}\ \ \ \ \ {{g}_{\mathrm{avg}}}>{{g}_{a0}}$

(21)${{g}^{*}}({{X}_{\mathrm{n}}})=g({{X}_{\mathrm{n}}})\ \ \ \ \ {{g}_{\mathrm{avg}}}\le {{g}_{\mathrm{a}0}}$

式中，${{g}_{\mathrm{avg}}}$表示该适应函数的平均值，${{g}_{a0}}$表示为大于0的参数。${{g}^{*}}({{X}_{\mathrm{n}}})$和$g({{X}_{\mathrm{n}}})$分别表示更新前后的适应值。

ACO经过全局搜索，可求解最佳解的范围。选择种群个体为L，选择比率为r，两者表达式为

(22)$L=M\centerdot r$

(23)$r=\frac{{{n}_{\max }}+{{n}_{\mathrm{x}}}}{{{n}_{\max }}}$

式中，${{n}_{\max }}$和${{n}_{x}}$表示全局搜索的最大迭代次数和已迭代次数。为进一步获得精确最优解，需要开展局部搜索。

在全局搜索和局部搜索之后，需要修正信息素，其方程为

(24)$\theta (n)=(1-\sigma )\theta (n)+\Delta \theta (n)$

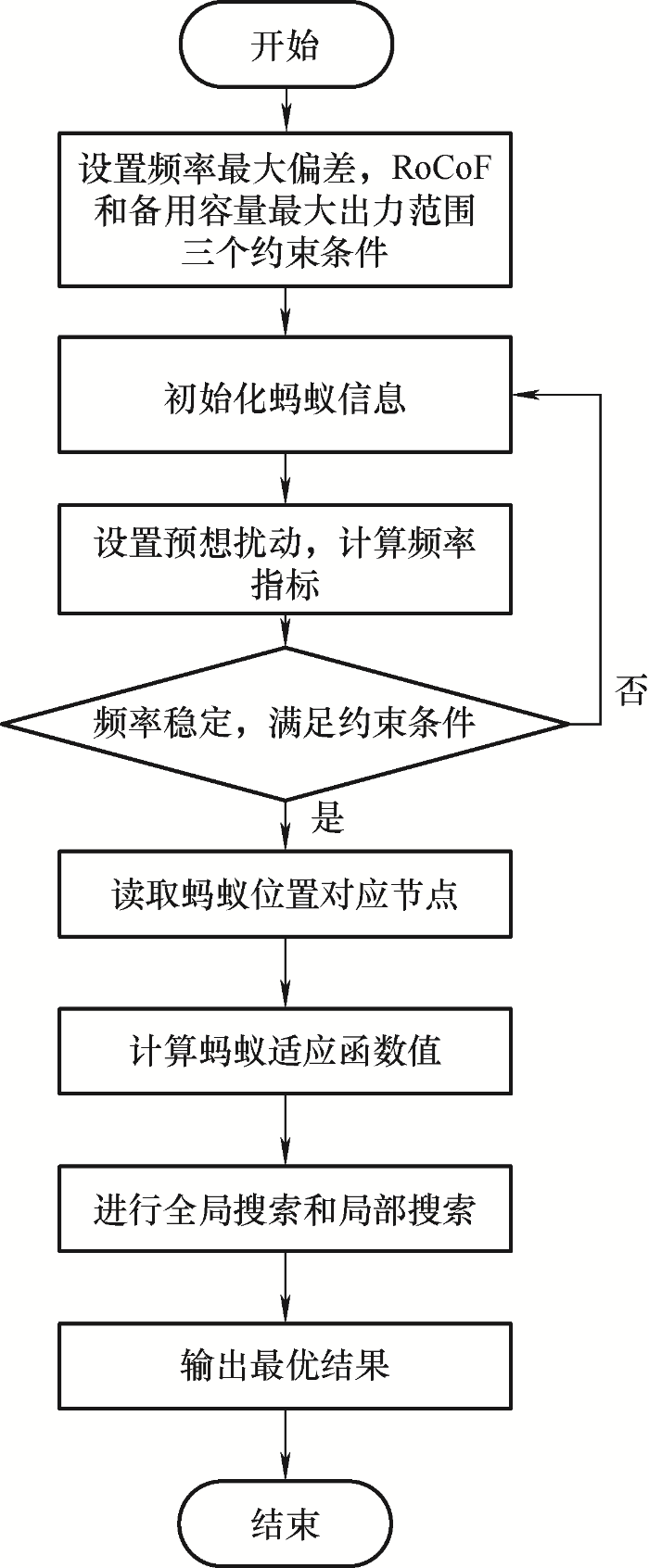
式中，$\sigma $表示信息素的发散系统，取值范围在0~1之间。最终获得目标函数的最佳蚁群位置，进而输出系统最低惯量值。具体流程如图4所示^[20]。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 电力系统最低惯量需求算法流程

4 算例分析

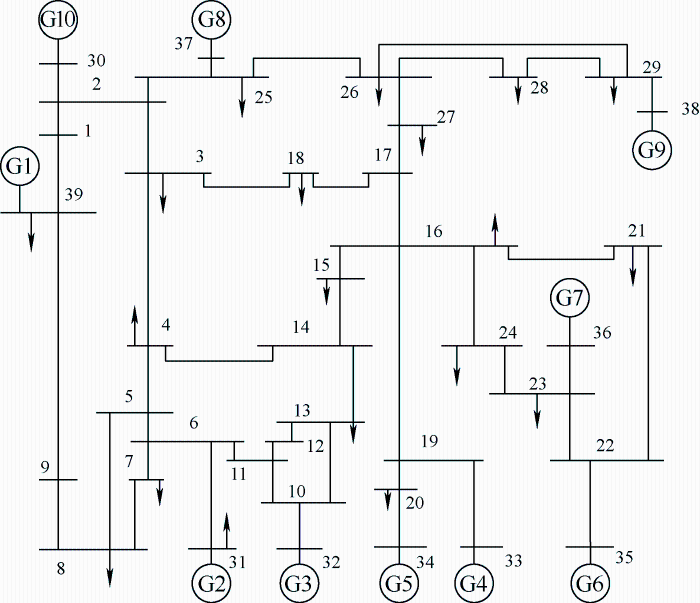
本文采用IEEE-39节点系统验证模型的准确性，系统网络拓扑如图5所示，通过Matlab/Simulink和PSASP平台搭建IEEE-39节点搭建系统仿真模型。在其中增设5个风电场，位于3、15、31、32和33节点，为尽可能消纳新能源，假定风电场和光伏电站均采用最大功率点跟踪(Maximum power point tracking，MPPT)控制。各机组与新增风电机组的参数如表1、2所示。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 IEEE-39节点系统网络拓扑

表1 同步发电机组参数

机组序号	额定功率/MW	惯性时间常数/s
G1	1 100	4.8
G2	646	5.0
G3	725	5.0
G4	652	5.4
G5	508	5.0
G6	687	5.6
G7	580	5.7
G8	564	4.7
G9	865	3.8
G10	1 040	4.5

新窗口打开| 下载CSV

表2 新能源发电机组参数

机组序号	额定功率/MW	虚拟惯性时间常数/s
W1	250	4.8
W2	180	5.0
W3	200	5.0
W4	250	5.4
W5	300	5.0

新窗口打开| 下载CSV

4.1 系统频率响应曲线

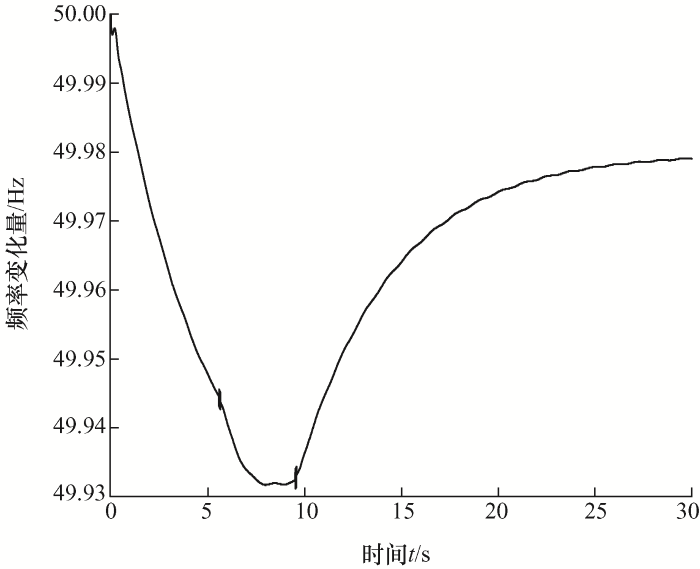
在$t=0$时刻，对系统PSASP仿真模型中相同节点施加一个$\Delta {{P}_{\text{d}}}=0.04\ \ \text{p}\text{.u}\text{.}$的负荷扰动，通过监测模型中频率变化量$\Delta f$的变化，进而判定系统频率响应模型的准确性。频率变化量结果以及nadir点如图6和表3所示。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 电力系统频率变化曲线

表3 系统频率nadir点

模型	时间t_nadir/s	频率变化量Δf_nadir/Hz
PSASP仿真模型	8.418 67	-0.066 4

新窗口打开| 下载CSV

由图6的曲线可知，电力系统经过惯量响应和一次调频系统的综合调节作用，系统频率经过nadir点后逐步恢复至稳定状态，在t = 8.418 67 s时刻，系统到达频率偏差最大点，系统频率最大偏差$\Delta {{f}_{\text{nadir}}}\text{=}-0.066\ 4\ \text{Hz}$。

4.2 系统最低惯量评估

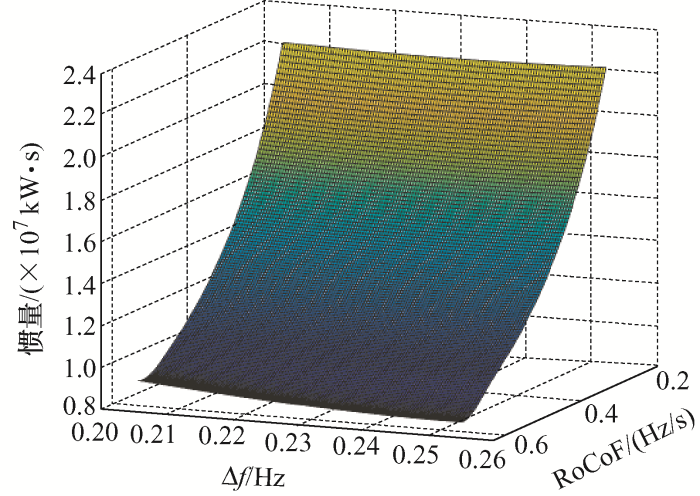
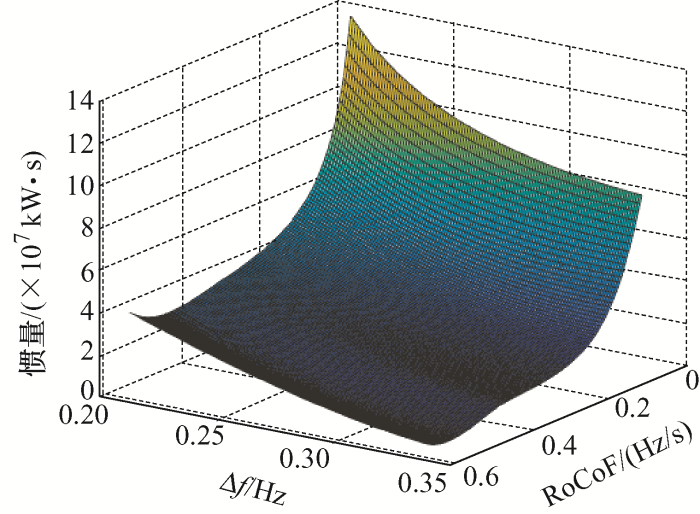
基于仿真模型，在$t=0$ s时刻针对负荷节点4施加一个有功功率扰动$\Delta {{P}_{\text{d}}}=0.03\ \text{p}\text{.u}\text{.}$。按照式(13)~(18)计算不同RoCoF和最大频率偏差约束条件下的系统最低惯量，最低惯量需求值为所设置约束条件下的最佳寻优结果，其中频率最大偏差以0.01 Hz为间隔，频率变化率RoCoF以0.01 Hz/s为间隔，时域仿真离线处理步长为0.02 s，平均仿真求解时间为30 s，最低惯量需求评估如图7、8所示。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 计及新能源虚拟惯量系统最低惯量需求评估

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 不计及新能源虚拟惯量系统最低惯量需求评估

由图7、8可知，系统频率变化率RoCoF约束和系统频率最大偏差$\Delta f$约束，与系统最低惯量呈负相关特性，具体表现为所设置约束条件$\mathrm{RoCo}{{\mathrm{F}}_{\max }}$和$\Delta {{f}_{\max }}$越小，系统最低惯量需求越大。且计及新能源虚拟惯量的电力系统相较于不计及新能源虚拟惯量的电力系统，由于系统具备附加新能源的惯性支撑能力，其频率响应能力更好，在相同约束条件下系统对于惯量需求更小。

以设置系统$\mathrm{RoCo}{{\mathrm{F}}_{\max }}\text{=}0.3\ \text{Hz/s}$、$\Delta {{f}_{\max }}=0.2\ \text{Hz}$为例，两个不同系统所需最低惯量如表4所示。

表4 不同新能源出力百分比的系统最低惯量需求

系统	系统最低惯量E_SVS/(kW·s)
计及新能源	18 503 700
不计及新能源	29 228 700

新窗口打开| 下载CSV

文献[8]综合考虑了RoCoF和频率偏差双重指标约束，建立了在孤岛和并网模式下保持频率稳定性的最低惯量需求评估模型。文献[8]和本文均是基于频率约束求得系统最低惯量值，本文相较于文献[8]约束上增加了对发电机组的处理约束，并考虑在发电侧的新能源发电机组虚拟惯量的作用。具体对比如表5所示。

表5 方法对比

对比项	文献[8]	本文
能否计及最大频率偏差约束	能	能
能否计及RoCoF约束	能	能
能否计及备用容量约束	否	能
能否分析新能源虚拟惯量作用	否	能
能否求解系统最低惯量值	能	能

新窗口打开| 下载CSV

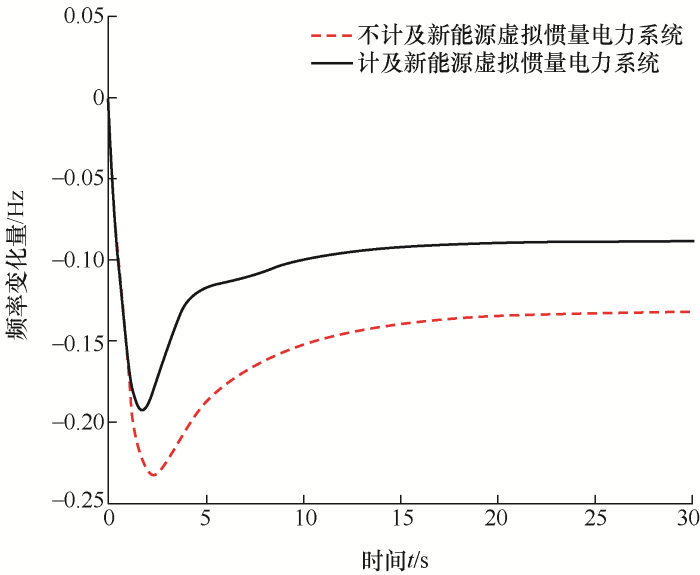
图9对比了相同在惯量E_sys=4×10⁷kW·s的系统频率响应曲线。由曲线可知，在相同惯量相同扰动情况下，计及新能源虚拟惯量的电力系统具有更好的抗干扰能量且具有更好的频率稳定性，验证了本文所提计及新能源虚拟惯量的电力系统最低惯量频率响应模型的准确性和有效性。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 两系统频率曲线对比

5 结论

本文构建了计及新能源虚拟惯量的电力系统最低惯量评估体系，实现了计及新能源虚拟惯量的电力系统最低惯量估计，并基于IEEE-39节点模型验证所提方法的准确性，所得结论如下所述。

(1) 研究表明，电力系统频率响应惯量响应阶段对电网频率安全起着至关重要的作用，且惯量的大小直接影响着电力系统频率最大频率偏差值以及系统抗扰动能力。

(2) 本文所提考虑多重指标约束的电力系统最低惯量需求评估模型，能够在不同新能源出力比例的条件下准确评估电力系统最低惯量需求，维持系统在不同运行条件下的频率稳定。

(3) 本文所提计及新能源虚拟惯量的电力系统最低惯量评估相较于一般最低惯量评估模型，有效考虑了新能源发电机组的调频能力，提高了电力系统频率稳定性，为新型电力系统的频率稳定性构建提供了新的思路。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

周孝信, 鲁宗相, 刘应梅, 等.

中国未来电网的发展模式和关键技术

[J]. 中国电机工程学报, 2014, 34(29):4999-5008.